Diverse crystalline protein scaffolds through metal-dependent polymorphism
Review Editor: John Kuriyan
Abstract
As protein crystals are increasingly finding diverse applications as scaffolds, controlled crystal polymorphism presents a facile strategy to form crystalline assemblies with controllable porosity with minimal to no protein engineering. Polymorphs of consensus tetratricopeptide repeat proteins with varying porosity were obtained through co-crystallization with metal salts, exploiting the innate metal ion geometric requirements. A single structurally exposed negative amino acid cluster was responsible for metal coordination, despite the abundance of negatively charged residues. Density functional theory calculations showed that while most of the crystals were the most thermodynamically stable assemblies, some were kinetically trapped states. Thus, crystalline porosity diversity is achieved and controlled with metal coordination, opening a new scope in the application of proteins as biocompatible protein-metal-organic frameworks (POFs). In addition, metal-dependent polymorphic crystals allow direct comparison of metal coordination preferences.
1 INTRODUCTION
Protein crystals, due to high protein concentration and precise order within the crystal, are increasingly recognized for the potential applications in drug delivery, vaccine development, catalysis, biosensing and even chromatography, far beyond the “traditional” role of structure determination (Abe & Ueno, 2015; Artusio et al., 2020; Contreras-Montoya et al., 2019; Contreras-Montoya et al., 2021; Fernandez-Penas et al., 2021; Gavira et al., 2018; Hartje & Snow, 2019; Huber et al., 2018; Kowalski et al., 2019; Sun et al., 2019; Ward & Snow, 2020; Xu et al., 2021). Many applications would require crystal stabilization through chemical cross-linking to prevent the material from dissolution when removed from the crystallization medium (Ayala et al., 2002; Hartje et al., 2018; Margolin & Navia, 2001; Noritomi et al., 1998; Quiocho & Richards, 1964; Yan et al., 2015), although dissolving crystals have been used for slow-release drug delivery (Yang et al., 2003). If embraced and honed, protein crystals would represent a new class of functional materials, with applications in sorting and storage, but with highly customizable inner surfaces. The highly ordered crystal framework has been recognized as a functional assembly joining the ranks of other well established porous materials like zeolites or metal-organic frameworks (MOFs; Safaei et al., 2019; Xu et al., 2021; Yuan et al., 2018) or the recently described protein-metal-organic frameworks (POFs) that use metal–protein complexes in place of metal nodes (Bailey et al., 2017; Sontz et al., 2015).
One of the primary parameters determining the properties of such materials is porosity, that is, the pore sizes between the frame-forming units (Abe & Ueno, 2015; Cvetkovic et al., 2005; Hartje et al., 2017; Hartje et al., 2018; Ward & Snow, 2020). Novel crystalline protein scaffolds with varied pore sizes have been developed by protein symmetrization, that is, dimer pre-formation, crystal contact engineering, and chemical ligand-guided crystallization (Bailey et al., 2017; Cohen-Hadar et al., 2009; Cohen-Hadar et al., 2011; Laganowsky et al., 2011; Li et al., 2019; Orun et al., 2023; Sontz et al., 2015; Wine et al., 2009; Wine et al., 2010). Recently, porous crystals capable of encapsulating gold nanoparticles have been developed through hierarchical generation of interacting surfaces locking the proteins into predetermined lattices (Li et al., 2023). The aforementioned approaches, however, require extensive protein engineering or involve chemical synthesis. In the current study, crystals of variable porosity were grown from a single protein utilizing metal dependent polymorphism, with the metal alone determining the precise organization of the protein chains in the crystal lattice. Metal ions have strict geometric requirements for ligand coordination, arising from the electronic configurations, that result in well-defined complexes (Kuppuraj et al., 2009; Rulisek & Vondrasek, 1998; Venkataraman et al., 1997).
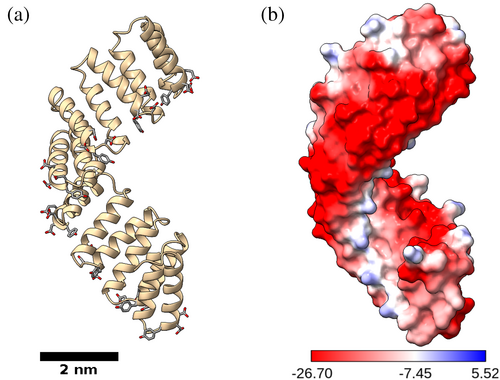
Any ligand capable of diverse assembly formation would be required to have the capacity to coordinate multiple metals and be structurally compatible with alternative spatial arrangements. Consensus tetratricopeptide repeat (CTPR) proteins were identified as potential targets for framework assemblies. CTPR proteins are composed of tandem helix-turn-helix motifs that fold into a rigid right-handed superhelical structure, with eight repeated modules (CTPR8) completing one full superhelical turn (Figure 1; Kajander et al., 2005, Kajander et al., 2006, Kajander et al., 2007). The elongated rod-like shape of the protein facilitates spatial packing, whereas a highly regular repeating surface provides long-range order for periodic interactions. In addition, the high content of negatively charged residues on the surface of CTPR proteins presents many potential sites for metal interactions, making the CTPR proteins suitable candidates for diverse framework development. The selection was further encouraged by the previous report of metal-driven polymorphic behavior of CTPR proteins (Kajander et al., 2007), with two distinct crystal forms forming in the presence of cadmium salts (1,2) and another one when grown with Sm3+ (3). While protein polymorphism is a well-known phenomenon (Campeotto et al., 2018; Gillespie et al., 2014; Vaney et al., 2001), the ability to strictly control the crystalline order through the use of metal ions has not been reported to date, and it enables rapid generation of novel crystalline frameworks.
In the current work, a thorough screening of CTPR protein interactions with a range of metal salts was carried out, and the resulting supramolecular arrangements have been analyzed according to their ion coordination. Analysis of the protein structures, along with density functional theory (DFT) calculations of the metal coordination sites, revealed how the geometric requirements for metal ion coordination drive the assembly of various crystal lattices. Solvent channel mapping showed how protein chain orientations influence the channel size and geometry inside the crystals.
2 RESULTS
CTPR8 protein was screened for interactions with a range of metals, and diffracting crystals grew in the presence Ca2+ (4, 5, 12, 13; two distinct polymorphs), Cu2+ (6), Zn2+ (7), Pb2+ (8), Ba2+ (9), Gd3+ (10), and Tb3+ (11) ions (Table 1). After structure solution, the solvent channels of the crystals were mapped out using MAP_CHANNELS (Juers & Ruffin, 2014).
| Crystal form | Metal salt | Growth conditions | Diffraction resolution, Å | PDB id | ||
|---|---|---|---|---|---|---|
| 1 | CdCl2, 20 mM | 100 mM NaOAc | pH 5.0 | 25% MPD | 2.05 | 2avpa |
| 2 | CdCl2, 10 mM | 100 mM NaOAc | pH 5.0 | 25% MPD | 2.3 | 2fo7a |
| 3 | SmCl3, 50 mM | 100 mM NaOAc | pH 5.0 | 25% MPD | 2.3 | 2hyza |
| 4 | CaCl2, 20 mM | 100 mM NaOAc | pH 5.5 | 30% MPD | 1.4 | 8bu0 |
| 5 | CaCl2, 10 mM | 100 mM NaOAc | pH 5.5 | 30% MPD | 1.7 | 8cqp |
| 6 | CuSO4, 10 mM | 100 mM NaOAc | pH 5.5 | 30% MPD | 2.6 | 8cqq |
| 7 | ZnCl2, 20 mM | 100 mM NaOAc | pH 5.5 | 30% MPD | 2.0 | 8chy |
| 8 | PbCl2, 20 mM | 100 mM NaOAc | pH 5.5 | 30% MPD | 1.62 | 8cp8 |
| 9 | BaCl2, 20 mM | 100 mM NaOAc | pH 5.5 | 30% MPD | 3.3 | 8ot7 |
| 10 | GdCl3, 5 mM | 100 mM TrisHCl | pH 8.0 | 30% MPD | 1.56 | 8ch0 |
| 11 | TbCl3, 5 mM | 100 mM TrisHCl | pH 8.0 | 30% MPD | 1.78 | 8cmq |
| 12 | CaCl2, 20 mM | 100 mM Hepes | pH 7.5 | 30% MPD | 1.3 | 8ckr |
| 13 | CaCl2, 20 mM | 100 mM TrisHCl | pH 8.0 | 30% MPD | 1.4 | 8cig |
- a Kajander et al. (2007).
The characteristic CTPR superhelical fold (Figure 1) is maintained by the interactions between key conserved amino acids at the interfaces of the α-helices (Kajander et al., 2005). As the same “connecting” residues are also exposed at the terminal helices, CTPR protein displays a strong tendency for head-to-tail interactions between individual protein units, mimicking the inter-repeat contacts inside the protein. As a result, the CTPR proteins are prone to assemble into extended superhelices (Kajander et al., 2007; Mejias et al., 2014) that provide a continuous essentially infinite helical rod with an ordered surface that facilitates protein packing. Thus, unsurprisingly, in the crystals of long-chain CTPR proteins, the extended helices run continuously through the length of the entire crystal as if made of a single protein chain, with metals coordinating the arrangement between the composite superhelices (Figures 2 and 3). As the individual protein chains interact head-to-tail, the gaps in the protein are not identifiable, giving the appearance of a continual protein chain.


The spatial arrangement of the superhelices inside the crystals could be broadly classed into two categories: all-parallel and intersecting (Table 2). In the crystals with all-parallel superhelices (1, 3, 6, 10, 11), all the constituent supercoils are simultaneously visible from the top or from the side (Figure 2), whereas, when the superhelices intersect (2, 4, 5, 7, 8, 9, 12, 13), several orientations of the protein chains are simultaneously visible (Figure 3). As the protein chains have directionality, parallel arrangements can be further sub-typed into lattices with parallel and anti-parallel superhelices. The Cu-based lattice 6 is an example of the former, whereas the lattices 1, 3, 10, and 11 are of the latter type. Coloring is used to depict superhelical directionality in Figure 2: same color is used to portray co-directional superhelices, whereas chains with opposite polarity have different colors. The lattices also exemplify alternatives for compact packing: in both 1 and 6, the CTPR chains are arranged in square grids, whereas crystals based on lanthanide ions Sm3+ (3), Gd3+ (10), and Tb3+ (11) have more compact packing. Sm3+-based lattice 3 shows hexagonal packing, which is the tightest form of circular packaging (hexagonal packing efficiency η ≈ 90.7% vs. square packing η ≈ 78.5%; Fejes, 1942). In effect, the lattice is constructed from planes of parallel superhelices (e.g., purple in Figure 2, lattice 3), rotated 180° with respect to the previous plane (gold in Figure 2, lattice 3). The lattice compactness is closely reflected by the protein densities inside the crystals (309.4 Da/nm3 for 1 vs. 377.2 Da/nm3 for 3) as well as water content (62.55% for 1 vs. 54.34% for 3; Table 2). Lattices 10 and 11 have yet another form of antiparallel arrangement that could be described as an intermediate between square and hexagonal, and correspondingly have intermediate protein densities and water content (Table 2). Interestingly, the copper-based lattice 6 is considerably less dense than 1, despite both having square arrangement. This is attributable to larger separation between the superhelices and likely reflects the requirements of all-parallel arrangement. In fact, 6 is the least dense of the whole set, with water content approaching 70%.
| Crystal form | Space group | Cell volume,a Å3 | Crystal density,b Da/nm3 | Solvent content, % | Helical arrangement | Maximum channel diameter,c Å | Repeats per asymmetric unit |
|---|---|---|---|---|---|---|---|
| 1 | P41212 | 211220.0 | 309.4 | 62.55 | Antiparallel; square | 8.2 | 2 |
| 2 | P3121 | 273595.4 | 358.3 | 56.63 | 120° | 9.4 | 4 |
| 3 | P212121 | 173252.0 | 377.2 | 54.34 | Antiparallel; hexagonal | 7.8 | 4 |
| 4 | P3221 | 285907.9 | 342.9 | 58.50 | 120° | 9.8 | 4 |
| 5 | P212121 | 479022.8 | 409.3 | 50.46 | 90° | 6.6 | 8 + 4 |
| 6 | I41d | 258911.5d | 252.4 | 69.45 | Parallel, square | 11.8 | 2d |
| 7 | P6122 | 1133397.3 | 346.0 | 58.12 | 120° | 9.8 | 8 |
| 8 | P3121 | 546599.8 | 358.7 | 56.58 | 120° | 11.2 | 2 × 4 |
| 9 | P32 | 314300.3 | 311.9 | 62.25 | 120° | 9.8 | 8 |
| 10 | P212121 | 194028.7 | 336.8 | 59.23 | Antiparallel | 6.2 | 4 |
| 11 | P212121 | 191980.5 | 340.4 | 58.80 | Antiparallel | 6.2 | 4 |
| 12 | P3221 | 292373.8 | 335.3 | 59.42 | 120° | 10.2 | 4 |
| 13 | P3221 | 289855.1 | 338.2 | 59.06 | 120° | 10.2 | 4 |
- a Cell dimensions are listed in Table S1.
- b Crystal density refers to mass of protein per unit volume of crystal.
- c Channel diameter refers to the maximum diameter of a sphere that could traverse the crystal through a solvent channel, as calculated using MAP_CHANNELS.
- d Values for solution with highest symmetry. For deposited data: space group: P1; cell volume: 131132.5 Å3, 8 repeats per asymmetric unit.
The differences in crystal densities are most apparent in the solvent channel maps (Figure 2). As parallel packing of the superhelices allows for compact side-to-side packaging, the inner cavities of the CTPR superhelix form a substantial part of the solvent channels. In the tightest lattice 3 and to a smaller extent 10 and 11, the solvent channels are helical in nature, following the path of the protein superhelices. In 1, additional large pockets form at the empty corners of the unit squares, although they are connected by the narrow channels. The copper-based lattice 6 is significantly more open, on the other hand. As the proteins have larger separation, broad water channels form around the protein chains, allowing potential guests of up to 11.8 Å to traverse the crystal (Table 2).
In the cases 2, 4, 7, 8, 9, 12, and 13 where the interacting proximal chains are rotated by 120°, more elaborate arrangements are possible, resulting in overall larger cavities and more spacious water channels (Figure 3). In the systems 2 and 7, the supramolecular assemblies form roughly hexagonal cavities, whereas 4, 8, 9, 12, and 13 form triangular “clover-shaped” channels. The solvent content does not rise significantly, however, remaining in the 55%–62% range (Table 2), because intersecting superhelices can dock in the inner cavities of the interacting chains. The lattices can be constructed from planes of parallel superhelices, with subsequent planes rotated 120° with respect to the previous plane, and then compressed into the previous plane, with the outer surface of one superhelix resting on the inner surface of the other chain. The individual planes can be clearly identified when viewed perpendicular to the C dimension of the lattice (Figure 3, right; like colors indicate co-directional superhelices, that form extended planes repeating every three planes). The partial docking of the neighboring planes is quite apparent in the projections, but the close contacts cannot be easily portrayed in two dimensions, and the full nature on the interaction can only be fully appreciated by structure analysis in 3D. The individual planes cannot be discerned when projected along the C dimension due to extensive overlap, but the central solvent channel becomes very apparent, showing unobstructed pathway for small compounds along the length of the crystal (Figure 3, left). The systems 2 and 7 have additional, narrower solvent channels spiraling around the central cavity, although, unlike with the all-parallel systems, these channels do not follow the path of the protein chains, but emerge from the higher order assembly of the superhelices. In the lattices with the “clover-shaped” channel, the central triangular cavity is the only clearly discernible open corridor along the crystal, with any additional paths sealed by the tight packing. The central cavity, however, is large enough to accommodate ≥10 Å guests, with the lead-based lattice 8 allowing unobstructed passage to particles up to 11.2 Å. This is only surpassed by the Cu-based system 6, where larger spacing between the protein chains increases the overall solvent content with the crystal.
To the contrary, superhelix rotation in lattice 5 resulted in denser packing. In lattice 5, the superhelices are rotated by 90° and are thus also capable to dock on the inner surface of the perpendicular helices, but this arrangement does not produce new solvent channels. Instead, the arrangement reduces the water content inside the crystal, resulting in the densest lattice of the whole set (Table 2).
An additional peculiarity of the formation of extended superhelices inside of crystals is the equalization of the constituent CTPR repeats, that is, it becomes impossible to determine where the protein chain begins. Furthermore, as sections of the protein become equivalent, the smallest asymmetric unit can contain only two or four sequence repeats, even though all crystals were grown from an eight-repeat protein CTPR8 (Table 2). However, even in cases when the asymmetric unit contains full eight repeats, as in 7, the gap in the electron density is not identifiable, supporting the earlier observations that the extended superhelices can translocate along the helical axis, producing equivalent electron density (Kajander et al., 2007). The B-factor values between the termini of individual repeats do not deviate substantially, further demonstrating that inability to identify chain termini is not a consequence of protein model mispositioning, but real protein translocation inside the crystal.
The overall symmetry of the crystals was determined by the arrangement of the superhelices and the metal binding (Table 2). Of the systems with all-parallel helices, the lattices with square helical arrangements 1 and 6 had 4-fold symmetry. A body-centered lattice was obtained for 6, where all the helices run co-directionally; primitive cells were obtained in all other cases. Nevertheless, the system 6 was deposited with P1 symmetry to show the whole chain (Table S1). The lanthanoid-based systems 3, 10, and 11 had lower, two-fold symmetry. The crystals with 120° between the superhelices had three-fold symmetry, with the exception of Zn-based lattice 7 that had a higher six-fold symmetry. The higher symmetry of the latter system is likely attributable to heavier metal loading.
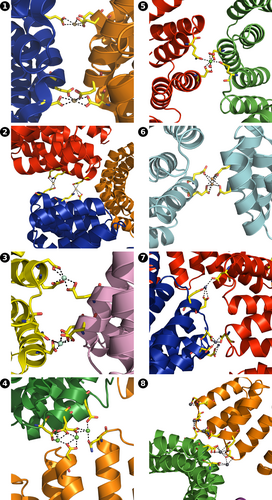
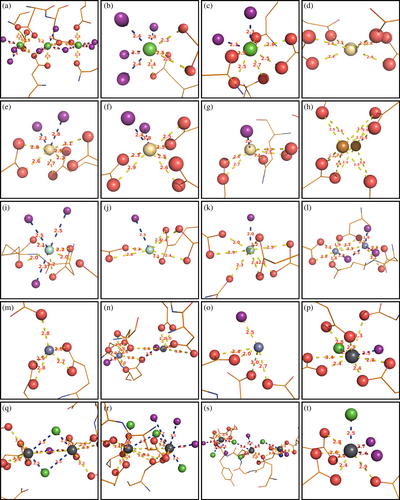
The principal contacts between protein chains are maintained by metal ions (Figure 4, Figure S2, Table S2). The outer surface of CTPR proteins is densely populated by negatively charged residues, presenting many potential metal binding sites. Despite the multiple binding options, a small negatively charged cluster 16DYDE19 in the turn region between two repeat-forming α-helices (Figure 1a) is responsible for metal-protein interactions in all cases, able to coordinate the multiple metal ions that supported crystal growth, with additional interactions serving to stabilize the contacts. The coordinating amino acid labels are omitted for clarity in Figure 4, with full identification provided in Figure S2 and listed in Table S2. The 16DYDE19 turn region appears to be in a privileged position for interaction, as the CTPR fold puts the turn at the highest radial distance from the superhelical axis, making the region the first point of contact between interacting chains. In addition, the close positioning of three charged residues allows the region to create a wider range of geometries, compatible with metal ion geometric requirements. The arrangement of protein chains into crystalline lattices was driven primarily by the geometric requirements of individual metal ions, resulting in distinct lattices on the macro-crystalline scale. For example, calcium ions inside the crystals were observed in octahedral arrangements, and copper ions had a near-perfect square-planar coordination environment (see below). Remarkably, calcium and cadmium ions had very distinct binding environments (and, as a result, created different lattices), despite often being considered as interchangeable in protein crystallography due to the similar atomic radii (0.97 Å for Ca2+ vs. 0.99 Å for Cd2+; Lawson et al., 1991). On the other hand, metals with equivalent electron spheres/coordination preferences facilitated the growth of similar crystal lattices. Crystals based on lanthanide ions, that have identical outer electron shells, that is, Sm3+ (3), Gd3+ (10), and Tb3+ (11), resulted with similar orthorhombic arrangements. Likewise, crystals grown with Ca2+ (4) and Ba2+ (9) were isomorphous with same trigonal lattices, except barium-based crystals diffracted to a lower resolution, as the larger Ba2+ ions could not bring the protein chains to the same proximity to establish the additional hydrogen bond network. The greater ionic size of Ba2+ (1.35 Å; Shannon, 1976) was reflected in the slight expansion of the crystal lattice (Table S1). The increased disorder of barium-based lattice 9 was likely the reason why better refinement statistics was obtained when processed with lower symmetry (P32 for 9 vs. P3221 for 4). Nevertheless, the two lattices have identical overall architecture (Figure 2). Interestingly, lead-based crystals 8 also had the same architecture. Lead ions were able to mimic calcium ions, which led to the assembly of a lattice with identical “clover-like” aqueous channels. However, Pb2+ ions can also be observed bound to various other amino acids where Ca2+ could not bind (Figure 4, Figure S2, Table S2). The “excess” metal binding resulted in different unit cell and symmetry between 8 and 4, despite the same overall lattice architecture, and also provided a more tightly held lattice that diffracted to 1.6 Å, not suffering the consequences of incorporating large ions.
Metal concentration also played an important role on crystal growth, with the most prominent effects observed with calcium and cadmium, whereby the metals were able to support the formation of distinct lattices in a concentration-dependent manner. As all ions are coordinated by the protein through oxygen atoms (mainly aspartate and glutamate sidechains), pH was expected not to impact crystallization, as the protonation state of acidic residues is not affected in the tested 5.0–8.0 range. Indeed, no effect was observed on the calcium-based systems 4, 12, and 13 that were grown at different pH. However, it remains to be determined whether the pH change, through modification of protein–protein interactions, or the intrinsic properties of the lanthanide ions are responsible for the differences in helical packing between 3 and 10, 11.
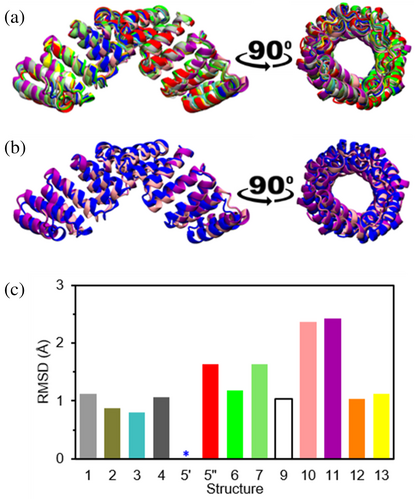
Despite the different crystal lattices, the protein retained the characteristic CTPR fold in all cases (Figure 5), indicating that the metals had no impact the CTPR structure. The superimposed structures show a clear overlap of all the different CTPRs against structure 5 (Figure 5a), suggesting a minimal effect of the different polymorphs in the structure of the CTPR. The RMSD between one of the CTPR chains in structure 5 (denoted 5′) and the structures with different cations, calculated using only the backbone atoms to minimize potential noise associated with the different side chains orientations, do not exceed 2.5 Å (Figure 5c), and even the structures 10 and 11 that render the highest RMSD value preserve the CTPR superhelix (Figure 5b). The lack of conformational change among the different structures discards any influence of the internal structure of the CTPR proteins on the crystal packing and shows that the different spatial arrangements are caused by the interplay among proteins mediated by the cations.
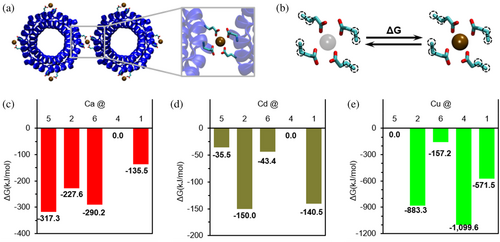
To better understand how the metals have such a strong influence on the assembly of significantly larger proteins, the binding energy contribution of the ions was calculated using DFT for select cases (Figure 6a). The stabilizing effect of the cations was calculated using the exchange free energy of each metal using magnesium as reference in each assembly (Figure 6b; Babu et al., 2003, Dudev & Lim, 2012). The results were then normalized to the highest energy and are shown as the free energy landscape of each cation in the studied polymorphs 1, 2, and 4–6 (Figure 6c–e). The results show strong differences in the scale of the binding strength among the metals, with Cu2+ showing the strongest binding energy and Cd2+ the weakest. Additionally, the results clearly show that the conformational free energy landscape fully depends on the cation, with the three different ions showing totally different trends (Figure 6c–e). The differences in the absolute value of the binding energies (Tables S3–S26, Figures S3 and S4) and the relative order of the structures between Ca2+ and Cd2+ support the experimentally observed different structures, despite Ca2+ and Cd2+ often considered exchangeable, as mentioned before. For both Ca2+ and Cd2+, assembly 4 is the least stable, but they differ in the relative order of the other tested cases. The most stable conformation with Ca2+ is 5, matching the experiments and suggesting that the thermodynamic crystallization process is cation driven (Figure 6c). Similarly, the most stable calculated disposition of Cd2+ matches the experimentally observed crystal structure 2 (Figure 6d). Although the structure that Ca2+ presents at higher ion concentrations shows the lowest stability, with a difference of 317.3 kJ/mol, this may explain why larger amounts of cation are required to force the formation. Instead, the conformation induced experimentally by a larger concentration of Cd2+ involves only a penalty of 9.5 kJ/mol. Oppositely, assembly 4 is the most stable for Cu2+, even though experimentally this ion has been proven to form structure 6, which is the second least stable in the calculations. This suggests that the crystal structure 6 obtained experimentally in the presence of Cu2+ is a kinetically trapped state. This is further supported by the simplicity of the protein disposition in the structures and the precipitation observed when adding Cu2+ amounts over the reported 10 mM, as well as by the binding strengths calculated for this cation (Table S10). Overall, the computational results show that the cations drive the formation of specific structures overcoming energetic penalties, and the binding energy gain of each cation is critical in determining the final structural arrangement of the proteins.
Metals play important roles in protein functionality, and the ability of the proteins to correctly select the metal cofactor is critical for correct protein function; binding a wrong metal can lead to devastating consequences. Thus, the mechanisms of protein metal selection are an important and active field of research, not only for the study of biological systems, but also protein engineering and design (Arnesano et al., 2011; Barber-Zucker et al., 2017; Dokmanic et al., 2008; Dudev & Lim, 2008; Dudev & Lim, 2014; Falini et al., 2008; Fermani et al., 2013; Kuppuraj et al., 2009; Rulisek & Vondrasek, 1998; Venkataraman et al., 1997). Trends of protein metal coordination are predominantly based on x-ray data of metalloproteins that have pre-formed metal coordination sites. Thus, metal coordination is determined solely by the protein scaffold, obscuring the influence of the metal ions. In the current study, the metal ions assemble the coordination environments by bridging several protein chains. The crystallization process requires a compromise between creating a suitable geometric environment for the binding ions and the arrangement of protein chains to form a stable lattice, revealing the tolerance of the ions for coordination sphere distortions. Consistently with reported trends (Kuppuraj et al., 2009; Rulisek & Vondrasek, 1998; Venkataraman et al., 1997), calcium showed a strong preference for octahedral arrangements, and copper formed a near-perfect square planar system. However, for many metals, the geometries were distorted (Figure 7). The largely open elongated shape of CTPR proteins enables the system to assemble in a large diversity of arrangements, allowing to study the interaction behavior of the multiple metals using the same supramolecular counter-ion. Additionally, CTPR proteins do not contain histidines, cysteines, or methionines, which have chemical preferences for select metals (Dokmanic et al., 2008; Laganowsky et al., 2011; Radford et al., 2011; Salgado et al., 2007; Salgado et al., 2009; Salgado, Ambroggio, et al., 2010; Salgado, Radford, & Tezcan, 2010); instead, all interactions with the protein are mediated through oxygen atoms, with key interactions established via the same 16DYDE19 turn region, thus showcasing true geometric preferences of the selected metals.
3 DISCUSSION
The variety of obtained crystal lattices demonstrates the diversity of arrangements that the streamlined CTPR superhelices can adopt to create unique environments for metal binding, compatible with innate geometric requirements of the metal coordination sphere. Likewise, the strict metal-dependent polymorphism showcases the influence metal ions can exert on protein arrangements, effectively allowing the proteins to be regarded as large hard ligands with multiple polydentate metal binding sites. In this context, protein crystals can be considered a type of POF. In previous works (Bailey et al., 2017; Sontz et al., 2015), alternate POF crystals packing was achieved by mixing engineered metal coordinating proteins with small chemical ligands with different coordination topologies. In the current study, the CTPR protein is the sole organic component of the POF.
As the physical spaces between the assembly forming units are often key determinants of the functional properties of the assemblies, the ability to strictly control the spatial arrangement of CTPR proteins through metal-driven supramolecular assembly boosts their potential as functional materials. Many proteins exhibit crystal polymorphism (Campeotto et al., 2018; Gillespie et al., 2014; Vaney et al., 2001), and metal–protein interactions are often pivotal in the maintenance of lattice structure (Hegde et al., 2017), but direct dependence of supramolecular protein assembly on metal identity is not common. Polymorphic peptides whose multimeric state depends on metal identity have been developed, but the interactions rely on chemical affinity of specifically introduced histidine residues (Radford et al., 2011; Salgado et al., 2007; Salgado et al., 2009; Salgado, Ambroggio, et al., 2010; Salgado, Radford, & Tezcan, 2010). Similarly, the introduction of histidine pairs into test proteins led to crystals with different crystal morphologies depending on the metal (Laganowsky et al., 2011). However, metal-dependent protein crystal polymorphism has not been systematically explored. This is likely because polymorphism is not seen as valuable in the context of structural determination. In the current system, multiple spatial arrangements were achieved via metal interactions with innate negative sidechains. More notably, every metal promoted growth of a unique lattice, with related lattices grown in the presence of related metals (e.g., alkaline earth metals, lanthanoids). This suggests that the protein organization is driven exclusively by the electronic properties of the metal ions, and not by the presence of a generic positive charges. This has an added benefit of broad pH stability, as the protonation state of the carboxylate sidechains does not vary around physiological pH. As many proteins naturally display solvent exposed charged/polar residues for solubility, metal-dependent crystal polymorphism might be quite common among proteins.
The current study showcases the potential of using metal–protein interactions for the construction of ordered assemblies at the macroscopic scale. Most notably, the different crystal forms had very distinct porosities, which is a prominent determinant of the material properties. The variety of the systems can likely be explained by the rigidity of the CTPR superhelical structure and the largely open elongated shape of proteins, allowing for more freedom for 3D packing. The involvement of a single region on the protein surface in metal coordination in all observed polymorphs provides valuable clues for the considerations needed for using metal coordination to organize proteins in a manner that is reminiscent of MOFs. Metal-based crystal polymorphism has an untapped potential for the design of protein-based assemblies, that is, crystalline POFs, allowing a single design to become multiple designs and thus reduce the design costs, as demonstrated by this analysis using CTPR proteins.
4 MATERIALS AND METHODS
4.1 Protein production
CTPR8 was produced as described previously (Kajander et al., 2006). The gene for CTPR8 was constructed through sequential ligations of shorter repeat sequences and was inserted into pProEX-HTb vector. The protein was expressed in Escherichia coli C41 (DE3) cells, cultured in LB with ampicillin. Upon induction with IPTG, the culture was incubated with shaking overnight at 37°C, followed by pelleting by centrifugation. The pellet was resuspended in buffer (50 mM Tris, pH 8, 300 mM NaCl) and lysed through repeated flash freeze/defrost cycles, followed by probe-tip sonication of 2 × 5 min with 0.5 s on/off cycles at 0°C, using Sartorius stedim biotech Labsonic® P sonicator. Cell debris were subsequently removed by 45 min × 10,000 g centrifugation at 4°C. The protein was isolated from the supernatant using HisTrap™ FF crude 5 mL metal affinity column following the manufacturer's guidelines. The his-tag was then cleaved using TEV protease overnight at room temperature, and the protein was purified passing through HisTrap™ FF crude 5 mL metal affinity column a second time, collecting the flow-through. Finally, the protein was purified by size exclusion chromatography on ÄKTApure purifier with GE Fraction collector F9-R, using HiLoad™ 16/600 SuperdexTM 75 pg column and eluting with 10 mM Tris, pH 8, 10 mM NaCl buffer.
4.2 Protein crystallization
Crystallization was carried out by hanging-drop vapor-diffusion method using EasyXtal 15-Well plates from Qiagen or by sitting-drop vapor diffusion method using MRC2 well crystallization plates from Swisssci. CTPR8 (20 mg ml−1) in 10 mM Tris, pH 8, 10 mM NaCl buffer was mixed in 2:1 or 1:1 ratio with reservoir solution. Exact crystallization conditions are listed in Table 1. Crystals suitable for structure determination were obtained within a week.
4.3 Data collection
Crystals were frozen without additional cryo-protectant, as the crystallization solutions had substantial (≥20% v/v) MPD content. Diffraction data were collected at BL13–XALOC beamline at ALBA synchrotron. The collection was carried out at the absorption edge wavelength specific for each metal, where possible; in the cases of calcium and cadmium where the absorption edge is outside the available energy range, data was collected at 0.9795 nm.
4.4 Structure refinement
Structure refinements were carried out on refmac 5.8.0257 as implemented in CCP4 (Winn et al., 2011), and models were built with Coot (Emsley & Cowtan, 2004). Initial phases were obtained with molrep or phaser using a published structure PDB ID: 2hyz (Kajander et al., 2007) as an initial model, or using the balbes pipeline as implemented in CCP4 online (Krissinel et al., 2018). Metal ion positions were determined from anomalous scattering data.
4.5 Solvent channel mapping
Solvent channels were mapped from the pdb files using MAP_CHANNELS program (Juers & Ruffin, 2014), running as a plug-in in Coot. Grid stepsize was set to 0.20 Å. Maxtime was increased to 10 min, but the calculation never exceeded 3 min.
4.6 Model building for DFT calculations
Binding sites were identified from the crystal structures. Models for calculations include all residues with at least an atom in the coordination sphere of the ion as well as the waters and residues interacting with one of those water molecules. Only the side chain and α-carbon were kept, thus, removing most of the backbone to reduce the computational cost, except in the case where a backbone is involved in the binding. The rigidity resulting of being connected to a protein was modeled through fixing the α- and β-carbons in the calculation.
4.7 DFT Calculation
These were calculated for the crystal structures of Ca2+ and Cd2+ at 10 and 20 mM as well as Cu2+, evaluating the energy of each cation in each binding site. Results are presented per cation to assess the stabilizing effect that it has in the structure, and they are normalized to the highest energy.
AUTHOR CONTRIBUTIONS
Mantas Liutkus: Writing – original draft; conceptualization; investigation; methodology. Ivan R. Sasselli: Investigation; methodology. Adriana L. Rojas: Methodology; validation. Aitziber L. Cortajarena: Supervision; conceptualization; writing – review and editing.
ACKNOWLEDGMENTS
A.L.C. acknowledges support by the Agencia Estatal de Investigación Grant PID2022-137977O-BI00 funded by MCIN/AEI/10.13039/501100011033, and Grants PDC2021-120957-I00, TED2021-131641B-C41 funded by MCIN/AEI/10.13039/501100011033 and by the “European Union NextGenerationEU/PRTR.” A.L.C. acknowledges support by European Union's Horizon 2020 Research and Innovation Programme under Grant Agreement No. 964593 (eProt). This work was performed under the Maria de Maeztu Units of Excellence Program from Q5 the Spanish State Research Agency grant no. MDM-2017-0720. X-ray diffraction experiments were performed at XALOC beamline at ALBA Synchrotron with the collaboration of ALBA staff. DFT calculations were carried out at the ATLAS HPC Cluster at Donostia International Physics Center.