RESEARCH ARTICLE

Free Access

Assessing computational tools for predicting protein stability changes upon missense mutations using a new dataset

Feifan Zheng

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Visualization, Validation, Data curation, Investigation, Methodology, Software, Formal analysis

Search for more papers by this author

Yang Liu,

Yang Liu

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Investigation, Methodology, Validation, Software, Formal analysis, Data curation

Search for more papers by this author

Yan Yang,

Yan Yang

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Visualization

Search for more papers by this author

Yuhao Wen,

Yuhao Wen

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Software

Search for more papers by this author

Minghui Li,

Corresponding Author

Minghui Li

[email protected]

orcid.org/0000-0002-7657-6589

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Correspondence

Minghui Li, MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, Jiangsu 215123, China.

Email: [email protected]

Contribution: Conceptualization, Supervision, Project administration, Writing - original draft, Writing - review & editing, Funding acquisition, Investigation, Visualization, Validation

Search for more papers by this author

Feifan Zheng,

Feifan Zheng

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Visualization, Validation, Data curation, Investigation, Methodology, Software, Formal analysis

Search for more papers by this author

Yang Liu,

Yang Liu

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Investigation, Methodology, Validation, Software, Formal analysis, Data curation

Search for more papers by this author

Yan Yang,

Yan Yang

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Visualization

Search for more papers by this author

Yuhao Wen,

Yuhao Wen

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Contribution: Software

Search for more papers by this author

Minghui Li,

Corresponding Author

Minghui Li

[email protected]

orcid.org/0000-0002-7657-6589

MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, China

Correspondence

Minghui Li, MOE Key Laboratory of Geriatric Diseases and Immunology, School of Biology and Basic Medical Sciences, Suzhou Medical College of Soochow University, Suzhou, Jiangsu 215123, China.

Email: [email protected]

Contribution: Conceptualization, Supervision, Project administration, Writing - original draft, Writing - review & editing, Funding acquisition, Investigation, Visualization, Validation

Search for more papers by this author

First published: 11 December 2023

https://doi.org/10.1002/pro.4861

Citations: 1

Feifan Zheng and Yang Liu contributed equally.

Review Editor: Nir Ben-Tal

Share a link

Email
Wechat
Bluesky

Abstract

Insight into how mutations affect protein stability is crucial for protein engineering, understanding genetic diseases, and exploring protein evolution. Numerous computational methods have been developed to predict the impact of amino acid substitutions on protein stability. Nevertheless, comparing these methods poses challenges due to variations in their training data. Moreover, it is observed that they tend to perform better at predicting destabilizing mutations than stabilizing ones. Here, we meticulously compiled a new dataset from three recently published databases: ThermoMutDB, FireProtDB, and ProThermDB. This dataset, which does not overlap with the well-established S2648 dataset, consists of 4038 single-point mutations, including over 1000 stabilizing mutations. We assessed these mutations using 27 computational methods, including the latest ones utilizing mega-scale stability datasets and transfer learning. We excluded entries with overlap or similarity to training datasets to ensure fairness. Pearson correlation coefficients for the tested tools ranged from 0.20 to 0.53 on unseen data, and none of the methods could accurately predict stabilizing mutations, even those performing well in anti-symmetric property analysis. While most methods present consistent trends for predicting destabilizing mutations across various properties such as solvent exposure and secondary conformation, stabilizing mutations do not exhibit a clear pattern. Our study also suggests that solely addressing training dataset bias may not significantly enhance accuracy of predicting stabilizing mutations. These findings emphasize the importance of developing precise predictive methods for stabilizing mutations.

1 INTRODUCTION

Protein stability is a critical determinant of protein function, activity, and regulation, playing a pivotal role in the adaptation and survival of proteins during evolution (Tanford, 1968). Perturbations in protein stability, often caused by mutations, have been associated with various diseases, leading to functional impairment and the onset of genetic disorders (Casadio et al., 2011; Hartl, 2017; Shoichet et al., 1995). In the fields of biotechnology and biopharmaceuticals, protein stability holds significant importance in the design of therapeutic proteins and enzymes (Goldenzweig & Fleishman, 2018; Korendovych & DeGrado, 2020). Enhanced protein stability can improve the shelf life, bioactivity, and resistance to environmental stresses, thereby increasing the efficacy of drugs and therapeutic agents (Mitragotri et al., 2014). Accurate determination of the impact of mutations on protein stability is therefore indispensable in understanding the molecular basis of diseases and devising appropriate therapeutic interventions. Experimental measurements of protein stability changes can be laborious and may not be feasible for all proteins, especially those that are difficult to purify. As a result, computational tools have emerged as valuable resources for predicting the impact of mutations on protein stability in recent years (Baek & Kepp, 2022; Benevenuta et al., 2021; Blaabjerg et al., 2023; Capriotti et al., 2005; Chen et al., 2020; Cheng et al., 2006; Dehouck et al., 2011; Deutsch & Krishnamoorthy, 2007; Dieckhaus et al., 2023; Fariselli et al., 2015; Guerois et al., 2002; Kellogg et al., 2011; Laimer et al., 2015; Li et al., 2020; Li et al., 2021; Masso & Vaisman, 2014; Montanucci, Capriotti, et al., 2019; Pancotti et al., 2021; Parthiban et al., 2006; Rodrigues et al., 2021; Savojardo et al., 2016; Wang et al., 2022; Zhou et al., 2023).

These computational methods leverage a diverse array of information derived from protein sequence, structure, and evolution. The integration of this information is facilitated through a broad spectrum of machine learning techniques, ranging from simple linear regression to more advanced algorithms. The prediction performances of these computational methods have undergone rigorous evaluation and comparison, utilizing various datasets of experimentally characterized mutants. Some excellent reviews and comparative tests have been performed on these methods (Benevenuta et al., 2022; Caldararu et al., 2020; Fang, 2020; Iqbal et al., 2021; Kepp, 2015; Marabotti et al., 2021; Montanucci, Martelli, et al., 2019; Pan et al., 2022; Pancotti et al., 2022; Pandey et al., 2023; Pucci et al., 2018; Pucci et al., 2022; Sanavia et al., 2020; Usmanova et al., 2018). For instances, a recent review by Marabotti et al. (2021) comprehensively summarized the primary methodologies employed in the development of these tools and provides an overview of various assessments conducted over the years. Pucci et al. (2022) conducted a critical examination of these predictors, delving into their algorithms, constraints, and biases. Additionally, they discussed the key challenges that the field is likely to encounter in the future to fortify the influence of computational methodologies in protein design and personalized medicine. Iqbal et al. (2021) offered evolving insights into the significance and relevance of features that can discern the impacts of mutations on protein stability. Pancotti et al. (2022) conducted a thorough comparison of prediction methods using a completely novel set of variants never tested before. While protein stability prediction tools vary in accuracy, they generally perform better at predicting destabilizing variations than stabilizing ones. Benevenuta et al. (2022) explored the factors contributing to this disparity, examining the connection between experimentally-measured ΔΔG and seven protein properties. Their findings emphasize the importance of developing tools that can effectively leverage features associated with stabilizing variants for enhanced accuracy.

Given the extensive body of research mentioned above, we aim to explore several issues here. Firstly, while many of these methods have been trained or optimized using different or partially overlapping data, this poses challenges when attempting to conduct a fair comparison. Therefore, we meticulously compiled a new dataset sourced from three recently published databases: ThermoMutDB (Xavier et al., 2021), FireProtDB (Stourac et al., 2021), and ProThermDB (Nikam et al., 2021). This dataset comprises 4038 single-point mutations, including over 1000 stabilizing mutations, which were carefully selected to avoid any overlap with the well-established S2648 dataset (Dehouck et al., 2009). Subsequently, we computed stability changes values for these mutations using different computational methods, including both machine learning and non-machine learning approaches. For machine learning methods, we gathered their respective training datasets and excluded entries from S4038 with any overlap or significant similarity to the training datasets used in the development of these computational approaches to ensure a fair comparison.

Secondly, we included 27 widely recognized and available tools from the past 20 years (Baek & Kepp, 2022; Benevenuta et al., 2021; Blaabjerg et al., 2023; Capriotti et al., 2005; Chen et al., 2020; Cheng et al., 2006; Dehouck et al., 2011; Deutsch & Krishnamoorthy, 2007; Dieckhaus et al., 2023; Fariselli et al., 2015; Guerois et al., 2002; Kellogg et al., 2011; Laimer et al., 2015; Li et al., 2020; Li et al., 2021; Masso & Vaisman, 2014; Montanucci, Capriotti, et al., 2019; Pancotti et al., 2021; Parthiban et al., 2006; Rodrigues et al., 2021; Savojardo et al., 2016; Wang et al., 2022; Zhou et al., 2023), encompassing the latest AI tools that leverage extensive mega-scale stability datasets, deep neural networks, and transfer learning techniques that have never been tested before (Blaabjerg et al., 2023; Dieckhaus et al., 2023). We provide a brief introduction for each tool, summarizing important information, including their features and methodologies.

Thirdly, a significant challenge currently faced by these methods is their tendency to be less accurate in predicting stabilizing mutations compared to destabilizing ones (Benevenuta et al., 2022; Pancotti et al., 2022; Pucci et al., 2018). The widely accepted explanation for this challenge is dataset bias, resulting from an overrepresentation of destabilizing mutations. Here, we conducted a detailed investigation into stabilizing and destabilizing mutations. We found that none of the methods could accurately predict stabilizing mutations, even those that performed well in anti-symmetric property analysis. While most methods displayed consistent trends in predicting destabilizing mutations across various properties (solvent exposure, secondary conformation, conservation, and mutation type), stabilizing mutations did not exhibit a clear pattern. Additionally, our study suggests that solely addressing training dataset bias may not significantly improve the accuracy of predicting stabilizing mutations.

Finally, our study could provide researchers and practitioners with the knowledge to make informed decisions and recognize the limitations of the application of these methods. Moreover, we hope that our findings will aid developers in advancing their methods and lead to the development of more effective and reliable computational tools for predicting the impact of mutations on protein stability.

2 METHODS

2.1 Benchmark dataset of S4038

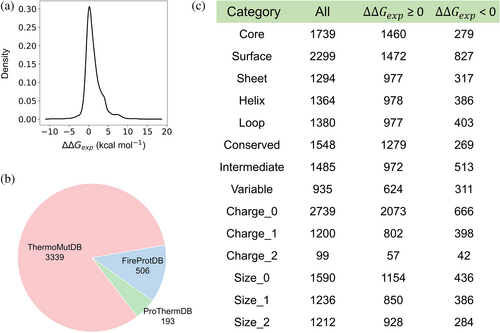
We compiled a new dataset from the latest versions of three databases: ThermoMutDB (v1.3) (Xavier et al., 2021), FireProtDB (v1.1) (Stourac et al., 2021), and ProThermDB (2020.12) (Nikam et al., 2021). These databases include experimentally measured protein stability changes upon mutations (∆∆G), along with corresponding three-dimensional protein structures. First, we selected single-point missense mutations. Then, we excluded the entries lacking experimental stability changes values. As a result, the total count of mutations from ThermoMutDB, FireProtDB, and ProThermDB stands at 5858, 5176, and 4523 respectively. The overlapping of data among the three databases is shown in Figure S1.

To integrate the data from the three databases, we initially matched the respective identifiers (PDB ID and mutation ID) from each database to the corresponding identifiers for proteins (UniProt ID) and mutations using SIFTS (Dana et al., 2019). With this, we were able to identify identical mutations across multiple databases. Subsequently, we integrated entries by UniProt ID and mutation ID. As certain mutations appeared in different databases and may have different ΔΔG values, we retained these mutations in accordance with the following priority order: ThermoMutDB > FireProtDB > ProThermDB. For instance, in cases where a mutation existed across all three databases, we only chose the mutation and its associated value and protein structure from the ThermoMutDB database. For mutations in the database that match those in S2648 (Dehouck et al., 2009), we directly used the experimental values from S2648. The S2648 dataset is a well-established and widely recognized compilation, encompassing 2648 distinct non-redundant single-point mutations derived from 131 globular proteins. For other entries, we conducted a manual inspection of the ∆∆G values and mutation details for each entry, utilizing the literature resources furnished by the respective databases. This meticulous scrutiny led us to pinpoint and rectify a total of 169 erroneous data entries (see Data 1). In situations where identical mutations are associated with multiple ∆∆G values, we first selected a single ∆∆G value based on its proximity to neutral pH and/or closest temperature (T) to room temperature. Then, the average ∆∆G value is employed for mutations exhibiting standard deviations of multiple ∆∆G values less than 1.0 kcal mol⁻¹. Entries with significant standard deviations are excluded. We obtained 3339, 506, and 193 unique mutations from ThermoMutDB, FireProtDB, and ProThermDB, respectively, forming our dataset S4038, which does not contain mutations overlapping with those found in S2648. This dataset now comprises 318 structures across 280 proteins.

Finally, we performed updates on the protein structures for each individual entry. The criteria for updating the structures were based on the sequence identity and structural coverage shared between the structures and protein sequences. We retained the structures with higher sequence identity and greater structural coverage. It was mandatory for all structures to have a resolution of less than 3 Å. In total, we updated 177 structures (refer to Data 2). As a result, the S4038 dataset includes 287 structures corresponding to 280 proteins (Table S1). The S4038 dataset and the computational results of all evaluated methods are available from Data 3.

2.2 Benchmark datasets of S594, S^sym, and S2000

To ensure a fully consistent and fair comparison among all the methods, we established the S594 dataset by extracting data from S4038. This dataset comprises proteins and variants that have not been previously encountered and possess less than 25% sequence identity with the proteins in the training sets of all the evaluated methods. The MMseqs2 software (Steinegger & Soding, 2017) was utilized for conducting sequence similarity comparisons with the following criteria: a sequence identity threshold of 25% is applied, and the alignment covers at least 50% of both query and target sequences. To assess the bias of the antisymmetric property, we proceeded to model the reverse mutations corresponding to these 594 mutations. The antisymmetric property refers to that the sum of the ΔΔG_F value for a forward mutation and the ΔΔG_R value for its corresponding reverse mutation should equate to zero. Regarding the forward mutations, the 3D structures of wild-type proteins were acquired from the Protein Data Bank (PDB) (Berman et al., 2000). For the reverse mutations, the initial 3D structures of proteins were generated using the BuildModel module of FoldX (Guerois et al., 2002), utilizing the wild-type protein structures as templates. It is noteworthy that FoldX solely focuses on optimizing the surrounding side chains near the mutation site during the creation of mutant structures.

To further assess the bias of the antisymmetric property, we employed two commonly used datasets, S^sym (Pucci et al., 2018) and S2000 (Usmanova et al., 2018). S^sym is a balanced dataset comprising a total of 684 mutations, each accompanied by experimentally measured ΔΔG values. Notably, half of the mutations within S^sym pertain to forward mutations, while the remaining half correspond to reverse mutations, for which both the wild-type and mutant proteins are solved by X-ray crystallography with a resolution of at most 2.5 Å. S2000, the other balanced dataset, consists of 1000 pairs of single-site mutations, where the protein sequences for each pair differ by only one residue. High-resolution protein 3D structures are available for all pairs, although experimental ΔΔG values are lacking. The number of protein structures and mutations in these datasets are presented in Table S1.

2.3 Evaluated methods for predicting the impact of single-point mutations on protein stability

We computed the stability changes for all the aforementioned datasets using 27 widely recognized and available tools in recent 20 years. These tools are listed below, accompanied by a brief introduction of their attributes. The training datasets for each machine learning tool are presented in Table S2. The methods within each category are organized chronologically by their publication dates.

2.3.1 Machine learning methods—Structure-based

ThermoMPNN (Dieckhaus et al., 2023), a deep neural network, utilizes an extensive mega-scale stability dataset, which includes stability measurements inferred from protease sensitivity experiments on hundreds of thousands of mutations from approximately 300 proteins. It leverages transfer learning by incorporating features from a 3D structure-based sequence prediction model. Stand-alone tool: https://github.com/Kuhlman-Lab/ThermoMPNN.
DDMut (Zhou et al., 2023) is constructed using a Siamese network architecture that includes two separate sub-networks, one designed for processing forward mutations and the other dedicated to reverse mutations. The input data are derived from two distinct sets of features: graph-based signatures and complementary features. The training set incorporates data from both S2648 and FireProtDB and comprises 4514 mutations and their corresponding reverse mutations. Web server: https://biosig.lab.uq.edu.au/ddmut.
RaSP (Blaabjerg et al., 2023) begins with training a self-supervised 3D convolutional neural network on high-resolution protein structures, predicting amino acid labels based on local atomic environments. In the second step, a supervised fully-connected neural network is trained to forecast stability changes, using the 3D network's internal representation along with wild type and mutant amino acid labels and frequencies. The downstream model was trained using ΔΔG values of all possible mutations from 45 proteins generated by saturation mutagenesis using Rosetta. Stand-alone tool: https://github.com/KULL-Centre/_2022_ML-ddG-Blaabjerg.
BayeStab (Wang et al., 2022) is a deep graph neutral network-based method. The inputs to the GNN are the adjacency matrix and the 30-dimensional initial node features, which consists of molecular information such as atom types, the number of adjacent hydrogen atoms, and aromatic bonds. The training dataset used is S2648. Web server: http://www.bayestab.com/.
SimBa2 (Baek & Kepp, 2022) consists of two linear regression models: SimBa-IB and SimBa-SYM. SimBa-IB performs better on data with a destabilization bias, while SimBa-SYM is suitable for applications where both forward and reverse mutations, as well as stabilizing and destabilizing mutations, have approximately equal influence. Both models rely on three distinct feature types: relative solvent accessibility, molecular volume differences, and hydrophobicity disparities. Both models were trained on a dataset containing 940 mutations. Stand-alone tool: https://github.com/kasperplaneta/SimBa2/.
DynaMut2 (Rodrigues et al., 2021) combined optimized graph-based signatures to represent the global environment of the wild-type residues and incorporates normal mode analysis to capture conformational change. The model is trained using the random forest algorithm and utilizes 2298 forward mutations derived from S2648 and 1724 reverse mutations. Only mutations with an absolute ΔΔG value less than 2 kcal mol⁻¹ were considered in the construction of reverse mutations. Web server: https://biosig.lab.uq.edu.au/dynamut2/.
ACDC-NN (Benevenuta et al., 2021), short for Antisymmetric Convolutional Differential Concatenated Neural Network, specifically designed to address the challenges posed by the antisymmetric property. The ACDC-NN takes two separated inputs for forward and reverse variations. Each of the two inputs consists of 620 elements to encode sequence, structural, and variation information. The model was trained using S2648 and its reverse mutations, as well as S2000. Stand-alone tool: https://github.com/compbiomed-unito/acdc-nn.
PremPS (Chen et al., 2020) utilizes the random forest regression scoring function and encompasses a set of 10 features derived from evolutionary and structural considerations. The training set consists of S2648 and its reverse mutations, constructed based on the antisymmetric principle. The web server is accessible at https://lilab.jysw.suda.edu.cn/research/PremPS/.
ThermoNet (Li et al., 2020) is constructed using a deep, 3D-convolutional neural network architecture that treats protein structures as multi-channel 3D images. The inputs are uniformly transformed into multi-channel voxel grids, which are created by integrating seven biophysical properties extracted from raw atom coordinates. The training set comprises a dataset consisting of 1744 mutations and their reverse mutations. Stand-alone tool: https://github.com/gersteinlab/ThermoNet.
INPS3D (Savojardo et al., 2016) is constructed using a support vector machine algorithm and integrates nine distinct features as inputs. These features include six sequence-based features, two structure-based features, and one evolutionary-based feature. The training set used is S2648. Web server: https://inpsmd.biocomp.unibo.it/inpsSuite/default/index2.
MAESTRO (Laimer et al., 2015) is a multi-agent prediction system that relies on artificial neural networks, support vector machines, and linear regression. For all agents, nine input features were employed, including three statistical scores and six global and local protein properties. The model was trained using 1765 single-point mutations. Web server: https://pbwww.services.came.sbg.ac.at/maestro/web.
AUTO-MUTE 2.0 (Masso & Vaisman, 2014) includes two regression models: REPTree using random forest and SVMreg using support vector machine. It utilized a four-body, knowledge-based statistical potential function obtained through coarse graining of protein structures at the residue level to represent mutations as a feature vector. The training set used is S1925. Stand-alone tool: http://binf.gmu.edu/automute/.
PoPMuSiC 2.1 (Dehouck et al., 2011) uses a linear combination of 16 terms, including 13 statistical potentials, two dependent on amino acid volumes, and an extra term. Coefficients are sigmoid functions tied to solvent accessibility of the mutated residue. Sigmoid parameters were optimized using a neural network trained on S2648 dataset. Web server: http://babylone.ulb.ac.be/popmusic.
I-Mutant2.0 (Capriotti et al., 2005) is based on support vector machine, with an input vector consisting of 42 values. This vector includes temperature, pH, 20 values defining residue mutation types, and 20 values encoding the spatial environments of the residues. It was trained on the 1948 mutations obtained from ProTherm. The web server is https://folding.biofold.org/i-mutant/i-mutant2.0.html.

2.3.2 Machine learning methods—Sequence-based

ACDC-NN-Seq (Pancotti et al., 2021) architecture is the sequence-based counterpart of the 3D version introduced above. It consists of 160 elements to code variation and sequence evolutionary information. Stand-alone tool: https://github.com/compbiomed-unito/acdc-nn.
SAAFEC-SEQ (Li et al., 2021) is a gradient boosting decision tree learning approach that utilizes sequence-based physicochemical properties, sequence neighbor features, and evolutionary information for prediction purposes. It was trained on the S2648 dataset. Web server: http://compbio.clemson.edu/SAAFEC-SEQ/.
INPS (Fariselli et al., 2015) differs from the structural model INPS3D is that INPS did not integrate two structure-based features. Web server: https://inpsmd.biocomp.unibo.it/inpsSuite/default/index2.
MUpro (Cheng et al., 2006) is an SVM-based predictive method composed of 140-dimensional sequence-based features that consider a local window of size 7 centered around the mutated residue as its input. The training set includes 1615 mutations. Web server: http://mupro.proteomics.ics.uci.edu/.
I-Mutant2.0-Seq (Capriotti et al., 2005) differs from the structural model I-Mutant2.0 in the encoding of the residue environment. When the protein structure is available, this environment corresponds to a spatial environment. Conversely, when only the protein sequence is available, the residue environment encompasses the nearest sequence neighbors. Web server: https://folding.biofold.org/i-mutant/i-mutant2.0.html.

2.3.3 Non-machine learning methods—Structure-based

DDGun3D (Montanucci, Capriotti, et al., 2019) employs a linear combination of four anti-symmetric scores. The weights assigned to these scores are proportional to their correlation with the ∆∆G values obtained from the VariBench dataset. These scores include three sequence-based terms derived from the Blosum62 substitution matrix, Skolnick statistical potential, and hydrophobicity, along with a structure-based term from Bastolla statistical potential. Subsequently, this composite score is further adjusted by multiplying the relative solvent accessibility of the wild-type residue. Web server: https://folding.biofold.org/ddgun/.
Rosetta (Kellogg et al., 2011) calculates the energy of a structure using energy functions that combine physical and statistical terms. To evaluate the effects of mutations, it computes the total interaction energies of residues at the mutation site. In our study, we carried out the calculation using the cartesian_ddg protocol and the ref2015 energy function. Stand-alone tool: https://www.rosettacommons.org/software.
MultiMutate (Deutsch & Krishnamoorthy, 2007) is a method that employs a Delaunay tessellation-based four-body scoring function. It predicts the effects of mutations on protein stability and reactivity by calculating the change in total score between wild-type and mutant proteins. Stand-alone tool: https://www.math.wsu.edu/math/faculty/bkrishna/DT/Mutate/.
CUPSAT (Parthiban et al., 2006) is a stepwise multiple regression predictive model founded upon the distribution of torsion angles and the potentials associated with amino acid atoms. It evaluates the local amino acid environment surrounding the substituted position, incorporating considerations of secondary structure specificity and solvent accessibility into the assessment. The model weights were optimized using data from 1538 point mutations. Web server: https://cupsat.brenda-enzymes.org/.
FoldX (Guerois et al., 2002) is an empirical force field-based method that employs a linear combination of several terms, including van der Waals interactions, solvation effects, electrostatic contribution, hydrogen bonds, water bridges, and entropy effects. The weights were optimized on 339 mutants across nine different proteins. Stand-alone tool: https://foldxsuite.crg.eu/.

2.3.4 Non-machine learning methods—Sequence-based

DDGun (Montanucci, Capriotti, et al., 2019) is the sequence-based version of the method, and it exclusively relies on three sequence-based terms derived from the Blosum62 substitution matrix, Skolnick statistical potential, and hydrophobicity as input features. Web server: https://folding.biofold.org/ddgun/.

2.4 Exploring the performance of different methods across different properties

We assessed the performance of all methods for five different aspects of properties (Figure 1):

Location of the mutated residue: Residues were classified as buried in the protein core or exposed on the protein surface. A residue is designated as “buried in the protein core” or “exposed on the surface” when the ratio of its solvent accessible surface area (SASA) within the protein to that within the extended tripeptide is less than or more than 0.2 (Hou et al., 2020). The SASA of a residue within the protein and in the extended tripeptide was calculated by DSSP program (Joosten et al., 2011) and obtained from (Rose et al., 1985), respectively.
Secondary structure conformation of the mutated residue: The secondary structure elements are assigned using the DSSP program and categorized into Helix, Sheet, and Loop.
Conservation of the mutated residue: Conservation scores for residues were derived from ConSurf-DB (Ben Chorin et al., 2020). In cases where the protein structure lacked pre-computed evolutionary conservation profiles within ConSurf-DB, we performed the calculation using the ConSurf webserver with default parameters (Glaser et al., 2003). A total of 70 mutations from five proteins in S4038 do not have conservation scores due to the limited availability of homologous sequences. The mutated sites were categorized into three tiers (conserved, intermediate, and variable) based on their conservation scores: Grades 1–3, Grades 4–6, and Grades 7–9.
Changes in amino acid charge: We assigned charge values to amino acid residues, considering lysine and arginine as positive (+1), aspartic acid and glutamic acid as negative (−1), and other amino acids as neutral (0). Mutations were categorized into three groups (charge_0, charge_1, and charge_2) based on the absolute value change in charge: 0, 1, and 2.
Changes in amino acid size: Residues were categorized into small group (Ala, Gly, Ser, Cys, Pro, Thr, Asp, Aln) (encoded as 0), medium group (Val, His, Glu, Gln) (encoded as 1), and large group (Ile, Leu, Met, Lys, Arg, Phe, Trp, Tyr) (encoded as 2). Mutations were classified into three categories (size_0, size_1, and size_2) based on the absolute change in residue size: 0, 1, and 2.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Overview of the S4038 dataset. (a) The distribution of experimental stability changes. (b) The number of mutations from each database. (c) The number of mutations for each property.

2.5 Performance evaluation

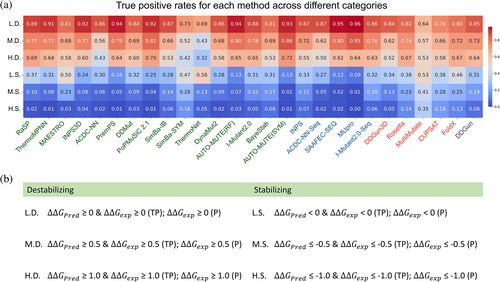
We employed two metrics, the Pearson correlation coefficient (R) and root-mean-square error (RMSE), to assess the agreement between experimentally observed and predicted values of unfolding free energy changes. A two-tailed t-test was employed to determine whether the correlation coefficient held statistical significance from zero. RMSE (kcal mol⁻¹) is the standard deviation of the prediction errors and is derived by taking the square root of the mean squared difference between predicted and experimental values. To evaluate the antisymmetric property of the prediction tools, we employed two additional metrics: R_FR and <δ>. R_FR represents the Pearson correlation coefficient between predicted ∆∆G values of the forward and reverse mutations. <δ> denotes the average bias and is calculated as the sum of (∆∆G_F + ∆∆G_R) divided by the number of pairs (Pucci et al., 2018). An unbiased prediction should have R_FR and <δ> equal to −1 and 0, respectively. To evaluate the performance of the assessed methods in classifying stabilizing or destabilizing mutations, we calculated the true positive rate (TPR) using the following formula: TPR = TP/P, where TP represents true positives and P denotes positives.

3 RESULTS AND DISCUSSION

3.1 Method performance on the unseen data

To assess the generalization capabilities of various machine learning protein stability change prediction methods, we conducted an analysis using three previously unseen datasets sourced from S4038. These datasets are denoted as S4038^[0%–25%], S4038^[25%–100%], and S594. S4038^[0%–25%] and S4038^[25%–100%] are two datasets of proteins and variants that have never been seen in each method, and the sequence identity of these proteins with the proteins in the training set of this method is less than 25% and more than 25%, respectively. For a detailed breakdown of the number of proteins and mutations within the S4038^[0%–25%] and S4038^[25%–100%] datasets for each method, please refer to Table S3. Lastly, to ensure a consistent and equitable comparison among all the methods, we created the S594 dataset. This dataset contains proteins and variants that have never been seen before, and these proteins have less than 25% sequence identity with the proteins present in the training sets of all the methods being evaluated. To evaluate the performance of non-machine learning methods, S4038 and S594 were utilized.

Table 1 provides the Pearson correlation coefficients (R) and root-mean-square-error (RMSE) values for all mutations, as well as the R values specifically for destabilizing and stabilizing mutations for each method tested on the unseen datasets. For all mutations, the correlations observed across all machine learning methods tested on the S4038^[0%–25%] and S4038^[25%–100%] datasets fall within the range of 0.09–0.49 and 0.32–0.60, respectively. The RMSE values fall within the range of 1.75–2.73 and 1.50–2.42 kcal mol⁻¹ for both datasets, respectively. The best-performing machine learning predictor for S4038^[0%–25%] is RaSP, followed by ThermoMPNN. For S4038^[25%–100%], the top-performing machine learning predictors are PremPS, RaSP, MAESTRO, and ThermoMPNN. The conclusion is further supported by the performance of combined dataset of 4038^[0%–25%] and S4038^[25%–100%] (Figure 2). These top-performing machine learning predictors make use of protein 3D structure information in their predictions. RaSP and ThermoMPNN are both recently developed methods and the only two among all methods that utilize a large number of large-scale stable datasets (Table S2), and leverage transfer learning techniques. If the 3D structure of a protein is unavailable, these sequence-based machine learning methods, SAAFEC-SEQ, ACDC-NN-Seq, and INPS, also demonstrate promising predictive performance (Table 1, Figure 2). In addition, for each method, mutations with higher sequence similarity to proteins in the training set demonstrate better prediction accuracy compared to mutations in dissimilar proteins.

TABLE 1. Performance of all methods on unseen data.

Method	All mutations						ΔΔG_exp ≥ 0			ΔΔG_exp < 0
	S4038 ^[0%–25%]		S4038 ^[25%–100%]		S594		S4038 ^[0%–25%]	S4038 ^[25%–100%]	S594	S4038 ^[0%–25%]	S4038 ^[25%–100%]	S594
	R	RMSE	R	RMSE	R	RMSE	R	R	R	R	R	R
Machine learning methods—structure-based
RaSP	0.49	1.99	0.59	1.54	0.32	2.14	0.48	0.52	0.28	−0.12	−0.13^#	0.10^#
ThermoMPNN	0.42	1.93	0.58	1.91	0.36	1.96	0.40	0.46	0.31	−0.03^#	0.07^#	0.02^#
MAESTRO	0.40	1.86	0.59	1.99	0.31	2.03	0.36	0.55	0.25	−0.13	−0.02^#	0.06^#
INPS3D	0.37	1.75	0.54	1.97	0.35	1.90	0.38	0.47	0.31	−0.01^#	0.02^#	0.11^#
ACDC-NN	0.36	1.82	0.53	2.02	0.32	2.02	0.35	0.50	0.29	0.06^#	−0.16	0.02^#
PremPS	0.36	1.78	0.60	1.90	0.35	1.97	0.43	0.55	0.39	−0.09^#	−0.09*	−0.09^#
DDMut	0.35	1.95	0.47	2.42	0.36	1.97	0.32	0.48	0.28	0.10^#	−0.21	0.13^#
PoPMuSiC 2.1	0.34	1.83	0.56	1.92	0.31	2.03	0.35	0.51	0.26	−0.01^#	−0.19	−0.01^#
SimBa-IB	0.33	1.89	0.47	2.06	0.31	2.04	0.36	0.42	0.24	−0.09^#	−0.07^#	0.07^#
SimBa-SYM	0.29	2.01	0.41	2.24	0.28	2.15	0.30	0.38	0.18	−0.03^#	0.01^#	0.14^#
ThermoNet	0.27	2.73	0.45	1.50	0.32	2.06	0.23	0.36	0.26	−0.07^#	0.04^#	0.07^#
DynaMut2	0.26	1.87	0.47	2.08	0.27	2.05	0.31	0.42	0.25	−0.04^#	−0.23	0.01^#
AUTO-MUTE(RF)	0.26	2.05	0.49	2.08	0.32	2.05	0.25	0.40	0.24	−0.05^#	0.08^#	0.06^#
I-Mutant2.0	0.25	2.09	0.56	1.98	0.27	2.10	0.27	0.49	0.29	−0.14	−0.03^#	−0.09^#
BayeStab	0.23	1.98	0.34	2.24	0.19	2.20	0.16	0.29	0.14	0.18	−0.14	0.23
AUTO-MUTE(SVM)	0.09	2.12	0.32	2.25	0.13	2.17	0.07*	0.28	0.07^#	−0.10*	−0.08*	0.01^#
Machine learning methods—sequence-based
INPS	0.33	1.84	0.46	2.09	0.31	2.04	0.30	0.42	0.22	0.02^#	−0.14	0.20*
ACDC-NN-Seq	0.31	1.93	0.48	2.06	0.29	2.05	0.28	0.42	0.23	0.03^#	−0.14	0.02^#
SAAFEC-SEQ	0.25	1.86	0.53	2.00	0.21	2.06	0.23	0.50	0.13*	−0.06^#	−0.21	0.02^#
MUpro	0.19	2.03	0.40	2.19	0.16	2.10	0.14	0.34	0.15	0.01^#	0.01^#	0.04^#
I-Mutant2.0-Seq	0.19	2.15	0.42	2.18	0.25	2.12	0.15	0.37	0.22	−0.03^#	−0.02^#	0.04^#

Method	S4038		S594		S4038	S594	S4038	S594
Method	R	RMSE	R	RMSE	R	R	R	R
Non-machine learning methods—structure-based
DDGun3D	0.49	1.94	0.30	2.07	0.47	0.24	−0.04^#	0.03^#
MultiMutate	0.45	2.76	0.29	2.95	0.47	0.17	0.02^#	0.26
Rosetta	0.41	2.16	0.34	2.17	0.39	0.24	−0.04^#	0.11^#
FoldX	0.36	2.88	0.26	2.64	0.33	0.20	0.02^#	0.18*
CUPSAT	0.25	2.70	0.10*	3.06	0.28	0.19	−0.09	−0.04^#
Non-machine learning methods—sequence-based
DDGun	0.38	2.10	0.27	2.17	0.36	0.20	−0.01^#	0.00^#

Note: Machine learning methods were assessed using S4038^[0%–25%], S4038^[25%–100%], and S594 datasets, and non-machine learning methods were assessed using S4038 and S594 datasets. The presentation order of the methods is based on the R values of the S4038^[0%–25%] dataset. All correlation coefficients are statistically significantly different from zero (p < 0.005, t-test), except for the R values denoted with superscripts of “^#” or “*”. ^#p > 0.05 and 0.005 < *p < 0.05 (t-test).
Abbreviations: R, Pearson correlation coefficient; RMSE, root-mean-square error (kcal mol⁻¹).

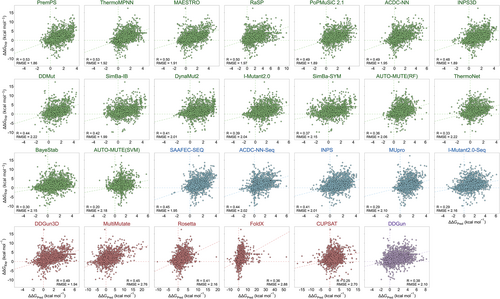
For non-machine learning methods, all mutations from S4038 were used to assess the performance. The Pearson correlation coefficients range from 0.25 to 0.49, and the RMSE ranges from 1.94 to 2.88 kcal mol⁻¹. The best-performing predictor is DDGun3D, a simple evolutionary-based mechanistic model, which achieves comparable performance to state-of-the-art prediction methods employing complex machine learning algorithms and utilizing up to a hundred features. DDGun3D can reach an impressive R value of 0.49 for the 4038 single-point mutations. For the S594 dataset, although the ranking of methods by R values differs somewhat from the S4038^[0%–25%] dataset, the methods that performed well for the S4038^[0%–25%] dataset also appear at the top for the S594 dataset. The highest R values for each category of methods applied on S594 are as follows: 0.36 for structure-based machine learning methods, 0.31 for sequence-based machine learning methods, 0.34 for structure-based non-machine learning methods, and 0.27 for sequence-based non-machine learning methods. Overall, structure-based methods outperform sequence-based methods, and machine learning methods outperform non-machine learning methods, but the differences are not very significant. The results indicate that there has been very limited improvement in accuracy over the past few years, despite the considerable efforts and the claimed enhanced performances by the authors of newly published methods.

Moreover, we analyzed the Pearson correlation coefficients for destabilizing (ΔΔG_exp ≥ 0) and stabilizing mutations (ΔΔG_exp < 0). The results in Table 1 indicate that none of the methods exhibit the capability to predict stabilizing mutations, as almost all R values do not have statistically significant differences from zero (p > 0.05, t-test). Only five R values are statistically significantly positive: 0.18 and 0.23 for BayeStab tested on S4038^[0%–25%] and S594; 0.20, 0.26, 0.18 for INPS, MultiMutate, and FoldX tested on S594. Recent studies proposed that the upper limits of Pearson correlation coefficient values depend on both experimental uncertainty and the distribution of target variables (Benevenuta & Fariselli, 2019; Montanucci, Martelli, et al., 2019). To investigate whether lower performance may arise from more intricate distribution patterns, we calculated the upper bounds of R values for all datasets presented in Table 1. The results in Table S4 reveal variations in upper bounds of R values across different datasets. Specifically, in the S4038 dataset, the upper bound of R for stabilizing mutations (R = 0.58) is lower than that for destabilizing mutations (R = 0.79). This difference is particularly pronounced in the S4038^[25%–100%] subset, where upper bound R values for stabilizing mutations range from 0.17 to 0.52. In contrast, both S4038^[0%–25%] and S594 datasets show no significant differences in upper bound R values between destabilizing and stabilizing mutations. Through careful observation and comparison of the R values in Table 1 with their corresponding upper bounds in Table S4, we found no direct or apparent dependency between them. For instance, there is a notable difference in the prediction R values for destabilizing and stabilizing mutations in both the S4038^[0%–25%] and S594 datasets, whereas the upper bound R values do not display significant distinctions.

In numerous scenarios, discerning destabilizing and stabilizing variants takes precedence over accurately predicting the specific ΔΔG value. Thus, we assessed the classification accuracy of the different methods by categorizing mutations into six conditions (Figure 3). For machine learning methods, we conducted the analysis using mutations from the combined dataset of S4038^[0%–25%] and S4038^[25%–100%]. For non-machine learning methods, the analysis encompassed all mutations within S4038. Regarding stabilizing mutations, the true positive rates (TPR) for L.S. range from 0.09 to 0.56. The methods with TPR values exceeding 0.50 are ranked as follows: ThermoNet, MultiMutate, and MAESTRO. However, the TPR values for M.S. and H.S. categories significantly decrease, with only TPR values of MultiMutate exceeding 0.30, reaching 0.41 and 0.35 for M.S. and H.S., respectively. For destabilizing mutations, the majority of the methods exhibit true positive rates exceeding 0.80 for L.D. Although these rates decrease as the degree of instability increases, it is noteworthy that for highly destabilizing mutations (H.D.), more than half of the methods achieve TPR values exceeding 0.60.

3.2 Method performance on antisymmetric property

To assess the predictive bias of the antisymmetric property (ΔΔG_F + ΔΔG_R = 0), we generated reverse mutations for the S594 dataset and conducted the analysis on this dataset along with two other widely discussed datasets, namely S^sym and S2000 (Table 2). When considering the reverse mutations, a first group of methods (ThermoNet, DDMut, PremPS, ACDC-NN, DynaMut2, ACDC-NN-Seq, DDGun3D, and DDGun) built to exhibit antisymmetric behavior performs well in terms of the antisymmetric property, with the exception of DynaMut2. The correlation coefficients (R_FR) between predicted ΔΔG values for forward and reverse mutations range from −0.79 to −1.00 across the three datasets with minimal bias. Among the remaining 19 predictors, SimBa-SYM, ThermoMPNN, SimBa-IB, and MultiMutate achieved high prediction accuracy for the antisymmetric property. They obtained R_FR values ranging from −0.66 to −0.99 for all mutations across the three datasets, even though the antisymmetric property was not explicitly incorporated into their method development. For FoldX and Rosetta, the R_FR values for S594 are −0.96 and −0.74, respectively, but they exhibit low R_FR values for the S^sym and S2000 datasets. The reason for this difference lies in the fact that the reverse mutations for the S594 dataset were generated using FoldX, which primarily focuses on optimizing the surrounding side chains near the mutation site during the creation of mutant structures. In contrast, experimentally determined 3D structures were employed for both wild-type and mutant proteins in the S^sym and S2000 datasets.

TABLE 2. The antisymmetric property of all methods tested on S594, S^sym, and S2000.

Method	All mutations						ΔΔG_exp ≥ 0				ΔΔG_exp < 0
	S594		S^sym		S2000		S594		S^sym		S594		S^sym
	R_FR	<δ>	R_FR	<δ>	R_FR	<δ>	R_FR	<δ>	R_FR	<δ>	R_FR	<δ>	R_FR	<δ>
Machine learning methods—structure-based
SimBa-SYM	−0.97	0.01	−0.99	0.01	−0.95	0.01	−0.97	0.02	−0.99	0.01	−0.96	0.00	−0.98	0.01
ThermoNet	−0.90	0.04	−0.90	0.05	−0.84	0.03	−0.90	0.04	−0.90	0.06	−0.90	0.03	−0.81	−0.01
DDMut	−0.90	0.10	−0.96	0.11	−0.88	0.10	−0.90	0.09	−0.96	0.15	−0.88	0.12	−0.91	−0.01
ThermoMPNN	−0.88	0.42	−0.66	0.70	−0.70	0.71	−0.89	0.42	−0.64	0.75	−0.80	0.42	−0.27*	0.54
PremPS	−0.87	−0.05	−0.93	0.04	−0.92	0.10	−0.87	−0.08	−0.93	0.12	−0.84	0.02	−0.76	−0.19
SimBa-IB	−0.85	0.83	−0.87	0.90	−0.83	0.82	−0.85	0.87	−0.88	0.98	−0.82	0.71	−0.82	0.66
ACDC-NN	−0.79	0.27	−0.98	0.05	−0.91	0.10	−0.79	0.33	−0.98	0.06	−0.72	0.10	−0.99	0.02
RaSP	−0.53	1.38	−0.26	1.65	−0.42	1.51	−0.52	1.44	−0.17*	1.84	−0.45	1.20	−0.37	1.05
PoPMuSiC 2.1	−0.47	1.55	−0.28	1.43	−0.34	1.41	−0.46	1.62	−0.27	1.55	−0.41	1.35	0.02^#	1.05
MAESTRO	−0.30	1.32	−0.33	1.25	−0.18	1.20	−0.29	1.35	−0.35	1.38	−0.13^#	1.24	0.07^#	0.84
AUTO-MUTE(RF)	−0.21	2.08	−0.05^#	1.97	−0.14	1.92	−0.19	2.18	−0.00^#	2.23	−0.12^#	1.81	−0.16^#	1.17
BayeStab	−0.12	1.47	0.08^#	1.49	−0.01^#	1.24	−0.17	1.41	0.08^#	1.62	0.07^#	1.63	0.14^#	1.10
I-Mutant2.0	−0.03^#	1.95	0.00^#	1.37	−0.09*	1.87	−0.01^#	2.05	−0.04^#	1.61	−0.05^#	1.69	0.19^#	0.62
AUTO-MUTE(SVM)	−0.01^#	2.13	−0.08^#	2.05	−0.21	2.07	0.01^#	2.17	−0.14*	2.17	−0.04^#	2.01	0.18^#	1.66
DynaMut2	0.01^#	1.48	−0.11*	1.56	0.00^#	1.33	−0.02^#	1.57	−0.14*	1.81	0.13^#	1.24	−0.16^#	0.76
Machine learning methods—sequence-based
ACDC-NN-Seq	−1.00	0.00	−1.00	0.01	−0.99	0.05	−1.00	0.00	−1.00	0.01	−1.00	0.00	−1.00	0.01
MUpro	−0.30	1.88	−0.02^#	1.93	−0.10	1.80	−0.27	1.87	−0.05^#	2.28	−0.34	1.88	0.15^#	0.85
I-Mutant2.0-Seq	−0.29	1.74	−0.34	1.29	−0.14	1.84	−0.28	1.84	−0.35	1.44	−0.30	1.47	−0.13^#	0.81
SAAFEC-SEQ	0.32	1.66	0.67	1.94	0.58	1.66	0.33	1.73	0.65	2.34	0.42	1.49	0.60	0.65
Non-machine learning methods—structure-based
DDGun3D	−0.98	0.05	−0.99	0.04	−0.97	0.04	−0.98	0.06	−0.99	0.05	−0.97	0.03	−0.99	0.01
FoldX	−0.96	0.11	−0.25	1.12	−0.15	1.48	−0.95	0.12	−0.16*	1.30	−0.96	0.07	−0.18^#	0.56
MultiMutate	−0.91	0.29	−0.91	0.34	−0.91	0.30	−0.92	0.27	−0.92	0.37	−0.87	0.36	−0.83	0.24
Rosetta	−0.74	0.33	−0.37	1.32	−0.06^#	1.42	−0.69	0.37	−0.32	1.33	−0.83	0.20	−0.16^#	1.29
CUPSAT	−0.69	1.09	−0.55	1.43	−0.43	1.26	−0.64	1.23	−0.59	1.63	−0.81	0.72	−0.50	0.79
Non-machine learning methods—sequence-based
DDGun	−0.96	0.08	−1.00	0.01	−0.98	0.03	−0.96	0.07	−1.00	0.01	−0.91	0.09	−1.00	0.02

Note: INPS and INSP3D were not included in the antisymmetric analysis due to a lack of computed data from the servers. The methods are presented in order based on the R_FR values calculated for all mutations in the S594 dataset. R_FR is the Pearson correlation coefficient between predicted ∆∆G values of the forward and reverse mutations. <δ> = ∑(∆∆G_F + ∆∆G_R)/N. A non-biased prediction should have R_FR = −1 and <δ> = 0. All correlation coefficients are statistically significantly different from zero (p < 0.005, t-test), except for the R_FR values denoted with superscripts of “^#” or “*”. ^#p > 0.05 and 0.005 < *p < 0.05 (t-test).

We also conducted a separate analysis of the bias effect for destabilizing and stabilizing mutations from S594 and S^sym (Table 2). S2000 dataset lacks ΔΔG values, which prevents us from performing a similar performance analysis on this dataset. For the 11 methods with high R_FR values for all mutations (ThermoNet, DDMut, PremPS, ACDC-NN, ACDC-NN-Seq, DDGun3D, DDGun, SimBa-SYM, ThermoMPNN, SimBa-IB, and MultiMutate), they consistently demonstrate a strong antisymmetric property for both destabilizing and stabilizing mutations. The only exception is ThermoMPNN, which has an R_FR value of −0.27 for stabilizing mutations from S^sym. The results indicate that the antisymmetric property for stabilizing mutations does not exhibit significant differences compared to that for destabilizing mutations, despite the notably poor performance in predicting stabilizing mutations. This finding suggests that while the antisymmetric property remains consistent between destabilizing and stabilizing mutations, the predictive challenges associated with stabilizing mutations are distinct and influenced by factors beyond the antisymmetric nature of the mutations. Further investigation is required to unravel the specific underlying reasons for the poor predictive performance of stabilizing mutations and to devise strategies for improvement in this area.

3.3 Performance on five types of properties

We conducted a further assessment to investigate how the performance of different methods varies on specific structural and sequence properties of the mutated residues and the mutations themselves. Figure 4 provides an overview of the performance of various methods across five distinct property types. The Pearson correlation coefficient values presented in Figure 4a indicate that all assessed methods consistently demonstrated superior performance when applied to buried residues as compared to exposed residues. For the secondary structure conformation of mutated sites, almost all methods achieved the highest R values for mutations occurred in sheet configurations, followed by helix, with loop configurations yielding the lowest performance. Regarding conservation, it was observed that all methods exhibited lower predictive performance for low-conservation mutation sites compared to conserved sites. Somewhat surprisingly, for highly conserved sites, the majority of methods did not perform better than for intermediate sites. In the context of mutations involving charge changes, mutations occurring between uncharged and charged residues displayed slightly higher R values compared to mutations where the charge remained unchanged, and mutations involving substantial changes in charge (charge_2) yielded the lowest R values. Finally, mutations that did not result in a change in amino acid size exhibited the lowest R values across the board. In summary, these findings highlight consistent trends observed for the majority of methods across the five property types under investigation. Among all approaches, ThermoMPNN consistently exhibited the best predictive performance for the properties of surface, loop, variable, charge_2, and size_0, in which the majority methods have poor performance.

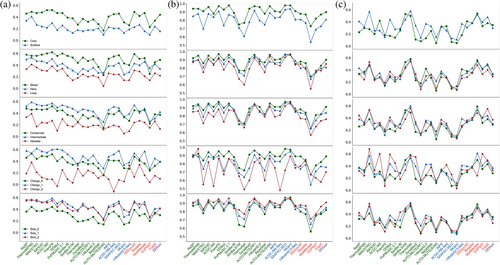
Subsequently, we performed an analysis of these five properties with respect to destabilizing and stabilizing mutations. Due to the lack of meaningful correlation values for stabilizing mutations, we utilized the true positive rates of L.D. and L.S. (see the definition in Figure 3b) for this portion of the analysis, with results presented in Figure 4b,c. Regarding the classification results for destabilizing mutations, the distinctions between different properties were not as pronounced as with R values, but the conclusions drawn are essentially consistent with those derived from the R values of all mutations. However, for stabilizing mutations, no discernible pattern was observed; for instance, some methods performed better on mutations occurring in the core than mutations occurring on the surface, while others exhibited higher performance on surface mutations than on core mutations. Overall, ThermoNet maintained the highest TPR values for all properties in the context of stabilizing mutations.

3.4 Is the poor prediction of stabilizing mutations due to the bias in dataset?

Based on the above testing, we have observed that the poor predictive performance for stabilizing mutations is a common challenge among current predictors. It is widely acknowledged that the primary reason for this challenge is dataset bias, which has a predominance of destabilizing mutations. Our objective here is to investigate whether the suboptimal performance of all tools in predicting stabilizing mutations is a consequence of dataset distribution bias. We used S2648 and its reverse mutations, as well as destabilizing and stabilizing mutations, as separate training sets for model construction. Additionally, we created a dataset called S1130 with a balanced distribution of $∆ ∆ G_{\exp}$ values between destabilizing and stabilizing mutations (Figure S2 and Table S5), which was also used for model construction. We then retrained our previously developed method of PremPS on these training datasets. Since mutations in the S2648 and S4038 datasets do not overlap, S4038 was utilized as the test set, further categorized into groups of similar proteins and dissimilar proteins (Table S5). In total, we employed six types of training sets, which include forward mutations, reverse mutations, a combination of both, forward destabilizing mutations, forward stabilizing mutations, and a dataset with balanced values of stability changes (as detailed in Table 3).

TABLE 3. Performance of PremPS after retraining on the six datasets.

Training set	Test set	All mutations		$∆ ∆ G_{\exp} \geq 0$		$∆ ∆ G_{\exp} < 0$
Training set	Test set	R	RMSE	R	RMSE	R	RMSE
Forward mutations as the training set
S2648	S4038	0.54	1.86	0.53	1.83	−0.11	1.92
	S2584	0.60	1.89	0.56	2.05	−0.12	1.43
	S1454	0.35	1.79	0.43	1.39	−0.09^#	2.71
Reverse mutations as the training set
S2648	S4038	0.24	2.38	0.17	2.65	0.07*	1.42
	S2584	0.22	2.56	0.17	2.99	−0.06^#	0.96
	S1454	0.30	2.01	0.21	1.98	0.17	2.11
Forward plus reverse mutations as the training set
S5296	S4038	0.53	1.86	0.53	1.86	−0.10	1.88
	S2584	0.60	1.90	0.55	2.08	−0.09*	1.39
	S1454	0.36	1.78	0.43	1.41	−0.09^#	2.66
Forward destabilizing mutations ( $∆ ∆ G_{\exp} \geq 0$ ) as the training set
S2080	S4038	0.52	1.90	0.55	1.72	−0.25	2.32
	S2584	0.60	1.93	0.57	1.96	−0.29	1.84
	S1454	0.33	1.86	0.45	1.24	−0.19	3.13
Forward stabilizing mutations ( $∆ ∆ G_{\exp} < 0$ ) as the training set
S568	S4038	−0.19	2.94	−0.26	3.38	0.27	1.14
	S2584	−0.31	3.13	−0.33	3.7	0.24	0.65
	S1454	−0.01^#	2.57	−0.18	2.77	0.20	1.81
Balanced dataset as the training set
S1130	S4038	0.47	2.16	0.45	2.35	−0.08	1.52
	S2584	0.53	2.27	0.47	2.63	−0.07*	1.00
	S1454	0.32	1.93	0.38	1.80	−0.08^#	2.30

Note: S2584 and S1454 are two datasets where the proteins exhibit sequence identity with S2648 of more than 25% and less than 25%, respectively. S1130 is derived from S2648, with a balanced distribution of $∆ ∆ G_{\exp}$ values between destabilizing and stabilizing mutations. All correlation coefficients are statistically significantly different from zero (p < 0.005, t-test), except for the R values denoted with superscripts of “^#” or “*”. ^#p > 0.05 and 0.005 < *p < 0.05 (t-test).
Abbreviations: R, Pearson correlation coefficient; RMSE, root-mean-square error.

As expected, using forward mutations as the training set, which primarily consists of destabilizing mutations (as indicated in Table S5), resulted in the model's inability to predict stabilizing mutations (Table 3). Incorporating reverse mutations to balance positive and negative data showed promise in predicting the antisymmetric property but fell short when predicting entirely new stabilizing mutations. Training the model exclusively with reverse mutations, which include a higher proportion of reverse stabilizing mutations, did not improve predictions for stabilizing mutations. Instead, it notably decreased performance for destabilizing mutations compared to the model trained with forward mutations. The absence of experimental mutant structures posed a challenge in generating reverse mutation data. To test if FoldX-generated structures affected performance, we used PremPS on the S^sym dataset. Results in Table S6 show that replacing experimental structures with FoldX-generated ones had no impact on performance. Therefore, one speculated reason is that reverse mutations, while including many stabilizing mutations, may not truly represent natural mutations.

Consequently, we proceeded to construct models using exclusively forward destabilizing and forward stabilizing mutations. Remarkably, when we exclusively employed forward stabilizing mutations for model construction, the R values for stabilizing mutations exhibited positive correlations ranging from 0.20 to 0.27. These correlations are higher than those observed in any other models. When we exclusively utilized forward destabilizing mutations to build the model, the R values display a significant positive correlation in predicting destabilizing mutations, ranging from 0.45 to 0.57. We acknowledge that training the model in this manner is susceptible to overfitting. Nevertheless, we can observe that the model built using destabilizing mutations performs significantly better in predicting destabilizing mutations than the model built using stabilizing mutations to predict stabilizing ones. Furthermore, even when we employed the S1130 dataset characterized by a balanced representation of both stabilizing and destabilizing mutations, the model still demonstrated an inability to effectively predict stabilizing mutations, at the expense of its predictive accuracy for destabilizing mutations.

Hence, our investigation suggests that merely addressing bias in the training dataset may not significantly enhance the accuracy of predicting stabilizing mutations. Further research and exploration are imperative to tackle these challenges. Potential areas for future investigation include: (1) data augmentation: Expanding the dataset with additional high-quality stabilizing mutation examples might help improve the model's understanding of these rare events. (2) Feature engineering: Exploring additional or refined features that specifically capture the characteristics of stabilizing mutations might lead to improved predictive models. (3) Model architecture: Experimenting with more sophisticated machine learning models or neural network architectures could enhance the model's ability to discern stabilizing mutations within the data.

AUTHOR CONTRIBUTIONS

Minghui Li: Conceptualization; supervision; project administration; writing – original draft; writing – review and editing; funding acquisition; investigation; visualization; validation. Feifan Zheng: Visualization; validation; data curation; investigation; methodology; software; formal analysis. Yang Liu: Investigation; methodology; validation; software; formal analysis; data curation. Yan Yang: Visualization. Yuhao Wen: Software.

ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China (32070665) and the Priority Academic Program Development of Jiangsu Higher Education Institutions. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

CONFLICT OF INTEREST STATEMENT

The authors declare no competing interests.

Open Research

DATA AVAILABILITY STATEMENT

The newly compiled experimental dataset of S4038 and the corresponding sequence and structure data are publicly accessible on GitHub at https://github.com/minghuilab/ACPSC. Additional data files that support the findings of this study are available from the corresponding authors upon request.

Supporting Information

Filename	Description
pro4861-sup-0001-Supinfo01.pdfPDF document, 597.1 KB	Appendix S1. Supporting Information.
pro4861-sup-0002-Supinfo02.xlsxExcel 2007 spreadsheet , 20.6 KB	Data S1. A total of 169 erroneous data entries were identified and corrected through manual inspection of the ΔΔG values and mutation details for each entry. These corrections were made while adhering to the following order of retention: ThermoMutDB > FireProtDB > ProThermDB, so the majority of erroneous data entries were found within ThermoMutDB.
pro4861-sup-0003-Supinfo03.xlsxExcel 2007 spreadsheet , 14.1 KB	Data S2. 177 updated structures along with their original structures from the databases.
pro4861-sup-0004-Supinfo04.xlsxExcel 2007 spreadsheet , 1.2 MB	Data S3. The S4038 dataset and the computational ΔΔG values of all evaluated methods.
pro4861-sup-0005-Supinfo05.xlsxExcel 2007 spreadsheet , 17.9 KB	Data S4. The counts of true positive and positive mutations for each category.
pro4861-sup-0006-Supinfo06.xlsxExcel 2007 spreadsheet , 25.5 KB	Data S5. The counts of mutations for each property along with the numbers of true positive and positive mutations.

Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.

REFERENCES

Baek KT, Kepp KP. Data set and fitting dependencies when estimating protein mutant stability: toward simple, balanced, and interpretable models. J Comput Chem. 2022; 43: 504–518.
10.1002/jcc.26810
CAS PubMed Web of Science® Google Scholar
Ben Chorin A, Masrati G, Kessel A, Narunsky A, Sprinzak J, Lahav S, et al. ConSurf-DB: an accessible repository for the evolutionary conservation patterns of the majority of PDB proteins. Protein Sci. 2020; 29: 258–267.
10.1002/pro.3779
CAS PubMed Web of Science® Google Scholar
Benevenuta S, Birolo G, Sanavia T, Capriotti E, Fariselli P. Challenges in predicting stabilizing variations: an exploration. Front Mol Biosci. 2022; 9:1075570.
10.3389/fmolb.2022.1075570
CAS PubMed Web of Science® Google Scholar
Benevenuta S, Fariselli P. On the upper bounds of the real-valued predictions. Bioinform Biol Insights. 2019; 13:1177932219871263.
10.1177/1177932219871263
Web of Science® Google Scholar
Benevenuta S, Pancotti C, Fariselli P, Birolo G, Sanavia T. An antisymmetric neural network to predict free energy changes in protein variants. J Phys D Appl Phys. 2021; 54:245403.
10.1088/1361-6463/abedfb
CAS Web of Science® Google Scholar
Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, et al. The protein data bank. Nucleic Acids Res. 2000; 28: 235–242.
10.1093/nar/28.1.235
CAS PubMed Web of Science® Google Scholar
Blaabjerg LM, Kassem MM, Good LL, Jonsson N, Cagiada M, Johansson KE, et al. Rapid protein stability prediction using deep learning representations. Elife. 2023; 12:e82593.
10.7554/eLife.82593
CAS PubMed Web of Science® Google Scholar
Caldararu O, Mehra R, Blundell TL, Kepp KP. Systematic investigation of the data set dependency of protein stability predictors. J Chem Inf Model. 2020; 60: 4772–4784.
10.1021/acs.jcim.0c00591
CAS PubMed Web of Science® Google Scholar
Capriotti E, Fariselli P, Casadio R. I-Mutant2.0: predicting stability changes upon mutation from the protein sequence or structure. Nucleic Acids Res. 2005; 33: W306–W310.
10.1093/nar/gki375
CAS PubMed Web of Science® Google Scholar
Casadio R, Vassura M, Tiwari S, Fariselli P, Luigi Martelli P. Correlating disease-related mutations to their effect on protein stability: a large-scale analysis of the human proteome. Hum Mutat. 2011; 32: 1161–1170.
10.1002/humu.21555
CAS PubMed Web of Science® Google Scholar
Chen Y, Lu H, Zhang N, Zhu Z, Wang S, Li M. PremPS: predicting the impact of missense mutations on protein stability. PLoS Comput Biol. 2020; 16:e1008543.
10.1371/journal.pcbi.1008543
CAS PubMed Web of Science® Google Scholar
Cheng J, Randall A, Baldi P. Prediction of protein stability changes for single-site mutations using support vector machines. Proteins. 2006; 62: 1125–1132.
10.1002/prot.20810
CAS PubMed Web of Science® Google Scholar
Dana JM, Gutmanas A, Tyagi N, Qi G, O'Donovan C, Martin M, et al. SIFTS: updated structure integration with function, taxonomy and sequences resource allows 40-fold increase in coverage of structure-based annotations for proteins. Nucleic Acids Res. 2019; 47: D482–D489.
10.1093/nar/gky1114
CAS PubMed Web of Science® Google Scholar
Dehouck Y, Grosfils A, Folch B, Gilis D, Bogaerts P, Rooman M. Fast and accurate predictions of protein stability changes upon mutations using statistical potentials and neural networks: PoPMuSiC-2.0. Bioinformatics. 2009; 25: 2537–2543.
10.1093/bioinformatics/btp445
CAS PubMed Web of Science® Google Scholar
Dehouck Y, Kwasigroch JM, Gilis D, Rooman M. PoPMuSiC 2.1: a web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinformatics. 2011; 12: 151.
10.1186/1471-2105-12-151
PubMed Web of Science® Google Scholar
Deutsch C, Krishnamoorthy B. Four-body scoring function for mutagenesis. Bioinformatics. 2007; 23: 3009–3015.
10.1093/bioinformatics/btm481
CAS PubMed Web of Science® Google Scholar
Dieckhaus H, Brocidiacono M, Randolph N, Kuhlman B. Transfer learning to leverage larger datasets for improved prediction of protein stability changes. 2023. bioRxiv.
Google Scholar
Fang J. A critical review of five machine learning-based algorithms for predicting protein stability changes upon mutation. Brief Bioinform. 2020; 21: 1285–1292.
10.1093/bib/bbz071
CAS PubMed Web of Science® Google Scholar
Fariselli P, Martelli PL, Savojardo C, Casadio R. INPS: predicting the impact of non-synonymous variations on protein stability from sequence. Bioinformatics. 2015; 31: 2816–2821.
10.1093/bioinformatics/btv291
CAS PubMed Web of Science® Google Scholar
Glaser F, Pupko T, Paz I, Bell RE, Bechor-Shental D, Martz E, et al. ConSurf: identification of functional regions in proteins by surface-mapping of phylogenetic information. Bioinformatics. 2003; 19: 163–164.
10.1093/bioinformatics/19.1.163
CAS PubMed Web of Science® Google Scholar
Goldenzweig A, Fleishman SJ. Principles of protein stability and their application in computational design. Annu Rev Biochem. 2018; 87: 105–129.
10.1146/annurev-biochem-062917-012102
CAS PubMed Web of Science® Google Scholar
Guerois R, Nielsen JE, Serrano L. Predicting changes in the stability of proteins and protein complexes: a study of more than 1000 mutations. J Mol Biol. 2002; 320: 369–387.
10.1016/S0022-2836(02)00442-4
CAS PubMed Web of Science® Google Scholar
Hartl FU. Protein misfolding diseases. Annu Rev Biochem. 2017; 86: 21–26.
10.1146/annurev-biochem-061516-044518
CAS PubMed Web of Science® Google Scholar
Hou Q, Kwasigroch JM, Rooman M, Pucci F. SOLart: a structure-based method to predict protein solubility and aggregation. Bioinformatics. 2020; 36: 1445–1452.
10.1093/bioinformatics/btz773
CAS PubMed Web of Science® Google Scholar
Iqbal S, Li F, Akutsu T, Ascher DB, Webb GI, Song J. Assessing the performance of computational predictors for estimating protein stability changes upon missense mutations. Brief Bioinform. 2021; 22:bbab184.
10.1093/bib/bbab184
PubMed Web of Science® Google Scholar
Joosten RP, te Beek TA, Krieger E, Hekkelman ML, Hooft RW, Schneider R, et al. A series of PDB related databases for everyday needs. Nucleic Acids Res. 2011; 39: D411–D419.
10.1093/nar/gkq1105
CAS PubMed Web of Science® Google Scholar
Kellogg EH, Leaver-Fay A, Baker D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins. 2011; 79: 830–838.
10.1002/prot.22921
CAS PubMed Web of Science® Google Scholar
Kepp KP. Towards a “Golden Standard” for computing globin stability: stability and structure sensitivity of myoglobin mutants. Biochim Biophys Acta. 2015; 1854: 1239–1248.
10.1016/j.bbapap.2015.06.002
CAS PubMed Web of Science® Google Scholar
Korendovych IV, DeGrado WF. De novo protein design, a retrospective. Q Rev Biophys. 2020; 53:e3.
10.1017/S0033583519000131
CAS PubMed Web of Science® Google Scholar
Laimer J, Hofer H, Fritz M, Wegenkittl S, Lackner P. MAESTRO—multi agent stability prediction upon point mutations. BMC Bioinformatics. 2015; 16: 116.
10.1186/s12859-015-0548-6
PubMed Web of Science® Google Scholar
Li B, Yang YT, Capra JA, Gerstein MB. Predicting changes in protein thermodynamic stability upon point mutation with deep 3D convolutional neural networks. PLoS Comput Biol. 2020; 16:e1008291.
10.1371/journal.pcbi.1008291
CAS PubMed Web of Science® Google Scholar
Li G, Panday SK, Alexov E. SAAFEC-SEQ: a sequence-based method for predicting the effect of single point mutations on protein thermodynamic stability. Int J Mol Sci. 2021; 22: 606.
10.3390/ijms22020606
CAS PubMed Web of Science® Google Scholar
Marabotti A, Scafuri B, Facchiano A. Predicting the stability of mutant proteins by computational approaches: an overview. Brief Bioinform. 2021; 22:bbaa074.
10.1093/bib/bbaa074
PubMed Web of Science® Google Scholar
Masso M, Vaisman II. AUTO-MUTE 2.0: a portable framework with enhanced capabilities for predicting protein functional consequences upon mutation. Adv Bioinformatics. 2014; 2014:278385.
10.1155/2014/278385
CAS PubMed Google Scholar
Mitragotri S, Burke PA, Langer R. Overcoming the challenges in administering biopharmaceuticals: formulation and delivery strategies. Nat Rev Drug Discov. 2014; 13: 655–672.
10.1038/nrd4363
CAS PubMed Web of Science® Google Scholar
Montanucci L, Capriotti E, Frank Y, Ben-Tal N, Fariselli P. DDGun: an untrained method for the prediction of protein stability changes upon single and multiple point variations. BMC Bioinformatics. 2019; 20: 335.
10.1186/s12859-019-2923-1
PubMed Web of Science® Google Scholar
Montanucci L, Martelli PL, Ben-Tal N, Fariselli P. A natural upper bound to the accuracy of predicting protein stability changes upon mutations. Bioinformatics. 2019; 35: 1513–1517.
10.1093/bioinformatics/bty880
CAS PubMed Web of Science® Google Scholar
Nikam R, Kulandaisamy A, Harini K, Sharma D, Gromiha MM. ProThermDB: thermodynamic database for proteins and mutants revisited after 15 years. Nucleic Acids Res. 2021; 49: D420–D424.
10.1093/nar/gkaa1035
CAS PubMed Web of Science® Google Scholar
Pan Q, Nguyen TB, Ascher DB, Pires DEV. Systematic evaluation of computational tools to predict the effects of mutations on protein stability in the absence of experimental structures. Brief Bioinform. 2022; 23:bbac025.
10.1093/bib/bbac025
PubMed Web of Science® Google Scholar
Pancotti C, Benevenuta S, Birolo G, Alberini V, Repetto V, Sanavia T, et al. Predicting protein stability changes upon single-point mutation: a thorough comparison of the available tools on a new dataset. Brief Bioinform. 2022; 23:bbab555.
10.1093/bib/bbab555
PubMed Web of Science® Google Scholar
Pancotti C, Benevenuta S, Repetto V, Birolo G, Capriotti E, Sanavia T, et al. A deep-learning sequence-based method to predict protein stability changes upon genetic variations. Genes (Basel). 2021; 12: 911.
10.3390/genes12060911
CAS PubMed Web of Science® Google Scholar
Pandey P, Panday SK, Rimal P, Ancona N, Alexov E. Predicting the effect of single mutations on protein stability and binding with respect to types of mutations. Int J Mol Sci. 2023; 24:12073.
10.3390/ijms241512073
CAS PubMed Web of Science® Google Scholar
Parthiban V, Gromiha MM, Schomburg D. CUPSAT: prediction of protein stability upon point mutations. Nucleic Acids Res. 2006; 34: W239–W242.
10.1093/nar/gkl190
CAS PubMed Web of Science® Google Scholar
Pucci F, Bernaerts KV, Kwasigroch JM, Rooman M. Quantification of biases in predictions of protein stability changes upon mutations. Bioinformatics. 2018; 34: 3659–3665.
10.1093/bioinformatics/bty348
CAS PubMed Web of Science® Google Scholar
Pucci F, Schwersensky M, Rooman M. Artificial intelligence challenges for predicting the impact of mutations on protein stability. Curr Opin Struct Biol. 2022; 72: 161–168.
10.1016/j.sbi.2021.11.001
CAS PubMed Web of Science® Google Scholar
Rodrigues CHM, Pires DEV, Ascher DB. DynaMut2: assessing changes in stability and flexibility upon single and multiple point missense mutations. Protein Sci. 2021; 30: 60–69.
10.1002/pro.3942
CAS PubMed Web of Science® Google Scholar
Rose GD, Geselowitz AR, Lesser GJ, Lee RH, Zehfus MH. Hydrophobicity of amino acid residues in globular proteins. Science. 1985; 229: 834–838.
10.1126/science.4023714
CAS PubMed Web of Science® Google Scholar
Sanavia T, Birolo G, Montanucci L, Turina P, Capriotti E, Fariselli P. Limitations and challenges in protein stability prediction upon genome variations: towards future applications in precision medicine. Comput Struct Biotechnol J. 2020; 18: 1968–1979.
10.1016/j.csbj.2020.07.011
CAS PubMed Web of Science® Google Scholar
Savojardo C, Fariselli P, Martelli PL, Casadio R. INPS-MD: a web server to predict stability of protein variants from sequence and structure. Bioinformatics. 2016; 32: 2542–2544.
10.1093/bioinformatics/btw192
CAS PubMed Web of Science® Google Scholar
Shoichet BK, Baase WA, Kuroki R, Matthews BW. A relationship between protein stability and protein function. Proc Natl Acad Sci U S A. 1995; 92: 452–456.
10.1073/pnas.92.2.452
CAS PubMed Web of Science® Google Scholar
Steinegger M, Soding J. MMseqs2 enables sensitive protein sequence searching for the analysis of massive data sets. Nat Biotechnol. 2017; 35: 1026–1028.
10.1038/nbt.3988
CAS PubMed Web of Science® Google Scholar
Stourac J, Dubrava J, Musil M, Horackova J, Damborsky J, Mazurenko S, et al. FireProtDB: database of manually curated protein stability data. Nucleic Acids Res. 2021; 49: D319–D324.
10.1093/nar/gkaa981
CAS PubMed Web of Science® Google Scholar
Tanford C. Protein denaturation. Adv Protein Chem. 1968; 23: 121–282.
10.1016/S0065-3233(08)60401-5
CAS PubMed Google Scholar
Usmanova DR, Bogatyreva NS, Arino Bernad J, Eremina AA, Gorshkova AA, Kanevskiy GM, et al. Self-consistency test reveals systematic bias in programs for prediction change of stability upon mutation. Bioinformatics. 2018; 34: 3653–3658.
10.1093/bioinformatics/bty340
CAS PubMed Web of Science® Google Scholar
Wang S, Tang H, Zhao Y, Zuo L. BayeStab: predicting effects of mutations on protein stability with uncertainty quantification. Protein Sci. 2022; 31:e4467.
10.1002/pro.4467
CAS PubMed Web of Science® Google Scholar
Xavier JS, Nguyen TB, Karmarkar M, Portelli S, Rezende PM, Velloso JPL, et al. ThermoMutDB: a thermodynamic database for missense mutations. Nucleic Acids Res. 2021; 49: D475–D479.
10.1093/nar/gkaa925
CAS PubMed Web of Science® Google Scholar
Zhou Y, Pan Q, Pires DEV, Rodrigues CHM, Ascher DB. DDMut: predicting effects of mutations on protein stability using deep learning. Nucleic Acids Res. 2023; 51: W122–W128.
10.1093/nar/gkad472
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume33, Issue1

January 2024

e4861

This article also appears in:

Tools for Protein Science 2024

Assessing computational tools for predicting protein stability changes upon missense mutations using a new dataset

Abstract

1 INTRODUCTION

2 METHODS

2.1 Benchmark dataset of S4038

2.2 Benchmark datasets of S594, S^sym, and S2000

2.3 Evaluated methods for predicting the impact of single-point mutations on protein stability

2.3.1 Machine learning methods—Structure-based

2.3.2 Machine learning methods—Sequence-based

2.3.3 Non-machine learning methods—Structure-based

2.3.4 Non-machine learning methods—Sequence-based

2.4 Exploring the performance of different methods across different properties

2.5 Performance evaluation

3 RESULTS AND DISCUSSION

3.1 Method performance on the unseen data

3.2 Method performance on antisymmetric property

3.3 Performance on five types of properties

3.4 Is the poor prediction of stabilizing mutations due to the bias in dataset?

AUTHOR CONTRIBUTIONS

ACKNOWLEDGMENTS

CONFLICT OF INTEREST STATEMENT

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Assessing computational tools for predicting protein stability changes upon missense mutations using a new dataset

Abstract

1 INTRODUCTION

2 METHODS

2.1 Benchmark dataset of S4038

2.2 Benchmark datasets of S594, Ssym, and S2000

2.3 Evaluated methods for predicting the impact of single-point mutations on protein stability

2.3.1 Machine learning methods—Structure-based

2.3.2 Machine learning methods—Sequence-based

2.3.3 Non-machine learning methods—Structure-based

2.3.4 Non-machine learning methods—Sequence-based

2.4 Exploring the performance of different methods across different properties

2.5 Performance evaluation

3 RESULTS AND DISCUSSION

3.1 Method performance on the unseen data

3.2 Method performance on antisymmetric property

3.3 Performance on five types of properties

3.4 Is the poor prediction of stabilizing mutations due to the bias in dataset?

AUTHOR CONTRIBUTIONS

ACKNOWLEDGMENTS

CONFLICT OF INTEREST STATEMENT

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Citing Literature

Figures

References

Related

Information

2.2 Benchmark datasets of S594, S^sym, and S2000