Network representation of protein interactions—Experimental results
Understanding the interactions of proteins with their natural targets is one of the most important tasks of modern molecular biology. Here the graph analytical investigation of different protein interactions reveals that the functional architecture of these interactions is always based on a common principle.
Abstract
A graph theoretical analysis of nuclear magnetic resonance (NMR) data of six different protein interactions has been presented. The representation of the protein interaction data as a graph or network reveals that all of the studied interactions are based on a common functional concept. They all involve a single densely packed hub of functionally correlated residues that mediate the ligand binding events. This is found independent of the kind of protein (folded or unfolded) or ligand (protein, polymer or small molecule). Furthermore, the power of the graph analysis is demonstrated at the examples of the Calmodulin (CaM)/Calcium and the Cold Shock Protein A (CspA)/RNA interaction. The presented approach enables the precise determination of multiple binding sites for the respective ligand molecules.
Introduction
The understanding of protein interactions is an important part of modern structural biology. In this regard nuclear magnetic resonance (NMR) constitutes a versatile tool, since it allows the determination of changes in chemical environment and structural dynamics of a protein at atomic resolution. Yet, the interpretation of protein NMR data is frequently not straightforward. Phenomena like allosteric restructuring or multiple binding sites render the analysis of these data a challenging task.1-3 In part one of this contribution we introduced means to interpret NMR data on the basis of graph theory. This method might aid to analyze even very complicated NMR data. The proposed data treatment is inspired by a network representation of a protein interaction. Such a representation highlights functional correlations between residues that are functionally involved in a ligand binding event. Hence, it can be regarded as a functional description of a protein interaction. This is especially useful in cases of intrinsically disordered proteins (IDPs), since these proteins lack a rigid three-dimensional structure, which impedes crystallographic analyses of their interactions.
We demonstrate how one can derive the network or graph representation of a protein interaction from the four differential NMR parameters ΔCS(1HN), ΔCS(15N), ΔR2, and Δη (the Δ here indicates the difference between a value measured for the holo-form minus the value found for the apo-form of a residue). These residue-resolved parameters were combined into an adjacency matrix with the dimension of the primary sequence of the protein under investigation. The construction of the graph representation of a protein interaction, which is represented through an associated adjacency matrix, was in detail explained in part one of this contribution at the example of the well-documented OPN/Heparin interaction. Here we show results of the analyses of five further protein interactions. Through this we validate the broad applicability of our method and demonstrate how it allows to precisely determine even complicated ligand binding patterns or multiple binding sites. Furthermore, it is shown that the graphs of all investigated interactions are based on a particular common architecture: that is, every graph description of a protein binding events reveals a single “hub” of strongly correlated residues independent of the kind of protein (folded or unfolded) or ligand (protein, polymer, or small molecule) underlying the graph.
This finding might aid to further develop modern thermodynamics models that explain allosteric effects that do not entail structural rearrangements. Complementarily, the graph representation of an interaction allows to understand the functional interaction and correlation between any two sites in a protein without the need for a structural explanation.
A second advantage of the presented method concerns the identification of binding residues. Reliable determination of interaction sites is a main feature of the graph analysis—even if the observed effects are not all present within the same NMR observable. Through this, also very diffuse data can be analyzed with high precision and details may be revealed that might remain unnoticed by means of conventional data analysis. At the examples of the Calmodulin/Ca2+ and the cold shock protein A/coldbox RNA interaction we show how our method—in agreement with crystallographic studies—allows for the accurate determination of multiple binding sites for multiple ligand molecules.
Results
Introduction to the analyzed protein interactions
Figure 1(A) displays adjacency matrices for six different protein interactions: Myc/BRCA1,4 OPN/Heparin,5 BASP1/CaM,6 CaM/Ca2+,7 YqcA/Flavin mononucleotide (FMN), CspA/coldbox RNA (CB-RNA).8 The graph theoretical treatment of the OPN–Heparin interaction was explained in part one of this contribution. Similarly, the construction, validation, and analysis of the five further matrices is demonstrated here in Supporting Information. The diagonal elements of the matrices in Figure 1 represent the nodes of a network or graph. Each node is associated with one residue of the protein whose interaction is investigated. Hence, the dimension of each adjacency matrix corresponds to the length of the primary sequence of the underlying protein. Non-zero off-diagonal elements indicate an edge between two nodes of the depicted network. These elements represent functional correlations between the two amino acids that they connect. These correlations were derived from coinciding changes in the measured NMR parameters of two residues (ΔCS(1HN), ΔCS(15N), ΔR2, and Δη) due to an interaction with a ligand molecule. (See part one of this contribution for a detailed description of this derivation.) Thus, the adjacency matrices in Figure 1(A) represents the particularities of the different protein binding events; that is, the functional correlations between protein residues in the different interactions named above. As will be shown below, these matrices are all constituted by a similar architecture indicating that the functional constitutions of the here investigated protein interactions have a common motif. This finding might shed some light on protein structure–function relationships.

(a) Adjacency matrices of the six investigated protein interactions as indicated on top of each matrix. The red dots indicate residues with the highest node degree. The binding sites for the respective ligands are indicated as a/b/c on the bottom of each matrix. For the Myc–BRCA1 interaction the position of the b/H1/L/H2/Zip motif is given. For the BASP1–CaM interaction details on the binding site are not available. (b) The adjacency matrices in (a) ordered by the node degree.
Yet, not only functional correlations behind a protein–ligand interaction are revealed through the adjacency matrices, but also complicated interaction patterns involving multiple ligands and binding sites are readily indicated (see part one of this contribution for a detailed explanation of the analysis of the adjacency matrices). These analyses would be cumbersome by conventional means as particular details of an interaction are frequently not represented in a single observable. In contrast, the here presented approach unifies different NMR observable in a single matrix, which renders the determination of a broader picture of the binding event possible.
While the OPN/Heparin interaction was introduced in part one of this contribution, the other five interactions are briefly characterized in the following:
Myc/BRCA1
The interaction between the proto-oncogenic transcription factor Myc and the breast cancer susceptibility protein 1 (BRCA1) is central to the regulation of cell proliferation in human tissues. Despite being characterized as an IDP,9 Wang et al. found that apo-Myc binds to BRCA1 via a “preformed,” that is, transiently sampled10 helix–loop–helix–Leucine zipper (HLH/LZ) motif localized between aa 364 and 411 of full-length Myc (our construct contains aa 310–440 of viral Myc). The HLH/LZ motif of Myc is fully developed only in its holo-state, that is to say, in the complex with the transcription factor MAX (Myc associated factor X). Here we investigate the binding of apo-Myc (the IDP without MAX) to a 285 aa long fragment of BRCA1 (aa 219–504 of full-length human BRCA1). This BRCA1 fragment contains a Myc binding motif, which was previously localized between aa 433 and 511 by means of GST pull-down assays.10
BASP1/CaM
The brain acid soluble protein 1 (BASP1) is a natively unfolded tumor suppressor lacking any significant secondary structure elements. Furthermore, it is involved in neurite outgrowth.6 It is well known that BASP1 binds holo-Calmodulin (CaM; Ca2+ loaded) at its N-terminus. The latter is myristoylated to a high degree in vivo.6 We investigate this interaction for the full length human BASP1 comprising 226 aa.
CaM/Ca2+
Calmodulin (CaM) is a messenger protein expressed in all eukaryotic life forms. It consists of two almost symmetric lobes. To adopt its functional holo-state it employs Calcium as a cofactor. Each of the two lobes of CaM binds two Ca2+ ions. Here we investigate data from the C-lobe of CaM (aa 78–148 of full length CaM), which interacts with two Ca2+ ions. The here investigated data were obtained from the work by Wang et al.7 The two binding sites for the Ca2+ ions on the CaM C-lobe are localized around aa 90–100 and 130–140. Due to the Calcium binding the quite flexible apo-form transforms into a rigid holo-state, which is readily crystallizable to reveal the structural peculiarities of Ca2+ the binding sites.
YqcA/FMN
YqcA is a Flavodoxin that non-covalently binds flavin mononucleotides (FMN). The functional holo-state acts as a redox center in electron transfer reactions. Flavodoxins are quite abundant in prokaryotes. Their function is probably best known for photosynthesis. We employ here data from the work by Ye and co-workers.11 They localized the FMN binding pockets of YqcA to aa 9–14, 57–68, and 94–101.
CspA/CB-RNA
The major cold shock protein A of Escherichia coli (CspA) binds to a special RNA sequence, the so-called cold-box (CB) motif. Through this it acts as a chaperone aiding nucleic acid folding at low temperatures.8, 12 CspA consists of a stably folded β-barrel structure. It is well known that surface exposed aromatic amino acid side-chains are distributed along the entire primary sequence. They act as anchor points for CB RNA on the lateral surface of the β-barrel8, 12 by intercalating between the base stacks of the RNA. For the present purpose we determined changes in residue resolved NMR parameters upon binding of CspA to a 23 bases long RNA fragment containing the CB motif.12 Newkirk et al. identified patches around aa 14–20, 30–45, and 50–65 to be important for RNA binding.7
Common features of protein interactions
The particularities of the five above introduced binding motives (as well as that of the OPN/Heparin interaction introduced in part 1 of this contribution) are represented by the associated adjacency matrices in Figure 1(A). Patches of densely packed edges around the diagonal elements of each protein indicate important sites in the different binding processes. All of the ligand binding sites mentioned in the previous section can be distinguished in the matrices in Figure 1(A) via these patches of densely packed edges; additionally, several correlations between different sites in a protein can be identified. The most correlated nodes/residues in each interaction with the highest degree, δ, are indicated in Figure 1(A) together with the documented binding sites. (δ corresponds to the node degree as defined in part one of this contribution. Likewise, W corresponds to the eigenvector centrality and C to the local clustering coefficient.) Note that the most correlated residues—as identified by our method—are lying within the interaction sites for the respective ligands in each case. Even multiple binding sites are identified. For the CspA-CB RNA interaction we find that one of the three binding sites (between aa 14 and 20) contains residues that distinguish themselves through a very high δ. This binding site is likely to be the primary binding site, while the other interactions sites might act stabilizing on the ligand interaction. This aspect will be investigated in more detail below.
Yet, a detailed analysis of all these matrices and the underlying interactions are beyond the scope of this article. Instead we want to focus on a common feature of the graphs/networks represented by these matrices.
In Figure 1(B) the six adjacency matrices for the six different protein interactions are shown in an alternative representation. The nodes are not ordered according to the amino acid primary sequence of the underlying proteins (recall that every node in the graph, i.e., every diagonal element of the matrices in Figure 1 represents a residue of a protein). Instead they are ordered by an increasing node degree, that is, by an increasing number of edges/connections per node. Note that this change in representation does not alter the actual architecture of the network/graph that is depicted by the adjacency matrices. While the matrices sorted by the primary protein sequence emphasize the structural peculiarities of each binding event, the matrices sorted by the node degree highlight a different aspect of the protein interactions. These matrices display a common architecture, that is, the edges are densely clustered in one single “hub.” The notion of a “hub” shell emphasize that all residues are connected to a cluster of residues that correspond to the functional core of the correlation network. The hub should not be mistaken as a single residue that is mediating the interaction between other residues. This would interfere with the idea of multiple binding sites.
The structure of the correlation network is peculiar also due to a second aspect. The nodes with the largest degree are connected to all other nodes. At the same time the residues at the bottom right of each matrix in Figure 1(b) become less connected as one moves away from this center of most connected residues. This means we may consider the nodes with the largest degree as the functional centers of the networks/graphs. This network configuration is reflected in a “triangular” agglomerate of nodes in the bottom right corner of the adjacency matrices in Figure 1(b). It is important to note that the network hub, the central cluster of residues, of the network is connected to all other residues with δ > 0, that is, these amino acids are correlated with all other residues that participate in the interaction. This center may further be regarded as the “hotspot” of the protein interaction. Most importantly, there is only one single cluster of residues visible in all the adjacency matrices independent of the number of binding sites or affected sites of a particular interaction: There is a single binding site for CaM on BASP1, but three binding sites for FMN on YqcA. Yet, in all cases we observe a single hotspot of these interaction in their respective network representations. This means that the functional architecture of a protein interaction is constituted by a single—not structural, but functional—motif, although its structural or spatial constitution might involve multiple binding or affected sites. In other words, spatially separate functional sites are nevertheless correlated via a single “hotspot” in the associated network representation. This is true for all the interactions studied here.
This finding might aid to understand modern theories of allostery. Hilser and co-workers13, 14 describe allosteric interactions in a thermodynamic model to avoid the conflicting view of structural bonds mediating “interactions at a distance.” In this model the binding event of an allosteric agent is energetically coupled to the ligand binding site. This allows for an explanation of the communication between the allosteric site and another ligand binding epitope anywhere in a molecule without the need for structural relations (allostery can take place without structural adaptions). The single-hub architecture of functional correlations shown in Figure 1(b) allows for communication between any two sites in a molecule that are involved in an interaction. The functional architecture of a protein discovered here is, hence, in excellent agreement with the allosteric model proposed by Hilser as it allows for communication between sites in a protein without the need for a structural explication. In other words, as novel allosteric models propose that functionally dissimilar proteins can share a common thermodynamic architecture, we here propose that these proteins share additionally a functionally common architecture.
This common pattern of correlation networks in protein interactions is found here for IDPs (Myc, OPN, BASP1) as well as for folded proteins (CaM, YqcA, CspA). Furthermore, the correlation networks exhibit the same architecture for different types of ligand molecules like the nucleic acid oligomer CB-RNA, the IDP BRCA1, the small molecule FMN and the organic polymer Heparin.
Moreover, this variety of ligands and proteins entails entirely different binding modes:
Considering IDPs, it was found that Heparin binds to OPN in a largely disordered fashion.5 The same is true for BRCA1 binding to Myc.4 The formed complexes display large motional freedom. In contrast, two precisely defined binding pockets for Ca2+ are documented for CaM as well as a single well-structured pocket for FMN in YqcA. In the case of CspA surface-exposed aromatic side chains that are distributed along the entire primary sequence intercalate into the RNA backbone. Yet, despite the significant structural and dynamic differences between the abovementioned interactions, the network representation (the functional correlations underlying the interactions) is always based on the same principle involving only one single strongly correlated hub of residues.
To visualize that the configuration of the matrices in Figure 1(B) is not a trivial consequence of any protein interaction alternative configurations are shown in the Supporting Information. The alternatives contain two uncorrelated interaction sites of different size and a node agglomerate without a “hub”-configuration. The single hub configuration with monotonously decreasing node degree is, thus, not a necessary outcome of a non-random interaction, although one node with the highest degree will always be found in any network. It is hence not a trivial finding that all the matrices in Figure 1(b) display the same “triangular” agglomerate of nodes.
In Figure 1(A) the nodes with the highest degree are indicated (red dots) for each of the here studied interactions. As mentioned above these are always located within a binding site. Taking the finding of similar hub architecture [cf. Fig. 1(B)] into account it can be deduced that these residues indicate the central spots of the interaction network. They thus indicate the functional centers of the different interactions. However, we want to emphasize that there are no single residues that constitute the “hub” or “hotspot” of an interaction. Instead, we find clusters of residues that are interconnected in a way that they constitute a single-hub architecture of the network. Thus, the hub of the functional network does not necessarily correspond to a single point in the primary sequence, but embraces several residues or patches of it that constitute the functional core of the protein interaction.
While the global (“triangular”) architecture of the matrices in Figure 1(B) remains similar for all here studied interactions, the degree density of the matrices varies. That is, the density of edges in the agglomerates in the bottom right corner of each matrix alters. This observation can be traced back to the fact that every of the studied binding events has its own particularities. In other words, while the particularities of the individual protein interactions may differ from case to case, the global functional architecture remains constant.
It is important to note that the matrices in Figure 1(B) display a high degree of order. This indicates a significant difference between the correlation networks found for protein interactions and (hypothetic) networks for random contacts between a protein and another molecule. The latter would display a homogeneous distribution of edges independent of the order of the nodes. The clustering of highly interconnected nodes, that is, the accumulation of edges in a single hub is not a general feature of a graph. Contrary, it renders protein interactions quite different from random. In other words, residues that are affected in a protein interaction are functionally interconnected among each other and centered around a single “hotspot” of the underlying process. This is not the case for a random event. In contrast, for a random interaction one would find a more homogeneous distribution of edges and a corresponding homogeneous distribution of W, δ, and C. This is exemplarily shown in Supporting Information.
Concluding, the nature of the network describing the functional correlations of a protein interaction appears to be always based on a common principle, independent of the particularities of the interaction and its structural and dynamical appearance. This finding might shed new light on protein structure-function relationships.
Analyses of protein interactions with respect to their molecular structures
In the following we will analyze selected properties of the graphs of the protein interactions and highlight interesting findings with respect to available crystal structures.
Binding sites for Ca2+ on CaM
Figure 2 shows residue plots of the eigenvector centrality, W, degree sequence, δ, and local clustering coefficient, C, for the CaM/Ca2+ interaction (cf. the related matrix in Fig. 1). All three parameters, W, δ and C, indicate (through increased values around these sites) that the Ca2+ binding sites can be localized roughly around aa 90–105 and 125–145. This is in agreement with earlier studies mapping the Calcium binding epitopes.7 For the case at hand we find nodes with very high δ (the central residues of the functional network) in both binding sites as indicated in Figure 1(A). The of residues around aa 100 is especially high. This is likely a consequence of the structural dissimilarities of the two binding sites. Most importantly, the residues identified as having the highest δ are in direct contact with the Ca2+ ions in the crystal structure of the CaM–Ca2+ complex exemplifying the applicability of the graph analysis for identification of multiple binding sites. The Supporting Information contains a graphical display of these contacts.
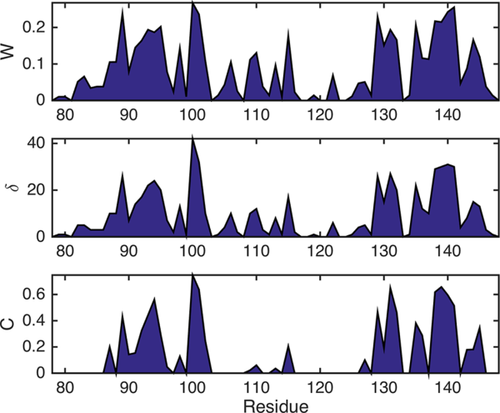
Connectivity and centrality measures W, δ, and C (see part 1 of this contribution for the definition of these parameters) corresponding to the matrix labeled CaM/Ca2+ in Figure 1.
Note that δ and W additionally highlight residues between aa 110 and 120. From earlier studies it is known that this site (central linker domain between the two Ca2+ binding sites) is subject to an allosterically induced restructuring due to the Calcium binding event.15 Thus, it is likely that the elevated values for W and δ observed between aa 110 and 120 are a consequence of this process.
Figure 3 shows the crystal structure of the CaM–Ca2+ complex (C-lobe).15 The Ca2+ binding sites, as determined from our method via elevated local clustering coefficient, C, are highlighted red (around aa 90–105 and 125–145). They indicate the Ca2+ binding epitopes in the crystal structure showing that our analysis allows to mark these sites precisely.
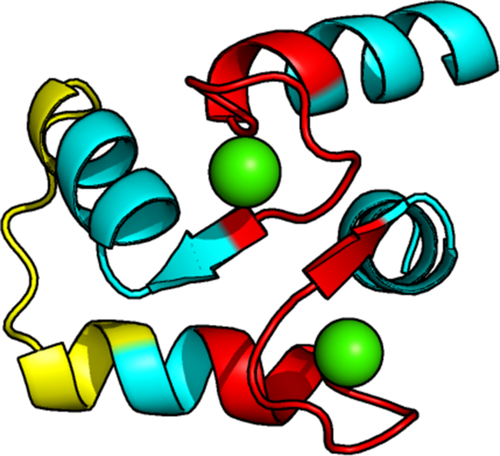
Crystal structure of the CaM C-lobe bound to two Ca2+ ions (green). The regions colored in red correspond to the two binding sites indicated by high C in Figure 2. The linker domain, indicated via high W but low C in Figure 2, is shown in yellow. (PDB code: 3CLN).
Recall that the determination of a binding site via W, δ, and C is possible since residues of a protein that are affected by a ligand show correlations among each other, hence, a large degree and centrality of these residues will be observed as well as strong edge clustering in their graph-theoretical neighborhood. A large C value, hence, indicates a strong functional connectedness of an underlying residue, which is typical for a binding site. (See part one of this contribution for a more detailed explanation.) The same argument holds for allosterically affected sites.
Binding of CB-RNA to CspA
Figure 4 shows the centrality and connectivity measures, W, δ, and C for the CspA/CB-RNA interaction (cf., the associated matrix in Fig. 1). The residues showing high W, δ, and C values are more diffusely distributed along the primary sequence than in the case of the CaM/Ca2+ interaction. Residues around aa 14–20, 30–45, and 50–65 appear to be important for the RNA binding as indicated by the elevated local clustering coefficient, C. This distribution of strongly correlated residues along the primary sequence can be expected, since the RNA binding aromatic side-chains are also distributed along the entire protein. In Figure 4 (bottom) the aromatic amino acids are indicated by red arrows. All of these positions, which constitute the RNA binding anchor points of CspA, are subject to large C-values. Yet, more residues than just the aromatic ones take part in the interaction as judged from the local clustering coefficient. Taking into account the three binding epitopes mapped earlier by Newkirk et al.8 (green bars in Fig. 4) we find that the residues showing elevated C are in excellent agreement with these three sites.
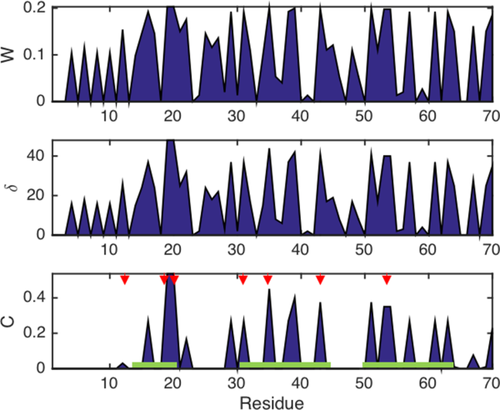
Connectivity and centrality measures W, δ, and C corresponding to the matrix labeled CspA/CB-RNA in Figure 1. The red arrows indicate the positions of the aromatic side chains of CspA. The green bars indicate the RNA binding sites found by Newkirk et al.8
Figure 5 shows the crystal structure of CspA.16 Residues associated with a large C are highlighted in blue. The RNA binding interface is clearly visible on the lateral surface of the β-barrel. It includes all aromatic side chains of the protein. Hence, while the W, δ, and C appear disordered in the residue plots, they in fact indicate the RNA binding epitope of CspA.
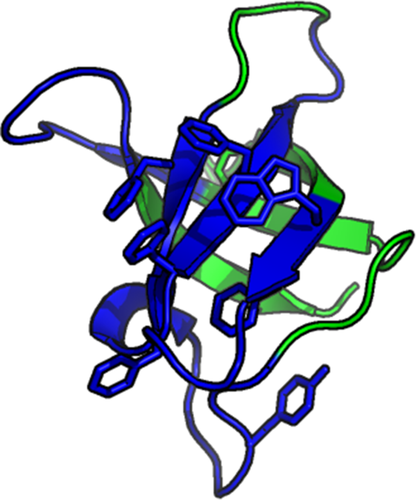
Crystal structure of CspA. Residues with elevated C in Figure 4 are highlighted in blue. (PDB code: 1JMC).
Note that the central residues of the correlation network of this interaction (with the highest δ) are located exclusively around aa 20 of the primary sequence [cf. Fig. 1(A)], although the local clustering coefficient, C, correctly identifies the aromatic residues distributed along the entire primary sequence. This indicates that the binding site around aa 14–20 might constitute the primary binding epitope and the anchor point for the CspA–CB RNA interaction, while the other binding sites might act as secondary interactions sites that stabilize the RNA interaction. This is in excellent agreement with earlier mutational studies that show that the aromatic side chains around aa 20 are most crucial for the CspA–nucleic acid interaction.17
Identification of binding epitopes from ambiguous data
In Figure 6 residue plots of the four normalized NMR parameters ΔCS(1HN)*, ΔCS(15N)*, Δ
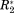 , and Δη* are shown for the CaM/Ca2+ and CspA/CB–RNA interactions. A visual inspection of these data sets is complicated by the fact that residues along the whole primary sequence of the proteins are likewise affected by the respective interactions. Moreover, it is difficult to distinguish the binding residues since the elevated differential values for a binding/affected site are not found within the same NMR observable.
, and Δη* are shown for the CaM/Ca2+ and CspA/CB–RNA interactions. A visual inspection of these data sets is complicated by the fact that residues along the whole primary sequence of the proteins are likewise affected by the respective interactions. Moreover, it is difficult to distinguish the binding residues since the elevated differential values for a binding/affected site are not found within the same NMR observable.
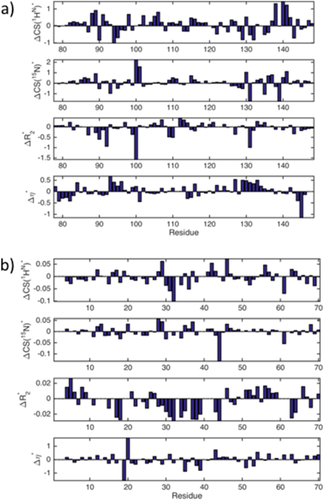
(a) ΔCS(1HN)*, ΔCS(15N)*, Δ
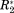 , and Δη* for the CaM/Ca2+ interaction. (b) ΔCS(1HN)*, ΔCS(15N)*, Δ
, and Δη* for the CaM/Ca2+ interaction. (b) ΔCS(1HN)*, ΔCS(15N)*, Δ
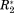 , and Δη* for the CspA/CB–RNA interaction.
, and Δη* for the CspA/CB–RNA interaction.
Thus, the binding epitopes can hardly be determined by a visual inspection of these data. In contrast, as demonstrated above, the analysis of the local clustering coefficients associated with the graph representation of these interactions allows for precise determination of the binding sites of the respective ligands. This is possible since the construction of the graph representation is based on the derivation of the correlation pattern that underlies all four NMR parameters. Hence, the correlations found via a graph analysis contain information of all the different NMR experiments, which yield ΔCS(1HN)*, ΔCS(15N)*, Δ
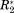 , and Δη*. These correlations represent the functional particularities of the unique structural ensemble of a protein–ligand complex and, hence, indicate the sites that are important for this interaction.
, and Δη*. These correlations represent the functional particularities of the unique structural ensemble of a protein–ligand complex and, hence, indicate the sites that are important for this interaction.
Discussion
The methodology presented here constitutes a versatile tool for the analysis of protein interactions. It allows for precise determination of ligand binding sites of a protein. This is possible even for data sets that appear ambiguous and challenging to analyze by visual inspection. Furthermore, the graph analysis allows for quantification of functional correlations between residues in terms of number of connections per residue, density of correlations and centrality of a node to a network.
Interestingly, we find that the networks of correlations of all here investigated examples of protein interactions are always constituted by the same architecture. That is, all the derived graphs are based on a single hub of densely correlated nodes. This hub exhibits a decreasing edge degree as one moves away from its center. This special architecture of the network of correlations between residues in a protein is found independent of the structural and dynamical peculiarities of the different protein interactions. One might speculate that this is a widespread feature of protein interactions. In this case this finding might help to understand the general principles behind structure–function relationship between proteins and their ligands.
Material and Methods
BRCA1 preparation
BRCA1 was subcloned into a Pet52b expression vector and transformed into E. coli Rosetta pLysS cells. Cells were grown at 37°C in LB and induced at an OD600 of 0.8 with 0.5 mM IPTG for 3 h. Cell pellets were lysed by sonication in 25 mM Tris, 100 mM NaCl, and 1 mM β-mercaptoethanol. For protein purification histidine and StrepTactin affinity chromatography were applied.
Myc preparation
Myc (b/H1LH2/LZ fragment) was expressed as published earlier.9, 18
Calmodulin preparation
For the expression of unlabeled calmodulin, the vector pETM11 with a cleavable His6-tag and a TEV cleavage site was used. Expression was done in E. coli strain T7. About 10 mL of an overnight culture in LB is added to 1 L of LB at 37°C. The expression is induced at an OD600 of 0.6–0.8 by adding 0.8 mM IPTG. Expression was carried out overnight (∼16 h) at 30°C. The cell pellet (after centrifugation at 5000 rpm for 15min) was resuspended using PBS containing 0.5mM EDTA and complete Mini protease inhibitor (Roche). Breaking the cells is done by sonication (3 min of 50% amplitude) and the supernatant after centrifugation at 18,000 rpm for 20 min was pressed through a 0.45 μm filter before loading it on a Ni2+-loaded HiTrap 5 mL affinity column (GE healthcare). After a washing step with PBS containing 1.5M NaCl, the protein was eluted using 100% HI-PBS (∼1–2 column volumes). The fractions containing the protein were concentrated using an Amnicon Ultra-15 centrifugal filter device 3000 NMWL to get an end volume of 1 mL. The sample was put on a shaker at 4°C overnight with 1 mg TEV protease for 50 mg protein added to the sample for an efficient cleavage of the tag. After cleavage, the sample was loaded on a column HiLoad16/60 to get rid of the tag. The protein concentration was measured by A (280 nm). Calmodulin is dialyzed into the same buffer as BASP1 for the NMR measurements (Bis Tris pH 6.0 containing 0.5 mM EDTA).
BASP1 preparation
BASP1 was expressed as published earlier.19
NGAL preparation
NGAL was expressed as published earlier.20
NMR measurements
NMR spectra were recorded at 25°C on Varian spectrometers operating at 600 and 800 MHz. Spectra were recorded in the PFG sensitivity-enhanced mode for quadrature detection in the 15N indirect dimension with carrier frequencies for 1HN and 15N of 4.73 and 120 ppm, respectively.
The 15N transverse relaxations experiments for evaluating T2 were performed with Carr Purcell Meiboom Gill (CPMG) delays of 0, 16, 32, 64, 128, 192, and 256 ms using a CPMG duty cycle delay of 0.5 ms.
Heteronuclear steady-state NOE 15N{1HN} attenuation factors were derived from the INOE/IREF ratio, where INOE and IREF denote the peak intensities in the experiments with and without proton saturation, respectively. In the case of spectra without presaturation, a net relaxation delay of 5 s was employed whereas a relaxation delay of 2 s prior to a 3 s proton presaturation period was applied for the NOE spectra.
NMR spectra were processed and analyzed with NMRPipe21 and SPARKY. A squared and 60° phase-shifted sine bell window function was applied in all dimensions for apodization. Time domain data were zero-filled to twice the data set size, prior to Fourier transformation.
Calculations
All calculations were performed with home-written scripts employing the MATLAB 2015 and Python 3 program packages.
Acknowledgment
The authors thank the Professors Robert Konrat and Geoffrey Bodenhausen for their support and meaningful discussions.




