Optimization approaches are important to design sustainable structures. In structural mechanics, different design objectives can be defined, for example, to minimize the required construction material or to maximize the structural durability. In this paper, the durability of a reinforced concrete (RC) structure is assessed by advanced finite element (FE) models to simulate the cracking behavior and the chloride transport process. The corrosion initiation time is used as durability measure to be maximized within an optimization approach, where the concrete cover is defined as design variable. The variability of structural loads and material parameters and unavoidable construction imprecision leads to a probabilistic reliability and durability assessment, where aleatory as well as epistemic uncertainties are quantified by random variables, intervals and probability-boxes. The FE simulation models cannot directly be applied to structural analyses and optimizations with polymorphic uncertain parameters and design variables because of the high computational demand of the multi-loop algorithm (Monte Carlo simulation, interval analysis, global optimization). In this paper, a new surrogate modeling strategy is presented, where artificial neural networks are trained sequentially to speed-up the coupled mechanical and transport simulation FE models. The new approach is applied to the uncertainty quantification and the structural durability optimization of a RC structure.

1 INTRODUCTION

Reinforced concrete (RC) structures are vulnerable to reinforcement corrosion especially in marine environments due to high chloride exposure. Chloride ions are transported with the moisture through the concrete. If a critical chloride ion concentration reaches the reinforcement, the corrosion process is initiated. The chloride ion transport is accelerated in case of larger cracks. According to the classical design guidelines, the concrete cover has to be selected according to the specific exposure class, which means that a thicker concrete cover is required, if moisture or chloride is expected to attack the concrete. However, a thicker concrete cover will result in larger cracks assuming the same area of reinforcement and the same dimensions of the RC structure. Therefore, it is important to optimize the concrete cover, which is realized in this paper by maximizing the corrosion initiation time considering aleatory and epistemic uncertainties of structural parameters.

Two independent finite element (FE) models are used to simulate the cracking and the subsequent chloride transport process. The first FE model is applied to compute the tensile cracking of a RC beam under mechanical loading. The second FE model calculates the coupled moisture and chloride transport within the most relevant crack to determine the corrosion initiation time.

The strategy of independent models is also tested for the surrogate modeling, which is realized by artificial neural networks (ANN) in this paper. Instead of training a global surrogate model to solve the optimization problem, also separate and partially nested surrogate models for the mechanical FE model and for the transport FE model are investigated.

2 POLYMORPHIC UNCERTAINTY QUANTIFICATION

Within the polymorphic uncertainty quantification concept, stochastic and non-stochastic uncertainty models are combined. Here, random variables and intervals are used to quantify uncertain parameters of a structural model. This leads to probability boxes (p-boxes) of the resulting quantities of interest, which have to be computed by a nested interval and stochastic analyses of the structural model.

A random variable A is defined by a stochastic distribution functions, for example, lognormal distribution or Gaussian distribution, which is represented by a probability density function (PDF) $f(a)$ and the corresponding cumulative distribution function (CDF) $F(a)$ .

An interval

\overline{d}

is defined by a range

\begin{equation} \overline{d}=[{}_{l}d,\;{}_{u}d] \;, \end{equation}

(1)

with a lower bound

{}_{l}d

and an upper bound

{}_{u}d

. In this paper, also the midpoint-radius-representation of an interval is used, where the midpoint is

\begin{equation} {}_{m}d=\frac{1}{2}\cdot {\left({}_{l}d+{}_{u}d\right)} \;, \end{equation}

(2)

and the radius is given by

\begin{equation} {}_{r}d=\frac{1}{2}\cdot {\left({}_{u}d-{}_{l}d\right)} \;. \end{equation}

(3)

A p-box $\overline{Z}$ is defined as an imprecise random variable with a lower bound CDF ${}_{l}F(z)$ and an upper bound CDF ${}_{u}F(z)$ . Here, free p-boxes according to [1] are used, where the lower and upper bound CDFs are represented by empirical distributions obtained from Monte Carlo simulations.

3 OPTIMIZATION WITH POLYMORPHIC UNCERTAIN PARAMETERS

In a strict sense, an optimization problem with uncertain parameters does not lead to a crisp optimum. The inherent variability and imprecision have to be modeled to enable the numerical treatment. In order to mathematically solve an optimization problem with polymorphic uncertain parameters, it has to be transformed into a quantified representation of the problem using corresponding uncertainty measures for random variables and intervals. In this paper, the optimization problem contains an interval design variable $\overline{d}$ (imprecise position of the reinforcement layer, that is, the concrete cover, with a fixed interval radius ${}_{r}d$ and an interval midpoint ${}_{m}d$ to be optimized) and two stochastic a priori parameters A₁ (structural load) and A₂ (modulus of elasticity) defined as random variables. This leads to a p-box of the quantity of interest (corrosion initiation time) to be maximized. Here, the uncertain optimization problem is represented by maximizing the lower bound (worst case) of the interval mean value of the quantity of interest $\text{max:}\;\lbrace {}_{l}\mu ({t}) \rbrace$ .

The described optimization problem with polymorphic uncertain parameters is solved by a four level algorithm. A deterministic structural model is computed at the first level. To consider the randomness of structural parameters, a stochastic analysis using Monte Carlo simulation is applied at level two of the algorithm. At level three, an interval analysis is performed. Because of the monotonicity of the models used in this paper, the interval analysis is solved just by analyzing the lower and upper interval bounds of the stochastic quantities of interest, for example, the lower bounds of the mean values. Finally, at level four, a particle swarm optimization algorithm [2] is applied to solve the optimization problem, see [3] for further details.

Because of the four level algorithm, a high number of deterministic structural simulations is necessary to solve the optimization problem, which is very time consuming or almost not possible in case of detailed FE simulation models. This means that the FE models have to be replaced by numerically efficient surrogate models, see for example [4].

4 ARTIFICIAL NEURAL NETWORK SURROGATE MODELS

In this paper, neural networks with feedforward architecture are used as surrogate models. They consist of an input layer, a number of hidden layers and an output layer. In the fully connected ANNs, the neurons of each layer are connected to all neurons of the previous layer. Here, several ANNs are generated for different models to be approximated (mechanical FE model, transport FE model and global surrogate model). The corresponding number of input and output neurons is defined by the problem to be solved. The number of hidden layers and hidden neurons is selected by trial and error according to the complexity of the mapping problem.

Within feedforward ANNs, the signals are processed layer by layer through the network. The signal

x^{(m)}_i

of neuron i in layer m is computed by

\begin{equation} x^{{\left(m\right)}}_i=\varphi ^{{\left(m\right)}}_i {\left(\nu ^{{\left(m\right)}}_i \right)} = \varphi ^{{\left(m\right)}}_i {\left(\sum _{h=1}^{H}{\left[ x^{{\left(m-1\right)}}_h\cdot w^{{\left(m\right)}}_{ih}\right]}+b^{{\left(m\right)}}_i\right)} \;, \end{equation}

(4)

where

\varphi ^{(m)}_i(.)

is the activation function. The hyperbolic tangent function is used in the hidden neurons and the linear activation function is applied to the output neurons. The argument

\nu ^{(m)}_i

of the activation function contains the sum of all

h = 1, \ldots, H

output signals

x^{(m-1)}_h

of the previous layer

(m-1)

multiplied by the corresponding synaptic weights

w^{(m)}_{ih}

and an added bias value

b^{(m)}_i

The weights and bias values of the ANN are identified during the network training, which is done by the Levenberg-Marquardt algorithm here. It should be noted, that a sufficient number of training, validation, and testing data are required to get a good approximation performance and to avoid overfitting. To produce these data, a mix of Latin hypercube sampling (for the concrete cover and the modulus of elasticity) and a regular grid (for the loading, which is increased incrementally in the FE model for each realization of the concrete cover and the modulus of elasticity) is applied.

5 OPTIMIZATION OF THE CONCRETE COVER OF A RC BEAM

5.1 Structural model and uncertain parameters

As an example for the maximization of the structural durability, a RC beam is investigated. The structure and the cross section with the reinforcement of a simply supported RC beam is shown in Figure 1.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

RC beam structure.

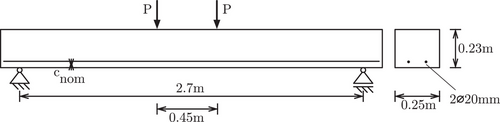
The beam is stressed with two single loads P, which are acting as fully correlated random variables to the structure. The a priori uncertain load parameter P is assumed as a random variable having a Gaussian distribution with a varying mean value $\mu (P_i)$ and a variance of ${\sigma (P) = 5\,}$ kN. The range of the mean value $\mu (P_i)$ is between 20 and 40kN with a discretization of 1kN, that is, $i=21$ cases of the varying mean value $\mu (P_i)$ are investigated. The second a priori uncertain parameter is the Young's modulus E, which is quantified as log-normal distributed random variable with a mean value of $\mu (E)= 34$ GPa and a variance of $\sigma (E) = 1.8$ GPa. All other concrete material parameters (tensile and compressive strength, fracture energy, porosity and crack tortuosity) are assumed to be fully correlated with the uncertain Young's modulus E.

The concrete cover $\bar{c}_{\mathrm{nom}}$ is defined as an interval design variable, with interval midpoint ${}_{m}c_{\mathrm{nom}}$ to be optimized an a fixed interval radius ${}_{r}c_{\mathrm{nom}}=5$ mm. This allows one to consider production imprecision of the RC beam within the design process.

In order to maximize the structural durability, the corrosion initiation time t is used as quantity of interest to be maximized. Because of the combination of two a priori random variables (P and E) and one interval design variable $\bar{c}_{\mathrm{nom}}$ , the resulting corrosion initiation time is quantified as a p-box $\bar{F}_{t}$ . Here, the worst case mean value, that is, the lower bound of the interval mean value ${}_{l}\mu (t)$ , of the corrosion initiation time is used as surrogate objective to be maximized.

To compute the corrosion initiation time, the crack pattern of the structure is required, which is influencing the moisture and chloride transport within the structure. In general, this would need a time consuming coupled FE simulation (mechanical model to compute the crack pattern and moisture and chloride transport model to compute the corrosion initiation time). Here, the problem is simplified by first computing the crack pattern of the structure with a 2D mechanical FE model, select the crack widths and the corresponding crack lengths of the maximal crack and finally compute the corrosion initiation time with a 1D FE transport model.

The crack patterns are computed by a 2D FE simulation model using zero-thickness cohesive interface elements [5, 6], which are inserted between linear-elastic finite triangular elements. At each Gauss point of the interface elements, the fracture behavior of plain concrete is modeled by a nonlinear traction-separation law. The reinforcement of the beam is modeled by discrete independent embedded rebar elements (geometrically linear truss elements), which are connected to the concrete elements by a bond-slip-law according to the fib Model Code 1990 [7].

The corrosion initiation time is computed by a coupled moisture and chloride transport model assuming an unsaturated, cracked concrete. The chloride ions are transported by a combination of diffusion and advection according to

\begin{equation} \dfrac{\partial (\theta \,c)}{\partial t} - \dfrac{\partial}{\partial x}\Biggl (\underbrace{\theta \,D_c\frac{\partial c}{\partial x}}_{\rm{diffusion}} +\underbrace{{c\,D_\theta \frac{\partial \theta}{\partial x}}}_{\text{advection}}\Biggr) = 0. \end{equation}

(5)

In Equation (5), θ is the volume fraction of the water content and c is the chloride concentration of the species in solution. The parameters

D_{\theta}

and

D_c

are the moisture and chloride diffusion coefficients, respectively, which both are depending on the crack width, the crack length and the concrete porosity (assumed to be correlated with the Young's modulus E), see for example [8-10]. This means that the results of the mechanical FE model (crack width and crack length) are required as input of the transport FE model to quantify the diffusion coefficients

D_{\theta}

and

D_c

and finally to compute the corrosion initiation time, which is defined as the point in time, when the chloride concentration at the reinforcement reaches a critical value of

C_{crit} = 0.6

% by mass of binder according to [11].

With respect to the optimization problem to be solved, the mechanical FE model has three varying inputs (P, c_nom, and E) and two output parameters (crack width w_cr and crack length l_cr). The transport FE model has four varying inputs (E, c_nom, w_cr and l_cr) and one output parameter (corrosion initiation time t).

5.2 ANN surrogate models for crack width and crack length

The FE simulation models are approximated by surrogate ANN models. Here, ANNs with feedforward architecture are used. In total, 48 000 FE simulation result samples are considered, of which 80% are used for training 15% for validation and 5% for testing, respectively.

First, the approximation of the mechanical model is investigated. To map the three varying input parameters (P, E, and c_nom) onto the two output parameters (w_cr and l_cr), either one ANN with two outputs or two ANNs with one output can be created. In Figure 2, the ANN surrogate model architecture with two outputs is shown together with the correlation plots (FE result vs. ANN prediction) for both outputs. The other option, that is, two separately trained ANNs with one output is visualized in Figure 3 together with the correlation plots. Whereas the crack length is approximated in a similar quality for both options, the crack width is predicted better by the independent ANN.

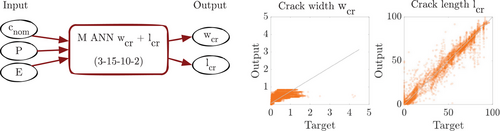
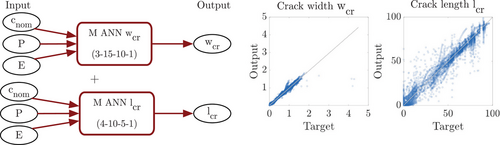
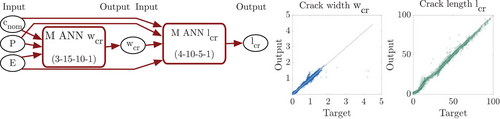
To further improve the crack length approximation, a third option is investigated, where two nested ANNs are trained sequentially. Both ANNs have one output, but the crack width predicted by the first ANN is used as an additional input of the second ANN for the crack length prediction, see Figure 4. As the results of the third option are the best, this ANN surrogate modeling strategy is used for the coupling with the moisture transport surrogate model.

5.3 ANN surrogate models for corrosion initiation time

For the transport FE model, the crack widths and the crack lengths calculated by the mechanical FE model are required as input parameters. In order to approximate the coupled FE models, which are used to finally compute the corrosion initiation time, a global surrogate model can be created, where the samples are obtained by running the mechanical FE model and the transport FE model sequentially, that is, with the same set of input parameters. The resulting global ANN is shown in Figure 5. Based on the correlation plot, it can be seen, that a good approximation quality is achieved.

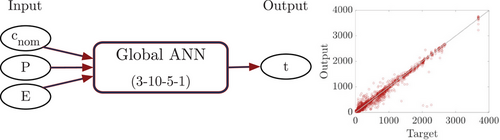
As two coupled FE models are used to compute the corrosion initiation time, it is investigated if also two coupled surrogate models can be created. Also if the advantage of a global ANN surrogate model compared to separate surrogate models for the mechanical problem and the transport problem is that no error accumulation can occur, because no intermediate results (crack width w_cr and crack length l_cr) are required for the global corrosion initiation time approximation, the disadvantage to work with a global surrogate model is that the training data generation needs to run both FE models sequentially. Here, the transport FE model needs far less computing time compared to the mechanical FE model. This means, that additional samples for a separate transport surrogate model can easily be produced and the surrogate models for the mechanical problem and the transport problem can be trained independently. In Figure 6, a nested ANN surrogate modeling strategy is shown together with the correlation plot of the finally predicted corrosion initiation time. It can be seen, that the prediction quality is worse compared to the global ANN surrogate model presented in Figure 5.

Several ANN architectures have been tested for all investigated options and variants. In Table 1, the best ANN results are summarized.

TABLE 1. Summary of the best ANN results; ANN architecture A, regression value R, and mean squared error

MSE

	Mechanical ANN					Global ANN
Output	w_cr		l_cr			t
	Option 1	Option 2	Option 1	Option 2	Option 3	Variant 1	Variant 2
A	[15 10]	[15 10]	[15 10]	[15 10]	[10 5]	[10 5]	-
R	0.825	0.993	0.998	0.997	0.999	0.998	0.993
$MSE$	0.03mm	0.001mm	4.49mm	5.78mm	0.26mm	732d	6690d

5.4 Uncertainty analysis of the corrosion initiation time and optimization results

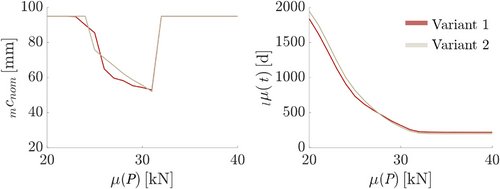
To investigate the influence of the different ANN surrogate modeling strategies to the uncertainty of the corrosion initiation time, the p-box is computed within an interval stochastic analysis for both surrogate modeling variants 1 and 2 described in the previous subsection. In Figure 7, the results are shown exemplified for the case $\mu (P)=30$ kN and ${}_{m}c_{\mathrm{nom}}=50$ mm. The upper bound cdfs of both p-boxes are almost identical. But the lower bound cdfs show remarkable different results for probabilities $F(t)>0.4$ . As the p-box of variant 2 is an envelope of the p-box of variant 1, it can be concluded that sequentially trained ANNs (variant 2) lead to an expansion of the p-box of the corrosion initiation time due to ignoring the physics of the coupled models within the ANN generation.

The final step is to investigated the influence of the different ANN surrogate modeling strategies on the optimization results, that is, the optimal concrete cover and the corresponding value of the objective function, which is the lower bound of the interval mean value ${}_{l}\mu (t)$ of the corrosion initiation time. Based on the results shown in Figure 8, it can be concluded that both surrogate modeling strategies lead to similar results of the optimization problem.

ACKNOWLEDGMENTS

This research is funded by the (DFG, German Research Foundation) – Project number: 312921814 within Subproject 6 of the Priority Programme SPP 1886 “Polymorphic uncertainty modelling for the numerical design of structures”.

Open access funding enabled and organized by Projekt DEAL.

REFERENCES

1Schöbi, R., & Sudret, B. (2017). Structural reliability analysis for p-boxes using multi-level meta-models. Probablistic Engineering Mechanics, 48, 27–38.
10.1016/j.probengmech.2017.04.001
Web of Science® Google Scholar
2Kennedy, J., & Eberhart, R. (1995). Proceedings of ICNN'95 - International Conference on Neural Networks, Vol. 4, (pp. 1942–1948). IEEE Press.
Google Scholar
3Edler, P., Freitag, S., Kremer, K., & Meschke, G. (2019). Optimization approaches for the numerical design of structures under consideration of polymorphic uncertain data. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems Part B: Mechanical Engineering, 5, 041013.
10.1115/1.4044153
Google Scholar
4Freitag, S., Edler, P., Kremer, K., & Meschke, G. (2020). Multilevel surrogate modeling approach for optimization problems with polymorphic uncertain parameters. International Journal of Approximate Reasoning, 119, 81–91.
10.1016/j.ijar.2019.12.015
Web of Science® Google Scholar
5Snozzi, L., Gatuingt, L., & Molinari, J. F. (2012). A meso-mechanical model for concrete under dynamic tensile and compressive loading. International Journal of Fracture, 178, 179–194.
10.1007/s10704-012-9778-z
Web of Science® Google Scholar
6Gudzulic, V., & Meschke, G. (2021). Multi-level approach for modelling the post-cracking response of steel fibre reinforced concrete under monotonic and cyclic loading. Proceedings in Applied Mathematics and Mechanics, 21, e202100194.
10.1002/pamm.202100194
Google Scholar
7 Comité Euro-International du Béton. (1993). CEB-FIP MODEL CODE 1990. Thomas Telford Publishing.
Google Scholar
8Ožbolt, J., Balabanić, G., Periškić, G., & Kušter, M. (2010). Modelling the effect of damage on transport processes in concrete. Construction and Building Materials, 24, 1638–1648.
10.1016/j.conbuildmat.2010.02.028
Web of Science® Google Scholar
9Schoen, S., Edler, P., Freitag, S., Gudzulic, V., & Meschke, G. (2022). Optimization of the corrosion initiation time of RC structures considering uncertainties. In G. Meschke, B. Pichler, & J. G. Rots (Eds.), Computational modelling of concrete and concrete structures – proceedings of EURO-C 2022 (pp. 545–554). Taylor & Francis.
10.1201/9781003316404-64
Google Scholar
10Zhang, R., Jin, L., Liu, M., Du, X. L., & Li, Y. (2017). Numerical investigation of chloride diffusivity in cracked concrete. Magazine of Concrete Research, 69, 850–864.
10.1680/jmacr.16.00511
Web of Science® Google Scholar
11Gehlen, C. (2000). Probabilistische Lebensdauerbemessung von Stahlbetonbauwerken, Dt. Ausschuß für Stahlbeton, (DAfStb-Heft 510DAfStb).
Google Scholar

Volume23, Issue4

Special Issue:93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM)

December 2023

e202300286

Artificial neural network surrogate modeling for uncertainty quantification and structural optimization of reinforced concrete structures

Abstract

1 INTRODUCTION

2 POLYMORPHIC UNCERTAINTY QUANTIFICATION

3 OPTIMIZATION WITH POLYMORPHIC UNCERTAIN PARAMETERS

4 ARTIFICIAL NEURAL NETWORK SURROGATE MODELS

5 OPTIMIZATION OF THE CONCRETE COVER OF A RC BEAM

5.1 Structural model and uncertain parameters

5.2 ANN surrogate models for crack width and crack length

5.3 ANN surrogate models for corrosion initiation time

5.4 Uncertainty analysis of the corrosion initiation time and optimization results

ACKNOWLEDGMENTS

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Artificial neural network surrogate modeling for uncertainty quantification and structural optimization of reinforced concrete structures

Abstract

1 INTRODUCTION

2 POLYMORPHIC UNCERTAINTY QUANTIFICATION

3 OPTIMIZATION WITH POLYMORPHIC UNCERTAIN PARAMETERS

4 ARTIFICIAL NEURAL NETWORK SURROGATE MODELS

5 OPTIMIZATION OF THE CONCRETE COVER OF A RC BEAM

5.1 Structural model and uncertain parameters

5.2 ANN surrogate models for crack width and crack length

5.3 ANN surrogate models for corrosion initiation time

5.4 Uncertainty analysis of the corrosion initiation time and optimization results

ACKNOWLEDGMENTS

REFERENCES

Figures

References

Related

Information