PAMM
Volume 23, Issue 4 e202300240
RESEARCH ARTICLE
Open Access

Detecting local spots in network materials prone to mechanical failure

Zhao Wu, 

Corresponding Author

Zhao Wu

Institute of General Mechanics, RWTH Aachen University, Aachen, Germany

Correspondence

Zhao Wu, Institute of General Mechanics, RWTH Aachen University, Eilfschornsteinstr. 18, 52062 Aachen, Germany.

Email: [email protected]

Search for more papers by this author
Bernd Markert, 

Bernd Markert

Institute of General Mechanics, RWTH Aachen University, Aachen, Germany

Search for more papers by this author
Franz Bamer, 

Franz Bamer

Institute of General Mechanics, RWTH Aachen University, Aachen, Germany

Search for more papers by this author
First published: 21 November 2023
https://doi.org/10.1002/pamm.202300240

Abstract

The prediction of the onset of fracture is a challenging issue in the mechanics of disordered materials. In this contribution, we show that the fracture process in network glasses, such as silica glass, turns out to be a complex phenomenon that originates from specific spots that have the size of a few hundred atoms only. We apply pure shear deformation to identify local rearrangement spots prone to material damage. These spots are analyzed using stress drop steps, originally used for densely packed disordered systems.

1 INTRODUCTION

Due to its exceptional properties, silica glass is highly valued in many industries and research. It can withstand extreme temperatures, allows light to pass through, is very resistant to chemicals, and has good electrical properties. These exceptional properties make silica glass highly versatile for various applications [1]. Unfortunately, on the macroscale, silica glass type breaks in a very brittle and somewhat unpredictable manner without any noteworthy foregoing plastic deformation, which limits the structural application of such materials. However, silica glass plastifies on the nanoscale and shows unusual behavior under shear and pressure [2]. Thus, extensive studies have been conducted to understand the dynamics of fracture in such a network-type of glass. These studies have employed both molecular simulations to understand the behavior of silica materials at the atomic level [3] and compare the simulation results with the experimental data [4].

Bamer et al. [5] used two-dimensional silica structures for the presentation of the main mechanical phenomena using molecular simulations due to several advantages. First, exploring a purely two-dimensional model offers a notable advantage in terms of visual representation, which enables enhanced classification and comprehension of intricate mechanical phenomena. Moreover, reducing one dimension results in computationally more economical models compared to three-dimensional counterparts of similar scales. Third, while dealing with such a theoretical model, it is less important for the model to be quantitatively accurate in terms of quantitative results while still providing a strong link to experimental images [6].

The main motivation of our study is to provide one step further to the understanding of an underlying molecular phenomenon behind the fracture of such two-dimensional silica structures. In this context, it has already been shown on densely packed systems, that is, models that describe the underlying physics of metallic glasses, that the material response originates from local rearrangements that involve a region of a few hundred atoms only and leads to an elastic response in the surrounding matrix [7, 8]. These small regions are predefined in the material prior to any deformation and may be activated during loading. One big issue in the community is to detect such “soft spots” prior to any mechanical deformation and preferably from the geometrical picture of the material only. In this context, Patinet et al. developed a model to detect this local rearrangement in amorphous solids by direct local probing of shear stress thresholds during remote loading in shear [9]. Furthermore, Bamer et al. [10] have investigated the reversibility of the local rearrangement and classified the reversibility using polynomial regression.

In this paper, we create a database of two-dimensional network glass samples and subject them to pure shear athermal quasistatic (AQS) deformation. This study focuses on detecting local rearrangements within the structures, which are as considered regions susceptible to future breakage. In order to identify and represent the size of the local rearrangements, we study the non-affine displacement fields of the structure under mechanical loading.

2 THEORY

2.1 Generating silica structure

William Holder Zachariasen successfully demonstrated the distinction between a crystalline and a vitreous silica state using a two-dimensional cartoon model [11]. Figure 1A presents an ordered or crystalline state of the material. However, this material also possesses a disordered arrangement of rings with diverse shapes and sizes, which he summarized through the random network theory. Figure 1B depicts such a disordered structure. To obtain such a kind of structure, one could generally employ a relaxation process in which the ensemble is brought to a state of zero temperature by minimizing the potential energy using an appropriate potential function. In this example, it is referred to a Yukawa-type potential. However, Zachariasen's random network theory demands that every Si-atom has to have exactly three oxygen neighbors, that is, full coordination. This ”rule” was supported by experimental images [6] in 2012. Out of obvious statistical reasons, the melting quenching procedure turns out to be ineffective in generating such networks. An alternative approach to achieve such a desired network structure is through the utilization of the Monte Carlo bond-switching algorithm. This algorithm involves a randomized sequence of bond switches [12]. After every switch, the following conditions must be satisfied to accept a bond switch as a valid configuration. First, the bond switch must meet the acceptance criteria defined by the Metropolis-Hastings condition outlined in Equation (1). Second, the resulting configuration must remain fully coordinated. Third, the sizes of the rings formed by the bonds must fall within an acceptable range, as determined by the statistics of experimental images. In the case of two-dimensional silica, ring sizes between four and ten members are allowed. The probability of one bond switch being accepted is shown here as:
P = min 1 , exp U b − U a k B T , $$\begin{equation} P=\min {\left\lbrace 1, \exp {\left(\frac{\mathcal {U}_b-\mathcal {U}_a}{k_B T}\right)}\right\rbrace} , \end{equation}$$ (1)
where U b $\mathcal {U}_b$ and U a $\mathcal {U}_a$ are the potential energy before and after the bond switch, k B $k_B$ is the Boltzmann constant, and T is the temperature of the system.
Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
(A). two-dimensional crystalline silica structure; (B). two-dimensional vitreous state of silica structure.
To prevent the formation of unphysical clusters of small or large rings, not a purely random sequence of switches is performed, but the Aboav and Weaire law is considered [13-15]. The Aboav-Weaire law provides a useful framework in this regard and can be expressed as follows:
m n = μ n 1 − α n + μ n 2 α n + σ n 2 n . $$\begin{equation} m_n=\mu _n{\left(1-\alpha _n\right)}+\frac{\mu _n^2 \alpha _n+\sigma _n^2}{n}. \end{equation}$$ (2)
In this paper, m n $m_n$ is the mean ring size from empirical observation around all rings of size n. The magnitudes μ n $\mu _n$ and σ n $\sigma _n$ are the mean and the variance of the ring statistics.

By following this procedure, artificial two-dimensional glass models that follow Zachariasen's framework were successfully generated using the Monte Carlo bond-switching algorithm.

In order to control the level of heterogeneity of ring statistics, we introduce the dual Monte Carlo bond-switching algorithm. To further control the level of heterogeneity of the network, the overall statistics of rings are considered in an additional objective function [5]. Figure 2A illustrates the target distributions of probability density function (PDF) of ring sizes ranging from four to nine. The PDFs exhibit a peak at six and indicate that rings with six members are the most commonly found in the network. This is not surprising since six-membered rings are energetically favorable. Additionally, there is a higher occurrence of five-membered rings compared to seven-membered rings, leading to an asymmetric effect. We approximated these statistics by a logarithmic distribution function, as discussed by Büchner et al. [16]. This is represented by the following equation:
P x n , μ ( m ) , σ ( m ) = 1 x n σ 2 π exp log x n − μ ( m ) 2 2 σ ( m ) 2 . $$\begin{equation} P{\left(x_n, \mu ^{(m)}, \sigma ^{(m)}\right)}= \frac{1}{x_n \sigma \sqrt {2 \pi }} \exp \frac{{\left(\log x_n-\mu ^{(m)}\right)}^2}{2 \sigma ^{(m)^2}}. \end{equation}$$ (3)
In this equation, x n $x_n$ represents the continuous counterpart to the integer value of the ring size, μ ( m ) $\mu ^{(m)}$ and σ ( m ) $\sigma ^{(m)}$ correspond to the target mean and target standard deviation, respectively, derived from the experimental topology. By adjusting the extracted standard deviation of the distribution, the desired level of heterogeneity within the network can be controlled. Increasing the standard deviation increases both small- and large-membered rings, like four- and nine-membered rings, while a decrease in the occurrence of six-membered rings. For generating the sample shown in Figure 2B, a target variance of 0.6 σ ( m ) $\sigma ^{(m)}$ was employed, indicating a lower target heterogeneity compared to the value extracted from the measurement. For the sample depicted in Figure 2C, a target variance of 1.4 σ ( m ) $\sigma ^{(m)}$ was used, leading to a higher target heterogeneity compared to the value derived from the measurement.
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
(A). The probability distribution function of the ring sizes for different levels of heterogeneity σ; (B). silica network structure with a heterogeneity σ = 0.6 $\sigma = 0.6$ ; (C). silica network structure with a heterogeneity σ = 1.4 $\sigma = 1.4$ .

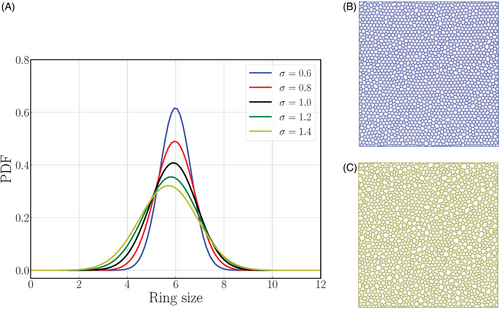
3 SIMULATION AND RESULTS

3.1 Pure shear deformation

Regarding shear deformation, simple shear and pure shear are considered. Noteworthy, the deformation gradient of simple shear is determined by combining the effects of pure shear deformation and rotation. This leads to a measurable stress response in the material and the contribution of rigid body motion [5].

In molecular simulations, a pure shear deformation protocol along the x and y directions can be easily implemented by subjecting the material to push-pull combined deformation and maintaining a constant cell volume. This approach proves convenient in molecular simulations.

Instead of using a time integration scheme, we employ an AQS deformation protocol. This approach involves increasing the strain incrementally and minimizing the potential energy without considering thermal effects. In other words, local energy basins can only be escaped through externally applied strain rather than thermal activation. This AQS protocol provides a physically meaningful description of glassy structures at temperatures significantly lower than the glass transition temperature. As a result, it enables a pure mechanical characterization of the disordered structure, free from thermal disturbances.

Figure 3 illustrates one of the outcomes obtained from the application of the AQS pure shear deformation on the generated lattice samples of heterogeneity σ = 1.2 $\sigma =1.2$ , where the deformation for each step is Δ x = 0.1 $\Delta x = 0.1$  Å. In Figure 3A, the initial state of the deformation is depicted, revealing an intact lattice structure without any damage or fracture. However, after subjecting the lattice to 200 steps of deformation, Figure 3B shows the occurrence of rearrangements within the lattice. These transformations can form irreversible large rings, which can be regarded as local fractures in the material. Continuing the deformation process, the voids depicted in Figure 3B continue to grow, as illustrated in Figure 3C. After 400 deformation steps, the voids become significantly larger and they have the potential to propagate throughout the entire lattice structure, which potentially leads to total rapture.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Silica network structure at different deformation steps; (A). Initial state; (B). 200 deformation steps; (C). 400 deformation steps.

3.2 Detecting identified regions of local rearrangement

We aim to find regions susceptible to mechanical failure or local rearrangements that are decoded in the material prior to deformation. This approach is motivated by the shear transformation zone (STZ) theory proposed by Falk and Langer in 1998 [7]. By analyzing the behavior and properties of these identified regions, one can gain insights into the mechanisms and patterns of mechanical failure in the simulated material.

Due to the change in the potential energy landscape (PEL) caused by external deformation, there is a possibility of encountering a point where the system can drop into an adjacent basin. This transition leads to a catastrophic and discontinuous rearrangement event. In other words, the system undergoes a sudden and significant change in its configuration as a result of this drop in the PEL. The strain step introduced to the cell is kept small enough to avoid significant alterations in the mechanical response behavior of the system. However, it is large enough to promote the occurrence of a specific saddle-node bifurcation that may emerge in the PEL as the shear strain increases. In other words, we took care that possible events were not skipped during strain increase. During each elastic AQS step, the objective of the minimization algorithm is to reposition the disturbed atom back into its minimum basin.

Following the stress-strain results, abrupt drops in stress are observed really interesting because of their inelastic behavior. These stress drops are accompanied by localized structural rearrangements at the atomic scale. In Figure 4, we present these stress-strain relations during deformation. Here we use σ x x $\sigma _{xx}$ to detect the stress drops. The inlay plots of Figure 4A represent a zoom-in of the first six stress drops, which may be identified by damage effects within the material. By analyzing the locations and magnitudes of these stress drops, one can detect the specific regions that experience localized rearrangement events. We evaluate the non-affine displacement field to visualize these local events within the structure. The calculation of the non-affine displacement field is realized by:
d nonaffine = d total − d affine . $$\begin{equation} \bm{d}_\mathrm{nonaffine} = \bm{d}_\mathrm{total} - \bm{d}_\mathrm{affine}. \end{equation}$$ (4)
Here, the total displacement dtotal is calculated by the difference in atomic position before and after the stress drop, while the affine displacement daffine is evaluated due to the affine mapping of the particles and the cell from the reference to the current configuration in an updated Lagrangian framework.
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Strain-stress curve of a two-dimensional silica lattice subjected to pure shear deformation; (A) stress in x-direction σ x x $\sigma _{xx}$ ; (B) stress in y-direction σ y y $\sigma _{yy}$ ; (C) shear stress τ.

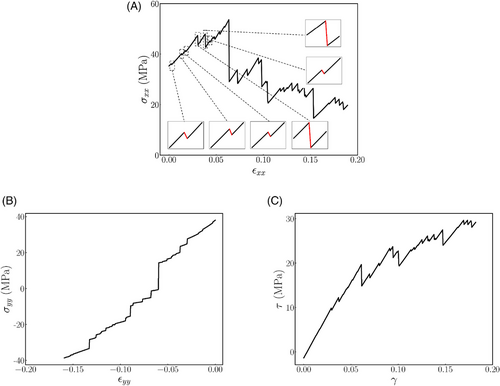
In Figure 5, we present the non-affine displacement field corresponding to the first six stress drops enlarged in Figure 4A. By examining these fields, one observes that the regions exhibiting significant non-affine displacements correspond to the damaged regions within the material. We emphasized this observation further by highlighting these regions with an orange circle. The center of each circle is chosen so that it coincides with the atom that experiences the maximum non-affine displacement. The radius of these circles may vary, allowing for flexibility in capturing the extent of the damaged region. Quantification of the size of these soft spots by finding the appropriate corresponding radii may help to better classify the extent of the damage for future studies.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Displacement fields for the first six stress drops.

4 CONCLUSION

In summary, we have constructed a database of two-dimensional silica network structures and subjected them to pure shear AQS deformation using molecular simulations. Through our analysis, we have identified and examined the occurrence of local rearrangements within the structures. These localized rearrangements can be regarded as regions susceptible to structural failure. We have identified local regions to represent these small damages, that allow for characterization and an understanding of potential failure mechanisms in the structures. Future work will aim to conduct investigations on the sizes of the identified regions of local rearrangement.

ACKNOWLEDGMENTS

This research was funded by the Federal Ministry of Education and Research (BMBF) and the Ministry of Culture and Science of North Rhine-Westphalia (MKW) under the Excellence Strategy of the Federal Government and the Länder.

Open access funding enabled and organized by Projekt DEAL.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.