Diagonally-Addressed Matrix Nicknack: How to improve SpMV performance
Abstract
We suggest a technique to reduce the storage size of sparse matrices at no loss of information. We call this technique Diagonally-Addressed (DA) storage. It exploits the typically low matrix bandwidth of matrices arising in applications. For memory-bound algorithms, this traffic reduction has direct benefits for both uni-precision and multi-precision algorithms. In particular, we demonstrate how to apply DA storage to the Compressed Sparse Rows (CSR) format and compare the performance in computing the Sparse Matrix Vector (SpMV) product, which is a basic building block of many iterative algorithms. We investigate 1367 matrices from the SuiteSparse Matrix Collection fitting into the CSR format using signed 32 bit indices. More than 95% of these matrices fit into the DA-CSR format using 16 bit column indices, potentially after Reverse Cuthill-McKee (RCM) reordering. Using IEEE 754 precision scalars, we observe a performance uplift of 11% (single-threaded) or 17.5% (multithreaded) on average when the traffic exceeds the size of the last-level CPU cache. The predicted uplift in this scenario is 20%. For traffic within the CPU's combined level 2 and level 3 caches, the multithreaded performance uplift is over 40% for a few test matrices.
1 INTRODUCTION
The key ingredient of the new storage technique is the observation that many matrices arising in, for example, finite element simulations have a very low matrix bandwidth (under certain permutations). That means, potentially after permutation, all non-zero matrix entries are located close to the matrix diagonal. This motivates storing the indices of these entries relative to the matrix diagonal rather than as an absolute position, which we call Diagonally-Addressed (DA) storage. Due to the small matrix bandwidth, the relative indices may be stored in a smaller (integer) data type. This technique is easily applicable to many sparse formats, for example, Compressed Sparse Rows (CSR), Block CSR (BSR), or (one of the vectors of) Coordinate (COO) storage. In this paper we apply DA storage to the Compressed Sparse Rows (CSR) format; obtaining the Diagonally-Addressed CSR (DA-CSR) format; and compare the SpMV performance against our implementation of CSR as well as the Intel Math Kernel Library (MKL) [4].
DA storage differs from Diagonal (DIA) storage in that the new technique still requires one index per non-zero, depending on the underlying technique, instead of one index per diagonal. Also, it does not impose a diagonal-major order of the entries, or require a potentially padded and full/dense storage for each of the diagonals. The Recursive Sparse Blocks (RSB) format [5] is another data structure for sparse matrices motivated by a cache-efficient and parallel implementation of the SpMV product. It divides a sparse matrix into a tree structure of sparse blocks, whose leaves are iterated in a Z- or Morton-order. The leaf blocks are stored in the COO, CSR, or Compressed Sparse Columns (CSC) format.
RSB was designed for arbitrary sparse matrices, in particular, matrices without an inherent low bandwidth (under certain permutations). RSB allows 16 bit indices as well, but only for its leaf matrices. Meanwhile, DA-CSR has a conceptually simpler non-recursive design, allowing 16 bit indices throughout, which leads to a much lower overhead in terms of Byte per non-zero. Therefore, DA storage does not directly compete with the RSB format, but could be used in the leaf blocks within the RSB format, to allow for an even smaller index type.
The remainder of this paper is structured as follows. Section 2 applies DA storage to the CSR format. Section 3 describes the selection of test matrices. Section 4 describes how to compute the SpMV product using that new DA-CSR format, and measures the performance of SpMV. We conclude the paper in Section 5.
2 DIAGONALLY-ADDRESSED STORAGE
The CSR storage of a matrix comprises three vectors, compare Listing 1, where nnz denotes the number of non-zero entries, oindex_t and iindex_t are integer data types, and scalar_t is an approximation of , for example, IEEE 754 or for . The “row pointers” stored in and “column indices” stored in do the bookkeeping imposed by only storing non-zero matrix entries.
Listing 1: (DA-) CSR storage of a matrix.
1 struct {
2 oindex_t rowptr[nrows+1];
3 iindex_t colids[nnz];
4 scalar_t values[nnz];
5 };
Example 2.1.The sample matrix shown in Figure 1 has , nnz = 5, and . Its CSR representation is given by
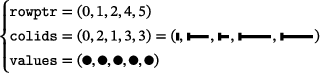 (3)
(3)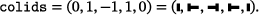 (4)
(4)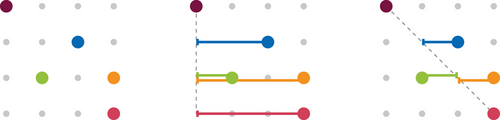
Sometimes it is necessary to reduce the bandwidth of a matrix before DA storage can be applied effectively, which we observe in the next example.
Example 2.2.The matrix GHS_posdef/ldoor from the SuiteSparse Matrix Collection [6] has dimension 952 203 and 46 522 475 pattern entries,2 distributed over a bandwidth of 686 979. On average, this matrix has 49 pattern entries per row. See Figure 2 (left) for its sparsity pattern. Due to its block structure, the original matrix bandwidth is fairly large. Still, a Reverse Cuthill-McKee (RCM) reordering [7] reduces the bandwidth to about 9100,3 which is only about 1% of the matrix dimension. Ignoring the colors, the corresponding sparsity pattern would look almost identical to Figure 2 (right). The reduced bandwidth is less than and therefore allows for the usage of 16 bit column indices in DA storage, while both the matrix dimension (for plain CSR storage) and the original bandwidth (for naive DA-CSR storage) would require 32 bit indices.
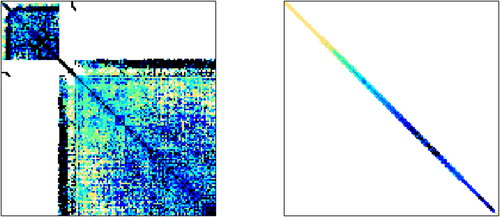
Example 2.3.The matrix Janna/Bump_2911 from the SuiteSparse Matrix Collection [6] has dimension 2 911 419 and 127 729 899 non-zeros, distributed over a bandwidth of only , which is only about 1% of the matrix dimension. On average, this matrix has 44 non-zeros per row. See Figure 2 (right) for its sparsity pattern. Therefore, standard CSR storage requires 32 bit indices for both oindex_t and iindex_t, which require 11 MiB and 487 MiB in total, respectively. DA-CSR allows for 16 bit iindex_t to be used, which requires only 244 MiB, thus reducing the bookkeeping traffic by , or from 4.09 to 2.09 Byte per nnz, irrespective of scalar_t. For 64 bit and 32 bit scalar_t, for example, IEEE 754 and , which in total require 975 MiB and 487 MiB, using DA-CSR instead of CSR results in an overall matrix-related traffic reduction of and , respectively.
For matrices with more than a few non-zeros per row, it is therefore reasonable to ignore the effect of oindex_t, i.e. to assume . The final percentages of the previous example would then be estimated by and . Figure 3 shows this approximate reduction in matrix-related traffic by means of formula (5). Note how smaller iindex_t; i.e. lower bookkeeping traffic; yield better approximations of the factor observed for dense storage.4 Recall that by Equation (1) a traffic reduction is tightly coupled with expected performance gains for memory-bound operations.
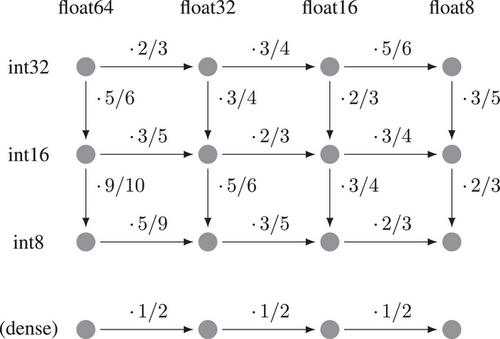
While the goal of multi-precision algorithms is to exchange scalar_t for a smaller data type (as in, for example, [8]), i.e. traversing the rows of Figure 3, DA storage focuses on iindex_t, i.e. traversing the columns of Figure 3. However, as the main motivation of multi-precision algorithms is the memory bottleneck, DA storage is expected to enable even larger speedups in that context. CSR using 64 bit scalars and 32 bit indices merely allows for a performance speedup when switching to 32 bit scalars. Meanwhile, if the matrix has a representation in DA-CSR using 16 bit indices, the expected speedup is . This speedup is much closer to the 2 × possible for dense storage, when using a scalar type half the size.
3 SELECTION OF MATRICES
The SuiteSparse Matrix Collection [6] contains 1367 square matrices having a CSR representation using 32 bit indices and a full structural rank.5 Only 993 of these matrices (72.6%) have a dimension less than 215, i.e. fit into CSR using 16 bit column indices. However, for 1302 matrices (95.2%) there exists a permutation that reduces the matrix bandwidth to below 215, such that these matrices fit into DA-CSR using 16 bit column indices. These are the matrices we select for further investigation.
Some of the investigated matrices are already stored in a bandwidth-reduced way. We applied an RCM reordering [7] to the ones that are not. Unfortunately, our implementation of the RCM permutation has not been able to sufficiently reduce the bandwidth of two matrices (Janna/Long_Coup_dt0 and Janna/Long_Coup_dt6), which reduces the number of matrices to 1300 (95.1%).
4 SPARSE MATRIX VECTOR PRODUCT
4.1 Implementation details and methodology
A prototypical implementation of the SpMV product for a matrix in DA-CSR format is given in Listing 2. Instead of reversing the index translation in the innermost loop, i.e. computing , we instead compute a shifted view into the factor one level up. This replaces nnz oindex_t-additions by nrows pointer-additions. Recall that in C/C++ the memory access is equivalent to . Applying associativity to the computation of the pointer address, we see that this access is also equivalent to and .
Listing 2: SpMV for DA-CSR
1 // Input: oindex_t *rowptr, nrows;
2 // iindex_t *colids;
3 // scalar_t *values, *x, *y, alpha, beta;
4 // Output: scalar_t *y;
5 for (oindex_t row = 0; row < nrows; ++row) {
6 scalar_t accumulator = 0;
7 scalar_t *xshift = x + row;
8 for (oindex_t i = rowptr[row]; i < rowptr[row+1]; ++i) {
9 iindex_t col = colids[i];
10 scalar_t val = values[i];
11 accumulator += val * xshift[col];
12 }
13 y[row] = alpha * accumulator + beta * y[row];
14 }
Remark 4.1. (Non-Square Matrices)For tall matrices, i.e. nrows > ncols, points to memory outside , and must therefore never be dereferenced directly. Within Listing 2 however, it will only be dereferenced at an offset that yields a memory address within .
The code has been compiled with GCC 10.3.0 using -O3 -NDEBUG -mavx2 -mfma. The benchmarks have been run on an Intel Xeon Skylake Silver 4110 running CentOS 7.9.2009,6 with threads pinned using taskset7. Runtime measurements have been taken using nanobench [9] with set to 100 ms, and both set to 10, using the minimum over 11 epochs.
We measured the performance of a naive implementation (with nnz additions instead of nrows) as well as several implementations akin to Listing 2, optionally using OpenMP with two, four, six, or eight threads, both for CSR and DA-CSR matrices. Among all implementations executed on the given hardware, the best performing ones were the naive implementation, the one using three accumulators, and the one using a single AVX2 accumulator (four scalars wide) accessing using unaligned load instructions. In the following, for each matrix, and each storage format tested, we select the implementations and number of threads yielding the highest performance.
For the MKL [4] implementation of the CSR format, we measured single-threaded as well as multithreaded performance. Again, for each matrix we select the number of threads yielding the highest performance.
4.2 Numerical results
For traffic within the size of the L1 cache, a single thread yields the best performance. Up to about 100 KiB, which is well within the size of a single L2 cache, the optimum number of threads increases gradually. For traffic larger than that, the maximum number of threads yields the best performance. This behavior is irrespective of the matrix format and the implementation vendor (ourselves or MKL [4]).
Our implementation of the SpMV product for the CSR format using 32 bit indices performs about the same as the MKL [4], see Table 1. Figure 4 shows the comparison of DA-CSR using 16 bit column indices to CSR. Using DA-CSR shows almost no change for traffic within the combined size of the L2 caches, i.e. up to . For traffic larger than that, up to the combined size of all caches, i.e. up to about 8 + 11 MiB, we observe a larger than 1.4 × speedup. For traffic beyond that, we observe an average speedup of about +17.5%, which is reasonably close to the expected +20%. However, the throughput drops slightly, indicating some unused potential on the given hardware. See Table 2 for the comparison of DA-CSR to MKL [4].
| Traffic | Singlethreaded | Multithreaded |
|---|---|---|
| L1d | 1.131 | 1.129 |
| L2 | 1.073 | 1.044 |
| L3 | 1.012 | 1.011 |
| Large | 0.982 | 0.994 |
- Abbreviations: CSR, Compressed Sparse Rows; MKL, Math Kernel Library; SpMV, Sparse Matrix Vector.
| Traffic | Single-threaded | Multithreaded |
|---|---|---|
| L1d | 1.103 | 1.098 |
| L2 | 1.073 | 1.055 |
| L3 | 1.052 | 1.032 |
| Large | 1.110 | 1.172 |
- Abbreviations: CSR, Compressed Sparse Rows; DA, Diagonally-Addressed; MKL, Math Kernel Library; SpMV, Sparse Matrix Vector.
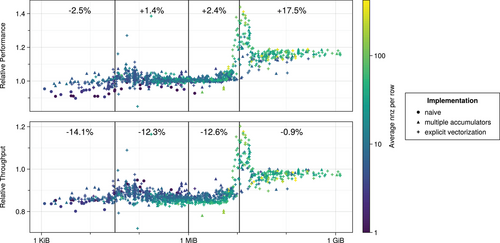
Remark 4.2. (CSR using 16 bit column indices)Recall that 933 matrices have a direct representation in CSR using smaller column indices. The DA-CSR format performs on par with CSR using the same index types for these matrices.
5 CONCLUSION AND OUTLOOK
DA storage allows to nearly halve the bookkeeping traffic in sparse matrix storage formats, when the matrix bandwidth allows for an index type half the size. On the hardware used, DA-CSR storage with 16 bit column indices improves the multithreaded SpMV performance over CSR storage with 32 bit column indices by more than 17%, for both our implementation and MKL [4] if the traffic exceeds the size of the L3 cache of the CPU. Meanwhile, DA-CSR performs no worse than CSR when using the same data types.
ACKNOWLEDGMENTS
Open access funding enabled and organized by Projekt DEAL.
Open Research
DATA AVAILABILITY STATEMENT
The source code is available at:
https://doi.org/10.5281/zenodo.8104335
The visualizations in this paper have been created using TikZ [10] and Makie.jl [11]. The SpMV performance measurements for the reported experiments are available at:
REFERENCES
- 1 The final entry is set to nnz for ease of use.
- 2 Technically, nnz refers to the number of pattern entries, which contains non-zeros as well as explicitly stored zeros.
- 3 Our implementation yields a bandwidth of 9120, while the SuiteSparse Matrix Collection [6] reports 9134.
- 4 Note that dense storage may be seen as having , i.e. having zero bit of bookkeeping (per nnz).
- 5 Eventually, we are interested in using DA storage when solving linear systems. We thus take full structural rank as a proxy for regularity, as the collection's metadata does not contain the numerical rank for all the matrices. Consequently, our selection of matrices contains irregular matrices as well.
- 6 https://www.mpi-magdeburg.mpg.de/cluster/mechthild
- 7 https://www.man7.org/linux/man-pages/man1/taskset.1.htmland https://github.com/util-linux/util-linux/blob/master/schedutils/taskset.c




