Double U-Net: Improved multiscale modeling via fully convolutional neural networks
Abstract
In multiscale modeling, the response of the macroscopic material is computed by considering the behavior of the microscale at each material point. To keep the computational overhead low when simulating such high performance materials, an efficient, but also very accurate prediction of the microscopic behavior is of utmost importance. Artificial neural networks are well known for their fast and efficient evaluation. We deploy fully convolutional neural networks, with one advantage being that, compared to neural networks directly predicting the homogenized response, any quantity of interest can be recovered from the solution, for example, peak stresses relevant for material failure. We propose a novel model layout, which outperforms state-of-the-art models with fewer model parameters. This is achieved through a staggered optimization scheme ensuring an accurate low-frequency prediction. The prediction is further improved by superimposing an efficient to evaluate U-net, which captures the remaining high-level features.
1 INTRODUCTION
When considering the size effect [1] for larger structures, a safety factor of up to 2 has to be adopted in order to ensure the material of a component will not break. This safety factor arises due to effects occurring on the microscale of the material, that is, due to accumulated damage on the microstructured material. In multiscale modeling, the material response on the macroscopic scale is obtained by considering the effects occurring on the microscale. Thus, enabling the engineering of high-performance materials suitable to effectively and efficiently fulfill the requirements of the deployed structure. In a multiscale simulation, at every material point on the macroscale, the microscopic behavior of the material is considered and modeled [2, 3], leading to prohibitively high computational cost. To circumvent the costly and repetitive simulation of the microscale, machine learning models are deployed to obtain an efficient, yet accurate prediction of the microscopic material behavior [4]. Artificial neural networks are a popular choice to predict the quantity of interest [5, 6], often being the homogenized response of the microstructured material, either obtained via a feature transform with a subsequent machine learning model [4, 5], or via the direct prediction using convolutional neural networks (Conv Net) [6]. The microstructured material is often represented as image data, for example, obtained via a CT-scan, making it suitable for Conv Nets to directly operate on the image input and efficiently yield an accurate prediction.
A subtype in the field of Conv Nets, that is, fully convolutional neural networks, yield another image as their prediction, which can be used to predict the full field solution in the context of microstructure modeling [7, 8]. An additional advantage of the predicted full field solution is that any quantity of interest can be extracted a posteriori, such that one is not constrained to the homogenized response, but one could also recover, for example, the peak stresses, which are relevant for material failure. The proposition of the U-net by Ronneberger et al. [9] surged the interest in the image to image prediction, which has an encoder–decoder structure, and first compresses the spatial resolution of the input image, before increasing it again to recover the prediction at the original resolution. Since the fully Conv Net operates on multiple resolutions, various approaches have emerged to utilize an approximation of the solution in a lower resolution, which contributes to the loss/model optimization and can be trivially obtained through coarse graining during training [10, 11]. Another approach simulates the material at the microscale in coarse resolution and uses the solution as input to the model while upsampling [7]. A different layout has also been considered, which incorporates information of the image on multiple spatial resolution levels [11, 12], starting at a very coarse resolution, on which the convolutional layers can consider large features within the image, and increasingly refining the prediction on each level when recovering the original resolution for its prediction.
This article diverts its attention to fully Conv Nets. We utilize the U-net structure and coarse grained solutions during the training for optimization. The model is designed to have comparatively few parameters to optimize, while being significantly more accurate than recent state-of-the-art models. This is achieved through a model layout, which ensures very accurate predictions on lower resolutions. To further refine the prediction of a model, a second efficient to evaluate U-Net is superimposed to capture high-level features. Due to the nature of the multiple interdependent prediction contributions, a staggered training scheme is proposed. The code of the model's implementation is made freely available in Lissner [13].
2 MULTISCALE MODELING
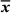 is governed by its underlying microscale with the domain Ω. For arbitrarily different length scales, that is,
is governed by its underlying microscale with the domain Ω. For arbitrarily different length scales, that is, 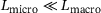 , a separation of length scale can be safely assumed. Further, it is assumed that the micro- and the macroscale follow the same material laws, which is described in more detail in Leuschner [14]. Thus, we will focus on the microscale and consider a microstructural unit cell Ω to motivate the materials behavior. For the sake of brevity, consider the equilibrium condition for the steady state heat equation
, a separation of length scale can be safely assumed. Further, it is assumed that the micro- and the macroscale follow the same material laws, which is described in more detail in Leuschner [14]. Thus, we will focus on the microscale and consider a microstructural unit cell Ω to motivate the materials behavior. For the sake of brevity, consider the equilibrium condition for the steady state heat equation
 (1)
(1)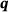 . The constitutive equation relating the heat flux
. The constitutive equation relating the heat flux 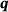 to the temperature gradient
to the temperature gradient 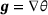 is given as
is given as
 (2)
(2) is introduced. The investigated microstructured material is subsided to periodic and antiperiodic boundary conditions with the fluctuating terms
is introduced. The investigated microstructured material is subsided to periodic and antiperiodic boundary conditions with the fluctuating terms  , being expressed as
, being expressed as
 (3)
(3) belongs to the periodic point set of the boundary
belongs to the periodic point set of the boundary 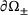 , respectively. The loading on the microscale is prescribed by its macroscopic counterpart. Once the materials response on the microscale is calculated, the homogenized quantity of interest
, respectively. The loading on the microscale is prescribed by its macroscopic counterpart. Once the materials response on the microscale is calculated, the homogenized quantity of interest 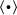 is recovered by the homogenization operation
is recovered by the homogenization operation
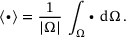 (4)
(4)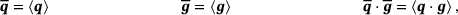 (5)
(5) is predicted.
is predicted.3 CONVOLUTIONAL NEURAL NETWORKS
3.1 Introduction
 (6)
(6) . After the addition of the bias term b, an activation function f is deployed to introduce nonlinearity between layers. To improve information processing between two layers, channels are introduced (represented as multiple rectangles in Figure 1), which are comparable to the number of hidden neurons in dense neural networks. Here, a brief motivation for convolutional neural networks is given to familiarize the reader with the relevant notion for the effective design of Conv Nets. Basic algorithmic operations are nicely illustrated in Dumoulin and Visin [16].
. After the addition of the bias term b, an activation function f is deployed to introduce nonlinearity between layers. To improve information processing between two layers, channels are introduced (represented as multiple rectangles in Figure 1), which are comparable to the number of hidden neurons in dense neural networks. Here, a brief motivation for convolutional neural networks is given to familiarize the reader with the relevant notion for the effective design of Conv Nets. Basic algorithmic operations are nicely illustrated in Dumoulin and Visin [16].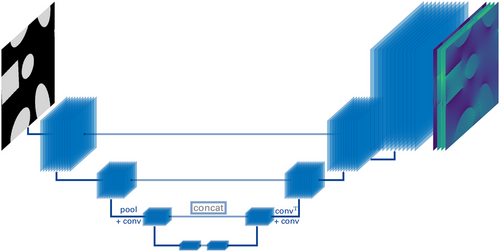
The forward pass via a convolution operation implies that each data point in the input image is processed by the same machine learned weights k. The underlying feature transform between layers is a global convolution operation, affected by the spatially local neighborhood. Therefore, we introduce the notion of the receptive field, that is, the number of adjacent pixels, which are at most considered by a single convolution operation. Since each 3 × 3 convolution increases the receptive field for all subsequent layers by two pixels, a prohibitive number of convolution operations would be required to achieve large receptive fields. When reducing the spatial resolution, which is implemented by evaluating the kernel each stride increment, the receptive field is virtually increased. After applying an operation with a stride of two, every subsequent operation has virtually doubled the receptive field with respect to the original spatial resolution of the input image. After resolution reduction, the number of feature channels can be increased while keeping memory usage constant. In terms of fully convolutional neural networks, the spatial resolution of the Conv Nets output has to match the resolution of the input image. To increase the resolution, either upsampling, or transpose convolutions[16] are used. In this end to end setting, Ronneberger et al. [9] proposed the U-net (Figure 1), which reuses the feature channels from the left while decreasing the resolution, and concatenates them to later layers on the right at the respective spatial resolution. This improves information processing in the model and provides low-level information to latter layers of the model.
Recent research has progressed in the direction of improved information processing [17-19], where shortcuts are used between two modules/layers. For the design of Conv Nets, modular blocks are generally used, which replace a single convolution operation between two layers by multiple operations. In Szegedy et al. [17], multiple parallel convolutions of differently sized kernels are deployed as inception modules. The ResNet [18] deploys blocks of two 3 × 3 convolutions, augmented by an identity mapping, which adds the previous features to the module's output, improving the gradient flow [19] and enabling deeper models to reliably converge.
In the field of fully convolutional neural networks, additional improvements have been found by infusing some knowledge of the approximate solution on lower resolutions into the model while the U-net structure increases the resolution. A popular option to infuse the knowledge is to assist the neural network during training by fitting the solution on multiple resolutions [11] to the coarse grained (average pooled) solution. Another interesting approach has been proposed by Zhou et al. [7], evaluating the simulation on a very coarse resolution, serving as a feature input on the respective spatial resolution.
3.2 Model proposition
The general structure of the U-net [9] is adopted, and the data usage of the model is optimized to reduce the computational overhead of the model while retaining/increasing accuracy. A main idea of the model is to have two prediction contributions, where the 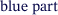 , the
, the  -net, aims to predict a good low-frequency field, while the
-net, aims to predict a good low-frequency field, while the  , the
, the  -net, is superimposed to capture the remainder of the high-level/frequency features.
-net, is superimposed to capture the remainder of the high-level/frequency features.
- I—the input image, also coarse grained to each spatial resolution.
- II—features obtained after decreasing the spatial resolution in the down path.
- III—features while increasing the spatial resolution in the up path (III* + the upsampled prediction of the previous level).
- IV—the prediction at current spatial resolution.
 -net is shown in Figure 2 (right). Note that the coarse grained prediction (IV) is not directly added to the next levels prediction, but combined with the feature channels used for upsampling and followed by a few convolution operations. This improved the models prediction quality significantly, since a Conv Net struggles to remove the introduced upsampling artifacts with a single convolution, or by adding a correction term after each upsampling operation. Such upsampling artifacts can be spotted by a critical eye in Marcato et al. [11].
-net is shown in Figure 2 (right). Note that the coarse grained prediction (IV) is not directly added to the next levels prediction, but combined with the feature channels used for upsampling and followed by a few convolution operations. This improved the models prediction quality significantly, since a Conv Net struggles to remove the introduced upsampling artifacts with a single convolution, or by adding a correction term after each upsampling operation. Such upsampling artifacts can be spotted by a critical eye in Marcato et al. [11].

 (7)
(7) -net is optimized, and frozen thereafter. As a next step, the
-net is optimized, and frozen thereafter. As a next step, the  -net is activated and trained to refine the prediction. In a final step, both predictors of the
-net is activated and trained to refine the prediction. In a final step, both predictors of the  -net are optimized in a combined manner.
-net are optimized in a combined manner. -net, the prediction
-net, the prediction 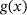 on each level
on each level 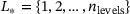 contributes to the total loss
contributes to the total loss 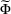 , that is,
, that is,
 (8)
(8)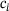 . The solution y is coarse-grained with the average pooling operation to match the current levels spatial resolution. In general, the smaller the spatial resolution, the more channels are used. Using the base number of channels of
. The solution y is coarse-grained with the average pooling operation to match the current levels spatial resolution. In general, the smaller the spatial resolution, the more channels are used. Using the base number of channels of 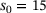 , the number of channels per level are scaled as
, the number of channels per level are scaled as
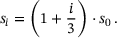 (9)
(9) -net and
-net and  -net, the
-net, the  -net is optimized in a staggered manner, while increasing the levels and the number of active modules, during a pretraining loop. One pretraining loop consists of a first optimization loop where the constant
-net is optimized in a staggered manner, while increasing the levels and the number of active modules, during a pretraining loop. One pretraining loop consists of a first optimization loop where the constant 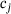 is zero for all but the current levels, that is,
is zero for all but the current levels, that is,
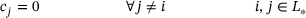 (10)
(10)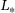 . Since the unconstrained optimization only ensures that the current level is a good approximation of the solution, in a second step, the approximation on each level is ensured with
. Since the unconstrained optimization only ensures that the current level is a good approximation of the solution, in a second step, the approximation on each level is ensured with
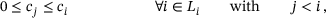 (11)
(11) -net is frozen except for the final predicting level, and the remainder of the
-net is frozen except for the final predicting level, and the remainder of the  -net is optimized as described above.
-net is optimized as described above.4 RESULTS
The proposed model is applied for the full-field prediction of the microstructured material characterized by representative volume elements (RVE), which is subsided to periodic boundary conditions (3). Thus, a single frame, that is, the input image to the fully convolutional neural network (Conv Net), suffices to fully characterize the material at the microscale. We consider the stationary heat equation outlined in Section 2 in a linear setting under constant loading conditions. Through superpositioning, the effective heat conduction tensor 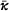 from Equation (2) can be recovered and generalized to arbitrary loading conditions.
from Equation (2) can be recovered and generalized to arbitrary loading conditions.
The proposed model is compared to the U-ResNet used in Santos et al. [15]. It has also been compared to the more recent models [11, 12], which have significantly underperformed the presented models. We deploy a data augmentation scheme during runtime outlined in Lißner and Fritzen [20], which utilizes the periodic boundary conditions to artificially generate new samples. In total, 1500 samples have been used for training, where the validation set contained 300 samples thereof. For optimization, all models have been trained using the mean squared error (MSE) as loss and the adam optimizer, with constant initial learning rate of 10−3 and early stopping. Each model is set out to predict all four components of the heat flux 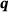 , that is, x and y response under x and y loading, respectively. The RVE image is the input to the model of fixed resolution of 128 × 128 voxels, where different input features following [15] did not improve the prediction. All error measures below refer to a test set consisting of 500 samples.
, that is, x and y response under x and y loading, respectively. The RVE image is the input to the model of fixed resolution of 128 × 128 voxels, where different input features following [15] did not improve the prediction. All error measures below refer to a test set consisting of 500 samples.
The effectiveness of the proposed optimization scheme of Section 3.2 has been investigated in an ablation study, where the results are summarized in Table 2. The table outlines statistical moments of the resulting heat flux distribution 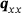 , as well as global MSE metrics. There it can be observed that the
, as well as global MSE metrics. There it can be observed that the  -net significantly outperforms the UResNet when utilizing the optimization scheme. Adding the
-net significantly outperforms the UResNet when utilizing the optimization scheme. Adding the  -net on top of the
-net on top of the  -net significantly improves the prediction, especially the errors on the peak values of the heat flux, which supports the design purpose of the
-net significantly improves the prediction, especially the errors on the peak values of the heat flux, which supports the design purpose of the  -net, delivering a good field prediction.
-net, delivering a good field prediction.
 -net is shown. The “conv” keyword before each layer has been omitted for readability. Each operation is read as “(conv) kernel size/stride.” “Max” refers to Max-pooling. Operations displayed in parallel are evaluated in parallel as an inception module.
-net is shown. The “conv” keyword before each layer has been omitted for readability. Each operation is read as “(conv) kernel size/stride.” “Max” refers to Max-pooling. Operations displayed in parallel are evaluated in parallel as an inception module. -net -net |
 -net -net |
||||
|---|---|---|---|---|---|
| Down path: IIVE | Up path IIIVE | PredictorVE | Down path IIV | Up path IIIV | PredictorV |
| 3/2–5/2–Max 3/2 | 2/2T–4/2T | 2· 3/1–1/1  |
3/2–5/2–Max/2 | Add ← IIV | 3· 3/1 |
| Concat | Concat | Add | Concat | 2/2T- 4/2T | 1/1 |
| 1/1 | 1/1 | 1/1 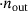 |
1/1 | Concat | |
Concat 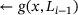 |
3· 3/1 | 1/1 | |||
| 3· 3/1 | |||||
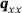 , whereas the error metrics in the right box are global over all components. The best performing model is marked with boldface in each metric.
, whereas the error metrics in the right box are global over all components. The best performing model is marked with boldface in each metric.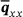 [%] [%] |
std 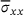 [%] [%] |
skew 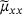 [%] [%] |
peak flux [%] [%] |
MSE [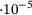 ] ] |
rel  [%](field) [%](field) |
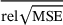 [%] (homogenized) [%] (homogenized) |
≈params | |
|---|---|---|---|---|---|---|---|---|
| U-ResNet | 0.35 | 1.95 | 19.80 | 3.31 | 9.35 | 2.74 | 1.11 | 780 000 |
 direct direct |
1.41 | 2.22 | 84.96 | 32.36 | 60.60 | 6.97 | 1.73 | 310 000 |
 pretrained pretrained |
0.21 | 0.61 | 14.14 | 7.79 | 6.71 | 2.32 | 0.51 | 310 000 |
 direct direct |
0.33 | 0.71 | 15.96 | 5.06 | 7.51 | 2.45 | 0.64 | 505 000 |
 pretrained pretrained |
0.19 | 0.61 | 10.13 | 2.33 | 3.11 | 1.58 | 0.46 | 505 000 |
 multi-pretrain multi-pretrain |
0.23 | 0.57 | 9.14 | 2.14 | 2.96 | 1.54 | 0.41 | 505 000 |
In the subsequent figures, the U-ResNet, which has been reimplemented from Santos et al. [15], is compared to the previously best performing model, that is, the  -net pretrained multiple times. In Figure 3, it is quantified how well the machine learned model recovers the actual distribution of the heat flux. As can be seen, the proposed
-net pretrained multiple times. In Figure 3, it is quantified how well the machine learned model recovers the actual distribution of the heat flux. As can be seen, the proposed  -net miss-classifies only ≈6% of the pixels, whereas the comparable U-ResNet has more than ≈12% of pixels wrongly predicted over the entire test set. The
-net miss-classifies only ≈6% of the pixels, whereas the comparable U-ResNet has more than ≈12% of pixels wrongly predicted over the entire test set. The  -net captures the underlying physics of the problem, delivers a smooth field prediction as well as accurate peak value predictions.
-net captures the underlying physics of the problem, delivers a smooth field prediction as well as accurate peak value predictions.
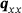 is compared using the models best predicting
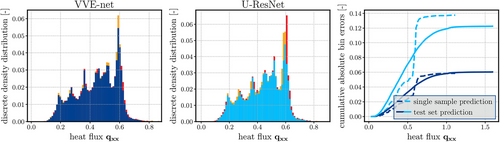
is compared using the models best predicting  -net and the U-ResNet for one random sample of the test set (left). The red bars denote the overestimation of the model in the current bin, and the orange bars denote the under estimation, respectively. On the right, the relative cumulative bin errors are shown, for the plotted sample (on the left) in dashed lines, and averaged over the entire test set in full lines, where the colors associate to each model shown on the left.
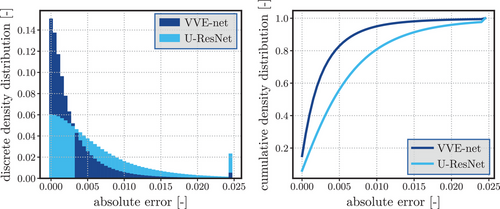
-net and the U-ResNet for one random sample of the test set (left). The red bars denote the overestimation of the model in the current bin, and the orange bars denote the under estimation, respectively. On the right, the relative cumulative bin errors are shown, for the plotted sample (on the left) in dashed lines, and averaged over the entire test set in full lines, where the colors associate to each model shown on the left.An increasingly strict error measure is considered in Figure 4, since Figure 3 disregards the position of the pixels, for example, a random permutation of the predicted pixels would not be reflected in the error metric. The pixel error compares each pixel with the solution at its position. Once again, a distribution over the entire test set and all components of 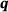 is presented. Every prediction error larger than
is presented. Every prediction error larger than 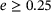 is capped and summarized to 0.25, which hides the long tail of the U-ResNet's prediction errors and ignores the single pixel maximum prediction error. In general, the left skew of the error distribution of the
is capped and summarized to 0.25, which hides the long tail of the U-ResNet's prediction errors and ignores the single pixel maximum prediction error. In general, the left skew of the error distribution of the  -net implies that most of the pixels have a very low prediction error, which is also reflected in the cumulative pixel error distribution, where more than 80% of pixels have a lower absolute error than
-net implies that most of the pixels have a very low prediction error, which is also reflected in the cumulative pixel error distribution, where more than 80% of pixels have a lower absolute error than 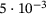 .
.
5 CONCLUSION
We developed a new efficient model layout of fully convolutional neural networks, which significantly outperforms recent state-of-the-art models while having fewer model parameters. There is multiple contributions improving the model, one being a staggered optimization scheme to ensure an excellent low-frequency prediction. The other improvement is found by superimposing a U-Net to refine the low-level prediction, reducing the errors on the peak values by 70%. The code of the model implementation is made freely available in Lissner [13]. The model has been applied in microstructure modeling under thermal boundary conditions, achieving a homogenization error of 0.2%. The model could be easily adopted to different physical boundary conditions once the data are readily available.
ACKNOWLEDGMENTS
Funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy—EXC 2075-390740016. Contributions by Felix Fritzen are funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the Heisenberg program DFG-FR2702/8-406068690 and DFG-FR2702/10-517847245. We acknowledge the support by the Stuttgart Center for Simulation Science (SimTech).
Open access funding enabled and organized by Projekt DEAL.




