Generative learning-based model for the prediction of 2D stress distribution
Abstract
In this study, we introduce a Generative learning-based approach to accelerate Finite Element simulations. The aim is to explore the ability of a Generative learning-based approach to predict the output of Finite Element simulations. Often, the drawback of classical regression models is that they are bound to the distribution of training data and cannot extrapolate outside of the training domain. In the current study, to overcome this, we propose a Generative Adversarial Network (GAN) based approach for learning to infer structural mechanics simulations. GANs have the ability to learn the underlying distribution of data and can efficiently extrapolate outside the training range. We train the proposed network on data obtained from classical Finite Element simulations based on linear elastic and Johnson-Cook plasticity models. The goal here is to understand the ability of a GAN to replace FEM by incorporating the underlying mechanics knowledge into the network to enhance the generalizing ability of the network for various materials on various loading and boundary conditions. We propose an encoder-decoder-like U-Net generator architecture with activated skip connections and a PatchGAN-based discriminator that discriminates based on local patches of data leading to a more robust critique for the generator. The advantage of the proposed framework is that it takes inputs such as the nodal information, their corresponding edges, nodal coordinates and the boundary conditions for each particular node from a Finite Element pre-processor and computes the von Mises stress at each node as output that can be read by a Finite Element post-processor. Also, the novelty of the proposed GAN is that, unlike the existing literature, it takes nodal values such as applied Boundary conditions and coordinates as inputs instead of images and performs nonlinear regression with Finite Element data and gives von-Mises stresses at each node as output.
1 INTRODUCTION
Finite Element simulations have become a crucial part of manufacturing and are extensively used in research, academics and industry. These numerical methods can, depending on the complexity of the boundary value problem (BVP) and geometry being solved, lead to computationally extensive and complex simulations. Often their high computational cost is controlled by using reduced order models or surrogates, but at the expense of accuracy [1-6]. Vehicle crash analysis, for instance, is one of the more complicated problems solved using FE methods that have high computational costs and consume a lot of time [7] due to their geometric, material and contact nonlinearity.
Machine learning-based algorithms are gaining a lot of momentum for accelerating the computation time of structural simulations. Deep learning methods have demonstrated excellent results when utilized to speed up the physical simulations and learn the underlying physics without prior knowledge of the mechanical model [8-11]. In [12, 13], CNN-based models have been used to accelerate FE simulations without penalizing accuracy. Also, CNN-based models have been extensively used in solid mechanical simulations for inhomogeneous non-linear materials [14] and in continuum mechanical simulations [15].
The success in deep learning has emerged from finding the right structural inductive bias to apply to the correct network architecture. The success of CNN models in modelling FE simulation results from their translation invariance, weight sharing and locality which are desirable inductive biases for these FE or continuum-based models. That said, CNNs have a huge drawback concerning the generalization of the model. They can only interpolate inside the training range but cannot extrapolate to unseen combinations of data. This is where Generative Adversarial Networks (GANs) come in. The generator is indirectly trained based on the loss of the discriminator. This helps the generator understand the training set's underlying data distribution and generate samples from a similar kind of distribution rather than mapping inputs to outputs. This quality of the GANs is very desirable in modelling networks that do not overfit and can generalize on new data. In [16], a hybrid FEM and GAN-based method was used to classify faults in rotor-bearing systems. TopologyGAN was proposed in [17] to perform topology optimization of structures with isotropic solid material behaviour. Simple body deformations with a simply supported structure loaded at the centre are modelled in [18]. The novelty of the present study is that, unlike existing literature where GANs are used to generate synthetic data or used for data augmentation, we implement the generator as an FE surrogate that solves the BVP predicting required outputs. Hence rather than generating synthetic data through GANs, we use them to accept input from a FE Pre-processor and generate an output of a FE solver which can be further read by an FE Post-processor.
In the literature, images have been predominantly used as input and output to the GANs and even in mechanics-based applications to model the physical problem. In this study, we take the discretized BVP from an FE pre-processor with inputs such as the nodal information, their corresponding edges, nodal coordinates and the boundary conditions for each particular node from a Finite Element pre-processor and compute the von-Mises stress at each node along with their edge connections as output that can be read by a Finite Element post-processor.
2 GENERATION OF DATA FROM FE SIMULATIONS
We chose a rectangular plate with a hole, a well-studied DFG benchmark problem, for our study. The dimensions of the plate are varied between 0.2 to 0.4 m and also the position and diameter of the hole. The plate has Dirichlet boundary conditions applied on its left and right edges with the left edge completely fixed and the right edge loaded with tensile and compressive displacements. The displacement is varied from 0.01 to 0.1 m with an increment set of [0.02,0.05,0.1] m depending on the sidelength of the geometry so as to prevent excessive deformation or unrealistically high load for the geometry. This resulted in 6 different cases which constitute 5 plates for each case and different loads resulting in 3200 samples. Figure 1 shows the 6 cases of plates with holes.

The plate is simulated using aluminium with elastoplastic material behaviour using the isotropic Johnson-Cook model with the following material properties [19] as shown in Table 1.
| Young's modulus (GPa) | Poisson's ratio (-) | A (MPa) | B (MPa) | n (-) |
|---|---|---|---|---|
| 70 | 0.33 | 520 | 477 | 0.52 |
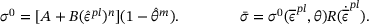 (1a)
(1a)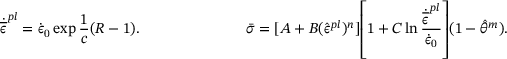 (1b)
(1b)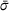 is the yield stress at nonzero strain rate,
is the yield stress at nonzero strain rate, 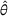 is the nondimensional temperature,
is the nondimensional temperature, 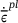 is the equivalent plastic strain rate,
is the equivalent plastic strain rate, 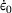 , n and C are material parameters measured from experiments,
, n and C are material parameters measured from experiments, 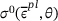 is the static yield stress and
is the static yield stress and 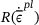 is the ratio of the yield stress at nonzero strain rate to the static yield stress.
is the ratio of the yield stress at nonzero strain rate to the static yield stress.The Finite Element solver ABAQUS is used to solve the BVP and generate data required for the GANs and the whole process is automated using Python scripting. Since the finite element solver does not output the results in an open-source format, an ODB2VTK interface is used to convert the ODB files into VTK format that is open-source and is imported into Python for training the GAN. From the discussed input combinations, a total of 3200 samples are generated.
3 GENERATIVE ADVERASARIAL NETWORKS
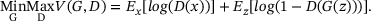 (2)
(2)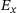 is the target or actual output over all the real data instances,
is the target or actual output over all the real data instances, 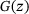 is the output generated by the generator with given noise z. The output of the discriminator for a generated input for a sample z is denoted by D(G(z)) and
is the output generated by the generator with given noise z. The output of the discriminator for a generated input for a sample z is denoted by D(G(z)) and 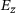 is the expected value over all random inputs to the generator. A lot of generator and discriminator architectures have been proposed since their inception. GANs have been widely used in large language models [20, 21], image segmentation, deepfakes and upscaling [22-24] and disease diagnosis [25, 26].
is the expected value over all random inputs to the generator. A lot of generator and discriminator architectures have been proposed since their inception. GANs have been widely used in large language models [20, 21], image segmentation, deepfakes and upscaling [22-24] and disease diagnosis [25, 26].In this study, we propose a residual U-net-based generator architecture with activated skip connections. The architecture comprises the encoder, decoder and symmetric skip connections between the encoder and decoder blocks. The encoder block consists of densely connected convolution blocks that help propagate the input features without any losses. The skip connections from the encoder to the decoder play a key role in reconstructing the fine details of the final prediction. Each block in the encoder consists of a convolutional layer, a batch normalization layer, and a swish activation.
The discriminator is based on a PatchGAN which differentiates data based on local patches rather than single probability output. This is rather desirable in this study because the local distribution of stresses plays a vital role in the global distribution. We employ binary cross entropy as a loss function for the discriminator with a gradient penalty and gradient clipping. For the generator, a combination of mean squared error and cross-entropy losses have been used for training. The architecture of the proposed generator is shown in Figure 2.
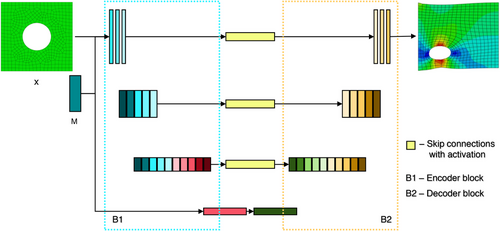
The generator receives the nodal information from the FE preprocessor and boundary conditions as input. The generator then tries to reconstruct and predict the von-Mises stress distribution in the output. The discriminator then takes the generated data and discriminates between the real and synthesized data and this process iteratively trains both the networks.
4 NETWORK TRAINING AND HYPERPARAMETER TUNING
Out of 3200 training data samples, 3000 samples are used for training the proposed network. The network was trained for 220k epochs. The network hyperparameters such as the number of filters of convolution layers, the dimension of the latent vector for the generator and the number of residual blocks in the generator and layers of the discriminator are critical to have good model performance. To achieve this, the Hyperband search algorithm [27] is employed. The hyperparameter sampling domain and the selected hyperparameters are shown in Table 2.
| Hyperparameters | Paremeter set | Selected Hyperparameters |
|---|---|---|
| Residual blocks | [1,2,…,8] | 4 |
| Latent vector dimension | [4,8,16,…,128] | 16 |
| Discriminator layers | [1,2,…,8] | 5 |
| Generator lrate | [1e-5 to 1e-3] | 5e-4 |
| Discriminator lrate | [1e-5 to 1e-3] | 1e-3 |
The network is optimized and trained using the Adam optimizer and mean squared error is used as the loss metric. A learning rate of 3E-3 is used with an exponential decay over epochs starting from the 200th epoch. This is done to eliminate the local minima that were being observed after 200 epochs into the training.
5 RESULTS AND DISCUSSION
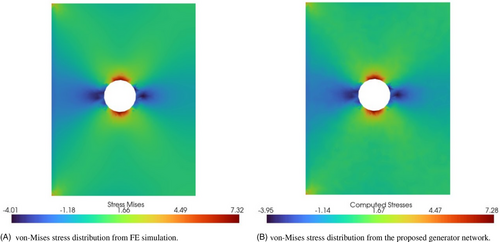
The network computed results are then embedded into the VTK file with a key named “Computed Stresses” to facilitate the comparison of the results in a FE post-processing environment. Here a comparison is drawn between the von-Mises stress distribution from the FE simulation with the generator-computed von-Mises stress distribution. A computational gain of 9.8% has been observed by using the GAN, also considering the computational effort for training the network. The results section is subdivided to discuss the performance of the GANs on extrapolation results.
5.1 From the trained limit
The proposed GAN is evaluated on the test set and an MSE error of 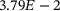 is achieved for the whole test batch, which roughly translated to an error of around
is achieved for the whole test batch, which roughly translated to an error of around 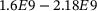 and
and  GPa for different input geometry and loading cases. The results from the generator show an excellent correlation to the FE simulations with a very small error in the magnitude. This shows that the GANs can efficiently replicate FEM simulations within the training range.
GPa for different input geometry and loading cases. The results from the generator show an excellent correlation to the FE simulations with a very small error in the magnitude. This shows that the GANs can efficiently replicate FEM simulations within the training range.
To determine the efficiency of purely data-driven models, in modelling FEM simulations, deformed displacements are also predicted using the same architecture and show good agreement with the FE results as shown in Figure 3. The prediction has a good overall structure but has some artefacts at the boundary which are discussed in the next section.
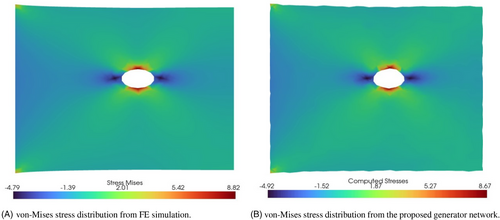
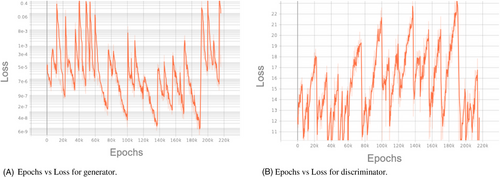
Figure 4 shows the epoch versus loss plot of the trained GAN. One can observe that the losses of the generator and discriminator follow opposite trends that is, when the generator loss increases, the discriminator loss decreases and vice versa. It is because the networks engage in a Zero-sum game and this is the reason for GANs to be notoriously hard to train.
5.2 From the extrapolation
The extrapolation ability of the proposed network is tested on a test sample as shown in Figure 5. The geometry and the loading condition are taken out of the training set for that particular case and the samples are evaluated using the trained generator. In Figure 5, although it looks identical, some artefacts can be observed in the stress distribution over the entire domain. This example is taken with a rectangular plate of side lengths 0.3 and 0.5 m (where the maximum side length of the training set is 0.4 m) respectively and a displacement of 0.125 m applied at the right end of the plate (maximum displacement applied in training is 0.1 m). The network although is able to predict the stress distribution and magnitude very well, it is not as accurate as that of the test samples with parameters in the bounds of the training range.
Although GANs have the ability to extrapolate and generate realistic samples, it is limited, in this case by the lack of physical knowledge in the network. Usually, GANs are applied to probabilistic data and trained on the likelihood of the generated data being close to realistic data. But in this case, the nature of the problem is nonlinear regression and it is a very unique scenario for GANs to be used for curve fitting. In this scenario, to improve the generalizing ability, physical information is also required to be introduced into the loss function by using a physics-informed GAN. Also, the convolution layers used in the generator are not efficient in dealing with temporal data. Hence the current architecture cannot be used to get the evolution of stresses over time. This limitation can be overcome by using recurrent-based layers inside the generator.
6 CONCLUSION
In the current study, we deploy a GAN-based Finite Element model, to compute the final deformations and von-Mises stress distribution that can be read by an FE postprocessor from a discretized FE Preprocessor input. We propose a novel approach where instead of generating synthetic data, we employ the generator to synthesize required FE output such as von-Mises stress at each node, in this case. The proposed architecture is based on a residual U-net generator architecture and PatchGAN-based discriminator architecture. A data-driven approach is employed to train the model and exploit the relational inductive bias of the GANs. A plate with a hole with various dimensions, positions and boundary conditions is simulated using an FE-Solver which is used for training the model. The trained generator shows a strong correlation with FE simulations and has the ability to extrapolate the data outside of training bounds to an extent. The model's extrapolation ability deteriorates when the data exceeds 20%–25% over the training bounds and cannot be used for any meaningful predictions. That said, the model can interpolate between the training set efficiently. The next steps will be to overcome the limitations of the current architecture by proposing a hybrid, data+physics-driven model, with an LSTM-based generator. The proposed architecture has a very low error relative to that of FEM (2.78%) and can generate results that can be read by an FE Postprocessor. We explore nonlinear regression for GANs using Finite Element methods in which the novelty of the study lies.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial support provided by Deutsche Forschungsgemeinschaft Priority Programme: SPP 2353 (DFG Grant No. STO 469/16-1).
Open access funding enabled and organized by Projekt DEAL.




