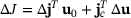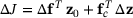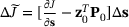Theoretical aspects and applications of goal-oriented reanalysis methods
Abstract
In this contribution, a method for goal-oriented reanalysis is presented. The process allows predicting the change in a quantity of interest due to structural modifications (design changes), for example, the shape, the topology, material properties, and so forth. The approach is based on a goal-oriented method using primal and dual problems. Furthermore, the procedure is easy to implement in existing finite element programs because no derivatives with respect to the design variables are necessary. The proposed method can be used in classical applications with successive design steps, such as structural optimization, reliability, or structural damage analysis. The repeated structural analysis and calculating quantities of interest involve significant computational effort. Goal-oriented reanalysis methods can reduce the overall computational cost in the numerical simulation.
1 INTRODUCTION
In many applications, design modifications (design changes) are investigated. The design variables are, for instance, parameters that describe the cross-sections, the geometry, the topology or material parameters, and so forth. Classical applications with successive design steps are, for example, structural optimization, reliability analysis, or structural damage analysis. Hundreds or even thousands of different design configurations are investigated in many cases, and the state equation must be solved for each design step. The repeated structural analysis of large problems involves significant computational effort.
An efficient reanalysis method can be used to reduce the overall computational cost. The goal of classical global reanalysis procedures is to evaluate the change in the state variables for some given design modifications efficiently and with sufficient accuracy without directly solving the set of modified equations of the changed problem. Reanalysis techniques for the computation of changes in the state variables due to given design changes have been extensively studied in the literature, for example [1-6], among many others. It has been formulated for static and dynamic problems. Furthermore, reanalysis methods have been applied to sensitivity analysis and optimization problems [7-9].
Very often, we are interested only in certain quantities of interest J, and so-called goal-oriented or duality techniques or adjoint state methods can be used to compute J. This is known as the concept of influence functions in structural mechanics, see for example [10]. The quantities of interest could be point values, for example, a displacement component, a stress component at a point, or some integral value.
This contribution presents a method for predicting the change in a quantity of interest 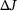 due to structural modifications using the primal and dual solutions changes. The changes in the primal and dual solutions are computed by using the residual increment approximation (RIA) method [6]. This reanalysis procedure is based on a formulation in terms of residual increments. In contrast to other existing reanalysis methods (e.g., the CA method [11]), which are based on the evaluation of changed stiffness matrices, only residual vectors must be computed and stored. Hence, this yields an efficient goal-oriented reanalysis method to compute the change in the quantities of interest due to given design modifications with sufficient accuracy without directly solving the set of modified equations of the changed problem.
due to structural modifications using the primal and dual solutions changes. The changes in the primal and dual solutions are computed by using the residual increment approximation (RIA) method [6]. This reanalysis procedure is based on a formulation in terms of residual increments. In contrast to other existing reanalysis methods (e.g., the CA method [11]), which are based on the evaluation of changed stiffness matrices, only residual vectors must be computed and stored. Hence, this yields an efficient goal-oriented reanalysis method to compute the change in the quantities of interest due to given design modifications with sufficient accuracy without directly solving the set of modified equations of the changed problem.
2 FORMULATION OF GOAL-ORIENTED ANALYSIS
2.1 The quantities of interest
We are interested in a quantity of interest J in goal-oriented or duality techniques. We consider a quantity of interest 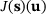 which depends on the state variables
which depends on the state variables 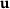 and on some design variables
and on some design variables  , that is, parameters which describe the cross-sections, the geometry, the topology or material parameter, and so forth. In this paper, the quantity
, that is, parameters which describe the cross-sections, the geometry, the topology or material parameter, and so forth. In this paper, the quantity  is linear in
is linear in  , but possibly nonlinear in
, but possibly nonlinear in  . Furthermore, we suppose that J is differentiable with respect to
. Furthermore, we suppose that J is differentiable with respect to 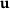 .
.
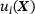 or a stress component
or a stress component 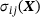 at a point
at a point 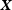 . Furthermore, it can be some integral value, for example,
. Furthermore, it can be some integral value, for example,
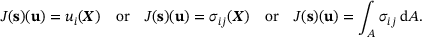 (1)
(1)2.2 The primal and dual (adjoint) problems
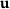 is determined by the primal problem in terms of a residual
is determined by the primal problem in terms of a residual  . This paper considers linear problems, that is,
. This paper considers linear problems, that is,  is linear in
is linear in 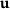 . For a given fixed design
. For a given fixed design  , the primal solution
, the primal solution 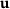 is given from
is given from
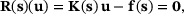 (2)
(2)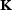 is the stiffness matrix and
is the stiffness matrix and 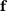 is the primal load vector. Both,
is the primal load vector. Both, 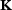 and
and 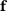 depend only on
depend only on  .
.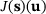 , the corresponding dual or adjoint solution, influence function or generalized Green's function
, the corresponding dual or adjoint solution, influence function or generalized Green's function is determined by the so-called dual problem written in terms of the dual residual vector
is determined by the so-called dual problem written in terms of the dual residual vector 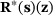 . For a given fixed design
. For a given fixed design  , the dual solution
, the dual solution  is given from
is given from
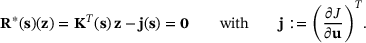 (3)
(3) is the so-called dual load vector. For self-adjoint problems, we have
is the so-called dual load vector. For self-adjoint problems, we have 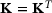 .
.It is important to note that the residual vectors 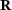 and
and 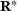 and the quantities of interest J are linear in
and the quantities of interest J are linear in 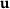 and
and  , respectively, but possibly nonlinear in
, respectively, but possibly nonlinear in  .
.
2.3 Computing the quantity of interest
The quantity of interest J can be computed in two different ways. Classically, the primal problem 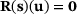 is solved and
is solved and 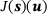 can be computed in a post-processing step.
can be computed in a post-processing step.
Alternatively, the dual solution  can be used, which can have a significant advantage.
can be used, which can have a significant advantage.
 and
and 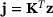 respectively, and hence
respectively, and hence
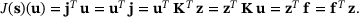 (4)
(4) , the quantity J is given by evaluating a scalar product, that is,
, the quantity J is given by evaluating a scalar product, that is,
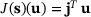 (5)
(5)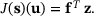 (6)
(6) is known, the quantity of interest
is known, the quantity of interest 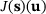 can be computed for arbitrary primal load vectors
can be computed for arbitrary primal load vectors 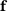 just by a simple scalar product of
just by a simple scalar product of  and
and 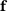 . This is, for instance, used in structural mechanics in the context of influence functions to compute J for many different load cases.
. This is, for instance, used in structural mechanics in the context of influence functions to compute J for many different load cases.3 GOAL-ORIENTED REANALYSIS
Reanalysis is used in many fields which are concerned with design modifications. Let 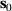 be a given initial design and let
be a given initial design and let 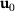 be the corresponding solution of (2). Assume a changed design
be the corresponding solution of (2). Assume a changed design 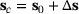 and let
and let 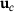 be the corresponding solution.
be the corresponding solution.
Furthermore, let 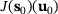 be the value of J for the initial design
be the value of J for the initial design 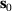 and let
and let 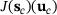 be the value of J for a given changed design
be the value of J for a given changed design 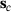 .
.
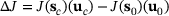 (7)
(7) with sufficient accuracy without solving the complete modified equations.
with sufficient accuracy without solving the complete modified equations.3.1 The initial and changed primal and dual problems
3.2 The change in the quantity of interest
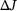 can be computed in two different ways. Firstly, we use a formulation with
can be computed in two different ways. Firstly, we use a formulation with 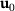 and the change
and the change 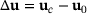 . With (5) we obtain after some manipulations
. With (5) we obtain after some manipulations
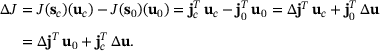 (12)
(12)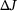 depends on
depends on 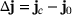 and the change
and the change 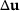 .
.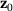 and the change
and the change 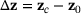 . By using (6) we obtain
. By using (6) we obtain
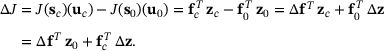 (13)
(13)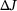 depends on
depends on 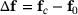 and the change
and the change 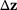 .
.Finally, according to (5) and (6), we obtain the two equivalent relations (12) and (13) to express the change 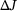 .
.
The big advantage of the second formulation (13) can be summarized as follows: If the dual solution 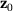 and the change
and the change 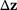 for a fixed
for a fixed 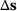 are known, the change in the quantity of interest
are known, the change in the quantity of interest 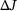 can be computed for arbitrary primal load vectors
can be computed for arbitrary primal load vectors 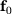 and changes
and changes 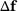 , that is,
, that is, 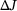 can be computed for many different primal load cases just by evaluating simple scalar products.
can be computed for many different primal load cases just by evaluating simple scalar products.
4 COMPUTING THE CHANGE IN THE QUANTITY OF INTEREST
To compute 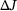 , we have to evaluate (12) or (13). The changes in the primal and dual loads
, we have to evaluate (12) or (13). The changes in the primal and dual loads 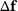 and
and  can easily be computed with less computational effort. The only challenge is the computation of approximations of the increments
can easily be computed with less computational effort. The only challenge is the computation of approximations of the increments 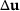 or
or 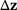 with sufficient accuracy. This can be done by using reanalysis methods. A general efficient reanalysis method for the computation of an approximation of
with sufficient accuracy. This can be done by using reanalysis methods. A general efficient reanalysis method for the computation of an approximation of 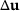 based on residual increment approximations (RIA method) has been presented in [6]. The paper uses this method to compute the changes
based on residual increment approximations (RIA method) has been presented in [6]. The paper uses this method to compute the changes 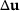 and
and 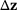 with sufficient accuracy without solving the complete modified equations.
with sufficient accuracy without solving the complete modified equations.
4.1 Reanalysis for the primal problem
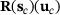 defined in (10). Although, the problem is linear in
defined in (10). Although, the problem is linear in 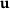 , the residual is in the general case nonlinear in
, the residual is in the general case nonlinear in  , that is,
, that is,
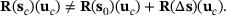 (14)
(14)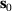 as
as
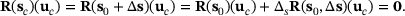 (15)
(15) is given as
is given as 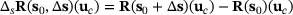 . Furthermore, we obtain with
. Furthermore, we obtain with 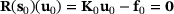 for the first term on the right side in (15) the relation
for the first term on the right side in (15) the relation
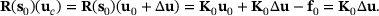 (16)
(16)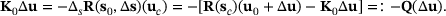 (17)
(17)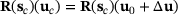 is not zero for some approximation of
is not zero for some approximation of 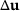 . The above equation can be expressed as the recurrence relation
. The above equation can be expressed as the recurrence relation
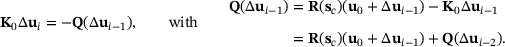 (18)
(18)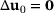 . Then, recurrence yields the first two values from
. Then, recurrence yields the first two values from

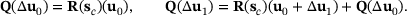
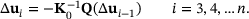 (19)
(19)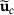 approximation for the changed design
approximation for the changed design 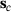 is obtained as
is obtained as 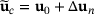 .
.The stiffness matrix 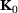 is the same as used for the solution of the initial design and, therefore, is usually already given in the decomposed form. Therefore, the computation of
is the same as used for the solution of the initial design and, therefore, is usually already given in the decomposed form. Therefore, the computation of 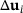 in (18) requires just forward and backward substitution. Only residual vectors must be computed and stored within the reanalysis method.
in (18) requires just forward and backward substitution. Only residual vectors must be computed and stored within the reanalysis method.
The reanalysis procedure adapted from Equation 18 is a local approximation based on information calculated at a single point (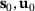 ). The results can be improved using a vector-valued rational approximation method introduced in [12] and applied to linear reanalysis problems in [4].
). The results can be improved using a vector-valued rational approximation method introduced in [12] and applied to linear reanalysis problems in [4].
This method is used within the numerical examples in the present paper. Details about this method and the overall algorithm of the reanalysis method are given in [6].
4.2 Reanalysis for the dual problem
In the same way, as for the primal problem, we can formulate a reanalysis method for the dual problem, that is, we want to compute an approximation of 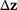 to evaluate the relation (13).
to evaluate the relation (13).
 as
as
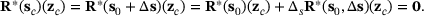 (20)
(20) is given as
is given as 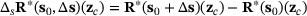 . Furthermore, we obtain with
. Furthermore, we obtain with 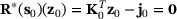 for the first term on the right side in (20) the relation
for the first term on the right side in (20) the relation
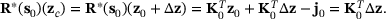 (21)
(21)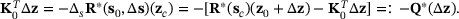 (22)
(22) is not zero for some approximation of
is not zero for some approximation of 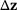 . Finally, this can be expressed as the recurrence relation in the form of
. Finally, this can be expressed as the recurrence relation in the form of
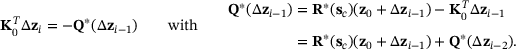 (23)
(23)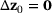 . Then, recurrence yields the first two values from
. Then, recurrence yields the first two values from

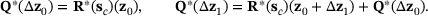
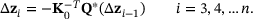 (24)
(24)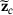 for the changed design
for the changed design 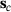 is obtained as
is obtained as 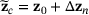 .
.In the same way, as for the primal problem, the results are improved by using a vector-valued rational approximation method. This is used within the numerical examples. Details and the overall algorithm are given in [6].
4.3 First-order adjoint sensitivity relation
In many applications, the classical first-order approximation (FOA) is used to predict the changes in the state variables or quantities of interest due to design modifications, see for example [13, 14]. The results are valid only for very small design changes. In this study, we compare the proposed reanalysis method with the classical FOA for completeness.
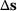 we obtain the first-order approximation
we obtain the first-order approximation 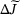 for the change in the quantity of interest in the form of
for the change in the quantity of interest in the form of
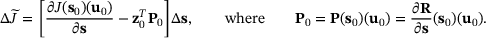 (25)
(25)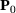 is the co-called pseudo load matrix, see for example [13, 14] for details and explicit formulations.
is the co-called pseudo load matrix, see for example [13, 14] for details and explicit formulations.The advantage of the first-order approximation (25) is that the relation depends only on the known initial primal and dual solutions 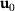 and
and 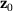 , that is, the changes in the primal and dual solutions are not required. The disadvantage of this method is that it requires the derivatives with respect to the design variables, that is, we have to compute
, that is, the changes in the primal and dual solutions are not required. The disadvantage of this method is that it requires the derivatives with respect to the design variables, that is, we have to compute 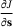 and
and 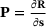 . This can be very difficult and expensive in many situations and model problems. However, it is a robust method and is used in many applications. Therefore, we compare the FOA with the other proposed methods within the numerical examples.
. This can be very difficult and expensive in many situations and model problems. However, it is a robust method and is used in many applications. Therefore, we compare the FOA with the other proposed methods within the numerical examples.
5 NUMERICAL EXAMPLE
In the above sections, we have considered three methods to compute an approximation of the change 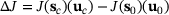 for a given fixed design change
for a given fixed design change  . The methods are summarized in Table 1 and investigated in the following numerical example. We consider the model problem of linear elasticity.
. The methods are summarized in Table 1 and investigated in the following numerical example. We consider the model problem of linear elasticity.
 .
.Approximations of the changes in the primal and dual solutions  and
and 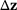 required in methods 1 and 2 are computed by using the reanalysis method from (18) and (23), respectively. Furthermore, the accuracy of
required in methods 1 and 2 are computed by using the reanalysis method from (18) and (23), respectively. Furthermore, the accuracy of 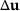 and
and 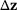 are improved using a vector-valued rational approximation method as described in [6].
are improved using a vector-valued rational approximation method as described in [6].
We examine a bi-material solid under tension with large deformations; see Figure 1A. The body is clamped on the left side and loaded by traction  . The design variables are the Young's moduli E1 and E2 in the two domains, that is,
. The design variables are the Young's moduli E1 and E2 in the two domains, that is, 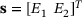 and
and 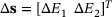 . For simplicity, we consider only changes in the second variable E2 and keep E1 constant. For the initial design
. For simplicity, we consider only changes in the second variable E2 and keep E1 constant. For the initial design 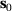 , we chose
, we chose 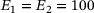 . The Poisson's ratio for both domains is
. The Poisson's ratio for both domains is 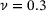 , and the finite element discretization consists of classical bilinear Q4 elements.
, and the finite element discretization consists of classical bilinear Q4 elements.
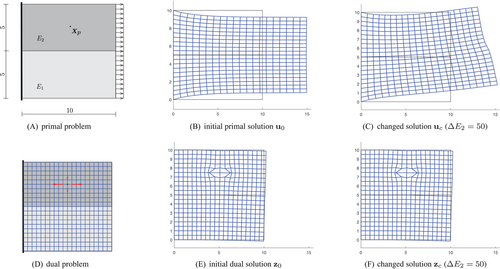
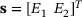 with the initial design
with the initial design 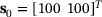 . A large design change
. A large design change 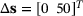 is investigated. The quantity of interest is the stress component
is investigated. The quantity of interest is the stress component 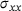 at point
at point 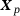 , that is,
, that is, 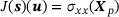 . The dual load case (red arrows in (d)) causes an approximation of a unit dislocation at point
. The dual load case (red arrows in (d)) causes an approximation of a unit dislocation at point 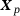 .
.The quantity of interest is the stress component 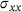 at point
at point 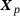 , that is,
, that is, 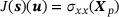 . The dual load case
. The dual load case 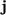 (red arrows in Figure 1D) causes an approximation of a unit dislocation at point
(red arrows in Figure 1D) causes an approximation of a unit dislocation at point 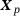 . The primal and dual solutions for the initial design are given in Figures 1B and E.
. The primal and dual solutions for the initial design are given in Figures 1B and E.
In this example, a significant change in Young's moduli is considered, that is, we investigate a design change 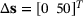 . This yields a significant change in the primal solution; see Figure 1C. The difference in the dual solution due to the design change is relatively small; see Figure 1F.
. This yields a significant change in the primal solution; see Figure 1C. The difference in the dual solution due to the design change is relatively small; see Figure 1F.
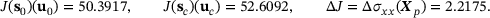 (26)
(26) ): Accuracy of the different methods (see Table 1).
): Accuracy of the different methods (see Table 1).Results for 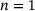 : : |
Results for 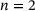 : : |
||||
|---|---|---|---|---|---|
| Method | Approximation of 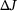 |
Rel. error [%] | Method | Approximation of 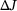 |
Rel. error [%] |
| 1 | 2.1349 | 3.7241 | 1 | 2.1878 | 1.3397 |
| 2 | 2.1619 | 2.5076 | 2 | 2.2175 | 0.0018 |
| 3 | 2.7415 | 23.628 | 3 | 2.7415 | 23.628 |
Results for 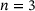 : : |
Results for 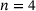 : : |
||||
|---|---|---|---|---|---|
| Method | Approximation of 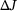 |
Rel. error [%] | Method | Approximation of 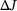 |
Rel. error [%] |
| 1 | 2.2179 | 0.0164 | 1 | 2.2175 | 0.0014 |
| 2 | 2.2176 | 0.0027 | 2 | 2.2175 | 0.0001 |
| 3 | 2.7415 | 23.628 | 3 | 2.7415 | 23.628 |
- Note: The results are given for different n, which is the number of iterations used within the reanalysis in methods 1 and 2. The relative errors are given w.r.t. the exact change
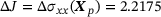 .
.
Method 1 and 2 yield very accurate results even for significant design changes. Method 3 is just a first-order relation and yields for significant design changes only a rough approximation. Furthermore, method 2 outperforms method 1 in this example because the change in the dual solution 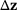 due to design changes
due to design changes  is relatively small. Hence, we can obtain a good approximation of
is relatively small. Hence, we can obtain a good approximation of 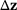 with few iterations within the reanalysis method. In contrast, the change
with few iterations within the reanalysis method. In contrast, the change 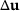 due to design changes
due to design changes 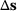 is huge. Therefore, we need more iterations within the reanalysis method to compute
is huge. Therefore, we need more iterations within the reanalysis method to compute 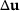 with high accuracy.
with high accuracy.
6 CONCLUSIONS
Reanalysis methods are very useful in reducing the computational effort within applications concerned with multiple design modifications, such as structural optimization, reliability analysis, or damage analysis. In this contribution, a goal-oriented reanalysis method for the prediction of the change in a quantity of interest due to structural modifications by using the changes in the primal and dual solutions has been presented.
The changes in the primal and dual solutions due to given design modifications are computed using the RIA method. This reanalysis procedure is based on a formulation in terms of residual increments. In contrast to other existing reanalysis methods (e.g., the CA method), which are based on evaluating changed stiffness matrices, only residual vectors must be computed and stored. The proposed method is very general and can be used for different design modifications. The overall goal-oriented reanalysis procedure is straightforward and can easily be implemented in existing finite element programs because no derivatives with respect to the design variables are necessary. The numerical example demonstrates that the method yields accurate results even for significant design changes. In the present paper, only linear problems are considered. The extension to nonlinear problems will be discussed in future work.
ACKNOWLEDGMENTS
Open access funding enabled and organized by Projekt DEAL.



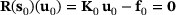
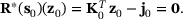
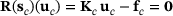
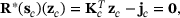
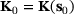 ,
, 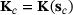 ,
, 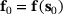 ,
, 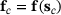 ,
, 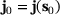 and
and 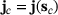 .
.