Can one hear the depth of the water?
Abstract
We discuss discrete-time dynamical systems depending on a parameter μ. Assuming that the system matrix 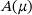 is given, but the parameter μ is unknown, we infer the most-likely parameter
is given, but the parameter μ is unknown, we infer the most-likely parameter 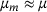 from an observed trajectory x of the dynamical system. We use parametric eigenpairs
from an observed trajectory x of the dynamical system. We use parametric eigenpairs 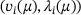 of the system matrix
of the system matrix 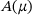 computed with Newton's method based on a Chebyshev expansion. We then represent x in the eigenvector basis defined by the
computed with Newton's method based on a Chebyshev expansion. We then represent x in the eigenvector basis defined by the 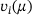 and compare the decay of the components with predictions based on the
and compare the decay of the components with predictions based on the 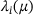 . The resulting estimates for μ are combined using a kernel density estimator to find the most likely value for
. The resulting estimates for μ are combined using a kernel density estimator to find the most likely value for 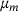 and a corresponding uncertainty quantification.
and a corresponding uncertainty quantification.
1 INTRODUCTION
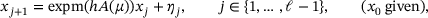 (1)
(1)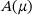 is a matrix depending on a parameter μ chosen from an interval
is a matrix depending on a parameter μ chosen from an interval 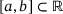 ,
,  is a noise term with
is a noise term with 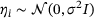 , h is the time increment of the discretization, and
, h is the time increment of the discretization, and 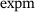 stands for the matrix exponential function. We assume that
stands for the matrix exponential function. We assume that 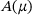 is diagonalizable for all
is diagonalizable for all 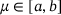 . We further assume that the dependency of A on μ is known, but the parameter μ itself is not. Estimating μ is the subject of this paper.
. We further assume that the dependency of A on μ is known, but the parameter μ itself is not. Estimating μ is the subject of this paper.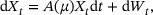
The paper focuses on the following example.
Example 1.1.Imagine we have a chain anchored below the water and on a pole above water. Submerged chain links are damped more than chain links in the air. The chain can be discretized by masses and springs like in Figure 1. We know the masses 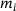 , the characteristics
, the characteristics 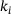 of the springs, and the damping when the masses are in the air as well as when they are in the water. However, we do not know the depth of the water μ or, if you like, how many of the masses are below water. The system is excited by external forces. We record the ensuing motion, that is we record the position of the masses at equidistant discrete time points, and try to infer the depth of water from said recording. Since the motion can be associated with the sound emitted one can arguably say that we are attempting to hear the depth of the water and hence the title of the paper.
of the springs, and the damping when the masses are in the air as well as when they are in the water. However, we do not know the depth of the water μ or, if you like, how many of the masses are below water. The system is excited by external forces. We record the ensuing motion, that is we record the position of the masses at equidistant discrete time points, and try to infer the depth of water from said recording. Since the motion can be associated with the sound emitted one can arguably say that we are attempting to hear the depth of the water and hence the title of the paper.
Discretization leads to a matrix 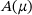 to describe this setup, where the parameter μ describes the depth of the water. We assume for simplicity that all masses are 1, that all spring characteristics are 1, and that the damping in water is 10, while the damping in air is 5. The mechanical system can be described with the second-order differential equation
to describe this setup, where the parameter μ describes the depth of the water. We assume for simplicity that all masses are 1, that all spring characteristics are 1, and that the damping in water is 10, while the damping in air is 5. The mechanical system can be described with the second-order differential equation
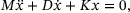 (2)
(2)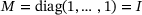 and
and 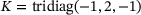 . The matrix D is diagonal with a transition on the diagonal from 5 for the parts in the air to 10 for the parts in water. To make this transition smooth and to account for a reduced damping near the surface caused by waves, we use sigmoid-functions on the diagonal,
. The matrix D is diagonal with a transition on the diagonal from 5 for the parts in the air to 10 for the parts in water. To make this transition smooth and to account for a reduced damping near the surface caused by waves, we use sigmoid-functions on the diagonal,
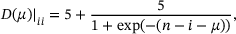
 . Equation (2) is a standard example of a quadratic eigenvalue problem that has been discussed in many publications, for instance in Refs. [2, 3]. We deliberately chose an overdamped system, that is one that fulfills
. Equation (2) is a standard example of a quadratic eigenvalue problem that has been discussed in many publications, for instance in Refs. [2, 3]. We deliberately chose an overdamped system, that is one that fulfills
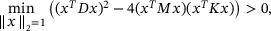
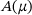 are real and nonpositive [2, 4]. We linearize this quadratic eigenvalue problem to
are real and nonpositive [2, 4]. We linearize this quadratic eigenvalue problem to
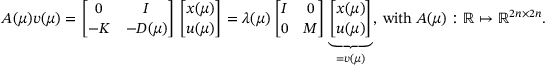
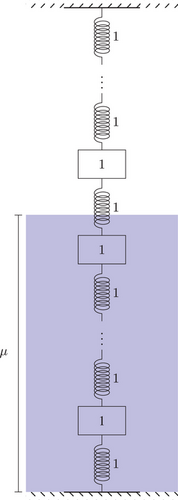
In this paper, we pursue the following idea: A discretized trajectory 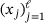 of the noisy dynamical system (1) is recorded. This is combined with approximations of the functions describing the eigenvalues
of the noisy dynamical system (1) is recorded. This is combined with approximations of the functions describing the eigenvalues 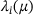 and eigenvectors
and eigenvectors 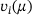 of
of 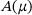 to estimate the most likely μ using a kernel density estimator. We choose a
to estimate the most likely μ using a kernel density estimator. We choose a 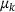 and use the
and use the 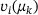 's for a coordinate transform to the eigenvector basis. We obtain new vectors
's for a coordinate transform to the eigenvector basis. We obtain new vectors 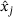 describing the trajectory in the eigenbasis. If we have chosen the correct
describing the trajectory in the eigenbasis. If we have chosen the correct 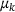 , then the components of
, then the components of 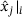 decrease like
decrease like 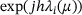 with time
with time 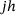 . Obviously, as soon as the components become too small, the influence of the noise η becomes dominant. Thus even with the correct
. Obviously, as soon as the components become too small, the influence of the noise η becomes dominant. Thus even with the correct 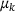 , the relation between
, the relation between 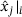 and
and 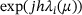 is not perfect. Nevertheless, each eigenpair i, each time step j, and each choice of
is not perfect. Nevertheless, each eigenpair i, each time step j, and each choice of 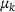 provide an estimate for μ. We combine all these estimates by employing a kernel density estimator, which will provide us with the most likely guess of μ based on the individual guesses and a corresponding probability density, that is an uncertainty extimate. This is demonstrated by the numerical example in Section 4. Before we discuss the experiments, we provide a brief review in Section 2 regarding the computation of parametric eigenpairs of
provide an estimate for μ. We combine all these estimates by employing a kernel density estimator, which will provide us with the most likely guess of μ based on the individual guesses and a corresponding probability density, that is an uncertainty extimate. This is demonstrated by the numerical example in Section 4. Before we discuss the experiments, we provide a brief review in Section 2 regarding the computation of parametric eigenpairs of 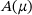 described in Mach and Freitag [5]. In Section 3, we discuss how μ is found.
described in Mach and Freitag [5]. In Section 3, we discuss how μ is found.
2 TAYLOR SERIES AND CHEBYSHEV EXPANSIONS OF 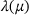 AND
AND 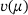
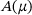 , see Mach and Freitag [5] for details. They show how one can compute an approximation to the eigenvalues and eigenvectors,
, see Mach and Freitag [5] for details. They show how one can compute an approximation to the eigenvalues and eigenvectors,
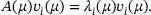
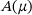 ,
, 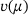 , and
, and 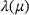 about an expansion point μ0. Under certain assumptions, the existence of such a series expansion for
about an expansion point μ0. Under certain assumptions, the existence of such a series expansion for 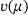 and
and 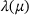 is shown in Kato's book on perturbation theory for linear operators [6]. In particular, if
is shown in Kato's book on perturbation theory for linear operators [6]. In particular, if 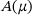 is real and symmetric such a series converges. The idea of using Taylor series expansions for the perturbation analysis is not new and goes at least as far back as 1939 [7]. The Taylor coefficients regarding the expansion point μ0 of v and λ can be successively computed by solving first
is real and symmetric such a series converges. The idea of using Taylor series expansions for the perturbation analysis is not new and goes at least as far back as 1939 [7]. The Taylor coefficients regarding the expansion point μ0 of v and λ can be successively computed by solving first
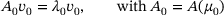
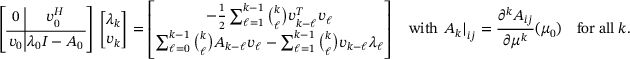
 and
and 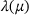 and the efficient implementation. In our numerical experiments, we are going to use the Matlab code provided by Mach [9]. In particular, if a Schur decomposition of A0 is computed in the initial step, recall we need to solve
and the efficient implementation. In our numerical experiments, we are going to use the Matlab code provided by Mach [9]. In particular, if a Schur decomposition of A0 is computed in the initial step, recall we need to solve 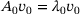 anyway, then this Schur decomposition can be used to transform
anyway, then this Schur decomposition can be used to transform
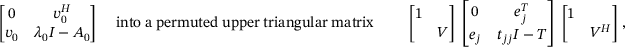
 [10-12]. The algorithm is described in many textbooks, among others in Aurentz et al. [13]. This enables us to compute the first p Taylor series coefficient for all eigenpairs in
[10-12]. The algorithm is described in many textbooks, among others in Aurentz et al. [13]. This enables us to compute the first p Taylor series coefficient for all eigenpairs in  .
.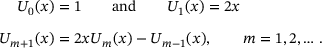
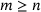 (follows with induction from Benjamin and Walton [14, Identity 3])
(follows with induction from Benjamin and Walton [14, Identity 3])
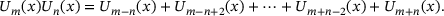
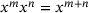 holds, means that the Chebyshev coefficients cannot be computed one-by-one as for the Taylor series coefficients, but have to be computed all at once. Nonetheless, approximating the products with
holds, means that the Chebyshev coefficients cannot be computed one-by-one as for the Taylor series coefficients, but have to be computed all at once. Nonetheless, approximating the products with 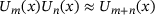 allows to use an approach similar to the Taylor polynomials to compute an initial approximation. Despite this rough approximation, the resulting eigenpairs are often accurate to three or four digits and serve as suitable starting points for a refinement with Newton's method, see Mach and Freitag [5] for further details. We observe that often the initial approximation places us within the area of quadratic convergence of Newton's method. Thus, three or four Newton steps often suffice to reach convergence to double precision.
allows to use an approach similar to the Taylor polynomials to compute an initial approximation. Despite this rough approximation, the resulting eigenpairs are often accurate to three or four digits and serve as suitable starting points for a refinement with Newton's method, see Mach and Freitag [5] for further details. We observe that often the initial approximation places us within the area of quadratic convergence of Newton's method. Thus, three or four Newton steps often suffice to reach convergence to double precision.Despite the increased costs, the Chebyshev expansion is preferable, due to the advantage of achieving a high approximation quality relatively homogeneously over the expansion interval. However, we observe a slight increase of the approximation error near the endpoints of the interval. The Taylor series approximation, by contrast, is mainly accurate near the expansion point μ0 and looses accuracy with increased distance from μ0. Thus, the numerical experiments in this paper solely use the Chebyshev expansion.
3 FINDING THE UNKNOWN PARAMETER μ
In this section, we discuss how μ can be found with the help of a trajectory 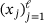 and the eigenpairs
and the eigenpairs 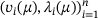 of
of 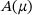 .
.
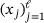 onto the eigenbasis. That is, we compute
onto the eigenbasis. That is, we compute
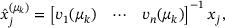
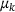 is an initial guess for μ. Initially, we use equispaced
is an initial guess for μ. Initially, we use equispaced 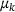 in the interval of interest. Other choices based on a prior distribution are possible and are subject to future research. This coordinate transformation depends on
in the interval of interest. Other choices based on a prior distribution are possible and are subject to future research. This coordinate transformation depends on 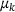 . Hence, we fix a
. Hence, we fix a 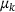 in the superscript. For
in the superscript. For 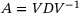 , we have (see, for instance, Higham [15])
, we have (see, for instance, Higham [15])
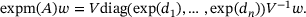
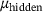 , the components of
, the components of 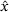 evolve like an exponential function,
evolve like an exponential function,
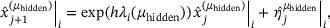
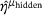 the representation of η in the eigenbasis for
the representation of η in the eigenbasis for 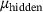 . For other μ, the
. For other μ, the 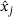 decay exponentially as well, but the effect is a mix of different
decay exponentially as well, but the effect is a mix of different 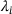 . Ignoring
. Ignoring 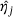 , we have
, we have
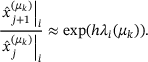
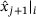 , the η term is negligible. If the system is close to being stationary, the noise becomes very relevant and a more elaborate approach for inferring μ is needed. (2) We also ignore that for different
, the η term is negligible. If the system is close to being stationary, the noise becomes very relevant and a more elaborate approach for inferring μ is needed. (2) We also ignore that for different 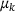 , the eigenbasis
, the eigenbasis 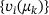 changes. We are going to use both simplifications and will demonstrate that the results are useful despite of them.
changes. We are going to use both simplifications and will demonstrate that the results are useful despite of them.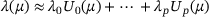 . Thus, the polynomial
. Thus, the polynomial  approximates
approximates 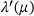 . We use this together with the difference between the quotient and the exponential of the eigenvalue to μ to guess μ by
. We use this together with the difference between the quotient and the exponential of the eigenvalue to μ to guess μ by
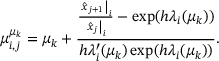 (3)
(3)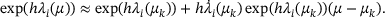
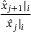 and
and 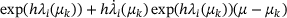 .
.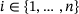 ,
, 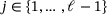 , and
, and 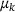 we get a new guess of μ.1 We combine all of the guesses inside our interval of interest using Matlab's kernel density estimator ksdensity. This function computes for selected ξ the following sum:
we get a new guess of μ.1 We combine all of the guesses inside our interval of interest using Matlab's kernel density estimator ksdensity. This function computes for selected ξ the following sum:
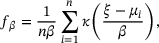
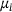 is smoothed out, and where
is smoothed out, and where
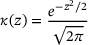
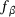 with
with 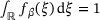 . We pick the mode
. We pick the mode 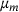 with
with
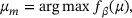
Alternatively, one can use the density function to draw a new set of guesses 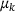 based on the new distribution. This process can be iterated, see Section 5.
based on the new distribution. This process can be iterated, see Section 5.
4 NUMERICAL EXPERIMENTS
This section is devoted to numerical experiments based on Example 1.1. For our numerical experiments, we use Matlab (R2020b) with IEEE 754 double precision arithmetic and a computer with Ubuntu 18.04.6 LTS, an Intel Core i7-10710U CPU (six physical cores), and 16 GB of RAM.
We first demonstrate the accuracy of the Chebyshev expansion approach by repeating some experiments from Mach and Freitag [5] with the matrix 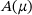 from Example 1.1. In Figure 2, we observe that a fourth-degree Chebyshev expansion with three Newton steps (solid blue line —) is sufficient to approximate the sampled eigenvalues (red crosses +) visually very well on the interval [2,4] and reasonably well outside the interval of interest. The visual impression of a small error is confirmed by the absolute error plot, see Figure 3.
from Example 1.1. In Figure 2, we observe that a fourth-degree Chebyshev expansion with three Newton steps (solid blue line —) is sufficient to approximate the sampled eigenvalues (red crosses +) visually very well on the interval [2,4] and reasonably well outside the interval of interest. The visual impression of a small error is confirmed by the absolute error plot, see Figure 3.
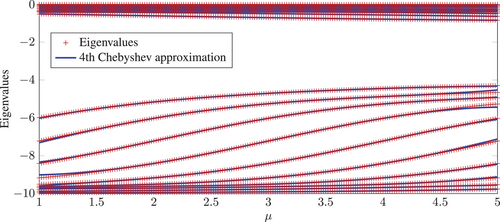
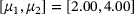 , eight Newton steps.
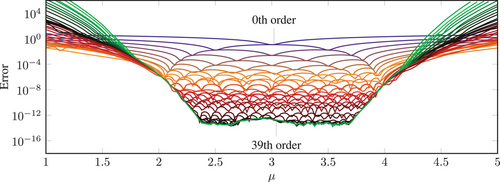
, eight Newton steps.Our penultimate experiment is a demonstration that we can find a good approximation to a hidden μ. Figure 4 depicts the results. We use one trajectory with 50 time steps of size 1/10 each. The chosen starting point x0 is randomly computed by 10*randn(20,1) and the added noise is computed by 1e-5*randn(20,1). We use a Chebyshev expansion up to degree 9 for the eigenvalues of Example 1.1 with 10 masses, that is 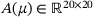 . The interval of interest is [2,4] in which we use 15 equidistant-spaced
. The interval of interest is [2,4] in which we use 15 equidistant-spaced 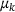 to compute guesses for μ, see Figure 5 for the contribution of each
to compute guesses for μ, see Figure 5 for the contribution of each 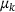 to the density. The kernel density estimator indicates that the most likely μ is
to the density. The kernel density estimator indicates that the most likely μ is 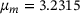 , while the actual μ used for the simulation of the trajectory was 3.2. This demonstrates that the described procedure is capable of inferring a good approximation of μ based on the parametric eigenpairs of
, while the actual μ used for the simulation of the trajectory was 3.2. This demonstrates that the described procedure is capable of inferring a good approximation of μ based on the parametric eigenpairs of 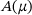 .
.

5 CONCLUSIONS AND FUTURE WORK
We have successfully demonstrated that we can estimate the depth μ based on a recorded trajectory, that is recording the sound emitted by the mass-spring system is sufficient to hear the depth of the water. The necessary computations were aided by initially computing a parametric eigendecomposition of 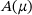 .
.
The guess of 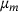 depends on the initial guess of μ. In the last section, we used 15 equidistant-spaced points in [2,4]. Using more points improves the accuracy and so does using points closer to the sought μ. Preliminary experiments reported in Figure 6 indicate that it is promising to draw new guesses for μ based on the estimated density and repeat the process with those. Beginning with the second iteration, we use 60 guesses for μ, which are shown as red crosses. We observe that the red crosses cluster closer and closer to the hidden
depends on the initial guess of μ. In the last section, we used 15 equidistant-spaced points in [2,4]. Using more points improves the accuracy and so does using points closer to the sought μ. Preliminary experiments reported in Figure 6 indicate that it is promising to draw new guesses for μ based on the estimated density and repeat the process with those. Beginning with the second iteration, we use 60 guesses for μ, which are shown as red crosses. We observe that the red crosses cluster closer and closer to the hidden 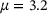 . Figure 6 indicates the density function that seem to converge toward a delta-pulse at
. Figure 6 indicates the density function that seem to converge toward a delta-pulse at 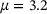 , see also Table 1. In the case of Table 1 the mode, the most likely μ, is a superior guess compared with the mean. These experiments are preliminary, since we observed different behavior for other examples. Once these differences are fully understood, we will report these experiments elsewhere. Other future work may involve investigations into the dependency on the noise level and extensions to 2 or more parameters.
, see also Table 1. In the case of Table 1 the mode, the most likely μ, is a superior guess compared with the mean. These experiments are preliminary, since we observed different behavior for other examples. Once these differences are fully understood, we will report these experiments elsewhere. Other future work may involve investigations into the dependency on the noise level and extensions to 2 or more parameters.
| it. | Mode | Mean | Variance |
|---|---|---|---|
| 1 | 3.2315 | 3.1682 | 0.1626 |
| 2 | 3.2095 | 3.1905 | 0.1089 |
| 3 | 3.2022 | 3.2090 | 0.0714 |
| 4 | 3.2006 | 3.2047 | 0.0372 |
| 5 | 3.2003 | 3.2013 | 0.0293 |
| 6 | 3.1999 | 3.1954 | 0.0199 |

ACKNOWLEDGMENTS
The title of this paper has been inspired by “Can you hear the shape of a drum?” by Marc Kac [16]. The research has been partially funded by the Deutsche Forschungsgemeinschaft (DFG)—Project-ID 318763901—SFB1294. In particular, we would like to acknowledge that this research started with a discussion at the annual SFB1294 Spring School 2023.
Open access funding enabled and organized by Projekt DEAL.
Open Research
DATA AVAILABILITY STATEMENT
The code used for the numerical experiments is available from GitHub, https://github.com/thomasmach/PEVP_with_Taylor_and_Chebyshev.
REFERENCES
- 1 An alternative would be to turn Equation (3) into a least squares problem. For the sake of brevity, we are not going to follow this idea here.



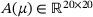 , Chebyshev expansion on the interval
, Chebyshev expansion on the interval 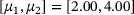 .
. ,
, 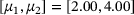 , unknown hidden
, unknown hidden 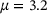 , best guess
, best guess 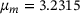 , noise
, noise 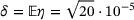 .
.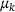 separately.
separately.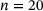 ,
, 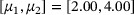 , hidden
, hidden 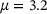 , 60 different μ per iteration, best guess
, 60 different μ per iteration, best guess 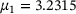 ,
, 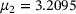 ,
, 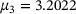 ,
, 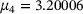 ,
, 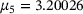 ,
, 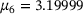 .
.
