Simplified description of hard particles in tribological systems using statistical sample particles
Abstract
Technical applications often include tribological systems in which friction and wear occur. Hard particles, such as sand, are often present in the contact between the surfaces of two bodies in contact and affect both the system dynamics and the resulting surface topography of the contacting bodies. Real tribological systems can contain a very high number of particles. Hence, for performance reasons of numerical studies, the explicit representation of each particle in a simulation is often not practical. The approach presented here is based on a model simplification by grouping several particles to form statistical sample particles (SSPs). SSPs can only move as a whole, and thereby simplify the motions of the individual particles, but the contact stiffness and orientation dependence of the force are still determined by the set of individual particles that are part of the statistical sample. Using sample size 1, each individual particle is represented without simplification, while using a sample size larger than one, the total number of particles in the system reduces to a minimum of one SSP representing all particles in the system. This approach provides a very efficient way to specify the model complexity and desired level of detail for the particle representation within a model of a tribological system.
1 INTRODUCTION
Tribological systems often contain loose, hard particles, which lead to abrasive wear. Abrasive wear depends besides the material combination and external load in such systems also on a variety of other parameters, such as particle shape and size, but also on the kinematics of the particles [1]. The wear is called two-body wear if the particles are fixed to one of the two adjacent body surfaces, otherwise, if the particles can move independently, it is called three-body wear [1]. The present study focuses on three-body wear systems. Depending on the technical application, low wear, for example due to sand particles in a gearbox [2], or an intentional change of the surface topography, for example in lapping processes, is desired.
Besides experiments, simulation models can also be used to investigate the behavior of tribological systems. However, the large number of elements and properties of a real tribological system can only be represented in a simplified way in a model. Depending on the investigation, various approaches are adopted for this purpose. Modeling of particles in tribological systems is often accomplished using simplified particle geometry by assuming the particle shape to be spherical [3, 4]. However, depending on their geometry, hard particles influence both dynamics of the tribological system, as shown in previous publications [5, 6], and the resulting topography of the adjacent body surfaces [7]. For this reason, there also exist models that can represent non-spherical particle geometries. For example, simulations of lapping processes exist in which the particle cross sections are represented as irregular polygons with rounded corners [8] and simulations of particle motion in polishing processes exist in which the particle geometries are represented by various three-dimensional regular convex polyhedrons [9]. In a preliminary work [10] to the current publication, simulations of tribological systems with particles of three-dimensional, irregular particle geometry are presented. However, for tribological systems with very many particles in the contact zone, modeling each particle individually is not efficient.
Summarizing multiple particles to simplify a model is not new in general. However, in tribological systems with a single layer of particles, different parameters are relevant than in systems of granular bulk material with many particle layers between adjacent boundaries. Therefore, in other applications it may be useful to scale the particle size and use so-called coarse grained particles to artificially reduce the particle number in Discrete Element Method simulations [11]. However, scaling the particle size is not useful when modeling tribological three-body systems containing a single layer of hard particles, as this would affect the equilibrium distance between the two first bodies. For example, the distance between the two first bodies has a very strong effect on forces caused by fluids in the contact zone, which can be shown using analytical solutions of the Reynolds equation even for simple squeeze flows [12].
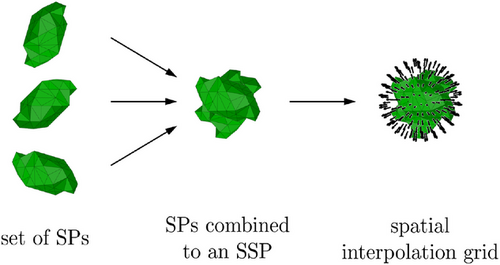
This publication presents an approach which can be used for simplified representation of a single layer of hard, non-spherical particles in tribological systems. On the one hand, the objective is the creation of statistical sample particles (SSPs) in order to drastically reduce the number of particles to be modeled in a simulation. On the other hand, the use of SSPs should make it possible to reproduce the overall behavior of a tribological system without significant changes in its properties. The idea is to combine multiple individual particles using already existing data and functions to form SSPs, which in turn can move through a tribological system as an entity in the same way as the original individual particles.
Section 2 presents the procedure for creating SSPs, and Section 3 investigates the influence on simulation results caused by the use of SSPs by means of illustrative scenarios. Section 4 summarizes the key aspects of the approach.
2 PROCEDURE
This section explains the basic procedure for creating and using SSPs on the basis of non-spherical particle shapes. Starting point is an individual single particle (SP), see Figure 1. The shown particle geometry is the same as already used in literature [10], but all dimensions are reduced by a factor of 100, so that the particle has an orientation-dependent diameter between 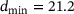
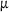 m and
m and 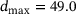
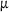 m.
m.
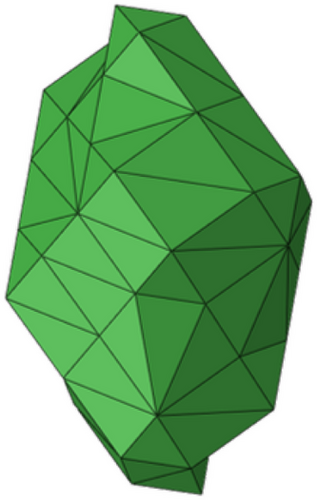
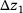 into the body surface of the lower first body. Likewise, the relationships between the force F and the indentation depth
into the body surface of the lower first body. Likewise, the relationships between the force F and the indentation depth 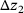 into the upper first body are determined. Since the same force F acts between the particle and the upper first body and between the particle and the lower first body under quasi-static loading, the gap height
into the upper first body are determined. Since the same force F acts between the particle and the upper first body and between the particle and the lower first body under quasi-static loading, the gap height 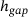 (i.e., the distance between the two first bodies) for each orientation simulated can be expressed in the form
(i.e., the distance between the two first bodies) for each orientation simulated can be expressed in the form
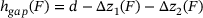 (1)
(1)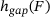 can be inverted to obtain the force-gap height relationship
can be inverted to obtain the force-gap height relationship 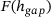 . Between orientations, for which reaction force-gap height relationships are already determined using finite element simulations, an approximation is made by interpolation based on barycentric coordinates [10].
. Between orientations, for which reaction force-gap height relationships are already determined using finite element simulations, an approximation is made by interpolation based on barycentric coordinates [10].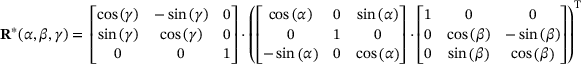 (2)
(2)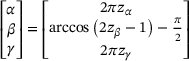 (3)
(3)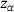 ,
, 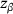 , and
, and 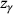 uniformly distributed in the interval
uniformly distributed in the interval 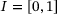 based on [13] as previously described in [10]. The set of randomly oriented SPs generated in this way are combined to form the SSP. The SSP is intended to be used in dynamics simulations the same way SPs are used. This means that for the SSP, the force-gap height relationship is also determined for selected orientations to act as support points for the interpolation of this relationship between orientations. While the force-gap height curves of the SPs are obtained for particle geometry-dependent orientations (that is, maxima and minima of the orientation-dependent particle diameter), the SSPs rely on a regular grid of support points to limit the number of orientations to be analyzed, especially when the SSP comprises a large sample size
based on [13] as previously described in [10]. The set of randomly oriented SPs generated in this way are combined to form the SSP. The SSP is intended to be used in dynamics simulations the same way SPs are used. This means that for the SSP, the force-gap height relationship is also determined for selected orientations to act as support points for the interpolation of this relationship between orientations. While the force-gap height curves of the SPs are obtained for particle geometry-dependent orientations (that is, maxima and minima of the orientation-dependent particle diameter), the SSPs rely on a regular grid of support points to limit the number of orientations to be analyzed, especially when the SSP comprises a large sample size 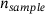 . The orientations are defined here using the vertices of a recursively subdivided icosahedron mesh [14]. This provides the SSP with a number of
. The orientations are defined here using the vertices of a recursively subdivided icosahedron mesh [14]. This provides the SSP with a number of 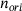 of, for example, 12, 42, 162, 642, or 2562 fairly uniformly distributed orientations as support points for subsequent interpolations of the force-gap height relationships. For each orientation, the force-gap height relationship is sampled with
of, for example, 12, 42, 162, 642, or 2562 fairly uniformly distributed orientations as support points for subsequent interpolations of the force-gap height relationships. For each orientation, the force-gap height relationship is sampled with 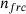 data points. In contrast to the SPs, however, for the SSPs the force-gap height relationship is not determined with the aid of complex finite element simulations, but based on the existing force-gap height relationships of the SPs. For each orientation for which the force-gap height relationship of the SSP is to be determined, the reaction forces of the individual particles are summed to a total force for specified gap height values. This way, apart from numerical inaccuracies, the SSP reacts like the
data points. In contrast to the SPs, however, for the SSPs the force-gap height relationship is not determined with the aid of complex finite element simulations, but based on the existing force-gap height relationships of the SPs. For each orientation for which the force-gap height relationship of the SSP is to be determined, the reaction forces of the individual particles are summed to a total force for specified gap height values. This way, apart from numerical inaccuracies, the SSP reacts like the 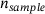 SPs when it lies between the two first bodies for a specific gap height. The SSP generated by this method can move in a simulation of a tribological system exactly like an SP. SSPs can be generated in simulations just like SPs with random initial positions and initial orientations. As a consequence, the use of SSPs of this type does not require profound changes in the implemented model for simulating the dynamics of tribological systems. Besides, both the amount of data and the computation time of simulations with many particles can be significantly reduced by using SSPs.
SPs when it lies between the two first bodies for a specific gap height. The SSP generated by this method can move in a simulation of a tribological system exactly like an SP. SSPs can be generated in simulations just like SPs with random initial positions and initial orientations. As a consequence, the use of SSPs of this type does not require profound changes in the implemented model for simulating the dynamics of tribological systems. Besides, both the amount of data and the computation time of simulations with many particles can be significantly reduced by using SSPs.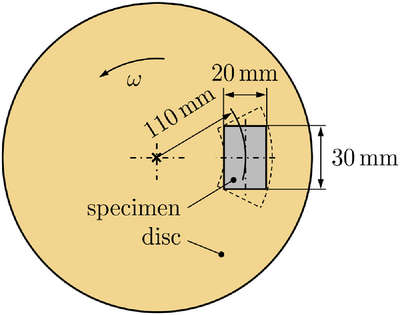
3 RESULTS AND DISCUSSION
To test the suitability of the SSP model, some SSPs are generated as described in Section 2 and the behavior of the SSPs is compared with the behavior of the original SPs. For this purpose, the contact force of a tribological system under static loading without tangential relative motion is evaluated as a function of gap height and the impact due to the use of SSPs versus SPs is compared, see Subsection 3.1. Furthermore, some simulations are performed to investigate the effects on the dynamic behavior of a tribological system using SSPs, see Subsection 3.2. This publication only uses the particle geometry shown in Figure 1, that is an SSP comprises multiple instances of the same SP.
3.1 Contact forces under static loading
In a first analysis, not the time histories of simulations are investigated, but directly the force-gap height relationships that arise under a pure static loading, that is when two plane and parallel first bodies approach each other perpendicularly. This test is performed with 1, 10, 100, and 1000 particles between the two first bodies, as qualitatively demonstrated in Figure 4.

Figure 5 provides diagrams comparing the force-gap height relationships for one randomly oriented SSP (dashed colored curves) of a certain sample size with a corresponding set of randomly oriented SPs (solid black curves). Each diagram includes 5 random realizations of these reaction force-gap height relationships. Depending on the orientations of the SPs or SSPs, different relationships are obtained. In particular, when only one SP is located between the first bodies, large differences are observed between the five repetitions of the force-gap height curves due to the non-circular shape of the particle. The influence of the random orientations has a smaller effect for larger particle quantities between the first bodies. This behavior is equally reflected by the SPs as well as the SSPs. The relationships of the SSPs and the SPs, including the variance of the curves caused by the random orientations, show an excellent agreement. The different rows of diagrams in Figure 5 show these relationships for interpolation grids with different resolutions. However, increasing the number of support points in the SSP model does not result in a significant improvement. Accordingly, with respect to contact stiffness, the resolution of the SSP with 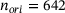 orientations and
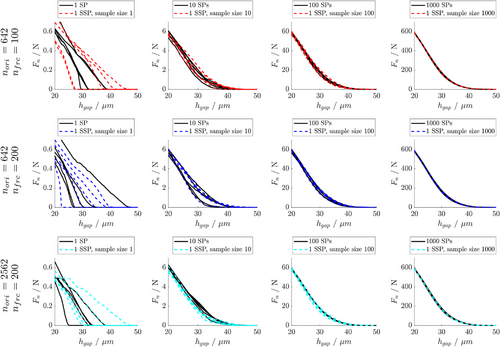
orientations and 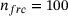 force-gap data points per orientation is considered to be sufficient.
force-gap data points per orientation is considered to be sufficient.
 dependent on the gap height
dependent on the gap height 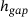 , if the given number of particles in the gap (1, 10, 100, 1000) for the columns from left to right) with random particle orientation are loaded. The five black solid curves in each diagram represent the five force-gap height relationships for different realizations of randomly oriented SPs between the first bodies. The colored dashed lines represent the same scenario modeled using a SSP of according sample size. Row 1 uses SSPs resolved with
, if the given number of particles in the gap (1, 10, 100, 1000) for the columns from left to right) with random particle orientation are loaded. The five black solid curves in each diagram represent the five force-gap height relationships for different realizations of randomly oriented SPs between the first bodies. The colored dashed lines represent the same scenario modeled using a SSP of according sample size. Row 1 uses SSPs resolved with 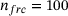 and
and 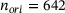 , row 2
, row 2 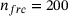 and
and 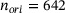 , row 3
, row 3 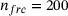 and
and 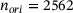 . SPs, single particles; SSP, statistical sample particle.
. SPs, single particles; SSP, statistical sample particle.3.2 Dynamic simulation of a tribological system
In this section, the effects on dynamic simulations of a tribological system by using SSPs of different sample sizes are investigated. The arrangement, geometries and movements of the two first bodies are based on the simulations already discussed in publication [10], with the dimensions given in Figure 2. The lower first body is a flat disc rotating at a constant angular velocity such that the sliding velocity 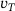 under the center of the upper first body corresponds to
under the center of the upper first body corresponds to 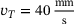 . Within the simulation time
. Within the simulation time 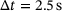 the sliding distance is
the sliding distance is 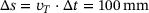 . The upper first body is a plane rectangular specimen with
. The upper first body is a plane rectangular specimen with 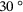 chamfers of 1.2 mm width along the short edges. The specimen center, as shown in Figure 2, is positioned at a distance of 110 mm from the rotational axis of the disc. The upper first body (mass m) can only move vertically, but cannot tilt. A constant gravitational force
chamfers of 1.2 mm width along the short edges. The specimen center, as shown in Figure 2, is positioned at a distance of 110 mm from the rotational axis of the disc. The upper first body (mass m) can only move vertically, but cannot tilt. A constant gravitational force 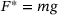 with gravitational acceleration
with gravitational acceleration 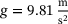 and mass
and mass 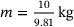 leads to the resultant external load
leads to the resultant external load 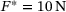 due to the dead weight of the upper first body. Between the first bodies, in the range
due to the dead weight of the upper first body. Between the first bodies, in the range 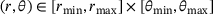 with
with 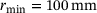 ,
, 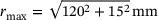 ,
, 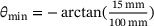 and
and 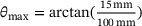 , which corresponds to the region surrounded by the dashed line in Figure 2, the particles can move. A total of 1000 individual particles, 1000 SSPs of sample size 1, 100 SSPs of sample size 10, respectively 10 SSPs of sample size 100 are generated. The particles are rolling, if they are contacting the disc and the specimen. Otherwise, they remain on the disc and undergo the same motion as the disc. The time-resolved vertical motion of the upper body is determined by the external force
, which corresponds to the region surrounded by the dashed line in Figure 2, the particles can move. A total of 1000 individual particles, 1000 SSPs of sample size 1, 100 SSPs of sample size 10, respectively 10 SSPs of sample size 100 are generated. The particles are rolling, if they are contacting the disc and the specimen. Otherwise, they remain on the disc and undergo the same motion as the disc. The time-resolved vertical motion of the upper body is determined by the external force 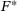 and the acting particle forces and it is solved considering its inertia using the ordinary differential equation solver ode15s in Matlab R2023a.
and the acting particle forces and it is solved considering its inertia using the ordinary differential equation solver ode15s in Matlab R2023a.
An extract of the time history of the normal force 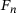 , gap height
, gap height 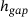 and gap height velocity
and gap height velocity 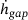 is shown in Figure 6. While similar ranges of values occur at the beginning of all simulations, the range of values for the remaining simulated time span moves in a bandwidth that decreases with increasing sample size. While virtually no difference in the time courses can be detected by using SSPs of sample size 1, the simulations show very little variance in the time courses when using SSPs with sample size 100.
is shown in Figure 6. While similar ranges of values occur at the beginning of all simulations, the range of values for the remaining simulated time span moves in a bandwidth that decreases with increasing sample size. While virtually no difference in the time courses can be detected by using SSPs of sample size 1, the simulations show very little variance in the time courses when using SSPs with sample size 100.
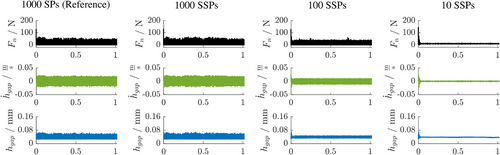
 , gap height
, gap height  and gap height velocity
and gap height velocity  during the first second of simulation time for simulation using SPs (first column), SSPs of sample size 1 (second column), SSPs of sample size 10 (third column), SSPs of sample size 100 (fourth column). SPs, single particles; SSP, statistical sample particle.
during the first second of simulation time for simulation using SPs (first column), SSPs of sample size 1 (second column), SSPs of sample size 10 (third column), SSPs of sample size 100 (fourth column). SPs, single particles; SSP, statistical sample particle.Figure 7 shows the respective time histories of normal force 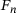 , gap height
, gap height 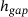 , and gap height velocity
, and gap height velocity 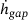 using error bars with attached estimated probability density functions. In order to visualize influences on the result variables that occur due to the random initial positions and orientations of the particles, five simulations with the same parameters (except for the random initial conditions) are run in each case and depicted in the diagrams. It can be seen that the variations within the repetitions are relatively small. Extreme values occur at the beginning of the simulation, as can be seen from the time histories. The probability distributions, on the other hand, represent the entire time history of the result variables. In the simulations using SPs (first column in Figure 7), the normal forces show a skewed distribution with many low values representing detachments between upper body and particles and few high values when the upper body hits the particle layer again. The vertical velocities
using error bars with attached estimated probability density functions. In order to visualize influences on the result variables that occur due to the random initial positions and orientations of the particles, five simulations with the same parameters (except for the random initial conditions) are run in each case and depicted in the diagrams. It can be seen that the variations within the repetitions are relatively small. Extreme values occur at the beginning of the simulation, as can be seen from the time histories. The probability distributions, on the other hand, represent the entire time history of the result variables. In the simulations using SPs (first column in Figure 7), the normal forces show a skewed distribution with many low values representing detachments between upper body and particles and few high values when the upper body hits the particle layer again. The vertical velocities 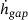 of the upper first body show a relatively broad spectrum. The gap height also reaches values that are exceeding the maximum particle diameter. This can only be true if the upper body partially loses contact with the particles due to the vertical motion and falls back onto the particles in free fall, which is in agreement with the analysis of the occurring forces. In comparison, simulations with SSPs with sample size 1 show no significant difference with respect to the reference simulations with SPs. SSPs with sample size 10, on the other hand, show distributions with smaller variances, but the shape of the distribution is essentially preserved. In contrast, the simulations with a sample size of 100 show very narrow distributions around the mean. The vertical movement of the upper body is therefore strongly underestimated in this case. This also reduces the proportion of gap height values that occur, at which the upper first body moves in free fall. Due to the underestimated vertical movement, the mean value of the gap height decreases by several percent with increasing sample size.
of the upper first body show a relatively broad spectrum. The gap height also reaches values that are exceeding the maximum particle diameter. This can only be true if the upper body partially loses contact with the particles due to the vertical motion and falls back onto the particles in free fall, which is in agreement with the analysis of the occurring forces. In comparison, simulations with SSPs with sample size 1 show no significant difference with respect to the reference simulations with SPs. SSPs with sample size 10, on the other hand, show distributions with smaller variances, but the shape of the distribution is essentially preserved. In contrast, the simulations with a sample size of 100 show very narrow distributions around the mean. The vertical movement of the upper body is therefore strongly underestimated in this case. This also reduces the proportion of gap height values that occur, at which the upper first body moves in free fall. Due to the underestimated vertical movement, the mean value of the gap height decreases by several percent with increasing sample size.
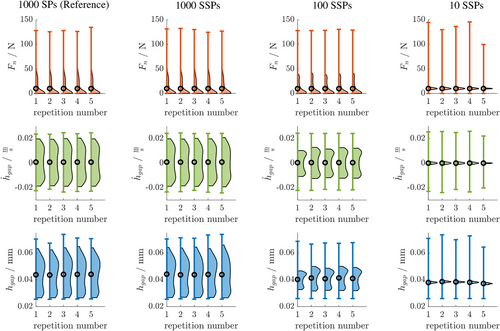
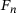 , gap height
, gap height 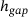 , and gap height velocity
, and gap height velocity 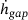 with error bars describing minimum and maximum, a black circle marking the mean and an estimated probability density function from 1st to 99th percentile attached for simulation using SPs (first column), SSPs of sample size 1 (second column), SSPs of sample size 10 (third column), SSPs of sample size 100 (fourth column). SPs, single particles; SSP, statistical sample particle.
with error bars describing minimum and maximum, a black circle marking the mean and an estimated probability density function from 1st to 99th percentile attached for simulation using SPs (first column), SSPs of sample size 1 (second column), SSPs of sample size 10 (third column), SSPs of sample size 100 (fourth column). SPs, single particles; SSP, statistical sample particle.4 CONCLUSION
An approach is presented which, based on an existing model for the reaction force of a SP between two first body surfaces, generates a SSP, which is a model of the combined reaction force of several particles. SSPs can be used in dynamic simulations in the same way as SPs due to the same structure of the particle model.
Although the representation of every SP in a dynamics simulation of a tribological system is suitable for calculating the topography change subsequently to a dynamic simulation, this detailed representation is not suitable for systems with a very large number of particles due to the high computational effort and memory requirements. The use of SSPs presented in Section 2 reduces the number of particles to be modeled and thereby simplifies the model of the tribological system by combining multiple individual particles in the SSP model.
When exposed to static loads, SSPs show the same force-gap height behavior as a corresponding set of SPs in the gap. For this reason, SSPs can also be used in combination with SPs or in combination with the previously published gap height-sensitive fluid force model [15]. Dynamics simulations show an increasing underestimation of the variance of dynamic quantities such as the occurring normal force between the first two bodies due to a reduced variance in vertical motion with increasing sample size. Nevertheless, SSPs can effectively reduce the number of degrees of freedom of models for tribological systems. With a reduction of the degrees of freedom by a factor of 10, it was not possible to reproduce the variance of the reference simulation, but at least the shape of the probability distribution.
Using SPs in conjunction with SSPs can also enable the calculation of the resulting topography of the first bodies' surfaces in tribological systems with a very large number of particles. For this purpose, the particles in a certain region of the contact area are represented by SPs and the remaining particles are represented by SSPs. Subsequently to a dynamics simulation, the first bodies' topography change caused by the SPs can be calculated by evaluating their imprints into the first bodies' surfaces, analogously to the literature [10].
ACKNOWLEDGMENTS
The present publication was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 172116086 – SFB 926.
Open access funding enabled and organized by Projekt DEAL.




