Efficient integration of deep neural networks in sequential multiscale simulations

1 INTRODUCTION

Multiscale computations often rely on finite elements for spatial discretization on both macro- and microscale, as explained, for example, in the literature [1]. However, the evaluation of heterogeneous microstructures, frequently represented using representative volume elements (RVEs), is a computationally expensive task. This evaluation typically involves solving boundary value problems (BVPs) or initial BVPs, especially when dealing with inelastic or viscous constitutive behavior, followed by a subsequent homogenization step. Recently, neural network-based surrogate models have become invaluable to substantially accelerate these computations or make them even feasible, when considering three-dimensional RVEs as well as complex constitutive or multiphysical behavior.

Machine learning methods, including deep neural networks (DNNs), have already been applied in multiscale computations, as comprehensively reviewed in the literature [2]. Among other approaches, [3] choose clustering techniques in a data-driven two-scale approach for the prediction of homogenized quantities from the microscale. An adaptive switching between the evaluation of a reduced order model and a neural network is presented by literature [4] to ensure accurate predictions. Beyond simple feedforward DNNs, as applied in this work, more complex architectures are applied to multiscale problems as well, see [5-7] and the cited references. Moreover, [8] introduced a data-driven multiscale framework coupled with autonomous data mining for multiscale computations. A current trend is the incorporation of physics into neural networks, see, exemplarily, [9, 10] and the literature cited therein, which is beyond the scope of this contribution. Moreover, Sobolev training [11], as demonstrated by literature [12], has proven to enhance the accuracy of the neural network-based surrogate models and is therefore followed also in this work together with reverse mode automatic differentiation (AD).

In this contribution, we begin by briefly summarizing the use of DNN surrogate models in sequential multiscale analyses. Afterward, the architecture and training process of a straightforward data-driven DNN surrogate is explained, which can be constructed directly from RVE evaluations, specifically homogenized stress and strain quantities. We intentionally omit the evaluation of other approaches, such as those involving the local strain-energy, as carried out, for instance, in the literature [13]. Our focus in this contribution is primarily on the efficient integration into an existing finite element code, for which a simple model is sufficient. Finally, a particular application example of a plate with a hole is studied, where non-linear elastic constitutive behavior is present in the microstructure. This example considers three key aspects: first, the prediction accuracy, second, the load-step size behavior, and third, the speed-up compared to classical concurrent multiscale FE² computations. The novelty of this work lies in the efficient integration of a Python-based DNN surrogate model into a Fortran-written finite element code while facilitating just-in-time compilation techniques, leading to a significant speed-up compared to reference FE² computations. Furthermore, we demonstrate the applicability of a simple data-based DNN surrogate model in load-step size controlled simulations.

Regarding the notation, column vectors and matrices at the global finite element level are symbolized by bold-type italic letters and column vectors and matrices on the local (element) level using bold-type Roman letters A. Here, microscale quantities are denoted by 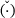. Further, calligraphic letters 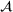denote DNN surrogate models.

2 SEQUENTIAL MULTISCALE ANALYSES WITH DEEP NEURAL NETWORK SURROGATE MODEL

In multiscale analyses, the goal is to incorporate the effective constitutive behavior of a heterogeneous microstructure into a macroscale analysis. Typically, concurrent multiscale FE² computations are carried out as follows: first, the macroscale strains 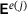are used to impose boundary conditions on the surface of the RVE, representing the microstructure. Subsequently, a BVP is solved on the microscale, followed by a homogenization step to obtain the macroscopic stresses 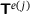and the consistent tangent 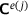. The notation 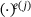denotes a quantity associated with macroscale integration point j of element e. However, the solution of the microscale BVPs can be efficiently replaced by the evaluation of a surrogate model to reduce computational costs. This leads to sequential multiscale analyses because the RVE has to be evaluated beforehand. In this context, the general assumptions still hold, that is the effective constitutive behavior has to be an intrinsic material property that is not influenced by the specific macroscale BVP. Additionally, scale separation between micro- and macroscale is assumed to use first-order homogenization. Moreover, since we apply periodic displacement boundary conditions on the RVE in this work, it is assumed that no discontinuities are present, and thus, composite phases are perfectly bonded in the microstructure. Further, it should be mentioned that we restrict ourselves to problems in the small strain domain.

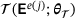Rather than repeatedly solving a microstructural BVP, we employ a common feedforward DNN as a surrogate model. This means that the microscale evaluations are entirely replaced by the surrogate model. In our case, the surrogate model is evaluated depending on the macroscale strains 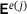, while parametrized with the trainable parameters 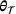. The DNN outputs are the homogenized stresses 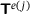, which are used to employ reverse mode AD, see [14], on the surrogate model 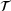to obtain 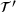and predict the consistent tangent matrix ,

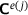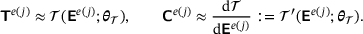(1)

The architecture is depicted in Figure 1.

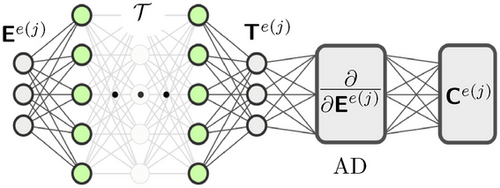
In the literature [15] it was shown that employing reverse mode AD with a single neural network surrogate model to obtain 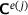is superior to an approach that uses two separate neural networks for predicting 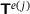and 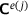 independently.

3 DEEP NEURAL NETWORK SURROGATE MODEL

In this work, we restrict ourselves to two-dimensional examples in the small strain domain, that is the macroscale strains 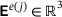, , 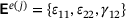is the vector of input quantities for the surrogate model and the output quantities are 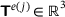, 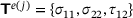and 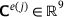. Here, the strains and stresses can be arranged in column vectors since the corresponding tensors are symmetric in the small strain case. Furthermore, the coefficients of the consistent tangent matrix, which is here a symmetric 3 × 3 matrix, are compiled in a column vector as well, .

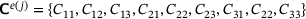The DNN surrogate model is developed by drawing on two different frameworks, TensorFlow [16] and JAX [17]. The data for the surrogate modeling is generated by performing RVE computations with different prescribed macroscale strains that are generated by Latin hypercube sampling [18]. Thereby, particular symmetry relations of the constitutive models, which are applied in the RVE, are employed leading to an essential reduction of the required RVE computations for the data generation. We refer to [15] for further details regarding the data generation. The macroscale strains are restricted to a domain of 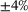as maximum strain for each strain component. Further, the inputs and outputs of the model are scaled with their mean and standard deviation to obtain efficient training. There, the scaling of the consistent tangent output has to retain the relationship between consistent tangent and homogenized stress.

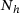The influence of three hyperparameters of the DNN (i.e. number of hidden layers , the number of neurons per each hidden layer 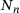, and the activation function) on the performance of the model is investigated. A summary of the obtained results is reported in Table 1 only for three different sizes of the DNN with swish activation function, for the sake of brevity. Based on the results, we choose a DNN architecture of eight hidden layers, each with 128 neurons and employing the swish activation function. The weights and biases are initialized by drawing on the Glorot uniform algorithm [19]. The training is done with 80% of the data for training and 20% for validation, using the Adam optimizer [20]. Here, different sizes of the dataset containing 10³ to 10⁶ samples are chosen. The training is done for 4000 epochs with an exponential decay of the learning rate η, which is initially chosen to 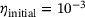. The decay step is 1000 and the decay rate 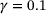. The dataset is decomposed to obtain 100 batches and the mean squared error is selected for the loss function,

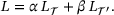(2)

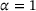Here, and 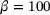denote the weighting factors for the two loss components of the predicted stresses and consistent tangent, respectively. Note that we track the validation loss during the training process and select the model parameters based on the lowest validation loss to avoid overfitting. The DNN surrogate model is implemented into the MPI-parallelized FORTRAN in-house code TASAFEM using the FORPy library [21]. It should be noted that utilizing more sophisticated DNN models, for example physics-informed NNs, see [10], could improve the performance of the model. However, here we focus more on developing an efficient framework for integrating DNN models into finite-element codes for sequential multiscale simulations by employing modern scientific computing tools such as just-in-time compilation and efficient FORTRAN-Python communication. Further, we show the applicability of our framework for load-step size controlled simulations in the following numerical example.

TABLE 1. Summary of the results obtained for training and validation losses and the required time of training for different sizes of the deep neural network.

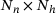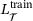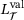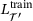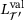					Training time (min.)
32× 2	1.81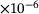	1.79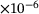	3.07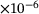	2.98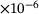	10.9
64× 4	3.74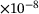	4.28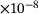	1.29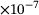	1.28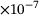	14.5
128× 8	3.78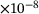	3.55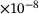	3.02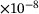	2.97	31.2

• Note: Results are reported for models with swish activation function. A dataset with the size of 10⁵ is employed for training.

4 NUMERICAL EXAMPLE

The framework explained earlier, which utilizes a DNN surrogate model to predict the homogenized stress 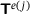and consistent tangent matrix 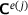, is employed to analyze the mechanical response of a two-dimensional plate with a hole subjected to shear load. Here, we focus on three aspects: the prediction quality using the DNN, the load step-size behavior in load-step controlled simulations, and the speed-up.

4.1 Problem setup

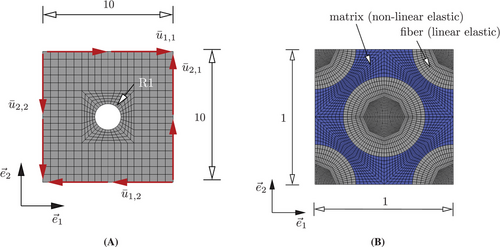
The macroscale geometry for the numerical example is shown in Figure 2A.

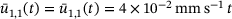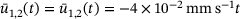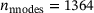The load functions are defined as follows: and . The plate is discretized using eight-noded quadrilateral elements, leading to elements and nodes. In the analysis, a plane strain state is assumed. The corresponding RVE is depicted in Figure 2B and comprises matrix material and fiber sections. The matrix material is modeled with a non-linear elasticity relation,

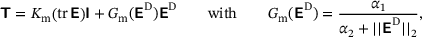(3)

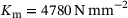where the bulk modulus and the parameters 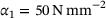and are the material parameters of the matrix material.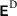

denotes the deviatoric strains and 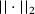represents the Euclidean norm. In contrast, the fibers are assumed to be linear elastic with bulk modulus 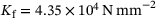and shear modulus 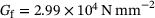. The RVE is spatially discretized with 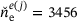eight-noded quadrilateral elements and  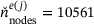nodes.

4.2 Prediction quality

To evaluate the prediction quality using the DNN surrogate model, which is described in Section 3, we introduce the absolute percentage error of the predicted stresses

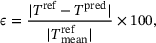(4)

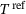where is the corresponding stress quantity for a reference FE² solution and 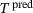represents the prediction from the DNN surrogate model. Since some of the stresses are zero, we use 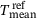as the mean value of the stresses in the reference solution to obtain a relative error measure. Results are summarized in Table 2 for different sizes of the training/validation dataset 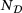, where 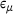and indicate the mean and the standard deviation of the absolute percentage error ε over all the integration points and stress components. It can be observed that the DNN model trained on a dataset with only 10³ samples can provide very accurate results with 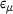and 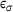of around 1%. Moreover, the error is decreased by employing a larger dataset for training and validation. In the following, we will focus on the results obtained from the DNN model trained on the dataset with 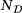of 10⁵.

TABLE 2. Results obtained from deep neural network surrogates trained using varying sizes of the training/validation datasets.

	(%)	(%)
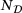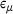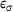103	1.08	1.14
104	0.14	0.13
105	0.04	0.03
106	0.02	0.03

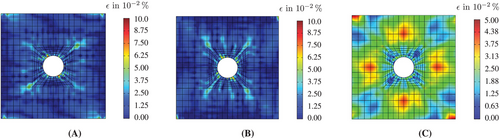
The absolute percentage errors for the predicted stresses are shown in Figure 2 for the final evaluation time of the applied load. Apparently, the DNN surrogate model is able to precisely predict the stresses in the present example, with the maximum error in the stresses being about 0.10%. As depicted in Figures 3A,B, the absolute error across a large domain is below 0.01%, with only a few integration points in the vicinity of the hole exhibiting slightly larger errors in the normal stresses. However, it is worth mentioning that the prediction of the shear stress τ₁₂ is less accurate compared to σ₁₁ and σ₂₂. This discrepancy could be attributed to the geometry of the RVE and the different stiffness of the constituents, which results in higher differences in the orders of magnitude for stresses and components of the consistent tangent matrix when subjected to shear load. Similar behavior has been previously reported for different macroscale problems in the literature [15].

4.3 Load-step size behavior

FE² computations usually utilize a load-step control since the initial load-step (or time-step, respectively) size is often very small to avoid convergence issues. Therefore, it is essential to investigate the performance of the DNN surrogate model in step-size controlled computations.

For both reference FE² computation and DNN-enhanced computation, an initial time-step size  s is selected. The incremental application of the prescribed load, which can be interpreted as time integration, is performed using the Backward-Euler method. The system of linear equations arising in non-linear elastic finite element computations can be formally extended with 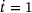to obtain a system of differential-algebraic equations as it is common in computations dealing with inelastic or viscous constitutive behavior. The determination of the time-step size for the next time-step 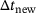is based on the number of global Newton iterations 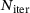and the current time-step size ,

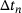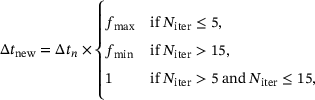(5)

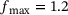where we choose the coefficients and 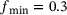. The step-size behaviors for reference FE² computation and the multiscale computation using a DNN surrogate model are shown in Figure 4.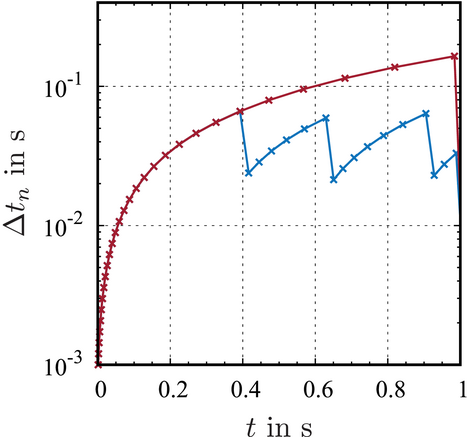

In this specific example, the initial time-step size 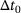is suitable for both methods. Moreover, both methods exhibit a similar behavior in the first iterations. However, the reference FE² computation shows a certain limit for the time-step size 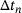at around  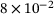s, which appears due to non-convergence of the RVE computations for certain load-increments. In contrast, the evaluation of the DNN surrogate model allows a continuously increasing time-step size. Thus, the application of a DNN surrogate model for the microscale evaluations even extends the applicable time-step sizes, at least for the non-linear elastic problem studied here.

4.4 Speed-up

In general, the application of a DNN surrogate model for multiscale simulations aims at significantly decreasing the computational time. Here, the speed-up is calculated by dividing the total computation time of the reference FE² simulation by that of the multiscale simulation with DNN surrogate ,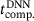

(6)

The simulations with DNN surrogate model are performed on an 11th Gen Intel(R) Core(TM) i7-11850H @ 2.50GHz CPU with 16 threads. In contrast, the reference simulations are performed on a 2nd Gen Intel(R) Xeon(R) Silver 4216 @ 2.10GHz CPU with 16 processes and one thread per process. For the example of a plate with a hole, the speed-up is 524× using the TensorFlow implementation of the DNN. However, as mentioned afore, we also apply the JAX framework for the development of a surrogate model with the neural network library Flax [22]. JAX facilitates the just-in-time compilation of the prediction function, that is the compilation of the Python code into machine code just before the execution to reduce resource consumption. As demonstrated in the literature [15], just-in-time compilation significantly increases the speed-up in multiscale simulations with surrogate models. Here, we obtain a speed-up of 6048× for the specific example of a plate with a hole.

5 CONCLUSIONS

As it is well-known, (deep) neural network surrogate models can significantly reduce the computational expenses of multiscale computations. In this contribution, an efficient integration of such a DNN surrogate model into an existing finite element code is explained, utilizing the open-source library FORPy [21] for Fortran-Python interoperability. This integration already results in a speed-up of around 500× for the specific example of a plate with a hole. Furthermore, using just-in-time compilation has significantly increased the speed-up to around 6000× . In load-step size controlled simulations, where non-linear elastic material behavior is present in the microstructure, it is observed that the surrogate model can overcome specific step-size limitations inherent in the RVE computations. Therefore, the use of a DNN surrogate model can even extend the feasible load-step sizes for multiscale computations.