Convergent spectral inclusion sets for banded matrices
Abstract
We obtain sequences of inclusion sets for the spectrum, essential spectrum, and pseudospectrum of banded, in general non-normal, matrices of finite or infinite size. Each inclusion set is the union of the pseudospectra of certain submatrices of a chosen size n. Via the choice of n, one can balance accuracy of approximation against computational cost, and we show, in the case of infinite matrices, convergence as 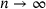 of the respective inclusion set to the corresponding spectral set.
of the respective inclusion set to the corresponding spectral set.
1 INTRODUCTION
In many finite difference schemes or in physical or social models, where interaction between objects is direct in a finite radius only (and is of course indirect on a global level), the corresponding matrix or operator is banded, also called of finite dispersion, meaning that the matrix is supported on finitely many diagonals only. In the case of finite matrices this is of course a tautology; in that context one assumes that the bandwidth is not only finite but small compared to the matrix size, where the bandwidth of a matrix A is the distance from the main diagonal in which nonzeros can occur. (Precisely: it is the largest 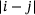 over all matrix positions
over all matrix positions 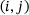 with
with 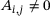 .) So this is our setting: finite, semi-infinite or bi-infinite banded matrices.
.) So this is our setting: finite, semi-infinite or bi-infinite banded matrices.
We equip the underlying vector space with the Euclidian norm, so our operators act on an ℓ2 space over 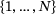 or
or 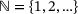 or
or 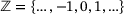 . In the two latter cases (semi- and bi-infinite matrices), we assume each diagonal to be a bounded sequence, whence the matrix acts as a bounded linear operator, again denoted by A, on the corresponding ℓ2 space.
. In the two latter cases (semi- and bi-infinite matrices), we assume each diagonal to be a bounded sequence, whence the matrix acts as a bounded linear operator, again denoted by A, on the corresponding ℓ2 space.
 , the pseudospectrum,
, the pseudospectrum,
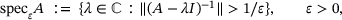
 . Note that, by agreeing to say
. Note that, by agreeing to say 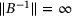 if B is not invertible, one has
if B is not invertible, one has 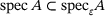 for all
for all 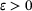 . For an impressive account of pseudospectra and their applications, see the monograph [1].
. For an impressive account of pseudospectra and their applications, see the monograph [1].Our aim in this paper is to derive inclusion sets for 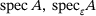 as well as the essential spectrum,
as well as the essential spectrum, 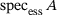 , in terms of unions of pseudospectra of moderately sized (but many) finite submatrices of A of column dimension n. Moreover, if the matrix is infinite, we prove convergence, as
, in terms of unions of pseudospectra of moderately sized (but many) finite submatrices of A of column dimension n. Moreover, if the matrix is infinite, we prove convergence, as  , of the respective inclusion set to each of
, of the respective inclusion set to each of 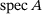 ,
, 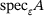 , or
, or 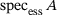 .
.
2 APPROXIMATING THE LOWER NORM ON 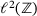
Our arguments are, perhaps surprisingly, tailor-made for the case of bi-infinite vectors and matrices on them. In fact, instead of 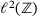 , everything also works for
, everything also works for 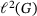 with a discrete group G, for example,
with a discrete group G, for example, 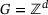 , subject to Yu's so-called Property A [2, 3]. Only later, in Section 6, we manage to work around the group structure and to transfer results to
, subject to Yu's so-called Property A [2, 3]. Only later, in Section 6, we manage to work around the group structure and to transfer results to 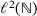 and
and 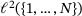 , hence: to semi-infinite and finite matrices.
, hence: to semi-infinite and finite matrices.
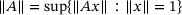 , we look at the so-called lower norm1
, we look at the so-called lower norm1
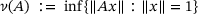
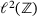 . Fixing
. Fixing 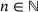 and limiting the selection of unit vectors x to those with a finite support of diameter less than n, further limits how small
and limiting the selection of unit vectors x to those with a finite support of diameter less than n, further limits how small 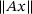 can get. Precisely,
can get. Precisely,
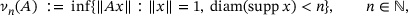 (2.1)
(2.1)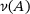 – but (and this is remarkable) only larger by at most the amount of a certain
– but (and this is remarkable) only larger by at most the amount of a certain 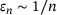 that we will quantify precisely below. Let us first write this important fact down:
that we will quantify precisely below. Let us first write this important fact down:
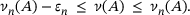 (2.2)
(2.2)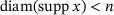 in (2.1) translates to
in (2.1) translates to 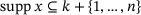 for some
for some 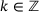 . Hence,
. Hence,
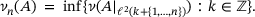 (2.3)
(2.3)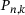 for the operator of multiplication by the characteristic function of
for the operator of multiplication by the characteristic function of 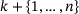 and agree on writing
and agree on writing
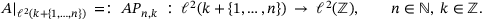
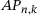 corresponds to the matrix formed by columns number
corresponds to the matrix formed by columns number 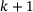 to
to 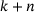 of A. By the band structure of A, that submatrix is supported in finitely many rows only, even reducing it to a finite
of A. By the band structure of A, that submatrix is supported in finitely many rows only, even reducing it to a finite 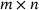 matrix, where m equals n plus two times the bandwidth of A. Then
matrix, where m equals n plus two times the bandwidth of A. Then 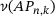 , as in (2.3), is the smallest singular value of this
, as in (2.3), is the smallest singular value of this 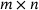 matrix, making this a standard computation.
matrix, making this a standard computation.3 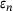 AND THE REDUCTION TO TRIDIAGONAL FORM
AND THE REDUCTION TO TRIDIAGONAL FORM
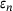 is particularly optimized in the case of tridiagonal matrices, that is when A has bandwidth one, so that it is only supported on the main diagonal and its two adjacent diagonals. Let
is particularly optimized in the case of tridiagonal matrices, that is when A has bandwidth one, so that it is only supported on the main diagonal and its two adjacent diagonals. Let 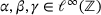 denote, in this order, the sub-, main- and superdiagonal of A, with entries
denote, in this order, the sub-, main- and superdiagonal of A, with entries 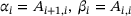 and
and 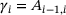 with
with 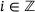 . In that case (see refs. [4, 12, 13]),
. In that case (see refs. [4, 12, 13]),
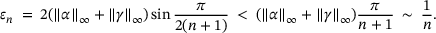 (3.1)
(3.1)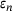 for the very general setting of all tridiagonal matrices, formula (3.1) turns out to be best possible in some nontrivial examples such as the shift operator [12].
for the very general setting of all tridiagonal matrices, formula (3.1) turns out to be best possible in some nontrivial examples such as the shift operator [12].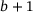 :
:
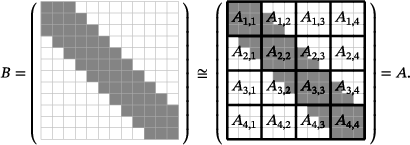
Here, a matrix B with bandwidth 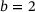 is identified with a block-tridiagonal matrix A with 3 × 3 blocks, noting that
is identified with a block-tridiagonal matrix A with 3 × 3 blocks, noting that 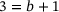 .
.
Since the blocks of A can be operators on a Banach space X, one can even study 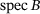 and
and 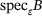 by our techniques for bounded operators B on
by our techniques for bounded operators B on 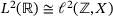 , where
, where 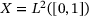 , for example, for integral operators B with a banded kernel
, for example, for integral operators B with a banded kernel 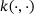 .
.
4 THE ROLE OF THE LOWER NORM IN SPECTRAL COMPUTATIONS
 with norm
with norm  then, clearly,
then, clearly, 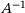 , bringing
, bringing 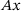 back to x, has to have at least norm four. The lower norm,
back to x, has to have at least norm four. The lower norm, 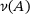 , is pushing this observation to the extreme. By minimizing
, is pushing this observation to the extreme. By minimizing 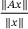 , it minimizes
, it minimizes 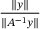 and hence computes the reciprocal of
and hence computes the reciprocal of 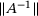 – with one possible exception: non-invertibility of A due to
– with one possible exception: non-invertibility of A due to 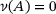 or
or 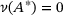 . Properly: since
. Properly: since 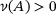 iff A is injective and has a closed range (e.g., [10, Lemma 2.32]), A is invertible iff both
iff A is injective and has a closed range (e.g., [10, Lemma 2.32]), A is invertible iff both 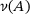 and
and 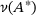 are nonzero2. Keeping this symmetry of A and
are nonzero2. Keeping this symmetry of A and 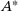 in mind,
in mind,
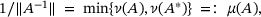
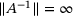 signals non-invertibility and where
signals non-invertibility and where 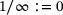 . From here it is just a small step to
. From here it is just a small step to
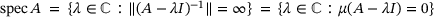
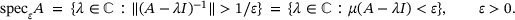 (4.1)
(4.1)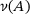 , up to
, up to 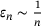 , by
, by 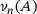 , enables us to approximate
, enables us to approximate 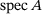 and
and 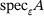 , with a controllable error, by sets built on
, with a controllable error, by sets built on 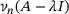 and
and 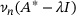 .
.5 APPROXIMATING THE PSEUDOSPECTRUM IN THE BI-INFINITE CASE
Combining this with (2.3) and (4.1), we conclude (cf. [4, Thm. 4.3 & Cor. 4.4]):
Proposition 5.1. (Bi-infinite case)For bounded band operators A on 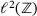 and corresponding
and corresponding  from (3.1)3, one has
from (3.1)3, one has
 (5.1)
(5.1)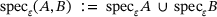 .
.
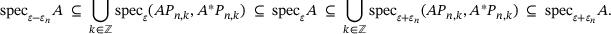
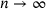 , we have
, we have 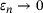 , by (3.1), and then Hausdorff-convergence
, by (3.1), and then Hausdorff-convergence 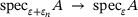 as well as
as well as 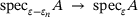 , see for example, [14]4. We conclude (cf. [4, Sec. 4.3]):
, see for example, [14]4. We conclude (cf. [4, Sec. 4.3]):
Proposition 5.2.The subsets and supersets of 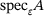 in (5.1) both Hausdorff-converge to
in (5.1) both Hausdorff-converge to 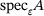 as
as 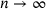 .
.
6 APPROXIMATING THE PSEUDOSPECTRA OF SEMI-INFINITE AND FINITE MATRICES
Now take a bounded and banded operator A on 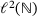 . In ref. [13] we show how to reduce this case (via embedding A into a bi-infinite matrix plus some further arguments) to the bi-infinite result:
. In ref. [13] we show how to reduce this case (via embedding A into a bi-infinite matrix plus some further arguments) to the bi-infinite result:
Proposition 6.1. (Semi-infinite case)For bounded band operators A on 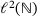 and corresponding
and corresponding 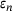 from (3.1), one has
from (3.1), one has

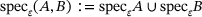 . Also here the sub- and supersets Hausdorff-converge to
. Also here the sub- and supersets Hausdorff-converge to 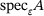 as
as 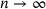 .
.
The technique that helps to deal with one endpoint on the axis can essentially be repeated for a second endpoint:
Proposition 6.2. (Finite case)For finite band matrices A on 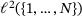 with some
with some 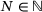 , one has
, one has
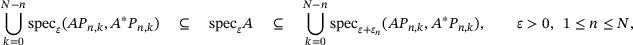
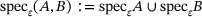 .
.
This time, of course, there is no way of sending 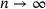 , hence no Hausdorff-convergence result.
, hence no Hausdorff-convergence result.
7 APPROXIMATING SPECTRA
 for
for 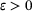 . The spectrum,
. The spectrum, 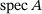 , can now be Hausdorff-approximated via sending
, can now be Hausdorff-approximated via sending  . However, there is a more direct approach: introducing closed-set versions of pseudospectra,
. However, there is a more direct approach: introducing closed-set versions of pseudospectra,
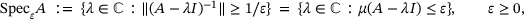
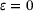 , see ref. [13]. The latter brings convergent supersets for
, see ref. [13]. The latter brings convergent supersets for 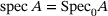 right away, without the need for a further limit
right away, without the need for a further limit  . Here is the new formula for the bi-infinite case, evaluated for
. Here is the new formula for the bi-infinite case, evaluated for 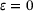 .
.
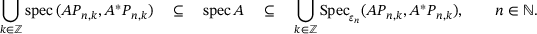 (7.1)
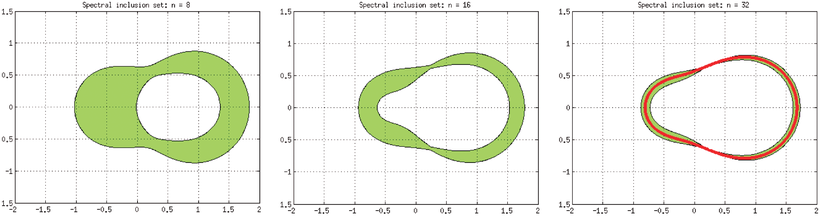
(7.1)8 EXAMPLES
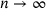 ) superset bounds on
) superset bounds on 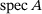 from (7.1). All three operators are given by tridiagonal bi-infinite matrices. Moreover, all three matrices are periodic, so that we can analytically compute the spectrum by Floquet-Bloch; that is, treating the 3-periodic matrix as a 3 × 3-block convolution on
from (7.1). All three operators are given by tridiagonal bi-infinite matrices. Moreover, all three matrices are periodic, so that we can analytically compute the spectrum by Floquet-Bloch; that is, treating the 3-periodic matrix as a 3 × 3-block convolution on 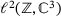 and turning that, via the corresponding block-valued Fourier-transform, into a 3 × 3-block multiplication on
and turning that, via the corresponding block-valued Fourier-transform, into a 3 × 3-block multiplication on 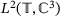 , whose spectrum is obvious, see, for example, Theorem 4.4.9 in ref. [15]. For comparison, the exact spectrum is superimposed in each example as a red curve in the last column.
, whose spectrum is obvious, see, for example, Theorem 4.4.9 in ref. [15]. For comparison, the exact spectrum is superimposed in each example as a red curve in the last column.
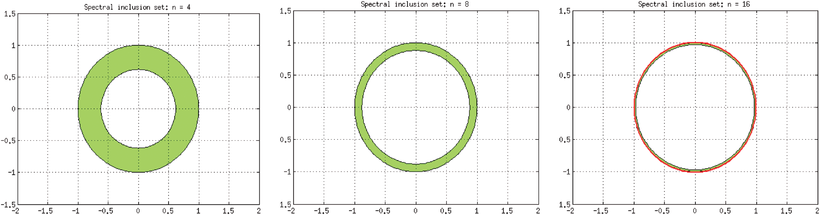
- a)
We start with the right shift, where the subdiagonal is
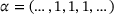 and the main and superdigonal are
and the main and superdigonal are  . The spectrum is the unit circle, and here are our supersets for
. The spectrum is the unit circle, and here are our supersets for 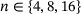 :
:
- b)
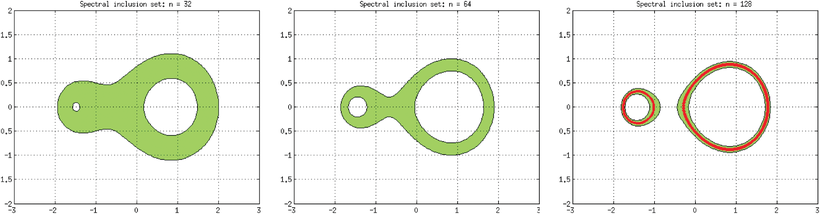
Our next example is 3-periodic with subdiagonal
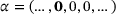 , main diagonal
, main diagonal 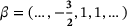 and superdiagonal
and superdiagonal 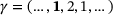 , where
, where 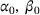 and γ0 are highlighted in boldface. The spectrum consists of two disjoint loops, and we depict our supersets for
and γ0 are highlighted in boldface. The spectrum consists of two disjoint loops, and we depict our supersets for 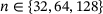 :
:
- c)
Our third example is also 3-periodic with subdiagonal
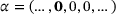 , main diagonal
, main diagonal 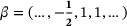 and superdiagonal
and superdiagonal 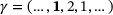 , where
, where 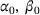 and γ0 are highlighted in boldface. The spectrum consists of one loop, and we depict our supersets for
and γ0 are highlighted in boldface. The spectrum consists of one loop, and we depict our supersets for 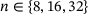 :
:
Another effect of the 3-periodicity of the diagonals in A is that there are only three distinct submatrices 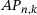 and
and 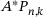 each for
each for 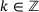 . In fact, for many operator classes, the infinite unions in (5.1), (7.1) and so on, reduce to finite unions. For example, for a
. In fact, for many operator classes, the infinite unions in (5.1), (7.1) and so on, reduce to finite unions. For example, for a 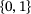 -valued aperiodic diagonal [16], there are only
-valued aperiodic diagonal [16], there are only 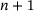 different subwords of length n, and for a
different subwords of length n, and for a 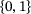 -valued random diagonal, there are 2n (again, finitely many) different subwords of length n. Also, for non-discrete diagonal alphabets, the infinite union can be reduced to a finite one via compactness arguments, see our discussion in ref. [12].
-valued random diagonal, there are 2n (again, finitely many) different subwords of length n. Also, for non-discrete diagonal alphabets, the infinite union can be reduced to a finite one via compactness arguments, see our discussion in ref. [12].
9 APPROXIMATING ESSENTIAL SPECTRA
In the case where A is an infinite matrix there is large interest also in the approximation of the essential spectrum, 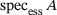 , which is the spectrum in the Calkin algebra, that is, the set of all
, which is the spectrum in the Calkin algebra, that is, the set of all 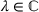 where
where 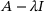 is not a Fredholm operator, that is, is not invertible modulo compact operators.
is not a Fredholm operator, that is, is not invertible modulo compact operators.
Our results in this section apply when each 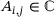 , but also when each
, but also when each 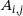 is a bounded linear operator on a Banach space X, as long as X is finite-dimensional or the operators
is a bounded linear operator on a Banach space X, as long as X is finite-dimensional or the operators 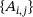 are collectively compact in the sense of refs. [17, 18].
are collectively compact in the sense of refs. [17, 18].
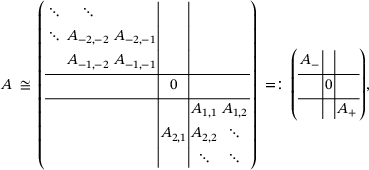
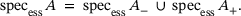
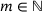 ,
,
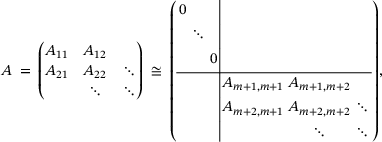
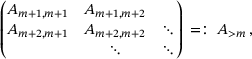
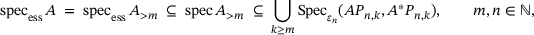
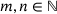 gives
gives
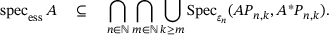 (9.1)
(9.1)In ref. [13], using results from ref. [2], we prove the following:
Proposition 9.1. (Semi-infinite)For bounded band operators A on 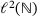 , formula (9.1) holds in fact with “⊆” replaced by equality. In addition, after this replacement,
, formula (9.1) holds in fact with “⊆” replaced by equality. In addition, after this replacement,
ACKNOWLEDGMENTS
Open access funding enabled and organized by Projekt DEAL.
REFERENCES
- 1 It is not a norm! Our terminology is that of refs. [10, 11].
- 2 By
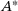 we denote the Banach space adjoint of A. In particular,
we denote the Banach space adjoint of A. In particular, 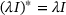 , not
, not 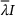 .
. - 3 Note that
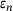 , if using (3.1), has to be computed for the block-tridiagonal representation of A, see Section 3.
, if using (3.1), has to be computed for the block-tridiagonal representation of A, see Section 3. - 4 In the case of a Banach space-valued ℓ2, that Banach space should be finite-dimensional or subject to the conditions in Theorem 2.5 of ref. [14].



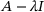 and
and 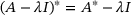 in place of A, we see that
in place of A, we see that
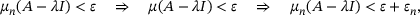
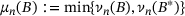 , noting that
, noting that 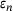 is independent of
is independent of 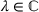 , by (
, by ( ” in (
” in ( ;
;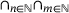 ” in (
” in (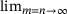 .
.
