QuantumNetSec: Quantum Machine Learning for Network Security
Funding: This work was partially supported by the São Paulo Research Foundation (FAPESP), projects 2020/04031-1, 2023/00811-0, and 2021/00199-8, CPE SMARTNESS, and project 2018/23097-3. It was also financed in part by the Coordination of Superior Level Staff Improvement (CAPES) Finance Code 001.
ABSTRACT
As the digital landscape becomes increasingly complex, traditional cybersecurity measures are struggling to keep pace with the growing sophistication of cyber threats. This escalating challenge calls for new, more robust solutions. In this context, quantum computing emerges as a powerful tool that can change our approach to network security. Our research addresses this by introducing QuantumNetSec, a novel intrusion detection system (IDS) that combines quantum and classical computing techniques. QuantumNetSec employs quantum machine learning (QML) personalized methodologies to analyze network patterns and detect malicious activities. Through detailed experimentation with publicly shared datasets, QuantumNetSec demonstrated superior performance in both binary and multiclass classification tasks. Our findings highlight the significant potential of quantum-enhanced cybersecurity solutions, showcasing QuantumNetSec's ability to accurately detect a wide range of cyber threats, paving the way for more resilient and effective IDSs in the age of quantum utility.
1 Introduction
The increasing number of cyber attacks has become a significant concern for organizations and individuals alike [1, 2]. As digital infrastructures grow more complex and interconnected, the frequency and sophistication of these attacks continue to rise [3]. This escalating threat underscores the urgent need for more advanced and effective security measures to protect sensitive information and critical systems from malicious activities [4].
In this context, the rapid development in quantum computing signals an important move towards quantum utility [5]. Current quantum computers can already solve complex problems more efficiently and accurately than some traditional methods [6, 7]. Although quantum computing has not yet consistently outperformed classical computing for specific tasks [8], these advancements are crucial for future applications across various fields. The progress in quantum technology is laying the groundwork for significant improvements in network security and other areas of research and industry.
Quantum technologies have the potential to transform network security by integrating with intrusion detection systems (IDS) using quantum machine learning (QML) techniques [9, 10]. This integration offers more accurate detection of network attacks and the ability to handle large datasets. This is essential for tackling the dynamic challenges of cybersecurity and represents a significant advancement in protecting digital infrastructures in today's fast-paced technological environment. By leveraging the strengths of QML, we can enhance the security measures that safeguard our digital world.
A key challenge is the current state of quantum devices, known as noisy intermediate-scale quantum (NISQ) devices [11]. These devices face limitations in the number of Qubits they can support, the complexity of quantum circuits they can run, and their ability to maintain quantum coherence over time due to noise and the delicate nature of Qubits [12]. Additionally, the lack of effective error correction mechanisms in NISQ systems presents a significant hurdle [13]. Any proposed quantum IDS must address these limitations to be practically useful with the current quantum computing technology [11]. Despite these challenges, the potential benefits of combining quantum computing with IDS are substantial.
In this paper, we propose QuantumNetSec, an attack detection system using QML tailored specifically for NISQ devices. Building upon our earlier research [14], where QML models were applied to network security using baseline circuits without optimization and subsequently with default circuit transpilation [15] via the IBM Qiskit framework [16], this study introduces significant advancements. We employ quantum personalized circuit optimization techniques and conduct more comprehensive experimentation. The outcomes of these approaches are thoroughly analyzed and compared in Section 6 (Table 4).
The primary goal is to create an adaptable system that can operate effectively within the constraints of current quantum computing technology. Our approach is based on QML techniques, leveraging the strengths of both classical and quantum computing. To optimize performance for NISQ devices, we incorporate the process of transpilation and circuit optimization, which helps minimize errors and improve the efficiency of quantum circuits. This ensures that QuantumNetSec can effectively utilize the available quantum resources, enhancing its applicability and performance in detecting cyber threats.
- Development of QuantumNetSec, a QML-based network IDS tailored for NISQ devices
- Evaluation of QuantumNetSec across different NISQ backends, highlighting its adaptability to various quantum device configurations.
- Thorough experimentation under various personalized circuit optimization techniques, demonstrating how these improvements enhance system performance.
- Analysis of four distinct QML techniques for network attack detection, with a detailed evaluation of the performance of each method.
The remainder of this paper is structured as follows: Section 2 provides an overview of QML techniques used in the study. Section 3 discusses related works in quantum-enhanced network security. Section 4 details the QuantumNetSec framework, including its design and implementation. Section 5 outlines the experimental setup and datasets used. The results and analysis are presented in Section 6. Finally, Section 7 concludes the paper and suggests directions for future research.
2 QML
QML represents the union of quantum computing principles such as superposition, interference, and entanglement, with traditional ML techniques to enhance tasks like classification, regression, and clustering. In this section, we introduce the foundational concepts of QML, including key quantum properties such as superposition, entanglement, and the use of quantum circuits. Following this, the section is structured into subsections that detail the main techniques employed in this study. Each subsection provides theoretical insights and implementation details, highlighting the advantages and potential applications of these techniques.
The unique properties of quantum computing enable QML to process information in fundamentally new ways, offering the potential for significant performance improvements over classical methods.
Superposition allows quantum systems to exist in multiple states simultaneously. In quantum computing, the basic unit of information is the qubit, which can represent a state as , or any quantum superposition of these states, written as , where and are complex numbers satisfying . This property enables quantum computers to process a vast amount of possibilities, significantly accelerating computations for specific ML tasks [17]. As depicted in Figure 1a, the bloch sphere represents the state of a Qubit, where any point on the sphere corresponds to a valid Qubit state. The north pole represents the state , the south pole represents , and any other point represents a superposition of these states. For example, the point represents an equal superposition of and .
Entanglement, on the other hand, is a unique quantum phenomenon where two or more Qubits become interconnected such that the state of one Qubit directly influences the state of the other, regardless of the distance separating them. When Qubits are entangled, the overall state of the system cannot be described independently of each Qubit's state. For example, in an entangled state , the measurement of one Qubit immediately determines the state of the other.
Quantum gates are the building blocks of quantum circuits, functioning similarly to classical logic gates but operating on Qubits. These gates manipulate Qubits through unitary transformations, enabling various quantum operations. Measurement is a crucial part of quantum computing, as it converts the quantum state of a Qubit into a classical state (0 or 1). This process collapses the superposition state into one of the basis states, providing the output of the quantum computation. Figure 1b illustrates a simple quantum circuit comprising Pauli-X (), Pauli-Z (), CNOT, and Hadamard () gates. The Pauli-X gate acts as a quantum equivalent of the classical NOT gate, flipping the state of a Qubit from to and vice versa. The Hadamard gate creates a superposition state, transforming into and into . The CNOT gate, or controlled-NOT gate, entangles two qubits by flipping the second qubit (target) if the first qubit (control) is in the state .
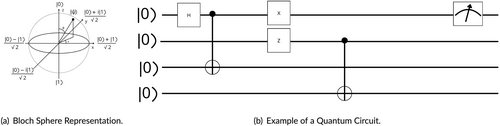
Quantum algorithms, such as those used in QML, are constructed by arranging these gates into circuits, such as the one presented in Figure 1b that perform specific computational tasks. By using superposition and entanglement, these circuits can process information in a new way, offering potential benefits for ML tasks. In this section, we will delve into the four QML methods employed in our proposal, explaining their mechanisms and the quantum advantages they provide.
2.1 Variational Quantum Classifier (VQC)
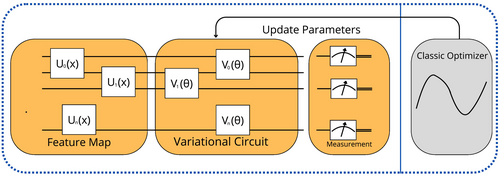
The VQC [18] is designed to bridge the gap between quantum computing and classical data classification methods. By integrating quantum circuits with classical optimization, the VQC is capable of tackling complex classification tasks. As depicted in Figure 2, the VQC process begins with the encoding of classical data into quantum states through a feature map. The quantum gates are employed to transform the input data into a quantum state. This step embeds the classical data into the quantum domain, leveraging the higher-dimensional space provided by quantum states.
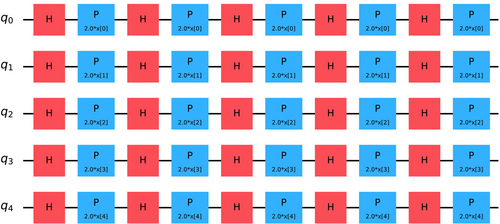
There are diverse types of feature maps in quantum computing, each designed to encode classical data into quantum states in a way that captures the essential features of the data. Figure 3 shows an example of a feature map circuit, where a combination of Hadamard gates (H) and parameterized Pauli-Z rotations (P) are used. The Hadamard gates create superposition. Then, the parameterized Pauli-Z rotations encode the classical input data into the quantum state by rotating the Qubits' phases according to the values of the input features. This arrangement of gates helps map the classical data into a quantum state that can be effectively utilized in QML algorithms.
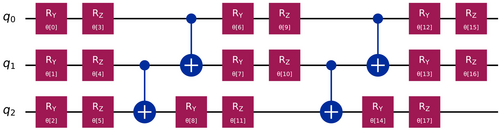
The core of the VQC lies in the variational quantum circuit (also known as Ansatz), as shown in Figure 4, where quantum gates are applied to the encoded states. These gates, controlled by adjustable parameters, enable the circuit to learn complex patterns within the data. The variational circuit typically consists of multiple layers of quantum gates, which may include rotation gates such as , where is the tunable parameter that controls the rotation angle around the y-axis of the Bloch Sphere. These quantum operations, combined with entangling gates, allow the VQC to explore a vast space of possible solutions, searching for the one that best separates the data into distinct classes.
The final stage in the VQC's process is the optimization of the Ansatz, which involves fine-tuning the parameters of the quantum circuit to minimize a cost function. This is accomplished through classical optimization techniques, where a classical optimizer iteratively adjusts the parameters to achieve the best possible classification accuracy. The measurement results are then used to compute a cost function that quantifies the accuracy of the classification. This process is essential for evaluating how well the current parameter set is performing in distinguishing between different classes. Finally, the measurement outcomes are fed into a classical optimizer, which adjusts the parameters of the variational circuit. This iterative process continues until the cost function is minimized, and the VQC finds the optimal parameters that define the decision boundary between different classes. By combining quantum circuits with classical optimization, the VQC leverages quantum properties to potentially enhance classification performance, particularly in areas where classical methods may be limited by computational complexity or data dimensionality.
2.2 Quantum Support Vector Machine (QSVM)
The QSVM [19] is a version of the classical support vector machine (SVM) [20] algorithm, designed to leverage the properties of quantum computing for enhanced data classification. Unlike its classical counterpart, the QSVM operates by mapping input data into a high-dimensional quantum feature space, as illustrated in Figure 5. This quantum feature space allows for the effective separation of data that may not be linearly separable in its original form. The QSVM achieves this by constructing a quantum kernel, a function that measures the similarity between pairs of data points within this quantum space. This quantum kernel is generated through specific quantum transformations applied to the quantum states that represent the input data, enabling the QSVM to tackle complex classification tasks that might be challenging for classical methods.
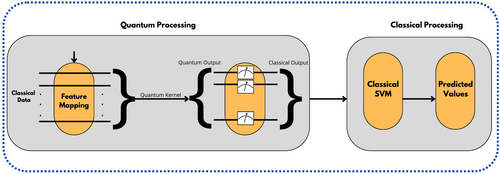
During the training phase, the QSVM utilizes a quantum circuit to project the training data into the quantum feature space. Within this space, the algorithm computes a kernel matrix, which captures the nuanced relationships between the training examples. The next step involves identifying support vectors, critical data points that help define the optimal hyperplane for separating different classes within the quantum feature space. This process is similar to the classical SVM but occurs within the quantum domain, potentially offering significant advantages in managing data structures and improving classification outcomes.
In the testing phase, the QSVM applies the same quantum mapping process to new, unlabeled data points. These points are classified based on their position relative to the quantum hyperplane established during the training phase. The ability to accurately classify data using quantum operations makes QSVM particularly valuable for datasets that challenge traditional classification methods.
To demonstrate the functionality of QSVM, an example can be provided involving two classes of data points: one class forms a circular pattern within a two-dimensional space, while the other class occupies the surrounding region. In this scenario, a classical SVM faces challenges in achieving linear separation within the original feature space. By contrast, QSVM addresses this limitation by mapping the data into a high-dimensional quantum feature space, where the circular pattern becomes linearly separable. Through the use of a quantum kernel specifically designed for such transformations, QSVM efficiently determines the optimal hyperplane, enabling accurate classification of the data points.
The performance of the QSVM is heavily influenced by the choice of the feature map and the design of the quantum kernel. These components are essential for capturing the key characteristics of the data in the quantum feature space, thereby enabling the QSVM to achieve superior classification accuracy.
2.3 Quantum Convolutional Neural Network (QCNN)
The QCNN [21] is a quantum-enhanced version of classical convolutional neural networks (CNNs) [22], designed to harness the power of quantum computing for advanced data processing tasks. As depicted in Figure 6, QCNNs retain the fundamental architecture of classical CNNs, consisting of convolutional layers, pooling layers, and fully connected layers, but they implement these components using quantum operations. In QCNNs, the convolutional layers are created through parameterized unitary operations applied to neighboring Qubits, analogous to the filters in classical CNNs. These quantum convolutions enable the detection and extraction of quantum features, operating on the quantum states of qubits rather than on pixel values as in classical CNNs.
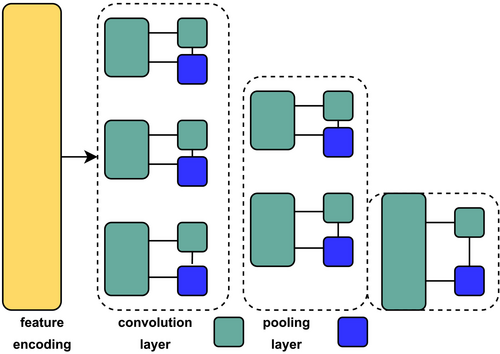
In classical CNNs, layers are designed to automatically learn and refine spatial hierarchies of features from input data, typically images. Convolutional layers apply filters that slide across the input, performing convolution operations that generate feature maps. These maps highlight various aspects of the input, such as edges, textures, and other patterns. The filters in classical CNNs are trained through backpropagation and gradient descent to identify specific features relevant to the task at hand. Pooling layers follow, reducing the dimensionality of these feature maps while retaining the most significant information. This process helps in creating a more abstract representation of the data as it moves deeper into the network.
QCNNs similarly incorporate quantum pooling layers, which serve a purpose akin to classical pooling but are executed within the quantum framework. In classical CNNs, pooling layers reduce the size of feature maps by selecting the most important information, typically through operations like max pooling or average pooling. In QCNNs, this dimensionality reduction is achieved by measuring a subset of qubits, effectively decreasing the number of qubits in the system. The selection of which qubits to measure is a crucial design decision in QCNNs, as it directly influences how information is condensed and propagated through the quantum network, impacting the overall performance of the model.
Training a QCNN involves optimizing the parameters of both the quantum convolutional and fully connected layers to minimize a loss function, much like in classical neural networks. However, because the operations within QCNNs are quantum in nature, traditional optimization techniques such as gradient descent must be adapted to work with quantum circuits. This often involves using classical optimization algorithms to adjust the parameters of the quantum operations based on measurement outcomes, creating a hybrid quantum-classical learning approach. The quantum-classical interplay in QCNNs opens up new possibilities for data processing, particularly in areas where quantum features can offer an advantage over classical methods, potentially leading to breakthroughs in fields such as quantum image processing and quantum pattern recognition.
An example of QCNN functionality can be demonstrated in a classification task involving quantum states representing two distinct categories. Each category is encoded into a set of qubits, with their quantum states containing patterns that distinguish one class from the other. In the quantum convolutional layer, parameterized unitary operations are applied to neighboring qubits to extract features such as correlations or entanglements specific to each category. These extracted features are processed through quantum pooling layers, where selected qubits are measured to reduce the dimensionality of the quantum system while preserving the most significant information. The reduced quantum representation is subsequently passed through additional quantum layers, culminating in a classification outcome.
2.4 Quantum K-Means (QKM)
QKM [23] is a quantum version of the classical k-means [24] algorithm, designed to improve the efficiency and effectiveness of clustering tasks by leveraging the unique properties of quantum computing. Like its classical counterpart, QKM aims to group data into distinct clusters by identifying and separating different categories based on their similarities. The fundamental mechanism of QKM, illustrated in Figure 7, involves a quantum circuit known as the swap-test circuit. This circuit plays a crucial role in determining the distance between data points and cluster centroids, a key step in the clustering process.
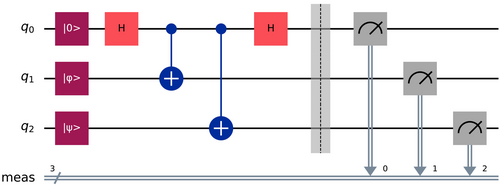
In the QKM algorithm, quantum states represent the centroids of clusters and the data points to be classified. For example, the quantum state represents the current centroid of a cluster, while represents a new data point whose cluster needs to be determined. To calculate the distance between these quantum states, an auxiliary qubit is introduced in the state. A Hadamard gate () is applied to this Qubit, placing it in a superposition state. The swap-test circuit, which involves controlled-NOT (CX) gates, is then used to calculate the distance between the quantum states and . Based on this distance, the algorithm assigns the data point to the nearest cluster, updating the centroids iteratively until the algorithm converges.
The QKM algorithm operates through three main subroutines: distance calculation using the swap-test circuit, cluster update, and centroid update. After each distance calculation, the algorithm updates the clusters and centroids, repeating these steps until the positions of the centroids stabilize, indicating that the clusters have been effectively formed.
Classical k-means is a well-established algorithm used to partition data into clusters by repeatedly assigning data points to the nearest centroid and recalculating the centroids until convergence is achieved. QKM enhances this process by utilizing quantum properties such as superposition and entanglement, which allow for potentially more efficient computations. The swap-test circuit in QKM enables the algorithm to measure the similarity between quantum states, representing the distance between data points and centroids in a quantum feature space.
3 Related Work
Multiple studies have explored the application of QML across various fields [25, 26]. These applications range from finance and drug discovery to optimization problems and image recognition, showcasing the broad potential of QML techniques across diverse fields. In this section, we highlight works that use QML in the context of network security and compare them with our proposal. Table 1 provides an overview of the related works.
| Techniques | NISQ optimization | Attacks | Target | Dataset | |
|---|---|---|---|---|---|
| This work | VQC, QSVM | ✓ | Various (23) | Binary | UNSW-NB15, CIC-IDS17, |
| QCNN, QKM | Multiclass | CICIoT23, TONIoT | |||
| [27] | QSVM | X | DDoS | Binary | CIC-DDoS2019 |
| [28] | VQC + NN | X | Various (4) | Binary | KDD99 |
| [29] | QSVM + NN | X | Various (6) | Binary | Own dataset |
| [30] | VQC + DL | X | DGA attack | Binary | Own dataset |
| [31] | qGAN | X | Various (4) | Binary | NSL-KDD |
| [32] | QSVM | X | Various (13) | Binary | UNSW-NB15, NLS-KDD |
| [33] | VQC, QSVM | X | Various (4) | Binary | KDD99 |
| [34] | QNNs, QCNN | X | Various (9) | Binary | UNSW-NB15 |
| [35] | QAE + SVM, RF, KNN | X | Various (34) | Binary | KDD99, IoT-23, CICIoT23 |
Said et al. (2023) [27] investigate the use of a QSVM model to detect distributed denial of service (DDoS) attacks in smart microgrids. Their study utilizes a sampled version of the CIC-DDoS2019 dataset [36], which contains data on both DDoS attacks and normal network behavior. The results indicate that the QML model outperforms the classical SVM approach. Similarly, Gouveia and Correia (2020) [32] apply QSVM to detect network attacks using the UNSW-NB15 [37] and NSL-KDD [38] datasets. Additionally, Venkatachalam and Liu (2023) [33] employ both VQC and QSVM to detect attacks in the KDD99 dataset [39].
Kalinin and Krundyshev (2023) [29] propose a hybrid model combining QSVM and neural networks (NN) for network attack detection. The authors tested on a custom-built database and compared it with techniques such as SVM and CNNs. Rahman et al. (2023) [31] introduce a quantum generative adversarial network (qGAN) for attack detection, which leverages the interaction between generative and discriminative networks to learn from training data. While these studies implement their solutions using noiseless quantum computing simulators, which do not accurately reflect current NISQ systems, our work distinguishes itself by implementing the proposed method on noisy quantum backends, providing a more realistic representation of current NISQ technology.
Suryotrisongko and Musahi (2022) [40] propose using a variational quantum circuit and a hybrid quantum deep learning (DL) model to detect botnet domain generation algorithm (DGA) attacks. The Hybrid DL model incorporates a quantum layer into a traditional neural network, while the VQC operates as a standalone model. Notably, while the DL model was tested on NISQ devices, the VQC was not. In a separate study, Gong et al. [28] propose a combination of a Neural Network (NN) with a VQC for network attack detection. This model was applied to a reduced subset of features from the KDD99 dataset [39], with a class balancing technique to improve classification accuracy. Their proposal was tested using both a noiseless quantum simulator on Google's Cirq framework 1 and the IBM Quantum platform 2.
Kukliansky et al. (2024) [34] tested four quantum neural network (QNN) architectures, TNN, MERA, QCNN, and a simple architecture using the IonQ quantum computing platform 3. They validated their proposal using the NF-UNSW-NB15 dataset [41]. Additionally, Hdaib et al. (2024) [35] introduced three frameworks combining quantum autoencoders (QAE) with classical ML methods, including SVM, random forest (RF), and K-nearest neighbors (KNN). Their experiments utilized the KDD99, IoT-23 [42], and CICIoT23 [43] datasets. Both Kukliansky et al. (2024) and Hdaib et al. (2024) conducted their experiments on the IBM quantum platform, running them on NISQ devices to evaluate the performance of their proposed frameworks in realistic quantum environments. However, none of these works used any NISQ circuit optimization technique.
In contrast to previous studies, our work addresses key limitations in the current literature by focusing on both practical and technical advancements in the application of QML to network security. While most prior works relied on noiseless quantum simulators or minimally optimized NISQ circuits [27-29, 31], our approach leverages advanced circuit optimization techniques tailored for NISQ devices. This directly enhances the feasibility of deploying QML models in real-world quantum hardware environments. Additionally, whereas earlier studies predominantly focused on binary attack detection with limited datasets (e.g., CIC-DDoS2019 or KDD99) [27, 32], our research expands the scope by incorporating multiclass attack detection and testing across four comprehensive datasets (UNSW-NB15, CIC-IDS17, CICIoT23, and TONIoT), covering a broader spectrum of 23 distinct attack types. Furthermore, unlike works such as [35] and [30], which introduced hybrid models without fully exploiting circuit optimization for performance gains, our proposal demonstrates the effectiveness of personalized optimization strategies in achieving better classification accuracy and robustness on noisy quantum backends. These distinctions not only address the scalability and practicality gaps in the field but also underline the significant advancements offered by our work over existing approaches.
In our previous research [14], QML models were initially tested within a network security context, through direct implementation of baseline circuits without circuit optimization and then with default circuit transpilation [15], available on IBM Qiskit framework [16]. In this study, we expand on that research by employing quantum personalized circuit optimization techniques alongside more thorough experimentation. We compare the results of these approaches in Section 6 (Table 4).
Thus, the research contributions presented in this work differ by presenting a comprehensive analysis of the application of various QML techniques (VQC, QSVM, QKM, QCNN), both for detection (binary scenario) and for the identification of attacks (multiclass scenario). Additionally, our work conducts tests on four reference datasets in network security: UNSW-NB15, CIC-IDS17, CICIoT23, and TONIoT [44] containing a wide variety of network attacks, with a total of 23 different attacks. Furthermore, unlike the related studies, we conducted tests in circuits with diverse optimization levels, incorporating personalized circuit optimization, which contributed to the improvement of our results.
4 QuantumNetSec: QML for Network Security
In this work, we propose QuantumNetSec, a network attack detection system that leverages QML techniques to enhance cybersecurity. The system integrates both quantum and classical computing methods to effectively detect network attacks. The operational workflow of QuantumNetSec is outlined in the flowchart presented in Figure 8, providing a clear visualization of the system's processes.
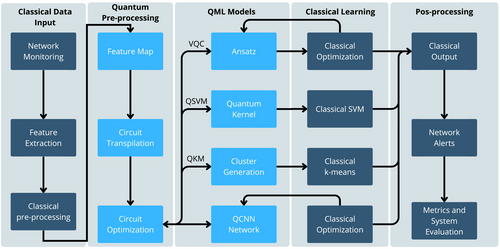
The system begins with the continuous monitoring of network traffic, which is a critical initial phase. During this stage, comprehensive data packets and metadata traversing the network are captured. This data collection is crucial as it provides the foundational dataset necessary for identifying potential security threats. The integrity and comprehensiveness of the collected data ensure a robust basis for subsequent analysis, making the monitoring phase essential for the system's effectiveness.
Following data collection, the system performs feature extraction, a process focused on deriving informative attributes from raw network data that may indicate normal or malicious activities. Feature extraction involves transforming unstructured or raw data into a structured representation by identifying and isolating patterns, such as traffic flow metrics, protocol behaviors, or anomaly indicators. This step is essential for enhancing the system's ability to detect irregularities in network traffic, laying the foundation for accurate attack detection. Importantly, feature extraction focuses on creating a comprehensive set of potential features rather than narrowing them down at this stage. Once feature extraction is complete, the data undergo classical preprocessing, which includes tasks such as normalization to scale feature values and handling missing data to ensure integrity. This phase can optionally include feature selection, a distinct process that identifies the most relevant features from the extracted set to reduce dimensionality and focus computational resources on key attributes. However, in this work, feature selection was not applied, as the full set of extracted features was retained for analysis. These preprocessing steps are critical for preparing the data in an optimal format and quality, which directly impacts the overall performance of the QML models.
The next phase involves mapping the preprocessed classical data to quantum states. This is achieved using a feature map. In this step, different architectures of feature map circuits can be employed, as will be further discussed in Section 5.2. Circuit transpilation then adapts these circuits to specific NISQ backends. During this stage, different circuit optimization techniques can be applied to enhance the efficiency of the quantum computations, as will be further discussed in Section 5.2, ensuring that the quantum processing is as effective and resource-efficient as possible.
The core of the QuantumNetSec system is the hybrid QML process, where both quantum and classical components work together according to the chosen QML technique. For example, in the case of variational quantum circuits, a variational quantum circuit ansatz is generated, with parameters adjusted by a classical optimizer. For QSVMs, a quantum kernel is generated and used to train a classical prediction model. For QKMs, the quantum process utilizes a swap-test circuit to calculate and generate clusters, while in QCNNs, the quantum network is generated and then optimized using classical methods. Each of these techniques is tailored to maximize the strengths of both quantum and classical approaches.
After the quantum models are constructed, their parameters are further optimized through a hybrid approach. This involves classical optimization techniques that refine the quantum circuits' parameters. These adjustments allow the models to adaptively improve based on performance feedback from the training data. The hybrid optimization process is key to ensuring that the QML models achieve their best possible performance, aligning with the overall goal of the system.
Upon completing the quantum processing, the results are converted back into a classical form. This conversion yields a classical output, which is then interpreted to generate attack alerts. Whenever suspicious patterns are detected, the system raises alerts, thereby contributing to the overall security of the network. The final interpretation of quantum results into actionable intelligence is a critical step in making the system practical and effective for real-world applications.
Importantly, the QuantumNetSec system is flexible and can incorporate various hybrid QML methods, adapting to the specific needs and characteristics of each method. In the next subsections, we further detail the QuantumNetSec quantum transpilation and circuit optimization process.
4.1 Quantum Transpilation
Transpilation is a fundamental process in quantum computing that involves transforming a given quantum circuit to perform on a specific quantum device. This adaptation is crucial because each quantum device has unique features and operational requirements. Instructions, such as what gate to use, that works well on one quantum backend may not be suitable for another. Figure 9 exemplifies this process by illustrating a quantum circuit before and after transpilation.
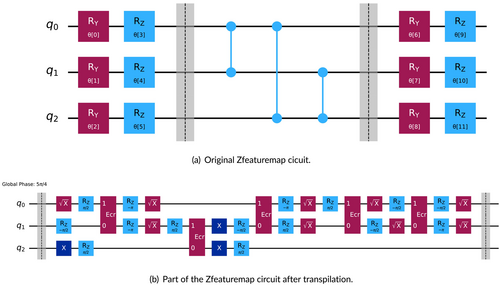
In Figure 9a, the original ZFeatureMap circuit is shown, which consists of parameterized and rotation gates applied to Qubits , and . This initial circuit is designed without consideration for a specific quantum device. Figure 9b shows part of the circuit after transpilation, where the quantum gates and their sequence have been modified to suit the architecture of the target quantum device. During transpilation, various elements such as the device's set of basic gates, the architecture of its quantum chips, and timing restrictions are considered. The primary goal of transpilation is to enhance performance on error-prone quantum hardware by modifying and refining circuits to mitigate the effects of noise and errors. These modifications align the circuit with the target device, improving the accuracy of computational results.
4.2 Circuit Optimization
In addition to adjusting circuits to meet the specific requirements of a quantum backend through transpilation, it is also necessary to address errors caused by noise. Decoherence, a significant type of noise, causes Qubits to lose information over time, particularly when they remain idle. Increased circuit depth increases this issue, leading to more substantial information loss.
Additionally, measurement errors present challenges when Qubits are measured incorrectly—for example, reading a 0 as a 1. Gate errors further contribute to noise; quantum gates are not flawless, and errors are particularly prevalent in two-qubit gates like the CX, which tend to have higher error rates than single-qubit gates. Crosstalk errors can also increase these issues, as activating a gate on one Qubit might inadvertently affect its neighbors.
Optimizing circuit transpilation can help reduce noise in quantum circuits. This can be done through a standardized six-step workflow, as illustrated in Figure 10.

As Figure 10 shows, the initial step, initialization, involves a basic check of circuit instructions and translates multiqubit gates into simpler configurations. Following initialization, the layout step assigns the circuit's virtual qubits to the physical qubits on the quantum device.
The routing phase integrates necessary SWAP gates into the quantum circuit to align with the backend's connectivity constraints. Since qubits in a quantum device are often not directly connected, SWAP gates are critical for repositioning Qubit states, enabling the execution of two-qubit gates between qubits that are not adjacent. This repositioning is essential for ensuring that all necessary interactions can occur despite physical layout limitations. The focus during this phase is on minimizing the use of SWAP gates because they introduce additional operations that are both noise-prone and computationally expensive. Therefore, the routing phase is typically optimized alongside the layout phase to efficiently manage qubit placement and connectivity.
In the translation phase, the circuit's gates are converted into the native gate set of the target backend. While quantum circuits can be designed with a variety of gate types, quantum hardware generally supports only a limited set of native gates. This translation ensures that the circuit is compatible with the specific backend but often results in increased circuit depth and a higher overall gate count. The addition of SWAP gates in the routing phase can contribute to this increased complexity, making efficient routing and translation crucial for optimizing quantum computations.
The optimization step runs a main optimization that aims to reduce the circuit's depth and gate count by combining or eliminating gates wherever possible. The success of this optimization varies; in some instances, it significantly reduces circuit complexity, while in others, the improvements might be minimal, especially on noisy quantum devices.
Finally, the Scheduling step manages the idle times between operations by strategically inserting delay instructions and optimizing the circuit's runtime on the backend in light of physical constraints and operational capabilities.
4.3 Personalized Circuit Optimization
Each step in the transpilation optimization process incrementally refines the quantum circuit, ensuring compatibility with the intended quantum hardware. While Qiskit offers four predefined transpilation levels, ranging from no optimization (level 0) to increasingly advanced optimizations (levels 1 through 3), these default settings may not fully exploit the potential of quantum hardware. Each step in the circuit optimization process presents opportunities for further refinement by utilizing nondefault configurations.
In our proposal, we implement a personalized circuit optimization approach, where we rigorously test all possible combinations of available optimization techniques for each step. This comprehensive exploration allows us to tailor the optimization process to the specific characteristics of the quantum hardware and the circuit at hand, potentially leading to better performance than standard methods. Table 2 presents the options available at each step of the circuit optimization process.
| Transpilation Process | Options |
|---|---|
| Init | UnitarySynthesis, HighLevelSynthesis, BasisTranslator, InverseCancellation, OptimizeSwapBeforeMeasure, RemoveDiagonalGatesBeforeMeasure |
| Layout | TrivialLayout, VF2Layout, DenseLayout, SabreLayout |
| Routing | basic, sabre, stochastic |
| Translation | translator, synthesis |
| Optimization | Collect2qBlocks, ConsolidateBlocks, UnitarySynthesis, Optimize1qGatesDecomposition, CommutativeCancellation, CXCancellation, approximation_degree |
| Scheduling | default, alap, asap |
The default circuit optimization level 0 is tailored for device characterization experiments. This level does not apply any optimizations to the input circuit, only mapping it to the constraints of the target backend. It employs the TrivialLayout 4 method for layout and routing, where the same numbers are assigned to both physical and virtual qubits. When necessary, it incorporates SWAP operations through StochasticSwap 5 to ensure the circuit functions within the backend's physical layout. Moving to optimization level 1, a light optimization is introduced, enhancing the basic mapping of circuits. Initially, TrivialLayout is used to establish a basic mapping; if this requires additional SWAPs, SabreSWAP [45] finds a layout with the minimal number of SWAPs necessary. Postlayout optimization is then applied using VF2LayoutPostLayout [46] to select optimal qubits within the graph. This level also includes InverseCancellation 6 to refine the circuit and 1Q gate optimization to streamline single-qubit operations.
The optimization further intensifies with Levels 2 and 3. Level 2 builds upon the foundation set by Level 1 but excludes TrivialLayout, instead employing more advanced heuristic methods with increased search depth and optimization trials. It also introduces CommutativeCancellation 7 to reduce redundancy. Level 3, offering the highest optimization, extends these methods further with exhaustive efforts and trials, particularly in layout and routing. It also features advanced techniques such as the resynthesis of two-qubit blocks using Cartan's KAK decomposition [47] and specific optimizations like RemoveDiagonalGatesBeforeMeasure 8, which streamline the circuit by altering or eliminating unnecessary gates and SWAPs in preparation for measurement.
Table 2 outlines the diverse methods available for each step of the transpilation process. By exploring these options, we aim to identify the most effective combination of techniques for minimizing circuit depth, gate count, and overall noise, thereby enhancing the reliability and efficiency of quantum computations. This approach ensures that the optimization process is not only thorough but also adaptable, maximizing the utility of the quantum hardware for specific tasks.
By systematically experimenting with these options, our personalized circuit optimization approach enables us to fine-tune the quantum circuits beyond what is possible with standard optimization levels. This method not only enhances the adaptability of the circuits to different quantum devices but also helps in mitigating the impact of various noise factors, thereby contributing to more robust and accurate quantum computations.
5 Experimental Setup
In this section, we outline the experimental setup used to evaluate the performance of QuantumNetSec. This includes a description of the datasets employed, the application of circuit optimization techniques, the configuration of both quantum and classical ML models, and the specifics of the NISQ devices used in the experiments. By providing a comprehensive overview of these elements, we aim to ensure the reproducibility and transparency of our evaluation methodology.
5.1 Datasets
To evaluate the proposed system, we conducted a comprehensive case study, leveraging four prominent network security datasets: UNSW-NB15, CIC-IDS17, TONIoT, and CICIoT23. These datasets include both normal traffic data and various types of attack network traffic data and are frequently utilized for the detection and classification of attacks using ML techniques [48, 49].
The UNSW-NB15 dataset is a benchmark network security dataset created for ML testing. It consists of 100 GB of labeled network flow data, including normal data and data from nine different types of attacks. The attack categories in this dataset are as follows: Analysis, Backdoor, DoS (Denial of Service), Exploits, Fuzzers, Generic, Reconnaissance, Shellcode, and Worms. This dataset provides a comprehensive set of network activities, making it suitable for evaluating the effectiveness of IDSs.
The CIC-IDS17 dataset was constructed by simulating the behavior of 25 users over a week. Network flow data were captured during this period, resulting in a detailed dataset that includes both normal and malicious activities. The types of attacks recorded in this dataset are BoT, BruteForce, DDoS, DoS, Infiltration, PortScan, and WebAttack. The comprehensive nature of this dataset allows for the thorough testing of IDS against various attack scenarios.
The TONIoT dataset contains a variety of IoT network attacks. The attacks included in this dataset are Backdoor, DoS, DDoS, Injection, MITM (Man-in-the-Middle), Password, Ransomware, Scanning, and XSS (Cross-Site Scripting). This dataset is particularly valuable for assessing the performance of IDS in protecting IoT networks from a wide range of cyber threats.
The CICIoT23 dataset is designed to test the robustness of IDSs in IoT networks. It includes a range of IoT-specific attacks such as BruteForce, DoS, DDoS, Mirai, Reconnaissance, Spoofing, and WebAttack. All attacks are executed by malicious IoT devices targeting other IoT devices, providing an environment for testing IDSs.
These datasets provide a diverse set of scenarios and attack types, enabling a thorough evaluation of QuantumNetSec's capabilities in different network environments. The variety of attacks and the comprehensive nature of these datasets ensure that the system is tested against a wide range of potential threats, highlighting its robustness and effectiveness in real-world applications.
5.2 Quantum and Classical ML Configuration
Four classical ML methods were selected and will serve as a comparison to the quantum counterparts results: SVM, convolution neural network, RF as a representative classifier to compare with VQC, and KNNs, all implemented using the scikit-learn9 and TensorFlow 10 frameworks.
To evaluate the performance of QuantumNetSec, four QML models were employed: VQC, QSVM, QKM, and QCNN, which were implemented using the Qiskit framework. For these models, the specific hyperparameters used are presented in Table 3.
| Feature maps | Ansatz | Classical optimizer |
|---|---|---|
| PauliFeatureMap | EfficientSU2 | COBYLA |
| RawFeatureVector | ExcitationPreserving | ADAM |
| ZFeatureMap | RealAmplitudes | SPSA |
| ZZFeatureMap | TwoLocal | GradientDescent |
We employ four feature maps from Qiskit for encoding classical data into quantum states, alongside four Ansatz and classical optimizers within the Qiskit framework. The RawFeatureVector offers a direct mapping of classical data to quantum states, establishing a baseline. The PauliFeatureMap and ZFeatureMap utilize quantum gates to simulate Pauli operators and employ Hadamard and unitary gates for transforming classical inputs into quantum states, enabling the capture of nonlinear patterns and facilitating first-order data encoding. The ZZFeatureMap extends these capabilities by incorporating second-order Qubit interactions for more complex correlation encoding [50].
The RealAmplitudes ansatz circuit consists of alternating layers of gate rotations and entanglements. It is named RealAmplitudes because the quantum states have only real amplitudes; thus, the complex part is always zero. On the other hand, EfficientSU2 circuit comprises layers of single qubit operations spanned by SU(2) and entanglements. The SU(2) stands for the special unitary group of degree 2, involving unitary matrices with determinant 1, like the Pauli rotation gates.
Another variational circuit used is the ExcitationPreserving. It is structured with layers of rotations and 2-qubit entanglements. We also used the TwoLocal ansatz, in which the circuit is a parameterized structure alternating between rotation layers, which apply single qubit gates to all qubits and entanglement layers that use two-qubit gates to entangle the Qubits.
For our experiments, we selected four classical optimization techniques, each with unique strengths. ADAM [51] is a gradient-based algorithm that adapts to lower-order moments, making it effective for nonstationary and noisy gradients. COBYLA [52] is used for constrained problems with unknown derivatives, iteratively refining solutions through linear approximations. SPSA [53] is well-suited for large-scale and complex systems, using a stochastic approximation of the gradient for efficient optimization. Finally, gradient descent [54] is a fundamental method that iteratively updates parameters in the direction of the negative gradient to find the function's minimum.
5.3 NISQ Devices
We evaluated the performance of QuantumNetSec across various NISQ backend configurations. Figure 11 presents the topology (physical positioning of Qubits) and noise levels per Qubit and connection for each of three of the backends used, with darker colors indicating lower noise levels. As illustrated in Figure 11, IBM Cairo has 27 Qubits with a distinct topology compared to IBM Kyoto, which has 127 Qubits, and IBM Torino with 133 Qubits.
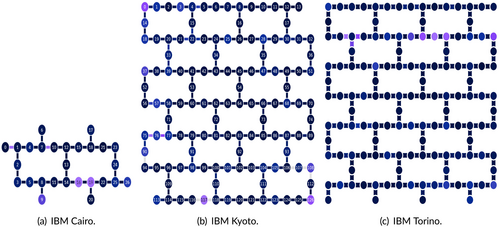
For this evaluation, seven different backends were utilized provided by IBM quantum platform: Cairo, Kyoto, Brisbane, Osaka, Sherbrooke, Torino, and Quebec. These environments incorporate the specific noise models, quantum logic gates, and topologies of actual quantum computers, providing a realistic assessment of quantum technologies in security applications.
6 Results
In this section, we present the results of our experiments. Then, we start with a comparison between the results obtained from different NISQ backends, examining three scenarios: no optimization, default optimization, and personalized optimization. We identify the best results across all NISQ backends using personalized optimization. Next, we discuss the results of attack identification using binary classification, followed by the results of attack classification using multiclass classification. Each subsection provides a detailed analysis of the performance improvements and the effectiveness of QuantumNetSec.
6.1 Circuit Optimization Impact on QuantumNetSec
In this subsection, we present the performance of various QML algorithms on different datasets under three optimization levels: no optimization, default optimization (using Qiskit's level 1, 2, 3 optimizations)11, and personalized optimization. Table 4 shows the results, where we report the F1 score percentage, a metric that balances precision and recall, for each configuration. We highlight the best results obtained across different NISQ backends in the attack detection task (binary classification). The results for configurations with no optimization and using default optimization were partially derived from our previous studies, as documented in [14] and [15].
| UNSW-NB15 | No Optimization | Default | Personalized | TONIoT | No Optimization | Default | Personalized |
|---|---|---|---|---|---|---|---|
| VQC | 88.99 | 89.15 | 89.9 | VQC | 97.78 | 97.89 | 97.95 |
| QSVM | 87.76 | 87.95 | 88.0 | QSVM | 96.12 | 97.15 | 97.35 |
| QKM | 86.78 | 87.22 | 87.8 | QKM | 96.11 | 97.15 | 97.35 |
| QCNN | 85.15 | 87.32 | 89.15 | QCNN | 97.4 | 97.95 | 98.16 |
| CIC-IDS17 | No Optimization | Default | Personalized | CICIoT23 | No Optimization | Default | Personalized |
| VQC | 95.78 | 95.90 | 96.12 | VQC | 74.53 | 78.92 | 79.55 |
| QSVM | 94.23 | 95.15 | 95.60 | QSVM | 76.15 | 82.40 | 83.70 |
| QKM | 93.67 | 93.80 | 93.95 | QKM | 79.15 | 80.15 | 82.99 |
| QCNN | 94.41 | 95.60 | 97.15 | QCNN | 78.60 | 82.56 | 84.55 |
- Note: Results in F1 score %.
For the UNSW-NB15 dataset, the VQC exhibited a progressive increase in performance, starting with an F1 score of 88.99% with no optimization, improving to 89.15% with default optimization, and reaching 89.9% with personalized optimization. The QSVM showed similar improvements, moving from 87.76% without optimization to 87.95% with default optimization and achieving 88.0% with personalized technique. QKMs started at 86.78% with no optimization, improved to 87.22% with default optimization, and further to 87.8% with personalized optimization. The QCNN demonstrated significant enhancement, increasing from 85.15% without optimization to 87.32% with default optimization, and achieving 89.15% with personalized optimization.
In the TONIoT dataset, the VQC showed high performance across all configurations, with an F1 score of 97.78% with no optimization, slightly increasing to 97.89% with default optimization, and reaching 97.95% with personalized optimization. The QSVM's performance improved from 96.12% without optimization to 97.15% with default optimization, and further to 97.35% with personalized optimization. The QKM algorithm displayed a similar pattern, starting at 96.11% with no optimization, improving to 97.15% with default optimization, and achieving 97.35% with personalized optimization. The QCNN also exhibited strong performance, increasing from 97.4% with no optimization to 97.95% with default optimization and reaching 98.16% with personalized optimization.
For the CIC-IDS17 dataset, the VQC's performance improved from 95.78% without optimization to 96.12% with personalized optimization, while the QSVM, QKM, and QCNN also showed similar improvements. In contrast, for the CICIoT23 dataset, the VQC saw a boost from 74.53% to 79.55%, and the QSVM, QKM, and QCNN experienced substantial gains, with QSVM reaching up to 83.70% with personalized optimization. Overall, Table 4 illustrates that across all datasets and QML algorithms, personalized optimization consistently yielded the highest F1 scores. This underscores the importance of tailored optimization strategies in maximizing the performance of QML algorithms on NISQ devices. Notably, the QCNN algorithm showed the most substantial improvements with personalized optimization.
The differences in performance across optimization levels can be attributed to the distinct strategies employed at each stage. The “No Optimization” configuration serves as a baseline, where circuits are implemented without modifications, often resulting in higher error rates due to inefficient qubit usage and excessive gate depth. Default optimization, as provided by Qiskit's transpiler, reduces gate count and circuit depth through predefined optimization techniques, leading to moderate improvements in F1 scores by mitigating noise and improving execution efficiency. Personalized optimization further refines this process by tailoring circuit modifications to the specific backend and dataset characteristics, allowing for maximized fidelity and performance. This progression explains the incremental yet consistent improvements observed across all datasets and QML algorithms, as personalized optimization exploits hardware-specific nuances and dataset requirements to achieve superior results.
6.2 Results Across Different NISQ Backends
Table 5 summarizes the performance of various QML algorithms across different datasets and NISQ backends, presenting F1 scores to highlight each algorithm's effectiveness under different conditions. Similar to Table 4, these results refer to the attack detection task (binary classification). However, this analysis exclusively considers outcomes achieved using personalized optimization. This focus allows for a clear assessment of how the personalized optimization strategy enhance algorithm performance on specific backends.
The performance of QML algorithms varies significantly across different NISQ backends for the datasets tested. For the UNSW-NB15 dataset, VQC performs best on the Kyoto backend with an F1 score of 89.9%, while QSVM shows strong results on the Osaka backend at 87.95%. QKM achieves consistent performance, peaking at 87.8% on the Osaka backend, and QCNN scores highest on the Kyoto backend with 89.15%. In the CIC-IDS17 dataset, VQC excels on both the Kyoto and Torino backends with an F1 score of 96.0%, while QSVM achieves 95.6% on the Brisbane backend. QKM performs best on the Quebec backend with 93.95%, and QCNN reaches 97.15% on both Torino and Quebec backends.
For the TONIoT dataset, VQC achieves the highest F1 score of 97.95% on the Sherbrooke backend, QSVM performs best on Kyoto with 97.35%, and QCNN demonstrates the highest efficiency on Osaka with 98.16%. For the CICIoT23 dataset, VQC reaches 79.55% on Brisbane, QSVM excels with 83.70% on Brisbane and Quebec, QKM achieves 82.99% on Sherbrooke and Torino, and QCNN stands out with 84.55% on Torino.
| UNSW-NB15 | Cairo | Kyoto | Brisbane | Osaka | Sherbrooke | Torino | Quebec |
|---|---|---|---|---|---|---|---|
| VQC | 87.91 | 89.9 | 87.78 | 89.2 | 87.31 | 87.3 | 88.15 |
| QSVM | 87.95 | 87.12 | 87.76 | 87.95 | 86.55 | 88.0 | 87.35 |
| QKM | 85.38 | 86.9 | 87.15 | 87.8 | 87.15 | 87.6 | 87.6 |
| QCNN | 85.78 | 89.1 | 89.15 | 89.0 | 89.0 | 89.12 | 88.9 |
| CIC-IDS17 | Cairo | Kyoto | Brisbane | Osaka | Sherbrooke | Torino | Quebec |
| VQC | 93.75 | 96.0 | 95.22 | 95.9 | 94.00 | 96.0 | 95.9 |
| QSVM | 92.95 | 94.6 | 95.6 | 94.55 | 94.38 | 94.15 | 94.4 |
| QKM | 92.38 | 93.67 | 93.55 | 93.0 | 93.55 | 93.8 | 93.95 |
| QCNN | 93.88 | 94.6 | 94.6 | 96.12 | 94.12 | 97.15 | 97.15 |
| TONIoT | Cairo | Kyoto | Brisbane | Osaka | Sherbrooke | Torino | Quebec |
| VQC | 95.65 | 97.6 | 97.9 | 97.9 | 97.95 | 97.85 | 97.88 |
| QSVM | 96.48 | 97.35 | 96.55 | 97.35 | 97.19 | 96.4 | 96.65 |
| QKM | 95.85 | 96.85 | 97.35 | 96.5 | 97.0 | 97.15 | 97.15 |
| QCNN | 95.9 | 97.3 | 97.9 | 98.16 | 97.6 | 98.0 | 98.0 |
| CICIoT23 | Cairo | Kyoto | Brisbane | Osaka | Sherbrooke | Torino | Quebec |
| VQC | 78.76 | 76.15 | 79.55 | 77.02 | 78.92 | 79.5 | 79.35 |
| QSVM | 79.85 | 80.0 | 83.70 | 80.55 | 80.12 | 83.6 | 83.6 |
| QKM | 79.56 | 79.25 | 81.0 | 81.86 | 82.99 | 82.99 | 82.95 |
| QCNN | 82.78 | 82.6 | 82.0 | 82.3 | 81.93 | 84.55 | 84.0 |
- Note: Results in F1 score %.
Overall, the results indicate significant variation in performance across different NISQ backends, reflecting the impact of each system's unique noise model, quantum logic gates, and topology. This underscores the importance of selecting and tuning QML models according to the specific characteristics of the quantum hardware in use. Notably, QCNN stands out with the highest F1 scores in several configurations, showcasing its effectiveness in handling the complexities of real quantum systems. The varying results emphasize the necessity for ongoing research and development in quantum computing to address the challenges posed by noise and other physical limitations in NISQ systems. The best results obtained in each model and backend combination will be discussed in detail in the following subsections.
6.3 QuantumNetSec: Attack Detection Results
In this subsection, we compare the performance of QML algorithms with classical ML algorithms in the context of binary classification for attack detection. The results, presented in Table 6 show the F1 scores for both QML and classical ML algorithms.
| Quantum ML | UNSW-NB15 | CIC-IDS17 | TONIoT | CICIoT23 |
|---|---|---|---|---|
| VQC | 89.90 | 96.0 | 97.95 | 79.55 |
| QSVM | 88.0 | 95.6 | 97.35 | 83.7 |
| QKM | 87.80 | 93.95 | 97.35 | 82.99 |
| QCNN | 88.90 | 97.15 | 98.16 | 84.55 |
| Classic ML | UNSW-NB15 | CIC-IDS17 | TONIoT | CICIoT23 |
| RF | 82.67 | 92.45 | 96.6 | 80.46 |
| SVM | 82.34 | 93.78 | 96.45 | 82.70 |
| KNN | 84.89 | 92.01 | 96.75 | 76.55 |
| CNN | 86.72 | 93.15 | 95.4 | 78.52 |
For the UNSW-NB15 dataset, the QCNN achieved the highest F1 score of 88.9%, outperforming classical ML algorithms. Among the classical ML models, CNN had the highest score of 86.72%. The VQC also performed well with an F1 score of 89.9%, surpassing the best classical result. In the CIC-IDS17 dataset, QCNN again led the performance with an F1 score of 97.15%, significantly higher than the top-performing classical model, SVM, which scored 93.78%. The VQC also demonstrated strong performance with an F1 score of 96.0%, highlighting the advantages of QML in this dataset.
For the TONIoT dataset, the QCNN achieved an high F1 score of 98.16%, outclassing all classical ML algorithms. The highest score among classical models was achieved by RF with an F1 score of 96.6%. The QSVM and QKM also performed exceptionally well, each scoring 97.35%. In the CICIoT23 dataset, QCNN again showed superior performance with an F1 score of 84.55%, compared to the best classical model, SVM, which scored 82.70%. The QSVM and QKM also performed well, with F1 scores of 83.7% and 82.99%, respectively, surpassing most classical algorithms. Overall, the results in Table 6 highlight that QML models generally outperform classical ML models across all tested datasets. The superior performance of QML, particularly the QCNN, underscores the potential of quantum computing to enhance attack detection capabilities in cybersecurity applications.
6.4 QuantumNetSec: Identification of Attacks
In this section, we present the multiclass F1 score results of various QML and classical ML algorithms for identifying different types of attacks (multiclass classification). The results are detailed in Tables 7–10, which correspond to the attack data from the UNSW-NB15, CIC-IDS17, TONIoT, and CICIoT23 datasets, respectively. The results highlight the performance of each algorithm in detecting specific attack categories.
For the UNSW-NB15 dataset, the QCNN consistently outperformed other models, achieving the highest F1 scores across multiple attack categories. Notably, QCNN scored 99.5% in both analysis and generic attack categories, indicating its superior capability in handling these types of attacks. The VQC also showed strong performance, particularly in the generic category with an F1 score of 97.05%. In contrast, classical models like SVM and RF performed well in certain categories but generally fell short of the top QML models.
| UNSW-NB15 | VQC | QSVM | QKM | QCNN | SVM | RF | KNN | CNN |
|---|---|---|---|---|---|---|---|---|
| Analysis | 96.3 | 88.15 | 94.58 | 99.5 | 96.45 | 90.23 | 56.78 | 95.15 |
| Backdoor | 84.45 | 83.22 | 88.31 | 94.5 | 90.78 | 92.11 | 49.34 | 90.13 |
| DoS | 90.15 | 88.68 | 84.55 | 93.23 | 92.45 | 82.56 | 76.89 | 80.26 |
| Exploits | 95.7 | 93.0 | 90.1 | 94.44 | 79.01 | 85.89 | 89.45 | 78.16 |
| Fuzzers | 76.3 | 94.0 | 83.17 | 93.14 | 77.56 | 79.78 | 76.23 | 76.89 |
| Generic | 97.05 | 96.0 | 94.65 | 99.5 | 99.34 | 99.01 | 98.45 | 94.83 |
| Reconn | 98.85 | 99.7 | 89.71 | 96.0 | 86.12 | 82.89 | 78.56 | 90.46 |
| Shellcode | 70.22 | 76.67 | 74.15 | 80.46 | 76.23 | 80.12 | 48.67 | 72.0 |
| Worms | 35.15 | 60.12 | 70.1 | 70.0 | 20.56 | 35.78 | 42.89 | 48.15 |
| CIC-IDS17 | VQC | QSVM | QKM | QCNN | SVM | RF | KNN | CNN |
|---|---|---|---|---|---|---|---|---|
| BoT | 88.41 | 98.22 | 99.0 | 99.54 | 94.67 | 92.12 | 98.89 | 91.45 |
| BruteForce | 96.5 | 100.0 | 98.9 | 100.0 | 93.45 | 96.24 | 95.18 | 94.42 |
| DDoS | 90.17 | 92.0 | 97.95 | 94.15 | 99.67 | 98.02 | 100.0 | 96.15 |
| DoS | 90.54 | 100.0 | 99.5 | 97.15 | 94.32 | 99.34 | 88.45 | 96.32 |
| Infiltration | 91.15 | 100.0 | 92.8 | 97.95 | 99.87 | 97.53 | 97.11 | 97.15 |
| PortScan | 96.12 | 98.5 | 97.5 | 98.15 | 97.89 | 97.45 | 99.76 | 96.88 |
| WebAttack | 93.18 | 98.4 | 97.65 | 98.0 | 98.21 | 96.89 | 89.45 | 96.55 |
| TONIoT | VQC | QSVM | QKM | QCNN | SVM | RF | KNN | CNN |
|---|---|---|---|---|---|---|---|---|
| Backdoor | 95.0 | 92.89 | 79.5 | 97.4 | 79.78 | 89.01 | 78.34 | 84.55 |
| DoS | 98.62 | 93.48 | 90.1 | 99.55 | 85.56 | 85.34 | 79.12 | 83.15 |
| DDoS | 98.0 | 92.7 | 93.4 | 98.2 | 76.89 | 88.45 | 88.23 | 80.78 |
| Injection | 90.39 | 93.0 | 91.0 | 94.4 | 91.34 | 90.23 | 65.78 | 74.12 |
| MITM | 98.75 | 99.65 | 92.47 | 100.0 | 88.78 | 86.34 | 78.67 | 86.61 |
| Password | 98.5 | 90.19 | 90.7 | 99.0 | 86.45 | 87.56 | 87.45 | 85.44 |
| Ransomware | 81.4 | 88.7 | 89.0 | 85.0 | 73.56 | 85.23 | 66.56 | 65.55 |
| Scanning | 82.22 | 89.7 | 88.7 | 91.1 | 94.01 | 82.45 | 90.12 | 80.0 |
| XSS | 88.1 | 86.41 | 91.4 | 92.14 | 84.78 | 80.45 | 86.01 | 79.55 |
| CICIoT23 | VQC | QSVM | QKM | QCNN | SVM | RF | KNN | CNN |
|---|---|---|---|---|---|---|---|---|
| BruteForce | 68.78 | 71.55 | 78.55 | 78.4 | 60.41 | 62.55 | 60.55 | 66.31 |
| DoS | 92.0 | 96.77 | 92.0 | 97.55 | 92.86 | 95.13 | 91.0 | 94.41 |
| DDoS | 92.0 | 97.0 | 90.11 | 97.1 | 92.52 | 95.78 | 89.0 | 95.27 |
| Mirai | 91.0 | 81.5 | 85.3 | 98.36 | 93.0 | 96.44 | 86.55 | 97.92 |
| Recon | 83.6 | 78.55 | 79.55 | 93.0 | 81.95 | 85.88 | 80.4 | 88.44 |
| Spoofing | 75.0 | 82.0 | 78.3 | 76.11 | 60.69 | 65.73 | 66.1 | 68.27 |
| WebAttack | 62.55 | 83.0 | 76.15 | 75.89 | 58.1 | 60.48 | 62.4 | 68.63 |
In the CIC-IDS17 dataset, QCNN again demonstrated exceptional performance, particularly in the BoT and BruteForce attack categories, where it achieved high F1 scores of 99.54% and 100%, respectively. QSVM also showed strong results, with a high score in the BruteForce and Infiltration categories. These results underscore the effectiveness of QML models, especially QCNN, in identifying a wide range of attack types with high accuracy compared to their classical counterparts.
For the TONIoT dataset, QCNN maintained its leading position with high F1 scores across most attack categories. It achieved a high score in the MITM, DoS, and Password attacks, highlighting its robustness and reliability. VQC also performed well, particularly in the DoS category with an F1 score of 98.62%. Classical models like SVM and RF performed adequately, but again, QML models demonstrated superior performance in most categories.
In the CICIoT23 dataset, QCNN continued to excel, achieving the highest F1 scores in categories such as Mirai (98.36%) and DoS (97.55%). QSVM also performed strongly in several categories, including DDoS and DoS, with scores of 97.0% and 96.77%, respectively. While classical models showed competitive performance in some categories, the QML models, particularly QCNN, consistently outperformed them, demonstrating their potential for more effective attack detection in complex IoT environments.
6.5 Results Discussion
The results from both binary and multiclass classification experiments demonstrate the significant potential of QuantumNetSec. In binary classification, the QML models consistently outperformed their classical counterparts across various datasets. QCNN emerged as the most effective model, achieving the highest F1 scores in almost all scenarios. This suggests that QCNN's ability to leverage quantum properties such as superposition and entanglement provides a tangible advantage in accurately distinguishing between attack and normal data.
In the multiclass classification results, the superiority of QML models was further confirmed. QCNN maintained its leading performance, particularly excelling in complex attack categories across all datasets. For instance, in the UNSW-NB15 dataset, QCNN achieved high scores in categories such as Analysis and Generic attacks. Similarly, in the CIC-IDS17 and TONIoT datasets, QCNN consistently delivered the highest F1 scores, highlighting its robustness and versatility. These findings underline the potential of QML models to handle a diverse range of attack types with high precision.
The comparison of QML models with classical ML models in both binary and multiclass classifications underscores the impact of quantum computing in cybersecurity applications. While classical models like SVM and RF showed competitive performance in certain categories, they generally lagged behind the QML models. The enhanced performance of QML models demonstrates their ability to address the limitations of classical approaches. This is crucial for improving the overall reliability and effectiveness of IDSs.
Moreover, the results highlight the importance of optimization techniques tailored to NISQ devices. The personalized optimization strategy employed in our experiments significantly boosted the performance of QML models. This indicates that, as quantum hardware continues to evolve, further improvements in optimization techniques could lead to even greater enhancements in the efficacy of QML-based cybersecurity solutions. These findings suggest a promising future for the integration of quantum computing in network security, paving the way for more advanced and resilient IDSs.
7 Conclusion
This work introduced QuantumNetSec, a QML-based attack detection system, designed to address emerging challenges in cybersecurity. Through experimental evaluations conducted on various public datasets, QuantumNetSec demonstrated its effectiveness in detecting attacks in both binary and multiclass classifications. The system achieved competitive results compared to traditional ML methods, highlighting the potential of QML solutions to enhance network security.
QuantumNetSec leverages the unique properties of quantum computing, such as superposition and entanglement, to analyze network patterns and more efficiently detect malicious activities. The results indicate that QuantumNetSec, particularly with the QCNN QCNN, can outperform classical models, showcasing its robustness and versatility across different attack types. These findings underscore the potential of integrating quantum computing into cybersecurity strategies to develop more resilient and effective IDSs.
7.1 Key Challenges
One of the primary challenges faced by QuantumNetSec lies in the limitations imposed by current quantum hardware. The constraints of NISQ devices, including noise, limited qubit counts, and restricted connectivity, present significant hurdles to achieving consistent scalability and reliability. These hardware limitations underscore the need for innovative, hardware-aware quantum algorithm development, and the incorporation of robust error mitigation techniques to bridge the gap between theoretical capabilities and practical deployment. Another notable challenge is the system's performance on complex IoT scenarios, as evidenced by the results on the CICIoT23 dataset. Although the implementation of personalized optimization techniques led to improved outcomes compared to baseline approaches, the performance still fell short of expectations. This highlights the difficulty in managing highly heterogeneous and intricate datasets typical of IoT environments and calls for further research into tailored feature extraction techniques and advanced quantum circuit designs to better address these complexities. These improvements could enable QuantumNetSec to handle such scenarios with greater accuracy and reliability.
Moreover, implementing QuantumNetSec in real-world scenarios introduces additional practical challenges. The constraints of quantum hardware, including the need for consistent operation under noisy conditions, limited access to high-performing quantum devices, and the costs associated with quantum computation, can hinder widespread adoption. Access to quantum devices is currently limited, often requiring significant investment or partnerships with providers, which may be prohibitive for many organizations. However, it is important to note that the field of quantum computing is advancing rapidly, with significant improvements in hardware capabilities and cost reductions expected in the near future. These developments provide optimism that the barriers to practical implementation will diminish, making systems like QuantumNetSec more accessible and viable for real-world applications.
7.2 Future Work
Building upon these challenges, several directions for future research can be proposed to enhance the capabilities of QuantumNetSec. The adaptability of the model to handle unknown attacks and emerging datasets is a critical area for further investigation. Integrating unsupervised learning approaches, such as quantum anomaly detection, could help identify patterns associated with previously unseen threats. Moreover, techniques like transfer learning and incremental learning should be explored to enable the model to adapt to new datasets without requiring complete retraining.
To improve performance on complex IoT scenarios, future work could refine feature extraction pipelines and develop advanced quantum circuit architectures. Hybrid approaches that combine quantum and classical preprocessing steps might better capture the intricate nature of IoT traffic. Additionally, incorporating domain-specific insights into the design of quantum feature maps and ansätze could enhance the system's capability to handle heterogeneous data.
Ensuring scalability as quantum hardware evolves will also be critical. Research should focus on optimizing quantum circuits to reduce computational overhead while maintaining or improving detection accuracy. Leveraging advancements in quantum hardware, such as error-corrected qubits and advanced transpilation techniques, will be essential in enhancing the system's applicability to large-scale, high-traffic network environments.
Finally, addressing the robustness of QuantumNetSec against adversarial attacks will be crucial for its long-term viability. Investigating the vulnerabilities of quantum-enhanced systems and developing quantum-specific defense mechanisms will be key. Techniques such as robust quantum circuit designs, adversarial training, and quantum cryptographic methods could be integrated to strengthen the system's defenses against sophisticated threats.
In conclusion, QuantumNetSec represents a significant advancement in leveraging QML for cybersecurity. By addressing these challenges and exploring these future directions, it has the potential to become a cornerstone of quantum-enhanced IDSs, paving the way for more secure and resilient digital infrastructures.
Acknowledgements
This work was partially supported by the São Paulo Research Foundation (FAPESP), projects 2020/04031-1, 2023/00811-0, and 2021/00199-8, CPE SMARTNESS, and project 2018/23097-3. It was also financed in part by the Coordination of Superior Level Staff Improvement (CAPES) Finance Code 001. The Article Processing Charge for the publication of this research was funded by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) (ROR identifier: 00x0ma614).
Conflicts of Interest
The authors declare no conflicts of interest.




