Using Population Dynamics to Model Harvest Regulation Impacts to Channel Catfish in the Monongahela River, West Virginia
Abstract
Channel Catfish Ictalurus punctatus were collected during 2018 and 2019 from the Monongahela River in West Virginia using hoop nets to estimate population dynamics. Length, weight, sex, fecundity, and age data were obtained from collected individuals. Population characteristics (e.g., relative abundance, size structure, age structure, growth, etc.) were modeled under three proposed length limits of 300, 375, and 450 mm. Simulation results indicated that growth overfishing may occur when exploitation rates reach 36% under a 300-mm minimum length limit. Furthermore, recruitment overfishing began to occur at 40% exploitation under a 300-mm minimum length limit. Additionally, simulations suggest that no recruitment or growth overfishing occur at minimum length limits of 375 mm or 450 mm until extremely high exploitation levels (>90%) are reached. Thus, future consideration should be given for implementation of a 375-mm minimum length limit of Channel Catfish in the Monongahela River to prevent growth and recruitment overfishing while also ensuring anglers are still able to harvest Channel Catfish.
Channel Catfish Ictalurus punctatus have gained popularity among anglers throughout their range since the 1980s (Arterburn et al. 2002). Although Channel Catfish regulations vary across North America, state agencies have recognized the need for potential management (Michaletz and Dillard 1999). As of 2014, 20 states had implemented some type of minimum length limit (MLL) for Channel Catfish fisheries. However, of the MLLs imposed, only five were statewide regulations (Eder et al. 2016). This could suggest regional variation in Channel Catfish populations or differences in regulation policy processes across regions.
Growth overfishing occurs when larger individuals are overexploited from the population, leading to an overall size reduction in the population (Hesse 1994; Pitlo 1997; Slipke et al. 2002). Growth overfishing commonly leads to recruitment overfishing in sport fish populations (i.e., once large numbers of sexually mature individuals are removed from a population, recruitment is hindered, leading to a decrease in yield; Berkely et al. 2004; Venturelli et al. 2009, 2010).
Minimum length limits are often implemented to curb growth overfishing in sport fisheries (Maceina et al. 1998; Allen et al. 2013; Graham et al. 2015; Eder et al. 2016), including commercial catfish fisheries (Hesse 1994; Pitlo 1997; Slipke et al. 2002). However, regulations targeting recreational catfish fisheries are sparse despite angler support (Arterburn et al. 2002; Reitz and Travnichek 2004).
Modeling simulations rely on knowledge of population demographics, such as recruitment, growth, mortality, and exploitation (Slipke and Maceina 2010). In comparison to recruitment, growth, and mortality, exploitation estimates are much more difficult to obtain, as they require intensive tagging studies (Eder et al. 2016). However, many agencies do not have the time, money, and/or personnel to implement these labor-intensive studies. Therefore, agencies often estimate this parameter in alternate ways by using modeling software. Modeling software provides a cost- and time-effective approach for managers to predict population-level responses to various harvest regulations and thus ensure sustainable management practices (Johnson 1995; Slipke and Maceina 2010). Simulations are often conducted before implementing length limits, with an aim of maximizing yield and preventing growth overfishing.
The West Virginia Division of Natural Resources (WVDNR) has recently recognized an increased interest in catfishing by the state’s anglers. Given this increased interest, efforts have been established throughout West Virginia to identify potential management needs for catfish populations. Regulations have recently been imposed on the Ohio and Kanawha rivers to conserve and enhance Flathead Catfish Pylodictis olivaris populations—specifically, a four-fish daily creel limit, with only one fish 889 mm (35 in) or longer. Research is also currently focused on Channel Catfish populations in the Ohio, Kanawha, and South Branch Potomac rivers. The WVDNR has also identified a potential need for catfish management on the Monongahela River, a large tributary of the Ohio River.
Historically, few studies have evaluated potential harvest regulations on Channel Catfish in West Virginia. Additionally, little information has been collected to assess population demographics of catfish within the Monongahela River, which can potentially inform management. Given that most species in the Monongahela River are recently recovered from decades of water quality impairment, an assessment of population characteristics would be beneficial for future management and monitoring. Therefore, this study aims to describe the age structure, size structure, growth, fecundity, and mortality of Channel Catfish within the Monongahela River, West Virginia. Specifically, we sought to utilize these data to model potential harvest regulations that may prevent growth overfishing and recruitment overfishing from occurring within the population.
METHODS
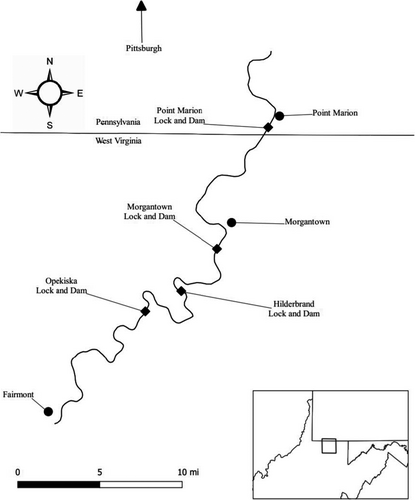
The Monongahela River is located within the Mississippi River basin. The river flows north from Fairmont, West Virginia, to Pittsburgh, Pennsylvania, where it meets the Allegheny River, which forms the Ohio River and eventually drains into the Gulf of Mexico. The Monongahela River watershed has a drainage area of approximately 7,692 km2 (Sotak 1968). Dams were installed on the Monongahela River during the 1800s for navigation and the transportation of coal. The upper 58-km section of the river located in West Virginia is segmented by four U.S. Army Corps of Engineers lock-and-dam structures (Figure 1). Instream habitat consists entirely of long, slow pools inundated by these locks and dams. Depths can reach over 10 m, but channels are maintained at a minimum depth of approximately 3 m for navigational purposes. Substrate type is generally soft (sand/silt), and large woody debris provides the main cover type. Much of the shoreline is still forested. The mean annual discharge of the Monongahela River in West Virginia from 2015 to 2018 was 152.06 m3/s (5,370 ft3/s) (U.S. Geological Survey station 03062235; USGS 2019).
The Monongahela River has a prominent history of acid mine drainage and pollution dating back to the 1800s, which ultimately led to a decrease in species richness and abundance, resulting in low biodiversity (Sotak 1968; Klarberg and Benson 1975). Before 1971, the only harvestable species in the Monongahela River were the Brown Bullhead Ameiurus nebulosus and Yellow Bullhead A. natalis (WVDNR, unpublished data). However, with the passing of new environmental legislation during the 1960s and 1970s, pollution began to decrease, subsequently leading to an improvement in water quality and ultimately the return of many fish populations, including Channel Catfish.
Sampling sites were located in each of the four pools of the Monongahela River located within West Virginia. These pools (listed from upstream to downstream; each pool is named after the corresponding lock and dam) include Opekiska, Hildebrand, Morgantown, and Point Marion pools (Figure 1). All pools are similar in habitat but do differ in size, with lengths of 20.9 km for Opekiska Pool, 11.3 km for Hildebrand Pool, 9.7 km for Morgantown Pool, and 16.1 km for Point Marion Pool.
Channel Catfish were collected seasonally (spring, summer, and fall) throughout 2018 and in June of 2019 using 25-mm bar-mesh hoop nets. Hoop nets were 3 m long, consisting of seven wooden hoops spanning 1 m in diameter. The first throat of each net was equipped with one 165-mm-diameter copper ring to prevent turtle bycatch. Hoop nets were set parallel to the flow with the open end facing downstream. Anchors were attached at each end to stabilize the net, and a buoy was attached at the open end. Channel Catfish were collected from each pool to obtain a representative sample of the river. We set 5 hoop nets·pool−1·survey−1 in 2018 and 10 hoop nets·pool−1·survey−1 in 2019. Nets were baited with two mesh bags of Zote Soap per net to increase catch and minimize turtle bycatch (Long et al. 2017). Hoop nets were fished for 48 h in depths ranging from 3 to 5 m. Fish collected in the field were euthanized using a cranial pith, immediately placed in an ice bath, and brought back to the laboratory for further examination.
Once in the laboratory, fish were weighed to the nearest gram and measured for TL to the nearest millimeter; the otoliths were extracted, and sex was determined for adults. During the spawning season (summer) in June 2019, eggs were removed and weighed. A subsample of eggs was weighed and enumerated to estimate fecundity. Lapillus otoliths were removed via cranial dissection, as otoliths are the best method for estimating ages of catfish older than 2 years (Buckmeier et al. 2002). Once dried, otoliths were mounted onto a dissecting slide using Crystalbond with the anterior placed down. Otoliths were then sanded down using dampened, 600-grit sandpaper until the nucleus was visible (Buckmeier et al. 2002). Ages were assigned to each fish by two independent readers. If the readers did not agree, a second otolith was mounted and read. In the circumstance that a consensus could not be reached, the fish was removed from the sample.
The predicted responses of Channel Catfish to 300-, 375-, and 450-mm MLL regulations were modeled using riverwide population characteristics. The yield resulting from the three modeled MLLs was used to identify exploitation levels leading to potential growth overfishing of the population. In addition, the spawning potential ratio (SPR) was used to assist in identifying exploitation levels that could lead to recruitment overfishing at the three MLLs. These MLLs were chosen based on recommendations from the WVDNR, providing that anglers commonly begin to harvest Channel Catfish at 300 mm. The 375-mm MLL was selected because it allows fish to reach sexual maturity (typically between 300 and 375 mm) and spawn at least once before harvest (Shepard and Jackson 2005). The 450-mm MLL was selected to demonstrate how a more conservative MLL would affect the Channel Catfish population.
All modeling was conducted using the Fishery Analysis and Modeling Simulator (FAMS) version 1.0 (Slipke and Maceina 2010). This model uses a yield-per-recruit (YPR) model and a static SPR to predict population response for various exploitation rates in 5% intervals, with fish of varying target harvest lengths (i.e., MLLs of 300, 375, and 450 mm; Slipke and Maceina 2010). All simulations were run with an initial population of 1,000 recruits. Both the YPR and SPR models evaluated multiple exploitation levels simultaneously (5–95%), in regard to the varied MLLs (Slipke and Maceina 2010).
Mean length at age was calculated from the pooled hoop-net data. Age and growth data from fish aged 3–18 were fit using a von Bertalanffy growth model, as this model was previously found to be the best fit for other Channel Catfish populations in northern West Virginia (Hilling et al. 2016). Age-classes with fewer than five fish were removed to ensure similar numbers from each age-class (Isely and Grabowski 2007). Weight-to-length ratios were calculated using log10 transformed data.
The YPR model utilizes length-at-age data to detect exploitation levels at which growth overfishing is occurring within a population. It is useful when exploitation rates are unknown or variable within a system, as natural mortality, exploitation, and length limits are varied in the YPR model to calculate various simulations (Slipke and Maceina 2010). The FAMS YPR model adapts the Beverton–Holt equilibrium yield equation (Ricker 1975) with the Jones (1957) modification to calculate yield (Slipke and Maceina 2010). Input parameters required for the YPR model include conditional fishing mortality, conditional natural mortality (cnm), number of fish in the initial population (N0), the intercept (a) and slope (b) of the weight–length regression, the average asymptotic length (Linf), the Brody growth coefficient (k), theoretical age at a length of zero (t0), maximum age, and the average asymptotic weight (Winf), which was calculated from the weight–length regression. Theoretical maximum age, total annual mortality (A), and total annual survival were calculated using the unweighted catch-curve analysis in FAMS.
The SPR model utilizes fecundity-at-length data to detect exploitation levels at which recruitment overfishing is occurring. The SPR represents the ratio of eggs produced over the cohort’s life span under fished conditions to eggs produced under conditions of no fishing. Critical SPR values for Channel Catfish have been found to vary among regions (Bueltman and Phelps 2015) but typically range between 10% and 30% (Goodyear 1993; Clark 2002; Slipke et al. 2002). Furthermore, a minimum SPR value of 20% was held constant to represent the minimum SPR threshold for protecting resilient populations, such as Channel Catfish populations, from recruitment overfishing given unknown exploitation rates. It was assumed in the SPR model that 50% of the adult breeding population (fish aged 4–18) are female and that 100% of those females are spawning annually. Additionally, it should be noted that YPR results are likely more reliable than SPR model results, as fecundity-at-length data have the potential to be impacted by seasonality and environmental stochasticity (Jackson and Ye 2004; Shepard and Jackson 2005), especially in systems affected by acid mine drainage (Fromm 1980; Jennings et al. 2008).
Both the YPR and SPR models were simulated using three MLLs (300, 375, and 450 mm) to determine when exploitation levels would begin to negatively impact yield, growth, and/or recruitment. The Hoenig method in FAMS was used to estimate the instantaneous natural mortality rate (M) as well as cnm (Hoenig 1983). We assumed a discrete (type I) fishery such that cnm = 1 − e−M. We calculated A by using a weighted catch-curve analysis (Chapman and Robinson 1960).
RESULTS
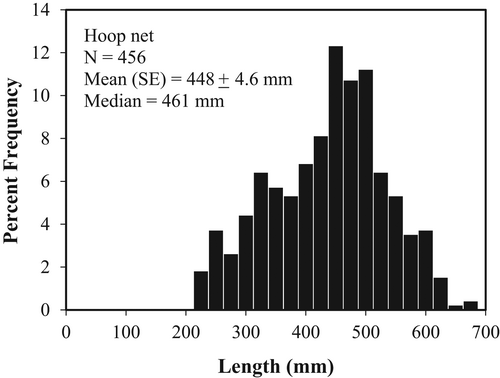
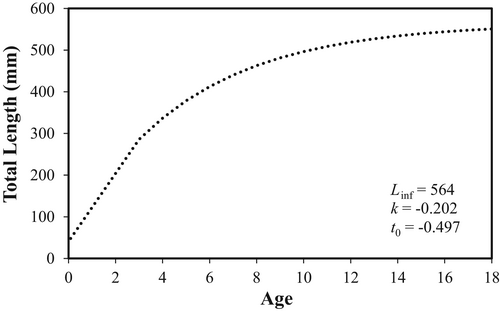
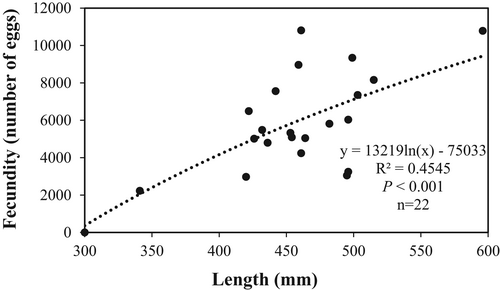
In total, 456 Channel Catfish were sampled throughout 2018 and 2019, with sizes ranging from 230 to 694 mm TL and a mean length of 448 mm (SE = 4.6; Figure 2). A total of 397 Channel Catfish were collected for aging purposes, and ages were estimated for 395 fish; two fish were removed from the sample due to reader differences. Ages spanned from 2 to 32 years, with a mean TL of 447 mm (SE = 4.8) at the most frequent age of 8 years (N = 54; Figure 3). A von Bertalanffy model was used to describe growth. The Linf was estimated to be 564 mm TL, while k was −0.202 and t0 was −0.497 year (Table 1; Figure 4). Total annual mortality was estimated as 23%, and cnm was estimated as 21%. Age at maturation was estimated to be 4 years (Figure 5). Fecundity was found to be highly variable with length (P < 2.3 × 10−6), ranging from 2,227 to 10,783 eggs/fish. The average female Channel Catfish in our study (mean length = 464 mm TL) had an estimated fecundity of 6,085 eggs/fish.

| Parameter | Value(s) or equation |
|---|---|
| Von Bertalanffy growth coefficients | Linf = 564, k = −0.202, t0 = −0.497 |
| Average asymptotic weight (Winf; g) | 1,730 |
| Maximum age (years) | 18 |
| Total annual mortality | 0.23 |
| Conditional natural mortality | 0.21 |
| Conditional fishing mortality | 0.05–0.95 |
| Log10(weight)–log10(length) coefficients | Intercept = −5.872, slope = 3.311 |
| Age (years) at sexual maturation | 4 |
| Fecundity-to-length relationship | log10(fecundity) = 2.2645 × log10(TL) = −2.2862 |
| Percentage of fish that are females | 50 |
| Percentage of females that spawn annually | 100 |
| MLLs (mm TL) | 300, 375, 450 |
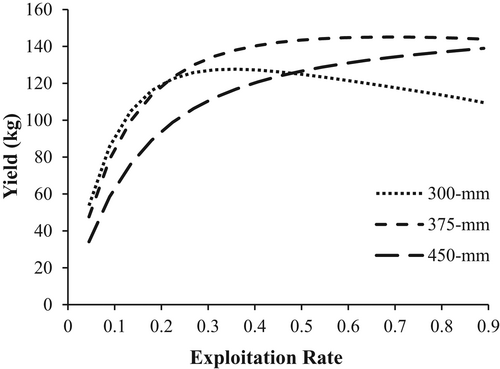
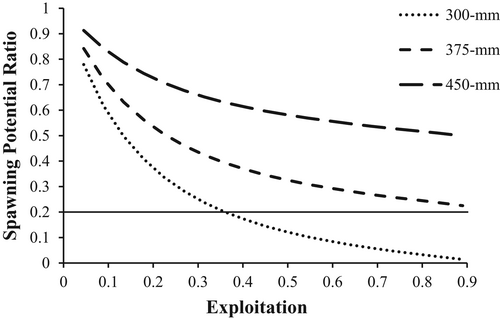
The YPR simulation model determined that growth overfishing could occur at a 300-mm MLL when the exploitation rate exceeded 36% (Figure 6). When simulating the 375- and 450-mm MLLs, growth overfishing did not occur until exploitation rates reached extremely high levels (>90%). The 375-mm MLL produced 15% more yield at a 50% exploitation rate and 20% more yield at 75% exploitation compared to the 300-mm MLL. In addition to YPR, the SPR model output indicated that recruitment overfishing also occurred at an exploitation level of 36% when the 300-mm MLL was implemented and SPR fell below 20%, the critical threshold needed to sustain recruitment for resilient populations (Figure 7). Additionally, neither a 375-mm MLL nor a 450-mm MLL reached levels of recruitment overfishing until exploitation rates exceeded 90%.
DISCUSSION
We found that Channel Catfish in the Monongahela River are slow growing and long lived and could be vulnerable to overfishing under moderate levels of exploitation. According to our model simulations, we found that under a 300-mm MLL, both growth overfishing and recruitment overfishing can occur when the exploitation rate reaches 36%. In contrast, under 375- and 450-mm MLLs our modeling simulations suggested that regardless of angler exploitation level (5–95%), there would be no reduction in YPR and the SPR would remain above the critical threshold (20%) for this population. Model simulation results suggest that consideration of regulation changes may be prudent to ensure sustainability of this population.
Currently, there are no length limits regulating Channel Catfish in the Monongahela River. However, many similar rivers have instituted MLLs for this species. Slipke et al. (2002) found that Channel Catfish in the upper Mississippi River experienced growth and recruitment overfishing, as well as a decrease in yield at exploitation rates greater than 40% under a 330-mm MLL. After the MLL was raised to 381 mm, the upper Mississippi River population was no longer experiencing overexploitation (Slipke et al. 2002). The FAMS input parameters used in this study were similar to those of Channel Catfish in the upper Mississippi River (Table 1; Slipke et al. 2002). In contrast, a decline in commercial harvest of Channel Catfish in the middle Mississippi River was previously thought to be attributable to a low MLL. However, Bueltmann and Phelps (2015) found that when modeling length limit simulations, no growth overfishing was occurring until exploitation rates reached 50–70%. Moreover, the authors determined that recruitment overfishing was not occurring, although SPR values were low (between 10% and 20%) at high exploitation rates of 45–80%. Ultimately, the decline in harvest was attributed to other external pressures (Bueltmann and Phelps 2015); thus, demonstrating the effectiveness of MLLs in managing Channel Catfish populations and the capabilities of modeling software to assist fisheries managers.
Population parameters estimated in this study indicate that the Monongahela River Channel Catfish population is longer lived and slower growing than most populations of this species in North America, with observed fish ages ranging from 2 to 32 years and a mean age of 8 years. Channel Catfish TL ranged from 230 to 694 mm, with a mean length of 448 mm and an Linf of 564 mm. Bueltman and Phelps (2015) found that the mean age of the Channel Catfish population in the middle Mississippi River was 6 years, and the mean length was 477 mm. Additionally, they noted a maximum age of 15 years and an Linf of 735 mm (Bueltman and Phelps 2015). In the Nebraska section of the Missouri River, Eder et al. (2016) collected fish ranging from 1 to 14 years, but they noted that fish older than 6 years were rare. The value of Linf in the Missouri River was also substantially larger (845 mm; Eder et al. 2016) than the Linf for the Monongahela River population. Furthermore, mortality rates for the Channel Catfish population in the Monongahela River are seemingly average in comparison with those of other North American populations (Colombo et al. 2008; Bueltmann and Phelps 2015; Eder et al. 2016; Hilling et al. 2016).
When analyzing population demographic data, researchers should be wary of shortcomings and should consider those limitations when making inferences about populations and suggesting regulatory changes. An inaccurate understanding of population dynamics could potentially lead to management errors, which in turn could produce undesirable conditions (McCain et al. 2011). However, conducting standardized sampling could help to reduce potential bias and better identify population trends within a system. These assessments should be conducted regularly—especially after conducting habitat modifications and implementing length limit changes—to accurately determine whether decreases in yield are observed, as such changes have the potential to alter population dynamics (Bueltmann and Phelps 2015). Long-term monitoring of potentially long-lived populations is critical for identifying natural fluctuations over time. Additionally, modeling of population dynamics can be important for ensuring proper management of populations (Phelps et al. 2011). Monitoring the same parameters over time, such as size structure, age structure, growth, recruitment, and mortality, will provide a robust understanding of the population dynamics and a basis upon which to evaluate whether regulations have the ability to provide sustainable fisheries.
When managing for a sustainable fishery, it is extremely important to understand and accurately monitor a population’s status. Gear types can be biased toward particular age- or size-classes (Bodine et al. 2013). A gear efficiency study (K. L. Chestnut-Faull, unpublished data) determined that the hoop nets used in the present study were the most appropriate for sampling Channel Catfish in the Monongahela River. Additionally, in Cheat Lake, an impoundment of the Cheat River, which flows into the Monongahela River, Hilling et al. (2016) sampled Channel Catfish by using gill nets and observed a mean length (466 mm) and Linf (595 mm) similar to those we obtained (448 and 564 mm, respectively). Furthermore, hoop nets that were equipped with excluder devices (Fratto et al. 2008) and baited with Zote Soap (Cartabiano et al. 2015; Long et al. 2017) helped to eliminate turtle bycatch without significantly impacting catch results, which is a growing concern for catfish sampling (Congdon et al. 1994; Midwood et al. 2015). When selecting a sampling gear, it is important to recognize and understand its limitations and the effect that it may have on data and subsequent simulation model results. Furthermore, seasonality may impact collection bias, as studies have observed seasonal movements of Channel Catfish between rivers and tributaries (Hesse et al. 1982; Dames et al. 1989; Newcomb 1989; Smith and Hubert 1989; Gerhardt and Hubert 1990; Coon and Dames 1991). Additionally, fecundity-to-length relationships were highly variable in this study, likely due to low sample size or annual oscillations within this system; however, these estimates may impact the validity of SPR model results. In conclusion, these biases could potentially influence our estimates of A, fecundity, mean length, mean age, etc. We recommend collecting a larger sample size over multiple years to more accurately depict fluctuations within this system and monitor gear effectiveness.
Currently, there are no regulations in place to protect the Monongahela River Channel Catfish population from overfishing. Simulation model results suggest that neither growth overfishing nor recruitment overfishing is currently occurring within this population at exploitation rates less than 36%. However, given the unknown exploitation rates within this system and the growing number of anglers targeting catfish, we feel that future consideration should be given to the implementation of a 375-mm (i.e., 15-in) MLL because it provides the best balance of conservation and angler acceptance, assuming higher exploitation levels. This regulation will prevent growth overfishing and recruitment overfishing from occurring if harvest exceeds critical levels currently or in the future. At the same time, this regulation also ensures that anglers have the ability to adequately harvest fish. Anglers likely already follow a de facto 300-mm MLL, as many states (e.g., Texas, Kentucky, and Oklahoma) have a 305-mm (12-in) MLL in place for Channel Catfish. However, additional creel data is needed to verify angler harvest in West Virginia. Although overfishing does not appear to be a problem currently, environmental or angler-induced population changes could increase the vulnerability of this population. A 450-mm MLL provides the greatest protection to SPR. However, additional data would have to be collected and analyzed to better understand whether this system can grow and/or support the larger individuals necessary for a 450-mm MLL to be considered. Additionally, a 450-mm MLL may be unnecessary, as the 375-mm MLL appears to provide ample protection to SPR under high exploitation rates. Furthermore, a 450-mm MLL substantially reduces predicted yield but with seemingly little benefit. Such a large MLL is unlikely to be acceptable to anglers, especially for a fishery with no prior length limit restrictions. Ultimately, additional data on Channel Catfish exploitation rates within this river will help to validify model estimates, which will in turn lead to more informed management decisions. In the event that a 375-mm MLL is implemented, it would be prudent to continue monitoring this fishery in the future to determine its impact and assess whether any further changes are warranted.
This study has demonstrated the applicability of modeling population demographic data to aid in determining the benefits of harvest regulations for catfish populations. Specifically, our modeling suggests that a 375-mm MLL for Channel Catfish in the Monongahela River should be considered in order to prevent the potential risks of growth overfishing and recruitment overfishing. Although catfish in other systems will likely exhibit different population characteristics, this same framework of investigation can be applied to determine the need for regulations on specific populations. An additional benefit of modeling population demographics is the ability to collect the data needed in a relatively short time period. At minimum, population evaluations like the one presented here provide important baseline data that biologists can reference when making future decisions regarding population changes.
Acknowledgments
We thank many West Virginia University undergraduate and graduate students for assisting with field and lab work during the course of this study. We also thank the reviewers for comments and suggestions that helped to improve the context and applicability of this manuscript. Funding and in-kind support was provided by the West Virginia Division of Natural Resources and West Virginia University. There is no conflict of interest declared in this article.




