Development, validation, qualification, and dissemination of quantitative MR methods: Overview and recommendations by the ISMRM quantitative MR study group
Sebastian Weingärtner and Kimberly L. Desmond contributed equally to this work.
Abstract
On behalf of the International Society for Magnetic Resonance in Medicine (ISMRM) Quantitative MR Study Group, this article provides an overview of considerations for the development, validation, qualification, and dissemination of quantitative MR (qMR) methods. This process is framed in terms of two central technical performance properties, i.e., bias and precision. Although qMR is confounded by undesired effects, methods with low bias and high precision can be iteratively developed and validated. For illustration, two distinct qMR methods are discussed throughout the manuscript: quantification of liver proton-density fat fraction, and cardiac T1. These examples demonstrate the expansion of qMR methods from research centers toward widespread clinical dissemination. The overall goal of this article is to provide trainees, researchers, and clinicians with essential guidelines for the development and validation of qMR methods, as well as an understanding of necessary steps and potential pitfalls for the dissemination of quantitative MR in research and in the clinic.
1 INTRODUCTION
MR probes a wide array of tissue contrasts, spectral properties, and anatomical information. Based on this wealth of contrast mechanisms, a variety of quantitative MR (qMR) methods that extract quantifiable information from MR acquisitions1-3 have been proposed and continue to emerge from the MR research community. Upon successful development and validation, qMR methods enable improved standardization in the detection, staging, and treatment monitoring of diseases, both in research and in clinical practice.4-7 On behalf of the International Society for Magnetic Resonance in Medicine (ISMRM) Quantitative MR Study Group, we provide an overview of the process of development of qMR methods, as well as guidelines for their technical validation, clinical qualification, application, and dissemination. To illustrate this process, we provide examples from two distinct qMR methods: quantification of liver proton-density fat fraction (PDFF), and T1 quantification in the myocardium (cardiac T1 mapping; see Figure 1). These two methods were selected based on their substantial interest within the MR research community, important existing and potential applications, and major advances toward widespread clinical use. Importantly, the current status of development and remaining challenges are different for these two methods, which helps illustrate the diversity in the field of qMR.
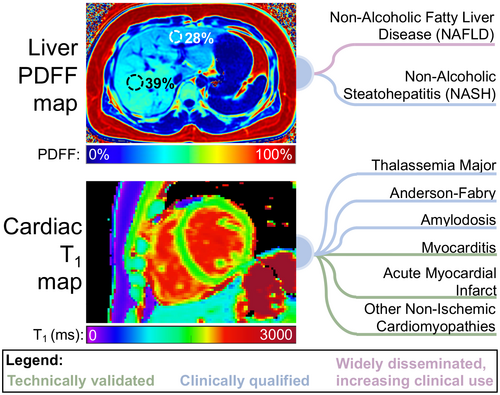
1.1 Liver PDFF quantification
PDFF has been developed, validated, and applied for the assessment of tissue triglyceride concentration.8 Although chemical shift encoded (CSE) fat-water imaging was introduced nearly 40 years ago,9 the development of quantitative techniques that measure PDFF has accelerated over the past two decades.10-17 Using either MRS16 or MRI8 acquisitions, PDFF measures the concentration of MR-visible triglyceride protons relative to all MR-visible protons (from triglycerides and water), which has multiple research and clinical applications. Recent technical developments and validation studies (see below) have led to widely available techniques. These techniques are particularly promising for the quantification of liver fat, e.g., in the assessment of non-alcoholic fatty liver disease (NAFLD).
1.2 Cardiac T1 mapping
Although cardiac T1 mapping was first developed in the 1990s,18 the field accelerated more recently when the promise to enable non-invasive assessment of diffuse fibrosis emerged.19 As the T1 relaxation time depends on the mobility in the macromolecular environment, over time cardiac T1 mapping has proved useful in many clinical applications.20 Initially, semi-quantitative relaxation measurements in the myocardium based on Look-Locker sequences were explored.21, 22 However, these methods lacked the reproducibility and reliability to serve as a quantitative tool in clinical application. With the introduction of the Modified Look-Locker Inversion Recovery (MOLLI)23 and shortened MOLLI (shMOLLI)24 methods, myocardial T1 mapping became feasible on a voxel-by-voxel basis in a single breath-hold and with high visual T1 map quality. This facilitated the widespread use and application to numerous ischemic and non-ischemic cardiomyopathies.25, 26 Continuous method development and refinement have led to increasingly sensitive and reliable T1 measurements of the heart, paving the way for routine clinical use.20
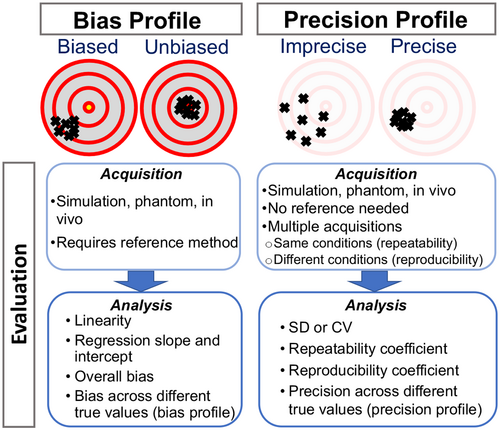
2 TECHNICAL PERFORMANCE OF qMR METHODS
The development and validation of qMR methods requires a framework for describing their technical performance. The two major technical performance properties of a qMR method (Figure 2) are: (1) the bias, which includes the properties of linearity, the regression slope and intercept, and the overall bias; and (2) the precision, which is described by the repeatability and reproducibility. These metrics are described in detail below and summarized in Table 1. Previous works in qMR have used deviating terminologies, including “accuracy” or “robustness,” to describe technical performance. However, in this work we use, and encourage others to use, metrics based on bias and precision, as established by the quantitative imaging metrology community.27, 28 A glossary of the terminology used throughout this paper can be found in Supporting Information Table S1, which is available online.
| Metric | Definition | Liver PDFF | Cardiac T1 (MOLLI) |
|---|---|---|---|
| Linearity | Ability to provide measurements that are proportional to the true value as described in Equation (1) | r2 = 0.96 and no evidence of significant higher-order terms in regression analysis of measurements vs true value48 | r2 = 0.996, magnitude of higher order terms < 0.000152 |
| Regression slope | β1 in Equation (1) | 0.97548 | 0.91952 |
| Fixed bias | β0 in Equation (1) | <0.2%48 | 4.2%52 |
| Bias (or precision) profile | A table or figure illustrating the estimates of the bias (or precision) over the range of true values and/or other relevant characteristics | See Yokoo et al., 201848 | See Roujol et al., 201452, 57 |
| Repeatability | A measure of precision describing the variability in measurements on a subject over a short period of time using the same imaging system and experimental conditions27 | Repeatability coefficient of 2.9%48 | Repeatability coefficient of 2.0%52–4.6%58 |
| Reproducibility | A measure of precision describing the variability in measurements on a subject using different experimental conditions (different systems, and/or pulse sequence parameters, and/or measurements separated by a long period of time, etc)27 | Reproducibility coefficient (across different hardware systems or reconstruction software) of 4.3%48 | Highly variable. In tightly controlled studies, 2.1% has been reported,59 however, a meta-analysis showed >7% reproducibility in healthy subjects.60 For this reason, it is not recommended to compare MOLLI T1 values across systems and parameters, due to system specific biases20 |
2.1 Bias
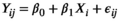(1)
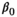is the intercept, 
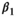is the regression slope, and 
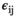is a random effect, which we assume is independently and identically distributed from a normal distribution with mean zero and variance 
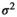(which captures the precision).To measure bias, the ground-truth value can sometimes be ascertained by using a reference method. Although the ground-truth should be conceptually well defined, its estimation via a reference method is generally imperfect and requires careful design. Such a reference method may be invasive or non-invasive, and based on MR or other modalities. Importantly, a reference method should be independent from the qMR method under evaluation (e.g., should not be obtained from the same source data), as any dependence between the two measurements may lead to an underestimation of the qMR method’s bias. Furthermore, to be accepted as a reference method, its measurements must be highly concordant with the ground truth, and its performance (bias and precision) must be substantially better than the performance of the method under evaluation.28 These requirements often complicate the acquisition of a reference method in vivo.
For this reason, investigators often rely on reference objects (“phantoms”) to assess bias. The design of phantoms is driven by the technique they will be testing and the specific tissues or MR properties they will mimic, as well as additional considerations such as traceability and long-term stability.31 It is important that phantoms themselves are systematically measured prior to use, which is sometimes achieved using gold standard NMR measurements,32 the best available reference method on MRI systems, or non-MR methods. With a standard phantom, such as the ISMRM/NIST system phantom,33 or a well-characterized home-built phantom, the technical performance of a qMR method can be estimated, as an approximation of in vivo technical performance. Although phantoms are highly effective in many qMR applications, there are cases where phantoms may be of limited value, as existing phantom designs do not adequately replicate the relevant signal properties, spatial distribution, or temporal dynamics found in tissue.34
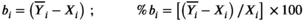(2)
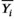is the mean over the potentially repeated measurements on the same phantom compartment (or subject). Over N observations, we can estimate the overall bias:
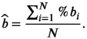(3)Finally, some qMR methods may present a constant bias that is not dependent on the true value of the measurand. In these cases, the fitted line in Equation (1) will be parallel to the identity line, with regression slope close to one, and regression intercept that provides an estimate of the overall bias.29 A 95% confidence interval (CI) for the estimate of the fixed bias should be reported.35 Note that small values of fixed bias are often well tolerated. For example, under typical conditions, confidence intervals for a new patient's measurement constructed under the no-bias assumption provide nominal coverage as long as the fixed bias is <12% of the within-subject SD (wSD).36
Because the bias sometimes depends on the true value of the measurand, the bias profile can be evaluated by plotting the estimate of bias from each value of Xi (i.e., bi) against the true values Xi. Note that the relationship between measurements and ground truth may generally be nonlinear, particularly when considering a broad range of measurand values. However, the assumption of linearity is often an appropriate approximation and greatly simplifies the statistical analysis. To assess the property of linearity, we fit an ordinary least squares (OLS) regression of the Yijs on Xis. One way to test the appropriateness of a linear model is to formally test for significant non-linearities (curvature).29 Sequential tests can be performed starting with a third-order (cubic) regression: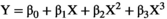 
. If the third order coefficient 
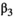is not significantly different from zero, then the process can be repeated with a second-order (quadratic) regression: 
. If the quadratic term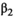 
is not significantly different from zero, then the hypothesis of a linear model cannot be rejected, and a linear fit can be used: 
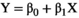.29 Ideally, R-squared (R2) will be greater than 0.90.35 The regression slope, 
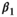, should be reported along with its 95% CI. As a general rule, a slope in the range [0.95, 1.05] is acceptable.35 Sometimes, the linear relationship in Equation (1) holds only for a certain range of the values of the measurand, so it is important to assess this property over the likely values of the measurand. It may be that linear relationships hold for various ranges of the true value, but 
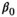and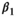 
differ for each range or even vary by subject characteristics (e.g., age or body mass index).
Finally, once the bias is known, the qMR method could, in principle, be calibrated to the reference to eliminate bias. However, this is not a common approach. Indeed, the bias itself often arises from uncorrected confounding factors that may affect various acquisitions or patients differently.37, 38 For this reason, bias is often not reproducible, and calibration-based correction should be approached with caution.
2.2 Precision
Precision describes the tendency of the measurement system, when used repeatedly in several “replicate” measurements on the same subject, to produce different values.27 The precision of a method has enormous practical importance. Indeed, the required number of participants for clinical studies increases with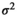 
and is, therefore, driven by the precision of a qMR method, which determines their cost and feasibility.39 The precision is also a major factor affecting the method’s ability (including sensitivity and specificity) to detect a specific condition, and determines the minimum detectable change (see Figure 3). In contrast to bias, the evaluation of precision does not require a reference method, and therefore in vivo evaluation of precision is often highly feasible.
Some studies use spatial variability in a homogeneous phantom or tissue as a heuristic to evaluate precision metrics. While this may be an acceptable approximation with certain simple imaging methods, spatial variability of system properties (e.g., B0 and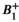 
heterogeneities) often render this approximation inadequate, even if the region of interest appears homogeneous to the observer. In particular, this spatial variability method cannot be used to evaluate precision metrics if spatial information is used in the image reconstruction or parametric mapping (e.g., regularization in compressed sensing). Instead, precision metrics should be evaluated in studies that obtain and compare multiple replicate measurements.
Test-retest studies allow estimation of precision. When the same MR system and experimental conditions (including acquisition parameters) are used for all replicate measurements on the same subject over a short span of time, we refer to this as the repeatability condition. When the replicates are obtained under different conditions (e.g., different field strengths, different MRI vendors, platforms, or software versions, different individual scanners, different pulse sequences or acquisition parameters, different image analysis software, different readers, or long delay between acquisitions), we call this the reproducibility condition [3]. With qMR, we often characterize precision by either the wSD, or the within-subject coefficient of variation, denoted wCV. Note from Equation (1),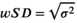 
, and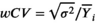 
. The wCV is often used when the variability in the measurements is much higher for large true values or when the measurements are log-normally distributed (thus, Xi and Yij in Equation (1) would need to be measured on a logarithmic scale).
Precision studies are often small because of cost, ethical, and technical concerns.29, 30, 40 For these reasons, meta-analysis is often required to pool estimates from multiple studies.41 A general rule of thumb to obtain a reliable estimate of precision is >35 subjects with two or more replicates.36
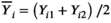and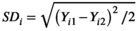 
. From the N subjects, we estimate the mean wSD or wCV as:
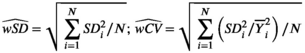(4)Importantly, 95% CIs for wSD and wCV should also be reported.35 Implicit in Equation (4) is the assumption that wSD (or wCV) is constant over the range of measurand values. This assumption should be assessed by calculating the estimates for several ranges of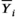 
or even for various patient and/or disease characteristics, to determine a precision profile.42, 43
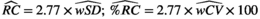(5)In evaluating reproducibility, the experimental conditions across replicate measurements can be altered in various different ways (see above). Ultimately, the widespread dissemination of a qMR method will require establishment of reproducibility across conditions such as different centers, MRI vendors, or patient populations. However, such multi-center, multi-vendor studies are expensive and complex, and may not be appropriate for a newly developed qMR method. A practical approach is to evaluate reproducibility in multiple studies of increasing complexity, beginning with relatively simple studies at a single center and vendor,44 while building up toward more ambitious studies.45
In evaluating precision, it is important to carefully design and describe the specific procedures followed. For example, repeatability may be evaluated by performing consecutive scans within the same scanning session, in order to establish the effects due to MR system adjustments and noise. However, repeatability is often determined by scanning the subject in separate sessions over a short time interval, including repositioning and re-localizing between sessions, in order to capture additional variability due to other factors such as subject positioning.29 In general, the experimental design to study precision may be different for different methods or applications. Thus, it is important to meticulously report the parameters and conditions that are kept identical and those which may have changed between replicate measurements, to enable replication and interpretation of the results.
2.3 Examples
2.3.1 Liver PDFF quantification
Liver PDFF quantification methods have been validated in multiple studies including evaluation of bias in PDFF phantoms (both commercially available and home-built),46, 47 in vivo liver imaging,48 and ex vivo livers.49 In a recent meta-analysis,48 liver PDFF had high linearity and low bias with respect to the MRS-determined reference PDFF value in 23 studies, which included a total of 1,679 subjects. Test-retest repeatability studies have also been performed.48, 50 Recently, high linearity and low bias of multi-center PDFF measurements47 has been demonstrated by shipping a phantom to multiple centers in a “round-robin” study, and evaluating measurements on the same phantom across centers, vendors, platforms, field strengths, and acquisition parameters. In addition, the reproducibility of PDFF measurements in the liver, including across field strengths and MRI vendors, has also been demonstrated in multiple studies.48, 51
2.3.2 Cardiac T1
Bias and precision have been the dominating criteria in analysis of cardiac T1 mapping methods [35]. Multiple studies have shown that different T1 mapping methods provide varying profiles of bias and precision.
Inversion recovery-based methods have been shown to exhibit good repeatability but large biases, while saturation recovery methods have been shown to reduce bias at the cost of reduced repeatability.52-54 For example, the most commonly used myocardial T1 mapping technique, the inversion recovery-based method MOLLI, is known to be subject to multiple confounding factors and exhibits substantial bias.55 However, given its excellent repeatability and visual image quality, the sequence is highly popular among users.23 Even though some studies have shown initial evidence of multi-center or multi-vendor reproducibility with tightly controlled protocols,56 the reproducibility is generally compromised due to the measurand confounders (see next section). Thus, it is recommended to obtain center and protocol specific reference ranges in healthy subjects, before using MOLLI for quantitative diagnosis.20
3 CONFOUNDING FACTORS IN MR
In qMR, a wide variety of confounding factors may introduce bias or poor precision. Table 2 provides illustrative categories and examples of qMR confounding factors. A poll distributed among the members of the ISMRM Quantitative MR Study Group queried the frequency, relevance, and potential correction mechanisms for confounding factors used in the quantitative MR community. Supporting Information Figures S1–S6, which are available online, summarize the poll results.
| Hardware/system imperfections | Physiological effects/motion | Signal model imperfections | Other artifacts and noise |
|---|---|---|---|
| B0 heterogeneities and off-resonance | Respiratory motion | Additional relaxation mechanisms (not included in model) | Partial volume |
| B1 heterogeneities | Cardiovascular motion/pulsation | Slice profile imperfections | |
| Eddy currents | Intestinal peristalsis | Spectral complexity (additional resonances, J-coupling, etc.) | Imperfect spoiling |
| Gradient nonlinearities | Bulk body motion | Parallel imaging artifacts | |
| System drift | Blood flow | Exchange (multi-pool) | Noise |
3.1 Hardware and system imperfections
The presence of magnetic field heterogeneities (both B0 and B1),61 gradient nonlinearities,62 concomitant gradients,63, 64 eddy currents,65 system drifts,66 timing errors,67 and other system imperfections, is unavoidable in MR applications. These effects may result in tolerable artifacts in qualitative MR as long as the relative visual contrast between tissues is preserved, but may introduce substantial bias and poor precision in qMR methods.
3.2 Physiological effects and motion
Physiological motion effects include respiration, cardiovascular motion and pulsation, intestinal peristalsis, and bulk patient motion, among others. These effects often result in artifacts, ghosting, and mis-registration in the acquired images,68 which can in turn introduce bias and poor precision in qMR. Blood and tissue motion during the acquisition can also introduce artifacts, phase offsets, and dephasing that confound the quantification.
3.3 Signal model imperfections
Practical qMR methods rely on simplified signal models. The presence of signal effects that are not included in the model introduces bias in qMR measurements. These effects may be due to additional relaxation mechanisms, incomplete approach to steady state, diffusion, spectral complexity, etc. Signal model imperfections can lead to poor reproducibility in qMR, as these effects will often manifest differently for varying experimental conditions, including different systems, field strengths, and acquisition parameters. Ideally, signal models should be based on specific biophysical assumptions about the tissues of interest. However, biophysical modeling is challenging in certain applications, and so signal “representations” are often used, which enable fitting of the acquired data but are not based on specific tissue models.69 For example, the diffusion tensor representation provides a useful approximation to the diffusion-weighted MR signal at moderate b-values, but is not based on specific tissue modeling assumptions.69 Such signal representations have demonstrated clinical value, but their quantitative performance needs cautious consideration. For example, bias may not be meaningful if the measurand does not represent a physical property of the tissue, and reproducibility across changes in acquisition parameters is often challenging.
3.4 Other artifacts and noise
A variety of additional imaging artifacts, including partial volume, slice profile imperfections, imperfect spoiling, parallel imaging artifacts, and noise can confound qMR methods. For example, imperfect slice profiles due to finite-duration excitation pulses lead to a distribution of flip angles across the slice and may also introduce crosstalk between slices.70, 71 In addition, noise in the acquired imaging data propagates into the subsequent qMR measurements. The propagation of noise is generally dependent on the acquisition parameters and the choice of signal model; more complicated models with many free parameters often result in higher noise amplification. Furthermore, manipulation of MR signals prior to qMR measurement can affect the noise distribution, which affects the bias and precision of qMR methods. For example, noise in complex MR data is well modeled by a Gaussian distribution. However, qMR sometimes relies on magnitude images (e.g., in diffusion MRI, or cardiac T1 mapping as discussed throughout this paper). This magnitude operation has several important effects, including the elimination of phase information, and the introduction of an additional bias. Indeed, regions of low signal magnitude, as commonly observed in methods such as diffusion MRI or relaxometry, deviate substantially from a Gaussian noise distribution.72 If subsequent qMR processing implicitly assumes a Gaussian noise distribution (e.g., in methods that rely on least-squares fitting, as described below), bias and poor reproducibility may result from the inaccurate noise assumptions.73, 74
For these reasons, different processing pipelines of the same data can lead to differences in the resulting qMR measurements. For example, even filtering of the image data can introduce biases in the quantification when nonlinear models are being used. Thus, using transparent open-source toolboxes or custom-built processing for qMR should be preferred over black-box tools, when reproducibility is targeted.
Finally, when using MR-based reference methods for validation of qMR, even the reference method itself may not be immune to the presence of confounding factors such as physiological effects and motion. This limitation of the reference method may complicate the evaluation of qMR bias in vivo.
3.5 Examples
3.5.1 Liver PDFF quantification
- T1 recovery: The short T1 relaxation time of fat compared to that of water in the liver can lead to bias (overestimation) of PDFF12 in acquisitions that include T1 weighting.
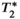relaxation:
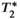decay across multiple echoes can appear as interference between fat and water signals, and therefore can introduce bias and poor reproducibility in PDFF quantification (see Figure 4).13, 14, 75, 76- Spectral complexity of fat signals: Unlike water signals, which result in a single MR resonance, fat signals arise from protons located in various positions within the triglyceride molecule. These protons, in turn, lead to a multi-peak spectrum from fat.15, 77 If unaccounted for, this spectral complexity leads to bias and poor reproducibility across acquisition parameters, particularly the echo time combination.
- Phase errors: Phase errors, such as those arising from eddy current effects, can introduce bias and poor reproducibility in PDFF quantification.78, 79
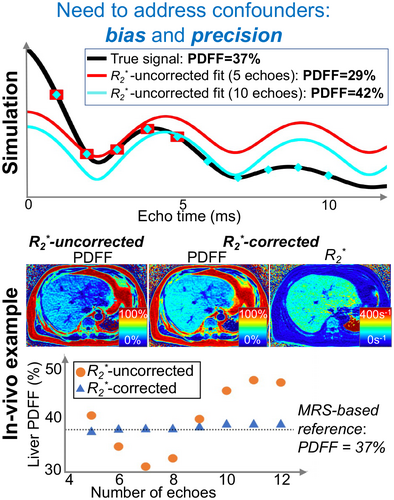
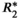decay, if uncorrected, can confound PDFF quantification, leading to bias, as well as poor precision (e.g., poor reproducibility across acquisitions with different number of echoes), particularly in patients with elevated liver 
= 1/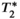
(
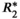= 160 s−1 at 1.5T, corresponding to mild iron overload). As shown though simulation and in vivo, 
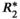-uncorrected signal fitting results are highly dependent on the choice of echo times. In contrast, 
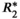-corrected PDFF quantification has low bias and high reproducibility across choices of echo times. For this illustration, a 12-echo liver CSE acquisition in a patient with high liver fat and iron overload was reprocessed retrospectively multiple times, using the first n echoes (for n = 5,…,12). In each case, both 
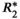-uncorrected and 
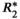-corrected PDFF mapping methods were usedOver the past two decades, these and other confounding factors have been systematically identified, characterized and addressed using various acquisition and post-processing-based approaches (see the Technical Development section below).
3.6 Cardiac T1
- Heart rate: Acquisitions commonly need to be synchronized with the heartbeat to minimize cardiac motion effects. The subject-specific heart rate may influence the bias and/or precision. Introduction of alternative mapping schemes or heart rate-resilient timing has helped to alleviate this confounder.55, 57, 80
- k-Space acquisition: In some methods, only the effect of the magnetization preparation is modeled. In this case the disruption of the magnetization by radiofrequency (RF) pulses used for the k-space acquisition can cause bias in the quantification. Specifically, this may render the quantification susceptible to physiological factors such as T2 relaxation57 or magnetization transfer,84 or system-related properties such as off-resonance85 or flip angles.86 The dependency on system-related parameters makes it paramount to use identical sequences and sequence parameters in cardiac T1 mapping, when reproducibility across centers and MRI scanners is desired.
- Partial-volume effect: Cardiac acquisitions are commonly limited in the achievable resolution due to motion constraints. This results in partial-voluming, where voxels are partially filled with different tissue types at tissue interfaces. As a result, the area that can reliably be evaluated is further reduced, rendering the quantification dependent on accurate delineation of the region of interest.87, 88
4 TECHNICAL DEVELOPMENT AND VALIDATION
The development of qMR methods is typically an iterative process including design of acquisition, modeling and signal fitting methods. This technical development can be framed as an optimization of bias and precision metrics (see Figure 5), subject to specific constraints such as scan time, or hardware performance.
4.1 Acquisition
Once the basic physical mechanism to be probed has been selected and potential confounders have been identified, aspects of protocol design and optimization can be considered. A common goal is to select pulse sequences and parameters such that the measurand can be determined with low bias and high precision, subject to a set of timing, hardware, and other constraints. Acquisition design will often begin by selecting a pulse sequence where the measurand of interest can be directly probed, while minimizing the effect of confounding factors. Next, an acquisition that includes multiple scans with different parameters can be designed to enable estimation of the measurand. In applications where thermal noise is the dominant source of noise (as opposed to, e.g., physiological noise), acquisitions with higher imaging SNR may substantially improve bias12 or precision.89 The choice of acquisition parameters may be driven by heuristics, and also refined using quantitative tools such as sensitivity analysis,90, 91 or noise propagation analysis (e.g., Cramer-Rao lower bounds, CRLB).11, 92-94
4.1.1 Liver PDFF quantification
The choice of pulse sequence for quantification of PDFF is driven by the desire to obtain chemical shift-encoded data with proton-density contrast (e.g., avoiding confounding effects due to T1 and T2 relaxation), and with rapid scan times (e.g., to enable whole-liver coverage in a single breath-hold while avoiding motion artifacts). For these reasons, the pulse sequence of choice for MRI-based liver PDFF quantification is a multi-echo spoiled gradient echo (SGRE) sequence, either using 2D multi-slice or 3D imaging.8, 17 In addition, small flip angles are used in order to avoid T1 bias.12 Other confounding factors are typically addressed by postprocessing/modeling (see below). Optimal acquisition parameters, such as echo times, have been determined using CRLB analysis.11
4.1.2 Cardiac T1
A multitude of pulse sequences for cardiac T1 mapping have been proposed and novel method development remains an active area of research. Generally, these acquisitions can be decomposed into three integral parts: 1) contrast sensitization; 2) k-space acquisition; 3) motion compensation.
Typically, preparation pulses are used to sensitize the imaging signal to the T1 relaxation time of the tissue. Inversion pulses are most widely used in T1 mapping, including the commonly used MOLLI sequence and its variants.23, 24, 55 Saturation recovery has also been proposed with the potential to minimize bias caused by various confounding factors as described above.57, 80 However, due to a decreased dynamic range, saturation recovery preparation typically results in lower T1 mapping precision as compared with inversion preparation.
Cardiac T1 mapping is typically performed using multiple electrocardiogram (ECG)-triggered snapshot images, with each image obtained during a single diastolic quiescence, i.e., all k-space lines necessary for image reconstruction of one snapshot image are acquired in one heartbeat. To achieve optimal SNR as well as minimal disruption of the longitudinal magnetization recovery curve, balanced steady state free precession (bSSFP) readouts are the method of choice. Spoiled gradient echo readouts have also been explored to minimize sensitivity to off-resonance and field heterogeneities, albeit at the cost of reduced precision.95 More recently, continuous imaging throughout the heartbeat have been proposed to allow cardiac phase-resolved T1 mapping.81, 82, 96
ECG triggering is almost universally used as the means for cardiac motion compensation in T1 mapping, with few notable exceptions.96, 97 Various schemes have been explored for respiratory motion compensation. Clinically available T1 mapping methods usually acquire a single-slice T1 map in a single breath-hold.26 However, free-breathing methods have also been explored with diaphragmatic navigator gating, tracking or self-gating.97-99 Importantly, free-breathing sequences allow for the acquisition of multiple slices or 3D volumes and can be used to enable T1 mapping with increased spatial resolution.83, 100, 101
4.2 Model selection
Many qMR methods rely on parametric mapping using a signal model that relates the acquired data to the underlying measurand. Selection of a signal model is typically an iterative process and seeks to balance bias and precision. Often the process begins with identifying the relevant degrees of freedom in the underlying tissue,69 such that these tissue properties can be related to, and estimated from, acquired MR signals. For example, this step may involve the identification of the major pools of nuclei with shared properties that will reasonably contribute to the signal. These pools can describe physical compartments, such as “intracellular” compartments, or local molecular environments such as lipid protons. The Bloch equations, describing the response to RF energy and relaxation properties, are defined for each pool. Next, a model may consider whether nuclei can travel between pools by chemical exchange or diffusion, or interact magnetically with other pools due to proximity and, thus, define the exchange kinetics. Models commonly describe the signal within a voxel independently of its spatial neighborhood, but one may also need to consider the influence of the neighboring voxels (e.g., in quantitative susceptibility mapping,102 or electrical properties tomography103, 104).
The next step is often to evaluate the signal model under modifications of the acquisition pulse sequence. It is often helpful to develop a working model for simple excitation-readout with Cartesian acquisition and long repetition time (TR) before considering advanced k-space trajectories or pulse trains. The requirements for each measurand are different, but major considerations in the presence of increasingly advanced pulse sequences may include relaxation effects, B0 and B1 heterogeneities, etc. It may also be necessary to consider the need for steady-state or non-steady state modeling. Finally, any signal manipulations that occur before analysis, such as magnitude operation or spatial filtering, need to be included.
In subsequent iterations, confounding factors are often identified and addressed through acquisition- and/or modeling-based refinements. Importantly, qMR methods necessarily use simplified models of the actual underlying physics. For this reason, it is always possible to “enhance” the models by including additional unknown parameters. However, these signal model enhancements generally lead to increased challenges in the parameter estimation (particularly noise amplification, sensitivity to artifacts, and computation time). Practical signal models, therefore, seek a balance between accurately capturing the underlying physics and enabling stable quantification within acceptable computation times. Once a satisfactory model is achieved, this model often needs to be re-evaluated upon subsequent refinements of the qMR method, including accelerated acquisitions.
4.2.1 Liver PDFF quantification
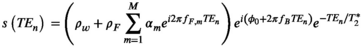(6)
and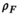 
are the proton density-weighted signal amplitudes of water and fat, respectively; fat signals are modeled as a pre-calibrated spectrum including M peaks with known relative amplitudes 
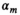and frequency offsets 
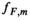77; initial phase 
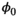; B0 related off-resonance frequency 
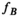; and transverse relaxation time 
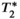. Upon data fitting (see below), this signal model allows estimation of 
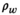and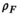 
, which lead to the calculation of PDFF as:
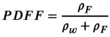(7)Importantly, the widely used signal model in Equation (6) constitutes a balance between bias and precision (noise performance).106 For example, this model addresses the spectral complexity of the fat signal by using a multi-peak signal model and also accounts for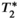 
decay. If unaccounted for, both of these effects have been shown to lead to substantial bias and poor reproducibility in PDFF quantification.17 However, the model in Equation (6) typically relies on a pre-calibrated multi-peak fat spectrum, where the relative frequencies and amplitudes of the fat peaks are assumed known a priori,107 and also assumes a common 
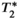decay time for water and all fat peaks.106 Each of these approximations help maintain acceptable noise performance and precision for PDFF quantification by limiting the number of unknown parameters, even though they may introduce a small bias in the estimation of liver PDFF when the model assumptions do not hold exactly.
4.2.2 Cardiac T1
T1 recovery is thoroughly studied and can be accurately described by the well-known phenomenological Bloch relaxation equations. However, the signal model needs to be adapted to the specific imaging sequence, as summarized next.
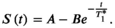(8)Here A and B describe fit parameters and 
is the apparent relaxation time. The T1 estimate is then extracted as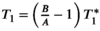 
. This adaptation is inspired by Deichmann et al108 and aims to reduce the effect of the RF pulses used for the k-space acquisition on the quantification. However, the acquisition commonly deviates from the assumptions underlying this correction, inducing residual susceptibility to various effects related to the RF pulses during the k-space acquisition. Numerical models have also been proposed to approximate the magnetization evolution during the k-space acquisition, using for example Bloch equation simulations or additional parameters.109, 110 While these methods commonly achieve lower bias, their applicability might be limited, and precision may be compromised.
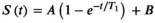(9)This saturation recovery-based approach has been shown to compensate for the effects of the RF pulses used for the k-space acquisition,57 which in turn enables cardiac T1 mapping with reduced bias. It has also been suggested to omit the B parameter to obtain a two-parameter model, in order to improve precision at the cost of bias in saturation recovery T1 mapping.55
4.3 Model fitting
Fitting a signal model to acquired data can typically be described in terms of a formulation and an algorithm, as described next.
The formulation is often an optimization problem, which describes in what sense the model should fit the acquired data. For example, least-squares fitting is often used for various linear or nonlinear models in quantitative MR. For nonlinear models based on exponential functions, a logarithm of the data is sometimes calculated to linearize the problem. This linearization simplifies the optimization, although it affects the noise propagation and may require additional manipulations to avoid excessive noise influence from low-SNR data points.111 Furthermore, some formulations rely on the acquired complex data, whereas others use magnitude data.79 Finally, the formulation may be constrained (where the set of allowable parameters is restricted based on physical or noise propagation considerations) or unconstrained. In addition to least-squares fitting, other formulations can be used, including those required for maximum-likelihood estimation in the presence of non-Gaussian noise.
Once a formulation is selected, an algorithm needs to be selected to solve the corresponding optimization problem. Depending on the formulation, various closed-form or iterative algorithms are typically available. Variations of Newton’s method, including Levenberg-Marquardt and Gauss-Newton algorithms, constitute common choices for iterative optimization.112 An ideal algorithm would be efficient (i.e., fast and requiring low resources) and would lead to the global solution of the optimization problem described in the formulation.
4.3.1 Liver PDFF quantification
Model fitting for PDFF mapping is typically performed using nonlinear least-squares fitting of the signal model (Equation 6) to the acquired multi-echo data, followed by calculation of PDFF at each pixel (Equation 7). Multi-echo data are often corrupted by phase errors that are inconsistent across echoes.78, 79 For this reason, some or all of the phase information is often discarded to avoid PDFF bias, and algorithms often rely partly on fitting the signal magnitude, instead of the original complex-valued signals. Magnitude fitting leads to reduced bias by avoiding phase related PDFF errors at the cost of reduced noise performance and precision (by discarding half of the acquired information, i.e., the phase).
4.3.2 Cardiac T1
Basic model fitting in cardiac T1 mapping is also most commonly performed using magnitude-based nonlinear least-squares fitting. When unsigned magnitude images are used in an inversion-recovery model, the signal polarity information is lost. To resolve this issue the images are commonly ordered by the inversion time and the polarity can be restored heuristically, by successively flipping the sign in the ordered sequence and accepting the solution with the lowest fit residual.20
However, this process might introduce additional noise variability. It has been proposed to incorporate phase information to perform hybrid fitting on a signed magnitude. Here, the background phase is extracted from a fully relaxed image, and the phase difference to other T1 weighted images can be used to restore the signal polarity.113
5 CLINICAL QUALIFICATION
For qMR methods, in addition to technical validation, which measures the bias and precision of the quantitative measurements, it is essential to perform clinical qualification (Figure 6).114 Clinical qualification seeks to establish the relationship between the qMR measurement and biological processes or clinical endpoints, as needed to determine the clinical utility of the method, e.g., whether it enables screening, diagnosis, staging, prognosis, or treatment monitoring for a particular condition and target population.115-119 For example, rather than focusing on technical performance metrics of bias and precision, clinical qualification may focus on metrics such as sensitivity, specificity, negative / positive predictive value, prediction accuracy, or odds ratio.114, 120 Upon successful clinical evaluation for a specific application, qMR methods may lead to qualified quantitative biomarkers (see Glossary in Supporting Information Table S1, which is available online).6
This marks an important distinction: while a qMR measurand usually relates to a physical property, this measurand, when being used as a clinical biomarker, indicates pathophysiological alterations or other changes in the physiological state. Often numerous biological and physiological processes affect the underlying physical property. Thus, a single qMR measurand can be qualified as a biomarker for multiple disease entities. In this case, while being sensitive to multiple diseases, the measurand may not be specific to any one physiological alteration.
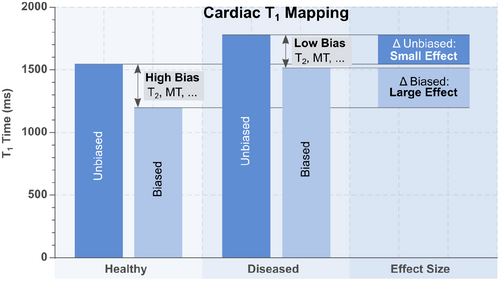
There are strong connections between technical validation and clinical qualification. For example, a qMR method with poor precision (e.g., poor test-retest repeatability) will likely also have poor sensitivity and specificity for detection of a specific condition. However, these are also important distinctions between both types of evaluation. For example, it is possible to develop a qMR method with excellent technical performance (low bias and high precision) for quantifying a measurand; however, this method may have poor clinical performance for a specific application, e.g., due to underlying biological variability that complicates the relationship between the measurand and the clinical endpoint of interest, such as survival, disease-free survival, or various surrogate endpoints.121-123 Furthermore, a biased method may reduce the desired effect size, as the bias itself may be different for various patient populations. Alternatively, it is possible that a biased (confounded) qMR method provides larger effect sizes for a specific disease entity than an unbiased measurement, e.g., if the confounders themselves are sensitive to the physiological alteration (see Figure 7). However, it is important to note that this enhancement usually comes at the cost of strongly reduced reproducibility as the variability in the bias is difficult to control.
For these reasons, it is essential to conduct both technical validation and clinical qualification of qMR methods. This need further highlights the importance of multi-disciplinary collaboration between technical imaging researchers, translation-focused radiologists, and other clinicians.
5.1 Examples
5.1.1 Liver PDFF quantification
Liver PDFF has been shown to be correlated with histologic steatosis grade. For example, PDFF can classify histologic steatosis (grade 0 vs. 1–3) with sensitivity 0.93 and specificity 0.94.124 Also, MRI-based liver PDFF quantification is emerging as a useful biomarker to assess longitudinal changes in liver fat within clinical trials.125 Furthermore, a reduction of MRI-PDFF by 30% is associated (odds ratio 6.98) with histologic improvement in NAFLD Activity Score.126
Liver PDFF values may be predictive of pediatric metabolic syndrome.127 In addition, liver steatosis is associated with cardiovascular diseases128, 129; for instance, liver fat is an independent risk factor (odds ratio 2.1) for high-risk plaque128 and other cardiovascular risk factors.129 Importantly, now that the required MRI technical development is mature and PDFF mapping methods are widely available, determination of the association between liver PDFF and various clinical outcomes constitutes an active area of research.
5.1.2 Cardiac T1
Native myocardial T1 times, in the absence of a contrast agent, have been evaluated against histologically determined fibrosis from myocardial biopsies in vivo and total collagen volume in animal studies130 and heart transplant patients.131 Variable degrees of correlation ranging from moderate to high have been reported depending on the disease model,131 indicating that T1 times are not reflective of fibrosis alone but of a number of factors. Extracellular volume (ECV) calculated from native T1, post-contrast T1, and hematocrit, generally showed better correlation to the amount of fibrosis but variability among disease models and studies remains. Accordingly, the clinical context needs to be considered in the interpretation of both native T1 and ECV, and alteration in either measurand cannot be directly linked to a single specific physiological process.20, 132-134
Nonetheless, cardiac T1 mapping-related markers have demonstrated high clinical diagnostic and prognostic value in an unexpectedly wide range of disease entities.25, 135 For example, in cardiac amyloidosis ECV showed excellent sensitivity and specificity (0.93 and 0.87, respectively) and an odds-ratio of 84.6.136 In patients with an acute infarct quantitative assessment of normal appearing myocardium in patients with an acute infarct using native T1 or ECV has proven to be a better predictor for all-cause mortality or major cardiac events than any other cardiac MRI marker,131 and accurate differentiator between reversible and irreversible myocardial damage (96.7% prediction accuracy).
Interestingly, MOLLI T1 mapping, which is most common in clinical use, is known to exhibit a large bias. However, it has been suggested that certain confounders to MOLLI T1 measurements may enhance clinical sensitivity.137 As illustrated in Figure 7, this somewhat counter-intuitive phenomenon arises because some confounders (e.g., magnetization transfer84, 137, 138) are sensitive to pathological alterations, leading to inflated effect size in certain disease entities compared to unbiased measurements. However, as a result of these confounders, the measurand in MOLLI is highly dependent on the sequence parameters (e.g., TR, flip angle, slice profile), the scanner specifications and tissue properties that are not related to the tissue T1 time. Hence, this inflated effect size is obtained at the cost of reduced reproducibility.
6 DISSEMINATION IN RESEARCH AND IN THE CLINIC
Although qMR methods have shown great potential to guide clinical decision-making and patient management for improved patient care and outcomes, very few qMR methods are used in routine clinical practice. Many promising qMR methods are only described in the scientific literature, without translation in clinical research studies or clinical use.
As recently stated in the Imaging Biomarker Roadmap for Cancer Studies,139 all imaging biomarkers, including quantitative MRI biomarkers, need to cross two “translational gaps” before they are ready to guide clinical decision making. These gaps are crossed through increasing technical validation and clinical qualification, as well as assessment of cost effectiveness and other considerations. Once technical and clinical performance evaluation demonstrate the reliability of a qMR biomarker to test medical research hypotheses, this biomarker can cross the first gap and become a useful “medical research tool”. At this stage, substantial additional validation and qualification are still needed in order to achieve clinical impact as a screening, diagnostic, or predictive biomarker. This may include validation of multi-center reproducibility,140 and large prospective clinical trials to demonstrate improved clinical diagnosis or outcomes. In combination with cost effectiveness and other considerations, these activities enable a biomarker to cross the second translational gap and become a “clinical decision-making tool” that influences patient care. Importantly, application of qMR methods in research or in the clinic requires rigorous quality assurance and quality control procedures.141-143
During the three processes of (1) technical development and validation, (2) clinical qualification, and (3) dissemination, additional substantial challenges (including regulatory issues and market-related factors) often arise before clinical dissemination is achieved (Figure 6). For example, the ability of healthcare providers to obtain reimbursement or take charge of the costs associated with quantitative imaging biomarkers may drive the clinical use of these tools. Oftentimes, a lack of CE/FDA (or equivalent) labeling limits the ability to apply a biomarker in clinical practice.
6.1 Examples
6.1.1 Liver PDFF quantification
CSE-based liver PDFF quantification has emerged as a major clinical and research tool to determine liver fat content. Importantly, this qMR method is commercially available on systems from various MRI vendors, including regulatory approvals such as FDA clearance and CE mark. A liver PDFF quantification profile is currently being developed by the Radiological Society of North America’s Quantitative Imaging Biomarkers Alliance (RSNA QIBA).144 Now that liver PDFF quantification methods have shown excellent technical performance (low bias, high precision), clinically relevant results are emerging, including population studies measuring prevalence in various populations145 and clinical studies showing the prognostic value of PDFF.146
6.1.2 Cardiac T1
In recent years, cardiac T1 mapping has become widely available on most clinical MRI systems. Some vendors have released dedicated product packages comprising one or more T1 mapping methods, while others have provided prototype methods. Several cardiac T1 mapping methods have regulatory approval such as FDA clearance and CE mark.
T1 mapping is widely used in cardiac MRI in academic centers and beyond. It has been successfully applied to an unexpectedly large spectrum of ischemic and non-ischemic cardiomyopathies20, 131 and is established as part of routine scanning in numerous clinical cardiac MR protocols. The effect of most heart diseases on myocardial T1 has been investigated, mostly in single center studies. Select pathologies have been studied in large cohorts or multi-center studies, including studies on amyloidosis147 and Anderson-Fabry disease.148 Additionally, cardiac T1 mapping has been adopted in multiple national cohorts, including the UK biobank protocol and the German national cohort.149, 150 These studies are some of the largest ongoing MRI projects to date. Following the clinical success demonstrated in the literature, cardiac T1 mapping was adopted in disease specific clinical guidelines.151 Further increases in clinical integration and use in a growing number of cardiac MRI protocols are likely.
7 RELATED INITIATIVES, CHALLENGES, AND OPPORTUNITIES
As described above, substantial efforts are needed for the development, validation and dissemination of quantitative MR techniques. These efforts require collaboration between technical researchers, translational researchers and clinicians, industry, and initiatives and institutions dedicated to the regulation and guidance of quantitative imaging measurements. Such initiatives and institutions include authorities for standardization of measurements such as Italy’s Istituto Nazionale di Ricerca Metrologica (INRIM), the Korea Research Institute of Science and Standards (KRISS), the U.S.’s National Institute of Standards and Technology (NIST), the UK’s National Physical Laboratory (NPL), Germany’s Physikalisch-Technische Bundesanstalt (PTB), and for the advancement of the development and use of imaging biomarkers, as performed by QIBA, the US National Cancer Institute through the Quantitative Imaging Network (QIN), the European Imaging Biomarkers Alliance (EIBALL), Japan-QIBA, the European Society of Radiology (ESR), and the ISMRM. Specifically, the major goal of the ISMRM Quantitative MR Study Group is to promulgate documentary and measurement standards for qMR methods in collaboration with national metrology institutes, academic and clinical MR sites, and through collaboration with existing study groups. Furthermore, ongoing qMR improvements occur in the context of broad efforts to evaluate and optimize the value of MRI in medicine.152 Ultimately, efforts to develop qMR methods should have broad value in medicine across countries and populations, beyond specialized research centers.
In addition, the development and validation of qMR methods is closely connected to the improvement of the reproducibility of MR research itself. There are multiple existing and emerging initiatives in this area, including the ISMRM Reproducible Research Study Group, and reproducibility has recently been emphasized by major journals, such as Magnetic Resonance in Medicine or the Journal of Magnetic Resonance Imaging. A related set of benchmarks for validation of quantitative imaging tools has been described by the Quantitative Imaging Network of the US’ National Cancer Institute.153 Importantly, multiple consensus efforts and community challenges have emerged in recent years for specific qMR methods or applications, as well as for general optimization of qMR.6, 20, 37, 142, 154-163 Data standards are also essential for reproducibility and interoperability, making it easier to create transparent qMR workflows. Two standards that are relevant for qMR are the ISMRM-Raw Data format (https://ismrmrd.github.io/apidocs/1.5.0/), and the Brain Imaging Data Structure (BIDS) extension proposal for quantitative MRI (https://github.com/bids-standard/bids-specification/pull/508).
Furthermore, various software packages developed, maintained and used by the community enable improved reproducibility by standardizing data processing pipelines. Supporting Information Figure S6 gives an overview of the user base of publicly available software with applications in qMR. Examples include various toolboxes hosted on the Matlab Central File exchange (https://www.mathworks.com/matlabcentral/fileexchange/), FSLTools (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslTools), OsiriX or Horos plugins, ImageJ (https://imagej.nih.gov/ij/), Bay Area Reconstruction Toolbox (BART, https://mrirecon.github.io/bart/), qMRlab (https://qmrlab.org),164 Gadgetron (http://gadgetron.github.io/), Quantitative Imaging Tools (https://github.com/spinicist/QUIT), Michigan Image Reconstruction Toolbox (MIRT, http://github.com/JeffFessler/MIRT.jl), hMRI (https://hmri-group.github.io/hMRI-toolbox/), LCModel (http://s-provencher.com/lcmodel.shtml), Total Mapping Toolbox (TOMATO) (https://mrkonrad.github.io/TOMATO/html), QMRI Tools (https://mfroeling.github.io/QMRITools/), and others (e.g., vendor proprietary software and in-house or personal code). RSNA QIBA and NIBIB have also sponsored the development of digital reference objects (DROs), which enable the testing of analysis tools to assess their bias and precision when working with quantitative data obtained with different acquisition parameters and varying levels of SNR. Example DROs for DCE-MRI and DWI are available from QIBA (https://qidw.rsna.org).
The transformation of MR into a truly quantitative diagnostic modality has enormous potential to impact research and clinical care. However, the development, validation, and dissemination of quantitative MR methods is faced with multiple challenges, particularly the complexity and cost of the required validation studies, as highlighted by the above networks and initiatives. These challenges reinforce the need for collaboration between technical MR researchers, academic radiologists, and other clinicians, as well as industry, such as original equipment manufacturers (OEMs)—vendors of MR systems and other MR equipment and software, pharmaceutical companies, contract research organizations, and others.
Finally, substantial recent efforts from the qMR community have focused on rapid multi-parametric mapping and machine learning (ML). Emerging multi-parametric mapping methods such as MR fingerprinting165 and multi-tasking81 enable quantitative mapping of several parameters with short scan times. These methods are highly promising for a variety of applications, and require careful development and validation to address a large number of potential confounding factors. ML methods, including radiomics and deep learning, have recently gained enormous interest in the field. Indeed, ML may contribute to different stages of the qMR pipeline, including image prescription, acquisition, reconstruction, post-processing, measurement, and analysis. Despite the potential impact of these methods, rigorous development and validation of ML-enabled qMR is needed. This development and validation pose new challenges and opportunities for ML-enabled qMR, including how to quantify and address confounding factors to achieve low bias and high reproducibility across patients, sites, and vendors, in much the same way as the more ‘traditional’ qMR methods highlighted in the present manuscript.
8 SUMMARY AND CONCLUSIONS
On behalf of the International Society for Magnetic Resonance in Medicine (ISMRM) Quantitative MR Study Group, this manuscript describes a framework for the development and validation of quantitative MR methods. With a focus on technical performance metrics (bias and precision), this framework highlights the challenges as well as the research opportunities associated with quantitative MR methods. Overall, rigorous development and validation are critical components of the transformation of MR into a truly quantitative diagnostic modality. A summary of concluding recommendations to achieve this aim is provided in Table 3. Upon successful implementation of qMR methods, as well as clinical qualification of qMR-based biomarkers, qMR has the potential to substantially advance imaging in clinical applications and clinical research, and build a cornerstone of precision radiology.
| Definitions | The measurand of interest needs to be clearly defined. How does the targeted measurand relate to other physical properties? For example, if a coefficient is determined, what is the reference quantity (e.g., MR-visible protons)? |
| Choice of pulse sequence | Select pulse sequences and parameters such that the measurand can be determined with low bias and high precision, subject to a set of timing, hardware, and other constraints. Acquisition design will often begin by selecting a pulse sequence where the measurand of interest can be directly probed, while minimizing the effect of confounding factors |
| Choice of models | Proper biophysical modeling is difficult, but may avoid the pitfalls of various signal representations. Indeed, various models can often fit the data, but models that are not grounded on specific tissue assumptions are often more difficult to validate, and are also likely to suffer from poor reproducibility |
| Rigorous validation | It is critical to perform systematic validation of the technical performance of emerging qMR methods. Importantly, even though early stage validation is often focused on bias, evaluation of precision (repeatability and reproducibility) is essential to enable further clinical qualification and dissemination |
| Structured evaluation | Well-structured reporting of the validation is an essential component of establishing a qMR method. The standard metrics being evaluated should be described clearly as discussed in the section “Technical Performance of qMR Methods” above. Future work from the community may establish a standardized structure for the Methods and Results sections of qMR manuscripts |
| Real-world validation | Even at the stage of technical validation, it is important to evaluate the performance of qMR methods under conditions that are relevant to the real-world clinical environment. For example, performance may depend on the hardware available at different sites (e.g., academic vs non-academic). In addition, technical validation in a relevant patient population helps pave the way for subsequent clinical qualification and application |
| Focus on reproducibility | Optimization and characterization of reproducibility across acquisition protocols, field strength, vendor, platform, etc, is critical in qMR. Indeed, in qualitative MR methods development, one is often interested in finding the optimal set of acquisition and processing parameters to maximize imaging performance (e.g., resolution, SNR). Although this optimal set of parameters is also relevant in qMR, the development of qMR methods that are reproducible across variations in the acquisition parameters is arguably even more important than the identification of the optimal parameters. This way, qMR methods are best suited for widespread dissemination across sites that may not be able to implement exactly optimized acquisitions |
| Reproducibility vs. standardization | Certain qMR methods are highly reproducible across variations in acquisition parameters (within a certain range). For example, this is the case for PDFF measurement in the liver: when correcting for all relevant confounders, PDFF measurement is highly reproducible across field strength, echo time combinations, spatial resolution, and various other acquisition parameters. However, other qMR methods have poorer reproducibility, and their widespread dissemination would benefit highly from standardization of acquisitions (as well as processing) across sites and systems, as well as harmonization (see below) |
| Harmonization | Quantitative MR can benefit from harmonized acquisitions and tools. For example, standardized reference objects and tool validation methods, such as the use of DROs, provide common ground for comparison of imaging protocols across sites, vendors, and software analysis packages |
| Realistic time-horizon | Development, validation, qualification, and dissemination of a qMR method is a slow, iterative process that may take more than a decade |
| Consider the end goal | In qMR, the end goal is often to enable improved diagnosis, staging, and/or treatment monitoring of disease and generate increased value in the clinical work up. This goal is generally relevant even for technically focused researchers |
| Mind the translational gap | Establishing new quantitative imaging biomarkers in actual clinical use is a lengthy process and requires many steps that may not be amenable to funding by traditional science-oriented grants or tenders. This may require creativity about the path to clinical integration and real-world use |
| Clinical qualification is key | Clinical qualification is critical to achieve translation of a quantitative MR method to the clinic. This may be the most time-consuming step in the entire pipeline of qMR method development and evaluation |
| Collaboration | Working together with stakeholders (technical, clinical, industrial) and across imaging modalities or scientific disciplines is critical. For example, accurate biophysical modelling will benefit from collaboration between clinical and preclinical MR scientists, but also between MR researchers and scientists studying tissues at smaller scales (e.g., cell cultures) or using different imaging technology (e.g., X-ray phase contrast imaging for tissue structure, near infrared spectroscopy for blood oxygenation properties, or microscopy). Collaboration with clinicians is of enormous value in qMR technique development, and helps create a virtuous loop of refinement of existing methods and conception of new methods that address existing clinical needs. Furthermore, early stage discussion and cooperation with industry is especially relevant, since CE/FDA-labeling is mandatory for clinical translation. A technique without labelling will not be widely adopted in clinical practice due to ethical concerns and regulatory issues |
ACKNOWLEDGMENTS
The authors thank the entire ISMRM Quantitative MR Study Group, including those who responded to the online poll, as well as those who provided feedback during the public presentation on June 23, 2021, for their thoughtful feedback, which has led to an improved manuscript. We also acknowledge the efforts of the endorsers, as listed in the Supporting Information Table S2. We also thank the ISMRM Publications Committee for reviewing the work and coordinating the ISMRM Board of Trustees approval process.
CONFLICT OF INTEREST
Nancy A. Obuchowski is a paid consultant for RSNA’s Quantitative Imaging Biomarker Alliance. Bettina Baessler is co-founder of Lernrad GmbH, Germany. Xavier Golay is a co-founder, CEO and shareholder of Gold Standard Phantoms. Diego Hernando is co-founder of Calimetrix, LLC.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were obtained or analyzed in this study.
