Mathematical Methods in the Applied Sciences
Volume 46, Issue 6 pp. 6756-6766
RESEARCH ARTICLE
Open Access

Sufficient conditions for regularity, positive recurrence, and absorption in level-dependent QBD processes and related block-structured Markov chains

Antonio Gómez-Corral, 

Corresponding Author

Antonio Gómez-Corral

Department of Statistics and Operations Research, Complutense University of Madrid, Madrid, Spain

Correspondence

Antonio Gómez-Corral, Facultad de Ciencias Matemáticas, Plaza de Ciencias 3, Universidad Complutense de Madrid, Madrid-28040, Spain.

Email: [email protected]

Communicated by: T. Wanner

Search for more papers by this author
Joshua Langwade, 

Joshua Langwade

Department of Applied Mathematics, School of Mathematics, University of Leeds, Leeds, LS2 9JT UK

Search for more papers by this author
Martín López-García, 

Martín López-García

Department of Applied Mathematics, School of Mathematics, University of Leeds, Leeds, LS2 9JT UK

Search for more papers by this author
Carmen Molina-París, 

Carmen Molina-París

Department of Applied Mathematics, School of Mathematics, University of Leeds, Leeds, LS2 9JT UK

T-6, Theoretical Biology and Biophysics, Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, 87545 USA

Search for more papers by this author
First published: 09 December 2022
https://doi.org/10.1002/mma.8938
Citations: 1

Abstract

This paper is concerned with level-dependent quasi-birth-death (LD-QBD) processes, i.e., multi-variate Markov chains with a block-tridiagonal q $$ q $$ -matrix, and a more general class of block-structured Markov chains, which can be seen as LD-QBD processes with total catastrophes. Arguments from univariate birth-death processes are combined with existing matrix-analytic formulations to obtain sufficient conditions for these block-structured processes to be regular, positive recurrent, and absorbed with certainty in a finite mean time. Specifically, it is our purpose to show that, as is the case for competition processes, these sufficient conditions are inherently linked to a suitably defined birth-death process. Our results are exemplified with two Markov chain models: a study of target cells and viral dynamics and one of kinetic proof-reading in T cell receptor signal transduction.

1 INTRODUCTION

Since the early 1960s, continuous-time Markov chains on the lattice points of ℕ 0 × ℕ 0 $$ {\mathbb{N}}_0\times {\mathbb{N}}_0 $$ have received significant attention in the literature, mainly due to their use in biological applications, e.g., representing some kind of interaction between individuals of two different species, where the point ( m 1 , m 2 ) $$ \left({m}_1,{m}_2\right) $$ represents the size of each population. Specifically, in the bi-variate competition process of Reuter1 the one-step transitions from any point ( m 1 , m 2 ) $$ \left({m}_1,{m}_2\right) $$ of the positive orthant ℕ × ℕ $$ \mathbb{N}\times \mathbb{N} $$ are allowed only to a neighboring point, ( m 1 + n 1 , m 2 + n 2 ) $$ \left({m}_1+{n}_1,{m}_2+{n}_2\right) $$ , with ( n 1 , n 2 ) ∈ { − 1,0 , 1 } × { − 1,0 , 1 } \ { ( − 1 , − 1 ) , ( 0,0 ) , ( 1,1 ) } $$ \left({n}_1,{n}_2\right)\in \left\{-1,0,1\right\}\times \left\{-1,0,1\right\}\backslash \left\{\left(-1,-1\right),\left(0,0\right),\left(1,1\right)\right\} $$ , which can be thought of as the natural generalization of the uni-variate birth-death process (see, e.g., Anderson2). Reuter1 and Iglehart,3 who extended the results of Reuter1 to the N $$ N $$ -dimensional orthant, derive sufficient conditions for a competition process to be specified uniquely by its transition rates, positive recurrent, absorbed with certainty, and to have finite mean absorption time. For details concerning two-dimensional nearest-neighbor random walks and their application in modelling traffic and computer networks, see for example the paper by Cohen4 and references therein.

A summary of the main results on multi-variate competition processes is given by Anderson,2 with special emphasis on processes in two dimensions and for different applications, such as epidemic models, predator-prey processes and bi-variate linear birth-death processes, which have been studied by a number of authors, including Almaraz et al.,5 Bailey,6 Hitchcock,7 Kester,8 and Ridler-Rowe.9 Gómez-Corral and López García10 investigate a two-species competition process previously analyzed by Ridler-Rowe,11 who derives the asymptotic distribution of the position at which the process first hits the subset of boundary points { ( m 1 , 0 ) : m 1 ∈ ℕ } ∪ { ( 0 , m 2 ) : m 2 ∈ ℕ } $$ \left\{\left({m}_1,0\right):{m}_1\in \mathbb{N}\right\}\cup \left\{\left(0,{m}_2\right):{m}_2\in \mathbb{N}\right\} $$ and an asymptotic result for the probability that the process accesses states in { ( m 1 , 0 ) : m 1 ∈ ℕ } $$ \left\{\left({m}_1,0\right):{m}_1\in \mathbb{N}\right\} $$ under the taboo of { ( 0 , m 2 ) : m 2 ∈ ℕ } $$ \left\{\left(0,{m}_2\right):{m}_2\in \mathbb{N}\right\} $$ (i.e., on those sample paths of the process satisfying that states in { ( 0 , m 2 ) : m 2 ∈ ℕ } $$ \left\{\left(0,{m}_2\right):{m}_2\in \mathbb{N}\right\} $$ are not to be visited), when the initial population sizes are large. Significantly different results for these hitting probabilities are derived in Gómez-Corral and López García10 under small and moderate initial population sizes, by considering an approximating process, for which the extinction time can be seen as a phase-type random variable. More recently, Ho et al12 focus on a tractable bi-variate extension of the birth-death process, where rates are allowed to be nonlinear, and present an efficient algorithm to evaluate its transition probabilities making use of a continued fraction representation of the Laplace transforms.

The methods used by Iglehart3 for a multi-variate competition process are similar to those of Reuter1 in that the proofs presented define the sum of all coordinates of a point (state) in the orthant as a level, i.e., points ( m 1 , ⋯ , m N ) ∈ ℕ 0 N $$ \left({m}_1,\cdots, {m}_N\right)\in {\mathbb{N}}_0^N $$ with ∑ n = 1 N m n = i $$ {\sum}_{n=1}^N{m}_n=i $$ are grouped into the i $$ i $$ th level, and where possible transitions represent the birth or the death of an individual affecting a single coordinate, or the “mutation” of an individual moving from one coordinate to another one. Therefore, the results of Iglehart3 cannot be applied to more general transitions involving simultaneous changes in three or more coordinates, even if those transitions are only between points belonging to the same or adjacent levels.

The results in this paper represent an extension of the work of Iglehart3 and Reuter1 to a wider class of processes, including level-dependent quasi-birth-death (LD-QBD) processes with and without total catastrophes.13-15 LD-QBD processes with total catastrophes —where the term total catastrophe16, 17 amounts to disaster,18, 19 killing20 or mass annihilation/exodus21— can be thought of as the multi-variate version of the uni-variate birth-death process with killing analyzed by Van Doorn and Zeifman,22, 23 where transitions from state m $$ m $$ may go to either state m − 1 $$ m-1 $$ or state m + 1 $$ m+1 $$ or an absorbing state. For a summary of analytical results and applications to queueing models and population processes, we refer the reader to the papers by Baumann and Sandmann,13 and Di Crescenzo et al.,24 and references therein. We aim to show that, in a similar manner to Reuter1 and Iglehart,3 the general theory of uni-variate birth-death processes can be used to prove the regularity (Section 2.1), the recurrence (Section 2.2), and the absorption with certainty and in a finite mean time (Section 2.3) of LD-QBD processes and related block-structured Markov chains. In our analysis, we adopt Iglehart's3 notation, which allows the interested reader to better observe the similarities and differences between Iglehart's results and our more general approach. Our theoretical results are applied to two Markov chain models: one for target cells and viral dynamics25 (Section 3.1), and a second for T cell receptor kinetic proof-reading26 (Section 3.2).

2 BLOCK-STRUCTURED MARKOV CHAINS AND LEVEL-DEPENDENT QBD PROCESSES

In this section, we investigate continuous-time Markov chains with infinitely many states, which are LD-QBD processes, but with the addition of total catastrophes. In particular, we are interested in the study of bi-variate processes X = { ( I ( t ) , J ( t ) ) : t ≥ 0 } $$ \mathcal{X}=\left\{\left(I(t),J(t)\right):t\ge 0\right\} $$ with state space
S = A ∪ T , $$ \mathcal{S}=\mathcal{A}\cup \mathcal{T}, $$
where states in A $$ \mathcal{A} $$ are absorbing and T $$ \mathcal{T} $$ consists of non-absorbing states. These sets of states are assumed to be of the form
A = ⋃ i = 0 ∞ l A ( i ) and T = ⋃ i = 0 ∞ l T ( i ) , $$ \mathcal{A}={\bigcup}_{i=0}^{\infty }{l}_{\mathcal{A}}(i)\kern0.4em \mathrm{and}\kern0.4em \mathcal{T}={\bigcup}_{i=0}^{\infty }{l}_{\mathcal{T}}(i), $$
where l A ( i ) = { ( i , j ) : j ∈ { 1 , ⋯ , M i ′ } } $$ {l}_{\mathcal{A}}(i)=\left\{\left(i,j\right):j\in \left\{1,\cdots, {M}_i^{\prime}\right\}\right\} $$ , l T ( i ) = { ( i , j ) : j ∈ { 1 , ⋯ , M i } } $$ {l}_{\mathcal{T}}(i)=\left\{\left(i,j\right):j\in \left\{1,\cdots, {M}_i\right\}\right\} $$ and M i ′ + M i $$ {M}_i^{\prime }+{M}_i $$ is strictly positive with M i ′ , M i ∈ ℕ 0 $$ {M}_i^{\prime },{M}_i\in {\mathbb{N}}_0 $$ , for i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ . This means that l ( i ) = l A ( i ) ∪ l T ( i ) $$ l(i)={l}_{\mathcal{A}}(i)\cup {l}_{\mathcal{T}}(i) $$ is a non-empty set of states—i.e., ( M i ′ , M i ) ≠ ( 0,0 ) $$ \left({M}_i^{\prime },{M}_i\right)\ne \left(0,0\right) $$ —for every integer i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ , whence if l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ (respectively, l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ ) is an empty set, then M i ′ = 0 $$ {M}_i^{\prime }=0 $$ and M i ∈ ℕ $$ {M}_i\in \mathbb{N} $$ (respectively, M i ′ ∈ ℕ $$ {M}_i^{\prime}\in \mathbb{N} $$ and M i = 0 $$ {M}_i=0 $$ ). Similarly as for QBD processes (see, for example, Latouche & Ramaswami27), the first coordinate I ( t ) $$ I(t) $$ of X $$ \mathcal{X} $$ is called the level variable and J ( t ) $$ J(t) $$ the phase variable. For convenience, we use here the term level to denote the subset l ( i ) $$ l(i) $$ .

An essential property of X $$ \mathcal{X} $$ , exploited in Sections 2.1–2.3, is the block-tridiagonal matrix structure of its q $$ q $$ -matrix on those sample paths under the taboo that the process X $$ \mathcal{X} $$ does not leave the subset T $$ \mathcal{T} $$ of non-absorbing states. In particular, under the assumption that the set A $$ \mathcal{A} $$ of absorbing states is empty (Section 2.2), X $$ \mathcal{X} $$ becomes a standard LD-QBD process; otherwise (Sections 2.1 and 2.3), a total catastrophe is said to occur whenever the process X $$ \mathcal{X} $$ jumps from non-absorbing states in a certain set l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ to any absorbing state in l A ( i − 1 ) $$ {l}_{\mathcal{A}}\left(i-1\right) $$ , l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ or l A ( i + 1 ) $$ {l}_{\mathcal{A}}\left(i+1\right) $$ , where it will remain forever.

2.1 Regularity of LD-QBD processes and related block-structured Markov chains

The processes to be studied in this section have conservative q $$ q $$ -matrices Q = ( q ( i , j ) , ( i ′ , j ′ ) : ( i , j ) , ( i ′ , j ′ ) ∈ S ) $$ Q=\left({q}_{\left(i,j\right),\left({i}^{\prime },{j}^{\prime}\right)}:\left(i,j\right),\left({i}^{\prime },{j}^{\prime}\right)\in \mathcal{S}\right) $$ of the following form:
  • (i)

    For states ( i , j ) ∈ T $$ \left(i,j\right)\in \mathcal{T} $$ and ( i ′ , j ′ ) ∈ l A ( i ′ ) $$ \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{A}}\left({i}^{\prime}\right) $$ with i ′ ∈ { max { 0 , i − 1 } , i , i + 1 } $$ {i}^{\prime}\in \left\{\max \left\{0,i-1\right\},i,i+1\right\} $$ ,

    q ( i , j ) , ( i ′ , j ′ ) = μ ′ ( ( i , j ) , ( i − 1 , j ′ ) ) , if ( i ′ , j ′ ) ∈ l A ( i − 1 ) and i ∈ ℕ , γ ′ ( ( i , j ) , ( i , j ′ ) ) , if ( i ′ , j ′ ) ∈ l A ( i ) , λ ′ ( ( i , j ) , ( i + 1 , j ′ ) ) , if ( i ′ , j ′ ) ∈ l A ( i + 1 ) , 0 , otherwise . $$ {q}_{\left(i,j\right),\left({i}^{\prime },{j}^{\prime}\right)}=\left\{\begin{array}{ll}{\mu}^{\prime}\left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{A}}\left(i-1\right)\kern0.4em \mathrm{and}\kern0.4em i\in \mathbb{N},\\ {}{\gamma}^{\prime}\left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{A}}(i),\\ {}{\lambda}^{\prime}\left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{A}}\left(i+1\right),\\ {}0,& \mathrm{otherwise}.\end{array}\right. $$ (1)
    That is, the functions μ ′ ( ( i , j ) , ( i − 1 , j ′ ) ) $$ {\mu}^{\prime}\left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right) $$ , γ ′ ( ( i , j ) , ( i , j ′ ) ) $$ {\gamma}^{\prime}\left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right) $$ and λ ′ ( ( i , j ) , ( i + 1 , j ′ ) ) $$ {\lambda}^{\prime}\left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right) $$ represent the transition rates of the process from ( i , j ) ∈ l T ( i ) $$ \left(i,j\right)\in {l}_{\mathcal{T}}(i) $$ to absorbing states in l A ( i − 1 ) $$ {l}_{\mathcal{A}}\left(i-1\right) $$ , l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ , and l A ( i + 1 ) $$ {l}_{\mathcal{A}}\left(i+1\right) $$ , respectively.

  • (ii)

    For states ( i , j ) ∈ T $$ \left(i,j\right)\in \mathcal{T} $$ and ( i ′ , j ′ ) ∈ l T ( i ′ ) $$ \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{T}}\left({i}^{\prime}\right) $$ with i ′ ∈ { max { 0 , i − 1 } , i , i + 1 } $$ {i}^{\prime}\in \left\{\max \left\{0,i-1\right\},i,i+1\right\} $$ ,

    q ( i , j ) , ( i ′ , j ′ ) = μ ( ( i , j ) , ( i − 1 , j ′ ) ) , if ( i ′ , j ′ ) ∈ l T ( i − 1 ) and i ∈ ℕ , γ ( ( i , j ) , ( i , j ′ ) ) , if ( i ′ , j ′ ) ∈ l T ( i ) and j ′ ≠ j , α ( i , j ) , if ( i ′ , j ′ ) = ( i , j ) , λ ( ( i , j ) , ( i + 1 , j ′ ) ) , if ( i ′ , j ′ ) ∈ l T ( i + 1 ) , 0 , otherwise. $$ {q}_{\left(i,j\right),\left({i}^{\prime },{j}^{\prime}\right)}=\left\{\begin{array}{ll}\mu \left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{T}}\left(i-1\right)\kern0.4em \mathrm{and}\kern0.4em i\in \mathbb{N},\\ {}\gamma \left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{T}}(i)\kern0.4em \mathrm{and}\kern0.4em {j}^{\prime}\ne j,\\ {}\alpha \left(i,j\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)=\left(i,j\right),\\ {}\lambda \left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right),& \mathrm{if}\kern0.4em \left({i}^{\prime },{j}^{\prime}\right)\in {l}_{\mathcal{T}}\left(i+1\right),\\ {}0,& \mathrm{otherwise}.\end{array}\right. $$ (2)
    That is, the functions μ ( ( i , j ) , ( i − 1 , j ′ ) ) $$ \mu \left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right) $$ , γ ( ( i , j ) , ( i , j ′ ) ) $$ \gamma \left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right) $$ and λ ( ( i , j ) , ( i + 1 , j ′ ) ) $$ \lambda \left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right) $$ represent the transition rates of the process from ( i , j ) ∈ l T ( i ) $$ \left(i,j\right)\in {l}_{\mathcal{T}}(i) $$ to non-absorbing states in l T ( i − 1 ) $$ {l}_{\mathcal{T}}\left(i-1\right) $$ , l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , and l T ( i + 1 ) $$ {l}_{\mathcal{T}}\left(i+1\right) $$ , respectively.

  • (iii)

    For states ( i , j ) ∈ A $$ \left(i,j\right)\in \mathcal{A} $$ , the rates q ( i , j ) , ( i ′ , j ′ ) $$ {q}_{\left(i,j\right),\left({i}^{\prime },{j}^{\prime}\right)} $$ are specified by q ( i , j ) , ( i ′ , j ′ ) = 0 $$ {q}_{\left(i,j\right),\left({i}^{\prime },{j}^{\prime}\right)}=0 $$ , for any state ( i ′ , j ′ ) ∈ S $$ \left({i}^{\prime },{j}^{\prime}\right)\in \mathcal{S} $$ , since ( i , j ) $$ \left(i,j\right) $$ is absorbing.

In Equation (2), the values α ( i , j ) $$ \alpha \left(i,j\right) $$ are given by
α ( i , j ) = − ( 1 − δ i , 0 ) ∑ j ′ = 1 M i − 1 ′ μ ′ ( ( i , j ) , ( i − 1 , j ′ ) ) + ∑ j ′ = 1 M i − 1 μ ( ( i , j ) , ( i − 1 , j ′ ) ) − ∑ j ′ = 1 M ′ i γ ′ ( ( i , j ) , ( i , j ′ ) ) − ∑ j ′ = 1 , j ′ ≠ j M i γ ( ( i , j ) , ( i , j ′ ) ) − ∑ j ′ = 1 M ′ i + 1 λ ′ ( ( i , j ) , ( i + 1 , j ′ ) ) − ∑ j ′ = 1 M i + 1 λ ( ( i , j ) , ( i + 1 , j ′ ) ) , $$ {\displaystyle \begin{array}{cc}\hfill \alpha \left(i,j\right)& =-\left(1-{\delta}_{i,0}\right)\left(\sum \limits_{j^{\prime }=1}^{M_{i-1}^{\prime }}{\mu}^{\prime}\Big(\left(i,j\right),\Big(i-1,{j}^{\prime}\left)\right)+\sum \limits_{j^{\prime }=1}^{M_{i-1}}\mu \left(\right(i,j\Big),\Big(i-1,{j}^{\prime}\left)\right)\right)\hfill \\ {}\hfill & \kern0.6060606060606061em -\sum \limits_{j^{\prime }=1}^{M_i^{\prime }}{\gamma}^{\prime}\left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right)-\sum \limits_{j^{\prime }=1,{j}^{\prime}\ne j}^{M_i}\gamma \left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right)-\sum \limits_{j^{\prime }=1}^{M_{i+1}^{\prime }}{\lambda}^{\prime}\left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right)-\sum \limits_{j^{\prime }=1}^{M_{i+1}}\lambda \left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right),\hfill \end{array}} $$
where the sums ∑ j ′ = 1 M ′ i ′ $$ {\sum}_{j^{\prime }=1}^{M_{i^{\prime}}^{\prime }} $$ and ∑ j ′ = 1 M i ′ $$ {\sum}_{j^{\prime }=1}^{M_{i^{\prime }}} $$ are equal to zero if M i ′ ′ = 0 $$ {M}_{i^{\prime}}^{\prime }=0 $$ and M i ′ = 0 $$ {M}_{i^{\prime }}=0 $$ , respectively, and where δ i , 0 $$ {\delta}_{i,0} $$ represents the Kronecker delta. It is also assumed that there exists an integer, i 0 ∈ ℕ 0 $$ {i}_0\in {\mathbb{N}}_0 $$ , which is the smallest level variable such that l T ( i 0 ) $$ {l}_{\mathcal{T}}\left({i}_0\right) $$ is a non-empty subset of non-absorbing states, and which satisfies the following inequalities:
∑ j ′ = 1 M ′ i + 1 λ ′ ( ( i , j ) , ( i + 1 , j ′ ) ) + ∑ j ′ = 1 M i + 1 λ ( ( i , j ) , ( i + 1 , j ′ ) ) > 0 , $$ \sum \limits_{j^{\prime }=1}^{M_{i+1}^{\prime }}{\lambda}^{\prime}\left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right)+\sum \limits_{j^{\prime }=1}^{M_{i+1}}\lambda \left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right)>0, $$ (3)
for states ( i , j ) $$ \left(i,j\right) $$ with i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0+1,\cdots \right\} $$ and j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ , and
∑ j ′ = 1 M i − 1 ′ μ ′ ( ( i , j ) , ( i − 1 , j ′ ) ) + ∑ j ′ = 1 M i − 1 μ ( ( i , j ) , ( i − 1 , j ′ ) ) > 0 , $$ \sum \limits_{j^{\prime }=1}^{M_{i-1}^{\prime }}{\mu}^{\prime}\left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right)+\sum \limits_{j^{\prime }=1}^{M_{i-1}}\mu \left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right)>0, $$ (4)
for states ( i , j ) $$ \left(i,j\right) $$ with i ∈ { i 0 + 1 , i 0 + 2 , ⋯ } $$ i\in \left\{{i}_0+1,{i}_0+2,\cdots \right\} $$ and j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ . As a result, the maximum rates λ i $$ {\lambda}_i $$ of upcrossing, defined by
λ i = max j ∈ { 1 , ⋯ , M i } ∑ j ′ = 1 M ′ i + 1 λ ′ ( ( i , j ) , ( i + 1 , j ′ ) ) + ∑ j ′ = 1 M i + 1 λ ( ( i , j ) , ( i + 1 , j ′ ) ) , $$ {\lambda}_i=\underset{j\in \left\{1,\cdots, {M}_i\right\}}{\max}\left\{\sum \limits_{j^{\prime }=1}^{M_{i+1}^{\prime }}{\lambda}^{\prime}\Big(\left(i,j\right),\Big(i+1,{j}^{\prime}\left)\right)+\sum \limits_{j^{\prime }=1}^{M_{i+1}}\lambda \left(\right(i,j\Big),\Big(i+1,{j}^{\prime}\left)\right)\right\}, $$ (5)
for i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ , and the minimum rates μ i $$ {\mu}_i $$ of downcrossing, defined by
μ i = min j ∈ { 1 , ⋯ , M i } ∑ j ′ = 1 M i − 1 ′ μ ′ ( ( i , j ) , ( i − 1 , j ′ ) ) + ∑ j ′ = 1 M i − 1 μ ( ( i , j ) , ( i − 1 , j ′ ) ) , $$ {\mu}_i=\underset{j\in \left\{1,\cdots, {M}_i\right\}}{\min}\left\{\sum \limits_{j^{\prime }=1}^{M_{i-1}^{\prime }}{\mu}^{\prime}\Big(\left(i,j\right),\Big(i-1,{j}^{\prime}\left)\right)+\sum \limits_{j^{\prime }=1}^{M_{i-1}}\mu \left(\right(i,j\Big),\Big(i-1,{j}^{\prime}\left)\right)\right\}, $$ (6)
for i ∈ ℕ $$ i\in \mathbb{N} $$ , are both strictly positive for integers i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0+1,\cdots \right\} $$ and i ∈ { i 0 + 1 , i 0 + 2 , ⋯ } $$ i\in \left\{{i}_0+1,{i}_0+2,\cdots \right\} $$ , respectively.

The distributional assumptions for process X $$ \mathcal{X} $$ extend Reuter's definition1 of a bi-variate competition process, as well as the extension of Iglehart3 to the N $$ N $$ -dimensional orthant, to the setting of continuous-time Markov chains with a block-tridiagonal structure for the q $$ q $$ -matrix, where jumps of X $$ \mathcal{X} $$ do not necessarily connect the nearest neighbors on the positive orthant in the N $$ N $$ -dimensional state space, and where the number of phases (i.e., states per level) is assumed to be level-dependent. In particular Iglehart3 and, consequently, Reuter1 (with N = 2 $$ N=2 $$ ) deal with levels l ( i ) $$ l(i) $$ consisting of M i ′ + M i = N − 1 + i N − 1 $$ {M}_i^{\prime }+{M}_i=\left(\genfrac{}{}{0ex}{}{N-1+i}{N-1}\right) $$ phases (i.e., states ( m 1 , ⋯ , m N ) ∈ ℕ 0 N $$ \left({m}_1,\cdots, {m}_N\right)\in {\mathbb{N}}_0^N $$ with ∑ n = 1 N m n = i $$ {\sum}_{n=1}^N{m}_n=i $$ ), and conditions (3) and (4) are assumed to hold for any non-absorbing state.

Remark 1.To explain, in a more explicit way, how the process X $$ \mathcal{X} $$ defined in (1)–(4) yields a wider class of Markov chains than the multi- and bi-variate competition processes of Iglehart3 and Reuter,1 we focus here on the special case N = 2 $$ N=2 $$ (Reuter1) and decompose level l ( i ) $$ l(i) $$ into the subsets l A ( i ) = { ( i , 0 ) , ( 0 , i ) } $$ {l}_{\mathcal{A}}(i)=\left\{\left(i,0\right),\left(0,i\right)\right\} $$ and l T ( i ) = { ( m 1 , m 2 ) ∈ ℕ 2 : m 1 + m 2 = i } $$ {l}_{\mathcal{T}}(i)=\left\{\left({m}_1,{m}_2\right)\in {\mathbb{N}}^2:{m}_1+{m}_2=i\right\} $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , which results in l T ( 1 ) = ∅ $$ {l}_{\mathcal{T}}(1)=\varnothing $$ and i 0 = 2 $$ {i}_0=2 $$ . Then, transitions between non-absorbing states occur from any state ( m 1 , m 2 ) ∈ l T ( i ) $$ \left({m}_1,{m}_2\right)\in {l}_{\mathcal{T}}(i) $$ , with i ∈ { 2,3 , . . . } $$ i\in \left\{2,3,\dots \right\} $$ , to states ( m 1 , m 2 − 1 ) $$ \left({m}_1,{m}_2-1\right) $$ and ( m 1 − 1 , m 2 ) $$ \left({m}_1-1,{m}_2\right) $$ in l T ( i − 1 ) $$ {l}_{\mathcal{T}}\left(i-1\right) $$ with respective rates μ ( ( m 1 , m 2 ) , ( m 1 , m 2 − 1 ) ) $$ \mu \left(\left({m}_1,{m}_2\right),\left({m}_1,{m}_2-1\right)\right) $$ and μ ( ( m 1 , m 2 ) , ( m 1 − 1 , m 2 ) ) $$ \mu \left(\left({m}_1,{m}_2\right),\left({m}_1-1,{m}_2\right)\right) $$ ; to states ( m 1 + 1 , m 2 − 1 ) $$ \left({m}_1+1,{m}_2-1\right) $$ and ( m 1 − 1 , m 2 + 1 ) $$ \left({m}_1-1,{m}_2+1\right) $$ in l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ with respective rates γ ( ( m 1 , m 2 ) , ( m 1 + 1 , m 2 − 1 ) ) $$ \gamma \left(\left({m}_1,{m}_2\right),\left({m}_1+1,{m}_2-1\right)\right) $$ and γ ( ( m 1 , m 2 ) , ( m 1 − 1 , m 2 + 1 ) ) $$ \gamma \left(\left({m}_1,{m}_2\right),\left({m}_1-1,{m}_2+1\right)\right) $$ ; and to states ( m 1 + 1 , m 2 ) $$ \left({m}_1+1,{m}_2\right) $$ and ( m 1 , m 2 + 1 ) $$ \left({m}_1,{m}_2+1\right) $$ in l T ( i + 1 ) $$ {l}_{\mathcal{T}}\left(i+1\right) $$ with respective rates λ ( ( m 1 , m 2 ) , ( m 1 + 1 , m 2 ) ) $$ \lambda \left(\left({m}_1,{m}_2\right),\left({m}_1+1,{m}_2\right)\right) $$ and λ ( ( m 1 , m 2 ) , ( m 1 , m 2 + 1 ) ) $$ \lambda \left(\left({m}_1,{m}_2\right),\left({m}_1,{m}_2+1\right)\right) $$ . From non-absorbing states in l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ with i ∈ { 2,3 , . . . } $$ i\in \left\{2,3,\dots \right\} $$ , it is seen that absorbing states in l A ( i − 1 ) $$ {l}_{\mathcal{A}}\left(i-1\right) $$ and l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ are accessible—via a one-step transition—only from states ( i − 1,1 ) $$ \left(i-1,1\right) $$ and ( 1 , i − 1 ) $$ \left(1,i-1\right) $$ , and the set l A ( i + 1 ) $$ {l}_{\mathcal{A}}\left(i+1\right) $$ of absorbing states is not accessible—via a one-step transition—from states in l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ . In a simple generalization of the Reuter1 model with the same decomposition of level l ( i ) $$ l(i) $$ into subsets l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ and l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , the process X $$ \mathcal{X} $$ defined by (1)-(4) may jump from any non-absorbing state ( m 1 , m 2 ) $$ \left({m}_1,{m}_2\right) $$ in l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , with i ∈ { 2,3 , . . . } $$ i\in \left\{2,3,\dots \right\} $$ , to any other non-absorbing state in l T ( i − 1 ) $$ {l}_{\mathcal{T}}\left(i-1\right) $$ , l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ and l T ( i + 1 ) $$ {l}_{\mathcal{T}}\left(i+1\right) $$ , as well as to any absorbing state in l A ( i − 1 ) $$ {l}_{\mathcal{A}}\left(i-1\right) $$ , l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ and l A ( i + 1 ) $$ {l}_{\mathcal{A}}\left(i+1\right) $$ .

Note that, for practical use, the structured form of the q $$ q $$ -matrix in (1)–(4) is often obtained directly, as in the case of the M / M / c $$ M/M/c $$ retrial queue,28 where the level I ( t ) $$ I(t) $$ and the phase J ( t ) $$ J(t) $$ variables correspond to the number of customers in orbit and the number of busy servers at time t $$ t $$ . However, it can be also derived from the use of a suitable labeling of states which translates a predetermined N $$ N $$ -dimensional continuous-time Markov chain—even with each coordinate taking values in a non-finite set of values, as in the models of Iglehart3 and Reuter,1 and our examples in Section 3—into a bi-variate process X $$ \mathcal{X} $$ with a finite number of phases per level.

Despite the general nature of the q $$ q $$ -matrix defined by (1)–(4), Iglehart's methods3 can be adapted to process X $$ \mathcal{X} $$ , as shown in the following result.

Theorem 1.A sufficient condition for the regularity of process X $$ \mathcal{X} $$ is

∑ i = i 0 ∞ 1 λ i σ i ∑ i ′ = i 0 i σ i ′ = ∞ , $$ \sum \limits_{i={i}_0}^{\infty}\frac{1}{\lambda_i{\sigma}_i}\kern3.0235pt \sum \limits_{i^{\prime }={i}_0}^i{\sigma}_{i^{\prime }}=\infty, $$
where σ i 0 = 1 $$ {\sigma}_{i_0}=1 $$ , σ i 0 + i = ∏ i ′ = 0 i − 1 λ i 0 + i ′ μ i 0 + i ′ + 1 $$ {\sigma}_{i_0+i}={\prod}_{i^{\prime }=0}^{i-1}\frac{\lambda_{i_0+{i}^{\prime }}}{\mu_{i_0+{i}^{\prime }+1}} $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , and rates λ i $$ {\lambda}_i $$ and μ i $$ {\mu}_i $$ are given by (5) and (6), respectively.

The proof of this result is very similar to that of Iglehart3 and is therefore left to the reader. The main idea is to replace the birth and the death of an individual in a single coordinate, and the “mutation” or movement of an individual from a coordinate to another one in the competition process considered in Ref.3 by jumps of our process X $$ \mathcal{X} $$ from any non-absorbing state ( i , j ) ∈ l T ( i ) $$ \left(i,j\right)\in {l}_{\mathcal{T}}(i) $$ , with i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0+1,\cdots \right\} $$ and j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ , to states in levels l ( i − 1 ) $$ l\left(i-1\right) $$ and l ( i + 1 ) $$ l\left(i+1\right) $$ , and states in l ( i ) \ { ( i , j ) } $$ l(i)\backslash \left\{\left(i,j\right)\right\} $$ , respectively.

We note that if we define the birth-death process X ′ $$ {\mathcal{X}}^{\prime } $$ , with state space { i 0 , i 0 + 1 , ⋯ } $$ \left\{{i}_0,{i}_0+1,\cdots \right\} $$ and birth and death parameters { λ i : i ∈ { i 0 , i 0 + 1 , ⋯ } } $$ \left\{{\lambda}_i:i\in \left\{{i}_0,{i}_0+1,\cdots \right\}\right\} $$ and { μ i : i ∈ { i 0 + 1 , i 0 + 2 , ⋯ } } $$ \left\{{\mu}_i:i\in \left\{{i}_0+1,{i}_0+2,\cdots \right\}\right\} $$ , similarly to Iglehart,3 the sufficient condition in Theorem 1 is a necessary and sufficient condition for X ′ $$ {\mathcal{X}}^{\prime } $$ to be regular (see, e.g., Karlin & McGregor29 and Reuter30). Specifically, the polynomials { Q i ( − s ) : i ∈ { i 0 − 1 , i 0 , ⋯ } } $$ \left\{{Q}_i\left(-s\right):i\in \left\{{i}_0-1,{i}_0,\cdots \right\}\right\} $$ satisfying Q i 0 − 1 ( − s ) = 0 $$ {Q}_{i_0-1}\left(-s\right)=0 $$ , Q i 0 ( − s ) = Q i 0 ∗ ( − s ) $$ {Q}_{i_0}\left(-s\right)={Q}_{i_0}^{\ast}\left(-s\right) $$ and s Q i ( − s ) = μ i Q i − 1 ( − s ) − ( λ i + μ i ) Q i ( − s ) + λ i Q i + 1 ( − s ) $$ s{Q}_i\left(-s\right)={\mu}_i{Q}_{i-1}\left(-s\right)-\left({\lambda}_i+{\mu}_i\right){Q}_i\left(-s\right)+{\lambda}_i{Q}_{i+1}\left(-s\right) $$ , for i ∈ { i 0 , i 0 + 1 , ⋯ , } $$ i\in \left\{{i}_0,{i}_0+1,\cdots, \right\} $$ , where Q i ∗ ( − s ) = max { P ( i , j ) ( − s ) : ( i , j ) ∈ l ( i ) } $$ {Q}_i^{\ast}\left(-s\right)=\max \left\{{P}_{\left(i,j\right)}\left(-s\right):\left(i,j\right)\in l(i)\right\} $$ , for i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ , and { P ( i , j ) ( − s ) : ( i , j ) ∈ S } $$ \left\{{P}_{\left(i,j\right)}\left(-s\right):\left(i,j\right)\in \mathcal{S}\right\} $$ is a non-negative solution of eq. (5.11) in Reuter30 for X $$ \mathcal{X} $$ , allow us to guarantee that, for every s > 0 $$ s>0 $$ , any non-negative, non-vanishing solution of eq. (5.11) in Reuter30 for the conservative birth-death process X ′ $$ {\mathcal{X}}^{\prime } $$ is unbounded as a function of i $$ i $$ . From the inequalities Q i ∗ ( − s ) ≥ Q i ( − s ) $$ {Q}_i^{\ast}\left(-s\right)\ge {Q}_i\left(-s\right) $$ and Q i ∗ ( − s ) − Q i − 1 ∗ ( − s ) ≥ Q i ( − s ) − Q i − 1 ( − s ) $$ {Q}_i^{\ast}\left(-s\right)-{Q}_{i-1}^{\ast}\left(-s\right)\ge {Q}_i\left(-s\right)-{Q}_{i-1}\left(-s\right) $$ , for i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0+1,\cdots \right\} $$ , it is then seen that the sequence { P ( i , j ) ( − s ) : ( i , j ) ∈ S } $$ \left\{{P}_{\left(i,j\right)}\left(-s\right):\left(i,j\right)\in \mathcal{S}\right\} $$ for process X $$ \mathcal{X} $$ is also unbounded as a function of ( i , j ) $$ \left(i,j\right) $$ , whence the system of equations described by eq. (5.11) in Ref.30 for X $$ \mathcal{X} $$ has no bounded non-negative solution other than P ( i , j ) ( − s ) = 0 $$ {P}_{\left(i,j\right)}\left(-s\right)=0 $$ , for every ( i , j ) ∈ S $$ \left(i,j\right)\in \mathcal{S} $$ and s > 0 $$ s>0 $$ .

Remark 2.Unlike Iglehart3 where (3) and (4) hold for every integer i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ and i ∈ ℕ $$ i\in \mathbb{N} $$ , respectively, we make no special assumption regarding λ i $$ {\lambda}_i $$ and μ i $$ {\mu}_i $$ , for i ∈ { 0 , ⋯ , i 0 − 1 } $$ i\in \left\{0,\cdots, {i}_0-1\right\} $$ . The assumption of strict block-tridiagonality of the q $$ q $$ -matrix over states in the finite subset ∪ i = 0 i 0 − 1 l ( i ) $$ {\cup}_{i=0}^{i_0-1}l(i) $$ can therefore be dropped.

2.2 Positive recurrence of level-dependent QBD processes

We consider here the particular case where X $$ \mathcal{X} $$ is regular and irreducible, so that A = ∅ $$ \mathcal{A}=\varnothing $$ . This means that X $$ \mathcal{X} $$ is a regular, irreducible LD-QBD process with q $$ q $$ -matrix
Q = Q 0,0 Q 0,1 Q 1,0 Q 1,1 Q 1,2 Q 2,1 Q 2,2 Q 2,3 ⋱ ⋱ ⋱ , $$ Q=\left(\begin{array}{ccccc}{Q}_{0,0}& {Q}_{0,1}& & & \\ {}{Q}_{1,0}& {Q}_{1,1}& {Q}_{1,2}& & \\ {}& {Q}_{2,1}& {Q}_{2,2}& {Q}_{2,3}& \\ {}& & \ddots & \ddots & \ddots \end{array}\right), $$
where Q i , i − 1 = ( μ ( ( i , j ) , ( i − 1 , j ′ ) ) : j ∈ { 1 , ⋯ , M i } , j ′ ∈ { 1 , ⋯ , M i − 1 } ) $$ {Q}_{i,i-1}=\left(\mu \left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right):j\in \left\{1,\cdots, {M}_i\right\},{j}^{\prime}\in \left\{1,\cdots, {M}_{i-1}\right\}\right) $$ and Q i , i + 1 = ( λ ( ( i , j ) , ( i + 1 , j ′ ) ) : j ∈ { 1 , ⋯ , M i } , j ′ ∈ { 1 , ⋯ , M i + 1 } ) $$ {Q}_{i,i+1}=\left(\lambda \left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right):j\in \left\{1,\cdots, {M}_i\right\},{j}^{\prime}\in \left\{1,\cdots, {M}_{i+1}\right\}\right) $$ . The diagonal and off-diagonal elements of sub-matrix Q i , i $$ {Q}_{i,i} $$ are given by α ( i , j ) $$ \alpha \left(i,j\right) $$ and γ ( ( i , j ) , ( i , j ′ ) ) $$ \gamma \left(\left(i,j\right),\left(i,{j}^{\prime}\right)\right) $$ , respectively, for phases j , j ′ ∈ { 1 , ⋯ , M i } $$ j,{j}^{\prime}\in \left\{1,\cdots, {M}_i\right\} $$ . For convenience, we limit ourselves to a process X $$ \mathcal{X} $$ with M 0 = 1 $$ {M}_0=1 $$ , which is general enough.

The necessary and sufficient condition for the birth-death process X ′ $$ {\mathcal{X}}^{\prime } $$ to be positive recurrent is also a sufficient condition for the positive recurrence of X $$ \mathcal{X} $$ , as stated below.

Theorem 2.If the process X $$ \mathcal{X} $$ is assumed to be regular and irreducible, then a sufficient condition for its positive recurrence is that ∑ i = 1 ∞ σ i $$ {\sum}_{i=1}^{\infty }{\sigma}_i $$ converges.

Proof.To prove the theorem, we make use of Anderson2 (see also Reuter1) and show that there exists a state ( i ∗ , j ∗ ) ∈ S $$ \left({i}^{\ast },{j}^{\ast}\right)\in \mathcal{S} $$ and a finite non-negative sequence { u ( i , j ) : ( i , j ) ∈ S } $$ \left\{u\left(i,j\right):\left(i,j\right)\in \mathcal{S}\right\} $$ such that

∑ j ′ = 1 M i + 1 λ ( ( i , j ) , ( i + 1 , j ′ ) ) u ( i + 1 , j ′ ) − u ( i , j ) + 1 ≤ ( 1 − δ i , 0 ) ∑ j ′ = 1 M i − 1 μ ( ( i , j ) , ( i − 1 , j ′ ) ) u ( i , j ) − u ( i − 1 , j ′ ) , $$ \sum \limits_{j^{\prime }=1}^{M_{i+1}}\lambda \left(\left(i,j\right),\left(i+1,{j}^{\prime}\right)\right)\left(u\left(i+1,{j}^{\prime}\right)-u\Big(i,j\Big)\right)+1\le \left(1-{\delta}_{i,0}\right)\sum \limits_{j^{\prime }=1}^{M_{i-1}}\mu \left(\left(i,j\right),\left(i-1,{j}^{\prime}\right)\right)\left(u\left(i,j\right)-u\Big(i-1,{j}^{\prime}\Big)\right), $$ (7)
for states ( i , j ) ∈ S \ { ( i ∗ , j ∗ ) } $$ \left(i,j\right)\in \mathcal{S}\backslash \left\{\left({i}^{\ast },{j}^{\ast}\right)\right\} $$ , since the condition
( 1 − δ i , 0 ) ∑ j ′ = 1 M i − 1 μ ( ( i , j ) , ( i − 1 , j ′ ) ) u ( i − 1 , j ′ ) + α ( i , j ) u ( i , j ) + ∑ j ′ = 1 , j ′ ≠ j M i γ ( ( i , j ) , ( i , j ′ ) ) u ( i , j ′ ) + ∑ j ′ = 1 M i + 1 λ ( ( i , j ) , ( i + 1 , j ′ ) ) u ( i + 1 , j ′ ) < ∞ $$ {\displaystyle \begin{array}{cc}\hfill &amp; \kern0.30em \left(1-{\delta}_{i,0}\right)\sum \limits_{j&#x0005E;{\prime }&#x0003D;1}&#x0005E;{M_{i-1}}\mu \left(\left(i,j\right),\left(i-1,{j}&#x0005E;{\prime}\right)\right)u\left(i-1,{j}&#x0005E;{\prime}\right)&#x0002B;\alpha \left(i,j\right)u\left(i,j\right)\hfill \\ {}\hfill &amp; &#x0002B;\sum \limits_{j&#x0005E;{\prime }&#x0003D;1,{j}&#x0005E;{\prime}\ne j}&#x0005E;{M_i}\gamma \left(\left(i,j\right),\left(i,{j}&#x0005E;{\prime}\right)\right)u\left(i,{j}&#x0005E;{\prime}\right)&#x0002B;\sum \limits_{j&#x0005E;{\prime }&#x0003D;1}&#x0005E;{M_{i&#x0002B;1}}\lambda \left(\left(i,j\right),\left(i&#x0002B;1,{j}&#x0005E;{\prime}\right)\right)u\left(i&#x0002B;1,{j}&#x0005E;{\prime}\right)&lt;\infty \hfill \end{array}} $$
holds irrespectively of the state ( i , j ) $$ \left(i,j\right) $$ . In particular, we can select the state ( i ∗ , j ∗ ) = ( 0,1 ) $$ \left({i}&#x0005E;{\ast },{j}&#x0005E;{\ast}\right)&#x0003D;\left(0,1\right) $$ and a sequence with u ( i , j ) = U ( i ) $$ u\left(i,j\right)&#x0003D;U(i) $$ , for ( i , j ) ∈ S $$ \left(i,j\right)\in \mathcal{S} $$ , where
U ( i + 1 ) = 1 λ i σ i ∑ i ′ = i + 1 ∞ σ i ′ + U ( i ) , i ∈ ℕ 0 , $$ U\left(i&#x0002B;1\right)&#x0003D;\frac{1}{\lambda_i{\sigma}_i}\sum \limits_{i&#x0005E;{\prime }&#x0003D;i&#x0002B;1}&#x0005E;{\infty }{\sigma}_{i&#x0005E;{\prime }}&#x0002B;U(i),\kern0.30em i\in {\mathbb{N}}_0, $$ (8)
and U ( 0 ) ≥ 0 $$ U(0)\ge 0 $$ is arbitrary. This choice turns (7) into the inequality
∑ j ′ = 1 M i + 1 λ ( ( i , j ) , ( i + 1 , j ′ ) ) U ( i + 1 ) − U ( i ) + 1 ≤ ∑ j ′ = 1 M i − 1 μ ( ( i , j ) , ( i − 1 , j ′ ) ) U ( i ) − U ( i − 1 ) , $$ \sum \limits_{j&#x0005E;{\prime }&#x0003D;1}&#x0005E;{M_{i&#x0002B;1}}\lambda \left(\left(i,j\right),\left(i&#x0002B;1,{j}&#x0005E;{\prime}\right)\right)\left(U\left(i&#x0002B;1\right)-U(i)\right)&#x0002B;1\le \sum \limits_{j&#x0005E;{\prime }&#x0003D;1}&#x0005E;{M_{i-1}}\mu \left(\left(i,j\right),\left(i-1,{j}&#x0005E;{\prime}\right)\right)\left(U(i)-U\left(i-1\right)\right), $$ (9)
for i ∈ ℕ $$ i\in \mathbb{N} $$ and j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ . From the definition of U ( i + 1 ) $$ U\left(i&#x0002B;1\right) $$ in (8), it is easily seen that
λ i ( U ( i + 1 ) − U ( i ) ) + 1 ≤ μ i ( U ( i ) − U ( i − 1 ) ) , i ∈ ℕ , $$ {\lambda}_i\left(U\left(i&#x0002B;1\right)-U(i)\right)&#x0002B;1\le {\mu}_i\left(U(i)-U\left(i-1\right)\right),\kern0.30em i\in \mathbb{N}, $$
so that (9) is shown for any integer i ∈ ℕ $$ i\in \mathbb{N} $$ and phase j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ , since { U ( i ) : i ∈ ℕ 0 } $$ \left\{U(i):i\in {\mathbb{N}}_0\right\} $$ is a strictly increasing sequence of non-negative values. □

2.3 Absorption of block-structured Markov chains

In this section, the interest is in a regular process X $$ \mathcal{X} $$ with non-empty subsets A $$ \mathcal{A} $$ and T $$ \mathcal{T} $$ . For states ( i , j ) ∈ T $$ \left(i,j\right)\in \mathcal{T} $$ and ( i ′ , j ′ ) ∈ A $$ \left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)\in \mathcal{A} $$ , let ρ ( i , j ) , ( i ′ , j ′ ) $$ {\rho}_{\left(i,j\right),\left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)} $$ be the probability that the process X $$ \mathcal{X} $$ starting in state ( i , j ) $$ \left(i,j\right) $$ will be absorbed in state ( i ′ , j ′ ) $$ \left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right) $$ , and ρ ( i , j ) $$ {\rho}_{\left(i,j\right)} $$ the probability of process X $$ \mathcal{X} $$ being ultimately absorbed in the set A $$ \mathcal{A} $$ having started in state ( i , j ) $$ \left(i,j\right) $$ . That is, we have ρ ( i , j ) = ∑ ( i ′ , j ′ ) ∈ A ρ ( i , j ) , ( i ′ , j ′ ) $$ {\rho}_{\left(i,j\right)}&#x0003D;{\sum}_{\left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)\in \mathcal{A}}{\rho}_{\left(i,j\right),\left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)} $$ .

Sufficient conditions for the process X $$ \mathcal{X} $$ to be non-dissipative and possess finite mean absorption times are derived in Theorem 3 below, by following Reuter's method.1 We note that, in a similar manner to Theorems 1 and 2, they correspond to necessary and sufficient conditions for the regular birth-death process X ′ $$ {\mathcal{X}}&#x0005E;{\prime } $$ to be absorbed almost surely in the state i 0 $$ {i}_0 $$ , and possess finite mean absorption times in the non-dissipative case, irrespectively of the initial state ( i , j ) $$ \left(i,j\right) $$ with i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0&#x0002B;1,\cdots \right\} $$ and j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ .

Theorem 3.A sufficient condition for a regular process X $$ \mathcal{X} $$ to be absorbed almost surely from any non-absorbing state ( i , j ) $$ \left(i,j\right) $$ is that ∑ i = i 0 ∞ ( λ i σ i ) − 1 $$ {\sum}_{i&#x0003D;{i}_0}&#x0005E;{\infty }{\left({\lambda}_i{\sigma}_i\right)}&#x0005E;{-1} $$ diverges. Moreover, the mean time to absorption τ ( i , j ) $$ {\tau}_{\left(i,j\right)} $$ is finite, regardless of the initial state ( i , j ) ∈ T $$ \left(i,j\right)\in \mathcal{T} $$ , provided that the absorption of process X $$ \mathcal{X} $$ is certain and ∑ i = i 0 ∞ σ i $$ {\sum}_{i&#x0003D;{i}_0}&#x0005E;{\infty }{\sigma}_i $$ converges.

Proof.The proof of the sufficient condition for non-dissipation (i.e., ρ ( i , j ) = 1 $$ {\rho}_{\left(i,j\right)}&#x0003D;1 $$ , for every state ( i , j ) ∈ T $$ \left(i,j\right)\in \mathcal{T} $$ ) is almost identical to that of Iglehart3: It is only necessary to construct a non-bounded sequence { u ( i , j ) : ( i , j ) ∈ T } $$ \left\{u\left(i,j\right):\left(i,j\right)\in \mathcal{T}\right\} $$ of non-negative values satisfying

∑ ( i ′ , j ′ ) ∈ S q ( i , j ) , ( i ′ , j ′ ) u ( i ′ , j ′ ) ≤ 0 , ( i , j ) ∈ T . $$ \sum \limits_{\left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)\in \mathcal{S}}{q}_{\left(i,j\right),\left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)}u\left({i}&#x0005E;{\prime },{j}&#x0005E;{\prime}\right)\le 0,\kern0.30em \left(i,j\right)\in \mathcal{T}. $$
The sequence can be defined as u ( i , j ) = U ( i ) $$ u\left(i,j\right)&#x0003D;U(i) $$ , for integers i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ and phases j ∈ { 1 , ⋯ , M i } $$ j\in \left\{1,\cdots, {M}_i\right\} $$ , with
U ( i ) = 0 , if i ∈ { 0 , ⋯ , i 0 − 1 } , 1 , if i = i 0 , 1 + μ i 0 ∑ i ′ = i 0 i − 1 ( λ i ′ σ i ′ ) − 1 , if i ∈ { i 0 + 1 , i 0 + 2 , ⋯ } , $$ U(i)&#x0003D;\left\{\begin{array}{ll}0,&amp; \mathrm{if}\kern0.4em i\in \left\{0,\cdots, {i}_0-1\right\},\\ {}1,&amp; \mathrm{if}\kern0.4em i&#x0003D;{i}_0,\\ {}1&#x0002B;{\mu}_{i_0}{\sum}_{i&#x0005E;{\prime }&#x0003D;{i}_0}&#x0005E;{i-1}{\left({\lambda}_{i&#x0005E;{\prime }}{\sigma}_{i&#x0005E;{\prime }}\right)}&#x0005E;{-1},&amp; \mathrm{if}\kern0.4em i\in \left\{{i}_0&#x0002B;1,{i}_0&#x0002B;2,\cdots \right\},\end{array}\right. $$
which yields a non-decreasing sequence of values U ( i ) $$ U(i) $$ , for i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ , such that lim i → ∞ U ( i ) = ∞ $$ {\lim}_{i\to \infty }U(i)&#x0003D;\infty $$ , since ∑ i = i 0 ∞ ( λ i σ i ) − 1 $$ {\sum}_{i&#x0003D;{i}_0}&#x0005E;{\infty }{\left({\lambda}_i{\sigma}_i\right)}&#x0005E;{-1} $$ diverges.

In proving that the mean absorption time τ ( i , j ) $$ {\tau}_{\left(i,j\right)} $$ is finite, for every initial state ( i , j ) ∈ S $$ \left(i,j\right)\in \mathcal{S} $$ , we make use of Reuter1 and, consequently, the argument for the finite sequence { u ( i , j ) : ( i , j ) ∈ S } $$ \left\{u\left(i,j\right):\left(i,j\right)\in \mathcal{S}\right\} $$ in Section 2.2 with an empty class, A $$ \mathcal{A} $$ , of absorbing states, referring to i 0 = 0 $$ {i}_0&#x0003D;0 $$ , merely needs rewording now for a non-empty subset A $$ \mathcal{A} $$ , so as to refer to the pre-determined integer i 0 ∈ ℕ $$ {i}_0\in \mathbb{N} $$ . □

3 TWO APPLICATIONS TO VIRAL DYNAMICS AND KINETIC PROOF-READING

In this section, we apply the theoretical results of Section 2 to two Markov chain models: one of target cells and viral dynamics,25 and a second one of kinetic proof-reading by T cell receptors.26 The first one will be used to illustrate Theorem 1 and Theorem 3, and the second example to do so with Theorems 1 and 2.

3.1 A Markov chain model for target cells and viral dynamics

Viruses are intra-cellular pathogens that infect cells in order to replicate. This means that the stochastic models typically considered to represent viral infection are inherently linked to multi-variate Markov chains that cannot be seen as competition processes. Here we consider a simple model of viral infection dynamics with cell proliferation,25 which consists of target cells T ( t ) $$ T(t) $$ , infected cells I V ( t ) $$ {I}_V(t) $$ , and extra-cellular virus V ( t ) $$ V(t) $$ at time t ≥ 0 $$ t\ge 0 $$ . These random variables lead to a Markov chain model Y = { ( T ( t ) , I V ( t ) , V ( t ) ) : t ≥ 0 } $$ \mathcal{Y}&#x0003D;\left\{\left(T(t),{I}_V(t),V(t)\right):t\ge 0\right\} $$ for viral infection (see Figure 1). In this model target cells get infected with rate β $$ \beta $$ , divide with rate γ $$ \gamma $$ , and die with rate μ T $$ {\mu}_T $$ . Infected cells produce virus (usually referred to as budding or bursting) with rate λ $$ \lambda $$ and die with rate μ I $$ {\mu}_I $$ . Viral particles decay with rate μ V $$ {\mu}_V $$ . This leads to the following non-vanishing infinitesimal transition rates:
q ( τ , ι , ν ) , ( τ ′ , ι ′ , ν ′ ) = β τ ν , if ( τ ′ , ι ′ , ν ′ ) = ( τ − 1 , ι + 1 , ν − 1 ) , μ T τ , if ( τ ′ , ι ′ , ν ′ ) = ( τ − 1 , ι , ν ) , μ I ι , if ( τ ′ , ι ′ , ν ′ ) = ( τ , ι − 1 , ν ) , μ V ν , if ( τ ′ , ι ′ , ν ′ ) = ( τ , ι , ν − 1 ) , γ τ , if ( τ ′ , ι ′ , ν ′ ) = ( τ + 1 , ι , ν ) , λ ι , if ( τ ′ , ι ′ , ν ′ ) = ( τ , ι , ν + 1 ) , $$ {q}_{\left(\tau, \iota, \nu \right),\left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)}\kern0.5em &#x0003D;\left\{\begin{array}{ll}\beta \tau \nu, &amp; \mathrm{if}\kern0.4em \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)&#x0003D;\left(\tau -1,\iota &#x0002B;1,\nu -1\right),\\ {}{\mu}_T\tau, &amp; \mathrm{if}\kern0.4em \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)&#x0003D;\left(\tau -1,\iota, \nu \right),\\ {}{\mu}_I\iota, &amp; \mathrm{if}\kern0.4em \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)&#x0003D;\left(\tau, \iota -1,\nu \right),\\ {}{\mu}_V\nu, &amp; \mathrm{if}\kern0.4em \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)&#x0003D;\left(\tau, \iota, \nu -1\right),\\ {}\gamma \tau, &amp; \mathrm{if}\kern0.4em \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)&#x0003D;\left(\tau &#x0002B;1,\iota, \nu \right),\\ {}\lambda \iota, &amp; \mathrm{if}\kern0.4em \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)&#x0003D;\left(\tau, \iota, \nu &#x0002B;1\right),\end{array}\right. $$
for states ( τ , ι , ν ) , ( τ ′ , ι ′ , ν ′ ) ∈ ℕ 0 3 $$ \left(\tau, \iota, \nu \right),\left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)\in {\mathbb{N}}_0&#x0005E;3 $$ with ( τ ′ , ι ′ , ν ′ ) ≠ ( τ , ι , ν ) $$ \left({\tau}&#x0005E;{\prime },{\iota}&#x0005E;{\prime },{\nu}&#x0005E;{\prime}\right)\ne \left(\tau, \iota, \nu \right) $$ , and q ( τ , ι , ν ) , ( τ , ι , ν ) = − ( ( γ + μ T ) τ + ( λ + μ I ) ι + ( β τ + μ V ) ν ) $$ {q}_{\left(\tau, \iota, \nu \right),\left(\tau, \iota, \nu \right)}&#x0003D;-\left(\left(\gamma &#x0002B;{\mu}_T\right)\tau &#x0002B;\left(\lambda &#x0002B;{\mu}_I\right)\iota &#x0002B;\left(\beta \tau &#x0002B;{\mu}_V\right)\nu \right) $$ , for ( τ , ι , ν ) ∈ ℕ 0 3 $$ \left(\tau, \iota, \nu \right)\in {\mathbb{N}}_0&#x0005E;3 $$ .
Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Diagram of a Markov chain model for viral infection dynamics [Colour figure can be viewed at wileyonlinelibrary.com]

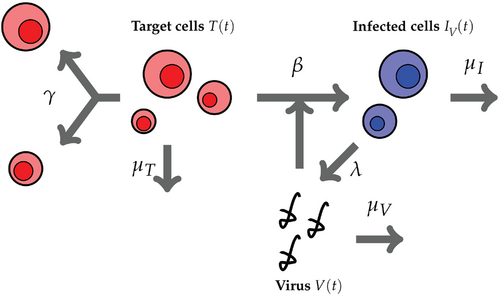
States in { ( τ , 0,0 ) : τ ∈ ℕ 0 } $$ \left\{\left(\tau, 0,0\right):\tau \in {\mathbb{N}}_0\right\} $$ are called infection-free states. An important question is whether the access of process Y $$ \mathcal{Y} $$ to any infection-free state is certain at late times. To answer this question, we first reformulate the process Y $$ \mathcal{Y} $$ as a bi-variate LD-QBD process X = { ( I ( t ) , J ( t ) ) : t ≥ 0 } $$ \mathcal{X}&#x0003D;\left\{\left(I(t),J(t)\right):t\ge 0\right\} $$ by letting the total size of the system, T ( t ) + I V ( t ) + V ( t ) $$ T(t)&#x0002B;{I}_V(t)&#x0002B;V(t) $$ , be the level variable I ( t ) $$ I(t) $$ , and the phase variable, J ( t ) $$ J(t) $$ , be suitably defined in such a way that the bi-variate subsets l A ( i ) $$ {l}_{\mathcal{A}}(i) $$ , for i ∈ ℕ 0 $$ i\in {\mathbb{N}}_0 $$ , and l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , correspond to the subsets { ( i , 0,0 ) } $$ \left\{\left(i,0,0\right)\right\} $$ and { ( τ , ι , ν ) ∈ ℕ 0 3 : τ + ι + ν = i , ι + ν ∈ ℕ } $$ \left\{\left(\tau, \iota, \nu \right)\in {\mathbb{N}}_0&#x0005E;3:\tau &#x0002B;\iota &#x0002B;\nu &#x0003D;i,\iota &#x0002B;\nu \in \mathbb{N}\right\} $$ , respectively. For example, bi-variate states ( i , j ) $$ \left(i,j\right) $$ of process X $$ \mathcal{X} $$ can be readily derived by labeling states ( τ , ι , ν ) ∈ l T ( i ) $$ \left(\tau, \iota, \nu \right)\in {l}_{\mathcal{T}}(i) $$ of the process Y $$ \mathcal{Y} $$ according to the lexicographical order.

By using the fact that λ i = a ( i − 1 ) + λ $$ {\lambda}_i&#x0003D;a\left(i-1\right)&#x0002B;\lambda $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , with a = max { λ , γ } $$ a&#x0003D;\max \left\{\lambda, \gamma \right\} $$ , an appeal to Theorem 1 with i 0 = 1 $$ {i}_0&#x0003D;1 $$ allows us to observe that X $$ \mathcal{X} $$ (equivalently, Y $$ \mathcal{Y} $$ ) is regular. In fact, we can also observe that the inequality
∑ i = 1 ∞ 1 λ i σ i ∑ i ′ = 1 i σ i ′ ≥ ∑ i = 1 ∞ 1 λ i $$ \sum \limits_{i&#x0003D;1}&#x0005E;{\infty}\frac{1}{\lambda_i{\sigma}_i}\sum \limits_{i&#x0005E;{\prime }&#x0003D;1}&#x0005E;i{\sigma}_{i&#x0005E;{\prime }}\ge \sum \limits_{i&#x0003D;1}&#x0005E;{\infty}\frac{1}{\lambda_i} $$
implies ∑ i = 1 ∞ ( λ i σ i ) − 1 ∑ i ′ = 1 i σ i ′ = ∞ $$ {\sum}_{i&#x0003D;1}&#x0005E;{\infty }{\left({\lambda}_i{\sigma}_i\right)}&#x0005E;{-1}{\sum}_{i&#x0005E;{\prime }&#x0003D;1}&#x0005E;i{\sigma}_{i&#x0005E;{\prime }}&#x0003D;\infty $$ , independently of the lineal incidence assumption for the death events. To determine whether the process X $$ \mathcal{X} $$ reaches the infection-free class of states at late times with certainty, we appeal to Theorem 3, from which it is established that the access to { ( τ , 0,0 ) : τ ∈ ℕ 0 } $$ \left\{\left(\tau, 0,0\right):\tau \in {\mathbb{N}}_0\right\} $$ is certain if the series ∑ i = 2 ∞ μ 2 ⋯ μ i λ 2 ⋯ λ i $$ {\sum}_{i&#x0003D;2}&#x0005E;{\infty}\frac{\mu_2\cdots {\mu}_i}{\lambda_2\cdots {\lambda}_i} $$ diverges. To be concrete, the inequalities μ i ≥ μ ∗ i $$ {\mu}_i\ge {\mu}_{\ast }i $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , with μ ∗ = min { μ T , μ I , μ V } $$ {\mu}_{\ast }&#x0003D;\min \left\{{\mu}_T,{\mu}_I,{\mu}_V\right\} $$ and
∑ i = 2 ∞ μ 2 ⋯ μ i λ 2 ⋯ λ i ≥ 1 λ ∑ i = 1 ∞ μ ∗ a i $$ \sum \limits_{i&#x0003D;2}&#x0005E;{\infty}\frac{\mu_2\cdots {\mu}_i}{\lambda_2\cdots {\lambda}_i}\ge \frac{1}{\lambda}\sum \limits_{i&#x0003D;1}&#x0005E;{\infty }{\left(\frac{\mu_{\ast }}{a}\right)}&#x0005E;i $$
imply that a sufficient condition for the process X $$ \mathcal{X} $$ to reach the infection-free class of states is a ≤ μ ∗ $$ a\le {\mu}_{\ast } $$ .
Furthermore, it is clear that
∑ i = 1 ∞ σ i ≤ ∑ i = 0 ∞ a μ ∗ i , $$ \sum \limits_{i&#x0003D;1}&#x0005E;{\infty }{\sigma}_i\le \sum \limits_{i&#x0003D;0}&#x0005E;{\infty }{\left(\frac{a}{\mu_{\ast }}\right)}&#x0005E;i, $$
which implies that X $$ \mathcal{X} $$ reaches an infection-free state with certainty in a finite mean time if a < μ ∗ $$ a&lt;{\mu}_{\ast } $$ . Specifically, the algebra used to derive a < μ ∗ $$ a&lt;{\mu}_{\ast } $$ as a sufficient condition for process X $$ \mathcal{X} $$ to reach the set of infection-free states in a finite mean time is based on the inequality
μ i ≥ min ( τ , ι , ν ) ∈ l T ( i ) { β τ ν } + μ ∗ i , i ∈ ℕ , $$ {\mu}_i\ge \underset{\left(\tau, \iota, \nu \right)\in {l}_{\mathcal{T}}(i)}{\min}\left\{\beta \tau \nu \right\}&#x0002B;{\mu}_{\ast }i,\kern0.30em i\in \mathbb{N}, $$
from which it follows that μ i ≥ μ ∗ i $$ {\mu}_i\ge {\mu}_{\ast }i $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ . More precise sufficient conditions could be then derived by evaluating μ i = min ( τ , ι , ν ) ∈ l T ( i ) { β τ ν + μ T τ + μ I ι + μ V ν } $$ {\mu}_i&#x0003D;{\min}_{\left(\tau, \iota, \nu \right)\in {l}_{\mathcal{T}}(i)}\left\{\beta \tau \nu &#x0002B;{\mu}_T\tau &#x0002B;{\mu}_I\iota &#x0002B;{\mu}_V\nu \right\} $$ in a more explicit form.

3.2 A Markov chain model of kinetic proof-reading by T cell receptors

In this example, we consider a Markov chain version of the ordinary differential equation model in previous studies26, 31-33 for kinetic proof-reading in T cell receptor signal transduction (Figure 2).

T cells are leukocytes which originate in the bone marrow and mature in the thymus, and play a central role in adaptive immune responses. During an infection T cells get activated and divide when the T cell receptors on their membrane (about 3 × 1 0 4 $$ 3\times 1{0}&#x0005E;4 $$ ) bind viral peptides (a short protein fragment) displayed on the membrane of professional immune cells, called antigen presenting cells (such as dendritic cells). The interaction between T cell receptors (TCRs) and viral peptides (or viral antigens) is the first step of a cellular immune response. This interaction needs to be specific and sensitive enough. Kinetic proof-reading has been proposed as a possible mechanism, which allows T cells to discriminate between foreign (i.e., viral) and self-antigens (derived from house-hold proteins). Kinetic proof-reading can explain, for example, how antigens of different affinities, when binding to TCRs, can potentially elicit qualitatively different intra-cellular responses.26

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Diagram of a Markov chain model of the kinetic proof-reading by T cell receptors (see McKeithan26)
The underlying multi-variate process Y = { ( T ( t ) , M x ( t ) , C 0 ( t ) , ⋯ , C N ( t ) ) : t ≥ 0 } $$ \mathcal{Y}&#x0003D;\left\{\left(T(t),{M}&#x0005E;x(t),{C}_0(t),\cdots, {C}_N(t)\right):t\ge 0\right\} $$ is defined in terms of the number T ( t ) $$ T(t) $$ of (unbound) TCR molecules on the surface of a T cell, the number M x ( t ) $$ {M}&#x0005E;x(t) $$ of extra-cellular x $$ x $$ -MHC peptides, the number C 0 ( t ) $$ {C}_0(t) $$ of nascent complexes (antigen bound to TCR), the number C s ( t ) $$ {C}_s(t) $$ of modified complexes at stage s $$ s $$ , for s ∈ { 1 , ⋯ , N − 1 } $$ s\in \left\{1,\cdots, N-1\right\} $$ , and the number C N ( t ) $$ {C}_N(t) $$ of active complexes at time t ≥ 0 $$ t\ge 0 $$ . The non-vanishing infinitesimal transition rates of process Y $$ \mathcal{Y} $$ have the form
q l , l ′ = k 1 τ m , if l ′ = ( τ − 1 , m − 1 , c 0 + 1 , c 1 , ⋯ , c N ) , μ T τ , if l ′ = ( τ − 1 , m , c 0 , ⋯ , c N ) , μ M m if l ′ = ( τ , m − 1 , c 0 , ⋯ , c N ) , μ C c s , if l ′ = ( τ , m , c 0 , ⋯ , c s − 1 , ⋯ , c N ) and s ∈ { 0 , ⋯ , N } , k p c s − 1 , if l ′ = ( τ , m , c 0 , ⋯ , c s − 1 − 1 , c s + 1 , ⋯ , c N ) and s ∈ { 1 , ⋯ , N } , k − 1 c s , if l ′ = ( τ + 1 , m + 1 , c 0 , ⋯ , c s − 1 , ⋯ , c N ) and s ∈ { 0 , ⋯ , N } , λ T , if l ′ = ( τ + 1 , m , c 0 , ⋯ , c N ) , λ M , if l ′ = ( τ , m + 1 , c 0 , ⋯ , c N ) , $$ {q}_{l,{l}&#x0005E;{\prime }}&#x0003D;\left\{\begin{array}{ll}{k}_1\tau m,&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau -1,m-1,{c}_0&#x0002B;1,{c}_1,\cdots, {c}_N\right),\\ {}{\mu}_T\tau, &amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau -1,m,{c}_0,\cdots, {c}_N\right),\\ {}{\mu}_Mm&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau, m-1,{c}_0,\cdots, {c}_N\right),\\ {}{\mu}_C{c}_s,&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau, m,{c}_0,\cdots, {c}_s-1,\cdots, {c}_N\right)\kern0.4em \mathrm{and}\kern0.4em s\in \left\{0,\cdots, N\right\},\\ {}{k}_p{c}_{s-1},&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau, m,{c}_0,\cdots, {c}_{s-1}-1,{c}_s&#x0002B;1,\cdots, {c}_N\right)\kern0.4em \mathrm{and}\kern0.4em s\in \left\{1,\cdots, N\right\},\\ {}{k}_{-1}{c}_s,&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau &#x0002B;1,m&#x0002B;1,{c}_0,\cdots, {c}_s-1,\cdots, {c}_N\right)\kern0.4em \mathrm{and}\kern0.4em s\in \left\{0,\cdots, N\right\},\\ {}{\lambda}_T,&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau &#x0002B;1,m,{c}_0,\cdots, {c}_N\right),\\ {}{\lambda}_M,&amp; \mathrm{if}\kern0.4em {l}&#x0005E;{\prime }&#x0003D;\left(\tau, m&#x0002B;1,{c}_0,\cdots, {c}_N\right),\end{array}\right. $$ (10)
for states l , l ′ ∈ ℕ 0 N + 3 $$ l,{l}&#x0005E;{\prime}\in {\mathbb{N}}_0&#x0005E;{N&#x0002B;3} $$ with l ′ ≠ l $$ {l}&#x0005E;{\prime}\ne l $$ , and q l , l = − k 1 τ m − μ T τ − μ M m − ( μ C + k − 1 ) ∑ s = 0 N c s − k p ∑ s = 0 N − 1 c s − λ T − λ M $$ {q}_{l,l}&#x0003D;-{k}_1\tau m-{\mu}_T\tau -{\mu}_Mm-\left({\mu}_C&#x0002B;{k}_{-1}\right){\sum}_{s&#x0003D;0}&#x0005E;N{c}_s-{k}_p{\sum}_{s&#x0003D;0}&#x0005E;{N-1}{c}_s-{\lambda}_T-{\lambda}_M $$ , for l ∈ ℕ 0 N + 3 $$ l\in {\mathbb{N}}_0&#x0005E;{N&#x0002B;3} $$ , with l = ( τ , m , c 0 , ⋯ , c N ) $$ l&#x0003D;\left(\tau, m,{c}_0,\cdots, {c}_N\right) $$ .

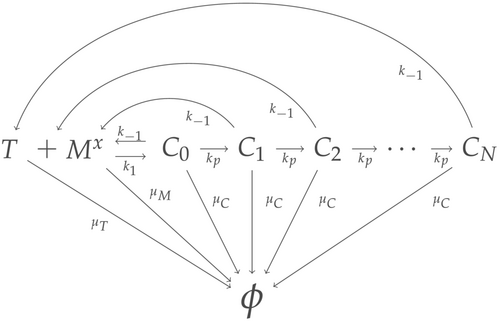
In (10), λ T $$ {\lambda}_T $$ is the TCR synthesis rate, λ M $$ {\lambda}_M $$ is the arrival rate of x $$ x $$ -MHC peptides to the proximity of the T cell, k 1 $$ {k}_1 $$ is the binding rate between antigen ( x $$ x $$ -MHC peptide) and a free (unbound) TCR, k − 1 $$ {k}_{-1} $$ is the bound antigen-TCR complex dissociation rate, k p $$ {k}_p $$ is the rate at which complexes are modified (i.e., towards activation, such as the rate of phosphorylation), and μ T $$ {\mu}_T $$ , μ M $$ {\mu}_M $$ and μ C $$ {\mu}_C $$ are the respective internalization (or degradation) rates for free TCR, x $$ x $$ -MHC peptides and bound TCR complexes.

We now make use of the results from Section 2. To that end the bi-variate process X $$ \mathcal{X} $$ can be formulated from Y $$ \mathcal{Y} $$ by using the level variable I ( t ) = T ( t ) + M x ( t ) + ∑ s = 0 N C s ( t ) $$ I(t)&#x0003D;T(t)&#x0002B;{M}&#x0005E;x(t)&#x0002B;{\sum}_{s&#x0003D;0}&#x0005E;N{C}_s(t) $$ and an appropriate phase variable, J ( t ) $$ J(t) $$ , such that the bi-variate subsets l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , correspond to the class of states ( τ , m , c 0 , ⋯ , c N ) ∈ ℕ 0 N + 3 : τ + m + ∑ s = 0 N c s = i $$ \left\{\left(\tau, m,{c}_0,\cdots, {c}_N\right)\in {\mathbb{N}}_0&#x0005E;{N&#x0002B;3}:\tau &#x0002B;m+{\sum}_{s&#x0003D;0}&#x0005E;N{c}_s&#x0003D;i\right\} $$ . Then, it is easy to show that λ i = λ T + λ M + k − 1 i $$ {\lambda}_i&#x0003D;{\lambda}_T&#x0002B;{\lambda}_M&#x0002B;{k}_{-1}i $$ and μ i ≥ μ ∗ i $$ {\mu}_i\ge {\mu}_{\ast }i $$ , for i ∈ ℕ $$ i\in \mathbb{N} $$ , where μ ∗ = min { μ T , μ M , μ C } $$ {\mu}_{\ast }&#x0003D;\min \left\{{\mu}_T,{\mu}_M,{\mu}_C\right\} $$ .

The regularity of the process X $$ \mathcal{X} $$ follows from Theorem 1 by noting that i 0 = 1 $$ {i}_0&#x0003D;1 $$ and ∑ i = 1 ∞ ( λ i σ i ) − 1 ∑ i ′ = 1 i σ i ′ = ∞ $$ {\sum}_{i&#x0003D;1}&#x0005E;{\infty }{\left({\lambda}_i{\sigma}_i\right)}&#x0005E;{-1}{\sum}_{i&#x0005E;{\prime }&#x0003D;1}&#x0005E;i{\sigma}_{i&#x0005E;{\prime }}&#x0003D;\infty $$ , since ∑ i = 1 ∞ ( λ i σ i ) − 1 ∑ i ′ = 1 i σ i ′ ≥ ∑ i = 1 ∞ λ i − 1 $$ {\sum}_{i&#x0003D;1}&#x0005E;{\infty }{\left({\lambda}_i{\sigma}_i\right)}&#x0005E;{-1}{\sum}_{i&#x0005E;{\prime }&#x0003D;1}&#x0005E;i{\sigma}_{i&#x0005E;{\prime }}\ge {\sum}_{i&#x0003D;1}&#x0005E;{\infty }{\lambda}_i&#x0005E;{-1} $$ . As in the previous example, the divergence of the series ∑ i = 1 ∞ ( λ i σ i ) − 1 ∑ i ′ = 1 i σ i ′ $$ {\sum}_{i&#x0003D;1}&#x0005E;{\infty }{\left({\lambda}_i{\sigma}_i\right)}&#x0005E;{-1}{\sum}_{i&#x0005E;{\prime }&#x0003D;1}&#x0005E;i{\sigma}_{i&#x0005E;{\prime }} $$ does not depend on the lineal incidence assumption for the degradation events. Moreover, Theorem 2 leads to the inequality k − 1 < μ ∗ $$ {k}_{-1}&lt;{\mu}_{\ast } $$ as a sufficient condition for the positive recurrence of X $$ \mathcal{X} $$ , since the convergence of the series ∑ i = 1 ∞ σ i $$ {\sum}_{i&#x0003D;1}&#x0005E;{\infty }{\sigma}_i $$ is equivalent to the convergence of the hypergeometric series 2 F 1 λ T + λ M k − 1 , 1 ; 1 ; k − 1 μ ∗ $$ {}_2{F}_1\left(\frac{\lambda_T&#x0002B;{\lambda}_M}{k_{-1}},1;1;\frac{k_{-1}}{\mu_{\ast }}\right) $$ .

4 CONCLUSIONS

In this paper we have generalized the results by Reuter1 and Iglehart3 to a wider class of LD-QBDs. We note that, as in the case of a competition process,3 direct transitions from non-absorbing states ( i , j ) ∈ l T ( i ) $$ \left(i,j\right)\in {l}_{\mathcal{T}}(i) $$ , with i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0&#x0002B;1,\cdots \right\} $$ , to other states in l ( i ) \ { ( i , j ) } $$ l(i)\backslash \left\{\left(i,j\right)\right\} $$ can be arbitrarily defined as far as regularity, positive recurrence and absorption with certainty in a finite mean time are concerned. This remark is closely related to the use of the uni-variate birth-death process X ′ $$ {\mathcal{X}}&#x0005E;{\prime } $$ and, more particularly, the fact that subsets l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , for i ∈ { i 0 , i 0 + 1 , ⋯ } $$ i\in \left\{{i}_0,{i}_0&#x0002B;1,\cdots \right\} $$ , are finite. In the case of infinitely-many states in l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ , the approach should necessarily incorporate transitions between points belonging to the same level into the underlying arguments, and this is the aim of future work.

The sufficient conditions in Theorems 1–3 are inherently linked to the labeling of states used for process X $$ \mathcal{X} $$ to have a finite number of phases per level and a block-tridiagonal matrix structure of its q $$ q $$ -matrix on the set T $$ \mathcal{T} $$ of non-absorbing states. Since the maximum rates λ i $$ {\lambda}_i $$ of upcrossing and the minimum rates μ i $$ {\mu}_i $$ of downcrossing depend on how subsets l T ( i ) $$ {l}_{\mathcal{T}}(i) $$ are defined, a certain labeling of states can lead to a sufficient condition—for either regularity or positive recurrence or absorption with certainty in a finite mean time—which could be different from its counterpart when another labeling of states is considered. This fact makes it difficult to study, in a general setting, whether the sufficient conditions in Theorems 1–3 may also be necessary for any labeling of states in some situations.

ACKNOWLEDGEMENT

The authors thank the editor and two anonymous referees for their constructive comments, which have improved the presentation of the paper. This research was supported by Ministerio de Ciencia e Innovación (Spanish Ministry of Science and Innovation), project PGC2018-097704-B-I00. JL was supported by an EPSRC-funded PhD studentship in partnership with the UK Ministry of Defence, Defence Science and Technology Laboratory (Dstl), project reference 1954851. The authors would like to thank Dr. Joseph J. Gillard (Dstl) for insightful discussions on viral dynamics. This manuscript has been internally reviewed at Los Alamos National Laboratory, and assigned the reference number LA-UR-22-21839.

    CONFLICT OF INTEREST

    The authors declare no potential conflict of interest.

    • * There is no real loss of generality in assuming that level l ( 0 ) $$ l(0) $$ consists of one state. Otherwise, we could re-define levels l ( 0 ) $$ l(0) $$ and l ( 1 ) $$ l(1) $$ so as to consist of { ( 0,1 ) } $$ \left\{\left(0,1\right)\right\} $$ and { ( 0 , j ) : j ∈ { 2 , ⋯ , M 0 } } ∪ l ( 1 ) $$ \left\{\left(0,j\right):j\in \left\{2,\cdots, {M}_0\right\}\right\}\cup l(1) $$ , respectively, so that l ( 0 ) $$ l(0) $$ has a single state.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.