Mathematische Nachrichten
Volume 298, Issue 1 pp. 244-281
ORIGINAL ARTICLE
Open Access

Polyharmonic fields and Liouville quantum gravity measures on tori of arbitrary dimension: From discrete to continuous

Lorenzo Dello Schiavo, 

Lorenzo Dello Schiavo

Institute of Science and Technology Austria, Klosterneuburg, Austria

Search for more papers by this author
Ronan Herry, 

Ronan Herry

IRMAR, Université de Rennes, Général Leclerc, Rennes Cedex, France

Search for more papers by this author
Eva Kopfer, 

Eva Kopfer

Institute for Applied Mathematics, University of Bonn, Bonn, Germany

Search for more papers by this author
Karl-Theodor Sturm, 

Corresponding Author

Karl-Theodor Sturm

Institute for Applied Mathematics, University of Bonn, Bonn, Germany

Correspondence

Karl-Theodor Sturm, Institute for Applied Mathematics, University of Bonn, Bonn, Germany.

Email: [email protected]

Search for more papers by this author
First published: 27 November 2024
https://doi.org/10.1002/mana.202400169
Citations: 1

Abstract

For an arbitrary dimension n $n$ , we study:

  • the polyharmonic Gaussian field h L $h_L$ on the discrete torus T L n = 1 L Z n / Z n $\mathbb {T}^n_L = \frac{1}{L} \mathbb {Z}^{n} / \mathbb {Z}^{n}$ , that is the random field whose law on R T L n $\mathbb {R}^{\mathbb {T}^{n}_{L}}$ given by
    c n e − b n ( − Δ L ) n / 4 h 2 d h , $$\begin{equation*} \hspace*{-4.5pc}c_n\, \text{e}^{-b_n{\left\Vert (-\Delta _L)^{n/4}h\right\Vert} ^2} dh, \end{equation*}$$
    where d h $dh$ is the Lebesgue measure and Δ L $\Delta _{L}$ is the discrete Laplacian;
  • the associated discrete Liouville quantum gravity (LQG) measure associated with it, that is, the random measure on T L n $\mathbb {T}^{n}_{L}$
    μ L ( d z ) = exp γ h L ( z ) − γ 2 2 E h L ( z ) d z , $$\begin{equation*} \hspace*{-7.5pc}\mu _{L}(dz) = \exp {\left(\gamma h_L(z) - \frac{\gamma ^{2}}{2} \mathbf {E} h_{L}(z) \right)} dz, \end{equation*}$$
    where γ $\gamma$ is a regularity parameter.
As L → ∞ $L\rightarrow \infty$ , we prove convergence of the fields h L $h_L$ to the polyharmonic Gaussian field h $h$ on the continuous torus T n = R n / Z n $\mathbb {T}^n = \mathbb {R}^{n} / \mathbb {Z}^{n}$ , as well as convergence of the random measures μ L $\mu _L$ to the LQG measure μ $\mu$ on T n $\mathbb {T}^n$ , for all γ < 2 n $\left|\gamma \right| < \sqrt {2n}$ .

1 INTRODUCTION

We study Gaussian random fields and the associated Liouville quantum gravity (LQG) measures on continuous and discrete tori of arbitrary dimension. The random field h $h$ on the continuous torus is a particular case of the copolyharmonic field introduced and analyzed in detail in [5] in great generality on all ‘admissible’ manifolds of even dimension. One of the main goals now is to study the approximation of these fields and the associated LQG measures by their discrete counterparts.

The polyharmonic fields h $h$ on T n ≅ [ 0 , 1 ) n $\mathbb {T}^n\cong [0,1)^n$ and h L $h_L$ on T L n ≅ { 0 , 1 L , … , L − 1 L } n $\mathbb {T}^n_L\cong \lbrace 0,\frac{1}{L},\ldots, \frac{L-1}{L}\rbrace ^n$ for L ∈ N $L\in {\mathbb {N}}$ are centered Gaussian random fields with covariance functions
E h ( x ) h ( y ) = k ( x , y ) ≔ 1 a n G ˚ n / 2 ( x , y ) , E h L ( x ) h L ( y ) = k L ( x , y ) ≔ 1 a n G ˚ L n / 2 ( x , y ) . $$\begin{align*} \mathbf {E}{\left[h(x)\,h(y)\right]}&=k(x,y)\coloneqq \frac{1}{a_n}\, \mathring{G}^{n/2}(x,y)\,\,\mathrm{,}\;\,\\[-4pt] \mathbf {E}{\left[h_L(x)\,h_L(y)\right]}&=k_L(x,y)\coloneqq \frac{1}{a_n}\, \mathring{G}_L^{n/2}(x,y)\,\,\mathrm{.} \end{align*}$$
given in terms of the integral kernel for the ‘grounded’ inverse of the (continuous and discrete, resp.) poly-Laplacian ( − Δ ) n / 2 $(-\Delta)^{n/2}$ and ( − Δ L ) n / 2 $(-\Delta _L)^{n/2}$ , and a normalization constant a n ≔ 2 Γ ( n / 2 ) ( 4 π ) n / 2 $a_n\coloneqq \frac{2}{\Gamma (n/2)\, (4\pi)^{n/2}}$ . Here and below,  ( − Δ ) s / 2 $(-\Delta)^{s/2}$ is, for every  s > 0 $s>0$ , the power of the Laplacian defined by means of the spectral theorem for self-adjoint operators on  L 2 ( T n ) $L^2(\mathbb {T}^n)$ . Its discrete counterpart  ( − Δ L ) s / 2 $(-\Delta _L)^{s/2}$ may be defined in the same way.

In particular, with the above choice of the normalization constant  a n $a_n$ ,

Lemma 1.1. (See Lemma 2.4)

| k ( x , y ) − log 1 d ( x , y ) | ≤ C . $$\begin{equation*} \Big |k(x,y)-\log \frac{1}{d(x,y)}\Big |\le C \,\,\mathrm{.} \end{equation*}$$

1.1 Characterization of the discrete polyharmonic field

Let n , L ∈ N $n,L\in {\mathbb {N}}$ be given and assume for convenience that L $L$ is odd, let Z L n = { − L − 1 2 , − L − 1 2 + 1 , … , L − 1 2 } n ${\mathbb {Z}}^n_L=\lbrace -\frac{L-1}{2},-\frac{L-1}{2}+1,\ldots, \frac{L-1}{2}\rbrace ^n$ , and set N ≔ L n $N\coloneqq L^n$ and
c n ≔ a n 2 π N N − 1 2 · ∏ z ∈ Z L n ∖ { 0 } 4 L 2 ∑ k = 1 n sin 2 π z k / L n / 4 . $$\begin{equation*} c_n\coloneqq {\left(\frac{a_n}{2\pi N}\right)}^{\frac{N-1}{2}}\cdot \prod _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace }{\left(4L^2\,\sum _{k=1}^n \sin ^2{\left(\pi z_k/L\right)}\right)}^{n/4} \,\,\mathrm{.} \end{equation*}$$
Define the measure ν ̂ ( h ) $\widehat{\bm{\nu }}(h)$ on R N ≅ R T L n ${\mathbb {R}}^{N}\cong {\mathbb {R}}^{\mathbb {T}_L^n}$ by
d ν ̂ ( h ) ≔ c n e − a n 2 N ∥ ( − Δ L ) n / 4 h ∥ 2 d L N ( h ) , $$\begin{equation*} d\widehat{\bm{\nu }}(h)\coloneqq c_n\,\text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}h\Vert ^2}\,d\mathcal {L}^N(h)\,\,\mathrm{,}\;\, \end{equation*}$$
and denote by ν $\bm{\nu }$ its push forward under the map
h ↦ h ˚ , h ˚ v ≔ h v − 1 N ∑ v = 1 N h v . $$\begin{equation*} h\mapsto \mathring{h}, \qquad \mathring{h}_v\coloneqq h_v-\frac{1}{N} \sum _{v=1}^{N} h_v \,\,\mathrm{.} \end{equation*}$$
In other words, ν = ν ̂ · | ∑ v = 1 N h v = 0 $\bm{\nu }=\widehat{\bm{\nu }}\left({\,\cdot \,}\big\vert \sum _{v=1}^{N} h_v=0\right)$ .
Furthermore,
T ˚ ∗ ν = P ˚ and T ˚ ∗ − 1 P ˚ = ν , $$\begin{equation*} \mathring{T}_*\bm{\nu }=\mathring{\mathbf {P}}\qquad \text{and}\qquad \mathring{T}^{-1}_*\mathring{\mathbf {P}}= \bm{\nu }\,\,\mathrm{,}\;\, \end{equation*}$$
where P ˚ $\mathring{\mathbf {P}}$ denotes the distribution of the ‘grounded white noise’ on T L n ${\mathbb {T}_L^n}$ , explicitly given as
d P ˚ ( Ξ ) = 1 ( 2 π ) N − 1 2 e − 1 2 N ∥ Ξ ∥ 2 d L H N − 1 ( Ξ ) $$\begin{equation*} d\mathring{\mathbf {P}}(\Xi)= \frac{1}{(2\pi)^{\frac{N-1}{2}}}\,\text{e}^{-\frac{1}{2N}\Vert \Xi \Vert ^2}\,d\mathcal {L}^{N-1}_H(\Xi) \end{equation*}$$
on the hyperplane H = { Ξ ∈ R N : ∑ v = 1 N Ξ v = 0 } $H=\lbrace \Xi \in {\mathbb {R}}^N: \ \sum _{v=1}^{N} \Xi _v=0\rbrace$ , and where
T ˚ : h ↦ Ξ = a n ( − Δ L ) n / 4 h , T ˚ − 1 : Ξ ↦ h = 1 a n G ˚ L n / 4 Ξ . $$\begin{equation*} \mathring{T}: h\mapsto \Xi =\sqrt {a_n}\, (-\Delta _L)^{n/4}h\,\,\mathrm{,}\;\,\qquad \mathring{T}^{-1}: \Xi \mapsto h=\frac{1}{\sqrt {a_n}}\, \mathring{G}_L^{n/4}\Xi \,\,\mathrm{.} \end{equation*}$$

Theorem 1.2. (cf. Theorem 3.4)The distribution of the discrete polyharmonic field on T L n ${\mathbb {T}_L^n}$ is given by the probability measure ν $\bm{\nu }$ on R T L n ≅ R N ${\mathbb {R}}^{\mathbb {T}_L^n}\cong {\mathbb {R}}^N$ .

1.2 Convergence of the random fields

As L → ∞ $L\rightarrow \infty$ , the polyharmonic fields h L $h_L$ on the discrete tori converge to the polyharmonic field h $h$ on the continuous torus. This convergence of the fields, indeed, holds in great generality.

For a precise formulation, one either has to specify classes of test functions on T n $\mathbb {T}^n$ which admit traces on T L n $\mathbb {T}^n_L$ , or unique ways of extending functions on T L n $\mathbb {T}^n_L$ onto T n $\mathbb {T}^n$ .

Theorem 1.3. (Thm. 4.11, Thm. 4.12)For all f ∈ ⋃ s > n / 2 H ˚ s ( T n ) $f\in \bigcup _{s>n/2}\mathring{H}^{s}(\mathbb {T}^n)$ ,

⟨ h L , f ⟩ T L n → ⟨ h , f ⟩ T n , ⟨ h L , ♭ , f ⟩ T n → ⟨ h , f ⟩ T n , in L 2 ( P ) as L → ∞ , $$\begin{equation*} \begin{aligned} {\langle h_L,f\rangle} _{\mathbb {T}^n_L} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \,\,\mathrm{,}\;\,\\ { {\langle h_{L,\flat },f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n}\,\,\mathrm{,}\;\,} \end{aligned} \qquad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{,}\;\, \end{equation*}$$
where  h L , ♭ $h_{L,\flat }$ denotes the piecewise constant extension to  T n $\mathbb {T}^n$ of  h L $h_L$ .

Let D L ⊂ C ∞ ( T n ) $\mathcal {D}_L\subset \mathcal {C}^\infty (\mathbb {T}^n)$ denote the linear span of the eigenfunctions φ z $\varphi _z$ for the negative Laplacian with associated eigenvalues 0 < λ z < ( L π ) 2 $0<\lambda _z<(L\pi)^2$ , or more explicitly,
D L ≔ f : f ( x ) = ∑ z ∈ Z L n α z cos ( 2 π x · z ) + β z sin ( 2 π x · z ) , α z , β z ∈ R . $$\begin{equation*} \mathcal {D}_L\coloneqq {\left\lbrace f: \ f(x)=\sum _{z\in {\mathbb {Z}}^n_L}{\left[ \alpha _z\cos (2\pi x\cdot z)+\beta _z\sin (2\pi x\cdot z)\right]},\ \alpha _z,\beta _z\in {\mathbb {R}}\right\rbrace} \,\,\mathrm{.} \end{equation*}$$

Theorem 1.4. (Thm. 4.13, Prop. 4.5)For all f ∈ H ˚ − n / 2 ( T n ) $f\in \mathring{H}^{-n/2}(\mathbb {T}^n)$ ,

⟨ h L , ♯ , f ⟩ T n → ⟨ h , f ⟩ T n , ⟨ h ♯ , L , f ⟩ T n → ⟨ h , f ⟩ T n , in L 2 ( P ) as L → ∞ , $$\begin{equation*} \begin{aligned} {\langle h_{L,\sharp },f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \,\,\mathrm{,}\;\,\\ {{\langle h_{\sharp,L},f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n}}\,\,\mathrm{,}\;\,\end{aligned} \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{,}\;\, \end{equation*}$$
where h L , ♯ ω $h_{L,\sharp }^\omega$ denotes, for every ω $\omega$ , the unique function in D L $\mathcal {D}_L$ which coincides with h L ω $h_L^\omega$ on T L n $\mathbb {T}^n_L$ , and  h ♯ , L $h_{\sharp, L}$ is the Fourier projection (23) of  h $h$ at scale  L $L$ .

The same convergence assertion also holds for the so-called spectrally reduced polyharmonic field  h L − ∘ $h_L^{{-\circ }}$ on T L n $\mathbb {T}^n_L$ given in terms of the eigenbasis { φ z } z ∈ Z L n $\lbrace \varphi _z\rbrace _{z\in {\mathbb {Z}}^n_L}$ of the discrete Laplacian Δ L $\Delta _L$ as
h L − ∘ ( x ) ≔ ∑ z ∈ Z L n L 2 π 2 | z | 2 ∑ k = 1 n sin 2 ( π z k / L ) − n / 4 ⟨ h L | φ z ⟩ T L n · φ z ( x ) . $$\begin{equation*} h^{{-\circ }}_L(x)\coloneqq \sum _{z\in {\mathbb {Z}}^n_L} {\left(\frac{L^2}{\pi ^2|z|^2}\sum _{k=1}^n \sin ^2(\pi z_k/L)\right)}^{-n/4}\, {\langle h_L| \varphi _z\rangle} _{\mathbb {T}^n_L}\cdot \varphi _z(x)\,\,\mathrm{.} \end{equation*}$$

Our convergence results apply to the case of arbitrary dimension  n $n$ . In dimension  n ≤ 4 $n\le 4$ , several results are available in the literature for the convergence of other discrete fractional Gaussian fields of integer order to the corresponding counterpart in the continuum, including, for example, the odometer for the sandpile model, or the membrane model. For a comparison of these results with those in this work, see Section 4.4.

1.3 Convergence of the random measures

The convergence questions for the associated random measures are more subtle. Again, of course, one expects that the Liouville measure  μ L $\mu _L$ on the discrete tori converge as  L → ∞ $L\rightarrow \infty$ to the Liouville measure μ $\mu$ on the continuous torus. This convergence of the random measure, however, only holds for small parameters γ $\gamma$ .

Theorem 1.5. (cf. Thm. 5.5)Assume | γ | < n e $|\gamma |<{\sqrt{\frac{n}{e}}}$ , and let a $a$ be an odd integer ≥ 2 $\ge 2$ . Then, in the sense of Definition 5.2,

μ a ℓ → μ as ℓ → ∞ . $$\begin{equation*} \mu _{a^\ell }\rightarrow \mu \qquad \text{as }\ell \rightarrow \infty \,\,\mathrm{.} \end{equation*}$$

Analogous convergence results hold for the random measures associated with the Fourier extensions of the discrete polyharmonic fields and the reduced discrete polyharmonic field, in the latter case even in the whole range of subcriticality γ ∈ ( − 2 n , 2 n ) $\gamma \in (-\sqrt {2n},\sqrt {2n})$ .

Theorem 1.6. (cf. Thm. 5.3)If  | γ | < n e $|\gamma |<{\sqrt {\frac{n}{e}}}$ , then in the sense of Definition 5.2,

μ L , ♯ → μ as L → ∞ , $$\begin{equation*} \mu _{L,\sharp }\rightarrow \mu \qquad \text{as }L\rightarrow \infty \,\,\mathrm{,}\;\, \end{equation*}$$
and for | γ | < 2 n $|\gamma |< {\sqrt {2n}}$ , again in the sense of Definition 5.2,
μ L , ♯ − ∘ → μ as L → ∞ . $$\begin{equation*} \mu ^{{-\circ }}_{L,\sharp }\rightarrow \mu \qquad \text{as }L\rightarrow \infty \,\,\mathrm{.} \end{equation*}$$

1.4 Uniform integrability of the random measures

As an auxiliary result of independent interest, we provide a direct proof of the uniform integrability of (discrete, semi-discrete, and continuous) random measures on the multidimensional torus.

Theorem 1.7. (cf. Thm. 5.6)Assume that | γ | < n e $|\gamma |< {}\sqrt{\frac{n}{e}}$ . Then

sup L E | μ L ( T L n ) | 2 < ∞ $$\begin{equation*} \sup _L\mathbf {E}{\left[\big\vert \mu _L(\mathbb {T}^n_L)\big\vert ^2\right]}<\infty \end{equation*}$$
and
sup L E | μ L , ♯ ( T n ) | 2 < ∞ . $$\begin{equation*} \sup _L\mathbf {E}{\left[\big\vert \mu _{L,\sharp }(\mathbb {T}^n)\big\vert ^2\right]}<\infty \,\,\mathrm{.} \end{equation*}$$

2 LAPLACIAN AND KERNELS ON CONTINUOUS AND DISCRETE TORI

2.1 Laplacian and kernels on the continuous torus

(a)

For n ∈ N $n\in {\mathbb {N}}$ , we denote by T n ≔ R / Z n $\mathbb {T}^n\coloneqq \left({\mathbb {R}}/{\mathbb {Z}}\right)^n$ the continuous n $n$ -torus. Where it seems helpful, one can always think of the torus T n $\mathbb {T}^n$ as the set [ 0 , 1 ) n ⊂ R n $[0,1)^n\subset {\mathbb {R}}^n$ . It inherits from R n ${\mathbb {R}}^n$ the additive group structure and the Lebesgue measure, denoted in the following by d L n ( x ) $d\mathcal {L}^n(x)$ or simply by d x $dx$ . The distance on T n $\mathbb {T}^n$ is given by
d ( x , y ) ≔ ∑ k = 1 n | x k − y k | ∧ | 1 − x k + y k | 2 1 / 2 . $$\begin{equation*} d(x,y)\coloneqq {\left(\sum _{k=1}^n {\left(|x_k-y_k|\wedge |1-x_k+y_k| \right)}^2\right)}^{1/2} \,\,\mathrm{.} \end{equation*}$$

(b)

For z ∈ Z n $z\in {\mathbb {Z}}^n$ and x ∈ T n $x\in \mathbb {T}^n$ put
Φ z ( x ) ≔ exp 2 π i z · x . $$\begin{equation*} \Phi _z(x)\coloneqq \exp {\left(2\pi \text{i}\, z\cdot x\right)} \,\,\mathrm{.} \end{equation*}$$
The family ( Φ z ) z ∈ Z n $(\Phi _z)_{z\in {\mathbb {Z}}^n}$ is a complete ON basis of L C 2 ( T n ) $L^2_{\mathbb {C}}(\mathbb {T}^n)$ . It consists of eigenfunctions of the negative Laplacian − Δ = − ∑ k = 1 n ∂ 2 ∂ x k 2 $-\Delta =-\sum _{k=1}^n\frac{\partial ^2}{\partial x^2_k}$ on T n $\mathbb {T}^n$ with corresponding eigenvalues given by
λ z ≔ ( 2 π | z | ) 2 . $$\begin{equation*} \lambda _z\coloneqq (2\pi |z|)^2\,\,\mathrm{.} \end{equation*}$$

(c)

The Fourier transform of the function f ∈ L C 2 ( T n ) $f\in L^2_{\mathbb {C}}(\mathbb {T}^n)$ is the function (or “sequence”) g ∈ ℓ 2 ( Z n ) $g\in \ell ^2({\mathbb {Z}}^n)$ given by
g ( z ) ≔ ⟨ f , Φ z ⟩ T n ≔ ∫ T n f ( x ) Φ ¯ z ( x ) d x . $$\begin{equation*} g(z)\coloneqq {\langle f,\Phi _z\rangle} _{\mathbb {T}^n}\coloneqq \int _{\mathbb {T}^n} f(x)\, \overline{\Phi }_z(x)\,dx\,\,\mathrm{.} \end{equation*}$$
Conversely, for g $g$ as above and a.e.  x ∈ T n $x\in \mathbb {T}^n$ ,
f ( x ) = ∑ z ∈ Z n g ( z ) Φ z ( x ) . $$\begin{equation*} f(x)=\sum _{z\in {\mathbb {Z}}^n} g(z) \Phi _z(x) \,\,\mathrm{.} \end{equation*}$$

(d)

To obtain a complete ON basis ( φ z ) z ∈ Z n $(\varphi _z)_{z\in {\mathbb {Z}}^n}$ for the real L 2 $L^2$ -space, choose a subset Z ̂ n $\hat{{\mathbb {Z}}}^n$ of Z n ∖ { 0 } ${\mathbb {Z}}^n\setminus \lbrace 0\rbrace$ with
Z n ∖ { 0 } = Z ̂ n ⊔ − Z ̂ n , $$\begin{equation*} {\mathbb {Z}}^n\setminus \lbrace 0\rbrace =\hat{{\mathbb {Z}}}^n\ \sqcup \ {\left(-\hat{{\mathbb {Z}}}^n\right)}\,\,\mathrm{,}\;\, \end{equation*}$$
and define
φ z ( x ) ≔ 1 2 Φ z + Φ − z ( x ) = 2 cos 2 π z · x if z ∈ Z ̂ n , 1 2 i Φ z − Φ − z ( x ) = 2 sin 2 π z · x if z ∈ − Z ̂ n , 1 if z = 0 . $$\begin{equation*} \varphi _z(x)\coloneqq {\begin{cases} \frac{1}{\sqrt 2}{\left(\Phi _z+\Phi _{-z}\right)}(x)=\sqrt 2\, \cos {\left(2\pi \,z\cdot x\right)}\quad &\text{if }z\in \hat{{\mathbb {Z}}}^n\,\,\mathrm{,}\;\,\\[10pt] \frac{1}{\sqrt 2\, i}{\left(\Phi _z-\Phi _{-z}\right)}(x)=\sqrt 2\, \sin {\left(2\pi \,z\cdot x\right)}\quad &\text{if }z\in -\hat{{\mathbb {Z}}}^n\,\,\mathrm{,}\;\,\\[10pt] {\bf 1}&\text{if }z=0 \,\,\mathrm{.} \end{cases}} \end{equation*}$$

(e)

Functions f $f$ on T n $\mathbb {T}^n$ will be called grounded if ∫ f d L n = 0 $\int f\,d\mathcal {L}^n=0$ . Let  L ˚ 2 ( T n ) $\mathring{L}^2(\mathbb {T}^n)$ be the subspace of  L 2 ( T n ) $L^2(\mathbb {T}^n)$ consisting of all grounded functions. For  s > 0 $s>0$ , we denote by  H ˚ s $\mathring{H}^s$ the grounded Sobolev space defined as
H ˚ s ( T n ) ≔ ( − Δ ) − s / 2 L ˚ 2 ( T n ) with norm f H ˚ s ≔ ∥ ( − Δ ) s / 2 f ∥ L 2 $$\begin{equation*} \mathring{H}^s(\mathbb {T}^n)\coloneqq (-\Delta)^{-s/2} \mathring{L}^2(\mathbb {T}^n) \qquad \text{with norm} \quad {\left\Vert f\right\Vert} _{\mathring{H}^s}\coloneqq \big \Vert (-\Delta)^{s/2}f\big \Vert _{L^2} \end{equation*}$$
and we define  H ˚ − s ( T n ) $\mathring{H}^{-s}(\mathbb {T}^n)$ as the completion of  L ˚ 2 ( T n ) $\mathring{L}^2(\mathbb {T}^n)$ w.r.t. the norm  f H ˚ − s ≔ ( − Δ ) − s / 2 f L 2 $\left\Vert f\right\Vert _{\mathring{H}^{-s}}\coloneqq \left\Vert (-\Delta)^{-s/2} f\right\Vert _{L^2}$ . (Note that  − Δ $-\Delta$ is a strictly positive self-adjoint operator on  L ˚ 2 ( T n ) $\mathring{L}^2(\mathbb {T}^n)$ , and thus its negative powers  ( − Δ ) − s $(-\Delta)^{-s}$ , with  s > 0 $s>0$ , may be defined again by means of the spectral theorem.)
For s ∈ R $s\in {\mathbb {R}}$ , the Sobolev space H ˚ s ( T n ) $\mathring{H}^s(\mathbb {T}^n)$ can be identified with a set of formal series:
H ˚ s ( T n ) = f = ∑ z ∈ Z n ∖ { 0 } α z φ z : α z ∈ R , ∑ z ∈ Z n ∖ { 0 } | z | 2 s | α z | 2 < ∞ . $$\begin{equation*} \mathring{H}^s(\mathbb {T}^n)={\left\lbrace f=\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\alpha _z\varphi _z: \ \alpha _z\in {\mathbb {R}}, \ \sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }|z|^{2s}\,|\alpha _z|^2<\infty \right\rbrace} \,\,\mathrm{.} \end{equation*}$$
Then for all f = ∑ z ∈ Z n ∖ { 0 } α z φ z ∈ H ˚ r ( T n ) $f=\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\alpha _z\varphi _z\in \mathring{H}^r(\mathbb {T}^n)$ and g = ∑ z ∈ Z n ∖ { 0 } β z φ z ∈ H ˚ s ( T n ) $g=\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\beta _z\varphi _z\in \mathring{H}^s(\mathbb {T}^n)$ with r + s ≥ 0 $r+s\ge 0$ ,
⟨ f , g ⟩ T n = ∑ z ∈ Z n ∖ { 0 } α z β z . $$\begin{equation*} {\langle f,g\rangle} _{\mathbb {T}^n}=\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\alpha _z\,\beta _z. \end{equation*}$$
The norm of  H ˚ s ( T n ) $\mathring{H}^s(\mathbb {T}^n)$ is given by the square root of ∑ z ∈ Z n ∖ { 0 } | z | 2 s | α z | 2 $\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }|z|^{2s}\,|\alpha _z|^2$ . Equivalently, it could be defined with  λ z s $\lambda _z^s$ in place of  | z | 2 s $|z|^{2s}$ . This is the convention adopted in [5]. The two norms differ only by a factor  ( 2 π ) s $(2\pi)^{s}$ .

(f)

The ℓ ∞ $\ell ^\infty$ -norm of  z ∈ R n $z\in {\mathbb {R}}^n$ is
∥ z ∥ ∞ ≔ max k = 1 , … , n | z k | . $$\begin{equation*} \Vert z\Vert _\infty \coloneqq \max _{k=1,\ldots,n}|z_k| \,\,\mathrm{.} \end{equation*}$$
Given any function u : Z n → C $u: {\mathbb {Z}}^n\rightarrow {\mathbb {C}}$ we define the principal value along cubes of the series ∑ z u ( z ) $\sum _z u(z)$ by
∑ z ∈ Z n □ u ( z ) : = lim L → ∞ ∑ z ∈ Z n , z ∞ < L / 2 u ( z ) $$\begin{equation*} \sum ^{\Box }_{z\in {\mathbb {Z}}^n} u(z):=\lim _{L\rightarrow \infty }\sum _{z\in {\mathbb {Z}}^n, \ {\left\Vert z\right\Vert} _{\infty } <L/2}u(z) \end{equation*}$$
provided the latter limit exists in C $\mathbb {C}$ or in R ∪ { ± ∞ } ${\mathbb {R}}\cup \lbrace \pm \infty \rbrace$ .

(g)

Since T n $\mathbb {T}^n$ is compact, there exists a unique grounded Green kernel G ˚ $\mathring{G}$ satisfying
G ˚ ( x , y ) ≃ x − y 2 − n . $$\begin{equation*} \mathring{G}(x,y) \simeq {\left|x-y\right|}^{2-n}. \end{equation*}$$
In particular, G ˚ ∈ L p ( T n × T n ) $\mathring{G} \in L^{p}({\mathbb {T}^n \times \mathbb {T}^n})$ for all p < n n − 2 $p < \frac{n}{n-2}$ . We claim that we have:
G ˚ ( x , y ) = ∑ z ∈ Z n ∖ { 0 } □ 1 ( 2 π | z | ) 2 φ z ( x ) φ z ( y ) = ∑ z ∈ Z n ∖ { 0 } □ 1 ( 2 π | z | ) 2 Φ z ( x ) Φ ¯ z ( y ) = ∑ z ∈ Z n ∖ { 0 } □ 1 ( 2 π | z | ) 2 Φ z ( x − y ) = ∑ z ∈ Z n ∖ { 0 } □ 1 ( 2 π | z | ) 2 cos 2 π z · ( x − y ) , $$\begin{align*} \mathring{G}(x,y)& = \sum ^\Box _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{(2\pi |z|)^2}\,\varphi _z(x)\, \varphi _z(y)= \sum ^\Box _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{(2\pi |z|)^2}\,\Phi _z(x)\, \overline{\Phi }_z(y)\\ & = \sum ^\Box _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{(2\pi |z|)^2}\,\Phi _z(x-y) =\sum ^\Box _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{(2\pi |z|)^2}\,\cos {\left(2\pi \,z\cdot (x-y)\right)}, \end{align*}$$
where the convergence holds almost everywhere and in L p $L^{p}$ for p < n / ( n − 2 ) $p < n/(n-2)$ . Indeed consider the filtration ( F L ) $(\mathfrak {F}_{L})$ where F L $\mathfrak {F}_{L}$ is the σ $\sigma$ -algebra generated by the φ z $\varphi _{z}$ for z ∈ Z n $z \in \mathbb {Z}^{n}$ , z ∞ < L / 2 $\left\Vert z\right\Vert _{\infty } < L/2$ , and the associated closed martingale G ˚ L = E [ G ˚ | F L ] $\mathring{G}_{L} = \mathbf {E} [ \mathring{G} | \mathfrak {F}_{L}]$ , where expectation is with respect to vol ⊗ vol $\mathsf {vol}\otimes \mathsf {vol}$ . Take z ∈ Z n $z \in \mathbb {Z}^{n}$ with z ∞ < L / 2 $\left\Vert z\right\Vert _{\infty } < L/2$ . Since φ z $\varphi _{z}$ is F L $\mathfrak {F}_{L}$ -measurable, we get that
∫ G ˚ k ( x , y ) φ z ( y ) d y = ∫ G ˚ ( x , y ) φ z ( y ) d y = − Δ − 1 φ z ( x ) = λ z − 1 φ z ( x ) . $$\begin{equation*} \int \mathring{G}_{k}(x,y) \varphi _{z}(y) dy = \int \mathring{G}(x,y) \varphi _{z}(y) dy = {\left(-\Delta \right)}^{-1} \varphi _{z}(x) = \lambda _{z}^{-1} \varphi _{z}(x). \end{equation*}$$
On the other hand, when z ∞ ≥ L / 2 $\left\Vert z\right\Vert _{\infty } \ge L/2$ , since the φ z $\varphi _{z}$ ’s form an orthonormal basis, we find that E [ φ z | F L ] = 0 $\mathbf {E}[ \varphi _{z} | \mathfrak {F}_{L}]= 0$ , and thus
∫ G ˚ L ( x , y ) φ z ( y ) d y = 0 . $$\begin{equation*} \int \mathring{G}_{L}(x,y) \varphi _{z}(y) dy = 0. \end{equation*}$$
This shows that
G ˚ L ( x , y ) = ∑ z ∈ Z L n ∖ { 0 } λ z − 1 φ z ( x ) φ z ( y ) , $$\begin{equation*} \mathring{G}_{L}(x,y) = \sum _{z \in \mathbb {Z}^{n}_{L} \setminus \lbrace 0\rbrace } \lambda _{z}^{-1} \varphi _{z}(x) \varphi _{z}(y), \end{equation*}$$
and thus the almost everywhere convergence of the series follows by the martingale convergence theorem.

(h)

The polyharmonic operator is defined as
a n · ( − Δ ) n / 2 with a n ≔ 2 Γ ( n / 2 ) ( 4 π ) n / 2 . $$\begin{equation*} a_n\cdot (-\Delta)^{n/2} \qquad \text{with} \qquad a_n\coloneqq \frac{2}{\Gamma (n/2)\, (4\pi)^{n/2}}\,\,\mathrm{.} \end{equation*}$$
The inverse operator admits a kernel denoted by k $k$ .

As for the Green kernel, we have the following representation.

Lemma 2.1.We have that

k = ∑ z ∈ Z n ∖ { 0 } □ 1 ( 2 π | z | ) n φ z ⊗ φ z , $$\begin{equation*} k = \sum ^{\Box }_{z\in \mathbb {Z}^n\setminus \lbrace 0\rbrace }\frac{1}{{(2\pi |z|)^n}}\,\varphi _z\otimes \varphi _z, \end{equation*}$$
where the series converges in L 2 ( T n × T n ) $L^2(\mathbb {T}^n\times \mathbb {T}^n)$ and almost-everywhere.

Remark 2.2.We conjecture that the convergence indeed holds everywhere but do not have a proof of this fact.

Proof.Since the series on the right-hand side is orthogonal, we find that

∑ z ∈ Z n ∖ { 0 } λ z − n / 2 φ z ⊗ φ z L 2 = ∑ z ∈ Z n ∖ { 0 } 2 π z − 2 n < ∞ . $$\begin{equation*} {\left\Vert \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-n/2} \varphi _{z} \otimes \varphi _{z}\right\Vert} _{L^{2}} = \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } {\left(2 \pi {{\left|z\right|}}\right)}^{-2n} < \infty . \end{equation*}$$
This shows that the series actually converges in L 2 $L^{2}$ . The rest of the claim is obtained by a martingale argument as for the previous lemma. □ $\Box$

We denote by  p ˚ t $\mathring{p}_t$ the grounded heat kernel
p ˚ t ( x , y ) ≔ p t ( x , y ) − 1 , x , y ∈ T n . $$\begin{equation*} \mathring{p}_t(x,y) \coloneqq p_t(x,y)-1\,\,\mathrm{,}\;\,\qquad x,y\in \mathbb {T}^n \,\,\mathrm{.} \end{equation*}$$

Lemma 2.3.The function

f : x ↦ k ( x , 0 ) = 1 Γ ( n / 2 ) ∫ 0 ∞ p ˚ t ( x , 0 ) t n / 2 − 1 d t $$\begin{equation} f: x\longmapsto k(x,0)=\frac{1}{\Gamma (n/2)}\int _0^\infty \mathring{p}_t(x,0)\, t^{n/2-1}dt \end{equation}$$ ()
is differentiable at every  x ∈ T n ∖ 0 $x\in \mathbb {T}^n\setminus \left\lbrace 0\right\rbrace$ , and, for every  k ≤ n $k\le n$ ,
∂ ∂ x k f ( x ) = 1 Γ ( n / 2 ) ∫ 0 ∞ ∂ ∂ x k p ˚ t ( x , 0 ) t n / 2 − 1 d t . $$\begin{equation} \frac{\partial }{\partial x_k}f(x)=\frac{1}{\Gamma (n/2)}\int _0^\infty \frac{\partial }{\partial x_k}\mathring{p}_t(x,0)\, t^{n/2-1}dt \,\,\mathrm{.}\end{equation}$$ ()

Proof.The heat-kernel representation in Equation (1) holds as in [6, Lemma 2.4]. For fixed  k ≤ n $k\le n$ , standard Gaussian upper heat kernel estimates provide the summability of the right-hand side in Equation (2), hence Equation (2) follows by differentiation under integral sign. Since  x ↦ ∂ ∂ x k p ˚ t ( x , 0 ) $x\mapsto \left({\frac{\partial }{\partial x_k}\mathring{p}_t}\right)(x,0)$ is continuous for every  k $k$ on the whole of  T n $\mathbb {T}^n$ , we have that  ∂ ∂ x k f $\frac{\partial }{\partial x_k} f$ is continuous away from 0, and the differentiability of  f $f$ follows by standard arguments in multivariate calculus. □ $\Box$

The constant a n $a_n$ is chosen such in such a way that k $k$ has exactly logarithmic divergence.

Lemma 2.4. ([[5], Prop. 2.13])There exists a constant  C = C ( n ) > 0 $C=C(n)>0$ such that

k ( x , y ) − log 1 d ( x , y ) ≤ C , x , y ∈ T n . $$\begin{equation} {\left|k(x,y)-\log \frac{1}{d(x,y)}\right|}\le C\,\,\mathrm{,}\;\,\qquad x,y\in \mathbb {T}^n \,\,\mathrm{.} \end{equation}$$ ()

Proof.Note that the estimate in Proposition 2.13 in [5] for the kernel G n / 2 ( x , y ) $G^{n/2}(x,y)$ of the n / 2 $n/2$ -power of the Green operator holds not only for even but also for odd  n $n$ . □ $\Box$

Remark 2.5.Let us note here that we rely—as in the proof of Lemma 2.3— on results in [5], proved there for copolyharmonic operators on admissible manifolds  M $M$ of even dimension  n $n$ . Copolyharmonic operators are pseudo-differential operators on  M $M$ with the same principal symbol as the (integer) power  ( − Δ g ) n / 2 $(-\Delta _g)^{n/2}$ of the Laplace–Beltrami operator  Δ g $\Delta _g$ on  M $M$ , with lower-order correction terms granting their covariance under conformal transformations. We call a manifold admissible if the copolyharmonic operator is non-negative definite, with kernel exactly the one-dimensional subspace consisting of all constant functions. While the fact that a copolyharmonic operator has non-negative spectrum depends on the geometry of  M $M$ , the assumption of  n $n$ even is sufficient to grant that copolyharmonic operators have no zero-order term, so that their kernel contains all constant functions.

In the case of n $n$ -dimensional flat tori with  n $n$ even, the copolyharmonic operators in [5] coincide with the (integer) power  ( − Δ ) n / 2 $(-\Delta)^{n/2}$ of the standard Laplacian on the torus. In this case however, it is readily verified for every integer  n $n$ that  ( − Δ ) n / 2 $(-\Delta)^{n/2}$ is non-negative definite and that its kernel is the one-dimensional subspace consisting of all constant functions. Thus, all results [5] concerned with the existence of Gaussian fields and their Gaussian multiplicative chaoses hold with identical proof on flat tori of arbitrary dimension.

2.2 Laplacian and kernels on the discrete torus

(a)

For the sequel, fix L ∈ N $L\in {\mathbb {N}}$ . For convenience, we assume that L $L$ is odd. Put
Z L n ≔ { z ∈ Z n : ∥ z ∥ ∞ < L / 2 } , $$\begin{equation*} {\mathbb {Z}}^n_L\coloneqq \lbrace z\in {\mathbb {Z}}^n: \, \Vert z\Vert _\infty <L/2\rbrace \,\,\mathrm{,}\;\, \end{equation*}$$
and let
T L n ≔ 1 L Z n / Z n $$\begin{equation*} \mathbb {T}^n_L\coloneqq {\left(\tfrac{1}{L} {\mathbb {Z}}\right)}^n\big /{\mathbb {Z}}^n \end{equation*}$$
denote the discrete n $n$ -torus with edge length 1 L $\frac{1}{L}$ . Where helpful, one can think of the discrete torus T L n $\mathbb {T}_L^n$ as the set 1 L Z L n = { k L : k ∈ Z , 0 ≤ k < L } ) n ⊂ R n $\frac{1}{L}{\mathbb {Z}}^n_L=\lbrace \frac{k}{L}: \ k\in {\mathbb {Z}},\, 0\le k<L \rbrace){}^n\subset {\mathbb {R}}^n$ . We always regard it as a subset of the continuous torus T n $\mathbb {T}^n$ . Furthermore, let
m L ≔ 1 L n ∑ z ∈ T L n δ z $$\begin{equation*} m_L\coloneqq \frac{1}{L^n}\sum _{z\in \mathbb {T}_L^n}\delta _z \end{equation*}$$
denote the normalized counting measure on T L n $\mathbb {T}^n_L$ . Points v , u ∈ T L n $v,u\in \mathbb {T}^n_L$ are neighbors, in short v ∼ u $v\sim u$ , if d ( v , u ) = 1 L $d(v,u)=\frac{1}{L}$ . Each point in T L n $\mathbb {T}^n_L$ has 2 n $2n$  neighbors.

(b)

We define the discrete Laplacian Δ L $\Delta _L$ acting on functions f ∈ L 2 ( T L n ) $f\in L^2(\mathbb {T}^n_L)$ by
Δ L f ( v ) ≔ L 2 · ∑ u ∼ v f ( u ) − f ( v ) = 2 n L 2 p L f − f ( v ) $$\begin{equation*} \Delta _L f(v)\coloneqq L^2\cdot \sum _{u\sim v}{\left[f(u)-f(v)\right]}=2nL^2 {\left({\sf p}_Lf-f\right)}(v) \end{equation*}$$
with the transition kernel on T L n $\mathbb {T}^n_L$ given by
p L ( v , u ) ≔ L n 2 n 1 v ∼ u $$\begin{equation*} p_L(v,u)\coloneqq \frac{L^n}{2n}{\bf 1}_{v\sim u} \end{equation*}$$
and its action by ( p L f ) ( v ) = L − n ∑ u p L ( v , u ) f ( u ) $({\sf p}_Lf)(v)=L^{-n} \sum _u p_L(v,u) f(u)$ . Furthermore, we define the grounded transition kernel by
p ˚ L ( v , u ) ≔ p L ( v , u ) − 1 . $$\begin{equation*} \mathring{p}_L(v,u)\coloneqq p_L(v,u)-1\,\,\mathrm{.} \end{equation*}$$
The discrete Green operator acting on grounded functions f ∈ L ˚ 2 ( T L n ) $f\in \mathring{L}^2(\mathbb {T}^n_L)$ is defined by
G ˚ L f ≔ 1 2 n L 2 ∑ k = 0 ∞ p L k f = 1 2 n L 2 ∑ k = 0 ∞ p ˚ L k f . $$\begin{equation*} \mathring{\sf G}_L f\coloneqq \frac{1}{2nL^2}\, \sum _{k=0}^\infty {\sf p}_L^kf=\frac{1}{2nL^2}\, \sum _{k=0}^\infty \mathring{\sf p}_L^kf \,\,\mathrm{.} \end{equation*}$$
In particular, the grounded discrete Green kernel is given by
G ˚ L ( v , u ) = 1 2 n L 2 ∑ k = 0 ∞ p ˚ L k ( v , u ) $$\begin{equation*} \mathring{G}_L(v,u)=\frac{1}{2nL^2}\, \sum _{k=0}^\infty \mathring{p}_L^k(v,u) \end{equation*}$$
and its action by ( G ˚ L f ) ( v ) = L − n ∑ y G ˚ L ( v , u ) f ( u ) $(\mathring{\mathsf {G}}_Lf)(v)=L^{-n} \sum _y \mathring{G}_L(v,u) f(u)$ .

(c)

A complete ON basis of the complex L C 2 ( T L n , m L ) $L^2_{\mathbb {C}}(\mathbb {T}^n_L,m_L)$ is given by ( Φ z ) z ∈ Z L n $(\Phi _z)_{z\in {\mathbb {Z}}^n_L}$ with
Φ z ( v ) ≔ exp 2 π i z · v , v ∈ T L n . $$\begin{equation*} \Phi _z(v)\coloneqq \exp {\left(2\pi \text{i}\, z\cdot v\right)}\,\,\mathrm{,}\;\,\qquad v\in \mathbb {T}^n_L\,\,\mathrm{.} \end{equation*}$$
The functions Φ z $\Phi _z$ are (normalized) eigenfunctions of the negative discrete Laplacian − Δ L $-\Delta _L$ with eigenvalues
λ L , z ≔ 4 L 2 ∑ k = 1 n sin 2 π z k / L . $$\begin{equation} \lambda _{L,z}\coloneqq 4L^2\,\sum _{k=1}^n \sin ^2{\left(\pi z_k/L\right)}\,\,\mathrm{.}\end{equation}$$ ()
Note that as L → ∞ $L\rightarrow \infty$ , the right-hand side converges to λ z = ( 2 π | z | ) 2 $\lambda _z=(2\pi |z|)^2$ for any z ∈ Z n $z\in {\mathbb {Z}}^n$ .

A complete ON basis of L R 2 ( T L n , m L ) $L^2_{\mathbb {R}}(\mathbb {T}^n_L,m_L)$ is given by the functions φ z $\varphi _z$ for z ∈ Z L n $z\in {\mathbb {Z}}^n_L$ whereas before φ 0 ≡ 1 $\varphi _0\equiv 1$ and φ z ( v ) = 2 cos 2 π z · v $\varphi _z(v)=\sqrt 2\, \cos \left(2\pi \,z\cdot v\right)$ if z ∈ Z ̂ n ∩ Z L n $z\in \hat{{\mathbb {Z}}}^n\cap {\mathbb {Z}}^n_L$ and φ z ( v ) = 2 sin 2 π z · v $\varphi _z(v)=\sqrt 2\, \sin \left(2\pi \,z\cdot v\right)$ if z ∈ ( − Z ̂ n ) ∩ Z L n $z\in (-\hat{{\mathbb {Z}}}^n)\cap {\mathbb {Z}}^n_L$ .

Remark 2.6.For even L $L$ , the previous definitions require some modifications. The set Z L n ${\mathbb {Z}}^n_L$ has to be re-defined as

Z L n ≔ { − L / 2 + 1 , … , L / 2 − 1 , L / 2 } n . $$\begin{equation*} {\mathbb {Z}}^n_L\coloneqq {\big \lbrace -{L}/2+1,\ldots, {L}/2-1,{L}/2\big \rbrace} ^n\,\,\mathrm{.} \end{equation*}$$
Each z ∈ Z L n $z\in {\mathbb {Z}}^n_L$ we decompose into z ′ ≔ ( z k ) k ∈ σ z $z^{\prime }\coloneqq (z_k)_{k\in \sigma _z}$ and z ∼ ≔ ( z k ) k ∈ τ z $\tilde{z}\coloneqq (z_k)_{k\in \tau _z}$ with σ z ≔ { k ∈ { 1 , … , n } : z k = L / 2 } $\sigma _z\coloneqq \lbrace k\in \lbrace 1,\ldots, n\rbrace: z_k=L/2\rbrace$ , τ z ≔ { k ∈ { 1 , … , n } : z k < L / 2 } $\tau _z\coloneqq \lbrace k\in \lbrace 1,\ldots, n\rbrace: z_k<L/2\rbrace$ . Similarly, for v ∈ T L n $v\in \mathbb {T}^n_L$ we put v ′ ≔ ( v k ) k ∈ σ z $v^{\prime }\coloneqq (v_k)_{k\in \sigma _z}$ and v ∼ ≔ ( v k ) k ∈ τ z $\tilde{v}\coloneqq (v_k)_{k\in \tau _z}$ . Then
Φ z ( v ) = ( − 1 ) L | v ′ | σ z · Φ z ∼ ( v ∼ ) with | v ′ | σ z ≔ ∑ k ∈ σ z v k . $$\begin{equation*} \Phi _z(v)=(-1)^{L\,|v^{\prime }|_{\sigma _z}}\cdot \Phi _{\tilde{z}}(\tilde{v})\quad \text{with }|v^{\prime }|_{\sigma _z}\coloneqq \sum _{k\in \sigma _z}v_k\,\,\mathrm{.} \end{equation*}$$
Thus, a complete ON basis of L R 2 ( T L n , m L ) $L^2_{\mathbb {R}}(\mathbb {T}^n_L,m_L)$ is given by the functions
φ z ( v ) ≔ ( − 1 ) L | v ′ | σ z · φ z ∼ ( v ∼ ) , z ∈ Z L n , $$\begin{equation} \varphi _z(v)\coloneqq (-1)^{L\,|v^{\prime }|_{\sigma _z}}\cdot \varphi _{\tilde{z}}(\tilde{v})\,\,\mathrm{,}\;\,\quad z\in Z^n_L\,\,\mathrm{,}\;\, \end{equation}$$ ()
where φ z ∼ $\varphi _{\tilde{z}}$ for z ∼ ∈ Z n $\tilde{z}\in {\mathbb {Z}}^n$ with ∥ z ∼ ∥ ∞ < L / 2 $\Vert \tilde{z}\Vert _\infty <L/2$ is defined as before.

(d)

In terms of the discrete eigenfunctions, the discrete grounded Green kernel, the integral kernel of the inverse of − Δ L $-\Delta _L$ acting on grounded L 2 $L^2$ -functions, is given as
G ˚ L ( v , u ) = ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z φ z ( v ) φ z ( u ) = ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z Φ z ( v ) Φ ¯ z ( u ) = ∑ z ∈ Z L n ∖ { 0 } 1 4 L 2 ∑ k = 1 n sin 2 π z k / L · cos 2 π z · ( v − u ) , $$\begin{align*} \mathring{G}_L(v,u)&= \sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}}\varphi _{z}(v)\, \varphi _z(u)= \sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}}\Phi _z(v)\,\overline{\Phi }_z(u)\\ & =\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{4L^2\,\sum _{k=1}^n \sin ^2{\left(\pi z_k/L\right)}}\cdot \cos {\left(2\pi \, z\cdot (v-u)\right)}\,\,\mathrm{,}\;\, \end{align*}$$
and the discrete polyharmonic kernel k L $k_L$ (Figure 1), the integral kernel of the inverse of a n ( − Δ L ) n / 2 $a_n(-\Delta _L)^{n/2}$ acting on grounded L 2 $L^2$ -functions, as
k L ( v , u ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 φ z ( v ) φ z ( u ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 Φ z ( v ) Φ ¯ z ( u ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 4 L 2 ∑ k = 1 n sin 2 π z k / L n / 2 · cos 2 π z · ( v − u ) . $$\begin{align} k_L(v,u)&=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda ^{n/2}_{L,z}}\varphi _z(v)\, \varphi _z(u)=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}\Phi _z(v)\,\overline{\Phi }_z(u)\nonumber \\ &=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{{\left(4L^2\,\sum _{k=1}^n \sin ^2{\left(\pi z_k/L\right)}\right)}^{n/2}}\cdot \cos {\left(2\pi \, z\cdot (v-u)\right)}\,\,\mathrm{.}\end{align}$$ ()
Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
k ( 0 , y ) $k(0,y)$ (orange) and k 11 ( 0 , y ) $k_{11}(0,y)$ (blue) for  y ∈ T 2 $y\in \mathbb {T}^2$ (sectional view with one quadrant removed).

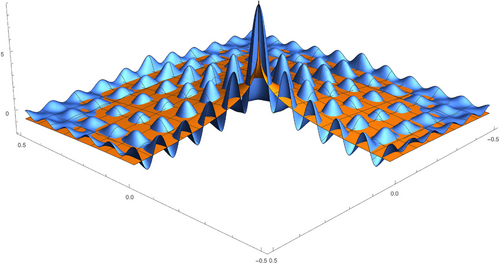
2.3 Extensions and projections

(a) Piecewise constant extension/projection

Set
Q L ≔ − 1 2 L , 1 2 L n and Q L ( v ) ≔ v + Q L , v ∈ T L n . $$\begin{equation} Q_L\coloneqq {\left[-\tfrac{1}{2L},\tfrac{1}{2L}\right)}^n \qquad \text{and}\qquad Q_L(v)\coloneqq v+Q_L\,\,\mathrm{,}\;\,\ v\in \mathbb {T}^n_L\,\,\mathrm{.}\end{equation}$$ ()
Observe that
T n = ⨆ v ∈ T L n Q L ( v ) . $$\begin{equation*} \mathbb {T}^n={\bigsqcup \limits _{v\in \mathbb {T}^n_L}} Q_L(v)\,\,\mathrm{.} \end{equation*}$$
Functions on T n $\mathbb {T}^n$ are called piecewise constant if they are constant on each of the cubes Q L ( v ) , v ∈ T L n $Q_L(v), v\in \mathbb {T}^n_L$ . Every function f $f$ on the discrete torus T L n $\mathbb {T}^n_L$ can be uniquely extended to a piecewise constant function f L , ♭ ( x ) $f_{L,\flat }(x)$ by setting f L , ♭ ( x ) ≔ f ( v ) $f_{L,\flat }(x)\coloneqq f(v)$ if x ∈ Q L ( v ) $x\in Q_L(v)$ . In other words,
f L , ♭ ( x ) = ( q ̇ L , f ) ( x ) ≔ ⟨ q L ( x , · ) , f ⟩ T L n $$\begin{equation*} f_{L,\flat }(x)=(\dot{\sf q}_{L,}f)(x)\coloneqq {\langle q_{L}(x,{\,\cdot \,}),f\rangle} _{\mathbb {T}_L^n} \end{equation*}$$
with the Markov kernel q L ( x , v ) ≔ L n 1 Q L ( v ) ( x ) $q_{L}(x,v)\coloneqq L^n\,{\bf 1}_{Q_L(v)}(x)$ on T n × T L n $\mathbb {T}^n\times \mathbb {T}^n_L$ . The latter is the restriction of the Markov kernel
q L = L n ∑ v ∈ T L n 1 Q L ( v ) ⊗ 1 Q L ( v ) on T n × T n . $$\begin{equation} q_L=L^n\,\sum _{v\in \mathbb {T}^n_L}{\bf 1}_{Q_L(v)}\otimes {\bf 1}_{Q_L(v)}\quad \text{on }\mathbb {T}^n\times \mathbb {T}^n. \end{equation}$$ ()
Note that ∫ T n q L ( x , y ) d y = 1 $\int _{\mathbb {T}^n}q_L(x,y)dy=1$ as well as ∫ T L n q L ( x , v ) d m L ( v ) = 1 $\int _{\mathbb {T}^n_L} q_L(x,v)dm_L(v)=1$ .
The projection from L 2 ( T n ) $L^2(\mathbb {T}^n)$ onto the set of piecewise constant functions on T n $\mathbb {T}^n$ is given by f ↦ f ♭ , L $f\mapsto f_{\flat,L}$ with
f ♭ , L ( x ) = ( q L f ) ( x ) ≔ ⟨ q L ( x , · ) , f ⟩ T n = L n ∑ v ∈ T L n ⟨ 1 Q L ( v ) , f ⟩ T n · 1 Q L ( v ) ( x ) . $$\begin{equation} f_{\flat,L}(x)= ({\sf q}_Lf)(x)\coloneqq {\langle q_L(x,{\,\cdot \,}),f\rangle} _{\mathbb {T}^n}= L^n\,\sum _{v\in \mathbb {T}^n_L}{\langle 1_{Q_L(v)},f\rangle} _{\mathbb {T}^n}\cdot 1_{Q_L(v)}(x)\,\,\mathrm{.}\end{equation}$$ ()

Here and in the following, the integral operators associated with kernels p , q , r $p,q,r$ will be denoted by p , q , r ${\sf p,q,r}$ , resp. In general, these are regarded as integral operators on T n $\mathbb {T}^n$ . If we want to regard them as integral operators on T L n $\mathbb {T}^n_L$ , we write p ̇ , q ̇ , r ̇ ${\sf \dot{p},\dot{q}, \dot{r}}$  instead.

(b) Fourier extension/projection

Let D L $\mathcal {D}_L$ denote the linear span of { φ z : z ∈ Z L n } $\lbrace \varphi _z: z\in {\mathbb {Z}}^n_L\rbrace$ . Every function f $f$ on the discrete torus T L n $\mathbb {T}^n_L$ can be uniquely represented as f = ∑ z ∈ Z L n α z φ z $f=\sum _{z\in {\mathbb {Z}}_L^n}\alpha _z\varphi _z$ with suitable coefficients α z ∈ R $\alpha _z\in {\mathbb {R}}$ for z ∈ Z L n $z\in {\mathbb {Z}}^n_L$ , and thus uniquely extends to a function f L , ♯ ∈ D L $f_{L,\sharp }\in \mathcal {D}_L$ on the continuous torus T n $\mathbb {T}^n$ . Formally,
f L , ♯ ( x ) ≔ ( r ̇ L f ) ( x ) ≔ ⟨ f , r L ( x , · ) ⟩ T L n ≔ ∑ z ∈ Z L n ⟨ f , φ z ⟩ T L n · φ z ( x ) $$\begin{equation*} f_{L,\sharp }(x) \coloneqq (\dot{\sf r}_{L}f)(x)\coloneqq {\langle f,r_{L}(x,{\,\cdot \,})\rangle} _{\mathbb {T}_L^n}\coloneqq \sum _{z\in {\mathbb {Z}}^n_L}{\langle f,\varphi _z\rangle} _{\mathbb {T}_L^n}\cdot \varphi _z(x) \end{equation*}$$
with the kernel
r L ≔ ∑ z ∈ Z L n φ z ⊗ φ z on T n × T n . $$\begin{equation} r_{L}\coloneqq \sum _{z\in {\mathbb {Z}}_L^n}\varphi _z\otimes \varphi _z\quad \text{on }\mathbb {T}^n\times \mathbb {T}^n. \end{equation}$$ ()
Regarded as a kernel on T L n × T n $\mathbb {T}_L^n\times \mathbb {T}^n$ , the latter defines the Fourier extension operator. As a kernel on T L n × T L n $\mathbb {T}_L^n\times \mathbb {T}_L^n$ it indeed is the identity.
Conversely, the projection from ⋃ s H s ( T n ) $\bigcup _{s}H^s(\mathbb {T}^n)$ onto D L $\mathcal {D}_L$ is given by f ↦ f ♯ , L $f\mapsto f_{\sharp,L}$ with
f ♯ , L ( x ) ≔ ( r L f ) ( x ) ≔ ⟨ f , r L ( x , · ) ⟩ T n ≔ ∑ z ∈ Z L n ⟨ f , φ z ⟩ T n φ z ( x ) . $$\begin{equation*} f_{\sharp,L}(x) \coloneqq ({\sf r}_{L}f)(x)\coloneqq {\langle f,r_{L}(x,{\,\cdot \,})\rangle }_{\mathbb {T}^n}\coloneqq \sum _{z\in {\mathbb {Z}}^n_L}{\langle f,\varphi _z\rangle} _{\mathbb {T}^n}\,\varphi _z(x). \end{equation*}$$
In particular, if f = ∑ z ∈ Z n α z φ z $f=\sum _{z\in {\mathbb {Z}}^n}\alpha _z\varphi _z$ then f ♯ , L = ∑ z ∈ Z L n α z φ z $f_{\sharp,L}=\sum _{z\in {\mathbb {Z}}_L^n}\alpha _z\varphi _z$ .

(c) Enhancement and reduction

For f = ∑ z ∈ Z L n α z φ z ∈ ⋃ s H s ( T n ) $f=\sum _{z\in {\mathbb {Z}}_L^n}\alpha _z\varphi _z\in \bigcup _{s}H^s(\mathbb {T}^n)$ we define its spectral reduction and its spectral enhancement, resp., by
f L − ∘ ≔ ∑ z ∈ Z L n λ L , z λ z n / 4 α z φ z , f L + ∘ ≔ ∑ z ∈ Z L n λ z λ L , z n / 4 α z φ z . $$\begin{equation*} f_L^{{-\circ }}\coloneqq \sum _{z\in {\mathbb {Z}}_L^n}{\left(\frac{\lambda _{L,z}}{\lambda _{z}}\right)}^{n/4}\alpha _z\varphi _z, \qquad f_L^{{+\circ }}\coloneqq \sum _{z\in {\mathbb {Z}}_L^n}{\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}\alpha _z\varphi _z. \end{equation*}$$
Note that
λ L , z λ z = L 2 π 2 | z | 2 ∑ k = 1 n sin 2 ( π z k / L ) ∈ ( 2 / π ) 2 , 1 and → 1 as L → ∞ . $$\begin{equation} \frac{\lambda _{L,z}}{\lambda _{z}}=\frac{L^2}{\pi ^2\,|z|^2}\sum _{k=1}^n \sin ^2(\pi z_k/L)\ \in \ {\left[ (2/\pi)^2, 1\right]}\quad \text{and }\rightarrow 1\text{ as }L\rightarrow \infty . \end{equation}$$ ()
Similarly, we define its integral reduction and its integral enhancement, resp., by
f L ∘ − ≔ ∑ z ∈ Z L n ϑ L , z α z φ z , f L ∘ + ≔ ∑ z ∈ Z L n 1 ϑ L , z α z φ z $$\begin{equation*} f_L^{{\circ -}}\coloneqq \sum _{z\in {\mathbb {Z}}_L^n}\vartheta _{L,z}\alpha _z\varphi _z,\qquad f_L^{{\circ +}}\coloneqq \sum _{z\in {\mathbb {Z}}_L^n}\frac{1}{\vartheta _{L,z}}\alpha _z\varphi _z \end{equation*}$$
with
ϑ L , z ≔ ∏ k = 1 n L π z k sin π z k L ∈ ( 2 / π ) n , 1 and → 1 as L → ∞ . $$\begin{equation} \vartheta _{L,z}\coloneqq \prod _{k=1}^n{\left(\frac{L}{\pi z_k}\, \sin {\left(\frac{\pi z_k}{L}\right)}\right)}\ \in \ {\left[ (2/\pi)^n, 1\right]}\quad \text{and }\rightarrow 1\text{ as }L\rightarrow \infty . \end{equation}$$ ()
In terms of integral operators this can be expressed as
f L − ∘ = r L − ∘ f , f L + ∘ = r L + ∘ f , f L ∘ − = r L ∘ − f , f L ∘ + = r L ∘ + f $$\begin{equation*} f_L^{{-\circ }}={\sf r}_L^{{-\circ }}f, \qquad f_L^{{+\circ }}={\sf r}_L^{{+\circ }}f, \qquad f_L^{{\circ -}}={\sf r}_L^{{\circ -}}f, \qquad f_L^{{\circ +}}={\sf r}_L^{{\circ +}}f \end{equation*}$$
with integral and enhancement kernels on T n × T n $\mathbb {T}^n\times \mathbb {T}^n$ defined as follows:
r L + = ∑ z ∈ Z L n λ z λ L , z n / 4 ϑ L , z − 1 φ z ⊗ φ z , r L − = ∑ z ∈ Z L n λ z λ L , z − n / 4 ϑ L , z φ z ⊗ φ z , r L + ∘ = ∑ z ∈ Z L n λ z λ L , z n / 4 φ z ⊗ φ z , r L − ∘ = ∑ z ∈ Z L n λ z λ L , z − n / 4 φ z ⊗ φ z , r L ∘ + = ∑ z ∈ Z L n ϑ L , z − 1 φ z ⊗ φ z , r L ∘ − = ∑ z ∈ Z L n ϑ L , z φ z ⊗ φ z . $$\begin{align*} r_L^{{+}}=& \sum _{z\in {\mathbb {Z}}_L^n}{\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}\vartheta _{L,z}^{-1}\ \varphi _z\otimes \varphi _z\,\,\mathrm{,}\;\,& r_L^{{-}}=& \sum _{z\in {\mathbb {Z}}_L^n}{\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{-n/4}\vartheta _{L,z}\ \varphi _z\otimes \varphi _z\,\,\mathrm{,}\;\,\\ r_L^{{+\circ }}=& \sum _{z\in {\mathbb {Z}}_L^n}{\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}\varphi _z\otimes \varphi _z\,\,\mathrm{,}\;\,& r_L^{{-\circ }}=& \sum _{z\in {\mathbb {Z}}_L^n}{\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{-n/4}\varphi _z\otimes \varphi _z\,\,\mathrm{,}\;\,\\ r_L^{{\circ +}}=& \sum _{z\in {\mathbb {Z}}_L^n}\vartheta _{L,z}^{-1}\ \varphi _z\otimes \varphi _z\,\,\mathrm{,}\;\,& r_L^{{\circ -}}=& \sum _{z\in {\mathbb {Z}}_L^n}\vartheta _{L,z}\ \varphi _z\otimes \varphi _z\,\,\mathrm{.} \end{align*}$$

Lemma 2.7.For f ∈ D L $f\in \mathcal {D}_L$ ,

q L f = f L ∘ − on T L n and q L ( f L ∘ + ) = f on T L n . $$\begin{equation*} {\sf q}_Lf=f_L^{{\circ -}}\text{ on }\mathbb {T}^n_L\quad \text{and}\quad {\sf q}_L(f_L^{{\circ +}})=f\text{ on }\mathbb {T}^n_L \,\,\mathrm{.} \end{equation*}$$

Proof.For f = Φ z $f=\Phi _z$ with z ∈ Z L n $z\in {\mathbb {Z}}^n_L$ , and for v ∈ T L n $v\in \mathbb {T}^n_L$ ,

q L f ( v ) = L n ∫ Q L ( v ) Φ z ( x ) d x = Φ z ( v ) · L n ∫ Q L Φ z ( x ) d x = Φ z ( v ) · ∏ k = 1 n L ∫ − 1 2 L 1 2 L cos ( 2 π x k z k ) d x k = Φ z ( v ) · ∏ k = 1 n L π z k sin π z k L . $$\begin{align*} {\sf q}_Lf(v)&=L^n\int _{Q_L(v)}\Phi _z(x)dx=\Phi _z(v)\cdot L^n\,\int _{Q_L}\Phi _z(x)dx\\ &=\Phi _z(v)\cdot \prod _{k=1}^n L\,\int _{-\frac{1}{2L}}^{\frac{1}{2L}}\cos (2\pi x_k z_k)dx_k=\Phi _z(v)\cdot \prod _{k=1}^n{\left(\frac{L}{\pi z_k}\, \sin {\left(\frac{\pi z_k}{L}\right)}\right)}. \end{align*}$$
Therefore, for f = φ z $f=\varphi _z$ with z ∈ Z L n $z\in {\mathbb {Z}}^n_L$ , and for v ∈ T L n $v\in \mathbb {T}^n_L$ ,
q L f ( v ) = f ( v ) · ϑ L , z . $$\begin{equation*} {\sf q}_Lf(v)=f(v)\cdot \vartheta _{L,z}\,\,\mathrm{.} \end{equation*}$$
Thus, the claim follows. □ $\Box$

(d) Continuous versus discrete scalar product

For functions f = ∑ z ∈ Z L n α z φ z $f=\sum _{z\in {\mathbb {Z}}_L^n}\alpha _z\varphi _z$ and g = ∑ w ∈ Z L n β w φ w $g=\sum _{w\in {\mathbb {Z}}_L^n}\beta _w\varphi _w$ , the scalar products in T L n $\mathbb {T}^n_L$ and in T n $\mathbb {T}^n$ coincide:
⟨ f , g ⟩ T L n = ⟨ f , g ⟩ T n = ∑ z ∈ Z L n α z β z . $$\begin{equation*} {\langle f,g\rangle} _{\mathbb {T}_L^n}={\langle f,g\rangle} _{\mathbb {T}^n}=\sum _{z\in {\mathbb {Z}}_L^n}\alpha _z\,\beta _{z} \,\,\mathrm{.} \end{equation*}$$
This simple identity, however, no longer holds if the Fourier representation of f $f$ and g $g$ also contains terms with higher frequencies.

Lemma 2.8.

  • ( i ) $(i)$ For f = ∑ z ∈ Z K n α z φ z $f=\sum _{z\in {\mathbb {Z}}_K^n}\alpha _z\varphi _z$ and g = ∑ w ∈ Z K n β w φ w $g=\sum _{w\in {\mathbb {Z}}_K^n}\beta _w\varphi _w$ ,
    ⟨ f , g ⟩ T L n = ∑ z ∈ Z K n ∑ w ∈ Z n , ∥ z + L w ∥ ∞ < K / 2 α z β z + L w . $$\begin{equation*} {\langle f,g\rangle} _{\mathbb {T}_L^n}=\sum _{z\in {\mathbb {Z}}_K^n}\sum _{w\in {\mathbb {Z}}^n, \Vert z+Lw\Vert _\infty <K/2} \alpha _z\,\beta _{z+Lw}\,\,\mathrm{.} \end{equation*}$$
  • ( i i ) $(ii)$ For any α : Z n → R $\alpha: {\mathbb {Z}}^{n}\rightarrow \mathbb {R}$ , the limit f = ∑ z ∈ Z n □ α z φ z $f = \sum ^{\Box }_{z\in {\mathbb {Z}}^n}\alpha _z\varphi _z$ exists in L 2 ( T L n ) $L^2(\mathbb {T}^n_L)$ if and only if
    sup K ∥ ∑ z ∈ Z K n α z φ z ∥ T L n 2 < ∞ $$\begin{equation} \sup _{K}\Big \Vert \sum _{z\in {\mathbb {Z}}_K^n}\alpha _z\varphi _z \Big \Vert ^2_{\mathbb {T}^n_L}<\infty \end{equation}$$ ()
  • ( i i i ) $(iii)$ For all f = ∑ z ∈ Z n □ α z φ z $f= \sum ^{\Box }_{z\in {\mathbb {Z}}^n}\alpha _z\varphi _z$ and g = ∑ w ∈ Z n □ β w φ w $g= \sum ^{\Box }_{w\in {\mathbb {Z}}^n}\beta _w\varphi _w$ in L 2 ( T L n ) $L^2(\mathbb {T}^n_L)$ ,
    ⟨ f , g ⟩ T L n = lim K → ∞ ∑ z ∈ Z K n ∑ w ∈ Z n : z + L w ∞ < K / 2 α z β z + L w , ⟨ f , g ⟩ T n = ∑ z ∈ Z n □ α z β z . $$\begin{equation*} {\langle f,g\rangle} _{\mathbb {T}_L^n} = \lim _{K \rightarrow \infty } \sum _{z \in \mathbb {Z}_{K}^{n}} \sum _{w \in \mathbb {Z}^{n}: {\left\Vert z+Lw\right\Vert} _{\infty } < K/2} \alpha _{z} \beta _{z + Lw} \,\,\mathrm{,}\;\,\qquad {\langle f,g\rangle} _{\mathbb {T}^n}=\sum ^{\Box }_{z\in {\mathbb {Z}}^n}\alpha _z\,\beta _{z}. \end{equation*}$$

Proof.

  • ( i ) $(i)$ We prove the analogous assertion in the complex Hilbert space: for all f = ∑ z ∈ Z K n a z Φ z $f={\sum_{z\in {\mathbb {Z}}_K^n}} a_z\Phi _z$ and g = ∑ w ∈ Z K n b w Φ w $g={\sum_{w\in {\mathbb {Z}}_K^n}} b_w\Phi _w$ ,
    ⟨ f , g ⟩ T L n = 〈 ∑ z ∈ Z K n a z Φ z , ∑ w ∈ Z K n b w Φ w 〉 T L n = ∫ T L n ∑ z ∈ Z K n ∑ w ∈ Z K n a z b ¯ w exp 2 π i v ( z − w ) d m L ( v ) = ∑ z ∈ Z K n ∑ w ∈ Z K n a z b ¯ w · ∫ T L n exp 2 π i v ( z − w ) d m L ( v ) = ∑ z ∈ Z K n ∑ w ∈ Z n , ∥ z + L w ∥ ∞ < K / 2 a z b ¯ z + L w $$\begin{align*} {\langle f,g\rangle} _{\mathbb {T}_L^n}&= {\Big \langle \sum _{z\in {\mathbb {Z}}^n_K}a_z\Phi _z, \sum _{w\in {\mathbb {Z}}^n_K} b_w\Phi _w\Big \rangle} _{\mathbb {T}_L^n} \\ &=\int _{\mathbb {T}^n_L}\sum _{z\in {\mathbb {Z}}^n_K}\sum _{w\in {\mathbb {Z}}^n_K} a_z\,\overline{b}_{w} \exp {\left(2\pi i\, v(z-w) \right)}\,dm_L(v) \\ &=\sum _{z\in {\mathbb {Z}}_K^n}\sum _{w\in {\mathbb {Z}}_K^n} a_z\, \overline{b}_{w}\cdot \int _{\mathbb {T}^n_L} \exp {\left(2\pi i\, v(z-w) \right)}\,dm_L(v) \\ &=\sum _{z\in {\mathbb {Z}}_K^n}\sum _{w\in {\mathbb {Z}}^n, \Vert z+Lw\Vert _\infty <K/2} a_z\,\overline{b}_{z+Lw} \end{align*}$$
    since for every z ∈ Z n $z\in {\mathbb {Z}}^n$
    ∫ T L n exp ( 2 π i v z ) d m L ( v ) = 1 , if z ∈ L Z n 0 , else . $$\begin{equation*} \int _{\mathbb {T}^n_L} \exp (2\pi \text{i}\, v z)\,dm_L(v)= {\begin{cases} 1,& \ \text{if }z\in L{\mathbb {Z}}^n \\ 0,&\ \text{else} \end{cases}} \,\,\mathrm{.} \end{equation*}$$
    The claim for the real Hilbert space then follows choosing a z = 1 2 ( α z + i α − z ) $a_z=\frac{1}{\sqrt 2}(\alpha _z+\text{i}\alpha _{-z})$ and a − z = 1 2 ( α z − i α − z ) $a_{-z}=\frac{1}{\sqrt 2}(\alpha _z-\text{i}\alpha _{-z})$ for z ∈ Z ̂ n $z\in \hat{{\mathbb {Z}}}^n$ and analogously b z $b_z$ .
  • ( i i ) $(ii)$ Assume first that f ∈ L 2 ( T L n ) $f \in L^{2}(\mathbb {T}^{n}_{L})$ . Then, ∑ z ∈ Z K n α z φ z $\sum _{z \in \mathbb {Z}^{n}_{K}} \alpha _{z} \varphi _{z}$ converges to f $f$ in L 2 ( T L n ) $L^{2}(\mathbb {T}_{L}^{n})$ . This implies Equation (13). Conversely, assume that Equation (13) holds. Then, a martingale argument similar to that of Lemma 2.1 shows that f $f$ is the limit in L 2 ( T L n ) $L^{2}(\mathbb {T}^{n}_{L})$ of ∑ z ∈ Z K n α z φ z $\sum _{z \in \mathbb {Z}_{K}^{n}} \alpha _{z} \varphi _{z}$ .
  • ( i i i ) $(iii)$ We only need to show the first equation. By linearity it is sufficient to show it for f = g $f = g$ . In view of what precedes, we have
    f T L n 2 = lim K → ∞ ∑ z ∈ Z K n α z φ z 2 = lim K → ∞ ∑ z ∈ Z K n ∑ w ∈ Z n : z + L w ∞ < K / 2 α z α z + L w , $$\begin{equation*} {\left\Vert f\right\Vert} _{\mathbb {T}_{L}^{n}}^{2} = \lim _{K \rightarrow \infty } {\left\Vert \sum _{z \in \mathbb {Z}_{K}^{n}} \alpha _{z} \varphi _{z}\right\Vert} ^{2} = \lim _{K \rightarrow \infty } \sum _{z \in \mathbb {Z}_{K}^{n}} \sum _{w \in \mathbb {Z}^{n}: {\left\Vert z+Lw\right\Vert} _{\infty } < K/2} \alpha _{z} \alpha _{z + Lw}, \end{equation*}$$
    which proves the claim. The convergence of the series is ensured by Equation (13). □ $\Box$

Remark 2.9.According to the previous lemma, in particular, for every f = ∑ z ∈ Z n □ α z φ z $f= \sum ^{\Box }_{z\in {\mathbb {Z}}^n}\alpha _z\varphi _z$ ,

∥ f ∥ T L n 2 = ∑ z ∈ Z n ∑ w ∈ Z n α z α z + L w $$\begin{equation*} \big \Vert f\big \Vert ^2_{\mathbb {T}_L^n}=\sum _{z\in {\mathbb {Z}}^n}\sum _{w\in {\mathbb {Z}}^n}\alpha _z\,\alpha _{z+Lw} \end{equation*}$$
if the latter series is absolutely convergent.

One can show (cf. proof of Theorem 4.11) that the latter series is absolutely convergent if f ∈ ⋃ s > n / 2 H s ( T n ) $f\in \bigcup _{s>n/2}H^s(\mathbb {T}^n)$ . This is in accordance with the Sobolev embedding theorem which asserts that in this case f ∈ C ( T n ) $f\in \mathcal {C}(\mathbb {T}^n)$ and thus guarantees that the pointwise evaluation of f $f$ (at the lattice points of T L n $\mathbb {T}^n_L$ ) is meaningful.

3 THE POLYHARMONIC GAUSSIAN FIELD ON THE DISCRETE TORUS

3.1 Definition and construction of the field

Throughout the following, fix integers n $n$ and L $L$ . For convenience, we assume that  L $L$ is odd, and we set  N ≔ L n $N\coloneqq L^n$ .

Definition 3.1.A random field h L = ( h L ( v ) ) v ∈ T L n $h_L=(h_L(v))_{v\in \mathbb {T}^n_L}$ —defined on some probability space ( Ω , A , P ) $(\Omega,\mathfrak {A}, \mathbf {P})$ —is called polyharmonic Gaussian field on the discrete torus T L n $\mathbb {T}^n_L$ (shortly: discrete polyharmonic Gaussian field) if it is a centered Gaussian field with covariance function  k L $k_L$ given by Equation (6).

Proposition 3.2.Given i.i.d. standard normals ξ z $\xi _z$ for z ∈ Z L n ∖ { 0 } ${z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }$ on a probability space ( Ω , A , P ) $(\Omega,\mathfrak {A}, \mathbf {P})$ , a polyharmonic Gaussian field on T L n $\mathbb {T}^n_L$ is defined by

h L ω ( v ) ≔ 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 4 · ξ z ω · φ z ( v ) v ∈ T L n , ω ∈ Ω . $$\begin{equation} h^\omega _L(v)\coloneqq \frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/4}} \cdot \xi _z^\omega \cdot \varphi _z(v) \qquad v\in \mathbb {T}_L^n\,\,\mathrm{,}\;\,\omega \in \Omega \,\,\mathrm{.}\end{equation}$$ ()

Here, λ L , z = 4 L 2 ∑ k = 1 n sin 2 π z k / L $\lambda _{L,z}=4L^2\,\sum _{k=1}^n \sin ^2\left(\pi z_k/L\right)$ for z ∈ Z L n $z\in {\mathbb {Z}}_L^n$ are the eigenvalues of the discrete Laplacian, see Equation (4), and the eigenvalue 0 is excluded in the representation of the random field.

Proof.For all v , u ∈ T L n $v,u\in \mathbb {T}_L^n$ ,

E h L ( v ) h L ( u ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 · φ z ( v ) φ z ( u ) = k L ( v , u ) . $$\begin{align*} \mathbf {E}{\left[h_L(v)\,h_L(u)\right]}= \frac{1}{a_n} \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}\cdot \varphi _z(v)\,\varphi _z(u) =k_L(v,u) \,\,\mathrm{.}& \end{align*}$$
□ $\Box$

Alternatively, the polyharmonic field on the discrete torus T L n $\mathbb {T}^n_L$ can be defined in terms of the white noise on the discrete torus. Recall that a random field Ξ = ( Ξ v ) v ∈ T L n $\Xi = (\Xi _v)_{v\in \mathbb {T}^n_L}$ is called white noise on ( T L n , m L ) $(\mathbb {T}^n_L,m_L)$ if the Ξ v $\Xi _v$ for v ∈ T L n ${v\in \mathbb {T}_L^n}$ are independent centered Gaussian random variables with variance L n $L^n$ . (This normalization guarantees that ∫ T L n Ξ v d m L ( v ) $\int _{\mathbb {T}^n_L}\Xi _vdm_L(v)$ is N ( 0 , 1 ) $\mathcal {N}(0,1)$ distributed.)

Proposition 3.3.Given a white noise Ξ = ( Ξ v ) v ∈ T L n $\Xi = (\Xi _v)_{v\in \mathbb {T}^n_L}$ on ( T L n , m L ) $(\mathbb {T}^n_L,m_L)$ , a polyharmonic Gaussian field on  T L n $\mathbb {T}^n_L$ is defined by

h L ω ( v ) = 1 a n L n ∑ u ∈ T L n G ˚ L n / 4 ( v , u ) Ξ u ω $$\begin{align*} h^\omega _L(v)& =\frac{1}{\sqrt {a_n}\,L^n}\,\sum _{u\in \mathbb {T}^n_L}\mathring{G}_L^{n/4}(v,u)\, \Xi ^\omega _u \end{align*}$$
with
G ˚ L n / 4 ( v , u ) = ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 4 · cos 2 π z ( v − u ) . $$\begin{equation*} \mathring{G}_L^{n/4}(v,u)=\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/4}}\cdot \cos {\left(2\pi z(v-u)\right)}\,\,\mathrm{.} \end{equation*}$$

Proof.For all v , w ∈ T L n $v,w\in \mathbb {T}^n_L$ ,

E h L ( v ) h L ( w ) = 1 a n L 2 n ∑ u ∈ T L n G ˚ L n / 4 ( v , u ) · G ˚ L n / 4 ( w , u ) · L n = 1 a n G ˚ L n / 2 ( v , w ) = k L ( v , w ) . $$\begin{align*} \mathbf {E}{\left[h_L(v)\,h_L(w)\right]}&= \frac{1}{a_n\, L^{2n}} \,\sum _{u\in \mathbb {T}^n_L}\mathring{G}_L^{n/4}(v,u) \cdot \mathring{G}_L^{n/4}(w,u) \cdot L^n\\ &=\frac{1}{a_n}\mathring{G}_L^{n/2}(v,w)=k_L(v,w)\,\,\mathrm{.} \end{align*}$$
□ $\Box$

In other words,
h L ω = 1 a n G ˚ L n / 4 Ξ ω $$\begin{equation} h^\omega _L=\frac{1}{\sqrt {a_n}}\,\mathring{\sf G}_L^{n/4} \, \Xi ^\omega \end{equation}$$ ()
with Ξ ≔ ( Ξ v ) v ∈ T L n $\Xi \coloneqq (\Xi _v)_{v\in \mathbb {T}^n_L}$ being a white noise on T L n $\mathbb {T}^n_L$ . The latter is a Gaussian random variable on R N ≅ R T L n ${\mathbb {R}}^N\cong {\mathbb {R}}^{\mathbb {T}_L^n}$ —recall that N = L n $N=L^n$ —with distribution
d P ( Ξ ) = 1 ( 2 π N ) N / 2 e − 1 2 N ∥ Ξ ∥ 2 d L N ( Ξ ) . $$\begin{equation*} d{\mathbf {P}}(\Xi)=\frac{1}{(2\pi N)^{N/2}}\,e^{-\frac{1}{2N}\Vert \Xi \Vert ^2}\,d\mathcal {L}^N(\Xi) \,\,\mathrm{.} \end{equation*}$$
Here, ∥ Ξ ∥ $\Vert \Xi \Vert$ denotes the Euclidean norm of Ξ ∈ R N $\Xi \in {\mathbb {R}}^N$ , and thus under the identification R N ≅ R T L n ${\mathbb {R}}^{N}\cong {\mathbb {R}}^{\mathbb {T}_L^n}$ ,
1 N ∥ Ξ ∥ 2 = ∥ Ξ ∥ L 2 ( T L n , m L ) 2 . $$\begin{equation*} \frac{1}{N} \Vert \Xi \Vert ^2=\Vert \Xi \Vert ^2_{L^2(\mathbb {T}^n_L,m_L)}\,\,\mathrm{.} \end{equation*}$$

3.2 A second look on the polyharmonic Gaussian field on discrete tori

(a)

Consider the orthogonal decomposition of R N ${\mathbb {R}}^N$ into the line R · ( 1 , … , 1 ) ${\mathbb {R}}\cdot (1,\ldots,1)$ and its orthogonal complement H ˚ ≔ { Ξ ∈ R N : ∑ v = 1 N Ξ v = 0 } $\mathring{H}\coloneqq \lbrace \Xi \in {\mathbb {R}}^N: \sum _{v=1}^N\Xi _v=0\rbrace$ . More precisely, consider the maps
A ¯ : R N ⟶ R , Ξ ↦ Ξ ¯ ≔ 1 N ∑ v = 1 N Ξ v $$\begin{equation*} \bar{A}: {\mathbb {R}}^N\longrightarrow {\mathbb {R}}, \quad \Xi \longmapsto \bar{\Xi }\coloneqq \frac{1}{\sqrt N}\sum _{v=1}^{N} \Xi _v \end{equation*}$$
and
A ˚ : R N ⟶ H ˚ , Ξ ↦ Ξ ˚ with Ξ ˚ j ≔ Ξ j − 1 N Ξ ¯ . $$\begin{equation*} \mathring{A}: {\mathbb {R}}^N\longrightarrow \mathring{H}, \quad \Xi \longmapsto \mathring{\Xi }\quad \text{with} \quad \mathring{\Xi }_j\coloneqq \Xi _j-\frac{1}{\sqrt N} \bar{\Xi }\,\,\mathrm{.} \end{equation*}$$
Note that A ≔ ( A ˚ , A ¯ ) : R N → H ˚ × R ⊂ R 1 + N $A\coloneqq (\mathring{A},\bar{A}): {\mathbb {R}}^N\rightarrow \mathring{H}\times {\mathbb {R}}\subset {\mathbb {R}}^{1+N}$ is a bijective linear map with A T A = E N $A^T\,A=E_N$ and inverse given by
B : H ˚ × R → R N , ( Ξ ˚ , t ) ↦ Ξ ˚ + t N · ( 1 , … , 1 ) . $$\begin{equation*} B:\mathring{H}\times {\mathbb {R}}\rightarrow {\mathbb {R}}^N, \quad (\mathring{\Xi },t)\mapsto \mathring{\Xi }+\frac{t}{\sqrt N}\cdot (1,\ldots,1) \,\,\mathrm{.} \end{equation*}$$
Thus, if L H ˚ N − 1 $\mathcal {L}^{N-1}_{\mathring{H}}$ denotes the ( N − 1 ) $(N-1)$ -dimensional Lebesgue measure on the hyperplane H ˚ $\mathring{H}$ then on R N ${\mathbb {R}}^N$ ,
L N = L H ˚ N − 1 ⊗ L 1 . $$\begin{equation*} \mathcal {L}^N=\mathcal {L}_{\mathring{H}}^{N-1}\otimes \mathcal {L}^1\,\,\mathrm{.} \end{equation*}$$
The push-forward A ¯ ∗ P $\bar{A}_*{\mathbf {P}}$ is the normal distribution N ( 0 , N ) $\mathcal {N}(0,\sqrt N)$ on the real line. The push forward  P ˚ ≔ A ˚ ∗ P $\mathring{\mathbf {P}}\coloneqq \mathring{A}_*{\mathbf {P}}$ , called (the law of) the grounded white noise, is a Gaussian measure on the hyperplane H ˚ $\mathring{H}$ given explicitly as
d P ˚ ( Ξ ) = 1 ( 2 π N ) N − 1 2 e − 1 2 N ∥ Ξ ∥ 2 d L H ˚ N − 1 ( Ξ ) . $$\begin{equation*} d\mathring{\mathbf {P}}(\Xi)= \frac{1}{(2\pi N)^{\frac{N-1}{2}}}\,e^{-\frac{1}{2N} \Vert \Xi \Vert ^2}\,d\mathcal {L}^{N-1}_{\mathring{H}}(\Xi) \,\,\mathrm{.} \end{equation*}$$
It can also be characterized as the conditional law P ( · | A ¯ = 0 ) $\mathbf {P}({\,\cdot \,}| \bar{A}=0)$ .

(b)

Let us define a measure on R N ≅ R T L n ${\mathbb {R}}^{N}\cong {\mathbb {R}}^{\mathbb {T}_L^n}$ by
d ν ̂ ( h ) ≔ c n e − a n 2 N ∥ ( − Δ L ) n / 4 h ∥ 2 d L N ( h ) , $$\begin{equation} d\widehat{\bm{\nu }}(h)\coloneqq c_n\,e^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}h\Vert ^2}\,d\mathcal {L}^N(h)\,\,\mathrm{,}\;\, \end{equation}$$ ()
where
c n ≔ a n 2 π N N − 1 2 · ∏ z ∈ Z L n ∖ { 0 } 4 L 2 ∑ k = 1 n sin 2 π z k / L n / 4 , $$\begin{equation} c_n\coloneqq {\left(\frac{a_n}{2\pi N}\right)}^{\frac{N-1}{2}}\cdot \prod _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace }{\left(4L^2\,\sum _{k=1}^n \sin ^2{\left(\pi z_k/L\right)}\right)}^{n/4}\,\,\mathrm{,}\;\, \end{equation}$$ ()
and consider the push-forward measures under the maps  A ¯ $\bar{A}$ and  A ˚ $\mathring{A}$ introduced above. On one hand, by the standard change-of-variable formula for push-forward measures and since  ( − Δ L ) n / 4 A ¯ h = 0 $(-\Delta _L)^{n/4} \bar{A} h=0$ for every  h ∈ R N $h\in {\mathbb {R}}^N$ , we have that
A ¯ ∗ ν ̂ = c n L 1 on R 1 . $$\begin{equation} \bar{A}_*\widehat{\bm{\nu }}=c_n\,\mathcal {L}^1\quad \text{on }{\mathbb {R}}^1 \,\,\mathrm{.}\end{equation}$$ ()
On the other hand, again by the standard change-of-variable formula for push-forward measures and since  ( − Δ L ) n / 4 A ˚ h = ( − Δ L ) n / 4 h $(-\Delta _L)^{n/4} \mathring{A} h=(-\Delta _L)^{n/4} h$ for every  h ∈ R N $h\in {\mathbb {R}}^N$ , we have that  ν ≔ A ˚ ∗ ν ̂ $\bm{\nu }\coloneqq \mathring{A}_*\widehat{\bm{\nu }}$ is a measure (actually, a probability measure as we will see below) on the hyperplane H ˚ ≔ { Ξ ∈ R N : Ξ ¯ = 0 } ≅ R N − 1 $\mathring{H}\coloneqq \lbrace \Xi \in {\mathbb {R}}^{N}: \bar{\Xi }=0\rbrace \cong {\mathbb {R}}^{N-1}$ given by
d ν ( h ) ≔ c n e − a n 2 N ∥ ( − Δ L ) n / 4 h ∥ 2 d L H ˚ N − 1 ( h ) . $$\begin{equation*} d{\bm{\nu }}(h)\coloneqq c_n\,\text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}h\Vert ^2}\,d\mathcal {L}^{N-1}_{\mathring{H}}(h) \,\,\mathrm{.} \end{equation*}$$
Furthermore, since  e − a n 2 N ∥ ( − Δ L ) n / 4 h ¯ ∥ 2 = 1 $\text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}\bar{h}\Vert ^2}=1$ for every  h ¯ ∈ R · ( 1 , … , 1 ) $\bar{h}\in {\mathbb {R}}\cdot (1,\ldots\,,1)$ , by orthogonality of  H ˚ $\mathring{H}$ and  R · ( 1 , … , 1 ) ${\mathbb {R}}\cdot (1,\ldots\,,1)$ in  R N ${\mathbb {R}}^N$ and the parallelogram identity, we have
e − a n 2 N ∥ ( − Δ L ) n / 4 h ˚ ∥ 2 = e − a n 2 N ∥ ( − Δ L ) n / 4 h ˚ ∥ 2 e − a n 2 N ∥ ( − Δ L ) n / 4 h ¯ ∥ 2 = e − a n 2 N ∥ ( − Δ L ) n / 4 h ∥ 2 , h = ( h ˚ , h ¯ ) . $$\begin{equation*} \text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}\mathring{h}\Vert ^2} = \text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}\mathring{h}\Vert ^2} \text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}\bar{h}\Vert ^2} = \text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4} h\Vert ^2}\,\,\mathrm{,}\;\,\qquad h=(\mathring{h}, \bar{h}) \,\,\mathrm{.} \end{equation*}$$
Thus, in light of Equation (18), we have the decomposition of measures
ν ̂ = c n ν ⊗ L 1 . $$\begin{equation*} \widehat{\bm{\nu }}= c_n\, \bm{\nu }\otimes \mathcal {L}^1 \,\,\mathrm{.} \end{equation*}$$

(c)

Now consider the map
T : R N → R N , h ↦ Ξ = a n ( − Δ L ) n / 4 h $$\begin{equation*} T: {\mathbb {R}}^{N}\rightarrow {\mathbb {R}}^{N}\,\,\mathrm{,}\;\,\qquad h\mapsto \Xi =\sqrt {a_n}\, (-\Delta _L)^{n/4}h \end{equation*}$$
as well as its restriction T ˚ : H ˚ → H ˚ $\mathring{T}: \mathring{H}\rightarrow \mathring{H}$ . The latter is bijective with inverse
T ˚ − 1 : H ˚ → H ˚ , Ξ ↦ h = 1 a n G ˚ L n / 4 Ξ , $$\begin{equation*} \mathring{T}^{-1}: \mathring{H}\rightarrow \mathring{H}\,\,\mathrm{,}\;\,\qquad \Xi \mapsto h=\frac{1}{\sqrt {a_n}}\, \mathring{\sf G}_L^{n/4}\Xi \,\,\mathrm{,}\;\, \end{equation*}$$
cf. Equation (15), and with determinant
det T ˚ = a n N − 1 2 · ∏ z ∈ Z L n ∖ { 0 } λ L , z n / 4 . $$\begin{equation*} \mathrm{det}\, \mathring{T}=a_n^{\frac{N-1}{2}}\cdot \prod _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace }\lambda _{L,z}^{n/4} \,\,\mathrm{.} \end{equation*}$$

Theorem 3.4.The distribution of the discrete polyharmonic field on T L n ${\mathbb {T}_L^n}$ is given by the probability measure ν $\bm{\nu }$ on R T L n ≅ R N ${\mathbb {R}}^{\mathbb {T}_L^n}\cong {\mathbb {R}}^N$ . (Indeed, it is supported there on the hyperplane of grounded fields.) Furthermore,

T ˚ ∗ ν = P ˚ . $$\begin{equation*} \mathring{T}_*\bm{\nu }=\mathring{\mathbf {P}} \,\,\mathrm{.} \end{equation*}$$

Proof.For bounded measurable f $f$ on H ˚ $\mathring{H}$ ,

∫ H ˚ f ( Ξ ) d T ˚ ∗ ν ( Ξ ) = ∫ H ˚ f ( T ˚ h ) d ν ( h ) = c n ∫ H ˚ f ( T ˚ h ) e − a n 2 N ∥ ( − Δ L ) n / 4 h ∥ 2 d L H ˚ N − 1 ( h ) = c n ∫ H ˚ f ( T ˚ h ) e − 1 2 N ∥ T ˚ h ∥ 2 d L H ˚ N − 1 ( h ) = c n det T ˚ − 1 ∫ H ˚ f ( Ξ ) e − 1 2 N ∥ Ξ ∥ 2 d L H ˚ N − 1 ( Ξ ) = c n det T ˚ − 1 ( 2 π N ) N − 1 2 ∫ H f ( Ξ ) d P ˚ ( Ξ ) . $$\begin{align*} \int _{\mathring{H}} f(\Xi)\,d\mathring{T}_*\bm{\nu }(\Xi)&=\int _{\mathring{H}}f(\mathring{T} h)\,d\bm{\nu }(h)\\ &= c_n\,\int _{\mathring{H}}f(\mathring{T} h)\, \text{e}^{-\frac{a_n}{2N}\Vert (-\Delta _L)^{n/4}h\Vert ^2}\,d\mathcal {L}^{N-1}_{\mathring{H}}(h)\\ &= c_n\,\int _{\mathring{H}}f(\mathring{T} h)\, \text{e}^{-\frac{1}{2N}\Vert \mathring{T} h\Vert ^2}\,d\mathcal {L}^{N-1}_{\mathring{H}}(h)\\ &= c_n\,\mathrm{det}\, \mathring{T}^{-1}\,\int _{\mathring{H}}f(\Xi)\, \text{e}^{-\frac{1}{2N}\Vert \Xi \Vert ^2}\,d\mathcal {L}^{N-1}_{\mathring{H}}(\Xi)\\ &= c_n\,\mathrm{det}\, \mathring{T}^{-1}\,(2\pi N)^{\frac{N-1}{2}}\,\int _Hf(\Xi)\,d\mathring{\mathbf {P}}(\Xi). \end{align*}$$
Since c n det T ˚ − 1 ( 2 π N ) N − 1 2 = 1 $c_n\,\mathrm{det}\, \mathring{T}^{-1}\,(2\pi N)^{\frac{N-1}{2}}=1$ according to our choice of c n $c_n$ , this proves the claim. □ $\Box$

3.3 Reduced polyharmonic Gaussian fields on the discrete torus

Besides the polyharmonic Gaussian field h L $h_L$ on the discrete torus, we occasionally consider two closely related random fields h L − ∘ $h_L^{{-\circ }}$ and h L − $h_L^{{-}}$ in the defining properties of which the eigenvalues λ L , z = 4 L 2 ∑ k = 1 n sin 2 π z k / L $\lambda _{L,z}=4L^2\,\sum _{k=1}^n \sin ^2\left(\pi z_k/L\right)$ of the discrete Laplacian are replaced by the eigenvalues λ z = ( 2 π | z | ) 2 $\lambda _z=(2\pi |z|)^2$ of the continuous Laplacian or by λ z · ϑ L , z − 4 / n $\lambda _z\cdot \vartheta _{L,z}^{-4/n}$ , resp., with ϑ L , z $\vartheta _{L,z}$ as in Equation (12).

Definition 3.5.We define

  • ( i ) $(i)$ the spectrally reduced discrete polyharmonic Gaussian field as the centered Gaussian field  h L − ∘ = ( h L − ∘ ( v ) ) v ∈ T L n $h_L^{{-\circ }}=(h^{{-\circ }}_L(v))_{v\in \mathbb {T}^n_L}$ with covariance function
    k L − ∘ ( v , u ) ≔ 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ z n / 2 φ z ( v ) φ z ( u ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 ( 2 π | z | ) n · cos 2 π z · ( v − u ) . $$\begin{align*} k^{{-\circ }}_L(v,u)&\coloneqq \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda ^{n/2}_{z}}\ \varphi _z(v)\, \varphi _z(u) =\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{(2\pi |z|)^{n}}\cdot \cos {\left(2\pi \, z\cdot (v-u)\right)}\,\,\mathrm{.} \end{align*}$$
  • ( i i ) $(ii)$ the reduced discrete polyharmonic Gaussian field as the centered Gaussian field  h L − = ( h L − ( v ) ) v ∈ T L n $h_L^{{-}}=(h^{{-}}_L(v))_{v\in \mathbb {T}^n_L}$ with covariance function
    k L − ( v , u ) ≔ 1 a n ∑ z ∈ Z L n ∖ { 0 } ϑ L , z 2 λ z n / 2 φ z ( v ) φ z ( u ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } ϑ L , z 2 ( 2 π | z | ) n · cos 2 π z · ( v − u ) . $$\begin{align*} k^{{-}}_L(v,u)&\coloneqq \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{\vartheta _{L,z}^2}{\lambda ^{n/2}_{z}}\ \varphi _z(v)\, \varphi _z(u) =\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{\vartheta ^2_{L,z}}{(2\pi |z|)^{n}}\cdot \cos {\left(2\pi \, z\cdot (v-u)\right)}\,\,\mathrm{.} \end{align*}$$

Similarly as before for h L $h_L$ , we obtain the following representation results.

Remark 3.6.

  • ( i ) $(i)$ Given a polyharmonic Gaussian field h L $h_L$ on T L n $\mathbb {T}^n_L$ , a reduced polyharmonic Gaussian field and a spectrally reduced polyharmonic Gaussian field on T L n $\mathbb {T}^n_L$ are defined by
    h L − ≔ r L − ( h L ) , h L − ∘ ≔ r L − ∘ ( h L ) . $$\begin{align*} h_L^{{-}}\coloneqq {\sf r}_L^{{-}}(h_L), \qquad h_L^{{-\circ }}\coloneqq {\sf r}_L^{{-\circ }}(h_L) \,\,\mathrm{.} \end{align*}$$
  • ( i i ) $(ii)$ Given i.i.d. standard normals ξ z $\xi _z$ for z ∈ Z L n ∖ { 0 } ${z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }$ , a reduced polyharmonic Gaussian field on  T L n $\mathbb {T}^n_L$ is defined by
    h L − ( v ) ≔ 1 a n ∑ z ∈ Z L n ∖ { 0 } ϑ L , z λ z n / 4 · ξ z · φ z ( v ) . $$\begin{equation} h_L^{{-}}(v)\coloneqq \frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{\vartheta _{L,z}}{\lambda _{z}^{n/4}} \cdot \xi _z\cdot \varphi _z(v) \,\,\mathrm{.}\end{equation}$$ ()
    and a spectrally reduced polyharmonic Gaussian field by
    h L − ∘ ( v ) ≔ 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ z n / 4 · ξ z · φ z ( v ) . $$\begin{equation} h^{{-\circ }}_L(v)\coloneqq \frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{z}^{n/4}} \cdot \xi _z\cdot \varphi _z(v) \,\,\mathrm{.} \end{equation}$$ ()

3.4 Extensions of the polyharmonic Gaussian field on the discrete torus

We consider the following extensions of discrete polyharmonic Gaussian fields to the continuous torus. Recall the definition of  Q L $Q_L$ and  Q L ( v ) $Q_L(v)$ in Equation (7).

Definition 3.7. (Extensions (Figure 4))Given a discrete polyharmonic Gaussian field  h L $h_L$ on  T L n $\mathbb {T}^n_L$ as in Definition 3.1, we define

  • ( i ) $(i)$ its piecewise constant extension by
    h L , ♭ ( x ) ≔ h L ( v ) , x ∈ Q L ( v ) with v ∈ T L n , $$\begin{equation*} h_{L,\flat }(x)\coloneqq h_L(v)\,\,\mathrm{,}\;\,\qquad x\in Q_L(v) \text{ with } v\in \mathbb {T}^n_L \,\,\mathrm{,}\;\, \end{equation*}$$
    which is a centered Gaussian field on T n $\mathbb {T}^n$ with covariance function
    k L , ♭ ( x ) ≔ k L ( v ) , x ∈ Q L ( v ) with v ∈ T L n ; $$\begin{equation*} k_{L,\flat }(x) \coloneqq k_{L}(v) \,\,\mathrm{,}\;\,\qquad x\in Q_L(v) \text{ with } v\in \mathbb {T}^n_L \,\,\mathrm{;}\;\, \end{equation*}$$
  • ( i i ) $(ii)$ its Fourier extension by
    h L , ♯ ( x ) ≔ r ̇ L h ( x ) = ⟨ h , r L ( x , · ) ⟩ T L N , x ∈ T n , $$\begin{equation} h_{L,\sharp }(x)\coloneqq \dot{\sf r}_L h(x) = {\langle h, r_L(x,{\,\cdot \,})\rangle} _{\mathbb {T}^N_L} \,\,\mathrm{,}\;\,\qquad x\in \mathbb {T}^n\,\,\mathrm{,}\;\,\end{equation}$$ ()
    which is a centered Gaussian field on T n $\mathbb {T}^n$ with covariance function
    k L , ♯ ( x , y ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 · cos 2 π z · ( x − y ) , x , y ∈ T n . $$\begin{equation} k_{L,\sharp }(x,y)=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}\cdot \cos {\left(2\pi \, z\cdot (x-y)\right)}\,\,\mathrm{,}\;\,\qquad x,y\in \mathbb {T}^n \,\,\mathrm{.}\end{equation}$$ ()

Similarly, given a spectrally reduced, resp. reduced, discrete polyharmonic Gaussian field  h L − ∘ $h^{-\circ }_L$ , resp.  h L − $h^-_L$ , as in Definition 3.5 ( i ) $(i)$ , resp.  ( i i ) $(ii)$ on the discrete torus  T L n $\mathbb {T}^n_L$ , we define (in the natural way)

  • ( i i i ) $(iii)$ their piecewise constant extensions  h L , ♭ − ∘ $h_{L,\flat }^{{-\circ }}$ , resp.  h L , ♭ − $h_{L,\flat }^{{-}}$ ;
  • ( i v ) $(iv)$ their Fourier extensions h L , ♯ − ∘ $h_{L,\sharp }^{{-\circ }}$ , resp.  h L , ♯ − $h_{L,\sharp }^{{-}}$ ;
which are centered Gaussian fields on  T n $\mathbb {T}^n$ .

Remark 3.8.As for  h L , ♭ $h_{L,\flat }$ , let us note that

⟨ h L , ♭ , f ⟩ T n = ⟨ h L , q L f ⟩ T L n , f ∈ L 2 ( T n ) , $$\begin{equation*} {\langle h_{L,\flat },f\rangle} _{\mathbb {T}^n} = {\langle h_L,{\sf q}_Lf\rangle }_{\mathbb {T}_L^n} \,\,\mathrm{,}\;\,\qquad f\in L^2(\mathbb {T}^n)\,\,\mathrm{,}\;\, \end{equation*}$$
with q L f ∈ L 2 ( T L n ) ${\sf q}_Lf\in L^2(\mathbb {T}^n_L)$ as in Equation (9). (Note that q L f ( v ) = L n ∫ Q L ( v ) f ( y ) d y ${\sf q}_Lf(v)= L^{n}\int _{Q_L(v)} f(y)dy$ for v ∈ T L n $v\in \mathbb {T}^n_L$ .)

As for  h L , ♯ $h_{L,\sharp }$ , let us note that, for every ω $\omega$ , the function h L , ♯ ω $h^\omega _{L,\sharp }$ is the unique function in  D L ${\mathcal {D}}_L$ with h L , ♯ ω = h L ω $h^\omega _{L,\sharp }=h^\omega _L$ on T L n $\mathbb {T}^n_L$ , cf. Equation (14). Furthermore, if a discrete polyharmonic Gaussian field  h L $h_L$ is given in its representation

h L ( v ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 4 · ξ z · φ z ( v ) , v ∈ T L n , $$\begin{equation*} h_L(v)= \frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/4}} \cdot \xi _z\cdot \varphi _z(v)\,\,\mathrm{,}\;\,\qquad v\in \mathbb {T}_L^n\,\,\mathrm{,}\;\, \end{equation*}$$
then,  h L , ♯ $h_{L,\sharp }$ can be represented as
h L , ♯ ( x ) ≔ r ̇ L h ( x ) = ⟨ h , r L ( x , · ) ⟩ T L N = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 4 · ξ z · φ z ( x ) , x ∈ T n . $$\begin{equation*} h_{L,\sharp }(x)\coloneqq \dot{\sf r}_L h(x) = {\langle h, r_L(x,{\,\cdot \,})\rangle} _{\mathbb {T}^N_L} =\frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/4}} \cdot \xi _z\cdot \varphi _z(x)\,\,\mathrm{,}\;\,\qquad x\in \mathbb {T}^n\,\,\mathrm{.} \end{equation*}$$

4 THE POLYHARMONIC GAUSSIAN FIELD ON THE CONTINUOUS TORUS AND ITS (SEMI-)DISCRETE APPROXIMATIONS

This section is devoted to the analysis of approximation properties for the polyharmonic field on the continuous torus in terms of Gaussian fields on the discrete torus and semi-discrete extensions of the latter on the continuous torus.
  • The basic objects are the polyharmonic field h $h$ on the continuous torus and its discrete counterpart, the polyharmonic field h L $h_L$ on the discrete torus.
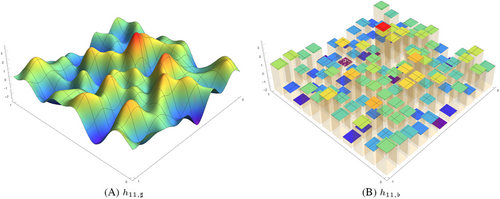
  • Starting from the field  h $h$ on T n $\mathbb {T}^n$ , we define its Fourier projection (i.e., eigenfunction approximation)  h ♯ , L $h_{\sharp,L}$ , its piecewise constant projection  h ♭ , L $h_{\flat,L }$ , its natural projection  h ∘ , L $h_{\circ,L }$ , and its enhanced projection h + , L $h_{+,L}$ . All of them are Gaussian random fields on T n $\mathbb {T}^n$ .
  • Starting from the field h L $h_L$ on T L n $\mathbb {T}^n_L$ , we define its Fourier extension h L , ♯ $h_{L,\sharp }$ and its piecewise constant extension h L , ♭ $h_{L,\flat }$ . Analogous extensions are defined for the spectrally reduced discrete field h L − ∘ $h_L^{{-\circ }}$ and the reduced discrete field h L − $h_L^{{-}}$ on T L n $\mathbb {T}^n_L$ . All these extensions are Gaussian random fields on T n $\mathbb {T}^n$ .
To summarize:
  • - ♭ $\flat$ stands for piecewise constant extension/projection, ♯ $\sharp$ for Fourier extension/restriction;
  • - h L , * $h_{L,\ast }$ with * ∈ { ♭ , ♯ } $\ast \in \lbrace \flat,\sharp \rbrace$ denotes the respective extension of the discrete field h L $h_L$ ; similarly for h L − ∘ $h_L^{{-\circ }}$ and h L − $h_L^{{-}}$ ;
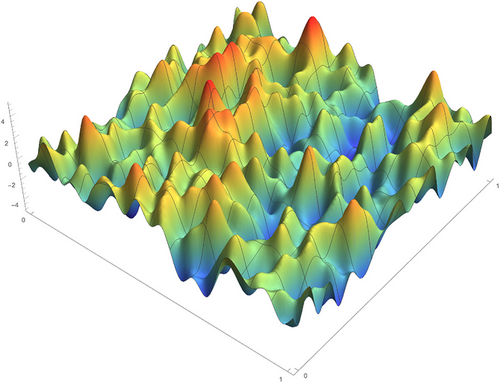
  • - h * , L $h_{\ast, L}$ with * ∈ { ♭ , ♯ , ∘ , + } $\ast \in \lbrace \flat,\sharp, \circ, +\rbrace$ denotes the projection of the continuous field h $h$ onto the respective class of fields of order L $L$ on the continuous torus (Figure 3).

4.1 The polyharmonic Gaussian field on the continuous torus and the convergence properties of its projections

Definition 4.1.A random field h = ( ⟨ h | f ⟩ ) f ∈ H n / 2 ( T n ) $h=(\langle h|f\rangle)_{f\in H^{n/2}(\mathbb {T}^n)}$ on the continuous n $n$ -torus is called polyharmonic Gaussian field if it is a centered Gaussian field with covariance function k $k$ in the sense that

E ⟨ h | f ⟩ · ⟨ h | g ⟩ = ∫ T n ∫ T n f ( x ) k ( x , y ) g ( y ) d y d x , f , g ∈ H n / 2 ( T n ) . $$\begin{equation*} \mathbf {E}{\left[\langle h|f\rangle \cdot \langle h|g\rangle \right]}=\int _{\mathbb {T}^n}\int _{\mathbb {T}^n} f(x) k(x,y) g(y)\,dy\,dx \,\,\mathrm{,}\;\,\qquad f,g\in H^{n/2}(\mathbb {T}^n)\,\,\mathrm{.} \end{equation*}$$

Proposition 4.2.The polyharmonic Gaussian field  h $h$ exists and can be realized in H ˚ − ε ( T n ) $\mathring{H}^{-\epsilon }(\mathbb {T}^n)$ . Furthermore, the pairing ⟨ h | f ⟩ $\langle h|f\rangle$ continuously extends to all f ∈ H ˚ − n / 2 ( T n ) $f\in \mathring{H}^{-n/2}(\mathbb {T}^n)$ .

Proof.For even n $n$ , the polyharmonic field to be considered here is just a particular case of the co-polyharmonic field considered in [5] on large classes of Riemannian manifolds. For flat spaces like the torus, the arguments for proving Theorem 3.2 and Remarks 3.4 and 3.5 there obviously apply also to odd  n $n$ . □ $\Box$

Recall that we set  λ z ≔ ( 2 π | z | ) 2 $\lambda _{z}\coloneqq (2\pi |z|)^2$ .

Definition 4.3. (Projections)Given a copolyharmonic Gaussian field  h $h$ on  T n $\mathbb {T}^n$ , we define

  • ( i ) $(i)$ its Fourier projection onto the space  D L $\mathcal {D}_L$ , see Section 2.3(a), by
    h ♯ , L ( x ) ≔ ⟨ h | r L ( x , · ) ⟩ , r L ≔ ∑ z ∈ Z L n ∖ { 0 } φ z ⊗ φ z , $$\begin{equation} h_{\sharp,L}(x)\coloneqq \langle h| r_{L}(x,{\,\cdot \,})\rangle, \qquad r_{L}\coloneqq \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \varphi _z\otimes \varphi _z \,\,\mathrm{,}\;\,\end{equation}$$ ()
    which is a centered Gaussian field on T n $\mathbb {T}^n$ with covariance function
    k ♯ , L ( x , y ) ≔ 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ z n / 2 · cos 2 π z · ( x − y ) ; $$\begin{equation} k_{\sharp,L}(x,y)\coloneqq \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{z}^{n/2}}\cdot \cos {\left(2\pi \, z\cdot (x-y)\right)} \,\,\mathrm{;}\;\,\end{equation}$$ ()
  • ( i i ) $(ii)$ its piecewise constant projection, cf. Section 2.3(b), by
    h ♭ , L ( x ) ≔ ⟨ h | q L ( x , · ) ⟩ , q L ≔ L n ∑ v ∈ T L n 1 Q L ( v ) ⊗ 1 Q L ( v ) , $$\begin{equation} h_{\flat,L}(x)\coloneqq \langle h| q_L(x,{\,\cdot \,})\rangle, \qquad q_L\coloneqq L^n\sum _{v\in \mathbb {T}^n_L}{\bf 1}_{Q_L(v)}\otimes {\bf 1}_{Q_L(v)}\,\,\mathrm{,}\;\,\end{equation}$$ ()
    which is a centered Gaussian field on  T n $\mathbb {T}^n$ with covariance function
    k ♭ , L ( x , y ) ≔ E h ♭ , L ( x ) h ♭ , L ( y ) = L 2 n ∑ v , w ∈ T L n 1 Q L ( v ) ( x ) 1 Q L ( w ) ( y ) ∫ Q L ( v ) ∫ Q L ( w ) k ( x ′ , y ′ ) d y ′ d x ′ ; $$\begin{equation} k_{\flat,L}(x,y)\coloneqq \mathbb {E}{\left[h_{\flat,L}(x)\,h_{\flat,L}(y)\right]}=L^{2n}\sum _{v,w\in \mathbb {T}^n_L} {\bf 1}_{Q_L(v)}(x)\, {\bf 1}_{Q_L(w)}(y)\, \int _{Q_L(v)}\int _{Q_L(w)} k(x^{\prime },y^{\prime })\,dy^{\prime }\,dx^{\prime } \,\,\mathrm{;}\;\,\end{equation}$$ ()
  • ( i i i ) $(iii)$ its enhanced piecewise constant projection (shortly: enhanced projection) by
    h + , L ( x ) ≔ ⟨ h | p + , L ( x , · ) ⟩ , p + , L ≔ q L ∘ r L + , r L + ≔ ∑ z ∈ Z L n 1 ϑ L , z · λ z λ L , z n / 4 · φ z ⊗ φ z , $$\begin{equation} { \def\eqcellsep{&}\begin{array}{c}h_{+,L}(x)\coloneqq \langle h| p_{+,L}(x,{\,\cdot \,})\rangle \,\,\mathrm{,}\;\,\qquad p_{+,L}\coloneqq q_{L}\circ r_L^{{+}}\,\,\mathrm{,}\;\,\\[3pt] r^{{+}}_L\coloneqq \sum _{z\in {\mathbb {Z}}^n_L} \, \frac{1}{\vartheta _{L,z}}\cdot {\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}\cdot \varphi _z\otimes \varphi _z\,\,\mathrm{,}\;\, \end{array} } \end{equation}$$ ()
    with  q L $q_L$ as in Equation (25), which is a centered Gaussian field on  T n $\mathbb {T}^n$ with covariance function
    k + , L ( x , y ) ≔ 1 a n ∑ z ∈ Z L n 1 ϑ L , z 2 · 1 λ L , z n / 2 · q L φ z ( x ) · q L φ z ( y ) ; $$\begin{equation} k_{+,L}(x,y)\coloneqq \frac{1}{a_n} \sum _{z\in {\mathbb {Z}}^n_L} \, \frac{1}{\vartheta _{L,z}^2}\cdot \frac{1}{\lambda _{L,z}^{n/2}}\cdot {\sf q}_L\varphi _z(x)\cdot {\sf q}_L\varphi _z(y) \,\,\mathrm{;}\;\, \end{equation}$$ ()
  • ( i v ) $(iv)$ its natural projection as the piecewise constant projection of its Fourier projection:
    h ∘ , L ( x ) ≔ q L ( r L ( h ) ) ( x ) = ⟨ h | p ∘ , L ( x , · ) ⟩ , p ∘ , L ≔ q L ∘ r L , $$\begin{equation} h_{\circ,L}(x)\coloneqq {\sf q}_L({\sf r}_L(h))(x)= \langle h| p_{\circ,L}(x,{\,\cdot \,})\rangle \,\,\mathrm{,}\;\,\qquad p_{\circ,L}\coloneqq q_{L}\circ r_L\,\,\mathrm{,}\;\,\end{equation}$$ ()
    with  r L $r_L$ as in Equation (23) and  q L $q_L$ as in Equation (25), which is a centered Gaussian field on  T n $\mathbb {T}^n$ with covariance function
    k ∘ , L ( x , y ) ≔ 1 a n ∑ z ∈ Z L n 1 λ z n / 2 · q L φ z ( x ) · q L φ z ( y ) . $$\begin{equation} k_{\circ,L}(x,y)\coloneqq \frac{1}{a_n} \sum _{z\in {\mathbb {Z}}^n_L} \, \frac{1}{\lambda _{z}^{n/2}}\cdot {\sf q}_L\varphi _z(x)\cdot {\sf q}_L\varphi _z(y) \,\,\mathrm{.} \end{equation}$$ ()

Remark 4.4.We note that the random fields  h + , L $h_{+,L}$ and  h ∘ , L $h_{\circ, L}$ are piecewise constant, and may thus be equivalently regarded as either piecewise constant random fields on the continuous torus  T n $\mathbb {T}^n$ or random fields on the discrete torus  T L n $\mathbb {T}^n_L$ .

Proposition 4.5. (cf. [[5], Props. 3.9, 3.11, and Ex. 3.12 ( i v ) $(iv)$ ])For all f ∈ H ˚ − n / 2 ( T n ) $f\in \mathring{H}^{-n/2}(\mathbb {T}^n)$ ,

⟨ h ♯ , L , f ⟩ T n → ⟨ h , f ⟩ T n in L 2 ( P ) as L → ∞ $$\begin{equation*} {\langle h_{\sharp,L},f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \quad \text{in\quad $L^2(\mathbf {P})$ as }L\rightarrow \infty \end{equation*}$$
and for every ε > 0 $\epsilon >0$ ,
h ♯ , L − h H − ε in L 2 ( P ) as L → ∞ . $$\begin{equation*} {\left\Vert h_{\sharp,L}- h\right\Vert} _{H^{-\epsilon }} \quad \text{in\quad $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{.} \end{equation*}$$

Proof.For the reader's convenience, we briefly summarize the argument from [5] for the first assertion:

E ⟨ h − h ♯ , L , f ⟩ 2 = 1 a n E ∑ z ∈ Z n ∖ Z L n 1 ( 2 π | z | ) n / 2 ξ z ⟨ φ z , f ⟩ 2 = 1 a n ∑ z ∈ Z n ∖ Z L n 1 ( 2 π | z | ) n ⟨ φ z , f ⟩ 2 → 0 $$\begin{align*} \mathbf {E}{\left[\langle h-h_{\sharp,L},f\rangle ^2\right]}&=\frac{1}{a_n} \mathbf {E}{\left[{\left|\sum _{z\in {\mathbb {Z}}^n\setminus {\mathbb {Z}}_L^n} \frac{1}{{(2\pi |z|)}^{n/2}}\,\xi _z\, \langle \varphi _z,f\rangle \right|}^2 \right]}\\ &=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n\setminus {\mathbb {Z}}_L^n} \frac{1}{{(2\pi |z|)}^{n}}\, \langle \varphi _z,f\rangle ^2 \rightarrow 0 \end{align*}$$
as L → ∞ $L\rightarrow \infty$ , since
∑ z ∈ Z n ∖ { 0 } 1 ( 2 π | z | ) n ⟨ φ z , f ⟩ 2 = ∥ ( − Δ ) − n / 2 f ∥ L 2 2 = ∥ f ∥ H ˚ − n / 2 2 < ∞ . $$\begin{equation*} \sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace } \frac{1}{{(2\pi |z|)}^{n}}\, \langle \varphi _z,f\rangle ^2 =\big \Vert (-\Delta)^{-n/2}f\big \Vert _{L^2}^2=\big \Vert f\big \Vert _{\mathring{H}^{-n/2}}^2<\infty \,\,\mathrm{.} \end{equation*}$$
□ $\Box$

Proposition 4.6.For all f ∈ L 2 ( T n ) $f\in L^2(\mathbb {T}^n)$ ,

⟨ h ♭ , L , f ⟩ T n → ⟨ h , f ⟩ T n in L 2 ( P ) as L → ∞ $$\begin{equation*} {\langle h_{\flat,L},f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \end{equation*}$$
and for every s > n / 2 $s>n/2$ ,
h ♭ , L − h H − s → 0 in L 2 ( P ) as L → ∞ . $$\begin{equation*} {\left\Vert h_{\flat,L} - h\right\Vert} _{H^{-s}} \rightarrow 0 \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{.} \end{equation*}$$

Proof.Since ⟨ h ♭ , L , f ⟩ T n = ⟨ h , q L f ⟩ T n ${\langle h_{\flat,L},f\rangle} _{\mathbb {T}^n} ={\langle h,{\sf q}_L f\rangle} _{\mathbb {T}^n}$ with ( q L f ) ( x ) ≔ ∫ T n q L ( x , y ) f ( y ) d y $({\sf q}_Lf)(x)\coloneqq \int _{\mathbb {T}^n} q_L(x,y)f(y)\,dy$ , we obtain

E ⟨ h ♭ , L − h , f ⟩ 2 = E ⟨ h , q L f − f ⟩ 2 = ∥ q L f − f ∥ H − n / 2 2 ≤ ∥ q L f − f ∥ L 2 2 → 0 as L → ∞ . $$\begin{align*} \mathbf {E}{\left[\langle h_{\flat,L}- h,f\rangle ^2\right]} &=\mathbf {E}{\left[\langle h,{\sf q}_Lf-f\rangle ^2\right]}=\big \Vert {\sf q}_Lf-f\big \Vert ^2_{H^{-n/2}}\\ &\le \big \Vert {\sf q}_Lf-f\big \Vert ^2_{L^2}\rightarrow 0\quad \text{as $L\rightarrow \infty $.} \end{align*}$$
To prove the second assertion, let h $h$ be given as
h = 1 a n ∑ z ∈ Z n ∖ { 0 } ξ z φ z λ z n / 4 $$\begin{equation*} h = \frac{1}{\sqrt {a_{n}}} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \xi _{z} \frac{\varphi _{z}}{\lambda _{z}^{n/4}} \end{equation*}$$
from which we get
h ♭ , L = 1 a n ∑ z ∈ Z n ∖ { 0 } ξ z q L φ z λ z n / 4 = 1 a n ∑ z ∈ Z n ∖ { 0 } ξ z λ z n / 4 ∑ w ∈ Z n ∖ { 0 } ⟨ φ w , q L φ z ⟩ φ w . $$\begin{equation*} h_{\flat,L} = \frac{1}{\sqrt {a_{n}}} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \xi _{z} \frac{\mathsf {q}_{L} \varphi _{z}}{\lambda _{z}^{n/4}} = \frac{1}{\sqrt {a_{n}}} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \frac{\xi _{z}}{\lambda _{z}^{n/4}} \sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \langle \varphi _{w}, \mathsf {q}_{L} \varphi _{z}\rangle \varphi _{w} \,\,\mathrm{.} \end{equation*}$$
Consequently
a n − Δ − s / 2 ( h − h ♭ , L ) = ∑ z ∈ Z n ∖ { 0 } ξ z λ z − n / 4 − s / 2 φ z − ⟨ φ z , q L φ z ⟩ φ z − ∑ z ∈ Z n ∖ { 0 } ξ z λ z − n / 4 ∑ w ∈ Z n ∖ { 0 , z } λ w − s / 2 ⟨ φ w , q L φ z ⟩ φ w . $$\begin{equation*} \begin{split} \sqrt {a_{n}} {\left(-\Delta \right)}^{-s/2} (h - h_{\flat,L}) &= \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \xi _{z} \lambda _{z}^{-n/4-s/2} {\left(\varphi _{z} - \langle \varphi _{z}, \mathsf {q}_{L}\varphi _{z}\rangle \varphi _{z} \right)} \\ &- \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \xi _{z} \lambda _{z}^{-n/4} \sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0,z\rbrace } \lambda _{w}^{-s/2} \langle \varphi _{w}, \mathsf {q}_{L} \varphi _{z}\rangle \varphi _{w} \,\,\mathrm{.}\end{split} \end{equation*}$$
Finally,
a n E h − h ♭ , L H − s 2 = ∑ z ∈ Z n ∖ { 0 } λ z − n / 2 − s 1 − ⟨ φ z , q L φ z ⟩ 2 + ∑ z ∈ Z n ∖ { 0 } λ z − n / 2 ∑ w ∈ Z n ∖ { 0 , z } λ w − s ⟨ φ w , q L φ z ⟩ 2 . $$\begin{equation} \begin{split} a_{n} \mathbf {E} \left[{ {\left\Vert h - h_{\flat,L}\right\Vert} _{H^{-s}}^{2} }\right] &= \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-n/2-s} {\left(1 - \langle \varphi _{z}, \mathsf {q}_{L}\varphi _{z}\rangle \right)}^{2} \\ &+ \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-n/2} \sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0,z\rbrace } \lambda _{w}^{-s} \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle ^{2} \,\,\mathrm{.}\end{split} \end{equation}$$ ()
Since | ⟨ φ z , q L φ z ⟩ | ≤ 1 $|\langle \varphi _{z}, \mathsf {q}_{L}\varphi _{z}\rangle | \le 1$ for all L $L$ and ⟨ φ z , q L φ z ⟩ → 1 $\langle \varphi _{z}, \mathsf {q}_{L}\varphi _{z}\rangle \rightarrow 1$ as L → ∞ $L \rightarrow \infty$ and
∑ z ∈ Z n ∖ { 0 } λ z − n / 2 − s 1 − ⟨ φ z , q L φ z ⟩ 2 ≤ ∑ z ∈ Z n ∖ { 0 } λ z − n / 2 − s < ∞ , $$\begin{equation*} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-n/2-s} {\left(1 - \langle \varphi _{z}, \mathsf {q}_{L}\varphi _{z}\rangle \right)}^{2} \le \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-n/2-s} < \infty \,\,\mathrm{,}\;\, \end{equation*}$$
we find that the first term on the right-hand side of Equation (31) vanishes as L → ∞ $L \rightarrow \infty$ . By Parseval's identity and the fact that λ z ≥ 1 $\lambda _z\ge 1$ for all z ≠ 0 $z\not=0$ , we get that
∑ z ∈ Z n ∖ { 0 } λ z − n / 2 ∑ w ∈ Z n ∖ { 0 , z } λ w − s ⟨ φ w , q L φ z ⟩ 2 ≤ ∑ w ∈ Z n ∖ { 0 } λ w − s ∑ z ∈ Z n ∖ { 0 , w } ⟨ φ w , q L φ z ⟩ 2 = ∑ w ∈ Z n ∖ { 0 } λ w − s q L φ w L 2 2 − ⟨ φ w , q L φ w ⟩ 2 ≤ ∑ w ∈ Z n ∖ { 0 } λ w − s $$\begin{align*} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-n/2} \sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0,z\rbrace } \lambda _{w}^{-s} \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle ^{2} &\le \sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{w}^{-s} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0,w\rbrace } \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle ^{2}\\ &=\sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{w}^{-s} \,{\left[{\left\Vert \mathsf {q}_{L}\varphi _{w}\right\Vert} ^2_{L^{2}}-\langle \varphi _{w}, \mathsf {q}_{L}\varphi _{w}\rangle ^{2} \right]}\\ &\le \sum _{w \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{w}^{-s} \end{align*}$$
which converges since s > n / 2 $s > n/2$ . Moreover, 0 ≤ q L φ w L 2 2 − ⟨ φ w , q L φ w ⟩ 2 ≤ 1 $0\le \left\Vert \mathsf {q}_{L}\varphi _{w}\right\Vert ^2_{L^{2}}-\langle \varphi _{w}, \mathsf {q}_{L}\varphi _{w}\rangle ^{2}\le 1$ for all w $w$ and L $L$ , and q L φ w L 2 2 − ⟨ φ w , q L φ w ⟩ 2 → 0 $\left\Vert \mathsf {q}_{L}\varphi _{w}\right\Vert ^2_{L^{2}}-\langle \varphi _{w}, \mathsf {q}_{L}\varphi _{w}\rangle ^{2}\rightarrow 0$ for all w $w$ as L → ∞ $L\rightarrow \infty$ . Thus, also the second term on the right-hand side of Equation (31) vanishes as L → ∞ $L \rightarrow \infty$ . □ $\Box$

Lemma 4.7.Let  ∗ $*$ denote either of the subscripts  + $+$ and  ∘ $\circ$ . Then,

  • ( i ) $(i)$ For all f ∈ L 2 ( T n ) $f\in L^2(\mathbb {T}^n)$ ,
    p ∗ , L f → f in L 2 ( T n ) as L → ∞ . $$\begin{equation*} {\sf p}_{*,L}f\rightarrow f\quad \text{in $L^2(\mathbb {T}^n)$ as $L\rightarrow \infty $}\,\,\mathrm{.} \end{equation*}$$
  • ( i i ) $(ii)$ On T n × T n $\mathbb {T}^n\times \mathbb {T}^n$ ,
    k ∗ , L → k in L 0 ( T n ) as L → ∞ . $$\begin{equation*} k_{*,L}\rightarrow k\quad \text{in $L^0(\mathbb {T}^n)$ as }L\rightarrow \infty \,\,\mathrm{.} \end{equation*}$$

Proof.We prove the assertions for  ∗ = + $*=+$ . A proof of corresponding assertions for  ∗ = ∘ $*=\circ$ is similar and simpler, and therefore it is omitted.

  • ( i ) $(i)$ Recall that p + , L = q L ∘ r L + ${\sf p}_{+,L}={\sf q}_L\circ {\sf r}_L^{{+}}$ . From (the proof of) Example 3.12 in [5] we know that ∥ q L f − f ∥ L 2 → 0 $\Vert {\sf q}_Lf-f\Vert _{L^2}\rightarrow 0$ as L → ∞ $L\rightarrow \infty$ and, by Jensen's inequality,
    ∥ q L f − q L r L + f ∥ L 2 ≤ ∥ f − r L + f ∥ L 2 . $$\begin{equation*} \big \Vert {\sf q}_Lf-{\sf q}_L{\sf r}_L^{{+}}f\big \Vert _{L^2}\le \big \Vert f-{\sf r}_L^{{+}}f\big \Vert _{L^2}\,\,\mathrm{.} \end{equation*}$$
    Moreover, the latter goes to 0 as L → ∞ $L\rightarrow \infty$ according to
    ∥ f − r L + f ∥ L 2 2 = ∑ ∥ z ∥ ∞ < L / 2 1 − 1 ϑ L , z · λ z λ L , z n / 4 · ⟨ f , φ z ⟩ φ z + ∑ ∥ z ∥ ∞ > L / 2 ⟨ f , φ z ⟩ φ z L 2 2 = ∑ ∥ z ∥ ∞ < L / 2 1 − 1 ϑ L , z · λ z λ L , z n / 4 2 · ⟨ f , φ z ⟩ 2 + ∑ ∥ z ∥ ∞ > L / 2 ⟨ f , φ z ⟩ 2 → 0 . $$\begin{align*} \big \Vert f-{\sf r}_L^{{+}}f\big \Vert _{L^2}^2&={\left\Vert \sum _{\Vert z\Vert _\infty <L/2} {\left[1- \frac{1}{\vartheta _{L,z}}\cdot {\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}\right]}\cdot \langle f,\varphi _z\rangle \,\varphi _z+ \sum _{\Vert z\Vert _\infty >L/2}\langle f,\varphi _z\rangle \,\varphi _z \right\Vert} ^2_{L^2}\\ &= \sum _{\Vert z\Vert _\infty <L/2} {\left[1- \frac{1}{\vartheta _{L,z}}\cdot {\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}\right]}^2\cdot \langle f,\varphi _z\rangle ^2 +\sum _{\Vert z\Vert _\infty >L/2}\langle f,\varphi _z\rangle ^2\ \rightarrow \ 0. \end{align*}$$
    The convergence of the last term here follows from the finiteness of ∑ z ⟨ f , φ z ⟩ 2 = ∥ f ∥ L 2 2 $\sum _{z}\langle f,\varphi _z\rangle ^2=\Vert f\Vert ^2_{L^2}$ . The convergence of the first term in the last displayed formula follows from the facts that 1 − 1 ϑ L , z · λ z λ L , z n / 4 ≤ C ≔ ( π 2 ) 3 n / 2 $\left|1- \frac{1}{\vartheta _{L,z}}\cdot \left(\frac{\lambda _z}{\lambda _{L,z}}\right)^{n/4}\right|\le C\coloneqq (\frac{\pi }{2})^{3n/2}$ for all L $L$ and z $z$ , that 1 − 1 ϑ L , z · λ z λ L , z n / 4 → 0 $\left|1- \frac{1}{\vartheta _{L,z}}\cdot \left(\frac{\lambda _z}{\lambda _{L,z}}\right)^{n/4}\right|\rightarrow 0$ for all z $z$ as L → ∞ $L\rightarrow \infty$ , and that ∑ z ⟨ f , φ z ⟩ 2 < ∞ $\sum _{z}\langle f,\varphi _z\rangle ^2<\infty$ .
  • ( i i ) $(ii)$ Denote by q L ⊗ 2 ${\sf q}_L^{\otimes 2}$ the two-fold action of q L ${\sf q}_L$ on functions of two variables, and put
    k L + ( x , y ) ≔ 1 a n ∑ z ∈ Z L n 1 ϑ L , z 2 · 1 λ L , z n / 2 · φ z ( x ) · φ z ( y ) . $$\begin{equation} k_L^+(x,y)\coloneqq \frac{1}{a_n} \sum _{z\in {\mathbb {Z}}^n_L} \, \frac{1}{\vartheta _{L,z}^2}\cdot \frac{1}{\lambda _{L,z}^{n/2}}\cdot \varphi _z(x)\cdot \varphi _z(y). \end{equation}$$ ()

Then, k + , L = q L ⊗ 2 k L + $k_{+,L}={\sf q}_L^{\otimes 2}k_L^+$ . The claimed convergence will follow from the three subsequent convergence assertions:

  • (1) q L ⊗ 2 k ( x , y ) → k ( x , y ) ${\sf q}_L^{\otimes 2}k(x,y)\rightarrow k(x,y)$ locally uniformly for all x ≠ y $x\not=y$
  • (2) ∫ ∫ q L ⊗ 2 k L + − q L ⊗ 2 k 2 d x d y ≤ ∫ ∫ k L + − k 2 d x d y $\iint\nolimits \left| {\sf q}_L^{\otimes 2}k_L^+-{\sf q}_L^{\otimes 2}k\right|^2dxdy\le \iint\nolimits \left| k_L^+-k\right|^2dxdy$
  • (3) ∫ ∫ k L + − k 2 d x d y → 0 $\iint\nolimits \left| k_L^+-k\right|^2dxdy\rightarrow 0$ .
Assertion (1) here is trivial since k $k$ is smooth outside the diagonal and since q L $q_L$ acts with bounded support ≤ 1 / L → 0 $\le 1/L\rightarrow 0$ . Assertion (2) follows from a simple application of Jensen's inequality. To prove assertion (3), observe that
∫ ∫ k L + − k 2 d x d y = 1 a n ∫ ∫ ∑ z ∈ Z n ∖ { 0 } 1 ϑ L , z 2 λ L , z n / 2 1 { ∥ z ∥ ∞ < L / 2 } − 1 λ z n / 2 φ z ( x ) φ z ( y ) 2 d x d y = 1 a n ∑ z ∈ Z n ∖ { 0 } 1 ϑ L , z 2 λ L , z n / 2 1 { ∥ z ∥ ∞ < L / 2 } − 1 λ z n / 2 2 = 1 a n ∑ z ∈ Z n ∖ { 0 } 1 ( 2 π | z | ) 2 n λ z n / 2 ϑ L , z 2 λ L , z n / 2 1 { ∥ z ∥ ∞ < L / 2 } − 1 2 . $$\begin{align*} \iint\nolimits {\left| k_L^+-k\right|}^2dxdy&=\frac{1}{a_n}\iint\nolimits {\left| \sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace } {\left(\frac{1}{\vartheta _{L,z}^2\,\lambda _{L,z}^{n/2}}\,{\bf 1}_{\lbrace \Vert z\Vert _\infty <L/2\rbrace }-\frac{1}{\lambda _z^{n/2}}\right)}\,\varphi _z(x)\,\varphi _z(y)\right|}^2dx\,dy\\ &=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace } {\left(\frac{1}{\vartheta _{L,z}^2\,\lambda _{L,z}^{n/2}}\,{\bf 1}_{\lbrace \Vert z\Vert _\infty <L/2\rbrace }-\frac{1}{\lambda _z^{n/2}}\right)}^2\\ &=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace } \frac{1}{(2\pi |z|)^{2n}} {\left(\frac{\lambda _z^{n/2}}{\vartheta _{L,z}^2\,\lambda _{L,z}^{n/2}}\,{\bf 1}_{\lbrace \Vert z\Vert _\infty <L/2\rbrace }-1\right)}^2. \end{align*}$$
The latter converges to 0 as L → ∞ $L\rightarrow \infty$ since the term ( λ z n / 2 ϑ L , z − 2 λ L , z − n / 2 ) 1 { ∥ z ∥ ∞ < L / 2 } − 1 $\left((\lambda _z^{n/2}\, \vartheta _{L,z}^{-2}\,\lambda _{L,z}^{-n/2})\,{\bf 1}_{\lbrace \Vert z\Vert _\infty <L/2\rbrace }-1\right)$ is bounded uniformly in L $L$ and z $z$ , since it converges to 0 for every z $z$ as L → ∞ $L\rightarrow \infty$ , and since the sum ∑ z ∈ Z n ∖ { 0 } 1 ( 2 π | z | ) 2 n $\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace } \frac{1}{(2\pi |z|)^{2n}}$ is finite. □ $\Box$

Corollary 4.8.Let  ∗ $*$ denote either of the subscripts  + $+$ and  ∘ $\circ$ . Then for all f ∈ L 2 ( T n ) $f\in L^2(\mathbb {T}^n)$ ,

⟨ h ∗ , L , f ⟩ T n → ⟨ h , f ⟩ T n in L 2 ( P ) as L → ∞ $$\begin{equation*} {\langle h_{*,L},f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \end{equation*}$$
and for every s > n / 2 $s>n/2$ ,
h ∗ , L − h H − s → 0 in L 2 ( P ) as L → ∞ . $$\begin{equation*} {\left\Vert h_{*,L} - h\right\Vert} _{H^{-s}} \rightarrow 0 \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{.} \end{equation*}$$

Proof.To prove the first assertion, we estimate similar as in the proof of Proposition 4.6. The fact that h ∗ , L ( x ) = ⟨ h | p ∗ , L ( x , · ) ⟩ $h_{*,L}(x)=\langle h | p_{*,L}(x,{\,\cdot \,})\rangle$ implies ⟨ h ∗ , L , f ⟩ T n = ⟨ h , p ∗ , L f ⟩ T n ${\langle h_{*,L},f\rangle} _{\mathbb {T}^n} ={\langle h,{\sf p}_{*,L} f\rangle} _{\mathbb {T}^n}$ and thus in turn

E ⟨ h ∗ , L − h , f ⟩ 2 = E ⟨ h , p ∗ , L f − f ⟩ 2 = ∥ p ∗ , L f − f ∥ H − n / 2 2 ≤ ∥ p ∗ , L f − f ∥ L 2 2 → 0 as L → ∞ . $$\begin{align*} \mathbf {E}{\left[\langle h_{*,L}- h,f\rangle ^2\right]} &=\mathbf {E}{\left[\langle h,{\sf p}_{*,L}f-f\rangle ^2\right]}=\big \Vert {\sf p}_{*,L}f-f\big \Vert ^2_{H^{-n/2}}\\ &\le \big \Vert {\sf p}_{*,L}f-f\big \Vert ^2_{L^2}\rightarrow 0\quad \text{as $L\rightarrow \infty $.} \end{align*}$$

To prove the second assertion, we follow the argument in Proposition 4.6. That is, we consider

h = 1 a n ∑ z ∈ Z n ∖ { 0 } ξ z φ z λ z n / 4 $$\begin{equation*} h = \frac{1}{\sqrt {a_{n}}} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \xi _{z} \frac{\varphi _{z}}{\lambda _{z}^{n/4}} \end{equation*}$$
from which we get
h ∗ , L ( x ) = 1 a n ∑ z ∈ Z n ∖ { 0 } ξ z ⟨ φ z , p ∗ , L ( x , · ) ⟩ λ z n / 4 . $$\begin{equation*} h_{*,L}(x) = \frac{1}{\sqrt {a_{n}}} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \xi _{z} \frac{\langle \varphi _z, \mathsf {p}_{*,L}(x,\cdot) \rangle }{\lambda _{z}^{n/4}}\,\,\mathrm{.} \end{equation*}$$
Then, the claim follows verbatim by noting that r L φ z = φ z $r_L\varphi _z=\varphi _z$ and r L + φ z = 1 ϑ L , z · λ z λ L , z n / 4 φ z $r_L^+\varphi _z= \frac{1}{\vartheta _{L,z}}\cdot \left({\frac{\lambda _z}{\lambda _{L,z}} }\right)^{n/4} \varphi _z$ , where | 1 ϑ L , z · λ z λ L , z n / 4 | $\big \vert \frac{1}{\vartheta _{L,z}}\cdot \left({\frac{\lambda _z}{\lambda _{L,z}} }\right)^{n/4} \big \vert$ is uniformly bounded and 1 ϑ L , z · λ z λ L , z n / 4 → 1 $ \frac{1}{\vartheta _{L,z}}\cdot \left({\frac{\lambda _z}{\lambda _{L,z}} }\right)^{n/4}\rightarrow 1$ as L → ∞ $L\rightarrow \infty$ . □ $\Box$

4.2 Identifications

Among the fields introduced above, we have the following identifications. We note that these identifications show that our notation of reductions/enhancements and projections/extensions is consistent, in the sense that it does not depend on the order in which the operations expressed by symbols are applied.

Lemma 4.9. (Fourier extensions/restrictions)Let  h $h$ be a polyharmonic Gaussian field on  T n $\mathbb {T}^n$ , and  h L $h_L$ be a discrete polyharmonic Gaussian field on  T L n $\mathbb {T}^n_L$ . Then,

  • ( i ) $(i)$ the spectral enhancement  h ♯ , L + ∘ $h^{{+\circ }}_{\sharp,L}$ of the Fourier projection  h ♯ , L $h_{\sharp,L}$ of  h $h$ coincides in distribution with the Fourier extension  h L , ♯ $h_{L,\sharp }$ of  h L $h_L$ ;
  • ( i i ) $(ii)$ the Fourier approximation  h ♯ , L $h_{\sharp,L}$ of  h $h$ coincides in distribution with the spectral reduction of the Fourier extension  h L , ♯ $h_{L,\sharp }$ of  h L $h_L$ and with the Fourier extension  h L , ♯ − ∘ $h^{-\circ }_{L,\sharp }$ of the spectrally reduced discrete polyharmonic field  h L − ∘ $h^{-\circ }_L$ .
  • ( i i i ) $(iii)$ the restriction to T L n $\mathbb {T}^n_L$ of the Fourier approximation  h ♯ , L $h_{\sharp,L}$ of  h $h$ coincides in distribution with a spectrally reduced polyharmonic field  h L − ∘ $h_L^{{-\circ }}$ (Figures 2-4).

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Fourier extension/projection of  h $h$ on  D 25 $\mathcal {D}_{25}$ with same realization of the randomness.
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
A realization of  h 25 , ♯ $h_{25,\sharp }$ .
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Two different approximations/extensions of the field  h $h$ with same realization of the randomness.

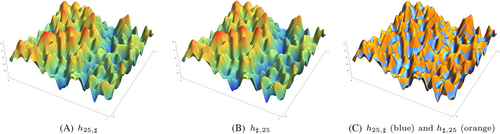
Proof. ( i ) $(i)$ and  ( i i ) $(ii)$ follow from simple manipulations of the symbols. ( i i i ) $(iii)$ is an immediate consequence of  ( i i ) $(ii)$ . □ $\Box$

Lemma 4.10. (Enhanced and natural extensions/restrictions)Let  h $h$ be a polyharmonic Gaussian field on  T n $\mathbb {T}^n$ , and  h L $h_L$ be a discrete polyharmonic Gaussian field on  T L n $\mathbb {T}^n_L$ . Then,

  • ( i ) $(i)$ the restriction to  T L n $\mathbb {T}^n_L$ of the enhanced projection h + , L $h_{+,L}$ of  h $h$ coincides in distribution with  h L $h_L$ ;
  • ( i i ) $(ii)$ the restriction to  T L n $\mathbb {T}^n_L$ of the natural projection  h ∘ , L $h_{\circ,L}$ of  h $h$ coincides in distribution with the reduced discrete polyharmonic field  h L − $h^-_L$ ;
  • ( i i i ) $(iii)$ the natural projection  h ∘ , L $h_{\circ, L}$ of  h $h$ coincides in distribution with the piecewise constant extension  h L , ♭ − $h^{{-}}_{L,\flat }$ of the reduced discrete polyharmonic field  h L − $h^-_L$ .

Proof.Without loss of generality, let  h $h$ be given in terms of standard i.i.d. normal variables ( ξ z ) z ∈ Z n ∖ { 0 } $(\xi _z)_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }$ as

h = 1 a n ∑ z ∈ Z n ∖ { 0 } □ 1 λ z n / 4 ξ z φ z . $$\begin{equation*} h=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{\lambda _z^{n/4}}\,\xi _z\,\varphi _z\,\,\mathrm{.} \end{equation*}$$
  • ( i ) $(i)$ We have
    r L + ( h ) = 1 a n ∑ z ∈ Z n ∖ { 0 } □ 1 ϑ L , z 1 λ L , z n / 4 ξ z φ z $$\begin{equation*} {\sf r}_L^{{+}}(h)=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{\vartheta _{L,z}}\,\frac{1}{\lambda _{L,z}^{n/4}}\,\xi _z\,\varphi _z \end{equation*}$$
    on T n $\mathbb {T}^n$ . Thus for v ∈ T L n $v\in \mathbb {T}^n_L$ ,
    h + , L ( v ) = 1 a n ∑ z ∈ Z n ∖ { 0 } □ 1 ϑ L , z 1 λ L , z n / 4 ξ z · L n ∫ Q L ( v ) φ z ( y ) d y = 1 a n ∑ z ∈ Z n ∖ { 0 } □ 1 λ L , z n / 4 ξ z φ z ( v ) $$\begin{align*} h_{+,L}(v)&=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{\vartheta _{L,z}}\,\frac{1}{\lambda _{L,z}^{n/4}}\,\xi _z\cdot L^n\,\int _{Q_L(v)}\varphi _z(y)dy \\ &=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{\lambda _{L,z}^{n/4}}\,\xi _z\,\varphi _z(v) \end{align*}$$
    according to Lemma 2.7. Therefore, by Proposition 3.2, h + , L $h_{+,L}$ is distributed according to the polyharmonic Gaussian field on the discrete torus T L n $\mathbb {T}^n_L$ .
  • ( i i ) $(ii)$ We have
    h ∘ , L ( x ) = 1 a n ∑ z ∈ Z n ∖ { 0 } □ 1 λ z n / 4 ξ z · ∑ v ∈ T L n 1 Q L ( v ) ( x ) · L n ∫ Q L ( v ) φ z ( y ) d y , $$\begin{align*} h_{\circ,L}(x)&=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{\lambda _{z}^{n/4}}\,\xi _z\cdot \sum _{v\in \mathbb {T}^n_L}{\bf 1}_{Q_L(v)}(x)\cdot L^n\,\int _{Q_L(v)}\varphi _z(y)dy, \end{align*}$$
    and thus for v ∈ T L n $v\in \mathbb {T}^n_L$ ,
    h ∘ , L ( v ) = 1 a n ∑ z ∈ Z n ∖ { 0 } □ 1 λ z n / 4 ξ z · L n ∫ Q L ( v ) φ z ( y ) d y = 1 a n ∑ z ∈ Z n ∖ { 0 } □ ϑ L , z λ z n / 4 ξ z φ z ( v ) $$\begin{align*} h_{\circ,L}(v)&=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{\lambda _{z}^{n/4}}\,\xi _z\cdot L^n\,\int _{Q_L(v)}\varphi _z(y)dy\\ &=\frac{1}{\sqrt {a_n}}\sum ^{\Box }_{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{\vartheta _{L,z}}{\lambda _{z}^{n/4}}\,\xi _z\,\varphi _z(v) \end{align*}$$
    according to Lemma 2.7. Therefore, the restriction of  h ∘ , L $h_{\circ,L}$ to  T L n $\mathbb {T}^n_L$ is distributed as the reduced discrete polyharmonic Gaussian field by the representation in Equation (19).
  • ( i i i ) $(iii)$ is an immediate consequence of  ( i i ) $(ii)$ and the fact that  h ∘ , L $h_{\circ, L}$ is piecewise constant on  T n $\mathbb {T}^n$ . □ $\Box$

4.3 Convergence of polyharmonic Gaussian fields on the discrete torus

We have the following first convergence result.

Theorem 4.11.Let  h L ∗ $h_L^*$ be either  h L $h_L$ ,  h L − ∘ $h^{-\circ }_L$ , or  h L − $h_L^-$ . Then, or all f ∈ ⋃ s > n / 2 H s ( T n ) $f\in \bigcup \limits _{s>n/2} H^{s}(\mathbb {T}^n)$ ,

⟨ h L ∗ , f ⟩ T L n → ⟨ h , f ⟩ T n in L 2 ( P ) as L → ∞ , $$\begin{align*} {\langle h_L^*,f\rangle} _{\mathbb {T}_L^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \quad &\text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{,}\;\, \end{align*}$$

Proof.We only show the assertion for  h L $h_L$ .

Given f = ∑ z ∈ Z n α z φ z ∈ ⋃ s > n / 2 H s ( T n ) $f=\sum _{z\in {\mathbb {Z}}^n}\alpha _z\varphi _z \in \bigcup \limits _{s>n/2} H^{s}(\mathbb {T}^n)$ , according to Lemma 2.8,

⟨ h , f ⟩ T n − ⟨ h L , f ⟩ T L n = 1 a n ∑ z ∈ Z L n ∖ { 0 } ξ z · 1 λ z n / 4 α z − 1 λ L , z n / 4 ∑ w ∈ Z n α z + L w + 1 a n ∑ z ∈ Z n , ∥ z ∥ ∞ ≥ L / 2 ξ z · 1 λ z n / 4 α z . $$\begin{align*} {\langle h,f\rangle} _{\mathbb {T}^n}-{\langle h_L,f\rangle} _{\mathbb {T}_L^n} =&\ \frac{1}{\sqrt {a_n}} \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }\xi _z\cdot {\left[\frac{1}{\lambda _{z}^{n/4}}\alpha _z-\frac{1}{\lambda _{L,z}^{n/4}}\sum _{w\in {\mathbb {Z}}^n}\alpha _{z+Lw} \right]} \\ &+\frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}^n, \, \Vert z\Vert _\infty \ge L/2}\xi _z\cdot \frac{1}{\lambda _{z}^{n/4}}\alpha _z\,\,\mathrm{.} \end{align*}$$
Thus
a n · E | ⟨ h , f ⟩ T n − ⟨ h L , f ⟩ T L n | 2 = ∑ z ∈ Z L n ∖ { 0 } 1 λ z n / 4 α z − 1 λ L , z n / 4 ∑ w ∈ Z n α z + L w 2 + ∑ z ∈ Z n , ∥ z ∥ ∞ ≥ L / 2 1 λ z n / 2 α z 2 ≤ 2 ∑ z ∈ Z L n ∖ { 0 } 1 λ z n / 4 − 1 λ L , z n / 4 2 α z 2 + 2 ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 ∑ w ∈ Z n ∖ { 0 } α z + L w 2 + ∑ z ∈ Z n , ∥ z ∥ ∞ ≥ L / 2 1 λ z n / 2 α z 2 ≤ 2 ( 2 π ) n ∑ z ∈ Z L n ∖ { 0 } 1 − λ z n / 4 λ L , z n / 4 2 1 | z | n α z 2 + 2 4 n ∑ z ∈ Z L n ∖ { 0 } 1 | z | n ∑ w ∈ Z n ∖ { 0 } α z + L w 2 + 1 ( 2 π ) n ∑ z ∈ Z n , ∥ z ∥ ∞ ≥ L / 2 1 | z | n α z 2 . $$\begin{align*} &{a_n\cdot \mathbf {E}{\left[\big\vert {\langle h,f\rangle} _{\mathbb {T}^n}-{\langle h_L,f\rangle} _{\mathbb {T}_L^n}\big\vert ^2\right]}}\\ =& \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }{\left[\frac{1}{\lambda _{z}^{n/4}}\alpha _z-\frac{1}{\lambda _{L,z}^{n/4}}\sum _{w\in {\mathbb {Z}}^n }\alpha _{z+Lw} \right]}^2 +\sum _{z\in {\mathbb {Z}}^n, \, \Vert z\Vert _\infty \ge L/2}\frac{1}{\lambda _{z}^{n/2}}\alpha _z^2 \\ \le &\ 2 \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }{\left[\frac{1}{\lambda _{z}^{n/4}}-\frac{1}{\lambda _{L,z}^{n/4}} \right]}^2\alpha _z^2 \\ &+ 2 \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }\frac{1}{\lambda _{L,z}^{n/2}}{\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\alpha _{z+Lw} \right]}^2 +\sum _{z\in {\mathbb {Z}}^n, \, \Vert z\Vert _\infty \ge L/2}\frac{1}{\lambda _{z}^{n/2}}\alpha _z^2 \\ \le &\ \frac{2}{(2\pi)^{n}} \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }{\left[1-\frac{\lambda _{z}^{n/4}}{\lambda _{L,z}^{n/4}} \right]}^2\frac{1}{|z|^n}\alpha _z^2 \\ &+ \frac{2}{4^{n}}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }\frac{1}{|z|^n}{\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\alpha _{z+Lw} \right]}^2 +\frac{1}{(2\pi)^{n}}\sum _{z\in {\mathbb {Z}}^n, \, \Vert z\Vert _\infty \ge L/2}\frac{1}{|z|^n}\alpha _z^2\,\,\mathrm{.} \end{align*}$$
Now as L → ∞ $L\rightarrow \infty$ , the last term vanishes since, in particular, f ∈ H − n / 2 ( T n ) $f\in H^{-n/2}(\mathbb {T}^n)$ , and also the first term vanishes, see the proof of Theorem 4.13. To estimate the second term, choose s > n / 2 $s>n/2$ with ∑ z ∈ Z n ∖ { 0 } | z | 2 s | α z | 2 < ∞ $\sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }|z|^{2s}|\alpha _z|^2<\infty$ , which exists by definition of  f $f$ . Then,
∑ z ∈ Z L n ∖ { 0 } 1 | z | n ∑ w ∈ Z n ∖ { 0 } α z + L w 2 ≤ ∑ z ∈ Z L n ∖ { 0 } ∑ w ∈ Z n ∖ { 0 } α z + L w 2 ≤ ∑ z ∈ Z L n ∖ { 0 } ∑ w ∈ Z n ∖ { 0 } 1 | z + L w | 2 s · ∑ w ∈ Z n ∖ { 0 } | z + L w | 2 s · | α z + L w | 2 . $$\begin{align*} &{\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }\frac{1}{|z|^n}{\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\alpha _{z+Lw} \right]}^2 \le \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }{\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\alpha _{z+Lw} \right]}^2}\\ &\le \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }{\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\frac{1}{|z+Lw|^{2s}} \right]}\cdot {\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }|z+Lw|^{2s}\cdot |\alpha _{z+Lw}|^2 \right]} \,\,\mathrm{.} \end{align*}$$
Estimating the term in the first bracket by
∑ w ∈ Z n ∖ { 0 } 1 | z + L w | 2 s ≤ ∑ u ∈ Z n ∖ { 0 } 1 | u | 2 s < ∞ , $$\begin{equation*} \sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\frac{1}{|z+Lw|^{2s}}\le \sum _{u\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{|u|^{2s}}<\infty \,\,\mathrm{,}\;\, \end{equation*}$$
we then obtain that
∑ z ∈ Z L n ∖ { 0 } 1 | z | n ∑ w ∈ Z n ∖ { 0 } α z + L w 2 ≤ ∑ u ∈ Z n ∖ { 0 } 1 | u | 2 s · ∑ z ∈ Z L n ∖ { 0 } ∑ w ∈ Z n ∖ { 0 } | z + L w | 2 s · | α z + L w | 2 $$\begin{align*} \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace }\frac{1}{|z|^n}{\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }\alpha _{z+Lw} \right]}^2 \le & {\left[\sum _{u\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace }\frac{1}{|u|^{2s}} \right]}\cdot \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } {\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }|z+Lw|^{2s}\cdot |\alpha _{z+Lw}|^2 \right]} \end{align*}$$
and it therefore suffices to show that the second factor vanishes as  L → ∞ $L\rightarrow \infty$ . Since  z , w ≠ 0 $z,w\ne 0$ , we have that  z + L w ≥ L / 2 $\left|z+Lw\right|\ge L/2$ , thus, relabeling  v ≔ z + L w $v\coloneqq z+Lw$ ,
∑ z ∈ Z L n ∖ { 0 } ∑ w ∈ Z n ∖ { 0 } | z + L w | 2 s · | α z + L w | 2 = ∑ v ∈ Z n , ∥ v ∥ ∞ ≥ L / 2 | v | 2 s · | α v | 2 → 0 as L → ∞ $$\begin{align*} \sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } {\left[\sum _{w\in {\mathbb {Z}}^n \setminus \lbrace 0\rbrace }|z+Lw|^{2s}\cdot |\alpha _{z+Lw}|^2\right]} =& {\left[\sum _{v\in {\mathbb {Z}}^n, \, \Vert v\Vert _\infty \ge L/2}|v|^{2s}\cdot |\alpha _{v}|^2 \right]}\rightarrow 0\qquad \text{as }L\rightarrow \infty \end{align*}$$
being the remainder of a convergent series. □ $\Box$

Theorem 4.12.Let  h L , ♭ ∗ $h_{L,\flat }^*$ be either  h L , ♭ $h_{L,\flat }$ ,  h L , ♭ − ∘ $h^{-\circ }_{L,\flat }$ , or  h L , ♭ − $h^-_{L,\flat }$ . Then, for all f ∈ ⋃ s > n / 2 H s ( T n ) $f\in \bigcup \limits _{s>n/2} H^{s}(\mathbb {T}^n)$ ,

⟨ h L , ♭ ∗ , f ⟩ T n → ⟨ h , f ⟩ T n in L 2 ( P ) as L → ∞ . $$\begin{equation} {\langle h^*_{L,\flat },f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{.}\end{equation}$$ ()
Furthermore, for every  s > n / 2 $s>n/2$ ,
∥ h L , ♭ − h ∥ H ˚ − s 2 → 0 in L 2 ( P ) as L → ∞ . $$\begin{equation} \big \Vert h_{L,\flat }-h\big \Vert _{\mathring{H}^{-s}}^2\rightarrow 0 \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \ . \end{equation}$$ ()

Proof.We only show the assertions for  h L , ♭ $h_{L,\flat }$ .

By construction,

⟨ h L , ♭ , f ⟩ T n − ⟨ h , f ⟩ T n = ⟨ h L , q L f − f ⟩ T L n + ⟨ h L , f ⟩ T L n − ⟨ h , f ⟩ T n $$\begin{equation*} {\langle h_{L,\flat },f\rangle} _{\mathbb {T}^n} - {\langle h,f\rangle} _{\mathbb {T}^n} = {\langle h_L,{\sf q}_Lf-f\rangle} _{\mathbb {T}_L^n}+ {\langle h_L,f\rangle} _{\mathbb {T}_L^n} - {\langle h,f\rangle} _{\mathbb {T}^n} \end{equation*}$$
and according to the previous Theorem 4.11, ⟨ h L , f ⟩ T L n − ⟨ h , f ⟩ T n → 0 $ {\langle h_L,f\rangle} _{\mathbb {T}_L^n} - {\langle h,f\rangle} _{\mathbb {T}^n} \rightarrow 0$ as L → ∞ $L\rightarrow \infty$ . The first claim thus follows from
E ⟨ h L , q L f − f ⟩ T L n 2 = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 ⟨ φ z , q L f − f ⟩ T L n 2 ≤ 1 4 n a n ∑ z ∈ Z L n ∖ { 0 } 1 | z | n ⟨ φ z , q L f − f ⟩ T L n 2 = 1 4 n a n ∥ q L f − f ∥ H − n / 2 2 ≤ 1 4 n a n ∥ q L f − f ∥ L 2 2 → 0 as L → ∞ $$\begin{align*} \mathbf {E}{\left[{\langle h_L,{\sf q}_Lf-f\rangle} _{\mathbb {T}_L^n}^2\right]}&=\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}{\langle \varphi _z, {\sf q}_Lf-f\rangle} _{\mathbb {T}_L^n}^2\\ &\le \frac{1}{4^n\, a_n}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } \frac{1}{|z|^n}{\langle \varphi _z, {\sf q}_Lf-f\rangle} _{\mathbb {T}_L^n}^2\\ &= \frac{1}{4^n\, a_n}\,\big \Vert {\sf q}_Lf-f\big \Vert ^2_{H^{-n/2}}\\ &\le \frac{1}{4^n\, a_n}\,\big \Vert {\sf q}_Lf-f\big \Vert ^2_{L^2}\rightarrow 0\quad \text{as $L\rightarrow \infty $} \end{align*}$$
since by Sobolev embedding
⋃ s > n / 2 H s ( T n ) ⊂ C ( T n ) . $$\begin{equation*} \bigcup \limits _{s>n/2} H^{s}(\mathbb {T}^n)\subset \mathcal {C}(\mathbb {T}^n) \,\,\mathrm{.} \end{equation*}$$

For the second claim, observe that

h L , ♭ = 1 a n ∑ z ∈ Z n ∖ { 0 } φ z ∑ w ∈ Z L n ∖ { 0 } λ w , L − n / 4 ξ w ⟨ φ w , q L φ z ⟩ . $$\begin{equation*} h_{L,\flat } = \frac{1}{\sqrt {a_{n}}} \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \varphi _{z} \sum _{w \in \mathbb {Z}^{n}_{L} \setminus \lbrace 0\rbrace } \lambda _{w,L}^{-n/4} \xi _{w} \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle . \end{equation*}$$
From this, we get
a n h L , ♭ H − s 2 = ∑ z ∈ Z n ∖ { 0 } λ z − s ∑ w ∈ Z L n ∖ { 0 } λ w , L − n / 4 ξ w ⟨ φ w , q L φ z ⟩ 2 . $$\begin{equation*} a_{n} {\left\Vert h_{L,\flat }\right\Vert} ^{2}_{H^{-s}} = \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-s} {\left(\sum _{w \in \mathbb {Z}^{n}_{L} \setminus \lbrace 0\rbrace } \lambda _{w,L}^{-n/4} \xi _{w} \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle \right)}^{2}. \end{equation*}$$
And thus
a n E h L , ♭ H − s 2 = ∑ z ∈ Z n ∖ { 0 } λ z − s ∑ w ∈ Z L n ∖ { 0 } λ w , L − n / 2 ⟨ φ w , q L φ z ⟩ 2 . $$\begin{equation*} a_{n} \mathbf {E} {\left\Vert h_{L,\flat }\right\Vert} ^{2}_{H^{-s}} = \sum _{z \in \mathbb {Z}^{n} \setminus \lbrace 0\rbrace } \lambda _{z}^{-s} \sum _{w \in \mathbb {Z}^{n}_{L} \setminus \lbrace 0\rbrace } \lambda _{w,L}^{-n/2} \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle ^{2}. \end{equation*}$$
On one hand, as L → ∞ $L \rightarrow \infty$ , the summand converges to λ z − s − n / 2 1 z = w $\lambda _{z}^{-s-n/2} 1_{z = w}$ . On the other hand, by Parseval's identity, we find that
∑ w ∈ Z L n ∖ { 0 } λ w , L − n / 2 ⟨ φ w , q L φ z ⟩ 2 = ( − Δ L ) − n / 2 q L φ z L 2 ( T L n ) 2 ≤ 1 . $$\begin{equation*} \sum _{w \in \mathbb {Z}^{n}_{L} \setminus \lbrace 0\rbrace } \lambda _{w,L}^{-n/2} \langle \varphi _{w}, \mathsf {q}_{L}\varphi _{z}\rangle ^{2} = {\left\Vert {(-\Delta _{L})}^{-n/2} \mathsf {q}_{L}\varphi _{z}\right\Vert} _{L^{2}(\mathbb {T}^{n}_{L})}^{2} \le 1. \end{equation*}$$
Thus, the sum is uniformly bounded since s > n / 2 $s > n/2$ . This shows that
E h L , ♭ H − s 2 → E h H − s 2 . $$\begin{equation*} \mathbf {E} {\left\Vert h_{L,\flat }\right\Vert} ^{2}_{H^{-s}} \rightarrow \mathbf {E} {\left\Vert h\right\Vert} ^{2}_{H^{-s}}. \end{equation*}$$
A similar computation shows that
E ⟨ h , h L , ♭ ⟩ H − s → E h H − s 2 . $$\begin{equation*} \mathbf {E} {\langle h, h_{L,\flat }\rangle} _{H^{-s}} \rightarrow \mathbf {E} {\left\Vert h\right\Vert} _{H^{-s}}^{2}. \end{equation*}$$
This concludes the proof of the second claim. □ $\Box$

Theorem 4.13.Let  h L , ♯ ∗ $h_{L,\sharp }^*$ be either  h L , ♯ $h_{L,\sharp }$ ,  h L , ♯ − ∘ $h^{-\circ }_{L,\sharp }$ , or  h L , ♯ − $h^-_{L,\sharp }$ . For all f ∈ H ˚ − n / 2 ( T n ) $f\in \mathring{H}^{-n/2}(\mathbb {T}^n)$ ,

⟨ h L , ♯ ∗ , f ⟩ T n → ⟨ h , f ⟩ T n in L 2 ( P ) as L → ∞ , $$\begin{equation} {\langle h^*_{L,\sharp },f\rangle} _{\mathbb {T}^n} \rightarrow {\langle h,f\rangle} _{\mathbb {T}^n} \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{,}\;\, \end{equation}$$ ()
and for all ε > 0 $\epsilon >0$ ,
∥ h L , ♯ − h ∥ H − ε 2 → 0 in L 2 ( P ) as L → ∞ . $$\begin{equation} \big \Vert h_{L,\sharp }-h\big \Vert _{H^{-\epsilon }}^2\rightarrow 0 \quad \text{in $L^2(\mathbf {P})$ as }L\rightarrow \infty \,\,\mathrm{.} \end{equation}$$ ()

Proof.We only show the assertions for  h L $h_L$ .

According to Proposition 4.5, we already know that ⟨ h ♯ , L , f ⟩ → ⟨ h , f ⟩ $\langle h_{\sharp,L},f\rangle \rightarrow \langle h,f\rangle$ . Thus, it suffices to prove ⟨ h L , ♯ − h ♯ , L , f ⟩ → 0 $\langle h_{L,\sharp }-h_{\sharp,L},f\rangle \rightarrow 0$ . This follows according to

E ⟨ h L , ♯ − h ♯ , L , f ⟩ 2 = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 − 1 λ z n / 2 ⟨ φ z , f ⟩ 2 = 1 a n ∑ z ∈ Z L n ∖ { 0 } λ z λ L , z n / 2 − 1 ⟨ φ z , f ⟩ 2 λ z n / 2 → 0 $$\begin{align*} &{\mathbf {E}{\left[\langle h_{L,\sharp }-h_{\sharp,L},f\rangle ^2\right]}}\\ &= \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } {\left(\frac{1}{\lambda _{L,z}^{n/2}} -\frac{1}{\lambda _z^{n/2}}\right)}\, \langle \varphi _z,f\rangle ^2\\ &= \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } {\left({\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/2}-1\right)}\, \frac{\langle \varphi _z,f\rangle ^2}{\lambda _z^{n/2}}\rightarrow 0 \end{align*}$$
as  L → ∞ $L\rightarrow \infty$ by the dominated convergence theorem since
∑ z ∈ Z n ∖ { 0 } 1 λ z n / 2 ⟨ φ z , f ⟩ 2 < ∞ , 0 ≤ λ z λ L , z n / 2 − 1 ≤ 2 n $$\begin{gather*} \sum _{z\in {\mathbb {Z}}^n\setminus \lbrace 0\rbrace } \frac{1}{\lambda _z^{n/2}}\langle \varphi _z,f\rangle ^2<\infty \,\,\mathrm{,}\;\,\\ 0\le {\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/2}-1\le 2^n \end{gather*}$$
for all z $z$ and L $L$ , and
λ z λ L , z n / 2 − 1 → 0 $$\begin{equation*} {\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/2}-1 \rightarrow 0 \end{equation*}$$
as  L → ∞ $L\rightarrow \infty$ for every z $z$ .

For the second claim, we use the fact that again by Proposition 4.5 for every ε > 0 $\epsilon >0$ ,

E ∥ h − h ♯ , L ∥ H ˚ − ε 2 → 0 as L → ∞ . $$\begin{equation*} \mathbf {E}{\left[\big \Vert h-h_{\sharp, L}\big \Vert _{\mathring{H}^{-\epsilon }}^2 \right]}\rightarrow 0\quad \text{as }L\rightarrow \infty \,\,\mathrm{.} \end{equation*}$$
Furthermore,
E ∥ h L , ♯ − h ♯ , L ∥ H ˚ − ε 2 = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 4 − 1 ( 2 π | z | ) n / 2 2 1 | z | 2 ε = 1 a n ( 2 π ) n ∑ z ∈ Z L n ∖ { 0 } λ z λ L , z n / 4 − 1 2 1 | z | n + 2 ε → 0 $$\begin{align*} \mathbf {E}{\left[\big \Vert h_{L,\sharp }-h_{\sharp, L}\big \Vert _{\mathring{H}^{-\epsilon }}^2 \right]} &= \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } {\left(\frac{1}{\lambda _{L,z}^{n/4}} -\frac{1}{{(2\pi |z|)}^{n/2}}\right)}^2\, \frac{1}{|z|^{2\epsilon }}\\ &= \frac{1}{a_n(2\pi)^n}\sum _{z\in {\mathbb {Z}}_L^n\setminus \lbrace 0\rbrace } {\left({\left(\frac{\lambda _z}{\lambda _{L,z}}\right)}^{n/4}-1\right)}^2\, \frac{1}{{|z|}^{n{+}2\epsilon }}\rightarrow 0 \end{align*}$$
as L → ∞ $L\rightarrow \infty$ by the same dominated convergence arguments as for the first claim. □ $\Box$

4.4 Related approaches and results

Remark 4.14. (Log-correlated Gaussian fields in the continuum)For  n = 1 $n=1$ , the field  h $h$ is the lower limiting case of the fractional Brownian motion with (regularity) parameter in  ( 1 2 , 3 2 ) $(\tfrac{1}{2},\tfrac{3}{2})$ , see, for example, [7, 12]. For  n = 2 $n=2$ , it is the celebrated Gaussian free field (GFF) on  T 2 $\mathbb {T}^2$ , surveyed in [16]. For  n = 1 $n=1$ , it coincides in distribution with the restriction of a GFF to a line ( T 1 ⊂ T 2 $\mathbb {T}^1\subset \mathbb {T}^2$ ). For  n ≥ 3 $n\ge 3$ , it is a log-correlated Gaussian field surveyed in [7]. The conformal invariance of  h $h$ on  T n $\mathbb {T}^n$ is a consequence of the conformal invariance of the Laplace–Beltrami operator on flat geometries. The correct (i.e., conformally covariant) construction of log-correlated Gaussian fields in general non-flat geometries may be found in [5].

Remark 4.15. (Discrete-to-continuum approximation)To the best of our knowledge, no discretization/discrete approximation results are available for log-correlated Gaussian fields in dimension  n ≥ 5 $n\ge 5$ . In small dimension however, Gaussian fields analogous to  h $h$ are known to be scaling limits of different discrete models. For n = 2 $n=2$ , in light of the celebrated universality property of GFFs, the field  h $h$ is a scaling limit for a huge number of different discrete Gaussian and non-Gaussian fields defined in various settings, from lattices to random environments, as, for example, the random conductance model [1]. For  n = 4 $n=4$ , the field  h $h$ is generated by the Neumann bi-Laplacian; the analogous field generated by the Dirichlet bi-Laplacian on  [ 0 , 1 ] 4 $[0,1]^4$ is the scaling limit of the membrane model [10, 13], see [2, 14], as well as of the odometer for the divisible sandpile model [11], see [4]. We stress that our convergence results for different discretizations of  h $h$ hold in  H ˚ − s $\mathring{H}^{-s}$ with  s > 2 $s>2$ , thus matching the same range of exponents as for the scaling limit of the sandpile odometer, see [3, Prop. 14]. On the other hand, the analogous scaling limit for the membrane model has so far been proven only in  H − s $H^{-s}$ for  s > 6 $s>6$ , see [2, Thm. 3.11].

5 Liouville quantum gravity MEASURES ON DISCRETE AND CONTINUOUS TORI

We will introduce and analyze LQG measures on discrete and continuous tori. Our main result in this section will be that as L → ∞ $L\rightarrow \infty$ the LQG measures on the discrete tori T L n $\mathbb {T}^n_L$ will converge to the LQG measure on the continuous torus T n $\mathbb {T}^n$ .

An analogous convergence assertion in greater generality will be proven for the so-called reduced LQG measures, random measures on the discrete tori T L n $\mathbb {T}^n_L$ defined in terms of the discrete polyharmonic fields h L $h_L$ .

5.1 Liouville quantum gravity measure on the continuous torus and its approximations

We define the parameters
γ ∗ ≔ n / e and γ ∗ ≔ 2 n . $$\begin{equation*} \gamma _*\coloneqq \sqrt {n/e} \qquad \text{and} \qquad \gamma ^*\coloneqq \sqrt {2n} \,\,\mathrm{.} \end{equation*}$$

We further make the following definitions of random measures on the common probability space  ( Ω , A , P ) $(\Omega,\mathfrak {A},\mathbf {P})$ supporting the polyharmonic field  h $h$ .

Definition 5.1.For γ ∈ R $\gamma \in {\mathbb {R}}$ , define

  • ( i ) $(i)$ the Fourier approximation μ ♯ , L $\mu _{\sharp,L}$ on T n $\mathbb {T}^n$ by
    d μ ♯ , L ( x ) = exp γ h ♯ , L ( x ) − γ 2 2 k ♯ , L ( x , x ) d L n ( x ) , $$\begin{equation*} d\mu _{\sharp,L}(x)=\exp {\left(\gamma h_{\sharp,L}(x)-\frac{\gamma ^2}{2} k_{\sharp,L}(x,x)\right)}\,d\mathcal {L}^n(x) \,\,\mathrm{,}\;\, \end{equation*}$$
    where h ♯ , L $h_{\sharp,L}$ denotes the Fourier projection (or eigenfunction approximation) of the polyharmonic field h $h$ and k ♯ , L $k_{\sharp,L}$ the associated covariance function (which takes the constant value 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 ( 2 π | z | ) n $\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{(2\pi |z|)^{n}}$ on the diagonal) as introduced in Definition 4.3 ( i ) $(i)$ .
  • ( i i ) $(ii)$ the piecewise-constant approximation μ ♭ , L $\mu _{\flat,L}$ on T n $\mathbb {T}^n$ by
    d μ ♭ , L ( x ) = exp γ h ♭ . L ( x ) − γ 2 2 k ♭ , L ( x , x ) d L n ( x ) , $$\begin{equation*} d\mu _{\flat,L}(x)=\exp {\left(\gamma h_{\flat .L}(x)-\frac{\gamma ^2}{2} k_{\flat,L}(x,x)\right)}\,d\mathcal {L}^n(x) \,\,\mathrm{,}\;\, \end{equation*}$$
    where h ♭ , L $h_{\flat,L}$ denotes the piecewise constant projection of the polyharmonic field h $h$ and k ♭ , L $k_{\flat,L}$ the associated covariance function (which is constant on the diagonal) as introduced in Definition 4.3 ( i i ) $(ii)$ .
  • ( i i i ) $(iii)$ the enhanced approximation μ + , L $\mu _{+,L}$ on T n $\mathbb {T}^n$ by
    d μ + , L ( x ) = exp γ h + , L ( x ) − γ 2 2 k + , L ( x , x ) d L n ( x ) , $$\begin{equation*} d\mu _{+,L}(x)=\exp {\left(\gamma h_{+,L}(x)-\frac{\gamma ^2}{2} k_{+,L}(x,x)\right)}\,d\mathcal {L}^n(x) \,\,\mathrm{,}\;\, \end{equation*}$$
    where h + , L $h_{+,L}$ denotes the enhanced projection of the polyharmonic field h $h$ and k + , L $k_{+,L}$ the associated covariance function as introduced in Definition 4.3 ( i i i ) $(iii)$ ;
  • ( i v ) $(iv)$ the natural approximation μ ∘ , L $\mu _{\circ,L}$ on T n $\mathbb {T}^n$ by
    d μ ∘ , L ( x ) = exp γ h ∘ , L ( x ) − γ 2 2 k ∘ , L ( x , x ) d L n ( x ) , $$\begin{equation*} d\mu _{\circ,L}(x)=\exp {\left(\gamma h_{\circ,L}(x)-\frac{\gamma ^2}{2} k_{\circ,L}(x,x)\right)}\,d\mathcal {L}^n(x) \,\,\mathrm{,}\;\, \end{equation*}$$
    where h ∘ , L $h_{\circ,L}$ denotes the natural projection of the polyharmonic field h $h$ and k ∘ , L $k_{\circ,L}$ the associated covariance function as introduced in Definition 4.3 ( i v ) $(iv)$ ;
  • ( v ) $(v)$ the semi-discrete approximation μ L , ♯ $\mu _{L,\sharp }$ (Figure 5) on T n $\mathbb {T}^n$ by
    d μ L , ♯ ( x ) = exp γ h L , ♯ ( x ) − γ 2 2 k L , ♯ ( x , x ) d L n ( x ) $$\begin{equation*} d\mu _{L,\sharp }(x)=\exp {\left(\gamma h_{L,\sharp }(x)-\frac{\gamma ^2}{2} k_{L,\sharp }(x,x)\right)}\,d\mathcal {L}^n(x) \end{equation*}$$
    where h L , ♯ $h_{L,\sharp }$ denotes the Fourier extension of the discrete polyharmonic field h L $h_L$ and k L , ♯ $k_{L,\sharp }$ the associated covariance function as introduced in Definition 3.7 ( i i ) $(ii)$ ;
  • ( v i ) $(vi)$ the spectrally reduced semi-discrete approximation μ L , ♯ − ∘ $\mu ^{{-\circ }}_{L,\sharp }$ on T n $\mathbb {T}^n$ by
    d μ L , ♯ − ∘ ( x ) = exp γ h L , ♯ − ∘ ( x ) − γ 2 2 k L , ♯ − ∘ ( x , x ) d L n ( x ) $$\begin{equation*} d\mu ^{{-\circ }}_{L,\sharp }(x)=\exp {\left(\gamma h^{{-\circ }}_{L,\sharp }(x)-\frac{\gamma ^2}{2} k^{{-\circ }}_{L,\sharp }(x,x)\right)}\,d\mathcal {L}^n(x) \end{equation*}$$
    where h L , ♯ − ∘ $h^{{-\circ }}_{L,\sharp }$ denotes the Fourier extension of the spectrally reduced discrete polyharmonic field  h L − ∘ $h^{{-\circ }}_L$ and  k L , ♯ − ∘ $k^{{-\circ }}_{L,\sharp }$ the associated covariance function as introduced in Definition 3.7 ( i v ) $(iv)$ .

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
The Gaussian multiplicative chaos  μ L , ♯ $\mu _{L,\sharp }$ on  T 2 $\mathbb {T}^2$ for  L = 15 $L=15$ , different values of  γ $\gamma$ and same realization of the randomness.

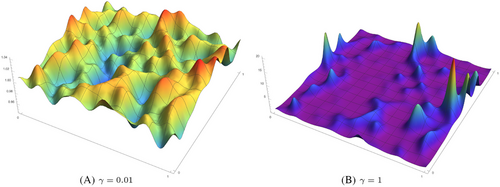
For a sequence  μ L L $\left(\mu _L\right)_L$ of random measures  μ L = μ L ω $\mu _L=\mu _L^\omega$ on  T n $\mathbb {T}^n$ and a random measure  μ = μ ω $\mu =\mu ^\omega$ , all defined on a same probability space  ( Ω , A , P ) $(\Omega,\mathfrak {A},\mathbf {P})$ , we further define the following mode of convergence.

Definition 5.2. (Convergence of random measures)We say that  μ L L $\left(\mu _L\right)_L$ converges to  μ $\mu$ as  L → ∞ $L\rightarrow \infty$ if both the following conditions hold:

  • P $\mathbf {P}$ -a.s. weak convergence, that is,
    lim L → ∞ ∫ T n f d μ L ω = ∫ T n f d μ ω for P -a.e. ω , for every f ∈ C ( T n ) ; $$\begin{equation*} \lim _{L\rightarrow \infty } \int _{\mathbb {T}^n} f d\mu _L^\omega = \int _{\mathbb {T}^n} fd\mu ^\omega \quad \text{for $\mathbf {P}$-a.e.\nobreakspace $\omega $, \quad for every\nobreakspace $f\in \mathcal {C}(\mathbb {T}^n)$} \,\,\mathrm{;}\;\, \end{equation*}$$
  • L 1 ( P ) $L^1(\mathbf {P})$ -convergence in  L 1 ( T n ) ∗ $L^1(\mathbb {T}^n)^*$ , that is,
    L 1 ( P ) - lim L → ∞ ∫ T n f d μ L · = ∫ T n f d μ · for every f ∈ L 1 ( T n ) . $$\begin{equation} L^1(\mathbf {P})\text{-}\lim _{L\rightarrow \infty } \int _{\mathbb {T}^n} f d\mu _L^{\,\cdot \,}= \int _{\mathbb {T}^n} fd\mu ^{\,\cdot \,}\quad \text{for every\nobreakspace $f\in L^1(\mathbb {T}^n)$} \,\,\mathrm{.}\end{equation}$$ ()

Theorem 5.3.Assume | γ | < γ ∗ $|\gamma |<\gamma ^*$ . Then, there exists a unique Borel random measure  μ = μ ω $\mu =\mu ^\omega$ on T n $\mathbb {T}^n$ , namely the polyharmonic LQG measure (also: polyharmonic Gaussian multiplicative chaos), satisfying—all convergences are in the sense of Definition 5.2

  • ( i ) $(i)$ μ ♯ , L → μ $\mu _{\sharp, L}\rightarrow \mu$ as L → ∞ $L\rightarrow \infty$ , and furthermore Equation (37) holds with  L 1 ( P ) $L^1(\mathbf {P})$ -convergence replaced by  L 2 ( P ) $L^2(\mathbf {P})$ -convergence if  γ < n $\left|\gamma \right|<\sqrt {n}$ ;
  • ( i i ) $(ii)$ μ ♭ , L → μ $\mu _{\flat,L}\rightarrow \mu$ as L → ∞ $L\rightarrow \infty$ ;
  • ( i i i ) $(iii)$ μ L , ♯ − ∘ → μ $\mu ^{{}{-\circ }}_{L,\sharp }\rightarrow \mu$ as L → ∞ $L\rightarrow \infty$ ;
  • ( i v ) $(iv)$ if  γ < n $\left|\gamma \right|<\sqrt {n}$ , then  μ ∘ , L → μ $\mu _{\circ,L}\rightarrow \mu$ as L → ∞ $L\rightarrow \infty$ ;
  • ( v ) $(v)$ if  γ < γ ∗ $\left|\gamma \right|<\gamma _*$ , then μ + , L → μ $\mu _{+,L}\rightarrow \mu$ as L → ∞ $L\rightarrow \infty$ ;
  • ( v i ) $(vi)$ if  γ < γ ∗ $\left|\gamma \right|<\gamma _*$ , then  μ L , ♯ → μ $\mu _{L,\sharp }\rightarrow \mu$ as L → ∞ $L\rightarrow \infty$ .

We note that the random measures  μ L , ♯ − ∘ $\mu ^{{}{-\circ }}_{L,\sharp }$ and  μ L , ♯ $\mu _{L,\sharp }$ are functions of the discrete fields  h L $h_L$ , while all other random measures above are functions of the continuum random fields  h $h$ .

Proof. ( i ) $(i)$ and  ( i i ) $(ii)$ respectively hold by combining [5, Thms. 4.1 and 4.14] and [5, Thms. 4.1 and 4.13]. ( i i i ) $(iii)$ follows from Lemma 4.9 and  ( i ) $(i)$ .

In order to prove the remaining assertions, we verify the necessary assumptions in [5, Lem. 4.5], a rewriting in the present setting of the general construction of Gaussian multiplicative chaoses by Shamov [15].

( i v ) $(iv)$ Lemma 4.7 provides the convergence results for the regularizing kernel p ∘ , L $p_{\circ,L}$ and for the covariance kernel k ∘ , L $k_{\circ,L}$ . The uniform integrability—even L 2 $L^2$ -boundedness—of the approximating sequence of random measures  μ ∘ , L $\mu _{\circ,L}$ follows from the L 2 $L^2$ -boundedness of the sequence of random measures  μ ♯ , L $\mu _{\sharp,L}$ as stated in  ( i ) $(i)$ and a straightforward application of Jensen's inequality with the Markov kernel q L $q_L$ :

sup L E μ ∘ , L ( T n ) 2 = sup L E ∫ T n exp γ h ∘ , L ( x ) − γ 2 2 k ∘ , L ( x ) d x 2 = sup L ∫ ∫ T n × T n exp γ 2 k ∘ , L ( x , y ) d y d x ≤ sup L ∫ ∫ T n × T n ∫ ∫ T n × T n exp γ 2 k ♯ , L ( x ′ , y ′ ) q L ( x , x ′ ) q L ( y , y ′ ) d y ′ d x ′ d y d x = sup L ∫ ∫ T n × T n exp γ 2 k ♯ , L ( x , y ) d y d x = sup L E μ ♯ , L ( T n ) 2 = E μ ( T n ) 2 < ∞ . $$\begin{align*} \sup _{L}\mathbb {E}{\left[{\left| \mu _{\circ,L}(\mathbb {T}^n)\right|}^2\right]}&= \sup _{L}\mathbb {E}{\left[{\left| \int _{\mathbb {T}^n} \exp {\left(\gamma h_{\circ,L}(x)-\frac{\gamma ^2}{2}k_{\circ,L}(x)\right)}dx\right|}^2\right]}\\ &=\sup _{L}\iint\nolimits _{\mathbb {T}^n\times \mathbb {T}^n}\exp {\left(\gamma ^2\,k_{\circ,L}(x,y)\right)}dy\,dx\\ &\le \sup _{L}\iint\nolimits _{\mathbb {T}^n\times \mathbb {T}^n}\iint\nolimits _{\mathbb {T}^n\times \mathbb {T}^n}\exp {\left(\gamma ^2\,k_{\sharp,L}(x^{\prime },y^{\prime })\right)} q_L(x,x^{\prime })\,q_L(y,y^{\prime })\,dy^{\prime }\,dx^{\prime }\,dy\,dx\\ &=\sup _{L}\iint\nolimits _{\mathbb {T}^n\times \mathbb {T}^n}\exp {\left(\gamma ^2\,k_{\sharp,L}(x,y)\right)}dy\,dx\\ &=\sup _{L}\mathbb {E}{\left[{\left| \mu _{\sharp,L}(\mathbb {T}^n)\right|}^2\right]}=\mathbb {E}{\left[{\left| \mu (\mathbb {T}^n)\right|}^2\right]}<\infty \,\,\mathrm{.} \end{align*}$$
Alternatively, we can also use Jensen's inequality directly at the level of h ∘ , L $h_{\circ,L}$ . Precisely, we find that
exp γ h ∘ , L ( x ) − γ 2 2 k ∘ , L ( x , x ) = exp ∫ γ h ♯ , L ( x ′ ) − γ 2 2 k ♯ , L ( x ′ , x ′ ′ ) q L ( x , x ′ ) q L ( x , x ′ ′ ) d x d x ′ d x ′ ′ ≤ ∫ exp γ h ♯ , L ( x ′ ) − γ 2 2 k ♯ , L ( x ′ , x ′ ′ ) q L ( x , x ′ ) q L ( x , x ′ ′ ) , $$\begin{equation*} \begin{split} \exp {\left(\gamma h_{\circ,L}(x) - \frac{\gamma ^{2}}{2} k_{\circ,L}(x,x)\right)} &= \exp {\left(\int {\left(\gamma h_{\sharp,L}(x^{\prime }) - \frac{\gamma ^{2}}{2} k_{\sharp,L}(x^{\prime }, x^{\prime \prime }) \right)} q_{L}(x, x^{\prime }) q_{L}(x, x^{\prime \prime }) dx dx^{\prime } dx^{\prime \prime } \right)} \\ &\le \int \exp {\left(\gamma h_{\sharp,L}(x^{\prime }) - \frac{\gamma ^{2}}{2} k_{\sharp,L}(x^{\prime }, x^{\prime \prime }) \right)} q_{L}(x,x^{\prime }) q_{L}(x,x^{\prime \prime }) \,\,\mathrm{,}\;\,\end{split} \end{equation*}$$
from which, we get
μ ∘ , L ( T n ) ≤ μ ♯ , L ( T n ) . $$\begin{equation*} \mu _{\circ,L}(\mathbb {T}^{n}) \le \mu _{\sharp,L}(\mathbb {T}^{n}) \,\,\mathrm{.} \end{equation*}$$

( v ) $(v)$ Lemma 4.7 provides the convergence results for the regularizing kernel p + , L $p_{+,L}$ and for the covariance kernel k + , L $k_{+,L}$ . The uniform integrability of the approximating sequence of random measures  μ + , L $\mu _{+,L}$ follows from Theorem 5.6 in the last section.

( v i ) $(vi)$ According to Lemma 4.9, the Fourier extension h L , ♯ $h_{L,\sharp }$ of the discrete random field h L $h_L$ coincides in distribution with the field obtained from the continuous field h $h$ by regularization with the kernel  r L + ∘ $r_{L}^{{+\circ }}$ . Conditions  ( i i ) $(ii)$ and  ( i i i ) $(iii)$ in [5, Lem. 4.5] can be verified exactly as in the proof of Lemma 4.7. The uniform integrability of the approximating sequence of random measures follows from Theorem 5.6 in the last section. □ $\Box$

5.2 Liouville quantum gravity measures on the discrete tori and their convergence

Let  m L $m_L$ be the normalized counting measure  1 L n ∑ u ∈ T L n δ u $\frac{1}{L^n}\sum _{u\in \mathbb {T}^n_L}\ \delta _u$ on the discrete torus  T L n $\mathbb {T}_L^n$ . Recall that if h L $h_L$ is a polyharmonic field on  T L n $\mathbb {T}_L^n$ as in Equation (14), then
h L − ( v ) ≔ r L − ( h L ) ( v ) = 1 a n ∑ z ∈ Z L n ϑ L , z λ z n / 4 ξ z φ z ( v ) , v ∈ T L n $$\begin{equation} h_L^{{-}}(v)\coloneqq {\sf r}_L^{{-}}(h_L)(v)=\frac{1}{\sqrt {a_n}}\sum _{z\in {\mathbb {Z}}^n_L}\frac{\vartheta _{L,z}}{\lambda _z^{n/4}}\,\xi _z\,\varphi _z(v) \,\,\mathrm{,}\;\,\qquad v\in \mathbb {T}^n_L \end{equation}$$ ()
defines a reduced polyharmonic field on the discrete torus.

Definition 5.4.For γ ∈ R $\gamma \in {\mathbb {R}}$ , define

  • ( i ) $(i)$ the polyharmonic LQG measure  μ L $\mu _L$ (also: discrete LQG measure) on  T L n $\mathbb {T}_L^n$ by
    d μ L ( v ) = exp γ h L ( v ) − γ 2 2 k L ( v , v ) d m L ( v ) , $$\begin{equation*} d\mu _L(v)=\exp {\left(\gamma h_L(v)-\frac{\gamma ^2}{2} k_L(v,v)\right)}\,dm_L(v) \,\,\mathrm{,}\;\, \end{equation*}$$
    where  h L $h_{L}$ is the polyharmonic Gaussian field on the discrete torus T L n $\mathbb {T}^n_L$ and  k L $k_{L}$ its covariance function (which takes the constant value  1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 $\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}$ on the diagonal of  T L n $\mathbb {T}^n_L$ ) as introduced in Equations (14) and (6);
  • ( i i ) $(ii)$ the reduced discrete LQG measure μ L − $\mu ^{{-}}_{L}$ on T L n $\mathbb {T}_L^n$ by
    d μ L − ( v ) = exp γ h L − ( v ) − γ 2 2 k L − ( v , v ) d m L ( v ) , $$\begin{equation*} d\mu ^{{-}}_{L}(v)=\exp {\left(\gamma h^{{-}}_{L}(v)-\frac{\gamma ^2}{2} k^{{-}}_{L}(v,v)\right)}\,dm_L(v) \,\,\mathrm{,}\;\, \end{equation*}$$
    where  h L − $h_{L}^-$ denotes the reduced polyharmonic field in Equation (38) and  k L − $k_{L}^-$ its covariance function.

In order to prove the convergence of the random measures  μ L $\mu _L$ on the discrete tori T L n $\mathbb {T}_L^n$ as L → ∞ $L\rightarrow \infty$ , we will restrict ourselves to subsequences for which the discrete tori are hierarchically ordered, say L = a ℓ $L=a^\ell$ as ℓ → ∞ $\ell \rightarrow \infty$ for some fixed integer a ≥ 2 $a\ge 2$ and ℓ ∈ N $\ell \in {\mathbb {N}}$ . For convenience, we will assume that a $a$ is odd.

Theorem 5.5.Let a $a$ be an odd integer ≥ 2 $\ge 2$ . Then,

  • ( i ) $(i)$ if | γ | < γ ∗ ≔ n e $|\gamma |<\gamma _*\coloneqq \sqrt {\frac{n}{e}}$ , then  μ a ℓ → μ $\mu _{a^\ell }\rightarrow \mu$ as ℓ → ∞ $\ell \rightarrow \infty$ in the sense that Equation (37) holds for every  f ∈ C ( T n ) $f\in \mathcal {C}(\mathbb {T}^n)$ ;
  • ( i i ) $(ii)$ if  γ < n $\left|\gamma \right|<\sqrt {n}$ , then  μ a ℓ − → μ $\mu ^{{-}}_{a^\ell }\rightarrow \mu$ as ℓ → ∞ $\ell \rightarrow \infty$ in the sense that Equation (37) holds for every  f ∈ C ( T n ) $f\in \mathcal {C}(\mathbb {T}^n)$ .

Proof.Given a $a$ as above, let us call a function f $f$ on T n $\mathbb {T}^n$ piecewise constant if it is constant on all cubes v + Q L $v+Q_{L}$ , v ∈ T L n $v\in \mathbb {T}^n_{L}$ , for some L = a ℓ ′ $L=a^{\ell ^{\prime }}$ .

  • ( i ) $(i)$

    For a piecewise constant  f $f$ and all ℓ ≥ ℓ ′ $\ell \ge \ell ^{\prime }$ ,

    ∫ f d μ a ℓ = ∫ f d μ + , a ℓ . $$\begin{equation} \int f\, d\mu _{a^{\ell }}=\int f\, d\mu _{+,a^{\ell }}. \end{equation}$$ ()
    Indeed, the field h + , a ℓ $h_{+,a^{\ell }}$ is constant all cubes v + Q a ℓ $v+Q_{a^\ell }$ , v ∈ T a ℓ n $v\in \mathbb {T}^n_{a^\ell }$ , and Lemma 4.10 ( i ) $(i)$ yields that the fields h a ℓ $h_{a^{\ell }}$ and h + , a ℓ $h_{+,a^{\ell }}$ coincide (in distribution) on the discrete torus T a ℓ n $\mathbb {T}^n_{a^\ell }$ . Thus, also the associated LQG measures of all cubes v + Q a ℓ $v+Q_{a^\ell }$ , v ∈ T a ℓ n $v\in \mathbb {T}^n_{a^\ell }$ , coincide.

    Hence, for a piecewise constant functions f $f$ , the convergence

    ∫ f d μ a ℓ → ∫ f d μ as ℓ → ∞ $$\begin{equation*} \int f\, d\mu _{a^\ell }\rightarrow \int f\, d\mu \qquad \text{as }\ell \rightarrow \infty \end{equation*}$$
    follows from the previous Theorem 5.3 ( v ) $(v)$ .

    For a continuous f $f$ , the claim follows by approximation of f $f$ by piecewise constant f j $f_j$ , j ∈ N $j\in {\mathbb {N}}$ . Indeed,

    E ∫ f d μ a ℓ − ∫ f j d μ a ℓ ≤ E ∫ f − f j d μ a ℓ = ∫ f − f j d x → 0 $$\begin{equation*} \mathbf {E}{\left[{\left|\int f\, d\mu _{a^\ell }-\int f_j\, d\mu _{a^\ell } \right|} \right]} \le \mathbf {E}{\left[\int {\left|f- f_j\right|}\, d\mu _{a^\ell } \right]}= \int {\left|f- f_j \right|} \, dx\ \rightarrow \ 0 \end{equation*}$$
    as j → ∞ $j\rightarrow \infty$ , uniformly in ℓ ∈ N $\ell \in {\mathbb {N}}$ , and similarly with μ $\mu$ in the place of μ a ℓ $\mu _{a^\ell }$ .

  • ( i i ) $(ii)$ For a piecewise constant  f $f$ , according to Lemma 4.10 ( i i ) $(ii)$ for all ℓ ≥ ℓ ′ $\ell \ge \ell ^{\prime }$ ,
    ∫ f d μ a ℓ − = ∫ f d μ ∘ , a ℓ . $$\begin{equation} \int f\, d\mu ^{{-}}_{a^{\ell }}=\int f\, d\mu _{\circ,a^{\ell }}. \end{equation}$$ ()
    Hence, for piecewise constant functions f $f$ , the convergence
    ∫ f d μ a ℓ − → ∫ f d μ as ℓ → ∞ $$\begin{equation*} \int f\, d\mu ^{{-}}_{a^\ell }\rightarrow \int f\, d\mu \qquad \text{as }\ell \rightarrow \infty \end{equation*}$$
    follows from the previous Theorem 5.3 ( i v ) $(iv)$ . For a continuous f $f$ , the claim follows by approximation of f $f$ by piecewise constant f j $f_j$ , j ∈ N $j\in {\mathbb {N}}$ , as in  ( i ) $(i)$ . □ $\Box$

5.3 Uniform integrability of discrete and semi-discrete Liouville quantum gravity measures

Finally, we address the question of uniform integrability of approximating sequences of LQG measures. We provide a self-contained argument for L 2 $L^2$ -boundedness, independent of Kahane's work [9].

Theorem 5.6.Assume | γ | < γ ∗ ≔ n e $|\gamma |<\gamma _*\coloneqq \sqrt {\frac{n}{e}}$ . Then

sup L ∫ T n exp γ 2 k L , ♯ ( 0 , y ) d L n ( y ) < ∞ , $$\begin{align} \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\sharp }(0,y)\right)}\,d\mathcal {L}^n(y)&<\infty \,\,\mathrm{,}\;\,\end{align}$$ ()
sup L ∫ T n exp γ 2 k L , ♭ ( 0 , y ) d L n ( y ) < ∞ , $$\begin{align} \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\flat }(0,y)\right)}\,d\mathcal {L}^n(y)&<\infty \,\,\mathrm{,}\;\,\end{align}$$ ()
sup L ∫ T n exp γ 2 k + , L ( 0 , y ) d L n ( y ) < ∞ . $$\begin{align} \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{+,L}(0,y)\right)}\,d\mathcal {L}^n(y)&<\infty \,\,\mathrm{.}\end{align}$$ ()

Proof.In order to prove Equation (41), recall from Equation (22) that for x , y ∈ T n $x,y\in \mathbb {T}^n$ ,

k L , ♯ ( x , y ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 λ L , z n / 2 · exp 2 π i z · ( x − y ) , $$\begin{align*} k_{L,\sharp }(x,y)=&\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}\cdot \exp {\left(2\pi \text{i}\, z\cdot (x-y)\right)}\,\,\mathrm{,}\;\, \end{align*}$$
were, as usual, λ L , z = 4 L 2 ∑ k = 1 n sin 2 π z k / L $\lambda _{L,z}=4L^2\,\sum _{k=1}^n \sin ^2\left(\pi z_k/L\right)$ . Given ε > 0 $\epsilon >0$ , choose R > 2 $R>2$ such that | z | + 1 2 n ≤ ( 1 + ε ) | z | $|z|+\frac{1}{2}\sqrt n\le (1+\epsilon)|z|$ for all z ∈ Z n $z\in {\mathbb {Z}}^n$ with ∥ z ∥ ∞ ≥ R / 2 $\Vert z\Vert _\infty \ge R/2$ , and S > 1 $S>1$ such that t ≤ ( 1 + ε ) sin ( t ) $t\le (1+\epsilon) \sin (t)$ for all t ∈ [ 0 , π 2 S ] $t\in [0, \frac{\pi }{2S}]$ . Decompose k L , ♯ $k_{L,\sharp }$ for L > R S $L>R\,S$ into k L , R , S + g L , R + f L , S $k_{L,R,S}+ g_{L,R}+f_{L,S}$ with
f L , S ( x , y ) = 1 a n ∑ z ∈ Z L n ∖ Z L / S n 1 λ L , z n / 2 · e 2 π i z · ( x − y ) , g L , R ( x , y ) = 1 a n ∑ z ∈ Z R n ∖ { 0 } 1 λ L , z n / 2 · e 2 π i z · ( x − y ) $$\begin{align*} f_{L,S}(x,y)=&\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus {\mathbb {Z}}^n_{L/S}} \frac{1}{\lambda _{L,z}^{n/2}}\cdot {\rm e}^{2\pi \text{i}\, z\cdot (x-y)}\,\,\mathrm{,}\;\,\qquad g_{L,R}(x,y)=&\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_R\setminus \lbrace 0\rbrace } \frac{1}{\lambda _{L,z}^{n/2}}\cdot {\rm e}^{2\pi \text{i}\, z\cdot (x-y)} \end{align*}$$
and
k L , R , S ( x , y ) = 1 a n ∑ z ∈ Z L / S n ∖ Z R n 1 λ L , z n / 2 · e 2 π i z · ( x − y ) . $$\begin{align*} k_{L,R,S}(x,y)=&\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_{L/S}\setminus {\mathbb {Z}}^n_R} \frac{1}{\lambda _{L,z}^{n/2}}\cdot {\rm e}^{2\pi \text{i}\, z\cdot (x-y)}\,\,\mathrm{.} \end{align*}$$

For fixed R $R$ , obviously g L , R ( x , y ) $g_{L,R}(x,y)$ is uniformly bounded in L , x , y $L,x,y$ . Similarly, since sin ( t ) ≥ 2 π t $\sin (t)\ge {\frac{2}{\pi }}\,t$ for t ∈ [ 0 , π / 2 ] $t\in [0,\pi /2]$ we have that for fixed S $S$ ,

| f L , S | ( x , y ) ≤ 1 a n ∑ z ∈ Z L n ∖ Z L / S n 1 λ L , z n / 2 ≤ 1 a n ∑ z ∈ Z L n ∖ Z L / S n 1 4 n | z | n ≤ 1 4 n a n ∫ B n L / 2 ( 0 ) ∖ B L / ( 2 S ) ( 0 ) 1 | x | n d L n ( x ) = C log ( n L / 2 ) − log ( L / ( 2 S ) ) = C ′ < ∞ . $$\begin{align*} \big\vert f_{L,S}\big\vert (x,y)&\le \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus {\mathbb {Z}}^n_{L/S}} \frac{1}{\lambda _{L,z}^{n/2}} \le \frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus {\mathbb {Z}}^n_{L/S}}\frac{1}{4^n|z|^n}\\ &\le \frac{1}{4^n\,a_n}\int _{B_{{\sqrt n}L/2}(0)\setminus B_{L/(2S)}(0)} \frac{1}{|x|^n}d\mathcal {L}^n(x)\\ &=C\,{\left[\log ({\sqrt n}L/2)-\log (L/(2S))\right]}=C^{\prime }<\infty \,\,\mathrm{.} \end{align*}$$

Thus, for Equation (41) to hold, it thus suffices to prove that

sup L ∫ T n exp γ 2 k L , R , S ( 0 , y ) d L n ( y ) < ∞ , $$\begin{equation} \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,R,S}(0,y)\right)}\,d\mathcal {L}^n(y)<\infty \,\,\mathrm{,}\;\,\end{equation}$$ ()
for some R > 2 $R>2$ as above.

In order to prove the latter, we follow the argument of the proof of Lemma 2, p. 611 in [17]. To start with, we use the multi-dimensional Hausdorff–Young inequality, which can be found in [8, p. 248]:

For p ≥ 2 ∫ T n | k L , R , S ( 0 , y ) | p d y ≤ ∑ z ∈ Z L / S n ∖ Z R n | c ( z ) | p ′ p − 1 , $$\begin{align*} \text{For } p\ge 2 \quad &\int _{\mathbb {T}^n}| k_{L,R,S}(0,y)|^p\, dy\le {\left(\sum _{z\in {\mathbb {Z}}^n_{L/S}\setminus {\mathbb {Z}}^n_R}|c(z)|^{p^{\prime }}\right)}^{p-1}, \end{align*}$$
where c ( z ) = 1 a n 4 L 2 ∑ k = 1 n sin 2 ( π z k / L ) − n / 2 $c(z)=\frac{1}{a_n}\left(4L^2\,\sum _{k=1}^n \sin ^2(\pi z_k/L)\right)^{-n/2}$ and p ′ ∈ [ 1 , 2 ] $p^{\prime }\in [1,2]$ is the Hölder-conjugate. Since π | z k | / L ≤ ( 1 + ε ) | sin ( π z k / L ) | $\pi |z_k|/L\le (1+\epsilon) |\sin (\pi z_k/L)|$ for all z k / L $z_k/L$ under consideration, we have that
∫ T n | k L , R , S ( 0 , y ) | p d y ≤ ( 1 + ε ) n p ′ ( p − 1 ) 1 a n p ′ ∑ z ∈ Z L / S n ∖ Z R n 1 ( 2 π | z | ) n p ′ p − 1 . $$\begin{align*} \int _{\mathbb {T}^n}| k_{L,R,S}(0,y)|^p\, dy\le (1+\epsilon)^{np^{\prime }(p-1)}\,{\left(\frac{1}{a_n^{p^{\prime }}}\sum _{z\in {\mathbb {Z}}^n_{L/S}\setminus {\mathbb {Z}}^n_R}\frac{1}{(2\pi |z|)^{np^{\prime }}}\right)}^{p-1}. \end{align*}$$
Let Q 1 ( z ) $Q_1(z)$ be the unit cube ∏ i = 1 n [ z − 1 2 e i , z + 1 2 e i ] $\prod _{i=1}^n[z-\frac{1}{2} e_i,z+\frac{1}{2} e_i]$ around z ∈ Z n $z\in {\mathbb {Z}}^n$ . Since by assumption
| x | ≤ | z | + 1 2 n ≤ ( 1 + 1 2 n ) | z | ≤ ( 1 + ε ) | z | $$\begin{align*} |x|\le |z|+\frac{1}{2}\sqrt {n}\le (1+\frac{1}{2}\sqrt {n})|z|\le (1+\epsilon)|z| \end{align*}$$
for all x ∈ Q 1 ( z ) $x\in Q_1(z)$ and all z $z$ with ∥ z ∥ ∞ ≥ R / 2 $\Vert z\Vert _\infty \ge R/2$ , we estimate
∑ z ∈ Z L / S n ∖ Z R n ∫ Q 1 ( z ) 1 | z | n p ′ d x ≤ ∑ z ∈ Z n ∖ Z R n 1 + ε n p ′ ∫ Q 1 ( z ) 1 | x | n p ′ d x ≤ 1 + ε n p ′ ∫ R n ∖ B R / 2 ( 0 ) 1 | x | n p ′ d x . $$\begin{align*} \sum _{z\in {\mathbb {Z}}^n_{L/S}\setminus {\mathbb {Z}}^n_R}\int _{Q_1(z)}\frac{1}{|z|^{np^{\prime }}}\, dx \le &\sum _{z\in {\mathbb {Z}}^n\setminus {\mathbb {Z}}^n_R}{\left(1+\epsilon \right)}^{np^{\prime }}\int _{Q_1(z)}\frac{1}{|x|^{np^{\prime }}}\, dx\\ \le &{\left(1+\epsilon \right)}^{np^{\prime }}\int _{{\mathbb {R}}^n\setminus B_{R/2}(0)}\frac{1}{|x|^{np^{\prime }}}\, dx. \end{align*}$$
With Cavalieri's principle the integral can be estimated by
∫ R n ∖ B R / 2 ( 0 ) 1 | x | n p ′ d x = ∫ R / 2 ∞ 2 π n / 2 Γ ( n / 2 ) r n − 1 1 r n p ′ d r = 2 π n / 2 Γ ( n / 2 ) 1 n ( p ′ − 1 ) R 2 n ( 1 − p ′ ) ≤ 2 π n / 2 Γ ( n / 2 ) p n $$\begin{align*} \int _{{\mathbb {R}}^n\setminus B_{R/2}(0)}\frac{1}{|x|^{np^{\prime }}}\, dx&=\int _{R/2}^\infty \frac{2\pi ^{n/2}}{\Gamma (n/2)}r^{n-1}\frac{1}{r^{np^{\prime }}}\, dr\\ &= \frac{2\pi ^{n/2}}{\Gamma (n/2)}\frac{1}{n(p^{\prime }-1)}{\left(\frac{R}{2}\right)}^{n(1-p^{\prime })}\le \frac{2\pi ^{n/2}}{\Gamma (n/2)}\frac{p}{n} \end{align*}$$
since p ′ > 1 $p^{\prime }>1$ and R ≥ 2 $R\ge 2$ . Hence, we obtain for k L , R , S $ k_{L,R,S}$ :
∫ T n | k L , R , S ( 0 , y ) | p d y ≤ ( 1 + ε ) 2 2 π n p 1 a n p 2 π n / 2 Γ ( n / 2 ) p n p − 1 . $$\begin{align} \int _{\mathbb {T}^n}|k_{L,R,S}(0,y)|^p\, dy\le {\left(\frac{(1+\epsilon)^2}{2\pi }\right)}^{np}\frac{1}{a_n^p}{\left(\frac{2\pi ^{n/2}}{\Gamma ({n}/2)}\frac{p}{n}\right)}^{p-1}. \end{align}$$ ()

Summing these terms over all p ∈ N ∖ { 1 } $p\in {\mathbb {N}}\setminus \lbrace 1\rbrace$ yields

∑ p ≥ 2 γ 2 p p ! ∫ T n | k L , R , S ( 0 , y ) | p d y ≤ ∑ p ≥ 2 γ 2 p p ! ( 1 + ε ) 2 n ( 2 π ) n a n p 2 π n / 2 Γ ( n / 2 ) p n p − 1 = n Γ ( n / 2 ) 2 π n / 2 ∑ p ≥ 2 γ 2 p p ! p ( 1 + ε ) 2 n ( 2 π ) n a n 2 π n / 2 p n Γ ( n / 2 ) p ∼ n Γ ( n / 2 ) 2 π n / 2 ∑ p ≥ 2 1 p 2 π p ( 1 + ε ) 2 n 2 π n / 2 e γ 2 ( 2 π ) n a n n Γ ( n / 2 ) p , $$\begin{align*} \sum _{p\ge 2}\frac{\gamma ^{2p}}{p!}\int _{\mathbb {T}^n}| k_{L,R,S}(0,y)|^p\, dy \le &\sum _{p\ge 2}\frac{\gamma ^{2p}}{p!}{\left(\frac{(1+\epsilon)^{2n}}{(2\pi)^{n}a_n}\right)}^p{\left(\frac{2\pi ^{n/2}}{\Gamma (n/2)}\frac{p}{n}\right)}^{p-1}\\ =&\frac{n\Gamma (n/2)}{2\pi ^{n/2}}\sum _{p\ge 2}\frac{\gamma ^{2p}}{p!\, p}{\left(\frac{(1+\epsilon)^{2n}}{(2\pi)^{n}a_n}\frac{2\pi ^{n/2}p}{n\Gamma (n/2)}\right)}^p\\ \sim &\frac{n\Gamma (n/2)}{2\pi ^{n/2}}\sum _{p\ge 2}\frac{1}{p\sqrt {2\pi p}}{\left(\frac{(1+\epsilon)^{2n}2\pi ^{n/2} e \gamma ^2}{(2\pi)^n a_n n\Gamma (n/2)}\right)}^p, \end{align*}$$
where we used Stirling's formula p ! ∼ 2 π p ( p e ) p $p!\sim \sqrt {2\pi p}(\frac{p}{e})^p$ . The last sum is finite if
( 1 + ε ) 2 n γ 2 < ( 2 π ) n a n n Γ ( n / 2 ) 2 π n / 2 e = n e = γ ∗ 2 , $$\begin{align} (1+\epsilon)^{2n}\gamma ^2<\frac{(2\pi)^n a_nn\Gamma (n/2)}{2\pi ^{n/2}e} =\frac{n}{e}=\gamma _*^2 \,\,\mathrm{,}\;\,\end{align}$$ ()
where we inserted a n = 2 ( 4 π ) n / 2 Γ ( n / 2 ) $a_n=\frac{2}{(4\pi)^{n/2}\Gamma (n/2)}$ . Since by assumption | γ | < γ ∗ $|\gamma |<\gamma _*$ and since ε > 0 $\epsilon >0$ was arbitrary, by appropriate choice of the latter, Equation (46) is satisfied.

To treat the cases p = 0 $p=0$ and p = 1 $p=1$ , observe that ( ∫ T n | k L , R , S ( 0 , y ) | d y ) 2 ≤ ∫ T n | k L , R , S ( 0 , y ) | 2 d y $(\int _{\mathbb {T}^n}| k_{L,R,S}(0,y)|\, dy)^2\le \int _{\mathbb {T}^n}| k_{L,R,S}(0,y)|^2\, dy$ . Thus, there exists a constant C n , γ R $C^R_{n,\gamma }$ such that

∑ p ≥ 0 γ 2 p p ! ∫ T n | k L , R , S ( 0 , y ) | p d y ≤ C n , γ R , $$\begin{align*} \sum _{p\ge 0}\frac{\gamma ^{2p}}{p!}\int _{\mathbb {T}^n}| k_{L,R,S}(0,y)|^p\, dy\le C^R_{n,\gamma }, \end{align*}$$
uniformly in L $L$ , and thus in turn there exists a constant C n , γ ♯ $C^\sharp _{n,\gamma }$ such that
sup L ∑ p ≥ 0 γ 2 p p ! ∫ T n | k L , ♯ ( 0 , y ) | p d y ≤ C n , γ ♯ , $$\begin{align*} \sup _L\,\sum _{p\ge 0}\frac{\gamma ^{2p}}{p!}\int _{\mathbb {T}^n}| k_{L,\sharp }(0,y)|^p\, dy\le C^\sharp _{n,\gamma }, \end{align*}$$
which proves Equation (41).

In order to show Equation (42), note that

∫ T n exp γ 2 k L , ♭ ( 0 , y ) d L n ( y ) = ∫ T L n exp γ 2 k L ( 0 , v ) d m L ( v ) $$\begin{equation*} \int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\flat }(0,y)\right)}\,d\mathcal {L}^n(y)=\int _{\mathbb {T}^n_L}\exp {\left(\gamma ^2 k_{L}(0,v)\right)}\,dm_L(v) \end{equation*}$$
for every L $L$ . Furthermore, for p ≥ 2 $p\ge 2$ ,
∫ T L n | k L ( 0 , v ) | p d m L ( v ) ≤ 1 a n p ′ ∑ z ∈ Z L n ∖ { 0 } | c ( z ) | p ′ p − 1 . $$\begin{align*} \int _{\mathbb {T}^n_L}|k_L(0,v)|^p\, dm_L(v)\le {\left(\frac{1}{a_n^{p^{\prime }}}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace }|c(z)|^{p^{\prime }}\right)}^{p-1}. \end{align*}$$
Indeed, for p = 2 $p=2$ this is due to Parseval's identity, and for p = ∞ $p=\infty$ this holds since | exp ( 2 π i z ( x − y ) ) | = 1 $|\exp (2\pi \text{i}z(x-y))|=1$ . The estimate holds for all intermediate p ∈ ( 2 , ∞ ) $p\in (2,\infty)$ by virtue of the Riesz–Thorin theorem. Then, the proof of Equation (42) follows the lines above.

In order to show Equation (43), recall that k + , L = q L ∘ k L + $k_{+,L}=q_L\circ k_L^+$ with k L $k_L$ given is Equation (32). Thus by Jensen's inequality, Equation (43) will follow from

sup L ∫ T n exp γ 2 k L + ( 0 , y ) d L n ( y ) < ∞ . $$\begin{equation} \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k^+_{L}(0,y)\right)}\,d\mathcal {L}^n(y)<\infty \,\,\mathrm{.}\end{equation}$$ ()
To prove this, we argue as before in (i), now with
k L + ( x , y ) = 1 a n ∑ z ∈ Z L n ∖ { 0 } 1 ϑ L , z 2 λ L , z n / 2 · exp 2 π i z · ( x − y ) $$\begin{align*} k_{L}^+(x,y)=&\frac{1}{a_n}\sum _{z\in {\mathbb {Z}}^n_L\setminus \lbrace 0\rbrace } \frac{1}{\vartheta _{L,z}^2\,\lambda _{L,z}^{n/2}}\cdot \exp {\left(2\pi \text{i}\, z\cdot (x-y)\right)} \end{align*}$$
in the place of k L , ♯ ( x , y ) $k_{L,\sharp }(x,y)$ . For given ε > 0 $\epsilon >0$ , choose R > 2 $R>2$ and S > 1 $S>1$ as before. In particular, then t ≤ ( 1 + ε ) sin ( t ) $t\le (1+\epsilon) \sin (t)$ for all t ∈ [ 0 , π 2 S ] $t\in [0, \frac{\pi }{2S}]$ and thus
1 ≥ ϑ L , z ≥ ( 1 + ε ) − n , z ∈ Z L / S n . $$\begin{equation*} 1\ge \vartheta _{L,z}\ge (1+\epsilon)^{-n}\,\,\mathrm{,}\;\,\qquad z\in {\mathbb {Z}}^n_{L/S} \,\,\mathrm{.} \end{equation*}$$
Thus, decomposing k L + $k_{L}^+$ intro three factors as before and then arguing as before will prove the claim. □ $\Box$

Corollary 5.7.If | γ | < γ ∗ $|\gamma |<\gamma _*$ , then for each f ∈ L 2 ( T n ) $f\in L^2(\mathbb {T}^n)$ ,

  • ( i ) $(i)$ the family ∫ T n f d μ L , ♯ L ∈ N $\left(\int _{\mathbb {T}^n} f\,d\mu _{L,\sharp }\right)_{L\in {\mathbb {N}}}$ is L 2 ( P ) $L^2(\mathbf {P})$ -bounded,
  • ( i i ) $(ii)$ the family ∫ T n f d μ L , ♭ L ∈ N $\left(\int _{\mathbb {T}^n} f\,d\mu _{L,\flat }\right)_{L\in {\mathbb {N}}}$ is L 2 ( P ) $L^2(\mathbf {P})$ -bounded.
  • ( i i i ) $(iii)$ the family ∫ T n f d μ + , L L ∈ N $\left(\int _{\mathbb {T}^n} f\,d\mu _{+,L}\right)_{L\in {\mathbb {N}}}$ is L 2 ( P ) $L^2(\mathbf {P})$ -bounded.

Proof.

  • ( i ) $(i)$ Given f ∈ L 2 ( T n ) $f\in L^2(\mathbb {T}^n)$ and γ $\gamma$ as above, consider the Gaussian variables
    Y L , ♯ ≔ ∫ T n f d μ L , ♯ = ∫ T n exp γ h L , ♯ ( x ) − γ 2 2 k L , ♯ ( x , x ) f ( x ) d L n ( x ) . $$\begin{equation*} Y_{L,\sharp }\coloneqq \int _{\mathbb {T}^n} f\,d\mu _{L,\sharp }= \int _{\mathbb {T}^n} \exp {\left(\gamma h_{L,\sharp }(x)-\frac{\gamma ^2}{2}k_{L,\sharp }(x,x)\right)}\, f(x)\,d\mathcal {L}^n(x) \,\,\mathrm{.} \end{equation*}$$
    Then
    sup L E | Y L , ♯ | 2 = sup L ∫ T n ∫ T n exp γ 2 k L , ♯ ( x , y ) f ( x ) f ( y ) d L n ( y ) d L n ( x ) ≤ sup L ∫ T n ∫ T n exp γ 2 k L , ♯ ( x , y ) d L n ( y ) f 2 ( x ) d L n ( x ) $$\begin{align*} \sup _L\mathbb {E}{\left[\big\vert Y_{L,\sharp }\big\vert ^2 \right]}&= \sup _L\int _{\mathbb {T}^n}\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\sharp }(x,y)\right)}\,f(x)\,f(y)\, d{\mathcal {L}^n}(y)\,d\mathcal {L}^n(x) \\ &\le \sup _L\int _{\mathbb {T}^n}{\left[\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\sharp }(x,y)\right)}\,d{\mathcal {L}^n}(y)\right]} f^2(x) \,d\mathcal {L}^n(x) \end{align*}$$
    and, by translation invariance of k L , ♯ $k_{L,\sharp }$ and Equation (41),
    ≤ ∥ f ∥ 2 · sup L ∫ T n exp γ 2 k L , ♯ ( 0 , y ) d L n ( y ) ≤ ∥ f ∥ 2 · C n , γ ♯ < ∞ . $$\begin{align*} &\le \Vert f\Vert ^2\cdot \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\sharp }(0,y)\right)}\,d{\mathcal {L}^n}(y)\le \Vert f\Vert ^2\cdot C^\sharp _{n,\gamma }<\infty . \end{align*}$$
  • ( i i ) $(ii)$ Similarly, again by translation invariance of  k L , ♯ $k_{L,\sharp }$ , and by Equation (42)
    sup L E | Y L , ♭ | 2 ≤ ∥ f ∥ 2 · sup L ∫ T n exp γ 2 k L , ♭ ( 0 , y ) d L n ( y ) ≤ ∥ f ∥ 2 · C n , γ ♭ < ∞ $$\begin{align*} \sup _L\mathbb {E}{\left[\big\vert Y_{L,\flat }\big\vert ^2 \right]}&\le \Vert f\Vert ^2\cdot \sup _L\int _{\mathbb {T}^n}\exp {\left(\gamma ^2 k_{L,\flat }(0,y)\right)}\,d{\mathcal {L}^n}(y)\le \Vert f\Vert ^2\cdot C^\flat _{n,\gamma }<\infty \end{align*}$$
    for Y L , ♭ ≔ ∫ T n f d μ L , ♭ = ∫ T n exp γ h L , ♭ ( x ) − γ 2 2 k L , ♭ ( x , x ) f ( x ) d L n ( x ) $Y_{L,\flat }\coloneqq \int _{\mathbb {T}^n} f\,d\mu _{L,\flat }=\int _{\mathbb {T}^n} \exp \left(\gamma h_{L,\flat }(x)-\frac{\gamma ^2}{2}k_{L,\flat }(x,x)\right)\, f(x)\,d\mathcal {L}^n(x)$ .
  • ( i i i ) $(iii)$ Analogously. □ $\Box$

ACKNOWLEDGMENTS

KTS is grateful to Christoph Thiele for valuable discussions and helpful references. LDS is grateful to Nathanaël Berestycki for valuable discussions on Gaussian Multiplicative Chaoses. The authors are grateful to an anonymous reviewer for suggestions which improved the presentation.

The authors gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft through the project ‘Random Riemannian Geometry’ within the SPP 2265 ‘Random Geometric Systems.'

LDS gratefully acknowledges financial support from the European Research Council (grant agreement No. 716117, awarded to J. Maas) and from the Austrian Science Fund (FWF). His research was funded by the Austrian Science Fund (FWF) project 10.55776/F65 and project 10.55776/ESP208.

RH, EK, and KTS gratefully acknowledge funding by the Hausdorff Center for Mathematics (project ID 390685813), and through project B03 within the CRC 1060 (project ID 211504053). RH and KTS also gratefully acknowledges financial support from the European Research Council through the ERC AdG ‘RicciBounds’ (grant agreement 694405).

Open access funding enabled and organized by Projekt DEAL.

    DATA AVAILABILITY STATEMENT

    Data sharing not applicable to this paper as no datasets were generated or analyzed during this study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.