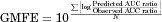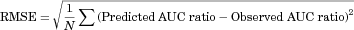Use of a Physiologically Based Pharmacokinetic Model for Quantitative Prediction of Drug–Drug Interactions via CYP3A4 and Estimation of the Intestinal Availability of CYP3A4 Substrates

INTRODUCTION

CYP3A4 is the major enzyme of the cytochrome P450 family of enzymes, accounting for 82% and 40% of the total P450 enzyme content in the human small intestine and liver, respectively,1 and is the enzyme responsible for the metabolism of more than 50% of the top 200 drugs prescribed in the United States.2 Therefore, drug–drug interactions (DDIs) via the inhibition of CYP3A4 sometimes result in serious problems in clinical practice. Recently, attempts have been made to predict DDIs taking into account interactions in the intestine as well as those in the liver, as the first-pass effect in the intestine greatly contributes to the interactions via CYP3A4.3-5

A previous study suggested that in vivo K_i values estimated from the plasma concentration–time profiles of the substrate in the presence and absence of inhibitor in clinical DDI studies were lower than the in vitro K_i values, and that for DDIs resulting from reversible CYP inhibition, the prediction using in vivo K_i values was more accurate than that using in vitro K_i values.6

In this study, clinical DDI studies involving nine CYP3A4 substrates, which are listed as “in vivo sensitive CYP3A substrates” in the DDI draft guidance published by the United States Food and Drug Administration (US FDA),7 were searched for using the Metabolism Transport Drug Interaction Database (DIDB) established by the University of Washington. Using a physiologically based pharmacokinetic (PBPK) model incorporating the inhibition of both intestinal and hepatic metabolism, the AUC ratios were predicted for interactions involving the six substrates for which intravenous data were available, and the accuracy was compared among the results obtained using the in vivo K_i values estimated from clinical DDI studies, predicted in vivo K_i values and in vitro K_i values. For the remaining three substrates for which intravenous data were not available, the F_g values were back-calculated from the plasma concentration–time profiles obtained with or without inhibitors.

METHODS

Collection of the Pharmacokinetic Data

Among the 31 drugs listed as “in vivo sensitive CYP3A substrates” in the DDI draft guidance published by US FDA,7 we have randomly selected nine drugs (aprepitant, dronedarone, eplerenone, ticagrelor, tolvaptan, vardenafil, dasatinib, everolimus, and quetiapine) for which PBPK modeling analysis for prediction of DDI had not been reported to the best of our knowledge. The bioavailability (F), fraction of unchanged drug excreted in urine (f_e), unbound fraction in the plasma (f_p), blood to plasma concentration ratio (R_b), and the contribution of CYP3A4 to the metabolism of the substrate (f_m) were obtained from the literature (Table 1 and Supplementary Table S1). If no information on the R_b was available, it was estimated by Eq. 1 using the f_p and a hematocrit (H_t) value of 0.45.8

()

The f_m was evaluated from in vitro inhibition studies conducted using a specific CYP inhibitor and a value of unity was assumed if no information was available, in consideration of the substrate being a “sensitive in vivo CYP3A substrate”.

Table 1. Pharmacokinetic Parameters of the Substrates and Inhibitors

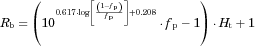		CLtot	CLr								CLh,intc	kac	V1c	k12c	k21c	Tlag
Substrate	F	(L/h)	(L/h)	Fh	Fg	Fa	fp	Rb	Kp,h	fmCYP3A4	(L/h)	(1/h)	(L)	(1/h)	(1/h)	(1/h)	Reference
Aprepitant	0.59	4.14	0	0.957	0.744	0.828	0.0035	0.615a	5.06	0.98	760	0.818	85.8	–	–	0.922	9, 10
											(37)	(0.160)	(4.8)			(0.061)
Dronedarone	0.04	64.2	1.54	0.351	0.114	0.996	0.003	0.628a	5.09	1b	20,800	0.791	415	0.239	0.0238	1.09	11
											(60,200)	(0.625)	(696)	(0.321)	(0.0498)	(0.15)
Eplerenone	0.69	8.26	0	0.914	0.788	0.958	0.41	0.923a	0.628	0.657	20.2	1.74	36.2	–	–	–	12
											(0.5)	(0.14)	(1.2)
Ticagrelor	0.36	14.4	0.00896	0.851	0.469	0.901	0.006	0.652	3.27	0.95	1860	0.491	49.3	0.191	0.0899	–	13
											(366)	(0.291)	(31.9)	(0.160)	(0.0686)
Tolvaptan	0.56	25.8	0	0.733	0.952	0.802	0.02	0.51	5.12	1b	890	0.876	108	–	–	–	14
											(40)	(0.134)	(10)
Vardenafil	0.145	65.6	0	0.321	0.503	0.9	0.0534	0.817	1.50	0.9	3040	1.96	206	–	–	–	15, 16
											(169)	(0.46)	(17)
	CLr						CLh,int	ka	V1	k12	k21	Ki,in vitro	Ki,in vivo	kinact	Ki,app
Inhibitord	(L/h)	Fg	Fa	fp	Rb	Kp,h	(L/h)	(1/h)	(L)	(1/h)	(1/h)	(μg/L)	(μg/L)	(1/h)	(μg/L)
Erythromycin	8.35	1.00	0.956	0.16	1	0.438	356	0.434	45.0	–	–			4.8	35,500
Fluconazole	0.388	0.948	0.950	0.89	1	0.714	0.118	0.861	60.1	–	–	2910	5270
Indinavir	6.59	1.00	1.00	0.4	1	0.529	114	2.13	41.4	–	–	411	0.264
Ketoconazole	0.558	1.00	1.00	0.01	0.632	5.84	1100	1.08	33.0	–	–	10.6	0.821
Itraconazole	1.55	1.00	0.885	0.002	0.58	6.67	10800	0.234	215	0.0797	0.0492	132	0.282

• ^a Calculated using Eq. 1.
• ^b Assumed to be 1 in consideration of being a sensitive in vivo CYP3A4 substrates.
• ^c Optimized by fitting analysis [fitted value (calculated S.E.)].
• ^d Parameters registered in DDI Simulator Ver. 2.1.

Calculation of the Pharmacokinetic Parameters for the CYP3A4 Substrates

The pharmacokinetic parameters of the six substrates for which intravenous data were available (aprepitant, dronedarone, eplerenone, ticagrelor, tolvaptan, and vardenafil) were estimated as follows.

The plasma–concentration profiles of these substrates were obtained from the literature and the plasma concentrations were converted to blood concentrations using the R_b values. Fixing F at the reported value, the substrate blood concentration profiles after a single oral administration was fitted to a one- or two-compartment model to obtain the optimized values of the elimination rate constant (k_e) and distribution volume of the central compartment (V₁) using Phoenix WinNonlin (Version 6.2; Pharsight, Mountain View, California). The total body clearance (CL_tot) and renal clearance (CL_r) were then calculated using Eqs. 2 and 3, respectively:

()

()

Hepatic availability (F_h) and intestinal availability (F_g) were calculated using Eqs. 4 and 5, respectively:

()

()

where the value of the hepatic blood flow (Q_h) was fixed at 96.6 L/h6 and the fraction absorbed (F_a) was either obtained from the literature or calculated by the method reported by Wakayama et al.17. For everolimus, F_a was assumed to be 1, because the reported results of a preclinical study suggested its high intestinal absorption.18

The unbound fraction in the blood (f_b) was calculated using Eq. 6:

()

The liver-plasma concentration ratio (K_p,h) was estimated based on Eq. 7:19

()

where P is the octanol–water partition ratio and was estimated using Eq. 8 from the computer-calculated log P (clog P) obtained using Chem draw (Version 12.0) or ACD/logD (Version 12.01):

()

f_h is the hepatic unbound fraction for specific binding to albumin, globulins, and lipoproteins, and was calculated using Eq. 9, assuming a value of 0.5 for the tissue interstitial fluid-to-plasma concentration ratios of albumin, globulins, and lipoproteins:

()

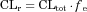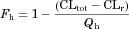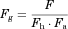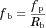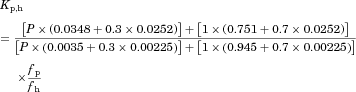Fitting Analyses of the Blood Concentration–Time Profiles of the CYP3A4 Substrates Based on a PBPK Model

Figure 1 shows a simple PBPK model consisting of the central compartment, liver compartment, peripheral compartment, and intestine compartment.6 According to this model, the concentration profiles of the substrate can be expressed by the following differential equations:

()

()

()

()

where C_b and C_h are the drug concentrations in the blood and liver, respectively, X_sub and X_g are the amounts of the drugs in the peripheral and intestine compartment, respectively, k₁₂ is the transfer rate constant from the central compartment to the peripheral compartment, k₂₁ is the transfer rate constant from the peripheral compartment to the central compartment, k_a is the absorption rate constant, CL_h,int is the hepatic intrinsic clearance, and T_lag is the time-lag in drug absorption.

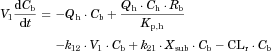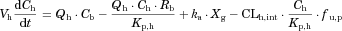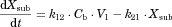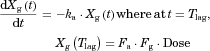The substrate blood concentration profiles after a single oral administration were fitted into Eqs. 10–13 to obtain the optimized values of CL_h,int, k_a, V₁, k₁₂, k₂₁, and T_lag using Phoenix WinNonlin. The hepatic volume (V_h) was fixed at 1.5 L.

Simulation of the Concentration Profiles of the CYP3A4 Substrates in Interaction Studies with Inhibitors

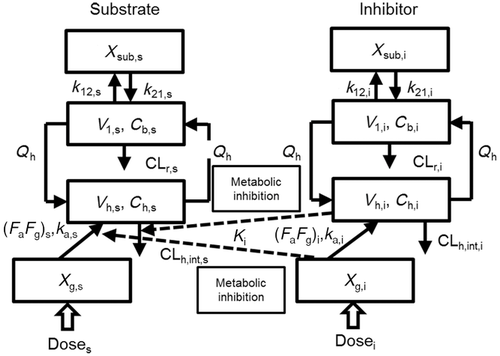
The changes in the concentrations of the substrates due to DDIs were predicted by simulating the concentration profiles of both substrates and inhibitors based on the PBPK model shown in Figure 1. According to this model, the concentration profiles of the substrate and the inhibitor can be expressed by the following differential equations, depending on the inhibition mechanism (reversible or time-dependent) and on whether the intestinal inhibition is incorporated or not. The parameters with subscripts “s” and “i” denote those for the substrate and inhibitor, respectively.

Method 1: Considering only Inhibition in the Liver

• Reversible inhibition (inhibitors except for erythromycin)

()

()

()

()

()

()

()

()

For each DDI, three values of K_i were used for the enzyme inhibition in the liver: in vitro K_i values calculated from metabolic inhibition experiments, in vivo K_i values estimated from other clinical DDI studies, and predicted in vivo K_i values calculated by Eq. 22 using the correlation between the log P and the in vivo K_i/in vitro K_i ratio.6

()

For fluconazole, with a log P value of 0.993, the in vitro K_i value was used as the predicted in vivo K_i value, based on the report by Kato et al.⁶ that the difference between the in vivo and in vitro K_i values of an inhibitor with a log P value of less than 1 is relatively small.

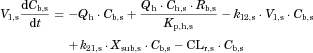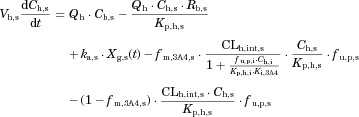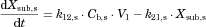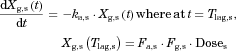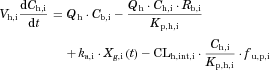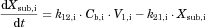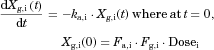• Time-dependent inhibition (erythromycin)

For DDIs involving erythromycin, a time-dependent inhibitor of CYP3A4, Eq. 23 was used instead of Eq. 15:

()

where RE_act,3A4 represents the ratio of the active enzyme relative to the total CYP3A4, expressed by Eq. 24 using the apparent dissociation constant between CYP3A4 and the inhibitor (K_i,app), the maximum inactivation rate constant (k_inact) and the degradation rate constant of CYP3A4 (k_deg). The value of k_deg was fixed at 0.0158 h⁻¹.20

()

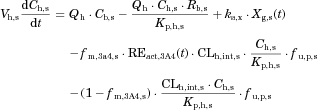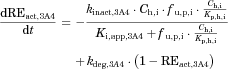Method 2: Considering Inhibition of both Intestinal and Hepatic Metabolism

The increase in the value of F_g,s due to intestinal CYP3A4 inhibition was estimated with Eq. 25 using the inhibitor concentration in the enterocytes ([I_g]) calculated using Eq. 26:22

()

()

In Eq. 25, the in vitro K_i for hepatic CYP3A4 was used for K_i, and the time-dependent inhibition parameters (k_inact, and K_i,app) were also assumed to be the same between the intestine and the liver. The k_deg for CYP3A4 in the intestine and the blood flow rate through the enterocytes were fixed at 0.029 h⁻¹21 and 14.9 L/h,22 respectively.

The estimated increase in the value of F_g,s was then incorporated into the PBPK model to accommodate the effect of metabolic inhibition in the intestine, using Eq. 27 as a substitute for Eq. 17:

()

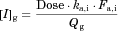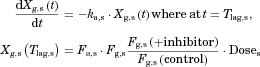The metabolic Inhibition in the liver was estimated in the same manner as that for method 1. Plasma concentration–time profiles of the substrates with and without co-administration of inhibitors were simulated by the above two methods, and the AUC ratio (AUC increase by the inhibitor) was calculated for each case using DDI Simulator (Version 2.1; Fujitsu Kyushu Systems, Fukuoka, Japan). All the parameters for the substrates and inhibitors used in the analyses are summarized in Table 1. The inhibitor parameters, including the in vivo K_i values, were those registered in DDI Simulator.

Comparison of the Model Predictability

The predictability of the AUC ratio was compared based on the geometric mean-fold error (GMFE, Eq. 28, the root mean square error (RMSE, Eq. 29 and % of the AUC ratios predicted within 2-fold accuracy.

()

()

RESULTS

Simulation of the CYP3A4 Substrates Concentration Profiles in Interaction Studies with Inhibitors

The substrate concentration changes due to DDIs were predicted by simulating the concentration profiles of both the substrates and inhibitors using Eqs. 14–27 based on the PBPK model shown in Figure 1, and the AUC ratios were calculated. Figure 2 shows the plasma concentration profiles of aprepitant and vardenafil with or without co-administration of ketoconazole simulated by methods 1 and 2. These two substrates were chosen because their concentration profiles with or without co-administration of typical strong inhibitor, ketoconazole, were available and also the profiles have been more successfully reproduced as compared to other substrates. For both aprepitant and vardenafil, the concentration profiles simulated by method 2, incorporating the inhibition of both intestinal and hepatic metabolism, were closer to the observed concentration profiles than those simulated by method 1, which only considered inhibition in the liver.

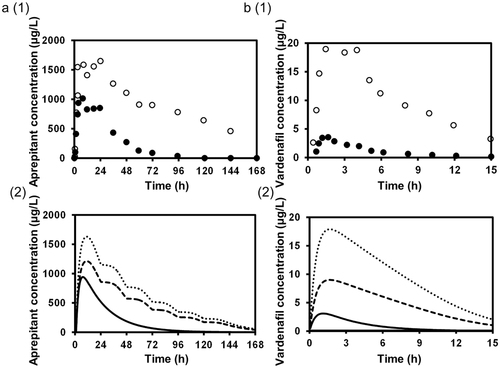
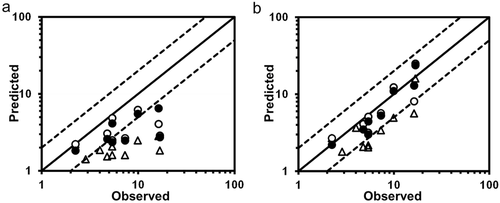
Table 2 summarizes the AUC ratios predicted by methods 1 and 2 using the in vitro K_i, predicted in vivo K_i and in vivo K_i values, and the relationship between the observed and predicted AUC ratios is shown in Figure 3. Method 1, which ignored the inhibition of intestinal metabolism, underestimated the observed AUC ratios in comparison to method 2. The smaller the original F_g of the substrate, the larger the difference tended to be between the observed AUC ratio and that predicted by method 1, and also the larger the prediction improvement by method 2. For the DDIs resulting from reversible inhibition of CYP3A4, the prediction using the predicted in vivo K_i values and in vivo K_i values estimated from clinical DDI studies was more accurate than that using the in vitro K_i values, for both methods 1 and 2. Table 3 shows the comparison of the predictability of the AUC ratios for DDIs resulting from reversible inhibition of CYP3A4. Both the GMFE values (2.11–3.59 and 1.31–1.99 for method 1 and 2, respectively) and RMSE values (6.65–8.14 and 3.02–4.81 for method 1 and 2, respectively) were lower for method 2 than for method 1. These values were lower when predicted in vivo K_i values or in vivo K_i values estimated from clinical DDI studies were used than when in vitro K_i values were used, for both methods 1 and 2. The AUC ratios for 12.5%–50.0% and 25.0%–100% of the eight studies were predicted within a 2-fold accuracy based on method 1 and 2, respectively, and the percentage was higher when predicted in vivo K_i values or in vivo K_i values estimated from clinical DDI studies were used than when in vitro K_i values were used, for both methods 1 and 2.

Table 2. The Observed AUC Ratios and Those Predicted by the PBPK Model

						AUC Ratio
								Predicted
Substrate			Inhibitor			Observed		In vitro Ki		Predicted in vivo Ki		In vivo Ki
	Dose (mg)	Schedule		Dose (mg)	Schedule		Reference	Method 1	Method 2	Method 1	Method 2	Method 1	Method 2
Aprepitant	125	Single dose (day 5)	Ketoconazole	400	QD (day1–10)	4.78	9	1.53	2.06	3.05	4.10	2.59	3.48
Dronedarone	200	Single dose (day 8)	Ketoconazole	200	QD (day 1–8)	16.8	11	1.83	15.9	2.87	24.9	2.73	23.7
Eplerenone	100	Single dose (day 7)	Erythromycin	500	BID (day 1–7)	2.87	23	1.41	1.78	–	–	–	–
Eplerenone	100	Single dose (day 6)	Fluconazole	200	QD (day 1–6)	2.24	23	2.22	2.68	2.22	2.68	1.83	2.20
Eplerenone	100	Single dose (day 6)	Ketoconazole	200	BID (day 1–6)	5.39	23	1.60	2.03	2.50	3.17	2.36	2.99
Ticagrelor	90	Single dose (day 4)	Ketoconazole	200	BID (day 1–10)	7.32	13	1.59	3.38	2.66	5.66	2.48	5.28
Tolvaptan	30	Single dose (day 2)	Ketoconazole	200	QD (day 1–3)	5.40	14	2.06	2.16	4.85	5.10	4.13	4.34
Vardenafil	20/5	Single dose (day 4)	Erythromycin	500	TID (day 1–4)	4.02	15	1.86	3.64	–	–	–	–
Vardenafil	10	Single dose (day 7)	Indinavir	800	TID (day 1–7)	16.3	15	2.82	5.60	4.06	8.06	6.48	12.9
Vardenafil	20/5	Single dose (day 4)	Ketoconazole	200	QD (day 1–4)	9.95	15	2.48	4.93	6.19	12.3	5.51	11.0

Table 3. Predictability of the Method 1 and Method 2

	In vitro Ki		Predicted in vivo Ki		In vivo Ki
	Method 1	Method 2	Method 1	Method 2	Method 1	Method 2
GMFE	3.59	1.99	2.11	1.37	2.20	1.31
RMSE	8.14	4.81	7.00	4.29	6.65	3.02
% within 2-fold error	12.5	25.0	50.0	87.5	50.0	100

• Method 1, the prediction assuming only inhibition in the liver; method 2, the prediction assuming inhibition of both intestinal and hepatic metabolism; GMFE, the geometric mean fold error; RMSE, the root mean square error.

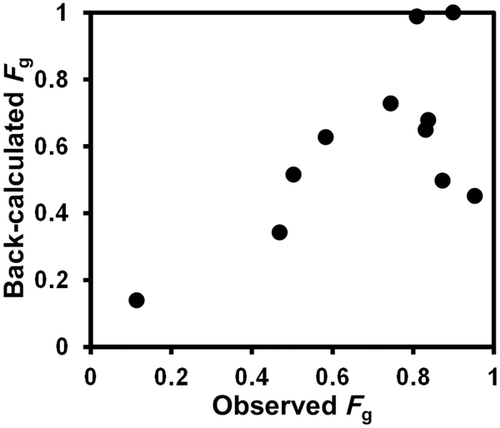
Estimation of F_g for the CYP3A4 Substrates

The F_g values of the CYP3A4 substrates for which intravenous data were available were back-calculated from their concentration–time profiles obtained with or without inhibitors (ketoconazole or itraconazole) using the parameters listed in Table 1 and Supplementary Table S1. As shown in Figure 4 and Supplementary Table S2, the back-calculated F_g values were comparable to those calculated from the intravenous data using Eq. 5.

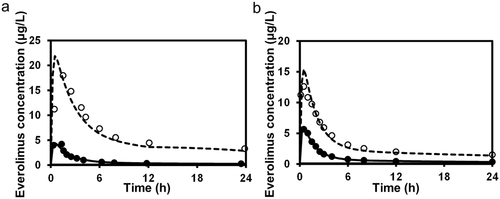
For the three substrates (dasatinib, everolimus, and quetiapine) for which intravenous data were not available, the substrate blood concentration profiles obtained with or without inhibitors (ketoconazole or erythromycin) were fitted into Eq. 14 based on the simultaneous analysis of Eqs. 14-16, 18-21, and 23-27 to obtain the optimized values of T_lag,s, CL_h,int,s, k_a,s, V_1,s, k_12,s, k_21,s, and F_g,s. The parameters fixed and optimized in the analyses are summarized in Supplementary Tables S1 and S4, respectively. The fitted curves were close to the observed profiles, as shown in Figure 5 (e.g., for the case of everolimus), and the F_g values of dasatinib, everolimus, and quetiapine were estimated as 0.744, 0.219–0.391, and 0.538–0.800, respectively. The values of F_g in the presence of inhibitor, calculated by multiplying those under the control condition and the increase estimated using Eq. 25, reached nearly 1 for all the cases, indicating complete inhibition of the intestinal metabolism in the presence of inhibitor. A larger contribution of inhibition in the intestine in the overall interaction was estimated in the case of a smaller F_g value under the control condition.

DISCUSSION

The present study investigated whether the DDIs via CYP3A4 can be quantitatively predicted by estimating the extent of hepatic CYP3A4 inhibition based on simple PBPK modeling of both the substrate and inhibitor and incorporating the increase in the F_g due to the intestinal enzyme inhibition.

For the DDIs resulting from reversible inhibition of CYP3A4, the prediction using predicted in vivo K_i values and in vivo K_i values was more accurate than that using in vitro K_i values (Table 2 and Fig. 3). The fold difference in the predicted and observed AUC ratios ranged from 0.55 (DDI between eplerenone and ketoconazole) to 1.41 (DDI between dronedarone and ketoconazole) using method 2 with the in vivo K_i, which we think is acceptable. Considering that ketoconazole is involved as an inhibitor in both of the above DDIs, the differences might be associated with the substrate characteristics, such as low bioavailability of dronedarone (4%), but the reasons are unknown.11 Because the prediction using in vitro K_i values underestimated the observed AUC ratios, either predicted in vivo K_i values or in vivo K_i values should be used for a more accurate prediction of DDIs. When the possibility of a candidate compound being a CYP3A4 inhibitor is to be evaluated and its in vivo K_i value is unavailable, use of predicted in vivo K_i values, estimated from the log P and the in vitro K_i value, is recommended.

The AUC ratios for 12.5%–50.0% and 37.5%–100% of the DDI studies were predicted within 2-fold accuracy based on method 1 and 2, respectively, indicating that the prediction by method 2 was more accurate than that by method 1 (Table 3). It is important for quantitative predictions of DDIs via CYP3A4 to take into account the interaction in the intestine as well as that in the liver. In the present study, the increase in the values of F_g due to the intestinal enzyme inhibition was estimated using a static model and incorporated into the PBPK model, whereas the ADAM (Advanced Dissolution Absorption and Metabolism) model is used in other prediction models such as the Simcyp Simulator (Simcyp Limited, Sheffield, UK) for dynamic prediction of intestinal absorption, transport, metabolism and DDIs.26 Although the ADAM model allows for estimation of the intestinal absorption of low-solubility compounds and also the DDI predictions considering the differential distribution of CYP3A4 along the intestine, it requires a large number of input parameters, some of which are not necessarily possible to estimate with accuracy. From that viewpoint, our prediction model with F_g estimation using a static model has the advantage of requiring much fewer parameters.

Four of the CYP3A4 substrates analyzed in the present study (aprepitant, 9 ticagrelor,13 tolvaptan,14, 27 and vardenafil28) are also reported as substrates of P-glycoprotein, and two of the CYP3A4 inhibitors (erythromycin29 and ketoconazole29) are also known to inhibit P-glycoprotein. Although DDIs via P-glycoprotein were not incorporated in the present model, the AUC ratios for DDIs involving these compounds were predicted within 2-fold accuracy by method 2 using in vivo K_i values (Table 3), suggesting a minor contribution of P-glycoprotein inhibition. In addition, membrane transport is unlikely to be a rate-limiting step in the intestinal absorption of a highly permeable and highly soluble drug such as vardenafil.15

For the three substrates (dasatinib, everolimus, and quetiapine) for which intravenous data were not available, the F_g values were back-calculated from the plasma concentration–time profiles obtained with or without inhibitors. To validate this method for F_g estimation, the F_g values of 12 substrates for which intravenous data were back-calculated from the concentration–time profiles obtained with or without inhibitors (ketoconazole or itraconazole). We found that the back-calculated F_g values were comparable to those calculated from the intravenous data (Fig. 4). Several methods of predicting F_g have been reported as follows: Nishimuta et al.³⁰ developed a method for predicting F_g that is applicable to low-permeability compounds based on metabolic clearance from metabolic stability assays using human liver microsomes for CYP3A4 substrates, and the permeability values obtained by parallel artificial permeability assay (PAMPA). Gertz et al.³¹ reported that F_g can be estimated from interaction studies with grapefruit juice, assuming complete inhibition of CYP3A4-mediated intestinal metabolism and no effects on the hepatic enzymes or the fraction absorbed of the drug. Hisaka et al.³² evaluated the F_g from the changes in the AUC and elimination half-life of the drug caused by DDIs. Because it is important for quantitative predictions of DDIs via CYP3A4 to take into account the increase in the values of F_g, the present method for estimating F_g would be useful for CYP3A4 substrates for which intravenous data are not available. The F_g values of dasatinib, everolimus, and quetiapine were estimated as 0.744, 0.219–0.391, and 0.538–0.800, respectively (Table 4). The F_g values of cyclosporin and midazolam have been estimated to be 0.4–0.79 and 0.29–0.68, respectively, based on intravenous and oral data obtained from different clinical studies,3 both showing 2-fold variation. Therefore, the 1.79-fold and 1.49-fold variation in the F_g values of everolimus and quetiapine, respectively, estimated from different clinical DDI studies, may be regarded as acceptable.

In conclusion, the present PBPK model for both CYP3A4 substrates and inhibitors, incorporating the increase in the F_g value due to the intestinal enzyme inhibition, was found to be useful for quantitative prediction of clinical DDIs when combined with the in vivo K_i values. Based on the present PBPK model, the F_g values for CYP3A4 substrates for which intravenous data were not available were also successfully back-calculated using the plasma concentration profiles obtained from clinical DDI studies.