Correlation between computed gas-phase and experimentally determined solution-phase infrared spectra: Models of the iron–iron hydrogenase enzyme active site
Abstract
Gas-phase density functional theory calculations (B3LYP, double zeta plus polarization basis sets) are used to predict the solution-phase infrared spectra for a series of CO- and CN-containing iron complexes. It is shown that simple linear scaling of the computed CO and CN stretching frequencies yields accurate predictions of the the experimentally determined ν(CO) and ν(CN) values for a variety of complexes of different charges and in solvents of varying polarity. As examples of the technique, the resulting correlation is used to assign structures to spectroscopically observed but structurally ambiguous species in two different systems. For the (μ-SCH2CH2CH2S)[Fe(CO)3]2 complex in tetrahydrofuran solution, our calculations show that the initial electrochemical reduction process leads to a simple one-electron reduced product with a structure very similar to the (μ-SCH2CH2CH2S)[Fe(CO)3]2 parent complex. For the iron–iron hydrogenase enzyme active site, our computations show that the absence or presence of a water molecule near the distal iron center (the iron center further from the [4Fe4S] cluster and protein backbone) has very little effect on the predicted infrared spectra. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 1454–1462, 2006
Introduction
Infrared (IR) spectroscopy is a powerful tool for studying metalloproteins that contain metal-bound diatomic ligands. When a diatomic ligand, such as CO, CN−, or NO is bound to a transition metal center, it becomes a sensitive indicator of its environment and its characteristic frequency is modulated by changes in the metal oxidation state, in the nature of nearby residues such as their protonation state, and in its hydrogen bond network.1 These diatomic ligands may be extrinsic (such as the NO and CO ligands present in the NO and CO inhibited forms of hemoglobin2, 3) or intrinsic (such as the CO and CN− ligands present in the hydrogenase enzymes4, 5) to the protein or enzyme being studied.
Infrared spectroscopy has proven particularly useful in the study of the hydrogenase (H2ases) enzymes. All H2ases studied to date have been shown to contain iron-bound CO ligands. The nickel–iron ([NiFe]) and iron–iron ([FeFe]) enzymes contain both CO and CN− as intrinsic ligands to their iron centers and when exposed to CO gas, both the [NiFe] and [FeFe] H2ases bind an additional CO ligand that inhibits catalysis.6-14 This extrinsic CO appears as a new ν(CO) band in their infrared spectra, and as an additional CO ligand in their solid-state structures (as determined by EXAFS or single-crystal X-ray diffraction).14-16
Protein crystallography has defined the basic framework of the [FeFe]H2ase active site (Fig. 1), as consisting of a typical [4Fe–4S] cluster bridged via a cysteinyl sulfur to a unique [FeFe] center.10, 13, 14 The two iron centers are bridged by the two sulfur atoms of a five-atom dithiolate linker. Each iron of the di-iron cluster is further coordinated by one terminal CO ligand and one terminal CN− ligand. A third CO ligand is found to either bridge the two iron centers or is terminally bound to the distal iron center. (The two iron centers are generally designated as either proximal or distal to the [4Fe–4S] cluster and protein backbone.) The nature of the L ligand bound to the distal iron center and the orientation of the bridging CO ligand apparently depends on the crystallization conditions and the redox state of the enzyme active site.14
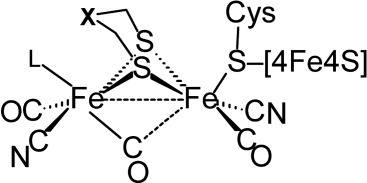
Consensus structure for the active site of [FeFe]H2ases. The two iron centers are commonly designated by their spatial relation to the [4Fe–4S] cluster, and thus are referred to as the distal iron (left) and proximal iron (right). The nature of the L ligand and the “bridging” CO ligand (fully bridging vs. semibridging vs. terminal to the distal iron) apparently depends on the redox state of the FeFe cluster.
At least four distinct forms of the di-iron active site of [FeFe]H2ase enzyme have been identified by the application of IR spectroscopy. Aerobic purification of the enzyme results in an overoxidized, catalytically inactive form of the enzyme, known alternatively as Has-isolated or H.14, 17, 18 Reduction of the enzyme (electrochemically or chemically with H2 gas or chemical reductants such as dithionite), leads to a reduced, catalytically active form of the enzyme, known as Hred.14, 17, 18 Oxidation of the Hred form (electrochemically or chemically by autooxidation via H2 loss or reaction with mild chemical oxidants) produces a species of intermediate oxidation state, known as Hox (i.e., Hox is more reduced than H, but more oxidized than Hred).14, 17, 18 The addition of CO gas to preparations of the catalytically active, Hox form, yields a catalytically inactive, CO-inhibited form known as Hox-CO.11, 14
Although the single-crystal X-ray diffraction studies of Peters, Fontecilla–Camps and their respective coworkers have defined the basic structure of the [FeFe]H2ase active site, important questions remain. Which, if any, spectroscopically observed form of the [FeFe] cluster (H, Hox, Hred) does each of the solid-state structures represent? Electron density centered at a distance of ∼2.6 Å from the distal iron in the native enzyme from Clostridium pasteurianum I (CpI) was modeled by the crystallographers as a terminally bound water molecule.10 Interestingly, a recent reevaluation of the X-ray structure of the Ni–A form of [NiFe] hydrogenase enzyme derived from Desulfovibrio fructosovorans showed that what was originally thought to be an oxo ligand (O, OH, or OH2) was determined to actually be a dioxo ligand (O2, O2H, or O2H2).19 Our calculations suggest that hydroperoxide (O2H) is the most likely candidate.20 Single-crystal X-ray diffraction studies are generally unable to accurately locate hydrogen atoms, and thus unable to distinguish between O, OH, and OH2. Therefore, the protonation states and oxidation states of the iron centers and iron-bound ligands in the various forms of the [FeFe]H2ase active site are often unclear.
The goal of this study is to develop and test a computational methodology for predicting and simulating the infrared spectra of di–iron models that are similar in composition and structure to the active site of the [FeFe]H2ase enzyme. In the present study, predicted IR frequencies and intensities are used in two examples: (1) to determine the best choice for the molecular structure for a spectroscopically observed, but structurally undetermined, intermediate in the electrochemical production of H2 by a synthetic model of the active site of [FeFe]H2ase; and (2) to predict the structure of one spectroscopically observed form of the [FeFe]H2ase active site, which has some unclear structural and electronic aspects. This methodology will be used in a subsequent study to discriminate between a series of structural candidates for various spectroscopically observed forms of the [FeFe]H2ase enzyme.
Computational Details
All DFT calculations were performed using a hybrid functional [the three-parameter exchange functional of Becke (B3)21 and the correlation functional of Lee, Yang, and Parr (LYP)22] (B3LYP) as implemented in Gaussian 03.23 The iron, phosphorus, and sulfur atoms use the effective core potential and associated basis set of Hay and Wadt (LANL2DZ).24, 25 For iron, the two outermost p functions were replaced by reoptimized 4p functions as suggested by Couty and Hall26 and an f polarization function27 was added. For sulfur and phosphorus, the basis set was augmented by the d polarization function of Höllwarth et al.28 The CO, CN− ligands, the nitrile CN unit of the CNMe ligands, amine nitrogens, and hydrogen atoms attached to amine nitrogens use the 6-31G(d′,p′) basis set.29-31 All other atoms use the 6-31G basis set.32 Solvation calculations use the Onsager model as implemented in Gaussian 03.33-38 Unless otherwise noted, all geometries are fully optimized and confirmed as minima or n-order saddle points by analytical frequency calculations at the same level.
Generation of Simulated Infrared Spectra
Results and Discussion
Selection of the Training Set
To be able to predict experimentally determined solution-phase IR spectra from DFT-derived gas-phase values, we must determine a scaling factor between the experimental and theoretical values. This scaling factor is determined by calculating with the same basis set and methodology a training set of complexes for which both the structures and infrared spectra are known. The selection of an appropriate training set is critical to the prediction of accurate ν(CO) and ν(CN) stretching frequencies. Three factors were considered in the selection of each member of this training set: (1) the total charge and chemical composition of the molecule is similar to the molecule of interest. Because the scaling factor adjusts the theoretically determined values for the effects of solvation and systematic error in the experimental and theoretical values, the use of a scaling factor determined for molecules that are drastically different from the molecule of interest is ill-advised. For example, the use of a series of ruthenium carbonyl complexes to determine the scaling factor for ν(CO) bands for an iron carbonyl complex may yield poor results because the systematic error arising from the Ru basis set is different than that arising from the Fe basis set. (2) The solvent used for the experimentally determined IR spectra are nonprotic. (3) For charged species, only complexes with large, weakly coordinating counterions were considered. Small, strongly coordinating counterions and highly polar, protic solvents may form strong interactions with the CO and CN− ligands, shifting their values, relative to the same complex with large, weakly coordinating and/or nonprotic, weakly polar solvent. Obviously, the latter conditions are more appropriate for predicting solution-phase spectra based on gas-phase calculations of the “naked” complex ion. The training set used in this article is presented in Table1 and Figure 2.
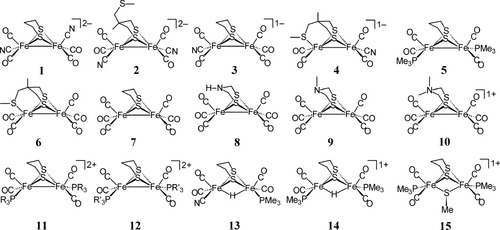
Structures for a series of synthetic models for the active site of [FeFe]H2ase. PR3 and PR′3 refer, respectively, to singly N-protonated and N-methylated 1,3,5-triaza-7-phosphaadamantane. References to the experimental data are given in Table 1.
| Complexa | Counterion(s) | Solvent | Reference |
|---|---|---|---|
| 1 | [18-crown-6-K]1+ | CH3CN | 39 |
| 2 | [18-crown-6-K]1+ | CH3CN | 40 |
| 3 | [NEt4]1+ | THF | 41, 42 |
| 4 | [NEt4]1+ | CH3CN | 40 |
| 5 | n/a | CH3CN | 43 |
| 6 | n/a | CH3CN | 40 |
| 7 | n/a | hexanes | 42, 44 |
| 8 | n/a | hexanes | 45 |
| 9 | n/a | CH3CN | 46 |
| 10 | n/a | CH3CN | 46 |
| 11 | [F3CSO3]1− | CH3CN | 47 |
| 12 | [PF6]1− | CH3CN | 47 |
| 13 | n/a | THF | 48 |
| 14 | [PF6]1− | CH3CN | 43 |
| 15 | [BF4]1− | CH2Cl2 | 49 |
- a Chemical structures of these complexes given in Figure 2.
Assignment of the Computed Spectra
Three cases are observed in examination of experimentally determined IR spectra: (case 1) The number of ν(CX) bands is the same as the number of CX ligands in the complex. (case 2) The number of ν(CX) bands is less than the number of CX ligands in the complex. For highly symmetric molecules, two or more of the C–X stretching modes may be degenerate [same ν(CX) value] or have no IR intensity by symmetry (case 2a). (A stretching mode that does not result in a change in the molecular dipole moment is not observed by IR spectroscopy.) Alternatively, one or more of the experimentally observed ν(CX) “bands” may, in fact, correspond to the accidental degeneracy (degeneracy that is not required by the symmetry of the molecule) of two or more fundamental stretching modes (case 2b), or the concentration of the sample may be such that one or more low-intensity ν(CX) bands are indistinguishable from the spectral baseline (case 2c). (case 3) The number of ν(CO) or ν(CN) bands is more than the number of CO and CN ligands in the complex. This situation occurs when there is a mixture of two or more CX-containing species present in the sample solution.
For case 1 situations, each of the computed ν(CX) stretching frequencies should correlate in a one-to-one manner with the experimentally observed ν(CX) bands, and the spectra should be simple to assign. The [(μ-S(CH2)3S)[Fe(CO)3][Fe(CO)2(CN)]]1− complex (3) provides an example of case 1. The experimentally determined IR spectrum of [(μ-S(CH2)3S)[Fe(CO)3][Fe(CO)2(CN)]]1− features five ν(CO) bands and one ν(CN) band.41 Each of the six C–X stretching frequencies of the computed spectrum of 3 is assigned to one of the bands of the experimentally determined IR spectrum (as shown in Fig. 3).
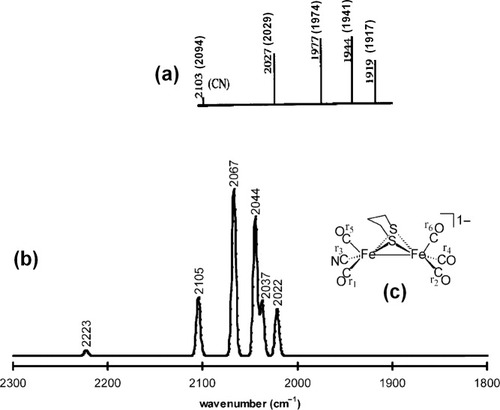
Simulation of the IR spectrum of [(μ-S(CH2)3S)[Fe(CO)3][Fe(CO)2(CN)]]1− (3). In (a), a line diagram of the experimental spectrum of 3 is reproduced from ref.42 with permission from Wiley-VCH Copyright 1999. The value of the corresponding experimentally determined ν(CX) band from ref. 41 is given in parentheses. In (b), the simulated IR spectrum of 3 is presented. A half-width of 5 cm−1 was used in the simulation of each ν(CX) band. The unscaled computed energy of each C–X stretching mode is given above the simulated ν(CX) band. In (c), the labeling scheme for the CO and CN ligands of complex 3 is given. These six calculated vibrations correspond to the group vibrations of the six CX ligands in the following manner: 2022 [r2–r6]; 2037 [r1–r5–r6]; 2044 [r2–r4–r5+r6]; 2067 [r1–r4+r5]; 2105 [r1+r2+r4+r5+r6]; 2223 [r3].
For case 2a situations, the assignment of the spectra should be simple if the “missing” bands correspond to degenerate stretching modes, or stretching modes that are not IR active by symmetry. In other words, for case 2a, the number of ν (CX) bands is the same as that one would predict by analyzing the molecule by group theory. In the case of degenerate vibrations, the computation should predict that two or more of the fundamental stretching modes will occur at approximately the same energy. In the case of vibrations that are not IR active, the computation should predict that these vibrations have little or no IR intensity. The (μ-S(CH2)3S)[Fe(CO)3]2 complex (7) provides one example of case 2. Simple group theoretical analysis of this pseudo-C2v molecule predicts five IR-active bands, and five ν(CO) bands are observed in the experimentally determined IR spectrum of 7 in hexanes.44 Consistent with these expectations and experiments, five of the six ν(CO) bands are computed to have nonnegligible IR intensities (The six computed intensities, given in order of increasing intensity, are 0.02, 35.81, 571.60, 828.89, 1180.05, and 2217.82.) The band with a computed intensity of 0.02 is the C–O stretch mode predicted by group theory to have no intensity in the IR spectrum. The assignment of the computed ν(CO) bands of 7 is given in Figure 4.
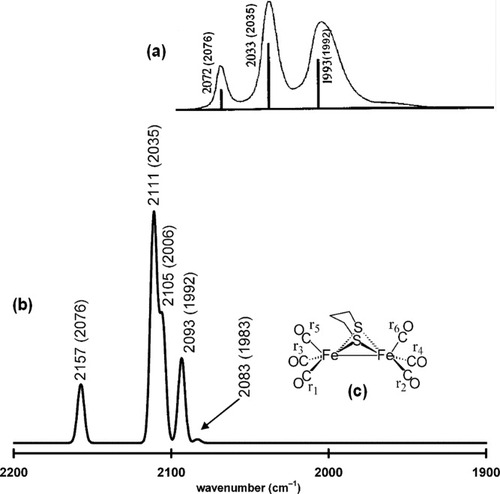
Simulation of the IR spectrum of (μ-S(CH2)3S)[Fe(CO)3]2 (7). In (a), the experimental spectrum of 7 is reproduced from reference 42 with permission from Wiley-VCH Copyright 1999. The value of the corresponding experimentally determined ν(CO) band from ref.44 is given in parentheses. In (b), the simulated IR spectrum of 7 is presented. A half-width of 5 cm−1 was used in the simulation of each ν(CO) band. The unscaled computed energy of each C–O stretching mode is given above the simulated ν(CO) band. In (c), the labeling scheme for the CO ligands of complex 7 is given. These six calculated vibrations correspond to the group vibrations of the six CO ligands in the following manner: 2083 [r1–r2+r3–r4–r5+r6]; 2089 (no IR intensity) [r1–r2–r3+r4]; 2093 [r1+r2+r3+r4–r5–r6]; 2105 [r1+r2–r3–r4]; 2111 [r1–r2+r3–r4+r5−r6]; 2157 [r1+r2+r3+r4+r5+r6].
For other case 2 examples, the situation is more complex when one or more of the experimentally observed ν(CX) “bands” corresponds to the overlap of two or more accidentally degenerate, fundamental C–X vibrational modes (case 2b), or when one or more bands with low relative intensities are present (case 2c). The (μ-S(CH2)3S)[Fe(CO)2(PMe3)]2 complex (5) provides such an example. The experimentally determined IR spectrum of 5 features ν(CO) bands at 1979, 1942, and 1898 cm−1.43 The computed ν(CO) stretching frequencies (and corresponding computed IR intensities) are 2060 cm−1 (22.47), 2040 cm−1 (1877.01), 2006 cm−1 (950.11), and 1990 cm−1 (568.45). In the absence of a graphical simulation of the experimental IR spectrum, one might be tempted to assign the three experimentally observed ν(CO) bands to the three computed C–O stretching frequencies with large relative intensities. The direct comparison of experimentally determined spectrum and the computed spectrum of 5 clearly shows that 1982, 1943, and 1899 cm−1 bands in the experimental spectrum correspond to the 2060, 2040, and {2006 + 1990} cm−1, C–O stretching frequencies of the computed spectrum (shown in Fig. 5).
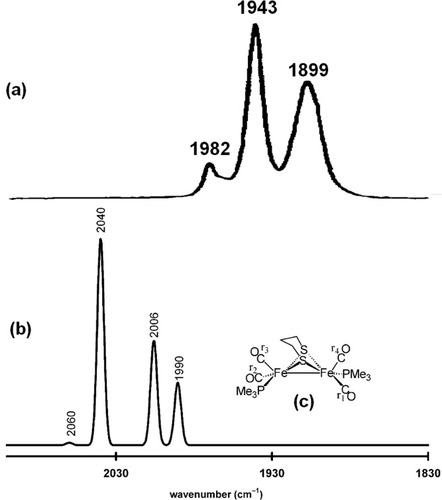
Simulation of the IR spectrum of (μ-S(CH2)3S)[Fe(CO)(PMe3)2]2 (5). In (a), the experimental spectrum of 5 is reproduced from reference 43 with permission from the American Society Copyright 2002. In (b), the simulated IR spectrum of 5 is presented. A half-width of 5 cm−1 was used in the simulation of each ν(CO) band. The unscaled computed energy of each C–O stretching mode is given above the simulated ν(CO) band. In (c), the labeling scheme for the CO ligands of complex 5 is given. These four vibrations correspond to the group vibrations of the six CO ligands in the following manner: 1990 [r1–r2+r3–r4]; 2006 [r1+r2–r3–r4]; 2040 [r1–r2–r3+r4]; 2060 [r1+r2+r3+r4].
In general, we find that the best method to accurately assign these spectra is to simulate the computed spectrum and visually compare it to the experimentally determined spectrum. Even when only ν(CX) values are reported and no graphic of the experimentally determined spectrum is available, simulation of the computed spectrum is beneficial for estimating which fundamental C–X stretching modes contribute to each ν(CX) band observed in the experimentally determined spectrum.
Evaluation of the Training Set
The experimentally determined ν(CO) and ν(CN) values are plotted vs. the corresponding computed C–X stretching frequencies as shown in Figure 6. We use a standard method of scaling computed frequencies with a multiplicative scaling factor (i.e., a linear regression in which the y-intercept is set to 0; y = mx).50-52 This method gave the equation y = 0.9526x, with an r2 value of 0.9477; the r2 value is the coefficient of determination.
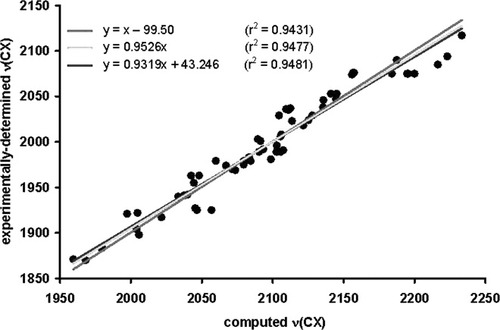
A plot of experimentally determined ν(CX) frequencies vs. computed ν(CX) frequencies.
Two other linear regressions have been performed on this data set and they will be discussed for illustrative purposes (see Fig. 6). If the slope is set to 1.0 and the y-intercept is optimized, this gives the equation y = x − 99.50, with an r2 value of 0.9431. If both the slope of the line and the y-intercept are allowed to optimize, this gives the equation y = 0.9319x + 43.246, with an r2 value of 0.9481. It is interesting that optimizing the y-intercept and slope, optimizing only the y-intercept, and optimizing only the slope give comparable descriptions of this data set in terms of the r2 value of the linear regression. In terms of basic statistics, these results show that the m and b values highly correlated, and there is no unique values of the y-intercept and slope of the line that define the data set. This phenomenon occurs when one is plotting a narrow set of values especially for deterministic data (data that contains only systematic errors, i.e., no random errors). The standard procedure for scaling frequency data (y-intercept = 0) will be used throughout the text.
The value of the scaling factor, 0.9526 (σ = standard deviation = 0.0067), calculated using the experimentally determined and computed values for the entire training set (complexes 1–15 in Fig. 2), is similar to the value that one may compute for the various subsets of molecules from the training set. [The subsets are designated as follows: FeIFeI dianionic complexes (1 and 2), FeIFeI monoanionic complexes (3 and 4), FeIFeI neutral complexes (5–9), an FeIFeI monocationic complex (10), FeIFeI dicationic complexes (11 and 12), an FeIIFeII neutral complex (13), FeIIFeII monocationic complexes (14 and 15).] The values vary from a low value of 0.9491 (σ = 0.0048) for the monocationic FeIIFeII complexes 14 and 15 to a high value of 0.9556 (σ = 0.0033) for monocationic FeIFeI complex, 10. The experimentally determined infrared spectra used in this correlation were measured using solvents with a wide range of polarity: hexane (dielectric constant at 20°C = ε20 = 1.9), THF (ε20 = 7.5), CH2Cl2 (ε20 = 8.9), CH3CN (ε20 = 36.6).53 The value of the scaling factor determined for the subsets based on solvent vary from 0.9502 (σ = 0.0055) for complex 15 in CH2Cl2 solvent to 0.9566 (σ =0.0059) for complexes 7 and 8 in hexanes solvent. These results indicate that there are no large systematic errors introduced by correlating computed gas-phase IR spectra with experimentally determined IR spectra in solvents with a wide range of polarity (ε20 values range from 1.9 to 36.6) or by using the same scaling factor for species of different charge.
To illustrate this point further, frequency calculations were performed on complex 7 in the gas phase and in the presence of a continuum solvent (Onsager method in Gaussian 03). Comparison of the phase–phase and ε = 5.0 continuum solvent computation shows an average shift of 6.9 cm−1 for each ν(CO) band of complex 7. Changing the solvent dielectric constant from 5.0 to 30.0 results in an average shift of 2.0 cm−1 for each ν(CO) band.)
The Prediction of ν(CO) Frequencies for Bridging CO Ligands
For terminal CO and CN− ligands, the experimentally determined ν(CO) and ν(CN) stretching frequencies are reproduced remarkably well by simple scaling of the computed ν(CO) and ν(CN) stretching frequencies. For bridging CO ligands, however, the predictions become more difficult. For example, the [(μ-CO)(μ-S(CH2)2S)[Fe(CNMe)3]2]2+ and [(μ-CO)(μ-S(CH2)3S)[Fe(CNMe)3]2]2+ complexes have been shown experimentally to have a ν(CO) stretching frequencies of 1914 cm−1 and Fe–Fe distances of ∼2.5 Å.54 Full geometry optimization of these complexes leads to predicted ν(CO) stretching frequencies of 1960 and 1985 cm−1 and Fe–Fe distances of 2.57 and 2.65 Å, respectively, for the [(μ-CO)(μ-S(CH2)2S)[Fe(CNMe)3]2]2+ complexes. Partial geometry optimization of these complexes with the Fe–Fe distance frozen at its experimentally determined distance of ∼2.5 Å led to predicted ν(CO) stretching frequencies of 1949 and 1951 cm−1, respectively, for the [(μ-CO)(μ-S(CH2)3S)[Fe(CNMe)3]2]2+ and (μ-CO)(μS(CH2)3S)[Fe(CNMe)3)2]2+ complexes. The predicted ν(CN) stretching frequencies of the terminal CNMe ligands are very similar to the experimental determined ν(CN) stretching frequencies in both cases, and are essentially unaffected by this small change in the Fe–Fe distance. The improved Fe–Fe distance improved agreement and brought the frequencies to the same value, but the calculated ν(CO) values for the bridging CO bands are still a little too high in part because the training set does not have any bridging CO ligands. Other functionals need to be tested to determine if another functional will yield a better Fe–Fe distance and improved ν(CO) frequencies for bridging CO ligands. For example, it is likely that a functional could be found that gives a slope of 1.0 for the ν(CO) training set, and therefore does not need scaling.
Example 1: Structural Assignment of a Transient, Electrochemically Generated Species
The close structural analogy between simple di–iron dithiolate complexes and the active site of [FeFe]H2ase has led several research groups to examine the ability of di–iron dithiolate assemblies to act as functional models of [FeFe]H2ase.47, 48, 55-59 The (μ-S(CH2)3S)[Fe(CO)3]2 complex, 7, has been shown to function as a simple and robust electrocatalyst for proton reduction.45, 49 In this context, the molecular details of the electrochemical reduction process of complexes such as complex 7 are of current interest.
Darensbourg, Best, and Pickett, and their respective coworkers have undertaken in-depth studies of the species generated upon reduction of 7 and related complexes at a graphite electrode.55, 59 These workers present evidence that complex 7 undergoes a one-electron reduction at ∼−1.1 V vs. SCE (SCE = standard calomel electrode) to form a one-electron reduced, odd-electron species. The early results of Darchen and coworkers on the electrochemistry of 7 at a mercury drop electrode suggest that this complex undergoes a simultaneous two-electron reduction at −1.17 V vs. SCE.60
Best, Pickett, and coworkers utilized thin-layer spectroelectrochemical techniques to obtain infrared spectroscopic data for a short-lived species resulting from the reduction of complex 7.59 Four possible structural candidates for this spectroscopically observed species are presented in Figure 7. Species [7-I]1− and [7-III]2−, respectively, are one- and two-electron reduced species in which both bridging thiolate sulfur atoms are fully bridging (i.e. a structure that is largely similar to 7). Species [7-II]1− and [7-IV]2−, respectively, are one- and two-electron reduced species in which a thiolate sulfur atom and one CO ligand bridges the two iron centers and the other thiolate sulfur is terminally coordinated to one of the iron centers. The experimentally determined IR spectrum of this species is given in Figure 8a, and the DFT-derived simulated spectra of four structural candidates for this species are given in Figure 8b–e. A comparison of the experimentally determined IR spectrum (Fig. 8a) and the DFT-derived simulated IR spectra clearly shows that the [7-I]1− species (given in Fig. 8b) is the best match to experimentally determined spectrum in terms of both the range and relative intensities of the ν(CO) bands. Comparison of the sum of the squares of the differences between the computed and experimentally determined ν(CO) bands of the electrochemically generated product and the candidate species shows that [7-I]1− (sum of the squares of the difference for the CO ligands = q = 587) is a much better structural candidate for this product form than the [7-II]1− (q = 8178), [7-III]2− (q = 26065), or [7-IV]2− (q = 13227) structural candidates.
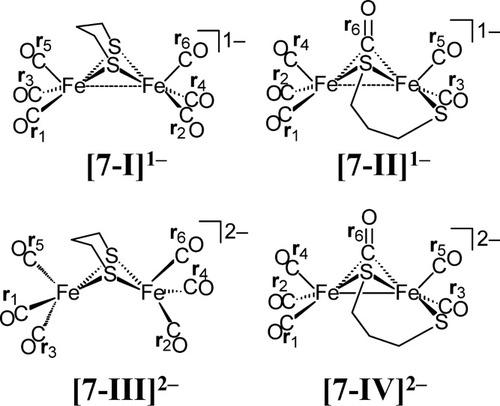
Structural candidates for a spectroscopically observed species resulting from the electrochemical reduction of complex 7.
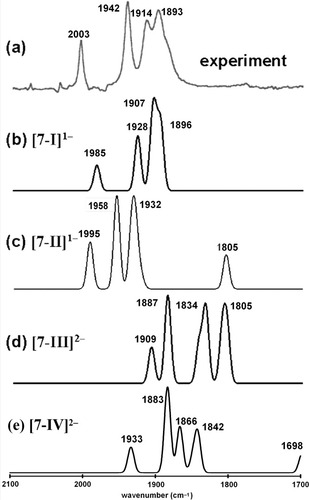
A comparison of an experimentally-determined IR spectrum (reproduced from ref.60, with permission from the American Chemical Society Copyright 2004.) for a species resulting from the reduction of complex 7 (a) and DFT-derived simulated spectra for various structural candidates for this species (b)–(e). Simulated spectra use a half-width of 10 cm−1 and the computed ν(CX) values are scaled using a factor of 0.9526. The labeling scheme for the CO ligands is given in Figure 7. The six vibrations of each model correspond to the group vibrations of the six CO ligands in the following manner: [7-I]1− 1896 [r5–r6]; 1904 [r4–r5–r6]; 1907 [r1–r2–r4]; 1911 [r1–r2–r3+r4]; 1928 [r1+r2–r3–r4]; 1985 [r1+r2+r3+r4+r5+r6], [7-II]1− 1805 [r6]; 1924 [r1+r2–r3–r4+r5]; 1932 [r1–r2+r3–r4–r5]; 1937 [r2–r4]; 1958 [r3+r5]; 1995 [r1+r2+r3+r4], [7-III]2−1805 [r2–r3+r5–r6]; 1811 [r1–r5–r6]; 1834 [r1+r2–r3–r4]; 1843 [r1–r2–r3+r4]; 1887 [r1+r2-r3+r4-r5+r6]; 1909 [r1+r2+r3+r4+r5+r6], [7-IV]2− 1698 [r6]; 1842 [r1+r2–r4]; 1848 [r1–r2+r4]; 1866 [r3–r5]; 1883 [r1+r2-r3+r4]; 1933 [r2+r3+r4].
Example 2: Structural Assignment of a IR Spectroscopically Observed Form of the Active Site of the [FeFe]H2ase Enzyme
The solid-state structure of the [FeFe]H2ase enzyme derived from CpI indicates the presence of a water molecule “coordinated” to the distal iron center with a rather long Fe-O distance of 2.6 Å.10 Although there is no definitive proof, it has been suggested on the basis of the crystallization conditions that this structure corresponds to the mixed valent, S = 1/2, Hox form of this enzyme.14 Four potential structural models for the Hox form were geometry-optimized and their predicted ν(CO) and ν(CN) stretching frequencies were computed. (The CH3SH ligand is used to model the CysS[Fe4S4] portion of the enzyme active site.) The geometry-optimized H2O-containing models do not show coordination of the water molecule to the iron center (Fe–O distance >3 Å). Representations of these four structural candidates for the Hox form are given in Figure 9.
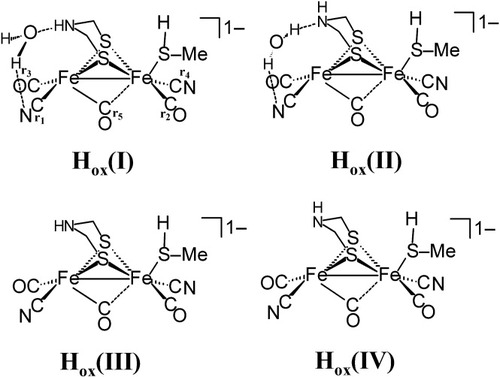
Structural candidates for the spectroscopically observed Hox form of the [FeFe]H2ase enzyme derived from CpI.
The experimentally determined IR spectrum of the EPR-active, S = 1/2, Hox form of the [FeFe]H2ase enzyme derived from CpI is compared to the predicted spectra for four structural candidates of the Hox form in Figure 10. In terms of their predicted stretching frequencies and relative intensities of the ν(CO) bands, all four of the structural candidates are qualitatively similar to one another and a fairly good match to the experimentally determined IR spectrum.
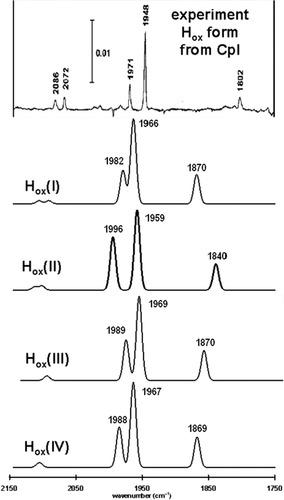
A comparison of the experimentally determined Hox form of the [FeFe]H2ase enzyme from CpI (reproduced from ref.11, with permission from the American Chemical Society Copyright 1999.) and predicted infrared spectra for various structural candidates. Simulated spectra use a half-width of 10 cm−1 and the computed ν(CX) values are scaled using a factor of 0.9526. The labeling scheme for the CO ligands is given in Figure 9. In all four models: The highest energy bands correspond to uncoupled vibrations of the cyanide ligands r4 and r1, respectively. The highest and intermediate energy CO bands correspond to r2 and r3, respectively. The lowest energy CO band corresponds to the bridging CO ligand, r5.
Comparison of the sum of the squares of the differences between the computed and experimentally determined terminal ν(CO) band shows that Hox(I) (sum of the squares of the difference for the terminal CO ligands = q = 29.7) is a slightly better structural candidate for the Hox form than the Hox(II) (q = 36.1), Hox(III) (q = 38.3), or Hox(IV) (q = 35.5) structural candidates.
These computations show that the FeIFeII formal oxidation state, in which the unpaired electron is localized on the distal iron center is a good model for the Hox form of the active site of the [FeFe]H2ase enzyme derived from CpI in terms of the predicted IR spectra.17, 18 Furthermore, Mulliken spin analysis shows that the unpaired electron density is localized on the distal iron center in all of these models, which agree with the EPR studies performed on the Hox form of the enzyme. In this context it is interesting to note that recent computations of Brunold and coworkers found that inclusion of the proximal [4Fe4S] is necessary to accurately reproduce the experimentally observed magnetic properties of the Hox and Hox–CO forms.61 The absence or presence of a water molecule near the distal iron center does not have a profound effect on the predicted IR spectra. Therefore, it is not expected that infrared spectroscopy will be able to determine if this water molecule is an important and intrinsic part of the active site of this [FeFe]H2ase.
Conclusions
We have been demonstrated that gas-phase DFT calculations can yield accurate estimates of experimentally determined solution-phase ν(CO) and ν(CN) stretching frequencies for a series of di–iron dithiolate complexes when multiplied by a scaling factor. The scaling factor that we determine for this series of complexes appears to be quite robust, but depends on the basis set and DFT functional. The value of the scaling factor predicted by each subset of complexes is very similar and demonstrates no obvious effect of the total charge or the formal oxidation states of the irons centers. Studies of these model complexes can improve the value of IR calculations on a larger, more complex model of the [FeFe]H2ase enzyme.




