Performance of DFT in modeling electronic and structural properties of cobalamins
Abstract
Computational modeling of the enzymatic activity of B12-dependent enzymes requires a detailed understanding of the factors that influence the strength of the CoC bond and the limits associated with a particular level of theory. To address this issue, a systematic analysis of the electronic and structural properties of coenzyme B12 models has been performed to establish the performance of three different functionals including B3LYP, BP86, and revPBE. In particular the cobalt–carbon bond dissociation energies, axial bond lengths, and selected stretching frequencies have been analyzed in detail. Current analysis shows that widely used B3LYP functional significantly underestimates the strength of the CoC bond while the nonhybrid BP86 functional produces very consistent results in comparison to experimental data. To explain such different performance of these functionals molecular orbital analysis associated with axial bonds has been performed to show differences in axial bonding provided by hybrid and nonhybrid functionals. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 1429–1437, 2006
Introduction
Derivatives of vitamin B12 that contain a unique CoC bond serve as a cofactor for many enzymatic reactions.1-6 Two biologically active forms of vitamin B12 are known to bear alkyl ligands: adenosylcobalamin (AdoCbl or coenzyme B12) with R = 5′-deoxy-5′-adenosyl, and methylcobalamin (MeCbl) with R = CH3 (Fig. 1). The stable CoC σ bond holds the key to the enzymatic activities of AdoCbl and MeCbl-dependent enzymes, which are quite different: the AdoCbl complex catalyzes radical rearrangement, while MeCbl transfers the methyl substituent to nucleophilic substrates. In the case of AdoCbl, the cleavage is homolytic, transiently yielding CoIICbl and an adenosyl radical,7 while in case of the MeCbl the cleavage is heterolytic, yielding CoICbl and a methyl cation.8 A precise understanding of the energetics of the cobalt–carbon bond and the factors that control this cleavage is an important goal in field of B12 chemistry. Substantial efforts have been devoted towards dissection of the dynamics of CoC bond homolysis and the spectacular rate acceleration, exceeding 12 orders of magnitude, achieved within the active site of enzyme in the presence of substrate.9-11 A variety of biochemical and biophysical methods have been applied to investigate how such a tremendous acceleration is achieved and controlled by B12-dependent enzymes. Despite these great efforts, the mechanism of the catalytic activation still remains poorly understood.
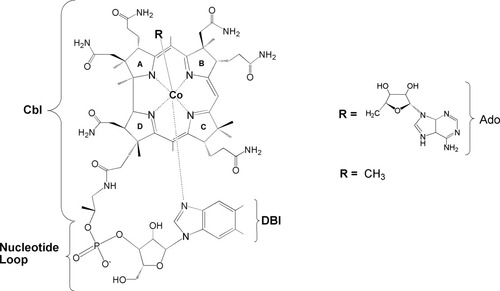
Molecular structures of coenzyme B12 (AdoCbl; 5′-deoxy-5′adenosyl-cobalamin) and methylcobalamin (MeCbl).
Computational modeling of the CoC bond activation employing realistic structural models of coenzyme B12 has been hampered for a long time by size of the cofactor and its complexity (Fig. 1). Earlier computations had only been carried out for simplified models, especially with respect to the corrin macrocycle12-14 or truncated cofactors without geometry optimization.15-17 Realistic quantum chemical calculations employing density functional theory (DFT) and models containing the entire corrin ring have been reported only recently18-22 (see also summary in ref. 23). Since this introductory work, there has been a growing interest in modeling structure and electronic properties of the coenzyme B12.24-36 Although these computational studies provided valuable insights into the structure and the electronic properties of the cofactor, the comparison with experimental data revealed that performance of the B3LYP functional, which has been used in majority of applications, is not as good as one could expect. In particular, theoretical prediction of the CoC bond dissociation energies (BDEs) showed that B3LYP functional underestimates experimental values by approximately 10 kcal/mol. Although the CoC bond length was reasonably well reproduced, the CoNB associated with axial base was found to be longer by more than 0.1 Å in comparison with experiment. It was suggested that shallowness of the potential energy surface associated with CoNB bond could be a plausible source of this discrepancy. Only Rovira et al.32 correctly reproduced the CoNB bond length in MeCbl using the Car–Parrinello approach.
The other unexpected result came from vibrational analysis of MeCbl.37, 38 The stretching frequency of the CoC bond was predicted to be 553 cm−1 in comparison to experimental value of 506 cm−1.39 To obtain a reasonable agreement with spectroscopic data unusually low scaling factor of 0.86 was required to develop Scaled Quantum Mechanical Force Field (SQM FF). This low scaling factor is more typically required for Hartree–Fock force constants and not for B3LYP, which is typically equal to 0.93.40
An important step toward resolving the issue of poor B3LYP performance was recently presented by Jensen and Ryde.41 They investigated why previously published B3LYP estimations of BDEs for models of MeCbl have given such poor results and provided a systematic analysis of possible BDE errors including such factors as zero-point vibrational energy, basis set superposition error, thermal, solvent or relativistic effects. They concluded that these factors are only of secondary importance, and that the problem is associated with the B3LYP functional, specifically related to the homolytic cleavage of metal–carbon bond. The problem with the accuracy of the B3LYP energy calculations arises from the fact that it is hybrid functional in combination with HF (Hartree–Fock) exchange. Thus, one of the reasons for its failure in energy calculations seems to be the inclusion of an exact HF exchange. This was a surprising outcome because the B3LYP functional is widely recognized as one of the most accurate for structures, energies, and frequencies as has been demonstrated for many models of metalloenzymes.42-44
Clearly, this issue requires further analysis and is the topic of the present work. This necessity is not only related to the strength of the CoC bond but is also required for the proper interpretation of spectroscopic and kinetic data. For example, recent theoretical work on NO binding to cobalamin45 has shown the results strongly depend on the type of functional used in DFT calculations. Systematic comparison of the experimental and theoretical data is further needed to understand how DFT methods perform in modeling electronic and structural properties of vitamin B12 derivatives. To accomplish this, six-coordinate cobalamins, denoted as B-[CoIII(corrin)]-R+ (Fig. 2), were employed in the current work. Following our recent work on metalloporphiryns excited states,46 three different functionals B3LYP (the Becke three-parameter hybrid functional with the Lee–Yang–Parr correlation), BP86 (Becke–Perdew 1986 with no HF exchange) and revPBE (revised Perdew–Becke–Ernzerhof) have been thoroughly tested and compared with experimental values of CoC BDEs (Table1) and with structural properties of cobalamins having different bond lengths associated with the NBCoC moiety (Table2). The particular focus in this work is placed only on the type of functional rather on the basis set, solvent, or relativistic effects, all of which have been recognized as factors having secondary importance. All reported calculations involving B3LYP and BP86 were carried out with the GAUSSIAN 03,47 while for revPBE the Amsterdam Density Functional (ADF)48, 49 suite of programs for electronic structure calculations was used. In the case of B3LYP and BP86 the 6-31g(d) [for H, C, N] and Ahlrich's VTZ [for Co]50 basis sets were used. In the case of revPBE calculations, the ADF standard Slater-type polarized split valence (DZP) basis set was used, with [1s] frozen cores on C, N, and [2p] frozen core on the Co atom.
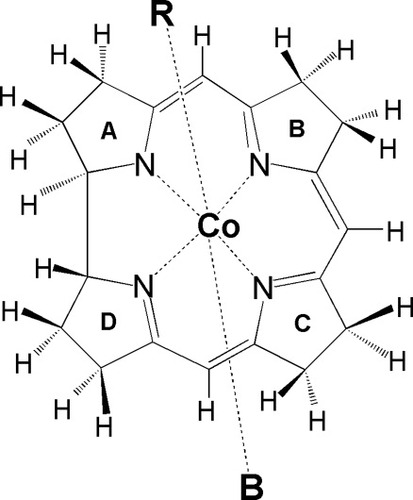
Molecular structure of B[CoIII(corrin)]R+ models.
| No. | System | Bond distances | Ref. | |||||
|---|---|---|---|---|---|---|---|---|
| CoN21 | CoN22 | CoN23 | CoN24 | CoC | CoNB | |||
| 1 | CNCbl | 1.875 (8) | 1.908 (8) | 1.917 (9) | 1.875 (8) | 1.858 (12) | 2.011 (10) | 62 |
| 2 | CNCbl (KCl) | 1.881 (3) | 1.911 (3) | 1.920 (3) | 1.883 (3) | 1.886 (4) | 2.041 (3) | 63 |
| 3 | CF3Cbl | 1.870 (9) | 1.951 (10) | 1.887 (10) | 1.917 (9) | 1.878 (12) | 2.047 (10) | 54 |
| 4 | CHF2Cbl | 1.894 | 1.911 | 1.891 | 1.887 | 1.949 (7) | 2.187 (7) | 64 |
| 5 | MeCbl | 1.88 (2) | 1.97 (2) | 1.93 (2) | 1.89 (2) | 1.99 (2) | 2.19 (2) | 65 |
| 6 | MeCbl | 1.877 (4) | 1.922 (4) | 1.918 (4) | 1.874 (4) | 1.979 (4) | 2.162 (4) | 66 |
| 7 | AdoCbl | 1.889 (9) | 1.909 (9) | 1.906 (9) | 1.885 (9) | 2.023 (9) | 2.214 (9) | 67 |
| 8 | AdoCbl | 1.880 | 1.916 | 1.914 | 1.866 | 2.030 (3) | 2.237 (3) | 68 |
| 9 | Im—CNa | 1.835 (9) | 1.899 (8) | 1.853 (9) | 1.880 (8) | 1.863 (11) | 1.968 (9) | 69 |
| 10 | Im—Meb | no data | 1.97 | 2.09 | 70 | |||
| 11 | cob(II)alamin | 1.89 | — | 2.13 | 71 | |||
| 12 | cob(II)alamin | 1.88 (2) | — | 1.99 (3) | 72 | |||
- a 1H-imidazolylCNcobamide.
- b 1H-imidazolylMecobamide.
Results and Discussion
Dissociation Energy of the CoC Bond
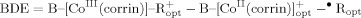 (1)
(1)
Theoretically determined BDEs plotted as a function of the CoC bond length in cobalamins with DBI as axial base (squares, B3LYP; diamonds, BP86; triangles, revPBE).
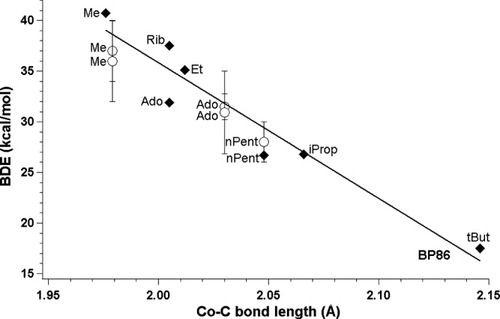
Theoretically and experimentally determined BDEs plotted as a function of CoC bond length in cobalamins with DBI as axial base (filled diamonds, BP86; empty circles, experiment).
| Ba | Ra | B3LYP | revPBE | BP86 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CoC | CoNB | BDE | CoC | CoNB | BDE | CoC | CoNB | BDE | ||
| DBI | CN | 1.871 | 2.125 | — | 1.856 | 2.177 | — | 1.852 | 2.110 | — |
| CF3 | 1.954 | 2.186 | — | 1.995 | 2.249 | — | 1.952 | 2.185 | — | |
| Me | 1.962 | 2.293 | 25.6 | 2.076 | 2.334 | 30.7 | 1.976 | 2.235 | 40.7 | |
| Rib | 1.989 | 2.333 | 23.6 | 2.035 | 2.362 | 32.7 | 2.005 | 2.252 | 37.5 | |
| Ado | 1.989 | 2.330 | 17.9a | 2.033 | 2.327 | 26.7 | 2.005 | 2.247 | 31.9a | |
| Et | 1.990 | 2.358 | 19.5 | 2.038 | 2.368 | 29.5 | 2.012 | 2.257 | 85.1 | |
| nPent | 2.021 | 2.505 | 12.3 | 2.078 | 2.589 | 23.6 | 2.048 | 2.346 | 26.7 | |
| iProp | 2.027 | 2.586 | 13.0 | 2.105 | 2.549 | 23.8 | 2.066 | 2.337 | 26.8 | |
| tBut | 2.091 | 2.841 | 3.1 | 2.199 | 2.645 | 16.0 | 2.146 | 2.471 | 17.5 | |
| DBIb | — | 2.251 | — | — | 2.227 | — | — | 2.160 | — | |
| Im | CN | 1.873 | 2.090 | — | 1.865 | 2.121 | — | 1.854 | 2.073 | — |
| CF3 | 1.954 | 2.122 | — | 1.997 | 2.176 | — | 1.949 | 2.127 | — | |
| Me | 1.962 | 2.218 | 28.0 | 2.010 | 2.236 | 33.7 | 1.976 | 2.170 | 41.3 | |
| Rib | 1.989 | 2.234 | 26.0 | 2.040 | 2.280 | 31.9 | 2.007 | 2.184 | 39.1 | |
| Ado | 1.988 | 2.227 | 18.9a | 2.038 | 2.273 | 28.6 | 2.001 | 2.179 | 31.9a | |
| Et | 1.989 | 2.261 | 21.9 | 2.047 | 2.280 | 30.1 | 2.008 | 2.202 | 35.7 | |
| nPent | 2.023 | 2.310 | 14.2 | 2.092 | 2.314 | 23.3 | 2.044 | 2.218 | 30.1 | |
| iProp | 2.033 | 2.325 | 14.1 | 2.104 | 2.340 | 24.7 | 2.054 | 2.258 | 28.5 | |
| tBut | 2.103 | 2.418 | 3.4 | 2.202 | 2.389 | 16.5 | 2.144 | 2.289 | 18.3 | |
| Imb | — | 2.213 | — | — | 2.199 | — | — | 2.126 | — | |
- a B and R refer to B-[CoIII(corrin)]-R+.
- b Axial base in B-[CoII(corrin)]+.
- cDifferent conformation of adenosyl radical was used thus providing lowering of BDE in comparison with previous results reported in Ref.22.
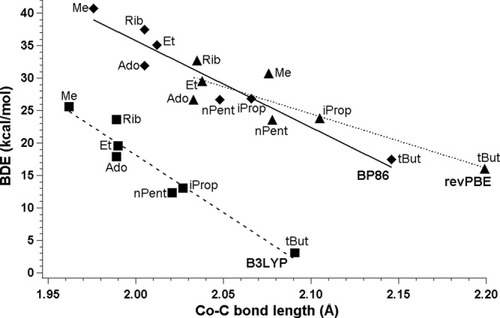
Following our previous studies, we plotted BDEs as a function of the CoC bond length and fitted line BDE ≈ A · r(CoC) + B to each set of points. Table4 summarizes parameters associated with line fitting and shows that in all cases good linear correlation is maintained, as can be judged from values of R2. For all three functionals, energies diminish correctly with the changes in the CoC bond length. Although in all cases the lowering of the dissociation energy correctly follows the CoC bond lengthening, comparison with experimental data shows that lines for both BP86 and B3LYP have a better linear fit than in case of revPBE. The impression which one can get from Figure 3 is that lines associated with BP86 and B3LYP are nearly parallel in comparison to experiment. The analysis of line parameters in Table 4 points out that B3LYP functional significantly underestimates dissociation energies, BP86 slightly overestimates while revPBE underestimates, but to less extend than B3LYP functional. Increase of the CoC bond length gives the biggest change in energy in the case of B3LYP, smallest in the case of revBPE, and nearly right for BP86 (Figs. 3 and 4). The lack of experimental data precludes making a similar assessment for much longer values of CoC bond lengths.
| A (kcal/mol Å−1) | B (kcal/mol) | R2 | |
|---|---|---|---|
| Experiment | −115.16 | 264.53 | 0.9720 |
| B3LYP | −176.80 | 371.77 | 0.9333 |
| BP86 | −133.69 | 303.19 | 0.9236 |
| revPBE | −83.69 | 200.27 | 0.7662 |
The best agreement with experiment is obtained in case of the BP86 functional, which only slightly overestimates experimental values (Fig. 4). Because the plotted data was not corrected for the zero-point vibrational energy (ZPVE) or basis set superposition error (BSSE), both these corrections should additionally lower the BDEs by few kcal/mol. The most significant correction is ZPVE, which for Im[CoIII(corrin)]Me+ is equal to 4.92 kcal/mol employing the BP86 functional and mixed basis set, while the BSSE correction should be around 1 kcal/mol according to Jensen and Ryde.41 Comparison of the theoretical data obtained with the revPBE functional implies that performance of this functional is not as reliable as BP86. The BDEs are slightly underestimated (Table 3), but the optimized CoC bond lengths are too long in average 0.05 Å in comparison to the experiment (Fig. 3). This overestimation of bond length causes a shift of the line representing the revPBE functional toward much longer cobaltcarbon distances. The worst performance in terms of BDEs is displayed by the B3LYP functional, which underestimates BDEs by more than 10 kcal/mol, but at the same time the optimized CoC bond lengths remain in good agreement with experiment. They are slightly shorter in comparison to the BP86 functional but more reliable than those provided by revPBE.
The trans axial base influence on BDEs was also examined in the present work by replacing DBI with Im (Table 3). Imidazole was combined with a series of axial ligands and for each of structures the BDE was computed. Systematic analysis of the energies associated with the homolytic cleavage of CoC bond shows that the influence associated with DBI replacement is small in term of energy and does not depend on the type of functional. In particular, results plotted for BP86 functional (Fig. 5) show that lines are almost parallel with very similar slopes (−133.69 and −131.10) and intercepts (303.19 and 298.70), respectively. The presence of DBI leads to lower values, but the average difference does not exceed 1 kcal/mol in terms of BDEs.
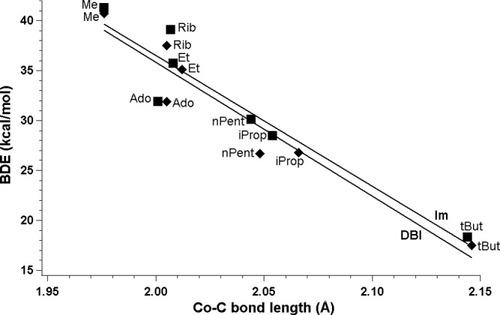
BP86-determined BDEs plotted as a function of the CoC bond length in cobalamins with DBI and imidazole as axial bases (squares, imidazole; diamonds, DBI).
NBCoC Axial Bond Lengths
The other performed test was analysis of the axial bonds lengths in models of c factors B12 (Fig. 2). Structural correlation between the nature of the axial ligands and bond distances in NBCoC moiety has been a topic of experimental and theoretical studies in conjunction with the anomalous trans effect.51-54 The anomalous (or inverse) trans effect emerges when the change in R lengthens or shortens both the interligand CoC and the CoNB distances. The origin of this effect is a consequence of an unusual combination of poor σ/π-donation by the base and unusually strong σ-donation by the alkyl group R.33 For the purpose of this analysis we selected nine structures with different electron donating/withdrawing character of the R groups (Table 3). The correlation between the CoC and the CoNB distances was plotted in Figure 6, together with values of optimized bond lengths. To each set of points, a line CoNB ≈ C·r(CoC) + D was fitted (Table 5) to establish qualitative correlation between axial bond lengths (Figs. 6 and 7). To obtain each line, only structures with DBI as an axial base were analyzed together with a set of nine different R groups to cover the experimentally determined bond lengths (Tables 2 and 3). However, the scarcity and concentration of experimental data limit the reliability of the computed slope.
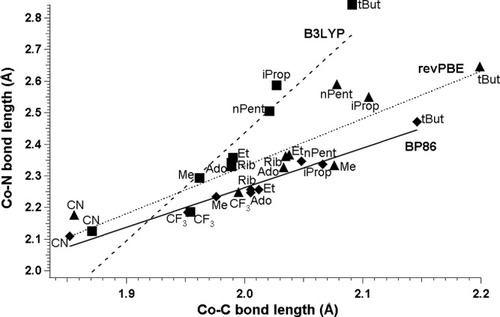
Theoretically determined CoNB distances plotted as a function of CoC distances in cobalamins with DBI as axial base (squares, B3LYP; triangles, revPBE; diamonds, BP86).
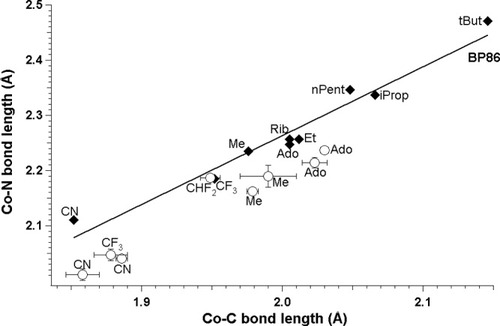
Theoretically and experimentally determined CoNBase distances plotted as a function of CoC distances in cobalamins with DBI as axial base (filled diamonds, BP86; empty circles, experiment).
| C | D (Å) | R2 | |
|---|---|---|---|
| Experiment | 1.2732 | −0.3455 | 0.9396 |
| B3LYP | 3.4151 | −4.3939 | 0.8754 |
| BP86 | 1.2484 | −0.2338 | 0.9569 |
| revPBE | 1.5035 | −0.6762 | 0.7571 |
The lines representing the BP86 and revPBE functionals (Fig. 6) are nearly parallel to experiment with similar slopes (Table 5). The B3LYP functional exhibits very different behavior and has a much bigger slope. The lines corresponding to experiment and to the B3LYP functional intersect each other around “short” distances representing electron withdrawing groups like CN or CF3. Although the optimized CoC bond lengths are close to experimental values, the CoNB distances are too long, which in consequence causes a very steep increase for the line representing B3LYP data. For this reason we noticed previously that for certain R groups like iProp or tBut the trans axial bases are not part of the Co coordination sphere.19, 33 This indeed is an artifact related to B3LYP functional; BP86 predicts much shorter distances. The revPBE functional produces both axial distances too long in comparison to experiment. The average overestimation in the case of CoNB bond is about 0.10 Å, while in the case of CoC 0.05 Å. Also, in the case of revPBE, the linear fit is much worse than in case of BP86 functional (Table 5).
Analysis of the optimized models with two different bases (DBI and Im) was also provided. This comparison for BP86 functional is shown on Figure 8. Analysis of all optimized structures allows us to establish that each trans axial base produces a positive linear correlation between the CoNB and CoC bonds, but the two lines fitted for the different bases have different slopes (−0.2338 and 0.5770) and intercepts (1.2484 and 0.8021). One can note that the CoC bond length stays basically identical for the same R substituent, when DBI is replaced by Im (Table 3). A different situation occurs for the CoNB bond lengths. DBI gives higher values of bond lengths, which most likely reflect its different basicity. For the two axial bases considered, the differences become more apparent with bond lengthening. For tBut, the difference is approximately 0.2 Å. The third set of points on Figure 8 represents the available experimental data for imidazole as the axial base (Table 2). One can note that BP86 accurately reproduces the CoC bond length, while in the case of CoNB BP86 it gives values about 0.1 Å too long, when compared with the experiment.
CoNB Bond Length in cob(II)alamins
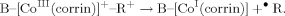 (2)
(2)The length of the CoIINDBI has been determined experimentally71 and its value 2.13 Å is shorter by about 0.1 Å in comparison to coenzyme B12 (CoIIINDBI = 2.237 Å). The optimized CoIINB bond employing B3LYP was found to be equal to 2.251 Å in the case of DBI[CoII(corrin)]+, while 2.213 Å for Im[CoII(corrin)]+. The same calculations were performed with BP86 and revPBE. BP86 gives 2.160 Å for DBI[CoII(corrin)]+ and 2.126 Å for Im[CoII(corrin)]+, while revPBE gives 2.227 and 2.199 Å, respectively. The calculated values confirm the trend observed in Figure 6, where the CoNB bond lengths calculated with B3LYP gives the highest values. All three functionals slightly overestimate experimental data; however, BP86 again gives the best comparison with the experiment among three investigated functionals. The higher values of CoNB bond length were obtained with DBI as axial base for all three functionals. This observation reflects data collected in Table 3, when values of CoNB bonds for DBI and imidazole are compared.
Interligand NBCoC Vibrations
Analysis of the interligand vibrations including the CoC and CoNB bonds can provide further insight into the performance of functionals under consideration. For this purpose DFT analysis of the Im[CoIII(corrin)]Me+ model was performed with B3LYP and BP86 functionals. The most important interligand vibration is the CoC stretch. The frequency of this vibration calculated using B3LYP functional is 553 cm−1, while 535 cm−1 corresponds to BP86. The same trend is observed for calculated values of CoNB stretching, where B3LYP displays a lower frequency (133 cm−1) while BP86 a higher frequency (148 cm−1), consistent with the inverse trans effect (Table 3). Although those results seem to confirm better performance of BP86 functional, this is not so critical for frequency analysis. For both functionals the frequencies for the CoC bond stretch are overestimated, and the force constants have to be scaled to obtain reasonable agreement with experiment. Although BP86 predicts closer value to the experiment, that is, 505 cm−1, the overall performance from a statistical point of view is better for B3LYP. Consequently, the latter was used in recent DFT analysis of Co-alkyl and Co-adenosyl vibrational modes in B12-cofactors.55
Summary and Discussion
DFT has become a popular method for studying the structure and electronic properties of large molecules. Its accuracy has been validated for wide range of organic molecules and molecules with transition metals. This is not yet the case for many biological complex systems including coenzyme B12.
Several structural models of coenzyme B12 have been investigated in the present work showing that the BP86 functional gives the best agreement with experimental data and should be further considered as more appropriate than more commonly used B3LYP functional. In that sense our present study confirms and extends previous work of Jensen and Ryde.41 Furthermore, they suggested that the basic problem with performance of B3LYP functional arises from Hartree–Fock inclusion, and that the general problem of the B3LYP functional for homolytic metal–carbon dissociation energies in tetrapyrollic system is cased by the differing correlation energies of open- and closed-shell complexes with a different number of unpaired electrons. Although this argument can be applied to explain difficulties associated with the cobal–carbon bond cleavage it cannot be simply extended to explain problematic performance associated with the correct reproduction of the NBCoC axial bond lengths (Fig. 6).
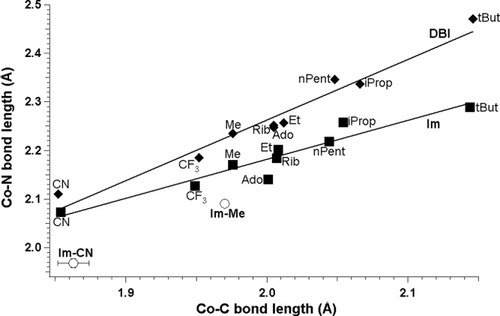
To further elucidate the problem associated with the B3LYP functional we performed population analysis for Im[CoIII(corrin)]Me+ model using both B3LYP and BP86 functionals and extracted six molecular orbitals (MOs) that are directly involved in the NImCoCMe bonding. Following previous analysis,33 the prerequisite for description of interligand bonding is formation of three MOs described as strongly bonding (ψ1), strongly antibonding (ψ3*) and of mixed character σ2, which is bonding with respect to CoCMe and antibonding with respect to CoNIm. The additional complication arises from mixing of σ's orbitals with the corrin π orbital, with the dxy orbital of Co and with px and py orbitals on NIm. The orbital energy diagram and contours of those orbitals for both B3LYP and BP86 functionals are summarized in Figure 9. Althopugh both functionals predict qualitatively the same orbital energy pattern, they give quantitatively different energetic description. The bonding orbitals resulting form B3LYP are energetically too low in comparison to BP86, while antibonding orbitals are too high. The same problem has been noticed in the case of excited states analysis for nickel porphyrins where it was found that B3LYP functional produces qualitatively incorrect energies of the d orbitals on the Ni atom leading to mislocations of states originating from a transfer of an electron between the metal and the porphyrin ring.46 Nonhybrid BP86 functional produces similar ordering of the excited electronic states as B3LYP, but gives better qualitative agreement with experimental results. In the case of cobalamins, the B3LYP functional gives too weak axial NBCoC bonding description which consequently affects strength of both axial bonds.
BP86-determined CoNB distances plotted as a function of CoC distances in cobalamins with DBI and imidazole as axial bases (filled squares, imidazole; filled diamonds, DBI; empty circles, experimental data for imidazole).
Orbital energy diagram for ψ1+, ψ1−, σ2+, σ2−, σ3+, and σ3− molecular orbitals of Im[CoIII(corrin)]Me+ determined with B3LYP and BP86 functionals and their contours determined with BP86 functional.




