On the O2 binding of Fe–porphyrin, Fe–porphycene, and Fe–corrphycene complexes
Abstract
Based on our previous study for the O2 binding of the Fe–Por complex, this study investigates the O2 binding mechanism in the Fe–porphyrin isomers, Fe–porphycene (FePc), and Fe–corrphycene (FeCor) complexes. By calculating the potential energy surface of the O2 binding, the present study explains the reason for the dramatic increase of O2 affinities observed in the FePc complex. In the case of FeCor–O2, the O2 binding process includes the intersystem crossing from a triplet to singlet state, as in the FePor–O2 complex. However, FePc–O2 uses only a singlet surface. This is because the ground state of the FePc complex in the deoxy state is a triplet state, while those of FePor and FeCor are a quintet state. Such difference originates from character of the SOMO. We estimated an equilibrium constant for the O2 binding that reasonably reproduced the trend observed in the experiments. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 1363–1372, 2006
Introduction
Hemoglobin and myoglobin play important roles in our daily life through the transport and storage of O2. These processes have been studied in detail both theoretically and experimentally.1-27 Hemoglobin and myoglobin are well-known heme proteins. They are also useful for engineering applications.28-43 To understand and control their functions, myoglobin has been subjected to extensive modifications. They are classified into two categories: amino acid mutation,28-32 and the replacement of the protoporphyrin by artificial porphyrin isomers.33-43 The former approach is mainly suitable for regulating delicate physiological reactions. In contrast, the latter approach is expected either to improve its functions or to introduce new functions, because the active center itself is replaced by another one. Several modified myoglobins have been experimentally realized using the latter approach. For example, the protoporphyrin has been replaced by aza-porphyrin, diaza-porphyrin, tetra-aza porphyrin, porphycene, corrphycene, etc.33-39
Among the interesting properties that the reconstituted myoglobins exhibit, we particularly focused on the O2 binding property. Hayashi et al.36, 37 reported that the replacement of porphyrin by porphycene in myoglobin had extremely high O2 affinity, which is by more than 1000 times higher than that of the native myoglobin. This finding indicates a possibility to realize tailor-made functional protein.37 In contrast, Neya et al.38, 39 reported that the replacement by corrphycene lowered the O2 affinity (about 1/100 times). These dramatic changes were introduced only by the substitution of the porphyrin ring. Porphycene36, 37 and corrphycene38, 39 are porphyrin isomers that have (2,0,2,0) and (2,1,0,1) carbon atoms between each pyrrole rings, respectively, as shown in Figure 1. These isomers interact to the Fe atom in different ways, and the electronic structures could be unique among the reconstituted heme. In this case, a theoretical study would provide important information about the electronic structure basis to understand the O2 affinity. It would be difficult by anything other than by the experimental studies to conclude which factor controls the O2 binding properties.
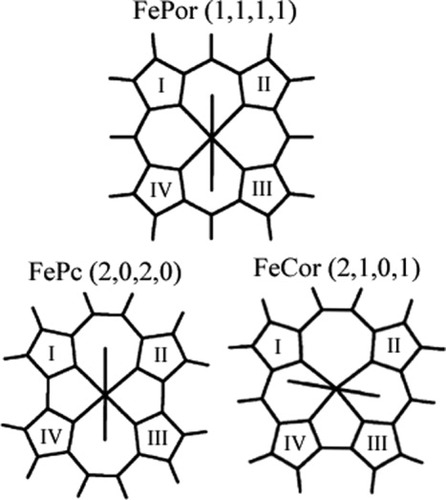
Structures of Fe–porphyrin (FePor), Fe–porphycene (FePc), and Fe–corrphycene (FeCor) complexes. Porphyrin has (1,1,1,1) carbons, porphycene has (2,0,2,0) carbons, and corrphycene has (2,1,0,1) carbons between pyrrole rings. The numbers in the parenthesis, (nI–II, nII–III, nIII–IV, nIV–I) are number of the carbon atoms between the pyrrole rings. The “nI–II,” “nII–III,” “nIII–IV,” and “nIV–I” denotes the number of the carbon atoms between the rings I and II, II and III, III and IV, and IV and I, respectively.
Several theoretical studies have been performed for the O2, CO, and NO bindings to the heme and their derivatives at several theoretical levels, MNDO/d,15 QM/MM,16-18 DFT with LSD schemes,19-21 CASSCF,22-24 CASPT2,25 and SAC/SAC-CI26 calculations. Recently, many DFT calculations were also performed, and the electronic structures of ligand-binding complexes or the effects of the proximal and distal sites in the protein environment were investigated.9-14 In the present study, we are interested in the O2 binding process to the heme and its isomers of proto-porphyrin. We discuss here the electronic structures of the O2 binding complexes, comparing our calculations with several other theoretical studies.
In our previous study,44 we investigated the electronic mechanism of the reversible O2 binding by heme (FePor). For the O2 binding process, we found that the spin state was primarily important. Out-of-plane deviation of the Fe atom from the porphyrin plane was also an important factor. Our conclusion for oxyheme is as follows. (1) The potential energy surface of the lowest singlet state is associative, while that of the lowest triplet state is dissociative. (2) The Fe atom locates in-plane in the singlet state, while it is out-of-plane in the triplet state. (3) The O2 binding process obviously include intersystem crossing from triplet to singlet states. (4) This crossing requires relativistic spin-orbit interaction. (5) Owing to such intersystem crossing, the activation energies for both O2 binding and dissociation become moderate, and hence, reversible. (6) The electronic structure of the ground state of the oxyheme would be an open singlet state.
In this study, we have extended our previous study to the Fe–porphycene–Imidazole (FePc) and Fe–corrphycene–Imidazole (FeCor) isomers and clarified the potential surface of the O2 binding processes. Based on these calculations, a reasonable explanation has been given to the previous experimental results. As seen later, the electronic and molecular structures of the deoxy-states and oxy-states are discussed, respectively. Then the potential energy surface and the O2 binding processes are discussed, and we estimated the equilibrium constant for the O2 binding, and the result was compared with the experimental data.
Computational Details
DFT (UB3LYP) calculations were performed with the Gaussian98 program package.45 The heme model used in this study is O2–Fe–X–Imidazole complex.44 For FePor, FePc, and FeCor, “X” is porphin, porphycene, and corrphycene, respectively. In myoglobin and its analogs, where the protoporphyrin of heme was replaced with the artificial porphyrin isomers (Pc and Cor), the electronic structure of the Fe atom is a ferrous state (Fe(II)) in the O2 dissociation limit.33-43 So, we calculated the ferrous states for deoxy complexes and the O2 binding states with the same number of electrons. As described in a later section, the electronic structure of the O2 binding state is close to the ferric state (Fe(III)), Fe(III)+ O2−. The basis sets for the Fe, O, and pyrrole N atoms were 6-31g* set.46 The rest of atoms are treated by 6-31g set for the other atoms.46 Solomon et al. did some extensive tests of the functional and basis set dependence for the O2 and NO bindings to the nonheme complexes.11 But, because we wanted to compare the results of the present isomers with the results of heme in our previous article, we used the same basis set and methodology.44
To determine the electronic structure of the ground states, we performed the geometry optimizations for deoxy complexes in singlet, triplet, and quintet states and oxy complexes in singlet and triplet states. As shown in a later section, the ground state of the O2 binding state has open-shell singlet nature. This state was calculated by using the guess of the triplet state having the same electronic configuration in the SCF step.
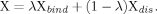 (1)
(1)
The computational model and the two reaction coordinates, d (the deviation of the Fe atom from the ring plane) and R (the distance between Fe and O2). The “Im,” “Por,” “Pc,” and “Cor” denote imidazole, porphyrin, porphycene, and corrphycene rings, respectively.
Results and Discussion
Ground States of the Deoxy Complexes: Electronic Structure and Geometry
The spin-multiplicity and the geometry of the deoxy complexes were determined by the geometry optimization in each spin multiplicity. Table1 shows some important structural parameters and relative energies of the complexes.
| FcPor | FePc | FcCor | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Quintet | Triplet | Singlet | Quintet | Triplet | Singlet | Quintet | Triplet | Singlet | |
| Relative energy (kcal/mol) | 0.00 | 0.671 | 6.48 | 4.70 | 0.00 | 9.97 | 0.00 | 3.59 | 12.6 |
| Optimized geometry | |||||||||
| Distance (Å) | |||||||||
| Fe–Im N | 2.13 | 2.21 | 1.91 | 2.12 | 2.21 | 1.92 | 2.12 | 2.19 | 1.92 |
| Fe–Pyr NI | 2.09 | 2.01 | 2.01 | 1.95 | 1.95 | 1.95 | 2.09 | 2.06 | 2.05 |
| Fe–Pyr NII | 2.09 | 2.01 | 2.02 | 1.95 | 1.95 | 1.95 | 2.10 | 2.07 | 2.05 |
| Fe–Pyr NIII | 2.09 | 2.01 | 2.01 | 1.95 | 1.95 | 1.95 | 2.10 | 1.95 | 1.96 |
| Fe–Pyr NIV | 2.09 | 2.01 | 2.01 | 1.95 | 1.95 | 1.95 | 2.10 | 1.95 | 1.96 |
| Fe–ring plane | 0.429 | 0.190 | 0.201 | 0.260 | 0.231 | 0.233 | 0.513 | 0.213 | 0.224 |
| Angle (degree) | |||||||||
| Pyr NI–Fe–Pyr NII | 88.8 | 89.1 | 89.7 | 94.2 | 96.2 | 96.1 | 107.6 | 102.7 | 103.4 |
| Pyr NII–Fe–Pyr NIII | 88.7 | 90.4 | 89.6 | 84.1 | 82.9 | 83.1 | 85.0 | 88.5 | 88.3 |
| Pyr NIII–Fe–Pyr NIV | 88.6 | 89.0 | 89.6 | 94.4 | 96.2 | 96.1 | 74.2 | 78.6 | 78.5 |
| Pyr NIV–Fe–Pyr NI | 88.7 | 90.4 | 89.7 | 84.1 | 82.9 | 83.1 | 85.6 | 88.7 | 88.3 |
| Pyr NI–Fe–Im N | 98.6 | 94.2 | 95.2 | 96.3 | 94.5 | 94.6 | 100.9 | 95.7 | 95.1 |
| Pyr NII–Fe–Im N | 99.9 | 94.2 | 94.2 | 96.4 | 94.5 | 94.5 | 98.0 | 94.7 | 94.5 |
| Pyr NIII–Fe–Im N | 96.6 | 93.9 | 94.6 | 97.3 | 95.5 | 95.1 | 102.3 | 93.5 | 94.0 |
| Pyr NIV–Fe–Im N | 99.9 | 93.9 | 94.2 | 97.4 | 95.4 | 95.1 | 101.1 | 94.9 | 94.4 |
| Dihedral angle (degree) | |||||||||
| Pyr NI–Fe–Im N–Im C | 90.4 | 135.4 | 135.0 | 46.5 | 46.8 | 46.9 | 105.8 | 149.7 | 142.6 |
| Pyr NII–Fe–Im N–Im C | 0.204 | 44.7 | 45.0 | −48.5 | −49.8 | −49.6 | −4.01 | 46.4 | 38.6 |
| Pyr NIII–Fe–Im N–Im C | −90.1 | −44.5 | −44.9 | −133.3 | −133.1 | −133.1 | −90.6 | −42.4 | −50.0 |
| Pyr NIV–Fe–Im N–Im C | −179.9 | −135.2 | −135.0 | 131.3 | 130.1 | 130.3 | −166.7 | −121.2 | −128.7 |
- The total energy of ground state is taken as 0.00 kcal/mol.
The ground state of FePor was calculated to be a quintet state.44 The triplet and singlet states are located 0.67 and 6.48 kcal/mol higher than the quintet state, respectively. The optimized geometry of the quintet state was quite different from those of the triplet and singlet states. In the quintet state, the deviation of the Fe atom from the ring plane was 0.421 Å, which was much larger than the case of the triplet (0.190 Å) and the singlet states (0.201 Å). The calculated geometry for the quintet state is in good agreement with the experimental X-ray crystallographic data44 for myoglobin and a biomimetic complexes.47-51 In the present calculations, the energy gap between the quintet and triplet state is so small (0.67 kcal/mol) that so we cannot justify the quintet state being the ground state from only the present theoretical result. However, fortunately, these experimental findings seem to support that the ground state may be the quintet state.47-51
For FeCor, the ground state was also a quintet state as in FePor. The energy gaps between the quintet state and the other states were, however, larger than the case of FePor. The Fe atom dislocation was 0.513 Å, which was larger than that of the triplet (0.213 Å) and singlet states (0.224 Å).
On the other hand, the ground state of FePc was calculated to be a triplet state. The quintet and singlet states are 4.70 and 9.97 kcal/mol higher than the triplet state, respectively. Moreover, the Fe atom deviation was not as significant (0.260 Å), which was clearly different from the case of FePor (0.421 Å). The triplet (0.231 Å) and singlet (0.233 Å) states showed similar deviations to the case of FePor, as shown in Table 1.
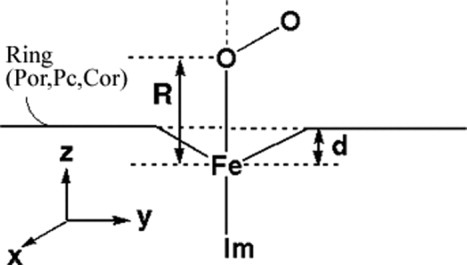
Among these three complexes, the optimized geometries and stabilities of the quintet states shows characteristic features. To figure out the reason, we analyzed the orbital energy of the complexes in the quintet state as shown in Figure 3. It showed the MO pictures of SOMOs and alpha spin MOs of the unrestricted DFT. In the quintet state, the SOMOs are important: they are the key orbitals dx2-y2 and ring π*. The orbital shown are characterized as Fe(d-orbital), Ring(π), and Ring(π*) of porphyrin. The orbital energy in in-plane (d = 0.0) and out-of-plane geometries are also compared.
Molecular orbital energy diagram (for SOMOs and alpha spin electrons) of the deoxy complexes in the quintet states. The results for the two structures, in-plane (d = 0.0) and out-of-plane, are compared.
Based on the diagram, the character of the highest singly occupied MO (HSOMO) explains why the Fe atom in FePor and FeCor prefer the out-of-plane position. The HSOMO of FePor and FeCor is the Fe dx2-y2 orbital, while that of FePc is the Ring(π*) orbital. Because the Fe dx2-y2 orbital has antibonding character with the lone pair of the pyrrole N, the dx2-y2 orbital becomes significantly stable when the Fe atom is in the out-of-plane position. The amount of the stabilization is 1.36 and 1.13 eV for FePor and FeCor, respectively. This would be the reason why the Fe atom stays in the out-of-plane position in the quintet state of FePor and FeCor.
In contrast, the HSOMO of FePc is the Ring(π*) orbital. The Ring(π) and Ring(π*) orbitals originate from the four orbitals of the porphyrin.52, 53 The energy levels of the Ring(π*) orbitals are very close each other in FePor, because of the symmetry. However, in FePc, one of the Ring(π*) orbitals is significantly more stable than the other. This is related to the orbital energy levels of the C20H202+ perimeter model, as clearly explained by a previous study.54, 55 As a result, the lowest quintet state of FePc has an unpaired electron in one of the Ring(π*) orbitals, but not in the Fe dx2-y2 orbital. This is also confirmed by Mulliken spin population analysis. In the optimized quintet states, the atomic spin populations of the Fe atom are 3.87 and 3.82 for FePor and FeCor, and in contrast, 2.86 for FePc. This is clearly different from the case of FePor and FeCor. In other words, FePc has a radical in the porphycene ring, and the Fe atom is in the quartet state [Fe(S = 3/2) + Pc(S = 1/2)]. In contrast, FePor and FeCor have Fe(II) ion in the quintet state [Fe(S = 2) + Por(S = 0)]. Therefore, FePc cannot be stable even when Fe atom is in the out of position. The amount of the stabilization is 0.22 eV (1.36 and 1.13 eV for FePor and FeCor, respectively).
Another remarkable orbital is dxy orbital, which is the lowest energy d-orbital of Fe atom for FePor and FePc. However, in FeCor, because the ring plane is distorted (symmetry broken), the dxy orbital interacts to the lone pair of the pyrrole N with antibonding character. As a result, this orbital is destabilized in in-plane geometry but stabilized in out-of plane geometry (the same reason for the stabilization of dx2-y2 orbital). In contrast, in FePor and FePc, the antibonding interactions vanishes, because the ring planes have high symmetry. The amount of the stabilization is 0.14, −0.12 and 1.11 eV for FePor, FePc, and FeCor, respectively. As a result, the quintet state of FeCor becomes more stable than that of FePor in the out-of-plane geometry.
Ground States of the Oxy-complex: Electronic Structure and Geometry
Next, we investigated the geometry and electronic structures of the ground state of the oxy-complexes. Table2 shows the optimized geometry and the relative energies in each spin multiplicity.
| FcPor–O2 | FePc–O2 | FeCor–O2 | ||||
|---|---|---|---|---|---|---|
| Triplet | Singlet | Triplet | Singlet | Triplet | Singlet | |
| Relative energy (kcal/mol) | 8.36 | 0.00 | 13.8 | 0.00 | 6.54 | 0.00 |
| Optimized geometry | ||||||
| Distance (Å) | ||||||
| Fe–Im N | 2.14 | 2.07 | 2.12 | 2.08 | 2.12 | 2.06 |
| Fe–Pyr NI | 2.09 | 2.01 | 1.95 | 1.95 | 2.09 | 2.04 |
| Fe–Pyr NII | 2.09 | 2.03 | 1.95 | 1.96 | 2.10 | 2.07 |
| Fe–Pyr NIII | 2.09 | 2.03 | 1.95 | 1.96 | 2.09 | 1.97 |
| Fe–Pyr NIV | 2.08 | 2.01 | 1.95 | 1.95 | 2.10 | 1.96 |
| Fe–O | 2.91 | 1.85 | 3.01 | 1.86 | 2.91 | 1.84 |
| O–O | 1.22 | 1.29 | 1.21 | 1.29 | 1.21 | 1.29 |
| Fe–ring plane | 0.394 | 0.0253 | 0.256 | 0.00141 | 0.468 | 0.0326 |
| Angle (degree) | ||||||
| Pyr NI–Fe–Pyr NII | 88.8 | 90.8 | 94.4 | 96.9 | 108.4 | 104.9 |
| Pyr NII–Fe–Pyr NIII | 88.9 | 88.9 | 84.1 | 82.8 | 85.4 | 87.6 |
| Pyr NIII–Fe–Pyr NIV | 89.0 | 90.7 | 94.5 | 97.0 | 74.4 | 79.0 |
| Pyr NIV–Fe–Pyr NI | 89.0 | 89.6 | 84.1 | 83.2 | 85.7 | 88.4 |
| Pyr NI–Fe–Im N | 98.9 | 89.7 | 95.7 | 89.0 | 99.8 | 88.5 |
| Pyr NII–Fe–Im N | 96.2 | 89.5 | 96.2 | 88.9 | 97.1 | 88.5 |
| Pyr NIII–Fe–Im N | 99.1 | 89.4 | 96.7 | 89.1 | 101.2 | 90.6 |
| Pyr NIV–Fe–Im N | 97.7 | 89.5 | 96.8 | 89.1 | 100.0 | 90.8 |
| Fe–O–O | 119.7 | 118.1 | 116.6 | 118.5 | 118.3 | 118.4 |
| Dihedral angle (degree) | ||||||
| Pyr NI–Fe–Im N–Im C | 86.6 | 135.7 | 38.0 | 45.3 | 103.7 | 136.6 |
| Pyr NII–Fe–Im N–Im C | −3.15 | 44.9 | −57.1 | −51.7 | −6.40 | 31.6 |
| Pyr NIII–Fe–Im N–Im C | −93.0 | −44.0 | −141.9 | −134.5 | −93.1 | −56.0 |
| Pyr NIV–Fe–Im N–Im C | 176.8 | −134.7 | 122.7 | 128.5 | −169.0 | −135.0 |
- The total energy of the singlet state is taken to be 0.00 kcal/mol for all complexes.
The ground states of the oxy-complex, FePor (Mulliken spin population: Fe: 1.15, O2: −1.08), FePc (Fe: 1.16, O2: −1.10), and FeCor (Fe: 1.13, O2: −1.07), were calculated to be a singlet state. There was no remarkable difference in the optimized geometries among the complexes in the single ground state. The Fe atom located in the in-plane position, and the deviations were calculated to be almost 0.0 Å. The Fe–O2 and O–O distances were about 1.85 and 1.29 Å, respectively. The electronic structures of the oxy-complexes in the ground state were also very similar. As shown in the previous article,44 the Fe dz2 and the O2 π* orbital interacts and compose the σ-bonding orbital. There is no apparent π-bonding orbital. Therefore, the electronic structure of the oxy-complexes is biradical character: spin population in the Fe dxz and the other π* orbital. Thus, there were no large differences regarding either the optimized geometry or the electronic structure among any of the complexes.
On the other hand, the triplet states located higher than that of the singlet states by 8.36, 13.8, and 6.54 kcal/mol for FePor–O2, FePc–O2, and FeCor–O2, respectively. The Fe–O2 and O–O distances were very close among the complexes. One characteristic feature was that the Fe atom located out of plane by 0.394, 0.256, and 0.468 Å in FePor−O2, FePc–O2, and FeCor–O2 complexes, respectively. Compared with FePor–O2 and FeCor–O2, the out-of-ring deviation was small in FePc–O2. The amount of the deviation is related to the structure of the deoxy-complexes in its ground state. The out-of-ring deviation was 0.429, 0.231, and 0.513 Å in FePor, FePc, and FeCor complexes, respectively. This is because the electronic structures of the triplet states can be described as the combination of the deoxy-complex and O2 in their ground states. They are described as Fe(S = 2) + O2(S = 1) for FePor–O2 (Mulliken spin population: Fe: 3.88, O2: −1.99) and FeCor−O2 (Fe: 3.82, O2: −1.99) and Fe(S = 1) + O2(S = 1) for FePc–O2 (Fe: 2.87, O2: −1.99). Therefore, from the same discussions as in the deoxy complexes (in the previous section), this explains the reason why the triplet state of FePc–O2 is unstable compared with those of FePor–O2 and FeCor–O2, and why the out-of-ring deviation of the Fe atom is small for FePc–O2.
The electronic structure of oxyheme (FePor–O2) has been studied with several theoretical methods but their results were very different to each other, which may indicate that the electronic structure of oxyheme is a rather difficult subject and may include strong electron correlation effects. Recently, elaborate DFT or CASPT2 calculations were performed, and we compare our results with them.9-14 Siegbahn et al. studied the O2, CO, and NO bindings to the heme with the histidine residue at the distal site by using the DFT method (B3LYP), although they replaced imidazole of the proximal site with NH3.14 Ghosh et al.9, 10 studied the effects of angular changes of the proximal imidazole ring, which can influence the ligand field and binding energies. The electronic structure of the ground state of oxyheme was the same as that of our calculations: open-shell singlet biradical state. The studies using multiconfigurational wave functions were also performed by Kashiwagi et al.22-24 10 to 20 years ago with the CASSCF level, in which they suggested that the Hartree–Fock closed-shell configuration Fe(S = 0)+O2(S = 0) was the main configuration. The SAC/SAC-CI study also suggested the same conclusion.26 The results of CASSCF calculations strongly depend on the choice of the active space.56 Ryde et al.56 studied the ground state of oxyheme with the CASPT2 level at a large active space and large basis set. They suggested the extensive multiconfigurational character of the ground state and a mixture of many different configurations, which were different from the previous CASSCF studies. These results indicate that strong electron correlations may exist in the electronic structures of oxyheme.
The Potential Energy Surfaces for the O2 Binding Processes
To understand the mechanism of O2 binding, we studied the potential energy surfaces in the O2 binding for the singlet and triplet states. Figure 4 shows the potential energy surfaces for the singlet and triplet states. See Figure 2 for the reaction coordinate, d and R.
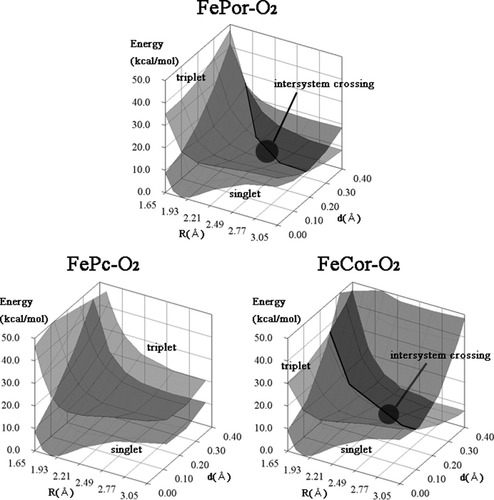
The potential energy surfaces of FePor–O2, FePc–O2, and FeCor–O2 in the lowest singlet and triplet states. The intersystem crossing could occur around d = 0.2–0.3 Å and R = 2.2–2.5 Å in FePor–O2 and around d = 0.1–0.2 Å and R = 2.1–2.5 Å in FeCor–O2. There is no intersystem crossing region in the FePc–O2 potential surface.
The Potential Energy Surface for FePor–O2 and FeCor–O2 Complex
For FePor–O2, the details have been described in the previous article.44 As shown in Figure 4, the potential energy surface of the singlet state is associative over the entire surface. In contrast, the triplet surface is dissociative over the entire area. Because the FePor moiety becomes the quintet ground state in the O2 dissociation limit, the Fe atom locates in the out-of-plane position. The potential surface clearly shows that the O2 binding requires the intersystem crossing from triplet to singlet state. The crossing region would be around d = 0.2–0.3 Å, R = 2.2–2.5 Å. The O2 binding process should include the intersystem crossing region to reach the singlet O2 binding state.
The O2 binding potential surface for the FeCor–O2 complex resembles that for FePor–O2. The ground state is singlet in the O2 binding state and changes into triplet state in the dissociation limit. There is intersystem-crossing region around d = 0.1–0.2 Å and R = 2.1–2.5 Å. Therefore, the O2 binding process would be very similar to that of FePor–O2.
The Potential Energy Surface for FePc–O2 Complex
Next, we explain the potential energy surface of the porphycenes complex. As seen in Figure 4, the potential energy surface of the singlet state is associative, and that of the triplet state is dissociative. This is the same feature generally seen in the porphyrin isomer complex. However, the important difference in the Pc case is that the singlet state is more stable than the triplet state in the dissociation limit. This is because the ground state of the deoxy complex is triplet, not quintet as the case of porphyrin and corrphycene as described earlier. The FePc + O2 system is singlet [Fe(S = 1) + O2(S = 1)] in the O2 dissociation limit. The FePc–O2 complex is also singlet after the O2 binding, as described above. Therefore, the O2 binding process does not require intersystem crossing. In this sense, the mechanism of O2 binding in the FePc–O2 complex is fundamentally different from that in the FePor–O2 and FeCor–O2 complexes.
The O2 Binding Mechanism
As shown in Figure 5, we extracted the energy-minimum pathway along the O2 binding process from the potential surface. For FePor–O2, the details have been reported in the previous article.44 In the O2 binding process, the complex reaches the intersystem crossing point on the triplet potential energy surface after climbing the energy barrier of 3.0 kcal/mol. The spin multiplicity changes into the singlet state, and Fe–O2 bond is formed. The overall reaction energy is 8.4 kcal/mol. In the O2 dissociation process, the system needs 11.4 kcal/mol to reach the intersystem crossing point.
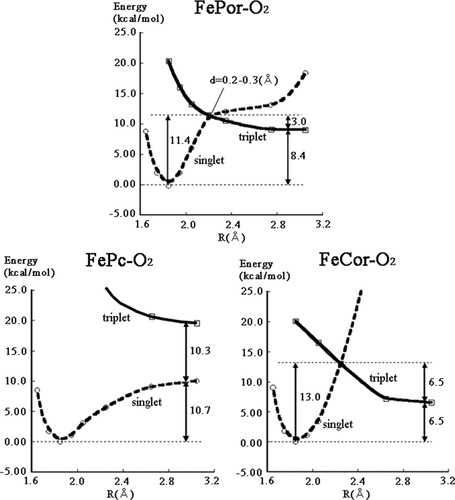
Potential curves for the O2 binding along the energy minimum pathway. The solid line (---) and dashed line (- - - -) denote the triplet and singlet states, respectively.
The potential curve of the FeCor–O2 as shown in Figure 5 is very similar to that of FePor–O2. The activation energy for the O2 binding is 6.5 kcal/mol, and the reaction energy is 6.5 kcal/mol as binding energy. In the O2 dissociation, the energy barrier is calculated to be 13.0 kcal/mol.
In contrast, FePc–O2 complex only uses the singlet surface for the O2 binding/dissociation without spin conversion. The binding energy is 10.7 kcal/mol. The O2 binding process has no energy barrier. We note that our calculations included only the O2–Fe–Porphycene–Imidazole and the O2 binding would be barrierless within the complex. In the actual system, the pathway to the heme might include some energy barrier due to van der waals interactions between O2 and the protein residues.
The O2 binding energy of the FePc–O2 complex is the largest, and that of FeCor–O2 is the smallest of the three porphyrin isomers. This tendency qualitatively explains the experimental fact that the FePc reconstituted heme exhibits very high O2 binding affinity36, 37 and the FeCor one shows only small O2 binding affinity.38, 39
On the Equilibrium Constant of O2 Binding
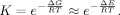 (2)
(2)| K [M−1] | Theoretical estimation | Experimental value |
|---|---|---|
| FePor | 1.8 × 106 (20°C) | 1.1 × 106 (20°C) |
| FePc | 7.0 × 107 (25°C) | 1.1 × 109 (25°C) |
| FeCor | 7.0 × 104 (20°C) | 1.5 × 104 (20°C) |
- The experimental values are also shown for the comparison.
The present estimations for the equilibrium constant reasonably agrees to the trend observed in the experiments for three isomers.36-39 Although we did not consider the effects of the surrounding proteins and the entropy, the present results could be a reasonable basis for explaining the experimental findings.36-39
Conclusion
There are several porphyrin isomers: porphycene and corrphycene. They were used for the alternative to the porphyrin in myoglobin. Such reconstituted myoglobins show singular O2 affinity, which is quite different from the native myoglobin. We theoretically investigated the mechanism of O2 binding to FePor, FePc, and FeCor complexes using the Density Functional Theory calculations.
First, the ground state of the deoxy and oxy complexes were determined. In deoxy complexes, the ground states of both FePor and FeCor are quintet states, and the Fe atom significantly deviates from the ring plane. In contrast, the ground state of FePc is a triplet state, and the Fe atom shows moderate deviation from the ring plane. In the quintet states, the dx2-y2 orbital (SOMO) is stabilized when the Fe atom locates the out-of-plane positions. This is because the dx2-y2 orbital has antibonding character between the Fe dx2-y2 and the porphyrin π orbitals. However, the dx2--y2 orbital is not occupied in the quintet state of FePc. Instead, the porphycene's Ring(π*) orbital becomes SOMO. Therefore, the quintet state of FePc is not stabilized as those of FePor and FeCor. This is the electronic-structural origin of the high O2 affinity in the porphycenes reconstituted myoglobin. In the oxy complexes, the ground states were calculated to be the singlet states for all complexes, and the Fe atom locates in-plane position. There are no large differences in the optimized geometries and the electronic structures among the isomers. The electronic structures of the triplet states are Fe(S = 2) + O2(S = 1), and the Fe–Ring–Im moieties are very close to that of the quintet states in deoxy complexes.
Next, we investigated the potential energy surfaces for the O2 binding. In all complexes, the potential energy surfaces of the singlet state are associative, while they are dissociative for the triplet states. For FePor–O2 and FeCor–O2, there is the intersystem crossing regions between the singlet and triplet states. This area is also the transition state in the O2 binding pathway. Therefore, the O2 binding process for both FePor–O2 and FeCor–O2 includes the intersystem crossing. In contrast, for FePc–O2, the triplet state is more unstable than the singlet state, and there is no crossing between the two surfaces. Therefore, the O2 binding of the FePc–O2 complex proceeds only on the singlet surface. There is no energy barrier in the O2 binding. These potential surfaces qualitatively explain the O2 affinity observed in the experiments.
We discussed the O2 affinities by estimating the equilibrium constant. The theoretical estimation reproduced the trend of the experimental equilibrium constant. This result also indicate that the potential energy surface reasonably explains the major part of the O2 affinities, FePc–O2 > FePor–O2 > FeCor–O2, observed in the experiments.
Acknowledgements
A part of the computations was performed in the Research Center for Computational Science, Okazaki, Japan.




