A DFT study on the relative affinity for oxygen of the α and β subunits of hemoglobin
Abstract
DFT calculations are carried out on computational models of the active center of the α and β subunits of hemoglobin in both its oxygenated (R) and deoxygenated (T) states. The computational models are defined by the full heme group, including all porphyrin substituents, and the four amino acids closer to it. The role of the protein environment is introduced by freezing the position of the α carbon atom of each of the four amino acids to the positions they have in the available PDB structures. Oxygen affinity is then evaluated by computing the energy difference between the optimized structures of the oxygenated and deoxygenated forms of each model. The results indicate a higher affinity of the α subunits over the β ones. Analysis of the computed structures points out to the strength of the hydrogen bond between the distal histidine and the oxygen molecule as a key factor in discriminating the different systems. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 1446–1453, 2006
Introduction
Oxygen transport is a fundamental process in most pluricellular organisms. In vertebrates, this role is undertaken by hemoglobin (Hb), a protein that picks up oxygen from the lungs and takes it to the tissues. It is one of the fundamental components of blood, and is responsible for its red color. The fixation center of oxygen in hemoglobin is the heme group. The heme group is composed by an iron atom and a porphyrin, a polycyclic planar ligand with four coordination sites. The heme group fixes oxygen through its attachment to iron.
Heme groups are common in biochemical systems. In oxygen transporters, like hemoglobin and myoglobin, the metal is in its ferrous oxidation state. In oxidation systems like cytochromes, iron is usually in its ferric oxidation state. The chemistry of the heme group is extensively studied, and an increasingly clear picture of its main characteristics is emerging thanks to the contributions of the experimental study of biological and biomimetical systems.1 A very significant effort has also been invested in the computational study of its features using quantum chemistry. This has allowed to clarify general aspects of the binding of dioxygen and other small molecules to heme,2-5 the dynamics of movement around heme,6, 7 the role of the axial histidine by cysteine ligand,8, 9 and the nature of intermediates and other mechanistic features of the catalytic cycle of cytochrome P450 and related enzymes.10-12
One of the main biological features of hemoglobin is the cooperativity behavior.13 There are four heme groups in a single hemoglobin protein, and their affinity for oxygen depends on the oxygenation state of the whole protein: the affinity increases with the number of oxygen molecules fixed. That is, it is easier to bind the fourth oxygen molecule in Hb(O2)3 than to bind the first one in Hb. This phenomenon has key biological consequences, because it makes the saturation curve of the protein vary sharply in response to the oxygen concentration. The protein thus loads, or unloads, the four oxygen molecules in response to slight changes, and this feature greatly improves its ability as transporter. There are a variety of theories aimed at explaining this cooperativity behavior,14 although its intepretation at the microscopic level remains controversial.15, 16
Hemoglobin is a tetramer composed of two α and two β subunits, each of them containing one heme attached to the subunit by a cordination bond between iron and histidine F8 (also called proximal histidine). The residues laying on the opposite side of the heme constitute the distal pocket. The key of the cooperativity mechanism is the transfer of information between the heme groups, which is triggered by the motion of the iron atom from the out-of-plane position in the absence of oxygen (pentacoordinate system) to the in-plane position in the presence of oxygen (hexacoordinate system). The understanding of this cooperativity requires the introduction of the whole protein for its computational study, and is a current subject of research with the joint use of molecular mechanics and molecular dynamics.17-19 The present study addresses a more modest, yet relevant, issue, which is the affinity that each subunit has for oxygen in the structure it adopts in both the deoxygenated (T) and oxygenated (R) forms of the protein. Direct measurement of this affinity is not possible, and a number of indirect approaches have been proposed. There is no consensus yet on the relative affinities,20 although some experiments suggest a higher affinity for the α subunit.21-23 Our tools are DFT calculations with a large basis set on a model defined by the heme group, the oxygen molecule, and the amino acids closer to the active center. The geometrical constraints associated to the protein chain are introduced by freezing the positions of the Cα atoms of the amino acids considered to the positions they have in the X-ray PDB structures of both the T and R forms of the protein.
Computational Details
Density functional calculations with the BP8624, 25 and B3LYP functionals26, 27 were performed with the Jaguar program.28 Two different basis sets were used. Most calculations were carried out with basis set I, which corresponds to that labeled as LACVP** in the program. This implies an effective core potential replacing the 10 innermost electrons of iron.29 The basis set is valence double-ζ for all atoms,29-31 and has a polarization shell for all atoms different from iron.31 An additional set of calculations was carried out with the larger basis set II, which is that labeled as LACV3P**++ in the program. This is a valence triple-ζ basis set.28, 32 It includes diffuse functions for all atoms,33 and it retains the same polarization shells of basis set I.31 For the oxygenated systems, basis set I contains 1342 basis functions, and basis set II, 2052.
Geometry optimizations were carried out with the BP86 functional and basis set I (BP86/I description). Most of the discussion on energetics is nevertheless based on single-point calculations with the B3LYP functional on the optimized BP86 geometries. The problem of the absolute energetics of the oxygen fixation is a difficult one from a computational view because of the involvement of different spin states. The energy comparison between different spin states is a challenge for DFT methods,34, 35 and B3LYP calculations on BP86 geometries seem to provide a reasonable balance.36 As will be shown below, the BP86 results suggest larger binding energies, but the trends between the different systems considered, which is the key issue in this article, are practically unchanged. The calculations used the unrestricted formalism for the quintet deoxygenated state, with the same ground state described in previous work.37 Spin contamination was always small. For the singlet oxygenated state, a restricted formalism was used.
Most of the energies presented are potential energies in the gas phase. An additional set of calculations was carried out introducing environmental effects through a continuum calculation with Jaguar's Poisson--Boltzmann solver.28 The dielectric constant is set to 4.0 and the probe radius to 1.40. Zero-point energies and entropic contributions have not been evaluated. The second derivative calculations would be very time consuming, and we think it is reasonable to assume that the additional contributions would be similar for all computed systems. In almost all cases, geometry optimizations were complete except for the frozen chain atoms. In the calculation of the subunit β in the T-state, the dihedral angle of the acidic hydrogen of one of the propionic substituents had to be frozen to avoid the formation of a spurious hydrogen bond with the distal histidine.
Computational Model
The model system used in these calculations is shown in Figure 1. It consists of the full heme group with all its substituents, and the four closest amino acids to the iron atom, His E7, Val E11, Phe CD1 for the distal side, and His F8 for the proximal side. The latter is bound to the iron through its ε nitrogen, and is trans to the coordination site of dioxygen. Its introduction is mandatory in any simple representation of the active center of hemoglobin, and it has been so considered in most previous calculations on the system. The other three amino acids are in the so-called distal side of the heme, where dioxygen binds to iron. The importance of this distal side of hemoglobin in dioxygen fixation is well established from experimental studies on mutant systems,38 and from molecular dynamics calculations.17 The three amino acids that have been considered are the same in both the α and β subunits. They are sensitive to oxygen fixation because they change notably their positions in the X-ray structures of the T and R forms of hemoglobin. Furthermore, it is well known that the distal histidine E7 is able to form a hydrogen bond with dioxygen, especially in the α chain.13
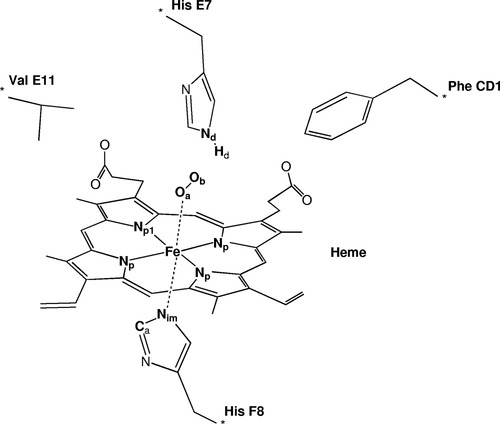
The model system used in the calculations, with the labeling of the atoms.
The structural features of the different subunits and states of hemoglobin are introduced in the calculation by constraining the coordinates of selected atoms to the values provided in the Protein Data Bank (PDB) (www.rcsb.org). The structures taken from the PDB are that with code 2HHB for the deoxygenated T form,39 and that labeled as 1HHO for the oxygenated R form.40 The computational approach consisted of freezing the α carbons of the amino acids to the position they have in the PDB structure. The peptidic bonds connecting these α carbons to the rest of the protein chain have been suppressed in our calculation, and their valence shell has been saturated with two hydrogen atoms, which have also been kept at the same orientation the CC and the CN bonds have in the PDB structure. The three CH bond distances were frozen to 1.090 Å. This procedure is illustrated graphically in Figure 2 for the case of histidine. There are thus four frozen atoms for each amino acid. The position for the rest of the atoms in each amino acid, as well as the full heme group (except for the dihedral angle of the propionate mentioned above) and the dioxygen, when present, are completely optimized without any additional constraint in the calculation. The propionate groups attached to the heme have been protonated to keep them in the neutral form. We could not introduce the amino acids neutralizing them in our calculation for a reason of size, and we assume that this aspect will not be critical for oxygen affinity.
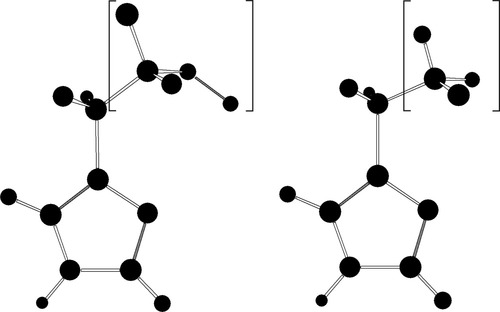
Real (left) and model (right) form of the histidine amino acid. Atoms in parenthesis are frozen in the calculation.
The geometry optimizations were carried out on a total of eight structures: RαD, RαO, TαD, TαO, RβD, RβO, TβD, and TβO. An additional pair of the calculations, in the presence and absence of dioxygen, were carried out on a simplified system with no distal amino acids, just an imidazole as the proximal ligand and the substituents of the porphyrin replaced by hydrogen atoms.
Energetics of Oxygen Affinity
The binding energies for dioxygen of each of the hemoglobin subunits computed with the different methods are collected in Table 1. Comparison of the first two columns shows a large difference between the B3LYP and BP86 binding energies. For BP86, the reaction is strongly exothermic, with the products ca. 30 kcal/mol below the reactants; while for B3LYP it is weakly endothermic, with the products between 5 and 15 kcal/mol above the reactants. This large difference between the two functionals is likely related to the known DFT problem of the unbalanced description of systems of different spin states. Functionals with pure DFT exchange like BP86 are known to overstabilize low spin states, while hybrid functionals with an exact exchange part are known to overstabilize high spin states.35 This problem is particularly visible in this specific system because of the large change of spin involved: the oxygenated complex, a singlet, breaks down into the deoxygenated complex, a quintet, and free oxygen, a triplet. The discrepancy between BP86 and B3LYP energies thus does not seem related to the interactions between dioxygen and the distal residues. This was further proved by a calculation on a more simple system where the distal residues are deleted, all porphyrin substituents are hydrogen atoms, and the proximal histidine is replaced by an imidazole. In this simplified model, the binding energy was −28.6 kcal/mol with the BP86 functional and +8.3 kcal/mol with B3LYP.
| BP86/I | B3LYP/I | B3LYP/I + SCRF | B3LYP/II | |
|---|---|---|---|---|
| Rα | −33.4 | +5.6 | +4.9 | +8.8 |
| Tα | −33.5 | +6.1 | +5.4 | +8.7 |
| Rβ | −27.4 | +11.2 | +10.2 | +13.9 |
| Tβ | −25.6 | +13.3 | +11.8 | +15.8 |
| Model | −28.6 | +8.3 | +8.0 | +11.3 |
- Data for the model system, with no amino acids or pending chains are also included.
There is no simple way to treat the relative stability of different spin states within the DFT formalism, but a consensus seems to emerge in that the correct value should be between those of B3LYP and pure functionals like BP86, and is usually closer to B3LYP. This would leave a reaction exothermic by a few kcal/mol, which agrees with the expected affinity for oxygen.
Therefore, it is difficult to give an accurate value for the absolute oxygen affinity from these calculations. However, the relative values between the different subunits are relatively independent from the method, and one can use either functional to obtain a reliable comparison between the different subunits, which is the main goal of this work. In what follows, we are going to focus on the B3LYP values.
B3LYP results are presented in three of the columns of Table 1. The second and third column differ only in the presence of solvent effects in the latter. Solvent effects are found to slightly favor the dissociation reaction, by values between 0.3 and 1.5 kcal/mol. The change does not however, alter, the relative ordering of the energies. The use of basis set II, in the fourth column, however, introduces some interesting nuances. The improvement of the basis set has a quite homogeneous effect on all four systems considered. Dissociation is always more difficult with the larger basis set, by a value between 2.5 and 3.2 kcal/mol. Because of the small differences involved, this forces a substantial approach between the dioxygen affinities for systems Rα and Tα, which for basis set II are only separated by 0.1 kcal/mol.
Concerning biochemical implications, a first observation from Table 1 is that the β subunit of the protein is able to discriminate between the R and T forms in terms of oxygen affinity. Binding is 1.9 kcal/mol stronger in the case of the R structure. This is not surprising, because R is the crystal structure where the oxygen is present, and the protein environment has logically arranged itself for an optimal interaction. This difference for the β subunit is not very large, but sufficient for a biological effect. This is not, however, the case for the α subunit, where the B3LYP/II result is, in fact, that the deoxygenated form has an affinity 0.1 kcal/mol higher. A difference of 0.1 kcal/mol is certainly not significant, but the result certainly points out to an inferior capacity to discriminate by the α subunit.
Another interesting analysis comes from the comparison of the affinities for the α and β subunits. The affinity of the α fragment is always larger than the β one with a difference of 5.1 kcal/mol for the R state and 7.1 kcal/mol for the T state. These values may be overestimated, but we think that they clearly indicate, based on the available structures of native Hb, that the coordination of oxygen to deoxygenated hemoglobin must start in the α subunits. Interestingly, Scherlis and Estrín41 obtained a different conclusion from a study where DFT single-point calculations where applied on structures partially optimized with the semiempirical SAM1 method. We believe that the current calculations are more reliable because of the more complete geometry optimization with a more accurate method. Our results are, furthermore, in agreement with the more extended experimental view.21-23 The values of oxygen affinity presented in Table 1 for the different computed systems can, in fact, be well accommodated in a proposal for the mechanism of the binding of the four molecules of oxygen to the protein.
In the deoxygenated T form, the affinity of the α subunit is significantly higher than that of the β subunit, and it is reasonable to assume that the oxygen uptake will start in the α subunits of the protein when it is still in the T form. Then, because of the low affinity of the β subunits in the T form, the transition from the T to the R form should take place, and the second pair of oxygen molecules would be loaded in the β subunits with the protein already in the R form. Thus, the transition from T to R should be induced by the oxygenation of the α subunits. This observation is in good agreement with what was observed by NMR studies22 and molecular dynamics simulations.17
The release of the four oxygen molecules from the oxygenated hemoglobin would follow the opposite direction. The β subunits would lose their oxygen molecules first because their affinity for oxygen is relatively low even in the R structure. Of course, within our simplified model, it is impossible to predict whether the transition between R and T states should be coupled with oxygen uptake or release, or if it would require oxygenation (or deoxygenation) of both subunits of the same type to be induced.
Computed Structures for the “PDB” Systems
X-ray data for four of the computed systems, the oxygenated R structure, and the deoxygenated T structure, have been reported in the PDB, and the frozen atoms of our constrained geometry optimizations have been, in fact, obtained from them. Accuracy of PDB structures is, however, not perfect, and it has been shown that they can be refined sometimes by DFT calculations.42 In what follows, we critically evaluate the quality of our computed structures.
Table 2 collects computed values for selected geometrical parameters for structures RαO, RβO, TαD, and TβD. The overall characteristics of the structures follow the trends that have been repeatedly reported in previous theoretical calculations,37 and that now seem to be generally accepted in the scientific community. The coordination sphere of iron in the deoxygenated species TαD, and TβD is that of the square pyramid, with the four porphyrin nitrogens occupying equatorial positions and the proximal histidine in the axial site. The iron atom is out of the porpyrin plane, towards the proximal side, as reflected by the average Nim–Fe–Np bond angles of 98.0° and 97.4° The axial Fe–Nim distance is quite long (2.172 and 2.170 Å), significantly longer than the average equatorial Fe–Np distances (2.064 and 2.089 Å). The oxygenated species RαO and RβO (Fig. 3) are better described as octahedral complexes, with the proximal histidine and the dioxygen ligand occupying trans sites. The octahedral arrangement results in the atom center lying very near the porpyrin plane, and this is reflected by bond angles around the iron center close to 90°. This is the case for the average Nim–Fe–Np angles of 88.7° and 88.5°. Dioxygen binds to iron through only one of its atoms, resulting in a quite short Fe–O distance of ca. 1.75 Å. The Fe–Oa–Ob bond angle is near 120° and 119.9° for RαO, and 121.0° for RβO.
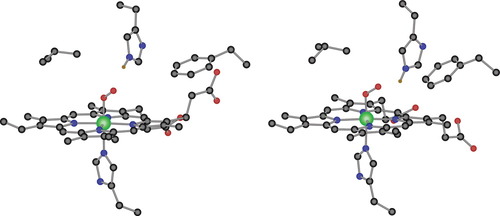
Computed BP86 geometries of structures RαO (left) and RβO (right). Hydrogen atoms different from Hd are omitted for clarity.
| RαO | RβO | TαD | TβD | |
|---|---|---|---|---|
| Fe–Nim | 2.082 (1.94) | 2.100 (2.07) | 2.172 (2.15) | 2.170 (2.15) |
| Fe–Npa | 2.018 (1.98) | 2.015 (1.96) | 2.064 (2.10) | 2.089 (2.03) |
| Nim–Fe–Npa | 88.7 (94.) | 88.5 (87.) | 98.0 (102.) | 97.4 (99.) |
| Ca–Nim–Fe–Np1 | −39.1 (−12.) | −24.6 (−27.) | −6.0 (−17.) | −5.8 (−21.) |
| Fe–Oa | 1.749 (1.66) | 1.745 (1.86) | — | — |
| Oa–Ob | 1.303 (1.22) | 1.295 (1.24) | — | — |
| Fe–Oa–Ob | 119.9 (153.) | 121.0 (159.) | — | — |
| Nd–Hd | 1.034 (1.05)b | 1.021 (1.05)b | — | — |
| Hd–Oa | 2.467 (2.03)b | 2.616 (2.31)b | — | — |
| Hd–Ob | 1.879 (1.69)b | 2.177 (2.87)b | — | — |
- Experimental PDB parameters are indicated in parentheses (see atom labels in Fig. 1).
- a Average value.
- b Assuming Nd–Hd is 1.05 Å.
It is interesting to compare these computed values with the PDB data also included in Table 2. The overall trends are the same, but differences are significant. This is particularly the case for the coordination of the dioxygen molecule. The PDB values in RαO and RβO for the Fe–Oa distances are 1.66 and 1.86 Å, respectively, which are 0.09 Å shorter for α and 0.12 Å longer for β than the corresponding computed values. The discrepancy is even larger for the Fe–Oa–Ob bond angle, which is experimentally reported around 155°, while the computed values are near 120°. We think that these discrepancies are essentially due to the intrinsic inaccuracy involved in the complicated X-ray measurement of proteins, which can, in fact, be corrected sometimes by accurate quantum chemistry calculations.42 Computed geometries around Fe are more similar for RαO and RβO than they are in the PDB structures. Furthermore, the computed structures are closer to those of the biomimetic systems, where the X-ray measurements are much more accurate.
It is reasonable that the larger inaccuracies in the PDB structures are in the position of dioxygen because different conformers exist associated to rotation around the Fe–Oa axis. In fact, for the particular case of RβO we computed three of them, and only the most stable one is reported in Table 2. The other two structures had energies 1.4 and 1.6 kcal/mol above. We did not compute the transition states connecting them, but the energy barriers are likely to be low. In this situation, disorder is likely to affect the X-ray diffraction, because of movements in the diffraction time scale or because of population of different conformers. This disorder will, in any case, hamper interpretation of the diffraction spectra, thus rendering data less accurate.
Not all discrepancies can be easily attributed to inaccuracies in the PDB data. For instance, the differences between computed and PDB structures in the dihedral angle Ca–Nim–Fe–Np1 can be as large as 27.1° (−39.1° vs. −12.°) in the case of RαO while insignificant (−24.6° vs. −27.°) in RβO. The variability of this angle, which essentially measures the rotation of the porphyrin ring around the Fe–Nim axis, can mainly be attributed to the lack of amino acids in our model, which most likely impede the rotation in the protein. We think that this particular parameter should have a minor effect on the oxygen affinity based on the low energy barriers calculated for this rotation.8 It would furthermore be pointless to seek perfect reproduction of the experimental structure, because our computational scheme is based on the frozen PDB positions of a set of atoms, and we have just seen above that the accuracy of this PDB data is not perfect to start with.
Table 2 also contains the parameters related to the hydrogen bond between the distal histidine and the dioxygen molecule, Nd–Hd, Hd–Oa, and Hd–Ob. In this case, the comparison is particularly complicated because the hydrogen atoms are not located in the X-ray structure, and their PDB position is assigned by assuming a N–H distance of 1.05 Å in the direction pointing away from the imidazole ring. The experimental relative distance to the oxygen atoms is furthermore affected by the uncertainty in the PDB position of oxygen discussed above. These parameters are included in Table 2, essentially because they will be discussed together with those of the “non-PDB” structures in the next subsection.
“PDB” vs. “non-PDB” Structures
This section presents the geometries of the so called “non-PDB” structures, emerging from the computational experiment resulting of substracting dioxygen from the R PDB conformations and adding it to the T PDB structures. Selected parameters from the calculated geometries of RαD, RβD, TαO, and TβO are collected in Table 3. The main features in the coordination sphere of iron follow the general trends described above. Deoxygenated structures are square pyramidal (Nim–Fe–Np values around 97°), and oxygenated structures are octahedral (Nim–Fe–Np values around 89°). The dioxygen ligand is bound η1 to iron and bent (Fe–Oa–Ob around 121°) in the oxygenated structures.
| RαD | RβD | TαO | TβO | |
|---|---|---|---|---|
| Fe–Nim | 2.168 | 2.156 | 2.103 | 2.093 |
| Fe–Npa | 2.087 | 2.089 | 2.018 | 2.020 |
| Nim–Fe–Npa | 96.9 | 97.1 | 88.7 | 88.7 |
| Ca–Nim–Fe–Np1 | −38.2 | −17.9 | −25.0 | −41.1 |
| Fe–Oa | — | — | 1.750 | 1.748 |
| Oa–Ob | — | — | 1.302 | 1.284 |
| Fe–Oa–Ob | — | — | 121.1 | 121.3 |
| Nd–Hd | — | — | 1.033 | 1.017 |
| Hd–Oa | — | — | 2.593 | 6.088 |
| Hd–Ob | — | — | 1.905 | 4.937 |
- a Average value.
The joint consideration of the data in Tables 1 to 3 shows a good correlation between the affinity for oxygen of a given subunit and the geometrical parameters describing the hydrogen bond between the distal histidine and dioxygen in its oxygenated form. From Table 1, the affinity of the different subunits for dioxygen follows the order Rα ≃ Tα > Rβ > Tβ. A stronger hydrogen bond will be geometrically reflected in a lengthening of the Nd–Hd distance and a shortening of the Hd–Ob distance. This is precisely what is found in Tables 2 and 3 for the series described above. The Nd–Hd is longer for the subunits with the higher oxygen affinities, with values of 1.034, 1.033, 1.021, and 1.017 Å for Rα, Tα, Rβ, and Tβ, respectively. The corresponding values for the Hd–Ob distance are 1.879, 1.905, 2.177, and 4.937 Å, respectively. This particular hydrogen bond plays a fundamental role on the relative oxygen affinity of the different subunits. Similar hydrogen bonds had been previously reported in related systems,41, 43 and have, in fact, been proposed to be responsible for the discrimination between oxygen and carbon monoxide in myoglobin44-46, a protein similar to one subunit (α or β) of hemoglobin.
Figure 4 presents the computed structures of the models for the TαO and TβO subunits. The geometry of TβO clearly shows that this is the only oxygenated structure with no hydrogen bond between the distal histidine and the dioxygen molecule, which is consistent with the fact that Tβ has the lowest affinity for oxygen. The joint observation of Figures 3 and 4, presenting the four oxygenated structures, shows how the hydrogen bond always takes place with Ob, the oxygen atom further away from iron. In all cases the Nd–Hd bond is in a direction mostly perpendicular to the Fe–Oa–Ob plane. Ob could actually get closer to Hd by rotating the dioxygen ca. 90° around the Fe–Oa axis. This orientation would, in fact, be the electronically preferred, as found in calculations where the distal histidine is left unconstrained.4 However, our attempts to optimize it in the case of RβO produced a structure with a higher energy. The strain introduced by the geometrical constraints in the Cα atoms of both the proximal and the distal histidine preclude this structure. Another alternative conformer, with Ob pointing away from the distal histidine, would favor a hydrogen bond between Hd and Oa. This was also tested, and found to have a higher energy than the reported structure. Moreover, the binding of oxygen to the Tβ structure induces an important shift of the porphyrin. This is due to steric hindrance of the distal amino acids in the deoxygenated conformation. This is consistent with observations made previously with molecular dynamics simulations where it was shown that the porphyrin must be displaced before binding of oxygen.17 The distal histidine thus plays a fundamental role both on the energetics and the structure of the dioxygen binding to the subunits of hemoglobin. However, the role of the other amino acids used in these calculations must not be overlooked. The proximal histidine is essential, because it actually fixes the position of the heme group in space. The role of the other two amino acids, valine and phenylalanine, is not so obvious, but from the structure of TαO in Figure 4 it seems that the distal histidine cannot reorientate itself to move Hd closer to the dioxygen because of the blocking presence of the valine amino acid.
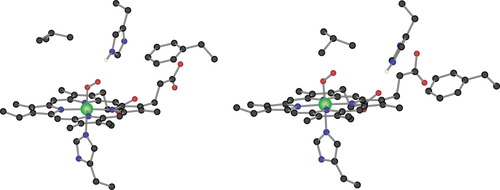
Computed BP86 geometries of structures TαO (left) and TβO (right). Hydrogen atoms different from Hd are omitted for clarity.
Conclusions
DFT calculations on a model system of the active center of the two subunits of hemoglobin give information on their relative oxygen affinities. In first place, the calculations correctly predict a higher affinity of the β subunits for oxygen in the R configuration than in the T configuration, which gives a certain confirmation to the validity of the computational model. The calculations also indicate a higher affinity for dioxygen in the case of the α subunit, a result that has been previously suggested from experimental data. From these results, a mechanism can be proposed where oxygen coordination starts in the α subunits of the T form of hemoglobin, which once oxygenated, can induce the transition from the T to the R form, and hence, coordination to the β subunits takes place. Deoxygenation would follow the opposite pathway, starting by the loss of oxygen from the β subunits. Analysis of the computed structures indicates a fundamental role of the distal histidine amino acid in the energetics of oxygen binding, in particular through the formation of a hydrogen bond with the oxygen atom further away from the metal center. A further understanding of the behavior of the affinity for oxygen by the α and β subunits, including the key cooperativity feature, would require introduction of the full protein, and is out of the scope of the current work.
Supplementary Material Available
Cartesian coordinates and total energies for the 10 optimized structures discussed in the text.
Acknowledgements
J.-D.M. thanks the financial support of the Training and Mobility of Researchers program of the European Union under contract No. ERBFMBICT97- 056. Part of the calculations were carried out on the IDRIS Supercomputer Center of the CNRS (France) and in CESCA of Barcelona (Spain). Financial support from the Spanish MCyT and FEDER (Projects CTQ2005-090000-CO1-01, CTQ2005-090000-CO1-02) and the ICIQ foundation is acknowledged.




