Theoretical, spectroscopic, and mechanistic studies on transition-metal dinitrogen complexes: Implications to reactivity and relevance to the nitrogenase problem
Abstract
Dinitrogen complexes of transition metals exhibit different binding geometries of N2 (end-on terminal, end-on bridging, side-on bridging, side-on end-on bridging), which are investigated by spectroscopy and DFT calculations, analyzing their electronic structure and reactivity. For comparison, a bis(μ-nitrido) complex, where the NN bond has been split, has been studied as well. Most of these systems are highly covalent, and have strong metal–nitrogen bonds. In the present review, particular emphasis is put on a consideration of the activation of the coordinated dinitrogen ligand, making it susceptible to protonation, reactions with electrophiles or cleavage. In this context, theoretical, structural, and spectroscopic data giving informations on the amount of charge on the N2 unit are presented. The orbital interactions leading to a charge transfer from the metals to the dinitrogen ligand and the charge distribution within the coordinated N2 group are analyzed. Correlations between the binding mode and the observed reactivity of N2 are discussed. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 1278–1291, 2006
Introduction
The reduction of molecular nitrogen (N2) to ammonia is one of the most complex and fascinating reactions of biology.1-4 It is catalyzed by the enzyme nitrogenase, the reactive center of which contains a unique metal cluster, the iron molybdenum cofactor (FeMoco).5, 6 The first X-ray structural information on nitrogenase was obtained from Azotobacter vinelandii and revealed that the FeMoco consists of two Fe4S3 cubane-like units, which are bridged by three μ2-sulfido ligands (Fig. 1).7, 8 In one of the subunits one iron is substituted by molybdenum, leading to a total composition of MoFe7S9. According to the original structural information, the central part of the FeMoco contains a trigonal prisma made up by six three-coordinated iron atoms. Recent crystallographic studies, however, identified the presence of an additional, μ6-coordinated ligand X in the central cavity.9 The identity of X (N, O, or another atom) has been subject to some controversy. Theoretical evidence was presented for the hypothesis that the central ligand most probably is nitrogen.10, 11 Hoffman et al.12 have shown by ESEEM/ENDOR spectroscopy that if X is N, it is not involved in catalytic turnover of the enzyme, which was supported by DFT calculations.11 Recently, however, spectroscopic evidence was presented that X is not N.13
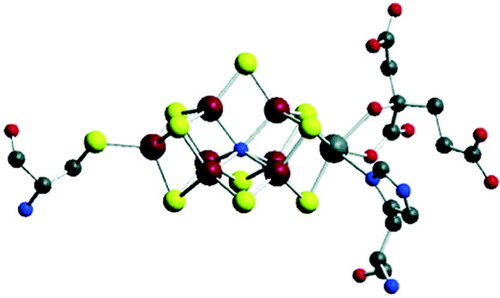
Structure of the FeMo cofactor of nitrogenase.
In view of the fact that even to date only limited experimental information exists as to where dinitrogen binds to the cofactor and how exactly it is transformed to ammonia,14 a large number of computational studies have been performed on this problem. Models of N2 binding to the cofactor can be classified according to the coordination mode: (1) end-on terminally to molybdenum,15-19 (2) end-on terminally to one of the six prismatic iron atoms,20-24 or (3) end-on bridging between two octahedrally coordinated iron atoms after opening of the cage.25–27 In the meantime, theoretical simulations on the entire reduction/protonation pathway of N2 at the FeMoco have appeared as well,28-31 which have provided detailed information on how the enzymatic process of nitrogen fixation could work on a molecular level.
From a synthetic perspective, many efforts have been undertaken in the recent years to create low molecular weight transition-metal complexes that represent structural or functional models of nitrogenase.1-3 Unfortunately, cubane clusters that are chemically and structurally related to the FeMoco only exhibit a limited reactivity with respect to N2 fixation.29, 32 Mono- and dinuclear transition-metal complexes, on the other hand, have been known for a long time to activate dinitrogen to various degrees, eventually making it accessible to protonation, functionalization, or cleavage. Correspondingly, we have divided dinitrogen complexes into weakly, moderately, and strongly activated systems, depending on N–N distances and stretching frequencies.33 Alternatively, dinitrogen complexes can be classified according to the N2 binding mode. This review considers a series of eight complexes (1–8), each of which is representative for a particular degree of activation and/or binding mode; a subset of these is shown in Figure 2. The least activated system is the iron(II)–N2 complex [Fe(N2)(H)(depe)2]+ (1a), which does not mediate the protonation of the coordinated N2 ligand. This reactivity at least requires moderately activated compounds like molybdenum and tungsten dinitrogen complexes that allow the transition metal-mediated generation of NH3 from N2.1-3, 34-36 An early representative of this class of compounds has been the Mo(0) dinitrogen complex [Mo(N2)(dppe)2] [2; dppe = 1,2-bis(diphenylphosphino)ethane], which can be protonated at the N2 ligand to give an NNH2 complex,37 the first step toward the synthesis of NH3.3 Corresponding complexes with monodentate phosphines stoichiometrically converted N2 to NH3.3 Recently, the mononuclear molybdenum complex [Mo(N2)(HIPTN3N)] (3) containing the sterically shielding ligand system HIPTN3N = hexaisopropyl-terphenyl-triamidoamine was even shown to catalytically transform dinitrogen to ammonia in six cycles with an overall yield of 65%.38-41 These experimental findings have been rationalized by DFT calculations, which demonstrated that the conversion of N2 to ammonia at room temperature and normal pressure is, in fact, feasible by a sequence of strictly alternating, thermally allowed protonation and reduction steps.42
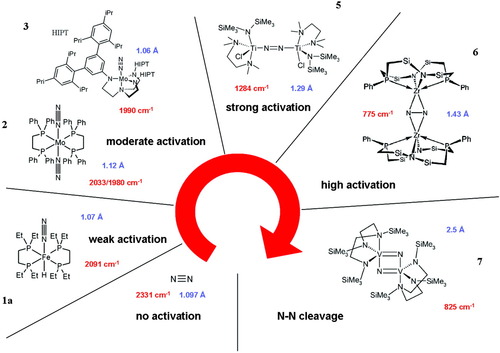
Activation scale of N2 complexes.
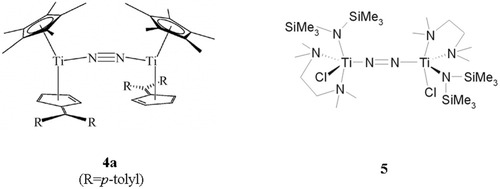
Going to the left in the d-block, the activation of coordinated dinitrogen increases. Group 4 transition-metal complexes are generally dinuclear and contain a dinitrogen ligand bridging the two metal centers, most commonly in a μ–η1:η1 geometry. The activation of the N2 ligand in such compounds ranges from moderate, as found in [{(η5-C5Me5)Ti(η6-C5H4CR2)}2(μ-η1:η1-N2)] (R = p-tolyl:4a; R = adamantyl:4b),43 to strong, as found in [{(Me3Si)2NTiCl(TMEDA)}2(μ-η1:η1-N2)] (5; TMEDA = tetramethylethylenediamine; Scheme 1.44
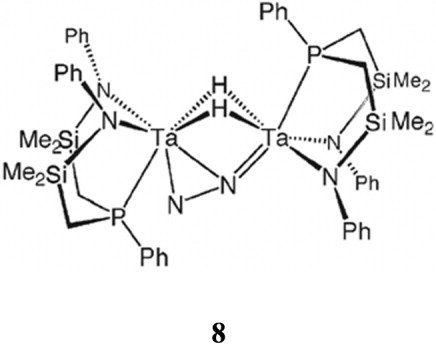
An even higher activation of N2 is observed for the side-on bridging mode of dinitrogen, which exhibits NN bond distances of about 1.5 Å. One example considered here is [{(P2N2)Zr}2(μ-η2:η2-N2)] (6; (P2N2) = PhP(CH2SiMe2NSiMe2CH2)PPh); cf. Fig. 2).45 Further increasing the activation of coordinated dinitrogen leads to cleavage of the NN bond, resulting in a bis(μ-nitrido) structure. This has been observed for the dinuclear vanadium complex [V(N{N″}2)(μ-N)] (7), where (N{N″}2)2− = ({Me3Si}N{CH2CH2N(SiMe3)}2)2−.46 The mechanistic pathway determined for this reaction assumes a preceding side-on coordination of N2.47 An intermediate position between strong and high activation, finally, is represented by the novel side-on end-on bridged dinitrogen complexes,48, 49 as exemplified by the compound [{(NPN)Ta}2(μ-H)2(μ-η1:η2-N2)] (8; NPN = PhN-SiMe2CH2)2PPh; cf. Scheme 2).
This system exhibits a pronounced tendency to form adducts with electrophiles,50-53 a reactivity that is related to protonation and thus of relevance to the enzymatic pathway of nitrogen fixation as well.
- 1
What is the charge on the N2 ligand?
- 2
How is it transmitted from the metals to N2?
- 3
How is it distributed between Nα and Nβ?
- 4
How does the binding mode correlate to reactivity?
If not stated otherwise, DFT calculations on 1–8 have been performed with the LANL2DZ basis set using the B3LYP functional. The general implications of the theoretical and spectroscopic results with respect to the nitrogenase problem are discussed.
End-On Terminal Coordination
Fe(II) Dinitrogen Complexes: Weak Activation Limit
Most of the characterized iron dinitrogen complexes have six-coordinate Fe(II) metal centers that do not activate dinitrogen towards protonation.54-59 Nevertheless, these systems are relevant to the area of nitrogen fixation, as they allow to obtain information about the influence of coligands on the bonding of N2 to metal centers, in particular, iron. On this background we prepared Fe(II) depe and dppe complexes with trans-hydrido and -halide ligands and investigated these compounds with respect to their reactivity with N2 (depe = 1,2-bis(diethylphosphino)ethane; dppe = 1,2-bis(diphenylphosphino)ethane).60-63 In the course of these studies, we performed a structural and spectroscopic investigation of the complexes [FeX(N2)(depe)2]BPh4 (X = Cl, Br) which have FeN2 bonds that are both thermally and photochemically labile.60, 61 The bonding of N2 in these systems proceeds in a spin-forbidden process that could be shown to be the origin of the lability of the FeN2 bond (Fig. 3) The analogous Fe(II) hydrido-dinitrogen complex, [FeH(N2)(depe)2]+ (1a), is thermally more stable.62 This also applies to the corresponding dppe system [FeH(N2)(dppe)2]+ (1b), which even forms in THF by reaction of the five-coordinate precursor [FeH(dppe)2]BPh4 with air.58, 59 The five-coordinate complex [FeCl(depe)2]+, in contrast, is extremely oxygen sensitive in solution.64 These remarkable differences in reactivity are correlated with different electronic ground states that we have determined by a combination of magnetic susceptibility measurements, various spectroscopic methods, and DFT calculations.
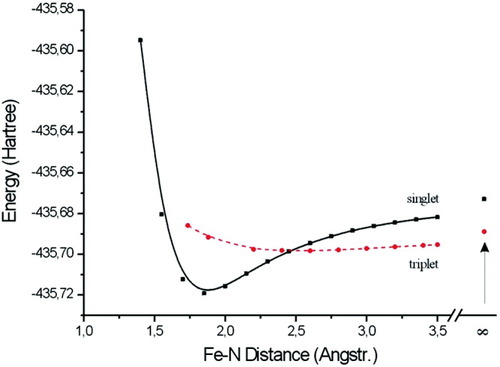
Singlet vs. triplet energy in the reaction of [FeCl(depe)2]+ with N2, plotted vs. the FeN distance.
Recently we investigated the reaction of the iron(II) hydrido complex [FeH(dppe)2]BPh4 with N2, leading to [FeH(N2)(dppe)2]BPh4 (1b).63 Importantly, the five-coordinate complex reacts with N2 both in the solid state and in THF solution.58, 59 Applying Mössbauer, NMR, UV/Vis, infrared and Raman spectroscopies as well as magnetic susceptibility measurements we found that the two dinitrogen adducts resulting from the reactions of [FeH(dppe)2]BPh4 with N2 in solution, and in the solid state differ in their physical and spectroscopic properties. Moreover, we observed that the five-coordinate precursor is paramagnetic in the solid state and diamagnetic in THF solution. DFT was employed to show that the relaxed geometry of the five coordinate complex [FeH(dppe)2]+ has a very small energy difference between the singlet and triplet states. The triplet state found experimentally is therefore due to a solid-state effect. In solution, diamagnetic [FeH(N2)(dppe)2]+ is formed from diamagnetic [FeH(dppe)2]+ upon reaction with N2. In the solid state, in contrast, the triplet state of the five-coordinate precursor is conserved upon reaction with N2, which again must be ascribed to a structural distortion imposed by the crystalline matrix. As evident from the different spectroscopic properties, the bonding properties of N2 appreciably differ for the solution and the solid-state reacted products. The corresponding depe system is simpler: here, [FeH(depe)2]+ is always diamagnetic and reacts with N2 to diamagnetic [FeH(N2)(depe)2]+ (1a).65
Structural and vibrational-spectroscopic data alone do not allow to draw conclusions with respect to relative stabilities of dinitrogen adducts, as exemplified by a vibrational-spectroscopic comparison between [FeH(N2)(depe)2]BPh4 (1a) and [FeCl(N2)(depe)2]BPh4.62 In agreement with the high ν(NN) values (2091 and 2086 cm−1, respectively), the N2 ligands in both compounds are weakly activated, which corresponds to the observation that N2 is not protonatable in Fe(II) systems (vide supra). Natural population analysis (NPA) predicts charges at the nitrogen atoms Nα/Nβ of the coordinated N2 group of −0.09/+0.11 for FeH(N2)(depe)2]+ and −0.05/+0.11 for [FeCl(N2)(depe)2]+.66 Importantly, the terminal nitrogen atom Nβ of the dinitrogen ligand thus is positively charged in both of these weakly activated systems, and therefore not susceptible to electrophilic attack. Normal coordinate analysis reveals that the force fields applying to the FeN2 units of both compounds are almost identical. Nevertheless, the thermal stability of these complexes with respect to loss of N2 is markedly different (vide supra). This indicates that the FeN potentials are unaffected in the vicinity of the respective equilibrium geometries by possible ground-state level crossing processes occuring at larger FeN bond lengths, which decisively influence the thermodynamic stability of these systems.
In summary, three types of reactions with N2 have been established for Fe(II) diphosphine complexes: spin-allowed S = 0 → S = 0 for [FeH(dppe)2]+ → [FeH(N2)(dppe)2]+ or [FeH(depe)2]+ → [FeH(N2)(depe)2]+ in solution; spin-allowed S = 1 → S = 1 for [FeH(dppe)2]+ → [FeH(N2)(dppe)2]+ in the solid state and spin-forbidden S = 1 → S = 0 for [FeX(depe)2]+ → [FeX(N2)(depe)2]+, X = Cl, Br. This class of compounds thus provides an excellent example for the fact that simple changes in the coordination sphere of transition-metal complexes can greatly influence their electronic structure and, correspondingly, their reactivity.
Mo(0) and W(0) Dinitrogen Complexes: Chatt Cycle and Ammonia Synthesis from N2
In contrast to their Fe(II) counterparts, molybdenum(0) and tungsten(0) dinitrogen complexes of the general formula [M(N2)2(diphos)2] (M = Mo,W; diphos = depe,dppe) allow the stepwise protonation and reduction of coordinated dinitrogen, ultimately leading to NH3.3 A cyclic production of ammonia has been demonstrated on the basis of these systems, although with very small yields.67 The corresponding chemistry proceeds within the Chatt cycle (Fig. 4).15, 68 Starting from the bis(dinitrogen) complexes, N2H, N2H2, and N2H3 intermediates can be generated through addition of mineral acids (HBF4, HCl, H2SO4).3 One of the N2 ligands is thereby exchanged against the conjugate base of the employed acid. We have characterized these systems using infrared, Raman, and UV/Vis absorption spectroscopies coupled to DFT calculations.69-75 Based on N–N stretching frequencies, the parent Mo(0) and W(0) dinitrogen complexes were characterized as moderately activated. NPA charge analysis performed for a model of these systems gave a charge of −0.07 on Nα and a charge of −0.06 on Nβ; that is, the terminal N-atom now is negatively charged.69 Using vibrational spectroscopy coupled to normal coordinate analysis, the reduction of the NN bond order from ∼3 to ∼1 upon stepwise protonation from N2 to NNH3− could be demonstrated.69-71 The metal-N bond strength, in turn, is increased up to a triple bond.71 This acts to prevent loss of the partly reduced intermediate from the metal center and to induce cleavage of the NN bond.
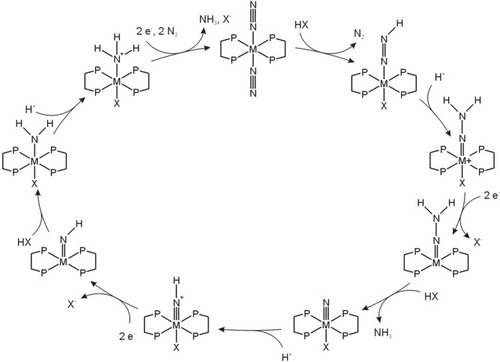
Chatt cycle. M = Mo,W; disphosphine = depe (see text).
The NN bond can be cleaved at the NNH2 stage by adding two electrons, followed by one additional protonation. Two-electron reduction of M(IV)–NNH2 systems leads to loss of the trans-ligand, generating five-coordinated M(II)–NNH2 intermediates (M = Mo,W). These species are favorably investigated based on alkylated derivatives.76 If the doubly reduced, five-coordinate intermediates [M(II)(dppe)2NNR2] are protonated, the NN bond cleaves and secondary amines as well as M(IV) nitrido or imido complexes are formed.77 We structurally and spectroscopically characterized the five-coordinate W(II) complex [W(NNC5H10)(depe)2] and kinetically followed the splitting of its NN bond upon protonation.78 The N cleavage process was found to occur much faster than in the corresponding Mo complex.77 Various mechanistic scenarios were explored by DFT to account for the experimental observations, and a theoretical comparison to the NN splitting process in the Schrock cycle was made. Importantly, DFT indicated that the NN cleavage process at the level of reduced hydrazidium complexes is strongly exothermic and occurs spontaneously, both in the Chatt and in the Schrock cycle.
In the second part of the Chatt cycle, the Mo(IV) and W(IV) nitrido complexes have to be converted to the corresponding low-valent ammine complexes that are able to exchange NH3 against N2. One of the problems associated with this chemistry are the strongly negative potentials, which, in particular, are needed to regenerate the +I and zerovalent Mo and W species.79 We recently showed that replacing the anionic trans ligands by acetonitrile shifts the reduction potentials to less negative values.80
Schrock-Cycle: Catalytic Ammonia Synthesis and Nitrogenase
Schrock et al. were the first to realize a truly catalytic ammonia synthesis proceeding under ambient conditions and through a series of well-defined intermediates.38-41 The corresponding reactive system is based on the moderately activated molybdenum complex [Mo(HIPTN3N] (3) with the specially designed triamidoamine ligand HIPTN3N (hexaisopropylterphenyl-triamidoamine), which provides a sterically shielded site for dinitrogen bonding and transformation to ammonia (Fig. 5). Using lutidinium tetrakis(3,5-bis-trifluoromethyl-phenyl)-borate (LutHBAr′4) as a proton source and decamethyl chromocene (Cp*2Cr) as reductant, ammonia was formed from N2 at room temperature and normal pressure, achieving six cycles with an overall yield of 65%. We performed DFT calculations on all possible intermediates occuring in the catalytic transformation of N2 to ammonia, including those characterized and invoked, respectively, by Schrock et al.38-41 Based on these calculations a detailed mechanism and a free enthalpy profile of the entire cycle were derived. The calculations were performed on models a–n, where the terminal HIPT (hexaisopropylterphenyl-) residues of the corresponding intermediates are replaced by hydrogen atoms (Fig. 6). Importantly, the energies of the reduction and protonation steps were explicitly calculated with respect to the oxidation and deprotonation processes Cp*2Cr → Cp*2Cr+ and LutH+ → Lut, respectively, which were treated withouth any simplifications on the involved molecules. All energies were evaluated on the B3LYP/TZVP level and are zero-point energy, thermally and solvent corrected. The corresponding standard free enthalpies are plotted in Figure 6 against the reaction coordinate.
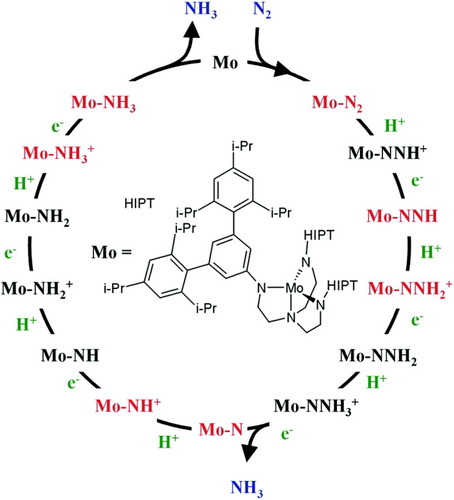
Schrock cycle.
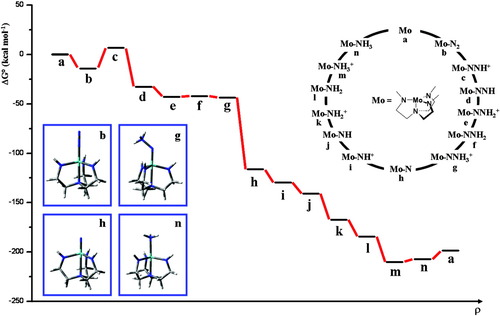
Catalytic cycle (upper right) and energy profile (center) of the reduction of dinitrogen to ammonia in the molybdenum triamidoamine system. Lower left: optimized structures of selected intermediates.
The calculations indicate that the catalytic cycle consists of a sequence of strictly alternating protonation and reduction steps. This agrees with the mechanism postulated by Schrock et al.,38-41 except for the transformation of the dinitrogen complex 3 (b) to the neutral NNH complex d (whereas the calculation predicts a primary protonation of coordinated N2 followed by reduction, Schrock et al. postulate a primary reduction of the Mo(III)-N2 complex to achieve the protonation leading to the NNH complex). All relevant intermediates thus are either neutral or singly positively charged while formation of negatively charged species appears to be excluded. Furthermore, most of the reactions are exergonic. The cleavage of the NN bond is by far the most exergonic step, which, in addition, proceeds spontaneously. Only three steps (b → c, m → n, n → a) of the cycle are endergonic, the most energy-demanding step being the first protonation of the N2 complex (b → c). The most difficult reduction process involves the final conversion of the Mo(IV)–NH3 complex m to its Mo(III) counterpart n, which is able to exchange NH3 for N2, closing the cycle.
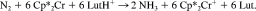 (1)
(1)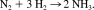 (2)
(2)The calculation gives a standard free enthalpy change ΔG0f of −12.3 kcal/mol for this reaction (in heptane; calculated gas phase value: 9.22 kcal/mol; gas phase literature value: 7.7 kcal/mol).81 186 kcal/mol are therefore required to generate the six molecules of reductant and the six molecules of acid from their oxidized and deprotonated counterparts, respectively, and H2. This value is very large, but appears to be necessary to overcome the kinetic hindrance of ammonia synthesis under ambient conditions. Remarkably, a very similar energy expenditure (180 kcal/mol) is experimentally determined for the enzyme nitrogenase to mediate the conversion of one mol N2 to 2 mol of NH3.82 This energy is mostly contained in the 16 molecules of ATP that are consumed in one catalytic turnover.
Superficially, the reaction path of the synthetic system bears some similarities to that theoretically derived for nitrogenase by Hinneman and Nørskov.28 As the most favorable N2 binding mode, these authors identify an end-on terminal coordination to one of the six iron atoms of the FeMoco that form the central trigonal prisma of the cluster. Then six hydrogenations (corresponding to combined protonation/reduction reactions) are simulated by DFT. Importantly, the authors find that the first hydrogenation of N2 is the most energy-demanding step in the entire reaction sequence (+66 to +119 kJ/mol, depending on n), which is related to our result obtained for the Schrock cycle. Moreover, all of the following hydrogenation steps are energetically downhill, and only the last step of the cycle, the desorption of NH3, is endothermic again. It should not be overlooked, however, that some details of this pathway also fundamentally differ from the Schrock cycle. Most conspicuosly, the two nitrogen atoms of the coordinated N2 molecule are hydrogenated in an alternating fashion, thus exluding formation of the hydrazidium (NNH3−) species, which cleaves the NN bond in the Schrock and Chatt cycles. In contrast, NN splitting occurs at the level of a hydrazinium (H2N-NH3+) species, which in turn, does not exist in the two synthetic systems. Thus, the above-mentioned synergism between the NN bond weakening and metal–N bond strengthening does not appear to apply for the enzymatic pathway. In particular, no metal–nitrido species is involved, which plays a central role in the two artificial systems. This appears to be connected with the fact that an iron–N triple bond necessarily is connected with a high-valent iron species, which may not accessible to the iron centers of the FeMoco.83
Quantum-chemical calculations of the Schrock cycle and the enzymatic pathway of ammonia synthesis on the FeMoco have also been performed by other groups.29-31 Cao et al.31 have applied DFT both to the biological and the synthetic system. With respect to the FeMoco, they postulate the binding of N2 to the molybdenum center. Then a sequence of protonation and reduction reactions is considered. The protonation steps are explicitly calculated with respect to the deprotonation of the weak acid NH4+ and the reduction steps with respect to the oxidation of a reduced cubance cluster, [Fe4S4(SEt)]2−. The authors thereby arrive at an energy profile for the total conversion of one N2 to ammonia, which in comparison with the experimentally determined energetics of nitrogenase (vide supra and ref.82), appears very exothermic (−18.5 eV = −426.6 kcal/mol/cycle). In their treatment of the Schrock system, the same authors consider a model of the Mo(III) HIPTN3N complex 3, with the HIPT residues being replaced by phenyl groups. On the basis of this structure, all intermediates of the Schrock cycle (N2, NNH+, …, NH3) are treated with DFT/BLYP. Again, the overall energy profile is found to be strongly exothermic (−16.1 eV = −371.3 kcal/mol for one turnover), which mainly derives from a strong exothermicity of the reduction steps. In contrast, all protonations are markedly endothermic (up to +3 eV = 69.2 kcal/mol), which would render these reaction steps difficult to achieve thermally.
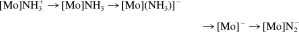
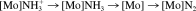
([Mo] = Mo(HIPTN3N)). The authors conclude that path 1 applies for strong reductants, whereas path 2 applies for weaker reductants (where reduction of the ammine complex cannot be achieved). Path 2 corresponds to the Schrock cycle (Figs. 5 and 6), whereas the practical relevance of path 1 to a catalytic ammonia synthesis has yet to be demonstrated. The authors further consider the first protonation/reduction of the N2 complex, leading to the [Mo]NNH intermediate. Based on the presently available computational data, an initial reduction of the N2 complex by Cp*2Cr (prior to protonation) can be excluded, in agreement with our theoretical results (vide supra). In addition, the authors consider an initial protonation of the triamidoamine ligand followed by reduction and subsequent proton transfer to the coordinated N2 group. They arrive at the conclusion that this alternative mechanism would provide a viable route for the first protonation/reduction step in the Schrock cycle. This may also apply to other protonation reactions of this system. After three protonations and two reductions, the [Mo]NNH3+ complex is formed. Although this intermediate is stable, it cleaves the NN bond after one additional electron transfer. This reaction is found to be strongly exothermic, and to occur spontaneously, in agreement with our theoretical findings.42, 78 Finally, it should be mentioned that Graham et al.85 have presented a comparison between DFT and coupled-cluster results at a three-coordinate molybdenum fragment giving dinuclear N2 complexes.
In contrast to Hinneman and Nørskov's quantum-chemical treatment of enzymatic ammonia synthesis, which involves an end-on coordination of N2 and leaves the cofactor intact, other groups postulate an opening of the cofactor to bind and/or transform N2. Kästner and Blöchl, thereby predict an end-on bridging coordination of N2 between two iron atoms of the FeMoco, which, after two combined protonation/reductions, leads to cis μ-1,2 bound diazene.30 We have termed this reaction mode “symmetric pathway” of ammonia synthesis, in contrast to the “asymmetric pathway” involving an initial end-on terminal coordination of N2.86 The former pathway is further considered in the next section.
End-On Bridging Coordination
The end-on bridging mode of N2 is considered on the basis of the three dinuclear titanium complexes 4a, 4b, and 5 (Scheme 1).87 They contain dinitrogen in a linear μ-1,2 geometry but have different sets of terminal ligands. Complexes 4a and 4b have the formula [{(η5-C5Me5)Ti(η6-C5H4CR2)}2(μ-η1:η1-N2)], R = p-tol (4a) and CR2 = adamantyl (4b), and exhibit a mixed cp*/fulvene ligation. With NN bond lengths of 1.160 Å they can be considered as moderately activated. The complex [{(Me3Si)2NTiCl(TMEDA)}2(μ-η1:η1-N2)] (2; TMEDA = tetramethylethylenediamine), on the other hand, exhibits a mixed amine/amide/chloride set of coligands and has an NN bond length of 1.29 Å, indicating a significantly higher activation of coordinated N2 than present in compounds 4a and 4b.
This picture is supported by vibrational spectroscopy. Resonance Raman studies performed on 4a and4b revealed NN stretching frequencies of 1749 and 1755 cm−1, respectively. These values are by more than 500 cm−1 lower than the NN stretch of free N2 (2331 cm−1),88 but, nevertheless, at the high end compared to other dinuclear end-on or side-on dinitrogen complexes of the early transition metals. In the case of 5, the NN stretching frequency was found at 1284 cm−1, about 500 cm−1 lower compared to 4a and4b and more than 1000 cm−1 lower in comparison to free N2. In conjunction with its large NN bond length, complex 2 thus can be described as strongly activated. This, however, would mean that the activation of N2 is higher in compound 2, formally a Ti2+–Ti2+ species, than in compounds 4a and 4b, formally Ti1+–Ti1+ complexes, which at first sight appeared difficult to understand.
This problem has been approached by employing DFT calculations on models IV and V of 4a/b and 5, respectively (Fig. 7). Model IV is oriented such that the x-axis is directed along the NN vector and the y-axis along the fulvene/cyclopentadienyl ligands. Figure 7 (left) shows contour plots of important molecular orbitals of IV. The HOMO of IV represents a bonding combination between the πz* orbital of dinitrogen and the metal dxz orbitals, forming a metal–dinitrogen π bond; this orbital has nearly equal contributions from the nitrogen p orbitals and the d orbitals of titanium. The LUMO of IV is the bonding combination of the N2 πy* orbital with the metal dxy orbital; the corresponding orbital has 19% metal and 40% nitrogen character. As only one π* orbital of the dinitrogen ligand is occupied, the N2 ligand is formally reduced by the Ti(I) centers of IV to an N22− oxidation state. However, in view of the fact that the HOMO πz_* dxz of IV has about 50% metal and 50% dinitrogen character, the dinitrogen ligand is more appropriately described as N2−. It should be noted that this description is also approximate; employing a natural population analysis (NPA), for example, a charge of −0.24 is obtained. Nevertheless, the N2− description corresponds quite well with the observed NN bond length and stretching frequency; the reasons for this finding are discussed below.
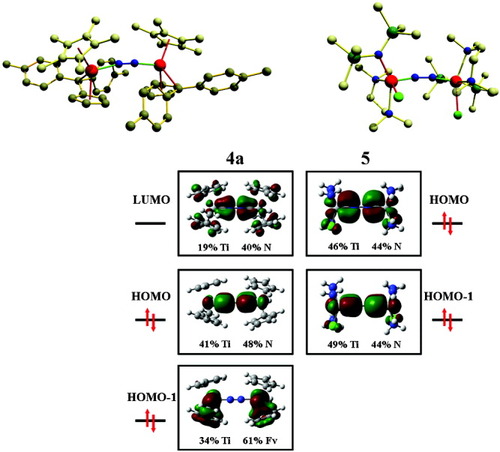
Contour plots of important molecular orbitals of 4a and 5 along with molecular structures.
To conclude, every Ti+ center donates one electron to the bridging dinitrogen ligand. The remaining two electrons of each metal center are located in two sets of dz2 orbitals (in-phase and out-of-phase combinations), both of which interact in a bonding fashion with fulvene π* orbitals to form two dz2_Fv orbitals. Both MOs have 61% fulvene character, indicative of a significant backbonding from the metals to these terminal ligands.
Model V is also oriented such that the x-axis is along the NN vector; the y-axis lies in the paper plane, between the amino and amido ligand on the one and the amido and chloro ligand on the other side of the dinuclear complex. The π* orbitals of the dinitrogen ligand (πz* and πy*) form the two dinitrogen–metal π bonding combinations πz*_dxz and πy*_dxy, respectively (Fig. 7, right). In the case of V, both of these orbitals are occupied, forming HOMO and HOMO-1. The dinitrogen ligand of 2 is therefore formally reduced by its two Ti(II) centers to a −4 charge state. Again, the corresponding molecular orbitals have about equal contributions from the dinitrogen p and metal d-orbitals such that the dinitrogen ligand would better be described as N22−. This description would coincide quite well with the observed NN bond length and stretching frequency of 5. However, the NPA charge of 5 again is much lower (−0.80).
In Figure 7 the orbitals of IV and V are arranged in a way that clarifies the relationship between the electronic structures of 4a/b and 5. Evidently, the dinitrogen part of the frontier orbitals is very similar and the major difference between the two systems lies in the fact that both π* orbitals of dinitrogen are occupied in 5, whereas for 4a and 4b one dinitrogen π* orbital (the HOMO) is occupied and the other one (the LUMO) is empty. This difference is due to the fact that the two Ti+ centers of 4a and 4b donate two electrons each to the terminal fulvene groups, making these ligands dinegative. The remaining electrons of the metal centers populate one of the dinitrogen π* orbitals, transmitting a moderate activation to this ligand. The titanium centers of 5, in contrast, are coordinated to a set of terminal donor ligands. The two electrons of each Ti2+center are therefore transferred to dinitrogen, rendering this ligand strongly activated. These investigations thus demonstrate that the set of coligands can have a decisive influence on the properties of the bridging dinitrogen ligand.
The dominant reactivity of strongly activated, end-on terminally bridged dinitrogen complexes of the early transition metal is protonation, primarily leading to coordinated diazene and hydrazine (“symmetric pathway,” vide supra). In some of these systems, the NN bond splits at the hydrazine stage, giving ammonia.3 If enough electrons are available, the NN bond can also be cleaved at the dinitrogen stage, without the assistance of protons (vide infra). The symmetric pathway proceeding via coordinated diazene has, in particular, been promoted by Sellmann and coworkers as a viable scenario for the nitrogenase reaction, which was assumed to proceed in an open-cage mechanism.25-27 We have characterized two Sellmann-type, trans-μ-1,2 diazene bridged dinuclear Fe(II) complexes with thioloate/thioether ligation using infrared and Raman spectroscopies, coupled to SCF-Xa calculations, and have discussed the further protonation/reduction of these systems along the symmetric pathway.86 More recently, in-depth theoretical treatments of these systems and the corresponding reduction pathway have been performed by Reiher and coworkers.89
In Kästner and Blöchl's open cage nitrogenase pathway (vide supra), diazene is protonated and reduced to give coordinated HNNH2, which rearranges to a μ-1,1 (end-on) bridging geometry and after further H+/e− transfer cleaves the NN bond, generating NH3 and bridging imide. The latter species is further reduced and protonated to give a second molecule of ammonia. Huniar and Ahlrichs' treatment of the nitrogenase reaction is also based on an open cage scenario. In contrast to Kästner and Blöchl, however, these authors have explicitly considered the possible involvement of a central nitrido ligand of the FeMoco in a catalytic cycle of enzymatic ammonia synthesis.29 They argue against the ESEEM/ENDOR results, which were taken as evidence that a central nitrogen ligand would not be involved in the catalytic turnover (vide supra).12 During most stages of their mechanism, the cage of the FeMoco is open; that is, one of the bonds to the μ2 sulfido ligands is broken. The latest results regarding the nature of the central X-ligand of the FeMoco,13 however, would cast doubts on the relevance of the derived mechanistic pathway to the nitrogenase reaction.
Side-On Bridging Coordination
The side-on bridging mode of dinitrogen is less common than its end-on counterpart and in conjunction with early transition-metal centers produces highly activated systems with NN bond lengths of about 1.5 Å. It should be noted that side-on dinitrogen bridged complexes also exist for some actinides and lanthanides,90-94 where, however, the activation of the dinitrogen ligand only ranges from zero to moderate. In this class of compounds the major bonding interactions between the dinitrogen ligand and the metal centers are mediated by metal f orbitals.95-97
Here, we consider the side-on N2 bridged Zr complex ([P2N2]Zr)2(μ-η2:η2-N2) (6; P2N2 = PhP(CH2SiMe2NSiMe2CH2)2 PPh) exhibiting an NN bond length of 1.43 Å (cf. Fig. 2).45 The vibrational properties of this system were investigated by Resonance Raman and infrared spectroscopy coupled to DFT calculations, allowing to identify the NN stretching frequency of 6 at 775 cm−1 (15N2 isotope shift of −22 cm−1).98 Importantly, this value is about 1500 cm−1 lower in energy than the NN stretch of free N2 and still 500 cm−1 lower in energy than that found for the strongly activated titanium complex 5. Complex 6 was therefore denoted to be highly activated.
To obtain more information on the electronic structure of 6, DFT was employed. It was found that in 6 both π* orbitals strongly interact with zirconium d-orbitals, forming a δ and a highly covalent σ bond. The corresponding molecular orbitals, πv*_dyz and πh*_dxy (v = vertical and h = horizontal with respect to the plane of the Zr2N2 unit), form the HOMO and HOMO-5 of 6, respectively (see Fig. 8). Importantly, these orbitals have predominantly dinitrogen character (up to 65%). Formally both π* orbitals of dinitrogen are thus occupied, corresponding to an N24− configuration.
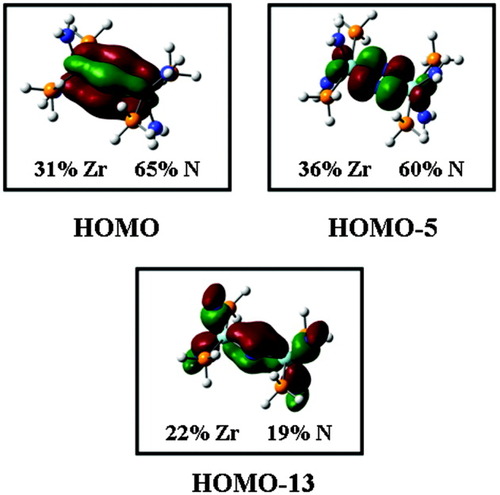
Contour plots of the HOMO, HOMO-5, and HOMO-13 of 6.
The actual charge on the N2 ligand is lower than indicated by this value as the π* orbitals are delocalized over the metal centers. Furthermore, the occupied π orbitals of the dinitrogen ligand also interact with empty zirconium d orbitals. The vertical π orbital, for example, interacts with zirconium d orbitals to form a π bond (see Fig. 8). Importantly, this leads to a transfer of charge from dinitrogen to the zirconium atoms and thus further decreases the charge of the dinitrogen ligand. Correspondingly NPA gives a charge of only −1.82 for the dinitrogen ligand, which is more compatible with an N22− description. In contrast, the NN bond lengths as well as the NN stretching frequency seem to indicate that this complex is at the hydrazido(4-) (N24−) stage. This apparent discrepancy is resolved by noting that both the transfer of electron density from the metal atoms to the π* orbitals of dinitrogen and the donation from the π orbitals of the dinitrogen to the metal atoms act to weaken the NN bond, causing an increase of the NN distance and a decrease of the NN stretching frequency.
The large NN distance of 6 together with the population of both π* orbitals of dinitrogen do not only indicate that the complex is highly activated, but also suggest that total cleavage of the NN bond should be feasible from this stage. This would require that the σ* orbital, which is unoccupied in 6, is populated with two electrons, a process that is considered in the next section. It should also be mentioned that 6 reacts with H2, forming a μ-η2:η2 NNH μ-hydrido complex under cleavage of the HH bond.45 This process has been treated by DFT calculations.99 Moreover, a side-on dinitrogen coordinated zirconium complex has been shown to react with H2 to ammonia.100
Bis(μ-nitrido) Complex
NN cleavage of side-on coordinated dinitrogen was observed for a dinuclear vanadium system, leading to the bis(μ-nitrido) VV2 complex [V(N{N″}2)(μ-N)] (7; (N{N″}2)2− = ({Me3Si}N {CH2CH2N(SiMe3)}2)2−; cf. Fig. 2).46 Employing DFT, a mechanism for this reaction was derived.47 Thereby, it was found that the dinitrogen molecule first coordinates side-on to a mononuclear metal fragment, followed by coordination to a second metal fragment. In the course of these reactions three electrons are transferred from each metal center to the dinitrogen unit, leading to splitting of the NN bond. The calculations further revealed that the NN cleavage process is highly exothermic and occurs without an activation barrier. Orbital analysis of the resulting bis(μ-nitrido) complex 7 clearly shows that the σ* orbital of the former dinitrogen unit, which is delocalized over the d-orbitals of the two metal fragments, now is occupied with two electrons (see Fig. 9).101
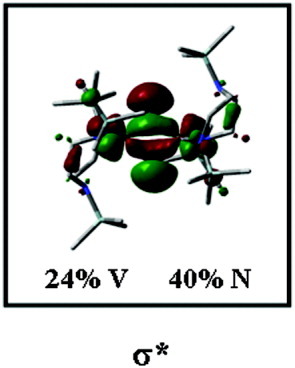
Contour plots of the occupied σ* orbital of 7.
In dealing with the electronic structure and the spectroscopic properties of complex 7 we were also interested in a correlation between its vibrational structure and that of the parent side-on dinitrogen bridged dimetal center. Eigenvectors of in-plane vibrations of the side-on and bis(μ-nitrido) cores of complex 6 and 7, respectively, are presented in Figure 10. The highest energy vibration of both units is a totally symmetric breathing mode which in both cases is dominated by motions along the NN axis. For the side-on dinitrogen bridged complex 6, this mode corresponds to the NN stretch, which has been observed at 775 cm−1 (vide supra).98 For the diamond core of 7, a corresponding vibration is theoretically predicted at ∼900 cm−1. This mode could be identified in the Raman spectrum at 825 cm−1, exhibiting a 15N isotope shift of 22 cm−1.101 This result is at first glance surprising, as it would imply that “νNN” in a complex were the NN bond is clearly broken is higher than in a species where the NN bond is elongated but still intact. Nevertheless, this result becomes understandable by noting that the “νNN” vibration of 7, in fact, corresponds to a breathing vibration of the metal–nitrido core. Due to the highly covalent character of the VN bonds in 7 this vibration is increased in energy with respect to the NN stretch of 6. This illustrates a common trend present in dinitrogen chemistry, that is, that a decrease in NN bond order generally is associated with an increase of metal–nitrogen bond order (vide supra).
Eigenvectors of the five in-plane normal modes of 6 (left) and 7 (right).
It should be mentioned that NN splitting of coordinated N2 is not restricted to side-on coordinated systems as, for example, an end-on N2 bridged dinuclear molybdenum complex has been synthesized, which, upon warming to 30°C, generates two Mo(VI) nitrido species, cleaving the NN bond.102 DFT calculations revealed that the activation barrier for this rate-determining step is substantial (about 21–41 kcal mol−1).103 These calculations further predicted that the NN splitting process is exothermic by about 3–27 kcal mol−1. The NN cleavage of heteronuclear, NN bridged transition metal dimers has also been treated computationally.104
Side-On End-On Coordination
Bridging coordination of dinitrogen in a side-on fashion to one metal and in an end-on coordination to another was observed for the dinuclear tantalum complex ([NPN]Ta(μ-H))2(μ-η1:η2-N2) (8; [NPN] = (PhNSiMe2CH2)2PPh), which additionally contains two μ-hydrido ligands (cf. Scheme 2).48, 49 Although this bonding mode has not explicitly been considered as a model for the nitrogenase, we discuss it in the present review as it has been shown to promote adduct formation at Nβ with various electrophiles,50-53 a reactivity that is related to protonation and thus of relevance to the nitrogenase problem as well.
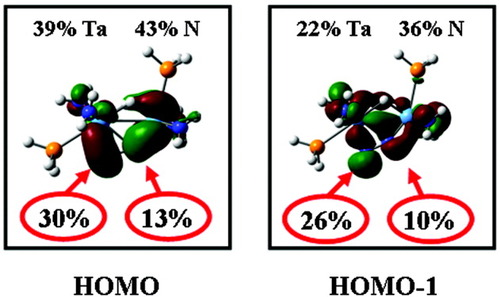
Based on its NN bond length (1.32 Å) and N–N stretching frequency (1165 cm−1; 15N2 isotope shift of −37 cm−1),105 the activation of the dinitrogen ligand in complex 8 is intermediate between that displayed by the side-on complex 6 and the end-on N2 complex 5, actually closer to the latter than to the former one. Both π* orbitals of the dinitrogen ligand strongly interact with the tantalum d orbitals, forming the HOMO and HOMO-1, which have about equal dinitrogen and metal contributions (see Fig. 11). Moreover, the total charge calculated for the dinitrogen ligand (−1.08) is found to be almost equally distributed over both nitrogens. On the other hand, both π* orbitals of the dinitrogen unit have higher contributions on the terminal nitrogen atom than on the bridging one, whereas the π orbitals, which also interact with the metals, have higher contributions on the bridging nitrogen atom than on the terminal one. We therefore assume that the reactivity towards electrophilic is governed by the dominant contributions of the terminal nitrogen atom in the π* orbitals of the coordinated N2 ligand, which would explain the experimental observation that electrophiles like AlMe3, GaMe3, and B(C6F5)3 preferentially react with complex 8 at Nβ. The corresponding Lewis acid-base adducts have been investigated spectroscopically and theoretically as well.53
Contour plots of the HOMO and HOMO-1 of 8.
Reaction of 8 with trimethylsilane, on the other hand, leads to addition of the silane across the TaN bond. After elimination of H2 the NN bond is cleaved, generating a μ-nitrido μ-imido structure, which is related to the diamond core of 7 and adds another silane.51 We have theoretically simulated this reaction cascade and identified the transition state in the unprecedented cleavage of the functionalized, μ-η1:η2 coordinated N2 unit.106
Summary and Conclusions
In the preceding sections the electronic structures and spectroscopic properties of dinitrogen complexes of transition metal have been considered. In the Fe(II) and Mo/W complexes, an end-on terminal coordination of N2 is found, which, in the case of moderate activation allows the protonation of N2, ultimately leading to NH3. The catalytic ammonia synthesis occuring in the Schrock cycle has been treated theoretically and understood on a molecular level. In the early transition-metal systems dinitrogen always coordinates in a bridging mode, albeit in different geometries (end-on terminal, end-on bridging, side-on bridging, and side-on end-on bridging). Of particular interest with respect to the reactivity of all of these dinitrogen complexes is the extent of activation exhibited by the coordinated dinitrogen ligands. Quantitative measures of this property are provided by NN bond lengths obtained from X-ray structure determinations, NN stretching frequencies obtained from Resonance Raman or infrared spectroscopies, and charges of the dinitrogen ligand obtained from quantum chemical calculations.
Dinitrogen activation in transition-metal complexes generally varies from weak to high. A particularly useful correlation with the activation of dinitrogen can be obtained from a consideration of NN stretching frequencies. As evident from Figure 2, the frequency differences between none, moderate, strong, and high activation are each in the order of about 500 cm−1, allowing to spectroscopically distinguish these four activation regimes. It should be noted that this correlation breaks down for the described bis μ-nitrido complex, which exhibits a cleaved NN bond (the reasons for this finding have been discussed above), and that weakly activated complexes have NN stretching frequencies between those of moderately activated systems and free N2.
Figure 12 shows a diagram where the three most important characteristics of dinitrogen ligands (NN distance, NN stretching frequency and NPA charge) are combined; Table 1 summarizes these values for 1–8. As discussed above, the NN stretching frequency decreases from 2331 cm−1 in free N2 to 775 cm−1 in the highly activated complex 6, which contains a side-on bridged dinitrogen ligand. The NN bond distance of 1.097107 found for gaseous N2 elongates with the degree of activation to about 1.15 (moderate), 1.30 (strong), and 1.4–1.5 Å (high); for weakly activated systems no significant elongation of N2 is found. Based on the NN stretching frequencies and bond lengths, the moderate activation is most appropriately associated with a N2− ligand; the same applies to N22− for strong and N24− for high activation. Notably, the charges of the various dinitrogen ligands derived by NPA are considerably lower than implied by these integer values. The highly activated complex 6, for example, formally having an N24− ligand was calculated to have a charge of only −1.82 on the N2 unit. The reasons for these discrepancies have been considered. Nevertheless, the general trend that the negative charge of the dinitrogen unit monotonously increases with the extent of activation also holds for the NPA charges (see also Table 1).
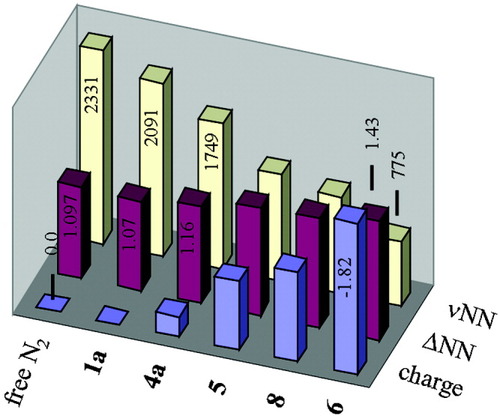
NPA charges, NN distances and NN stretching frequencies of N2 in complexes 1a, 4a, 5, 6, and 8.
| Compond | ΔNN in Å | νNN in cm−1 | NPA charge of N2 |
|---|---|---|---|
| free N2 | 1.097107 | 233188 | — |
| 1a | 1.0755 | 209162 | +0.0165 |
| 2 | 1.12a | 2033/198074 | −0.1370 |
| 3 | 1.0639 | 199039 | −0.2378 |
| 4a | 1.1643 | 174987 | −0.2487 |
| 5 | 1.2944 | 128487 | −0.8087 |
| 6 | 1.4345 | 77598 | −1.8298 |
| 7 | 2.5046 | 825101 | — |
| 8 | 1.3249 | 1165105 | −1.08105 |
- a Uchida, T; Uchida, Y; Hidai M; Kodama, T. Acta Crystallogr. 1975, B31, 1197.
Importantly, the activation determined by these methods allows for different reactivities: (1) protonation, (2) functionalization, and (3) cleavage. Within the early transition-metal complexes, NN cleavage appears to be most closely associated with the side-on mode of dinitrogen. Purely electronic splitting of the NN bond, however, was also observed for a moderately activated end-on bridged Mo(III) complex, indicating that it does not necessarily require a high activation of the N2 unit. Furthermore, NN cleavage is always possible after protonation or functionalization of N2 unit, and thus can occur in all binding modes. Protonation and functionalization are two aspects of the reactivity of coordinated dinitrogen towards electrophiles. They require a corresponding accumulation of negative charge on the N2 unit, which is transmitted to this ligand by the coordinated transition metal fragments.
With respect to a selective reactivity towards electrophiles at the terminal N-atom Nβ, an intrinsic “polarization” of the N2 ligand is advantageous. This can potentially arise in all asymmetric coordination modes like end-on terminal or end-on side-on bridging. Importantly, the end-on terminal coordination of N2 to mononuclear transition-metal centers has enabled the first (and, to date, only existing) catalytic conversion of N2 to ammonia proceeding under ambient conditions and in a sequence of well-defined steps (Schrock cycle). Spectroscopic investigations and DFT calculations on this system indicate that it contains a moderately activated dinitrogen ligand. The same applies to molybdenum and tungsten dinitrogen systems with phosphine coligands that mediate the stoichiometric conversion of N2 to ammonia (Chatt cycle). In the side-on end-on complex 8, the dominant contributions of the terminal nitrogen atom in the π* ligands of the coordinated N2 ligand similarly act to enhance its reactivity toward electrophilic attack at the terminal N-atom, and therefore, in conjunction with the high activation transmitted by the side-on coordination to an early transition metal, render this system suitable for the functionalization of N2.
Coming back to starting point, the nitrogenase problem, it certainly can be stated that density functional theory has greatly contributed to develop plausible mechanistic scenarios for the conversion of N2 to ammonia at the iron–molybdenum cofactor. There appears to be a growing consensus that dinitrogen is activated and reduced at an iron site of the FeMoco. The message from inorganic model chemistry is that, to be accessible to protonation, the dinitrogen ligand must at least be moderately activated. The spectacular successes in model chemistry and theoretical simulation of the biological process notwithstanding it has to be stressed, however, that up to now it is unclear how this is achieved by the FeMoco, as the activation of N2 in synthetic (at least, six-coordinate) iron(II) systems is always weak (vide supra). Efforts are underway to synthetically approach this problem by low-coordinate iron complexes.108, 109
Acknowledgements
F.T. thanks his students, his collaborators (M.D. Fryzuk, F.G.N. Cloke, R. Beckhaus), as well as their students involved in the projects covered by this review for their excellent contributions.




