Estimating intergenerational schooling mobility on censored samples: consequences and remedies
Abstract
In this paper we estimate the impact of parental schooling on child schooling, focus on the problem that children who are still in school constitute censored observations, and evaluate three solutions to it: replacement of observed with expected years of schooling, maximum likelihood approach, and elimination of all school-aged children. Using intergenerational data from the Wisconsin Longitudinal Study we test how the three correction methods deal with censored observations. The one that treats parental expectations as if they were realizations seems to fix the censoring problem quite well. Copyright © 2009 John Wiley & Sons, Ltd.
1. INTRODUCTION
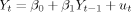 (1)
(1)In this paper we let Y be years of schooling, and focus on the problem that (some) children may still be in school at the time of data collection, which goes under the name of the censoring problem. We consider this a serious problem for three reasons. First, we cannot ignore censoring empirically because, if we do, least squares regression on censored samples would give us intergenerational persistency estimates that are too low. Second, we observe that censoring is a widely spread phenomenon. Of the recent studies that (aim to) estimate the causal effect of parents' schooling on children's schooling, almost all make use of samples with incomplete information on adult children. Among these studies are Behrman and Rosenzweig (2002, 2005); Plug (2004); Chevalier (2004); Black et al. (2005); Carneiro et al. (2007); Oreopoulos et al. (2006); and Maurin and McNally (2008). Third, the solutions offered to handle censored samples rely on assumptions that may not hold in practice, resulting in intergenerational mobility estimates that are biased.
Of course, the natural solution to the censoring problem is patience. If researchers were patient and could wait until all children in the censored sample finished their schooling to collect their data, we would not need to worry about censoring. Unfortunately, many researchers tend to be impatient. They are, presumably, more interested in the degree of intergenerational mobility among current generations than previous generations and are therefore willing to estimate parental schooling effects on censored samples using correction methods that do not always work.2 Since the latter approach certainly merits serious consideration, it is important to know (more) about how applied correction methods deal with censored observations.
One procedure for testing how effective available correction methods are in treating censored schooling observations is to apply these censoring solutions to one particular dataset. This is what we do in this paper. We focus our attention on three correction methods that are currently in use: maximum likelihood approach, replacement of observed with expected years of schooling, and elimination of all school-aged children. We apply these three different methods to one particular dataset: the most recent version of the Wisconsin Longitudinal Study (henceforth often WLS).
The WLS collects information on a large group of students who graduated from Wisconsin high schools in 1957. In 1975, 1992 and 2004 the same students were contacted again and asked about their children's schooling. The questions cover three different school stages. In 1975 most children are in school: the sample includes information on expected schooling. In 1992 some of these children have not yet completed their schooling: the sample is a censored sample. In 2004 all children have left school: the sample contains information on completed schooling.
Our contributions are twofold. First, we present new estimates of the intergenerational mobility of schooling. With updated 2004 samples, we are able to estimate the ultimate mobility models in which censored observations are absent. Second, we examine the validity of the different solutions to deal with the problem of censored data. With the 1975 and 1992 samples, we estimate the impact of parental schooling on children's schooling, applying the various procedures to correct for censored observations and use the difference between ultimate and corrected mobility estimates as a validity indicator.
This paper continues as follows. Section 2 models the intergenerational mobility of schooling, focuses on the problem that children who are still in school generate censored observations, and provides some intuition on the various solutions to it. Section 3 provides a brief description of the WLS. Section 4 presents and compares the parameter estimates. Section 5 evaluates the correction methods and presents a number of robustness tests. Section 6 concludes.
2. MOBILITY MODELS USING CENSORED DATA
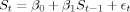 (2)
(2)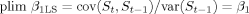 (3)
(3) such that
such that
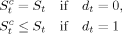 (4)
(4)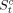 represents the child's years of schooling observed in the censored sample, and dt denotes whether observations are censored (dt = 1) or not (dt = 0). If we would ignore censoring, and treat the children's observed years of schooling as their completed years, the estimation of
represents the child's years of schooling observed in the censored sample, and dt denotes whether observations are censored (dt = 1) or not (dt = 0). If we would ignore censoring, and treat the children's observed years of schooling as their completed years, the estimation of 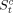 on St−1 using ordinary least squares gives us a β1 parameter that is too low. The intuition is as follows. We know that more schooled children (with more schooled parents) are more likely to be censored, and we know that observed school years are always smaller than or equal to the completed school years. Taken together, these observations imply that observed years of schooling covary less with parental years of schooling
on St−1 using ordinary least squares gives us a β1 parameter that is too low. The intuition is as follows. We know that more schooled children (with more schooled parents) are more likely to be censored, and we know that observed school years are always smaller than or equal to the completed school years. Taken together, these observations imply that observed years of schooling covary less with parental years of schooling 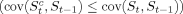 . When we take a censored sample and apply least squares to estimate the child–parent equation
. When we take a censored sample and apply least squares to estimate the child–parent equation
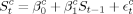 (5)
(5)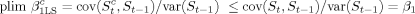 (6)
(6)Recent work on intergenerational mobility of schooling has taken various approaches to tackle the censoring problem: replacement of observed with expected years of schooling, maximum likelihood approach, elimination of all school-aged children, and intermediate school outcomes. Below we shortly discuss these different approaches.
2.1. Inserting Parental Expectations for Children Still in School
Behrman and Rosenzweig (2002) employ a mail survey, issued in 1994, to collect information on the families of identical twins born between 1936 and 1955, all drawn from the Minnesota Twin Registry (MTR). The survey contains information on the schooling of the twins, their parents and children, including information on expected schooling for children who had not yet completed their schooling; this is the case for more than 50% of their sample.3
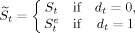 (7)
(7)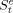 represents the school level the parent expects her child to complete. Suppose we model parental expectations about their children's completed years of schooling as follows:
represents the school level the parent expects her child to complete. Suppose we model parental expectations about their children's completed years of schooling as follows:
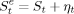 (8)
(8)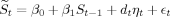 (9)
(9)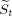 on St−1 gives us the following probability limit of the slope coefficient:
on St−1 gives us the following probability limit of the slope coefficient:
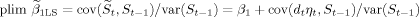 (10)
(10)Only if cov(dtηt, St−1) equals 0 does Behrman and Rosenzweig's original solution produce a consistent estimate of β1. If not, the validity of the method will depend on how much the prediction error correlates with parental education and on the number of censored observations. Whether or not cov(dtηt, St−1) equals 0 is an empirical issue, which we will put to the test later in this paper.
2.2. A Censored Regression Model
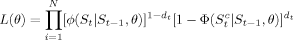 (11)
(11)2.3. Eliminating All School-Aged Children
Black et al. (2005) estimate the effect of parental schooling on child schooling using a reform in compulsory schooling in Norway during the 1960s and early 1970s to draw causal inferences. Because Black et al. focus on relatively young parents—only those between 42 and 53 years old are affected by the reform—many children have not yet finished their schooling by the time they appear in their sample. The authors take account of the censoring problem by eliminating all children younger than age 25.
Many of these children have parents who were very young when they were born. Because the parents' age at birth is likely related to observed and unobserved parental characteristics, censoring is no longer random. This means that Black et al. run the risk of introducing sample selection bias when they reduce their sample. With this form of non-random censoring, it is possible that their parental schooling effects estimated on the reduced sample in which younger parents are overrepresented are very different from the same parental schooling effects estimated on the full (but non-existing) sample without censored observations.
2.4. Intermediate School and Human Capital Outcomes
An alternative method to deal with censored observations is to work with multi-generational samples of parents with school-going children and consider intermediate outcomes of children that are both realized and available, such as birth weight (Currie and Moretti, 2003), test scores or grade repetition (Carneiro et al., 2007; Oreopoulos et al., 2006; Maurin and McNally, 2008). Without information on realized school outcomes of children, however, we do not really know how informative these intermediate outcomes are when it comes to assessing intergenerational schooling effects.
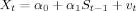 (12)
(12)Finding an intermediate outcome that fulfills these conditions is not easy. In fact, to the extent that similar performing children are treated differently in ways related to their parents' schooling, we may question whether most of the intermediate outcomes that are in use are informative about intergenerational schooling effects. If, for example, higher schooled parents find it easier to provide additional tutoring to young children who repeat a grade or receive low test scores than lower schooled parents, it is possible that the corresponding intermediate schooling estimates will not capture the parental treatment effects that children receive beyond their compulsory schooling years, and therefore miss the true impact of parental schooling on child schooling (Currie and Thomas, 2001; Erikson et al., 2005).
While we think it is useful to actually test how informative intermediate schooling outcomes are, we must leave this for future research. The present dataset does not contain information on birth weight, test scores or grade repetition.
3. DATA
Our main analysis employs the WLS of 10,317 randomly sampled graduates from Wisconsin high schools in 1957. After the initial wave of data collection, primary respondents were re-interviewed in 1975, 1992 and 2004. Together with their parents' interview of 1964, these waves provide information on, among others, educational attainment of the original graduates, their parents and children. The original sample is broadly representative for white men and women, who have completed at least 12 years of schooling. For more detailed information on the WLS we refer to Wollmering (2007) and references therein.
In this paper we use all three waves and exploit those questions that are targeted at the educational attainment of the respondents' children. In 1975 children are still in school and parents are asked to express their expectations about their child's schooling. In particular, parents are asked how far they think their children will go in school.5 In 1992 most children left school, but some children were still in school. Information is collected on the highest grade of regular school ever attended; whether the highest grade is completed or not; and whether the highest grade is obtained during the survey year. In addition, respondents are asked whether their child completed the grade or year and whether their child attended a regular school (elementary, secondary, college and university) in the past 12 months. In 2004 all children finished their education, and respondents are asked to update their information regarding their children's completed schooling.
Our sample includes married respondents with children, who are observed in the three years 1975, 1992 and 2004. In 2004 information is gathered from 7265 of the 10,317 original respondents, of whom 5660 are married and have children in 1992. Of these 5660 respondents, 316 drop out because relevant schooling information for themselves or their spouses is missing. In 1975 respondents are asked to express their school expectations for only one of their children. This child is randomly selected by the interviewer. Of the randomly selected children, we select only those for whom information is collected in 1975, 1992 and 2004. This leaves us with a final sample consisting of 4097 parents and own birth children.6 Note that the selected children are on average 10 years old when the parent forms expectations regarding the child's schooling. Expectations are elicited from the originally sampled graduates, which include both men and women, so the expectations are in some cases formed by the father and in other cases by the mother. Summary statistics appear in Table I.
| Mean | Std. Dev. | |
|---|---|---|
| Completed years of schooling (2004) | 14.50 | 2.30 |
| Observed years of schooling (1992) | 14.17 | 2.18 |
| Expected years of schooling (1975) | 14.78 | 1.93 |
| Years of schooling mother | 12.92 | 1.72 |
| Years of schooling father | 13.62 | 2.67 |
| Observation censored in 1992 | 0.22 | 0.41 |
| Gender (daughter) | 0.49 | 0.50 |
| Age (1992) | 26.92 | 3.97 |
| N | 4097 |
. RESULTS
Table II presents estimates that come from our child–parent schooling regressions run on uncensored and censored samples of own birth children and their parents. All regressions include individual controls for the child's age measured in years and gender. These parameters are not reported.
| Estimates without censoring | Estimates with censoring | Estimated differencesa | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
| Mother's schooling | 0.45 | 0.24 | 0.42 | 0.22 | − 0.03 | − 0.02 | |||
| 0.02*** | 0.02*** | 0.02*** | 0.02*** | 0.01*** | 0.01 | ||||
| Father's schooling | 0.35 | 0.27 | 0.32 | 0.25 | − 0.03 | − 0.02 | |||
| 0.01*** | 0.01*** | 0.01*** | 0.01*** | 0.01*** | 0.01*** | ||||
| N | 4,097 | 4,097 | |||||||
| Nc | 0 | 874 | |||||||
| Censored observations replaced with parental expectationsb | |||||||||
| Mother's schooling | 0.45 | 0.23 | − 0.00 | − 0.01 | |||||
| 0.02*** | 0.02*** | 0.01 | 0.01 | ||||||
| Father's schooling | 0.35 | 0.27 | 0.00 | 0.00 | |||||
| 0.01*** | 0.01*** | 0.01 | 0.01 | ||||||
| N | 4,097 | ||||||||
| Nc | 874 | ||||||||
| Censored regression model | |||||||||
| Mother's schooling | 0.53 | 0.30 | 0.08 | 0.05 | |||||
| 0.02*** | 0.03*** | 0.01*** | 0.01*** | ||||||
| Father's schooling | 0.39 | 0.30 | 0.04 | 0.03 | |||||
| 0.01*** | 0.02*** | 0.01*** | 0.01*** | ||||||
| N | 4,097 | ||||||||
| Nc | 874 | ||||||||
| Excluding all children younger than 25 | |||||||||
| Mother's schooling | 0.50 | 0.28 | 0.05 | 0.04 | |||||
| 0.03*** | 0.03*** | 0.02*** | 0.01*** | ||||||
| Father's schooling | 0.36 | 0.28 | 0.01 | 0.01 | |||||
| 0.02*** | 0.02*** | 0.01 | 0.01 | ||||||
| N | 2,990 | ||||||||
| Nc | 167 | ||||||||
- All regressions include additional controls or the child's age and gender.
- Standard errors are in italics; significant at: *10% level; **5% level; ***1% level.
- Nc is the number of censored observations.
- a Estimates come from previous school models using censored and uncensored samples where all coefficients vary by sample status. The interacted schooling estimates represent differences between mobility parameters. Insignificance suggests the absence of structural differences.
- b Parental expectations are expressed in levels. We convert level into years as follows: less than high school … 10; high school graduate … 12; technical and vocational education … 13; some college … 14; college graduate … 16; MA or MS degree … 18; law degree, MD, DDS, DVM degree … 19; PhD … 20.
In the first panel the first three columns report estimates using the completed school measures as recorded in the 2004 sample. These estimates will serve as the baseline throughout the paper. In columns (1) and (2) the mother's and father's schooling measures are included as separate regressors. The coefficients on maternal and paternal years of schooling are equal to 0.45 and 0.35, respectively. These estimates are fully in line with those commonly found in the literature (Haveman and Wolfe, 1995): more schooled parents have more schooled children, and more schooled mothers matter more than more schooled fathers, at least for the school outcomes of children. Note that the parental associations as estimated not only include the influence from the given parent but also the influence from the spouse, which is due to assortative mating and the ensuing correlation between the parents' schooling, or between everything else that correlates with schooling. In column (3) the mother's and father's schooling measures are therefore included simultaneously to control for assortative mating effects. We still find that more schooled parents get more schooled children, but that fathers and mothers now contribute equally to their offspring.
In the second three columns we estimate the same three equations using the observed school measures as recorded in the 1992 sample. With data that are partly censored we find, as expected, that all parental schooling estimates fall, but not by much. The last three columns, in which we express the difference between the child–parent estimates run on the censored and uncensored samples, indicate that the downward bias caused by the censoring is statistically significant and varies between 0.02 and 0.03.7
In the next three panels we report the estimates using alternative approaches to tackle the censoring problem: replacement of observed with expected years of schooling, maximum likelihood approach, and the elimination of all school-aged children. We find that the corrections do not affect our results qualitatively. In all three panels the estimates reported in columns (4), (5) and (6) show that more schooled parents get more schooled children and that mothers only matter more when parental schooling estimates include assortative mating effects. But we do find that most of the corrections affect our results statistically. When compared to the uncorrected regression results using the censored sample, all three approaches remove the downward bias and give us—as they should—higher persistency estimates. When compared to those estimates obtained using the ultimate uncensored sample, the estimated differences in columns (7), (8) and (9) are relatively small in magnitude. Of the three correction methods, we find that the maximum likelihood and elimination approaches lead to estimates that are a bit too high, at least in most specifications. With these two corrections, the medicine appears to be no better than the malady. The approach to treat parental expectations for young children as if they were realizations of completed schooling, however, works better. In fact, the replacement method fully eliminates the censoring bias, which we now precisely estimate at zero.
5. CAN WE TREAT EXPECTATIONS AS REALIZATIONS?
Our results in Table II suggest that parental expectations fix the censoring problem quite well. This is by no means a trivial result. After all, parents (in the WLS) form their expectations when their children are relatively young, about 10 to 15 years prior to school completion. In a recent paper Antonovics and Goldberger (2005, p. 1739) express their doubts regarding this particular correction method. We therefore perform additional robustness checks to see how sensitive the parental expectations solution is to a number of potential threats: the number of censored observations, prediction quality, and sample selection.
5.1. The Degree of Censoring
This is an expression we can actually test: least squares estimation of the regression of dtηt on parental schooling. To see whether our results are sensitive to the number of censored observations, we estimate the bias of the replacement method on samples where we gradually increase the number of censored observations. We do this by calculating how many children would still be in school if we had observed them some years before 1992. For example, if a mother, who reports in 1992 that her child, born in 1967, completed 15 years of schooling, were interviewed in 1984 we recode the same child as being censored, assuming he/she left school in 1988 (1967 + 6 + 15). In 1984 the same mother would have reported that her child had 11 years of schooling, assuming that children start school at age 6 and have uninterrupted school careers.
The first panel of Table III contains the estimates of the bias when using the replacement method, for increasing numbers of censored observations, with additional controls for age and gender of the child. Up to censoring percentages of 60, we find that all the bias estimates are statistically insignificant and virtually zero, confirming our baseline result that the replacement method yields consistent persistency estimates. Up to censoring percentages of 90, the bias is negative but small, and often statistically insignificant. The procedure to replace the censored observations with expectations is statistically rejected, but only at the margin. Only when the percentage of censored observations becomes very large does the corresponding method to adjust for censoring fail. The slopes are negative and statistically significant. Would we fully rely on parental predictions, the implication is that the corresponding intergenerational schooling estimates are biased downwards. The negative bias further suggests that expectations regress to the mean faster than realizations do.
| Samples with increasing number of censored observations | ||||||||
|---|---|---|---|---|---|---|---|---|
| 20–30% (1) | 30–40% (2) | 40–50% (3) | 50–60% (4) | 60–70% (5) | 70–80% (6) | 80–90% (7) | 100% (8) | |
| Censored observations replaced with parental expectations | ||||||||
| Mother's schooling | − 0.01 | − 0.02 | − 0.02 | − 0.02 | − 0.02 | − 0.03 | − 0.04 | − 0.05 |
| 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02** | |
| Father's schooling | 0.00 | − 0.01 | − 0.02 | − 0.02 | − 0.02 | − 0.03 | − 0.03 | − 0.04 |
| 0.01 | 0.01 | 0.01 | 0.01 | 0.01* | 0.01* | 0.01* | 0.02*** | |
| N | 4097 | 4097 | 4097 | 4097 | 4097 | 4097 | 4097 | 4097 |
| Nc | 874 | 1285 | 1712 | 2280 | 2859 | 3157 | 3388 | 4097 |
| Censored regression model | ||||||||
| Mother's schooling | 0.05 | 0.06 | 0.06 | 0.04 | 0.04 | − 0.01 | − 0.06 | x |
| 0.01*** | 0.02*** | 0.02*** | 0.03 | 0.03 | 0.04 | 0.04 | ||
| Father's schooling | 0.03 | 0.02 | 0.01 | 0.00 | − 0.02 | − 0.06 | − 0.09 | x |
| 0.01*** | 0.01** | 0.01 | 0.01 | 0.02 | 0.02*** | 0.02*** | ||
| N | 4097 | 4097 | 4097 | 4097 | 4097 | 4074 | 4006 | x |
| Nc | 874 | 1285 | 1712 | 2280 | 2859 | 3134 | 3297 | x |
| Excluding all children younger than 25 | ||||||||
| Mother's schooling | 0.04 | 0.07 | 0.03 | 0.02 | x | x | x | x |
| 0.02** | 0.04** | 0.06 | 0.18 | |||||
| Father's schooling | 0.01 | 0.02 | − 0.01 | − 0.00 | x | x | x | x |
| 0.01 | 0.02 | 0.03 | 0.06 | |||||
| N | 2990 | 1558 | 852 | 240 | x | x | x | x |
- All regressions include additional controls or the child's age and gender.
- Standard errors are in italics; significant at:
- * 10% level;
- ** 5% level;
- *** 1% level.
- Nc is the number of censored observations.
In the second and third panels we also show results for the censored regression and elimination models. In the case of the censored regression approach, we find for small censoring percentages that the estimated bias is somewhat larger than the bias reported in the previous panel. When we increase censoring percentages, we find that the bias consistently falls. For censoring percentages around 50% the bias goes to zero and then becomes negative for samples where the majority of the children are still in school.8 When we exclude all children below 25 from our sample, we find for small percentages that the bias is positive, statistically significant and comparable to the bias of the censored regression model. Together with falling sample sizes, the bias declines for censoring percentages up to 60%. For samples where more than 60% of the observations are censored, all children are below the age of 25 and the elimination method no longer works. Overall, we believe that of the three different solutions to the censoring problem the replacement method appears to be the least sensitive to the number of censored observations.
5.2. Prediction Quality and Generalizability
Our second concern is that the replacement trick might work because of the non-representative nature of the WLS. The WLS only collects information on high school graduates and (because of that) systematically undersamples the lower educated individuals. If more schooled parents form more accurate expectations about their children's schooling, it is possible that our observation—the best approach is to replace censored observations with parental expectations—is driven by the sample design of the WLS, and does not hold in other datasets.9
To get an idea whether the mechanism of more schooled parents forming more accurate expectations is present among WLS parents, we first ask ourselves whether WLS parents can accurately predict their child's education. Figure 1 shows a histogram of the difference between parental expectations and realizations. Although for almost 40% of the children parental expectations coincide with realizations, there is quite some variation in how well parents can predict their child's schooling.
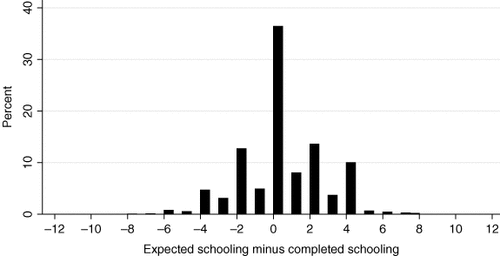
Difference between parental expectations and realized years of schooling
Figure 2 plots how the (absolute) difference between parental expectations and realizations varies with parental schooling, including the regression line that measures the relationship between (absolute) prediction error and parental schooling (controlling for age and gender of the child). In the top figures we see that the prediction error parents make is not fully independent of their amount of schooling. The slope coefficients (with standard error between brackets) which we estimate at − 0.084 [0.021] for mother's schooling and − 0.057 [0.013] for father's schooling indicate that higher schooled parents set their expectations a bit too low, while lower schooled parents set their expectations a bit too high. Since expectations that are too low can be as inaccurate as expectations that are too high, we also plot and estimate how prediction quality (measured as the absolute value of the prediction error) depends on parental schooling, age and gender of the child. The bottom figures show almost no visible relationship. The coefficients are 0.013 [0.017] for mother's schooling and − 0.021 [0.011] for father's schooling, respectively. If we look at mothers, there appears to be no evidence that more schooled mothers make better predictions. If we look at fathers, we do find that prediction quality improves with years of schooling, but it is only at the margin. These weak correlations, we think, raise the generalizability of our findings.
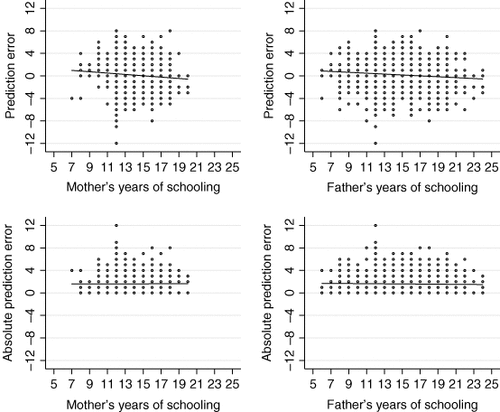
(Absolute) prediction errors and parental schooling
To get an idea whether WLS parents form expectations about their children's schooling in similar ways as other parents do in other datasets, we compare our WLS results with results that come from two more familiar multigenerational US samples drawn from the Michigan Panel Study of Income Dynamics (PSID)10 and the National Longitudinal Survey of Youth (NLSY).11 In all three samples we focus on mothers who expressed their expectations. The WLS and PSID samples are comparable with respect to the survey year expectations are elicited: all mothers were asked to form expectations in either 1975 or 1976. The WLS and NLSY samples are comparable with respect to the mother's age when expectations are elicited: all mothers are in their mid thirties when they report their expectations.
In the first panel of Table IV we report sample means and standard deviations for some of the variables we will study below. The summary statistics clearly illustrate that the mothers in our WLS sample are very different from the mothers in the PSID and NLSY samples. Compared to the PSID mothers, we observe that WLS mothers are much better educated. This result is perhaps not surprising given that we use the unbalanced version of the PSID sample in which low income families are oversampled. Compared to a representative sample of NLSY mothers, we find that WLS mothers have similar amounts of schooling. Despite these similarities, this result indicates that more schooled mothers are clearly oversampled in our WLS sample given that average schooling has increased over time, and that WLS mothers are almost 20 years older than NLSY mothers.
| Sample statistics | WLS | PSID | NLSY | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| Expected schooling | 14.66a | 1.93 | 14.40b | 1.88 | 15.42c | 2.13 | |||
| Mother's schooling | 12.93 | 1.65 | 12.00 | 2.28 | 12.83 | 2.40 | |||
| Father's schooling | 13.38 | 2.82 | 12.06 | 2.91 | 12.97 | 2.59 | |||
| Age mother | 36.08 | 0.44 | 29.47 | 8.29 | 35.00 | 2.24 | |||
| Age child | 10.68 | 3.87 | 9.65 | 2.70 | |||||
| N | 2225 | 1936 | 2635 | ||||||
| Regressing expected schooling on mother's and father's schooling | |||||||||
| Mother's schooling | 0.39 | 0.19 | 0.37 | 0.23 | 0.31 | 0.19 | |||
| 0.02*** | 0.03*** | 0.02*** | 0.02*** | 0.02*** | 0.03*** | ||||
| Father's schooling | 0.29 | 0.23 | 0.30 | 0.19 | 0.30 | 0.20 | |||
| 0.01*** | 0.02*** | 0.01*** | 0.02*** | 0.02*** | 0.02*** | ||||
- a Parents are asked: ‘How far do you think your child probably will go in school?’ Expectations reported in 1975 by mother in levels. We convert levels into years as follows: less than high school … 10; high school graduate … 12; technical and vocational education … 13; some college … 14; college graduate … 16; MA or MS degree … 18; law degree, MD, DDS, DVM degree … 19; PhD … 20.
- b Mothers are asked: ‘About how much education do you think your children will have when they stop going to school?’ Expectations reported in 1976 for children below 13 and/or future children in six levels: some high school … 10; high school … 12; high school plus non-academic training … 13; college but no degree … 14; college BA and no advanced degree … 16; college and advanced or professional degree … 19.
- c Mothers are asked: ‘Looking ahead, how far do you think your child will go in school?’ Expectations reported in 1996 for each child between 5 and 15 years old in five levels: leave high school before graduation … 10; graduate from high school … 12; get some college or other training … 14; graduate from college … 16; take further training after college … 19.
- In the second panel all regressions include additional controls for age of the mother at date of the interview.
- In the second panel standard errors are in italics; significant at: *10% level; **5% level; ***1% level.
In the second panel of Table IV we compare estimates that come from regressions of parental expectations on years of schooling of the mother, years of schooling of the father, and the mother's age (when information on expectations is collected) using the three different samples. In the first three columns we show results using our WLS sample. We find that more schooled mothers with more schooled spouses expect their children to do better in school. In the next six columns of Table IV we report the parental schooling estimates from the two other samples. Compared to the parental expectation results using WLS mothers, we find that the estimates obtained with the PSID and NLSY samples are quite similar. These findings imply that mothers in the WLS form expectations about their children's completed schooling in similar ways as mothers do in the PSID or the NLSY. But more importantly, these findings also imply that the replacement method will probably also work well in other more (or less) representative datasets.
5.3. Patience versus Impatience
Since the replacement method is not as disconcerting as Antonovics and Goldberger say it is, it is interesting to see what happens if a researcher is very impatient and wants to estimate the degree of intergenerational mobility when none of the children has finished their schooling. In Table IV we report those estimates researchers would get had they relied exclusively on the 1975 sample and replaced all observations by parental expectations.12 In the WLS specification, where we control for the schooling of both parents, we find child–parent associations of 0.19 and 0.23 for mothers and fathers, respectively. Compared to the associations of 0.24 and 0.27 obtained with the uncensored WLS sample, we see that the WLS estimates in Table IV are statistically but not substantially different, which is quite remarkable given that schooling expectations were measured when almost all children were still in primary school.
5.4. Maximum Likelihood and the Elimination Approach
So far, the sensitivity analysis has concentrated on mechanisms that could possibly invalidate the method to replace censored school observations with parental expectations. But perhaps it is also informative to understand why the maximum likelihood and elimination approach produce biased mobility estimates, even though the bias as reported in Table II is not substantial.
We begin with the maximum likelihood approach. One likely candidate to explain the upward bias of the maximum likelihood approach would be a normality violation. It is unlikely that schooling is normally distributed—the more appropriate distribution of the child's completed education is bimodal with peaks around 12 and 16 years (see also footnote 8). Another possibility is that heteroskedasticity is causing the inconsistent estimates. Using the uncensored 2004 sample we can test whether the normality and or homoskedasticity assumptions are violated. Our results show that the null hypotheses of normality and homoskedasticity are both rejected.13
A candidate to explain the inconsistencies caused by the elimination procedure would relate to the fact that by eliminating all children below 25 we are left with a sample consisting of parents who chose to have children at a relatively early age. These parents are likely different in both observed and unobserved characteristics which can cause the upward bias we observe in Table II. Parents who choose to have children at an early age, for example, are mostly lower educated. If mobility is lower at the lower end of the distribution (Oreopoulos et al., 2006) the elimination of mostly children from higher educated parents would lead to an estimate of the mobility parameter that is too high.
6. CONCLUDING REMARKS
Recent studies on intergenerational schooling mobility often rely on samples in which information on the child's completed schooling is not always available. Unfortunately, solutions offered to handle censored samples do not always work, and should be further scrutinized.
This is what we do in this paper. We first estimate the impact of mother's and father's schooling on child's schooling using censored and uncensored samples, and investigate the consequences of three different methods that deal with censored observations: replacement of observed with expected years of schooling, maximum likelihood approach, and elimination of all school-aged children.
Our basic result is that parental schooling effects fall, but not by much, when intergenerational mobility models are estimated on censored samples and rise, again not by much, when censored observations are tackled by any of the three correction methods. Of the three methods, the one that treats parental expectations as if they were realizations performs best.
This replacement result depends, however, on the degree of censoring. For samples that are largely incomplete the method does give a small (negative) bias. Nonetheless, it does not matter (much) whether researchers are patient or impatient: whether we fully rely on parental expectations, or whether we use realizations measured 30 years later, the mobility estimates are not substantially different.
An important question is whether our replacement result in this paper provides some guidance as to whether it might work in other datasets as well. We are quite confident it does, for two reasons. First, it is possible to apply the replacement method to other datasets. There are other, more familiar, intergenerational data sources available that collect information on expected schooling when children are still in school. Second, we find that parents in the WLS form expectations about their children's completed schooling in similar ways as many other parents do. It seems therefore reasonable to speculate that our replacement results will persist in other intergenerational data sources as well. We think, however, that further insights on these remarkable findings can be gained by more research investigating how parents actually form their expectations.
ACKNOWLEDGMENTS
The authors thank Reyn van Ewijk, Hessel Oosterbeek and participants in seminars/workshops at the Tinbergen Institute (Amsterdam, 2006), University of Oxford (Oxford, 2006), University of Essex (Essex, 2007), CEMFI (Madrid, 2007), IZA (2007) and LEaF conference (London, 2007), as well as three anonymous referees for their helpful comments. They further thank the Dutch National Science Foundation for its support under VIDI Grant 452.03.309. Support for collection and dissemination of data from the Wisconsin Longitudinal Study has been provided by the National Institute on Aging (AG-9775), the National Science Foundation (SBR-9320660), the Spencer Foundation, and the Center for Demography and Ecology and the Vilas Estate Trust at the University of Wisconsin–Madison. Data and documentation from the Wisconsin Longitudinal Study are available at http://www.ssc.wisc.edu/wlsresearch/documentation.




