Default priors and predictive performance in Bayesian model averaging, with application to growth determinants†
This article was published online on 11th August 2009. An error was subsequently identified. This notice is included in the online and print versions to indicate that both have been corrected [24 March 2010]
Abstract
Bayesian model averaging (BMA) has become widely accepted as a way of accounting for model uncertainty, notably in regression models for identifying the determinants of economic growth. To implement BMA the user must specify a prior distribution in two parts: a prior for the regression parameters and a prior over the model space. Here we address the issue of which default prior to use for BMA in linear regression. We compare 12 candidate parameter priors: the unit information prior (UIP) corresponding to the BIC or Schwarz approximation to the integrated likelihood, a proper data-dependent prior, and 10 priors considered by Fernández et al. (Journal of Econometrics 2001; 100: 381–427). We also compare two model priors: the uniform model prior and a prior with prior expected model size 7. We compare them on the basis of cross-validated predictive performance on a well-known growth dataset and on two simulated examples from the literature. We found that the UIP with uniform model prior generally outperformed the other priors considered. It also identified the largest set of growth determinants. Copyright © 2009 John Wiley & Sons, Ltd.
1. INTRODUCTION
Bayesian model averaging (BMA) is now widely accepted as a principled way of accounting for model uncertainty.1 Model uncertainty has played a particularly big role in economic growth research since the early 1990s, when a surge of new growth theories gave rise to a large literature that sought to evaluate the new growth determinants (see Durlauf et al., 2005, for a survey). Linear regression models dominate in growth research, and here we consider BMA for this class of models. The implementation of BMA involves solving the common challenge in Bayesian statistics of specifying the prior. For BMA, the prior has two parts: a prior for the parameters of each model, and the prior probability of each model.2 The implementation of BMA is, however, subject to the challenge that it requires prior distributions over all parameters in all models, and the prior probability of each model must also be specified.
If substantial prior information is available and can readily be expressed as a probability distribution, this should be used. Often, however, the prior information is small relative to the information in the data, and then it makes sense to use a default prior. Here we address the issue of which default prior to use.
We compare 12 candidate default parameter priors and two model priors that have been advocated in the literature. We do this on the basis of cross-validated predictive performance using a well-known growth dataset and two simulated examples from the literature. Predictive performance is a natural and neutral basis for such comparisons. We evaluate the predictive mean using the mean squared error, and the entire predictive distribution, using two different scoring rules.
We found substantial support for one of the priors evaluated: the unit information prior (UIP) that corresponds to the BIC (or Schwarz) approximation for the integrated (or marginal) likelihood, combined with a uniform prior over the model space. This also turned out to favor the largest number of growth determinants.
We are not the first to compare priors for BMA in growth regressions. FLS (2001a) applied a ‘benchmark prior’ (FLS, 2001b) to the growth context, but did not include the UIP, or alternative model priors. Sala-i-Martin et al. (2004, hereafter SDM) compared model prior distributions but did not compare different parameter priors. Ley and Steel (2007b, hereafter LS), following Brown et al. (1998, 2002), introduced a hierarchical prior on the model size and integrated out the prior model size in the model averaging. They used two parameter priors that we include in our set of 12 priors below, in combination with fixed and random model priors. However, LS did not include the UIP.3
The paper is organized as follows. Section 2 reviews BMA with a focus on prior specification. Section 3 describes how we use predictive performance to compare prior settings and gives results for the growth data. Section 4 gives the results of a simulation experiment, and Section 5 concludes.
2. BAYESIAN MODEL AVERAGING
2.1. Basic Ideas
We now briefly summarize the main ideas of BMA for linear regression.4 Given a dependent variable, Y, a number of observations, n, and a set of candidate regressors, X1, …, Xp, the variable selection problem is to find the most effective subset of regressors. We denote by M1, …, Mk the models considered, where each one represents a subset of the candidate regressors. When all possible subsets are considered, K = 2p. Model Mk has the form 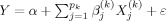 , where
, where 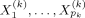 is a subset of X1, …, Xp,
is a subset of X1, …, Xp, 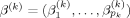 is a vector of regression coefficients to be estimated, and ε ∼ N(0, σ2) is the error term. We denote by θk = (α, β(k), σ) the vector of parameters in Mk.
is a vector of regression coefficients to be estimated, and ε ∼ N(0, σ2) is the error term. We denote by θk = (α, β(k), σ) the vector of parameters in Mk.
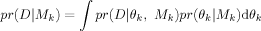 (1)
(1)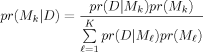 (2)
(2)BMA obtains the posterior inclusion probability of a candidate regressor, pr(βj ≠ 0|D), by summing the posterior model probabilities across those models that include the regressor. Posterior inclusion probabilities provide a probability statement regarding the importance of a regressor that directly addresses what is often the researcher's prime concern: ‘What is the probability that the regressor has an effect on the dependent variable?’5
BMA involves averaging over all the models considered. This can be a very large number; for example, the growth dataset we consider below features 41 candidate regressors (and so K = 241, or about two trillion models). Such a vast model space involves a major computational challenge as direct evaluation is typically not feasible. In this paper we use the leaps-and-bounds method developed by Raftery (1995) for BMA, based on the all-subsets regression algorithm of Furnival and Wilson (1974). This is implemented in the BMA R package, available at http://cran.r-project.org/ (Raftery et al., 2005, 2009).
Other approaches to dealing with the large model space are the coinflip importance sampling algorithm used by SDM, and the Markov chain Monte Carlo (MCMC) sampler used by FLS. We have experimented with all three algorithms using the FLS data and found that the results from the branch-and-bound and MCMC methods were very similar, while the coinflip method took substantially more computational time and produced less precise results. In particular, the coinflip algorithm failed to explore large parts of the model space, notably including the models with the highest posterior probabilities.
2.2. Prior Distributions of Parameters
The implementation of BMA in linear regression is subject to the challenge that prior distributions must be specified over all parameters in all models. Prior probabilities of all models must also be specified. If the researcher has information about the parameters, ideally this should be reflected in the priors, and informative priors should be used, as was done, for example, by Jackman and Western (1994).
However, often the amount of prior information is small and the effort needed to specify it in terms of a probability distribution is large. Thus there have been many efforts to specify default priors that could reasonably be used for all such analyses. These are sometimes called ‘noninformative’ or ‘reference’ priors, but there is debate about the extent to which a prior can be totally noninformative, and so we use the term ‘default prior’ here. Priors on parameters may affect results since they may influence the integrated likelihood (1), which is a key component of the posterior model weights (2). The integrated likelihood of a model is approximately proportional to the prior density of the model parameter evaluated at the posterior mode (Kass and Raftery, 1995). Thus the prior density should be spread out enough so that it is reasonably flat over the region of the parameter space where the likelihood is substantial. However, the prior density should also be no more spread out than necessary, since increasing the spread of the prior tends to decrease the prior ordinate at the posterior mode, which decreases the integrated likelihood and may unnecessarily penalize larger models (Raftery, 1996). The priors we discuss below make this trade-off in different ways.
We focus on a set of 12 candidate default priors that have been advocated in the literature (Table I): a prior which contains about the same amount of information as a typical single observation (Kass and Wasserman, 1995; Raftery, 1995); the data-dependent prior of Raftery et al. (1997), which was designed to be relatively flat over the region of the parameter space supported by the data but no more spread out than necessary; and third, the 10 automatic priors used by FLS (2001b), which do not rely on input from the researcher or information in the data, but only on the sample size and the number of regressors.
| Prior | Specification of g-prior | Comment | Source |
|---|---|---|---|
| 1 | Unit information prior | The prior contains information approximately equal to that contained in a single typical observation. The resulting posterior model probabilities are closely approximated by the Schwarz criterion, BIC | Kass and Wasserman (1995); Raftery (1995) |
| 2 | gk = pk/n | Prior information increases with the number of regressors in the model | FLS (2001b) |
| 3 | gk = p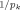 /n /n |
Prior information decreases with the number of regressors in the model | FLS (2001b) |
| 4 | 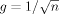 |
This is an intermediate case of Prior 1 suggested by FLS where a smaller asymptotic penalty is chosen for larger models | FLS (2001b) |
| 5 | 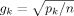 |
This is an intermediate case of Prior 2, suggested by FLS, where prior information increases with the number of regressors in the model | FLS (2001b) |
| 6 | g = 1/(ln n)3 | The Hannan–Quinn criterion. CHQ = 3 as n becomes large | Hannan and Quinn (1979) |
| 7 | gk = ln(pk + 1)/(ln n) | Prior information decreases even slower with sample size and there is asymptotic convergence to the Hannan–Quinn criterion with CHQ = 1 | Hannan and Quinn (1979) |
| 8 | gk = δγ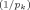 /(1 − δγ /(1 − δγ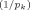 ) ) |
A natural conjugate prior structure, subjectively elicited through predictive implications. γ< 1 (so that g increases with kj) and delta such that g/(1 + g)€ [0.10, 0.15] (the weight of the ‘prior prediction error’ in the Bayes factors); for kj ranging from 1 to 15. FLS suggest covering this interval with the values of γ = 0.65 and δ = 0.15 | Laud and Ibrahim (1996) |
| 9 | g = 1/p2 | This prior is suggested by the risk inflation criterion (RIC) | Foster and George (1994) |
| 10 | 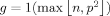 |
The preferred prior of Fernández et al. (2001), a mix of Prior 9 and Prior 1 | FLS (2001b) |
| 11 | β∼N(µ, σ2V) V = σ2ϕ2(1/nX′X)−1 vλ/σ2∼χ2 | Data-dependent prior. ϕ = 0.85, ν = 2.58, λ = 0.28 if the R2 of the full model is less than 0.9, and ϕ = 9.2, ν = 0.2, λ = 0.1684 if the R2 of the full model is greater than 0.9 | Raftery et al. (1997) |
| 12 | g = n−1 | Similar to the unit information prior, but with mean zero instead of MLE | FLS (2001b) |
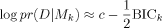 (3)
(3)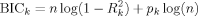 (4)
(4)In (4), 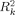 and pk are the coefficient of determination and the number of regressors, respectively, for model Mk, and c is a constant that does not vary across models and so cancels in the model averaging. BICk is the Bayesian information criterion for Mk, which is equivalent to the approximation derived by Schwarz (1978) for the regression model, as shown by Raftery (1995).6 The approximate integrated likelihood in (3) was the basis of the model averaging method of Raftery (1995) for linear regression, and was also used by SDM.
and pk are the coefficient of determination and the number of regressors, respectively, for model Mk, and c is a constant that does not vary across models and so cancels in the model averaging. BICk is the Bayesian information criterion for Mk, which is equivalent to the approximation derived by Schwarz (1978) for the regression model, as shown by Raftery (1995).6 The approximate integrated likelihood in (3) was the basis of the model averaging method of Raftery (1995) for linear regression, and was also used by SDM.
Raftery (1995, Section 4) showed that (3) gives an approximation to the integrated likelihood with an error that is O(n−1/2) when the prior for the regression parameters is multivariate normal centered at the maximum likelihood estimate with variance matrix equal to n times the inverse of the observed Fisher information matrix.7 This prior is much more spread out than the likelihood, and typically is relatively flat where the likelihood is substantial (Raftery, 1999). It contains the same amount of information as would be contained on average in a single observation and so, following Kass and Wasserman (1995), we call it the unit information prior (UIP). Because of its simplicity and intuitive appeal, we use the UIP as a baseline, and we compare other proposed default priors to it.8
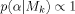 (5)
(5)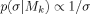 (6)
(6)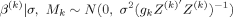 (7)
(7)The choice g = 1/n (Prior 12 in Table I) has the same variance as the UIP, but its mean is at zero instead of the MLE. Alternatives are Prior 4, 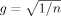 , which attributes a smaller asymptotic penalty than BIC, and Prior 2, gk = pk/n, where prior information increases with the number of regressors in the model. Other priors suggested by FLS (2001b) correspond to previous proposals: Priors 6 and 7 in Table I are versions of the Hannan and Quinn criterion (Hannan and Quinn, 1979), and Prior 9, gk = 1/p2, corresponds to the risk inflation criterion (RIC) of Foster and George (1994), designed to take account of the number of candidate regressors. Prior 10 is the preferred prior of FLS (2001b), developed on the basis of their experiments with their priors. It is composed of either the RIC-based prior (Prior 9) or Prior 12, depending on the number of observations and regressors in the particular dataset. For the datasets considered in this paper, Prior 10 is identical to Prior 9.
, which attributes a smaller asymptotic penalty than BIC, and Prior 2, gk = pk/n, where prior information increases with the number of regressors in the model. Other priors suggested by FLS (2001b) correspond to previous proposals: Priors 6 and 7 in Table I are versions of the Hannan and Quinn criterion (Hannan and Quinn, 1979), and Prior 9, gk = 1/p2, corresponds to the risk inflation criterion (RIC) of Foster and George (1994), designed to take account of the number of candidate regressors. Prior 10 is the preferred prior of FLS (2001b), developed on the basis of their experiments with their priors. It is composed of either the RIC-based prior (Prior 9) or Prior 12, depending on the number of observations and regressors in the particular dataset. For the datasets considered in this paper, Prior 10 is identical to Prior 9.
An alternative class of data-dependent priors can be viewed as approximating the subjective prior of an experienced researcher. Clearly, if such knowledge can be readily elicited in the form of a probability distribution, it should be introduced into the analysis. Raftery et al. (1997) specified conjugate data-dependent priors that are as concentrated as possible, subject to being reasonably flat over the region of parameter space where the likelihood is not negligible. Their prior (Table I, Prior 11) is specified by four hyperparameters that are explained in Table I. Another such data-dependent prior is based on Laud and Ibrahim (1996) (Table I, Prior 8) who specified g = δγ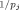 /(1 − δγ
/(1 − δγ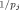 ). Given FLS's suggestions for γ and δ, they mention that model comparisons based on the resulting log integrated likelihood can roughly be compared to those based on the Akaike information criterion (AIC) (Akaike, 1974).
). Given FLS's suggestions for γ and δ, they mention that model comparisons based on the resulting log integrated likelihood can roughly be compared to those based on the Akaike information criterion (AIC) (Akaike, 1974).
2.3. Model Priors
The most common model prior in the literature is the uniform distribution that assigns equal prior probability all models, so that pr(Mk) = 1/K for each k. This was suggested first by Raftery (1988) and, for linear regression models, by George and McCulloch (1993). Hoeting et al. (1999) cite the extensive evidence that supports the good performance of the UIP, since the integrated likelihood on the model space is often concentrated enough for the results to be insensitive to moderate deviations from the uniform prior.
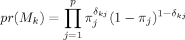 (8)
(8)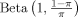 distribution. They evaluated parameter Priors 9 and 12 with fixed and random π. We adopt (8) and examine growth determinants as well as their predictive performance for a range of fixed model priors. We also compare our results with those in LS with fixed and random π.9
distribution. They evaluated parameter Priors 9 and 12 with fixed and random π. We adopt (8) and examine growth determinants as well as their predictive performance for a range of fixed model priors. We also compare our results with those in LS with fixed and random π.9There is a tradeoff between the prior inverse variance parameter g and the prior inclusion probabilities, πj in (8), pointed out by Taplin and Raftery (1994, Section 5.2) in a slightly different context, and also revealed by computations in LS. We now give a theoretical explanation for this, taking πj = π for j = 1, …, p for easier exposition.
Comparing the posterior probabilities for a given model in (2) for different priors, Kass and Raftery (1995) showed that an increase in the prior standard deviation by a factor c is approximately equivalent to a reduction in the prior odds for an increase in the model size by an additional variable, by the same factor of c.
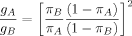 (9)
(9)This shows the nature of the tradeoff between the prior scale factor and the prior inclusion probability: a change in π has approximately the same effect as the change in g given by equation (9).
3. DETERMINING GROWTH DETERMINANTS
Since economic growth is the fundamental driver of living standards, it is of great interest to economists and policymakers alike to identify which of the numerous theories proposed receive support from the data and which determinants have a significant effect on growth. Attempts to identify robust growth determinants date back to Levine and Renelt (1992), who used extreme bounds analysis. Formal BMA analysis was conducted by Brock and Durlauf (2001), FLS (2001a) and SDM (2004). The dataset used across studies always contains a core of at least 41 candidate regressors, motivated by Sala-i-Martin (1997) and FLS (2001a). We base our growth analysis on the same dataset that FLS kindly shared with us.
3.1. Effects of Parameter Priors on Growth Determinants
For datasets with small numbers of observations such as our growth dataset with 72 observations, priors can play an important role. As can be seen in Figure 1, the precisions of the parameter priors vary widely; for example, the information contained in Prior 7 is three orders of magnitude greater than that in the FLS-preferred prior. It thus seems possible that the BMA results would vary considerably between priors.
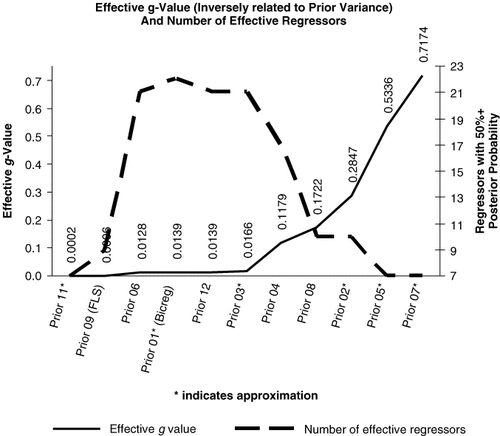
Effective g-value (inversely related to prior variance) and number of effective regressors. (1) When priors depend on the exact model size, pk, Figure 1 approximates the prior using the expected model size. Priors 11 and 1 are not exact g-priors, so the g-value is also an approximation. (2) Priors 9 and 10 are identical in the growth context
Table II reports the BMA posterior inclusion probabilities for all 12 prior distributions applied to the growth dataset. Posterior inclusion probabilities and the number of regressors that exhibit evidence of an effect on growth vary substantially across priors. The number of regressors whose inclusion probability exceeds 50% ranges from a low of seven regressors (Priors 5, 7, and 11) to a high of 22 regressors (Prior 1). Recall that, apart from the UIP, the prior distributions are all centered at zero and that Priors 5 and 7 have small prior variance that emphasizes the zero expected mean, while the variance of Prior 11 has the largest variance in the sample, which to emphasizes uncertainty (see Figure 1). Priors 5, 7, and 11 contain strong information against a large effect, and the information contained in the data is too weak to overwhelm that prior. As the priors over the parameter space become spread out enough to include those regions where the likelihood is large, the number of regressors that exhibit an effect increases. Figure 1 shows that both more diffuse and more precise priors (Priors 11, 7, and 5) lead to a decline in the integrated likelihood, thus reducing the number of regressors showing an effect.
| Priors arranged by effective g-value (increasing left to right) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior 11 | 9 (FLS) | Prior 6 | Prior 1 | Prior 12 | Prior 3 | Prior 4 | Prior 8 | Prior 2 | Prior 5 | Prior 7 | |
| Confucius | 99.5 | 99.9 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.9 | 99.2 | 98.5 |
| GDPsh560 | 99.9 | 99.9 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 99.5 | 98.5 |
| Life | 96.5 | 96.4 | 99.9 | 100.0 | 100.0 | 99.9 | 99.8 | 98.6 | 96.4 | 93.1 | 90.9 |
| RuleofLaw | 47.2 | 64.0 | 99.6 | 100.0 | 99.6 | 99.6 | 98.3 | 93.0 | 69.3 | 57.3 | 56.6 |
| SubSahara | 74.8 | 83.8 | 99.9 | 100.0 | 100.0 | 100.0 | 99.7 | 97.5 | 86.3 | 80.2 | 79.6 |
| EquipInv | 99.0 | 96.8 | 98.3 | 99.9 | 98.4 | 98.3 | 95.6 | 88.8 | 94.4 | 95.3 | 95.2 |
| Hindu | 3.2 | 10.3 | 96.6 | 99.9 | 97.0 | 96.8 | 88.7 | 42.8 | 16.7 | 15.0 | 18.5 |
| HighEnroll | 0.3 | 0.7 | 93.4 | 99.8 | 94.0 | 93.5 | 78.1 | 2.8 | 2.1 | 3.9 | 7.2 |
| LabForce | 0.4 | 1.3 | 94.5 | 99.8 | 95.0 | 94.6 | 81.6 | 11.6 | 3.9 | 5.6 | 9.2 |
| EthnoLFrac | 0.5 | 1.3 | 90.8 | 99.3 | 91.4 | 90.8 | 74.6 | 7.2 | 3.3 | 4.8 | 8.0 |
| Mining | 28.0 | 38.5 | 96.4 | 99.2 | 96.5 | 96.4 | 93.3 | 74.7 | 49.1 | 43.4 | 44.1 |
| LatAmerica | 9.2 | 13.4 | 79.5 | 97.2 | 80.3 | 79.4 | 61.0 | 30.2 | 17.7 | 17.5 | 19.1 |
| SpanishCol | 0.0 | 0.1 | 67.6 | 94.6 | 68.7 | 67.3 | 42.3 | 2.0 | 0.5 | 1.1 | 2.4 |
| FrenchCol | 0.3 | 0.2 | 65.4 | 93.9 | 66.5 | 65.1 | 39.4 | 0.0 | 0.3 | 1.0 | 2.2 |
| BritCol | 0.0 | 0.0 | 64.7 | 93.6 | 65.8 | 64.4 | 38.7 | 0.7 | 0.2 | 0.6 | 1.8 |
| PrSc | 19.3 | 12.0 | 72.2 | 90.7 | 72.8 | 72.2 | 58.0 | 8.1 | 14.1 | 16.1 | 17.5 |
| CivlLib | 5.2 | 3.3 | 66.8 | 85.7 | 67.5 | 66.7 | 51.2 | 3.7 | 4.4 | 5.4 | 7.1 |
| NEquipInv | 28.8 | 49.3 | 71.3 | 85.6 | 71.7 | 71.3 | 66.6 | 82.1 | 52.4 | 41.1 | 40.3 |
| English. | 0.5 | 1.1 | 58.0 | 84.5 | 58.9 | 57.7 | 36.7 | 2.7 | 2.2 | 2.4 | 3.5 |
| OutwarOr | 0.0 | 0.0 | 51.2 | 82.8 | 52.2 | 51.0 | 31.4 | 0.7 | 0.2 | 0.6 | 1.7 |
| BlMktPm | 5.1 | 12.2 | 63.8 | 72.5 | 63.9 | 64.1 | 67.6 | 45.4 | 19.6 | 17.4 | 19.9 |
| Muslim | 66.9 | 68.3 | 44.3 | 60.9 | 44.4 | 44.4 | 49.4 | 54.9 | 66.5 | 60.3 | 56.1 |
| Buddha | 4.1 | 10.2 | 19.5 | 36.5 | 19.7 | 19.7 | 21.5 | 31.1 | 13.4 | 10.6 | 11.4 |
| EcoOrg | 34.2 | 56.6 | 39.5 | 35.6 | 39.2 | 39.7 | 50.1 | 88.7 | 61.0 | 47.3 | 45.2 |
| X.PublEdu | 0.0 | 0.2 | 17.9 | 13.3 | 17.8 | 18.1 | 19.4 | 1.5 | 0.6 | 1.1 | 2.0 |
| PolRights | 2.0 | 2.7 | 16.4 | 12.4 | 16.5 | 16.5 | 14.6 | 10.1 | 4.5 | 4.4 | 4.8 |
| Protestants | 35.5 | 51.5 | 25.7 | 11.7 | 25.2 | 26.0 | 41.7 | 81.3 | 56.8 | 47.7 | 46.4 |
| WarDummy | 1.1 | 0.9 | 6.2 | 11.7 | 6.4 | 6.3 | 3.9 | 0.8 | 1.2 | 1.8 | 2.0 |
| Age | 0.4 | 0.7 | 14.6 | 11.4 | 14.7 | 14.7 | 12.2 | 3.3 | 1.3 | 1.7 | 2.3 |
| RFEXDist | 1.8 | 2.0 | 4.6 | 9.6 | 4.7 | 4.7 | 4.0 | 0.6 | 2.6 | 3.3 | 3.4 |
| Catholic | 4.1 | 8.7 | 3.5 | 7.5 | 3.5 | 3.6 | 7.1 | 20.3 | 11.0 | 8.3 | 8.2 |
| Popg | 0.2 | 0.3 | 2.2 | 3.6 | 2.2 | 2.3 | 2.2 | 0.2 | 0.5 | 0.5 | 0.5 |
| PrExports | 2.2 | 2.5 | 1.2 | 2.8 | 1.2 | 1.2 | 2.1 | 5.9 | 3.7 | 3.0 | 2.8 |
| Foreign | 0.5 | 0.3 | 0.7 | 2.0 | 0.7 | 0.7 | 0.4 | 0.0 | 0.2 | 0.6 | 0.7 |
| Jewish | 0.0 | 0.0 | 0.8 | 1.3 | 0.8 | 0.8 | 0.7 | 0.0 | 0.0 | 0.0 | 0.1 |
| std.BMP | 0.0 | 0.0 | 0.6 | 1.3 | 0.6 | 0.6 | 0.4 | 0.0 | 0.0 | 0.0 | 0.0 |
| Area | 0.0 | 0.0 | 0.8 | 1.1 | 0.9 | 0.9 | 1.1 | 0.0 | 0.1 | 0.1 | 0.2 |
| Work. pop. | 0.4 | 0.2 | 0.3 | 1.1 | 0.3 | 0.3 | 0.2 | 0.0 | 0.2 | 0.6 | 0.8 |
| AbsLat | 0.6 | 0.5 | 1.2 | 1.0 | 1.2 | 1.2 | 1.8 | 0.3 | 0.7 | 0.9 | 1.0 |
| YrsOpen | 57.8 | 40.9 | 1.2 | 1.0 | 1.1 | 1.2 | 3.4 | 15.3 | 37.3 | 44.2 | 42.4 |
| Rev.Coup | 0.1 | 0.2 | 0.4 | 0.7 | 0.4 | 0.4 | 0.7 | 1.1 | 0.5 | 0.4 | 0.4 |
| No. of relevant regressors | 7 | 9 | 21 | 22 | 21 | 21 | 17 | 11 | 10 | 7 | 7 |
- Note: Posterior inclusion probabilities that exceed 50% are in bold font (Jeffreys, 1961). Priors 9 and 10 are identical in the growth context.
Figure 2 shows scatterplots of posterior inclusion probabilities generated by the various priors against Prior 1. Since Prior 1 was the most optimistic, with 22 candidate regressors showing an effect in Table II, it is no surprise that most of the points in the scatterplots lie above the 45° line, indicating higher posterior inclusion probabilities under Prior 1 than under other priors. The scatterplots also show how the differences between Prior 1 and alternative priors increase as the implied g-prior diverges. Priors 1, 6, and 12 yielded similar results, but most other priors showed differing effects implied by the priors.
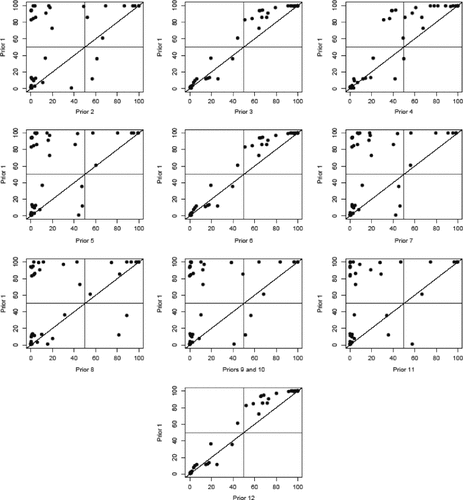
Correlation of posterior inclusion probabilities across parameter priors (growth dataset). Priors 9 and 10 are identical in the growth context
3.2. Combined Effects of Parameter and Model Priors on Growth Determinants
SDM advocated using a Mitchell–Beauchamp prior (8) with π = 7/ p, equivalent to a prior expected model size of 7 regressors. We combined this model prior with the 12 parameter priors considered, and the results are shown in Table III. As expected, this leads to smaller models than the uniform model prior, ranging from 3 to 10 effective regressors with posterior inclusion probabilities above 50%. Again the priors with intermediate variance have a slightly larger number of regressors (Priors 3, 4, and 12), and as before the number of regressors that exhibit an effect declines as the prior variance become large (Priors 6 and 9). The Mitchell–Beauchamp model prior has the least impact on Prior 11; for this prior, the rule of law variable loses significance but otherwise the results are identical to Table II.
| Prior 1 Model prior: uniform | Priors arranged by effective g-value (increasing left to right) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior 11 | Prior 9 | Prior 6 | Prior 1 | Prior 12 | Prior 3 | Prior 4 | Prior 8 | Prior 2 | Prior 5 | Prior 7 | ||
| Confucius | 100.0 | 92.0 | 95.8 | 99.7 | 99.9 | 99.7 | 99.7 | 98.7 | 97.2 | 96.5 | 87.1 | 84.8 |
| GDPsh560 | 100.0 | 91.6 | 91.7 | 99.8 | 100.0 | 99.8 | 99.8 | 99.0 | 97.3 | 96.8 | 71.8 | 50.1 |
| Life | 100.0 | 79.5 | 77.4 | 94.8 | 97.8 | 94.9 | 94.8 | 90.2 | 84.9 | 82.0 | 48.8 | 30.8 |
| RuleofLaw | 100.0 | 16.5 | 16.9 | 49.4 | 68.6 | 50.2 | 50.4 | 37.0 | 29.2 | 21.5 | 12.3 | 8.2 |
| SubSahara | 100.0 | 61.8 | 60.4 | 76.5 | 86.3 | 76.9 | 77.0 | 70.1 | 66.1 | 62.9 | 48.5 | 35.1 |
| EquipInv | 99.9 | 99.5 | 99.4 | 98.2 | 99.2 | 98.1 | 98.0 | 98.5 | 98.7 | 99.0 | 98.5 | 97.9 |
| Hindu | 99.9 | 0.0 | 0.0 | 4.8 | 9.6 | 5.0 | 5.1 | 2.3 | 1.1 | 0.1 | 0.0 | 0.0 |
| HighEnroll | 99.8 | 0.1 | 0.1 | 0.1 | 1.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.8 | 1.2 |
| LabForce | 99.8 | 0.0 | 0.0 | 0.3 | 1.5 | 0.3 | 0.3 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| EthnoLFrac | 99.3 | 0.2 | 0.2 | 0.4 | 0.9 | 0.5 | 0.5 | 0.4 | 0.4 | 0.4 | 0.5 | 0.3 |
| Mining | 99.2 | 4.1 | 6.9 | 31.2 | 33.7 | 31.8 | 32.2 | 25.8 | 19.6 | 12.0 | 3.8 | 1.7 |
| LatAmerica | 97.2 | 4.7 | 6.0 | 11.2 | 11.1 | 11.4 | 11.6 | 11.6 | 10.9 | 9.3 | 6.1 | 3.9 |
| SpanishCol | 94.6 | 0.0 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| FrenchCol | 93.9 | 0.3 | 0.3 | 0.3 | 0.0 | 0.3 | 0.3 | 0.6 | 0.7 | 0.7 | 0.3 | 0.1 |
| BritCol | 93.6 | 0.0 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| PrSc | 90.7 | 6.6 | 7.8 | 13.3 | 8.0 | 13.3 | 13.5 | 14.6 | 13.6 | 11.5 | 6.5 | 4.8 |
| CivlLib | 85.7 | 1.0 | 1.2 | 3.2 | 2.2 | 3.2 | 3.3 | 3.3 | 2.9 | 2.1 | 0.6 | 0.4 |
| NEquipInv | 85.6 | 3.2 | 5.6 | 34.7 | 56.2 | 35.4 | 35.5 | 23.0 | 16.6 | 9.8 | 5.2 | 4.1 |
| English | 84.5 | 0.0 | 0.0 | 0.8 | 0.1 | 0.8 | 0.9 | 0.7 | 0.4 | 0.1 | 0.1 | 0.3 |
| OutwarOr | 82.8 | 0.0 | 0.0 | 0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.3 |
| BlMktPm | 72.5 | 0.1 | 0.3 | 6.8 | 10.0 | 7.1 | 7.3 | 4.6 | 2.7 | 0.8 | 0.1 | 0.0 |
| Muslim | 60.9 | 21.5 | 29.2 | 65.6 | 69.1 | 65.9 | 65.8 | 56.5 | 46.9 | 37.2 | 13.0 | 7.2 |
| Buddha | 36.5 | 2.3 | 2.6 | 5.9 | 11.8 | 6.1 | 6.2 | 3.8 | 3.1 | 2.0 | 9.6 | 13.8 |
| EcoOrg | 35.6 | 4.7 | 7.6 | 40.7 | 61.9 | 41.6 | 41.7 | 27.4 | 19.7 | 11.9 | 6.2 | 5.0 |
| X.PublEdu | 13.3 | 0.0 | 0.0 | 0 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| PolRights | 12.4 | 0.3 | 0.5 | 1.9 | 0.8 | 1.9 | 2.0 | 2.0 | 1.7 | 1.2 | 0.4 | 0.5 |
| Protestants | 11.7 | 16.8 | 21.3 | 40.7 | 51.8 | 41.3 | 41.5 | 32.6 | 27.4 | 21.4 | 24.9 | 25.6 |
| WarDummy | 11.7 | 0.8 | 0.9 | 1.2 | 0.0 | 1.2 | 1.2 | 1.9 | 2.1 | 1.9 | 1.3 | 0.7 |
| Age | 11.4 | 0.4 | 0.6 | 0.6 | 0.1 | 0.6 | 0.7 | 0.9 | 1.1 | 1.0 | 1.8 | 2.0 |
| RFEXDist | 9.6 | 1.2 | 1.6 | 2.5 | 0.0 | 2.5 | 2.6 | 3.3 | 3.3 | 2.6 | 3.8 | 4.8 |
| Catholic | 7.5 | 0.6 | 1.1 | 5.3 | 9.0 | 5.5 | 5.5 | 3.3 | 2.3 | 1.4 | 1.9 | 1.6 |
| Popg | 3.6 | 0.0 | 0.0 | 0.2 | 0.0 | 0.2 | 0.3 | 0.2 | 0.1 | 0.0 | 0.1 | 0.2 |
| PrExports | 2.8 | 0.1 | 0.1 | 1.8 | 1.3 | 1.9 | 1.9 | 1.4 | 0.9 | 0.3 | 0.5 | 0.5 |
| Foreign | 2.0 | 0.6 | 0.9 | 0.6 | 0.0 | 0.6 | 0.6 | 1.1 | 1.3 | 1.5 | 1.0 | 0.7 |
| Jewish | 1.3 | 0.0 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.2 |
| std.BMP | 1.3 | 0.0 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4 | 0.8 |
| Area | 1.1 | 0.0 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.3 |
| Work.Pop | 1.1 | 1.1 | 1.2 | 0.5 | 0.1 | 0.4 | 0.5 | 1.0 | 1.5 | 1.7 | 2.2 | 2.2 |
| AbsLat | 1.0 | 0.2 | 0.3 | 0.6 | 0.0 | 0.6 | 0.6 | 0.8 | 0.8 | 0.7 | 0.2 | 1.0 |
| YrsOpen | 1.0 | 59.8 | 63.0 | 52.4 | 38.0 | 51.8 | 51.7 | 59.2 | 61.0 | 63.5 | 49.1 | 38.2 |
| Rev.Coup | 0.7 | 0.0 | 0.0 | 0.1 | 0.0 | 0.1 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| Relevant regressors | 22 | 6 | 6 | 7 | 10 | 8 | 8 | 7 | 6 | 6 | 3 | 3 |
The image plots in Figure 3, produced by the BMA R package, highlight how different the models are over which the various priors average. The figure shows models used in the averaging process on the horizontal axis. Each model's posterior probability is indicated by its horizontal width. Posterior means are indicated as positive (darker shading) or negative. Comparing Figure 3(a) and (c), we see that the model prior with prior expected model size 7 favors growth models with fewer variables. In addition, the image plots highlight that, while the procedure averages over the same number of models, many more models receive negligible weight if the model size is presumed to be small. On the other hand, we note the similarity between Figure 3(b) and (c), which feature two very different model and parameter priors. This similarity was first observed for these specific priors by Masanjala and Papageorgiou (2005). LS describe the similarity between the FLS uniform prior and Prior 1 with prior model size 7 as arising ‘mostly by accident’ and discuss specific parameter constellations that generate similar posterior probabilities. We showed in Section 2.3 that in fact this similarity has a theoretical explanation.
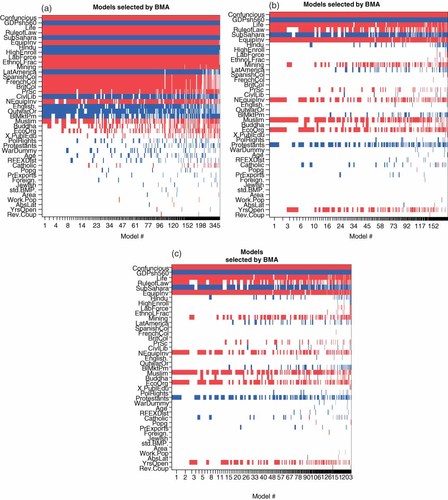
Regressors included in best models. (a) Prior 1 (uniform model prior). (b) Prior 9 (uniform model prior). (c) Prior 1 (prior model size = 7) Note: Posterior means are indicated as positive or negative (darker shading). Horizontal distances indicate posterior model weights. Priors 9 and 10 are identical in the growth context. This figure is available in colour online at wileyonlinelibrary.com/journal/jae
For the FLS dataset with n = 72 and p = 41, the FLS benchmark parameter prior implies gA = 1/p2, combined with the uniform model prior, 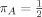 , in the notation of (9). When gB = 1/n as in the case of Prior 1, used by SDM, equation (9) holds when the prior inclusion probability is πA = 7.03/p, so that the prior expected model size is 7.03. It is therefore not surprising that for the SDM suggested prior expected model size of 7 the priors recommended by SDM and FLS yield similar results for the growth dataset, although they are based on very different parameter and model priors. Note that this similarity depends crucially on the number of candidate regressors in the dataset, p. Subjective priors that favor small models thus achieve their aim by punishing larger models (Figure 3(c)) or by increasing the prior variance on each individual parameter (Figure 3(b)).
, in the notation of (9). When gB = 1/n as in the case of Prior 1, used by SDM, equation (9) holds when the prior inclusion probability is πA = 7.03/p, so that the prior expected model size is 7.03. It is therefore not surprising that for the SDM suggested prior expected model size of 7 the priors recommended by SDM and FLS yield similar results for the growth dataset, although they are based on very different parameter and model priors. Note that this similarity depends crucially on the number of candidate regressors in the dataset, p. Subjective priors that favor small models thus achieve their aim by punishing larger models (Figure 3(c)) or by increasing the prior variance on each individual parameter (Figure 3(b)).
In summary, candidate default priors differed considerably in dispersion, and led to the choice of different sets of variables. As few as three and as many as 22 regressors were found to be related to growth, depending on the specific prior used.
3.3. Assessment of Prior Distributions Using Predictive Performance
We now compare the competing default priors on the basis of predictive performance on hold-out samples, a neutral criterion that allows the comparison of different methods on the same footing. We compare the performance of the full predictive distributions produced by the methods, as well as that of point predictions. Our routine (bma.compare, programmed in R and available from the first author on request) simultaneously evaluates all 12 different parameter priors and any specific prior expected model size, as well as their predictive performance.
We divide the dataset randomly into a training set, DT, which is used to estimate the BMA predictive distribution, and a hold-out set, DH, which is used to assess the quality of the resulting predictive distributions. We use three different criteria, or scoring rules: the mean squared error (MSE) of prediction, the log predictive score (LPS; Good, 1952), and the continuous ranked probability score (CRPS; Matheson and Winkler, 1976). All our scoring rules are negatively oriented, that is, lower is better.
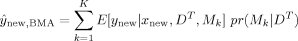
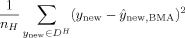
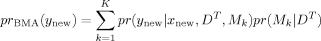
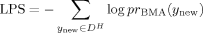
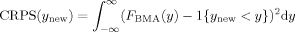
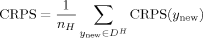
The CRPS measures the area between a step function at the observed value and the predictive cumulative distribution function. Unlike the LPS, it is defined when the prediction is deterministic; in that case it reduces to the mean absolute error (Hersbach, 2002).
The LPS and the CRPS assess both the sharpness of a predictive distribution and its calibration, namely the consistency between the distributional forecasts and the observations. However, the LPS assigns particularly harsh penalties to poor probabilistic forecasts, and so can be very sensitive to outliers and extreme events (Weigend and Shi, 2000; Gneiting and Raftery, 2007). The CRPS is more robust to outliers (Carney et al., 2009; Gneiting and Raftery, 2007), and hence it is our preferred measure of the performance of the predictive distribution as a whole. We also report the LPS for comparability with previous work, notably that of FLS (2001b) and LS.
We divided the dataset randomly into a training set that contains 80% of the data and thus leaves 20% of the data to be predicted, and we repeated the analysis for 400 different random splits, reporting the average over all splits. Table IV(A) shows the predictive performance of the 12 parameter priors in conjunction with uniform model priors as evaluated by the MSE, LPS and CRPS.
| Prior | Meana | Mediana | %b |
|---|---|---|---|
| MSE | |||
| 11 | 0.073 | 0.014 | 69*** |
| 9 | 0.075 | 0.012 | 69*** |
| 6 | 0.039 | 0.002 | 55** |
| 12 | 0.085 | 0.006 | 71*** |
| 3 | 0.083 | 0.005 | 69*** |
| 4 | 0.059 | 0.003 | 57*** |
| 8 | 0.051 | 0.003 | 58*** |
| 2 | 0.022 | 0.003 | 58*** |
| 5 | 0.008 | 0.003 | 55** |
| 7 | 0.013 | 0.004 | 56*** |
| CRPS | |||
| 11 | 0.854 | 0.030 | 69*** |
| 9 | 0.944 | 0.029 | 69*** |
| 6 | 0.233 | 0.005 | 57*** |
| 12 | 0.675 | 0.009 | 65*** |
| 3 | 0.533 | 0.007 | 65*** |
| 4 | 0.000 | 0.002 | 53 |
| 8 | 0.058 | 0.003 | 55** |
| 2 | 0.193 | 0.008 | 58*** |
| 5 | 0.708 | 0.012 | 60*** |
| 7 | 1.085 | 0.018 | 64*** |
| LPS | |||
| 11 | 0.711 | 0.711 | 61*** |
| 9 | 1.078 | 1.437 | 63*** |
| 6 | − 1.617 | − 0.715 | 41*** |
| 12 | 1.719 | 1.668 | 77*** |
| 3 | 1.337 | 1.348 | 73*** |
| 4 | − 1.557 | − 0.780 | 38*** |
| 8 | − 1.647 | − 0.846 | 39*** |
| 2 | − 1.181 | − 0.435 | 44*** |
| 5 | − 0.755 | 0.178 | 51 |
| 7 | −0.250 | 0.731 | 56*** |
The MSE and the CRPS agree that our baseline Prior 1 decisively outperformed all the other priors. The LPS suggests, however, that Priors 2, 4, 6, and 8 outperform Prior 1. Since this result runs counter to the results from the two other scoring rules, it seems possible that the difference is due to influential observations in the dataset or outliers in a particular subsample. Several of the regressors have extreme outlying values. When such cases are in the test set, they can have a large effect on the LPS, while the CRPS is more robust to individual cases. Given the known outlier sensitivity of the LPS, we discount the results it gives for this dataset, and conclude that Prior 1 performs best in this case.
Table IV(B) compares our results with those of LS (Table V), who did not consider the UIP, but who did include random model priors for parameter Priors 9 and 12, in which a prior distribution was put on the prior inclusion probability π. To achieve an exact comparison with the LS results, Table IV(B) is based on a 85/15 subsample split and we divide our LPS values by the number of held out observations (following LS's LPS formula). In addition, we report absolute log predicitve scores (LPS) in Table IV(B) (not values relative to the UIP LPS scores as we do in all of our other tables). Table IV(B) shows that Prior 1 outperformed Priors 9 and 12, whether the model priors are fixed or random.
| Model prior | Fixed, uniform | Random | |||
|---|---|---|---|---|---|
| Authors | EPR | LS | LS | ||
| Parameter prior | 1 | 9 | 12 | 9 | 12 |
| Min. | 0.16 | 1.11 | 0.86 | 1.20 | 1.11 |
| Mean | 0.97 | 1.63 | 1.65 | 1.63 | 1.61 |
| Max. | 2.32 | 2.85 | 2.76 | 2.47 | 2.64 |
| SD | 0.47 | 0.37 | 0.42 | 0.25 | 0.34 |
- Note: 100 random split trials (subsamples) and 15% hold-out sample. LS, Ley and Steel (2007b); EPR, Eicher, Papageorgiou, Raftery. Log predictive score: to conform to the Ley and Steel's LPS definition we divide here by the number of held out regressors
| Prior | Prior model size = 3 | Prior model size = 5 | Prior model size = 6 | Prior model size = 7 | Prior model size = 8 | Prior model size = 9 | Prior model size = 11 | Prior model size = 13 | Prior model size = 15 | Prior model size = 17 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | Mediana | %b | |
| MSE | MSE | MSE | MSE | MSE | MSE | MSE | MSE | MSE | MSE | |||||||||||
| 11 | 0.16 | 71*** | 0.13 | 72*** | 0.14 | 77*** | 0.13 | 71*** | 0.12 | 71*** | 0.16 | 79*** | 0.17 | 81*** | 0.11 | 71*** | 0.10 | 71*** | 0.10 | 72*** |
| 9 | 0.15 | 71*** | 0.12 | 71*** | 0.14 | 78*** | 0.12 | 71*** | 0.12 | 71*** | 0.16 | 81*** | 0.16 | 80*** | 0.11 | 73*** | 0.11 | 74*** | 0.10 | 73*** |
| 6 | 0.09 | 70*** | 0.08 | 71*** | 0.13 | 75*** | 0.09 | 73*** | 0.09 | 72*** | 0.15 | 79*** | 0.12 | 77*** | 0.08 | 80*** | 0.08 | 81*** | 0.07 | 79*** |
| 1 | 0.03 | 67*** | 0.02 | 67*** | 0.02 | 67*** | 0.02 | 69*** | 0.02 | 68*** | 0.04 | 58*** | 0.02 | 69*** | 0.01 | 68*** | 0.01 | 69*** | 0.01 | 70*** |
| 12 | 0.10 | 70*** | 0.09 | 71*** | 0.13 | 75*** | 0.09 | 72*** | 0.09 | 73*** | 0.15 | 80*** | 0.12 | 78*** | 0.08 | 82*** | 0.08 | 81*** | 0.07 | 81*** |
| 3 | 0.09 | 70*** | 0.08 | 71*** | 0.13 | 75*** | 0.09 | 73*** | 0.09 | 72*** | 0.15 | 79*** | 0.12 | 77*** | 0.08 | 80*** | 0.08 | 81*** | 0.07 | 79*** |
| 4 | 0.08 | 68*** | 0.06 | 67*** | 0.09 | 70*** | 0.05 | 65*** | 0.05 | 65*** | 0.13 | 78*** | 0.11 | 76*** | 0.06 | 69*** | 0.06 | 73*** | 0.05 | 73*** |
| 8 | 0.09 | 67*** | 0.08 | 65*** | 0.09 | 68*** | 0.05 | 65*** | 0.05 | 65*** | 0.13 | 74*** | 0.12 | 76*** | 0.05 | 66*** | 0.05 | 71*** | 0.05 | 71*** |
| 2 | 0.09 | 67*** | 0.07 | 68*** | 0.10 | 70*** | 0.07 | 68*** | 0.06 | 67*** | 0.12 | 74*** | 0.14 | 76*** | 0.05 | 63*** | 0.06 | 65*** | 0.05 | 65*** |
| 5 | 0.15 | 70*** | 0.13 | 69*** | 0.15 | 76*** | 0.11 | 67*** | 0.11 | 67*** | 0.17 | 73*** | 0.17 | 77*** | 0.09 | 65*** | 0.09 | 64*** | 0.08 | 65*** |
| 7 | 0.19 | 75*** | 0.17 | 73*** | 0.18 | 80*** | 0.16 | 73*** | 0.15 | 72*** | 0.20 | 75*** | 0.20 | 80*** | 0.13 | 69*** | 0.12 | 69*** | 0.10 | 68*** |
| CRPS | CRPS | CRPS | CRPS | CRPS | CRPS | CRPS | CRPS | CRPS | CRPS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 0.04 | 83*** | 0.04 | 80*** | 0.03 | 78*** | 0.03 | 79*** | 0.02 | 77*** | 0.03 | 72*** | 0.05 | 78*** | 0.01 | 77*** | 0.01 | 72*** | 0.01 | 71*** |
| 9 | 0.04 | 85*** | 0.03 | 77*** | 0.02 | 79*** | 0.02 | 79*** | 0.02 | 75*** | 0.02 | 71*** | 0.04 | 75*** | 0.01 | 73*** | 0.01 | 74*** | 0.01 | 71*** |
| 6 | 0.01 | 69*** | 0.01 | 66*** | 0.01 | 69*** | 0.01 | 66*** | 0.01 | 67*** | 0.01 | 62*** | 0.01 | 63*** | 0.00 | 71*** | 0.00 | 62*** | 0.00 | 63*** |
| 1 | 0.00 | 61*** | 0.00 | 59** | 0.00 | 62*** | 0.00 | 61*** | 0.00 | 61*** | 0.01 | 53 | 0.00 | 59** | 0.00 | 57** | 0.00 | 57** | 0.00 | 55** |
| 12 | 0.02 | 73*** | 0.01 | 68*** | 0.01 | 71*** | 0.01 | 71*** | 0.01 | 69*** | 0.01 | 62*** | 0.01 | 63*** | 0.00 | 68*** | 0.00 | 65*** | 0.00 | 68*** |
| 3 | 0.01 | 69*** | 0.01 | 66*** | 0.01 | 69*** | 0.01 | 66*** | 0.01 | 67*** | 0.01 | 62*** | 0.01 | 63*** | 0.00 | 71*** | 0.00 | 62*** | 0.00 | 63*** |
| 4 | 0.01 | 67*** | 0.00 | 56* | 0.00 | 59** | 0.00 | 56* | 0.00 | 53 | 0.01 | 59** | 0.00 | 53 | 0.00 | 59** | 0.00 | 57** | 0.00 | 57** |
| 8 | 0.01 | 65*** | 0.00 | 57** | 0.00 | 59** | 0.00 | 56* | 0.00 | 56* | 0.00 | 55*** | 0.00 | 56** | 0.00 | 53 | 0.00 | 55 | 0.00 | 56* |
| 2 | 0.01 | 72*** | 0.01 | 66*** | 0.01 | 66*** | 0.00 | 58** | 0.00 | 57** | 0.01 | 61*** | 0.01 | 65*** | 0.00 | 53 | 0.00 | 54 | 0.00 | 52 |
| 5 | 0.01 | 65*** | 0.01 | 65*** | 0.00 | 63*** | 0.00 | 61*** | 0.00 | 61*** | 0.01 | 59** | 0.01 | 57*** | 0.00 | 55 | 0.00 | 51 | 0.00 | 51 |
| 7 | 0.01 | 63*** | 0.01 | 58** | 0.00 | 60*** | 0.00 | 59** | 0.00 | 62*** | 0.01 | 60*** | 0.01 | 57*** | 0.00 | 55* | 0.00 | 52 | 0.00 | 51 |
| LPS | LPS | LPS | LPS | LPS | LPS | LPS | LPS | LPS | LPS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 1.50 | 62*** | 1.17 | 59** | 1.89 | 64*** | 1.23 | 58** | 1.15 | 57** | 3.58 | 82*** | 4.18 | 78*** | 0.82 | 55* | 0.89 | 57** | 0.99 | 57** |
| 9 | 1.53 | 62*** | 1.31 | 60*** | 1.96 | 64*** | 1.30 | 59** | 1.16 | 59** | 3.51 | 82*** | 4.28 | 78*** | 1.10 | 56* | 1.21 | 59** | 1.24 | 61*** |
| 6 | 0.40 | 54 | 0.66 | 54 | 1.72 | 59** | 0.68 | 55*** | 0.89 | 56 | 2.79 | 82*** | 3.23 | 75*** | 1.26 | 65*** | 1.41 | 70*** | 1.60 | 72*** |
| 1 | 0.86 | 62*** | 0.57 | 61*** | 0.43 | 61*** | 0.34 | 60*** | 0.42 | 59** | 1.63 | 60*** | 0.32 | 61*** | 0.22 | 61*** | 0.18 | 62*** | 0.10 | 63*** |
| 12 | 0.66 | 56* | 0.76 | 54 | 1.99 | 59** | 0.87 | 57** | 1.13 | 57** | 2.89 | 83*** | 3.34 | 76*** | 1.46 | 67*** | 1.58 | 72*** | 1.94 | 73*** |
| 3 | 0.40 | 54 | 0.66 | 54 | 1.72 | 59** | 0.68 | 55 | 0.89 | 56** | 2.79 | 82*** | 3.23 | 75*** | 1.26 | 65*** | 1.41 | 70*** | 1.60 | 72*** |
| 4 | 0.18 | 52 | − 0.28 | 47 | 0.92 | 57** | − 0.44 | 47 | − 0.44 | 47 | 2.36 | 77*** | 3.01 | 72*** | − 0.54 | 44*** | − 0.48 | 45* | − 0.53 | 43** |
| 8 | 0.45 | 53 | − 0.05 | 48 | 0.58 | 57** | − 0.43 | 47 | − 0.40 | 47 | 2.37 | 77*** | 3.11 | 73*** | − 0.62 | 42*** | − 0.61 | 43*** | − 0.82 | 44** |
| 2 | 0.46 | 53 | 0.10 | 51 | 0.99 | 58** | − 0.17 | 48 | − 0.28 | 48 | 2.65 | 78*** | 3.29 | 75*** | − 0.39 | 48 | − 0.40 | 46 | − 0.54 | 45* |
| 5 | 1.45 | 59** | 1.11 | 58** | 1.68 | 61*** | 0.81 | 56* | 0.69 | 55* | 3.43 | 88*** | 4.05 | 79*** | 0.20 | 52 | 0.02 | 50 | − 0.02 | 50 |
| 7 | 1.86 | 62*** | 1.69 | 61*** | 2.06 | 64*** | 1.45 | 58** | 1.30 | 58** | 4.22 | 91*** | 4.61 | 81*** | 0.83 | 55* | 0.69 | 54 | 0.57 | 53 |
- a Refers to the improvement in the score attained by the UIP compared to a given alternative prior.
- b Indicates percent of trials where ‘success’ is a better predictive score by the UIP than by the alternative prior. Asterisks indicate ***99%, **95%, and *90% significance levels based on binomial p-values, P(X ≥ z), for the given number of trials and successes, where success is defined as a better score for Prior 1 (the alternative) as compared to the alternative prior (UIP) if the percentage is above (below) 50%.
- Note: Priors 9 and 10 are identical in the growth context. Priors are arranged by effective g-value (see Figure 1).
Recall from Table IV(a) that Prior 1 had better (lower) LPS values than either Prior 9 or Prior 12 with uniform model priors. LS then show that uniform or random model priors generate similar means for Priors 9 and 12. Hence it is no surprise that UIP also has lower LPS values than Priors 9 or 12 with random model priors.
Overall, the unit information prior (Prior 1) with a uniform model prior performed best of the candidate default priors that we have evaluated in terms of cross-validated predictive performance on the growth dataset. Also, the prior expectation of a model size of about seven regressors is not supported by the predictive performance results.
4. SIMULATED DATA
We now examine the effects of the set of priors using simulated datasets from two models that have been prominent in the BMA literature: Model 1 that is based on Raftery et al. (1997) and was used by FLS; and Model 2 that is based on George and McCulloch (1993), which was also used by FLS.
 , where E is an n × 5 matrix of independent standard normal deviates. Model 1 implies small to moderate correlations between the first and last five regressors r1, …, r5 and r11, …, r15. The correlations increase from 0.153 to 0.561 for r1, …, r5 and are somewhat larger between the last five regressors, reaching 0.740. Each regressor is centered by subtracting its mean, which results in a matrix Z = (z1, …, z15). A vector of n observations is then generated according to
, where E is an n × 5 matrix of independent standard normal deviates. Model 1 implies small to moderate correlations between the first and last five regressors r1, …, r5 and r11, …, r15. The correlations increase from 0.153 to 0.561 for r1, …, r5 and are somewhat larger between the last five regressors, reaching 0.740. Each regressor is centered by subtracting its mean, which results in a matrix Z = (z1, …, z15). A vector of n observations is then generated according to
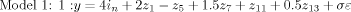 (10)
(10)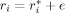 , i = 1, …, p, where
, i = 1, …, p, where  and e are n-dimensional vectors of independent standard normal deviates. This induces a pairwise correlation of 0.5 between all regressors. Let Z again denote the n × p matrix of centered regressors, and generate the n observations according to
and e are n-dimensional vectors of independent standard normal deviates. This induces a pairwise correlation of 0.5 between all regressors. Let Z again denote the n × p matrix of centered regressors, and generate the n observations according to
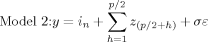 (11)
(11)For Model 1, the differences in the prior variances shown in Figure 4(a)–(c) are similar to the magnitudes observed for the growth dataset in Figure 1. Again about three orders of magnitude separate the most concentrated and most diffuse priors, although the level of concentration is a bit lower in the simulated datasets. Table VI(A) and (B) shows, however, that with well-behaved data all priors basically agree upon which regressors have an effect, even in a dataset that contains only 50 observations. For the larger simulated dataset in Model 2, with about three times the number of candidate regressors as in Model 1, we again find diversity in the number of regressors identified as having an effect on the dependent variable. Table VI(C) shows that several priors are clearly too concentrated, with Priors 2, 5, and 7 identifying only between three and seven of the 20 relevant regressors that in fact had an effect on the dependent variable. As the prior variance increases enough to cover the more substantive part of the likelihood, the priors are able to pick up more of the relevant regressors, getting closer to the correct number of regressors. Priors 3, 9, and 11 pick up 16 candidate regressors, although only Prior 1 shows appropriately high posterior inclusion probabilities.
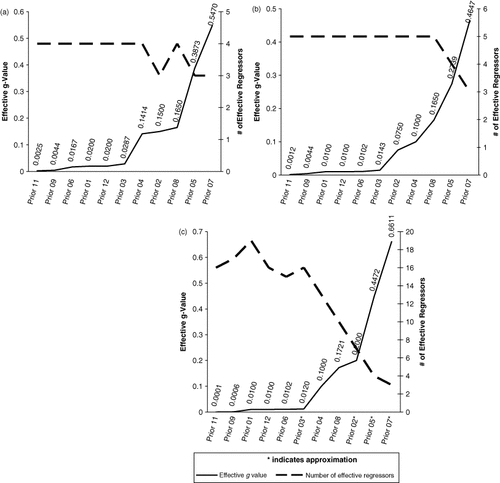
Effective g-value (inversely related to prior variance) and number of effective regressors (posterior > 50%). (a) Simulated data, Model 1 k = 15, n = 50. (b) Simulated data, Model 1, k = 15, n = 100. (c) Simulated data, Model 2, k = 40, n = 100. (1) Priors 9 and 10 are identical in the simulated datasets. (2) Priors 1 and 12 have the same g-value. (3) Priors are arranged by effective g-value (increasing left to right). (4) When priors depend on the exact model size, pk, (a)–(c) approximate the prior using the expected model size. Priors 11 and 1 are not exact g-priors, so the g-value is also an approximation
| Regressor | 11 | 9 | 6 | 1 | 12 | 3 | 4 | 2 | 8 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| z1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 99.9 | 99.5 |
| z7 | 100 | 100 | 99.3 | 100 | 100 | 100 | 99.8 | 99.2 | 99.6 | 94.4 | 90.9 |
| z11 | 99.6 | 99.6 | 96.9 | 99.9 | 99.7 | 99.7 | 98.6 | 95.6 | 97.9 | 84.3 | 79 |
| z5 | 70 | 67 | 65.5 | 73.7 | 70.5 | 71.2 | 67.8 | 46.2 | 65.1 | 36.9 | 34.5 |
| z2 | 18.5 | 23.6 | 37.3 | 34.9 | 32.2 | 34.9 | 37 | 20.9 | 35.7 | 22.6 | 22.3 |
| z4 | 19.9 | 23.1 | 36.7 | 32.9 | 30.7 | 33.2 | 35.8 | 22.1 | 34.9 | 26 | 26.3 |
| z14 | 18.8 | 13.8 | 32.5 | 27.4 | 23.4 | 26.8 | 31.1 | 11.2 | 29.2 | 14.7 | 15.9 |
| z9 | 10.6 | 8.7 | 31.3 | 20 | 16.7 | 20.1 | 28.2 | 8.8 | 26.3 | 11.4 | 12.5 |
| z3 | 9 | 9.3 | 29.2 | 21.7 | 18.1 | 21.5 | 27.3 | 8.4 | 25.4 | 11.4 | 12.5 |
| z13 | 10.7 | 7.5 | 22.1 | 14.1 | 12.5 | 14.4 | 19.6 | 7.7 | 18.6 | 11 | 12.4 |
| z12 | 10.2 | 8.9 | 20.2 | 15 | 13.6 | 15.2 | 18.6 | 8.2 | 17.7 | 10.5 | 11.3 |
| z8 | 6.7 | 5.3 | 18.1 | 9.5 | 8.7 | 10.1 | 15.2 | 7.2 | 14.7 | 11.2 | 12.6 |
| z15 | 6.4 | 6.1 | 15.3 | 9.7 | 9.1 | 10.3 | 13.5 | 6.3 | 13.1 | 7.8 | 8.4 |
| z6 | 5.1 | 4.2 | 7.3 | 4.9 | 5.1 | 5.4 | 6.4 | 5.2 | 6.5 | 6.8 | 7.2 |
| z10 | 5.2 | 4.4 | 7.1 | 4.9 | 5.2 | 5.4 | 6.3 | 5.3 | 6.4 | 7.1 | 7.5 |
| # effects | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 4 | 3 | 3 |
| Regressor | 11 | 9 | 1 | 12 | 6 | 3 | 2 | 4 | 8 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| z1 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| z7 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 99.6 | 97.9 |
| z11 | 99.4 | 99.4 | 99.7 | 99.5 | 99.5 | 99.5 | 97.6 | 99.1 | 98.1 | 86.5 | 75.6 |
| z5 | 92.9 | 92.9 | 95.6 | 94.5 | 94.5 | 94.9 | 83.8 | 93.9 | 90.5 | 57.6 | 43.6 |
| z15 | 79.9 | 81.1 | 87.8 | 85 | 85.1 | 86.2 | 63.2 | 85.1 | 78.8 | 35.8 | 28.3 |
| z6 | 15.6 | 15.4 | 22.1 | 21.2 | 21.3 | 23.7 | 14.9 | 39 | 38 | 13 | 12.3 |
| z12 | 13.7 | 13.2 | 19.2 | 18.3 | 18.4 | 20.5 | 12.4 | 33.2 | 32.2 | 10.9 | 10.4 |
| z4 | 134.3 | 15.8 | 17.3 | 17.9 | 18 | 19.1 | 23 | 27.5 | 29.7 | 33.6 | 34.2 |
| z13 | 7.7 | 6.9 | 9.9 | 9.7 | 9.7 | 10.9 | 7.1 | 16.7 | 16.6 | 7.9 | 8.8 |
| z10 | 4.8 | 5.1 | 7.9 | 7.6 | 7.6 | 8.7 | 5.2 | 17.7 | 17.8 | 5.3 | 5.4 |
| z3 | 4 | 6.1 | 7.4 | 7.6 | 7.6 | 8.3 | 7.7 | 12.3 | 13.1 | 9.1 | 8.7 |
| z2 | 3.2 | 5 | 7 | 6.9 | 6.9 | 7.8 | 5.4 | 13.2 | 13.4 | 5.9 | 5.9 |
| z8 | 6 | 5.6 | 7 | 7 | 7.1 | 7.7 | 6.4 | 11 | 11.3 | 7.4 | 7.7 |
| z9 | 4.9 | 4.6 | 6.8 | 6.6 | 6.7 | 7.6 | 4.9 | 14.3 | 14.4 | 5.2 | 5.2 |
| z14 | 4.6 | 4.3 | 6 | 5.9 | 6 | 6.7 | 4.6 | 10.9 | 11.1 | 5 | 5.3 |
| # effects | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 3 |
| Regressor | 11 | 9 | 1 | 12 | 6 | 3 | 4 | 8 | 2 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| z1 | 1.5 | 1.8 | 2.8 | 2.4 | 2 | 2.7 | 0.8 | 1.3 | 0.8 | 2.1 | 2 |
| z2 | 0.9 | 1.2 | 8.6 | 1.7 | 1.5 | 2 | 0.2 | 0.1 | 0 | 0 | 0 |
| z3 | 4.1 | 4.8 | 13.9 | 4.9 | 4.5 | 5.6 | 0.4 | 0.2 | 0 | 0.4 | 0.9 |
| z4 | 0.6 | 0.6 | 1.6 | 1.1 | 1.3 | 1.2 | 0.1 | 0 | 0 | 1 | 2.1 |
| z5 | 0.3 | 0.4 | 1.9 | 0.8 | 0.5 | 0.9 | 0.2 | 0.6 | 0.7 | 0.2 | 0.1 |
| z6 | 0.4 | 0.5 | 3.9 | 1 | 0.5 | 1.1 | 0.1 | 0 | 0 | 0 | 0 |
| z7 | 0.3 | 0.3 | 1.5 | 0.8 | 0.1 | 0.9 | 0.2 | 0.5 | 0.9 | 0.5 | 0.3 |
| z8 | 0.4 | 0.6 | 4.5 | 1 | 0.1 | 1.1 | 0.1 | 0.1 | 0.1 | 1 | 1.1 |
| z9 | 0.3 | 0.4 | 2.5 | 0.8 | 0.5 | 0.9 | 0.1 | 0 | 0 | 0 | 0 |
| z10 | 0.4 | 0.4 | 1.6 | 0.9 | 0.6 | 0.9 | 0.1 | 0 | 0.1 | 1.3 | 1.9 |
| z11 | 6.1 | 6.7 | 14.3 | 6.1 | 6.2 | 6.8 | 0.5 | 0.2 | 1.2 | 6.3 | 7 |
| z12 | 10.7 | 14.2 | 33.2 | 11.7 | 10.7 | 13.2 | 1.8 | 0.7 | 0 | 0 | 0 |
| z13 | 0.3 | 0.4 | 3 | 0.9 | 0.6 | 1 | 0.1 | 0 | 0 | 0 | 0.2 |
| z14 | 12.7 | 12.6 | 6.8 | 15.7 | 14.7 | 16 | 12 | 7.8 | 0.5 | 0.4 | 0.2 |
| z15 | 0.4 | 0.5 | 3.9 | 0.9 | 0.1 | 1.1 | 0.1 | 0 | 0 | 0 | 0.1 |
| z16 | 1.5 | 1.8 | 4.9 | 2.1 | 2.3 | 2.4 | 0.2 | 0.1 | 0 | 0.6 | 1.2 |
| z17 | 0.5 | 0.6 | 2.5 | 1 | 1 | 1.1 | 0.2 | 0.4 | 0.4 | 2.6 | 3.4 |
| z18 | 10.4 | 10.6 | 7.1 | 8.8 | 9.6 | 9.3 | 14.7 | 22.4 | 29.9 | 23.7 | 17.8 |
| z19 | 0.8 | 1 | 6.1 | 1.4 | 1.3 | 1.7 | 1.4 | 3.6 | 9.3 | 10.6 | 9 |
| z20 | 0.6 | 0.7 | 2.7 | 1.2 | 1.4 | 1.3 | 1.7 | 1.5 | 1.9 | 1.2 | 1.2 |
| z21 | 4.4 | 7 | 57.1 | 4.2 | 4 | 5.3 | 0.4 | 0.9 | 2.1 | 1 | 0.6 |
| z30 | 35.3 | 41.9 | 94 | 26.5 | 26.5 | 30 | 3.8 | 1.5 | 0 | 0.4 | 1.1 |
| z38 | 44.6 | 50.9 | 95.9 | 38.4 | 38.4 | 41.2 | 20.1 | 11.9 | 1.3 | 0.6 | 0.3 |
| z33 | 98.7 | 99 | 100 | 93.3 | 93.2 | 93.7 | 38.2 | 19.8 | 0.5 | 3.8 | 5.3 |
| z22 | 72.2 | 75.4 | 98.6 | 50.9 | 49.7 | 54.8 | 7.4 | 9.1 | 21.8 | 40.4 | 45.2 |
| z25 | 99.7 | 99.8 | 100 | 96.8 | 96.6 | 97.1 | 29.1 | 14.7 | 1.1 | 1.1 | 0.8 |
| z27 | 100 | 100 | 100 | 99.3 | 99.4 | 99.3 | 64.5 | 39.4 | 0.9 | 0.3 | 0.3 |
| z32 | 99 | 99.3 | 100 | 94.2 | 93.8 | 94.7 | 50.8 | 30.9 | 1.3 | 1 | 1.4 |
| z35 | 100 | 100 | 100 | 100 | 100 | 100 | 72.5 | 45.7 | 2.6 | 2.7 | 2.9 |
| z23 | 100 | 100 | 100 | 100 | 100 | 100 | 81.9 | 56.9 | 3.1 | 2 | 2.3 |
| z37 | 100 | 100 | 100 | 100 | 100 | 100 | 83.1 | 57.8 | 4.6 | 1.6 | 1.1 |
| z39 | 100 | 100 | 100 | 100 | 100 | 100 | 97.3 | 86.7 | 31 | 13.4 | 10.4 |
| z31 | 100 | 100 | 100 | 99.4 | 99.5 | 99.4 | 77.4 | 79 | 67.6 | 45.7 | 35.2 |
| z29 | 100 | 100 | 100 | 100 | 100 | 100 | 99.9 | 98.7 | 78.3 | 37.3 | 24.6 |
| z24 | 100 | 100 | 100 | 100 | 100 | 100 | 99.4 | 95 | 55.7 | 26.6 | 19.9 |
| z36 | 100 | 100 | 100 | 100 | 100 | 100 | 80.7 | 61.4 | 28.4 | 19.6 | 14 |
| z28 | 100 | 100 | 100 | 100 | 100 | 100 | 99.9 | 99.2 | 90.2 | 64.5 | 50.5 |
| z26 | 99 | 99.2 | 100 | 92.7 | 93.5 | 93.3 | 55.8 | 66.7 | 82.2 | 85.6 | 86.1 |
| z40 | 100 | 100 | 100 | 99.5 | 99.4 | 99.5 | 85.1 | 89.3 | 100 | 95.3 | 86.8 |
| # effects | 16 | 17 | 19 | 16 | 15 | 16 | 13 | 10 | 6 | 3 | 3 |
- Note: Shaded variables should have an effect. Posterior inclusion probabilities that exceed 50% are in bold font (Jeffreys, 1961). Priors 9 and 10 are identical in the simulated datasets. Uniform model priors throughout. Priors arranged by effective g-value.
In summary, our simulation experiment shows that priors can matter, especially when there are many candidate regressors. The UIP is the only one that was robust across simulations, coming closest to identifying the right regressors in all cases.
Table VII shows the UIP's generally superior predictive performance. The MSE was consistently better for the UIP than for all other priors. The LPS was too, except for Prior 3 in Model 2. The CRPS preferred the UIP to all other priors for Model 2, but for Model 1 it preferred Priors 3, 4, 6, and 8 to Prior 1.
| (a) Model 1, k = 15, n = 50 | (b) Model 1, k = 15, n = 100 | (c) Model 2, k = 40, n = 100 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior | Meana | Mediana | %b | Prior | Meana | Mediana | %b | Prior | Meana | Mediana | %b |
| MSE | MSE | MSE | |||||||||
| 11 | 0.004 | 0.003 | 55** | 11 | 0.114 | 0.120 | 70*** | 11 | 0.010 | 0.007 | 90*** |
| 9 | 0.003 | 0.002 | 56** | 9 | 0.127 | 0.127 | 71*** | 9 | 0.007 | 0.006 | 90*** |
| 6 | 0.029 | 0.026 | 67*** | 6 | 1.689 | 2.041 | 85*** | 6 | 0.027 | 0.026 | 75*** |
| 12 | 0.000 | 0.001 | 55** | 12 | 0.019 | 0.057 | 61*** | 12 | 0.003 | 0.003 | 79*** |
| 3 | 0.000 | 0.000 | 52 | 3 | − 0.015 | 0.043 | 56** | 3 | 0.002 | 0.001 | 64*** |
| 8 | 0.010 | 0.008 | 59*** | 8 | 1.025 | 1.303 | 77*** | 8 | 0.018 | 0.017 | 71*** |
| 4 | 0.009 | 0.007 | 59*** | 4 | 0.467 | 0.697 | 69*** | 4 | 0.008 | 0.007 | 62*** |
| 2 | 0.015 | 0.010 | 60*** | 2 | 0.398 | 0.668 | 70*** | 2 | 0.026 | 0.022 | 84*** |
| 5 | 0.064 | 0.054 | 75*** | 5 | 2.541 | 2.802 | 90*** | 5 | 0.063 | 0.059 | 88*** |
| 7 | 0.097 | 0.088 | 79*** | 7 | 4.116 | 4.440 | 94*** | 7 | 0.105 | 0.097 | 93*** |
| CRPS | CRPS | CRPS | |||||||||
| 11 | 0.021 | 0.007 | 72*** | 11 | 0.015 | 0.007 | 80*** | 11 | − 0.011 | − 0.002 | 47 |
| 9 | 0.010 | 0.004 | 69*** | 9 | 0.016 | 0.008 | 82*** | 9 | − 0.012 | 0.000 | 50 |
| 6 | − 0.002 | − 0.001 | 42*** | 6 | − 0.012 | − 0.005 | 27*** | 6 | 0.031 | 0.014 | 76*** |
| 12 | 0.000 | 0.000 | 47 | 12 | − 0.001 | 0.000 | 46* | 12 | 0.001 | 0.001 | 54* |
| 3 | − 0.001 | − 0.001 | 42*** | 3 | − 0.005 | − 0.003 | 26*** | 3 | 0.006 | 0.002 | 57*** |
| 8 | − 0.002 | − 0.001 | 42*** | 8 | − 0.012 | − 0.005 | 25*** | 8 | 0.028 | 0.013 | 73*** |
| 4 | − 0.002 | − 0.002 | 41*** | 4 | − 0.012 | − 0.006 | 23*** | 4 | 0.028 | 0.012 | 71*** |
| 2 | 0.001 | 0.001 | 54* | 2 | − 0.002 | 0.000 | 48 | 2 | 0.001 | 0.004 | 58** |
| 5 | 0.001 | 0.001 | 54* | 5 | − 0.010 | − 0.003 | 33*** | 5 | 0.022 | 0.013 | 71*** |
| 7 | 0.002 | 0.002 | 57*** | 7 | − 0.009 | − 0.003 | 38*** | 7 | 0.027 | 0.016 | 74*** |
| LPS | LPS | LPS | |||||||||
| 11 | 0.022 | 0.057 | 56** | 11 | 0.114 | 0.120 | 70*** | 11 | 0.443 | 0.463 | 81*** |
| 9 | 0.044 | 0.053 | 55** | 9 | 0.127 | 0.127 | 71*** | 9 | 0.279 | 0.331 | 79*** |
| 6 | 1.076 | 1.542 | 76*** | 6 | 1.689 | 2.041 | 85*** | 6 | 3.885 | 2.734 | 77*** |
| 12 | − 0.091 | 0.030 | 52 | 12 | 0.019 | 0.057 | 61*** | 12 | − 0.418 | 0.016 | 51 |
| 3 | − 0.114 | 0.049 | 56** | 3 | − 0.015 | 0.043 | 56** | 3 | − 0.543 | − 0.092 | 45** |
| 8 | 0.414 | 0.817 | 71*** | 8 | 1.025 | 1.303 | 77*** | 8 | 2.955 | 1.872 | 73*** |
| 4 | 0.374 | 0.768 | 71*** | 4 | 0.467 | 0.697 | 69*** | 4 | 1.784 | 0.954 | 67*** |
| 2 | 0.428 | 0.849 | 70*** | 2 | 0.398 | 0.668 | 70*** | 2 | 2.824 | 1.475 | 76*** |
| 5 | 1.823 | 2.330 | 84*** | 5 | 2.541 | 2.802 | 90*** | 5 | 5.782 | 4.274 | 87*** |
| 7 | 2.453 | 2.962 | 87*** | 7 | 4.116 | 4.440 | 94*** | 7 | 7.684 | 6.124 | 92*** |
- a Refers to the improvement in the score attained by the UIP compared to a given alternative prior.
- b Indicates percent of trials where ‘success’ is a better predictive score by the UIP than by the alternative prior. Asterisks indicate ***99%, **95%, and *90% significance levels based on binomial p-values, P(X ≥ z), for the given number of trials and successes, where success is defined as a better score for prior 1 (the alternative) as compared to the alternative prior (UIP) if the percentage is above (below) 50%.
- Note: Priors 9 and 10 are identical in the simulated dataset
5. CONCLUSION
Model uncertainty is intrinsic in economic analysis and the economic growth literature has been a showcase for model uncertainty over the past decade. Over 140 growth determinants have been motivated by the empirical literature, and the number of competing theories has grown dramatically since the advent of the New Growth Theory. Bayesian model averaging (BMA) provides a solid theoretical foundation for addressing model uncertainty as part of the empirical strategy.
However, BMA faces an important challenge. In this paper we showed that for a well-known growth dataset the results of BMA were sensitive to the prior specification. To identify the best prior for our growth dataset, we examined the predictive performance of 12 candidate default parameter priors that have been proposed in the statistics and economics literatures, as well as several model priors that have been advocated. We argue that predictive performance is a natural and neutral criterion for comparing different priors, and suggest the CRPS as a preferred measure. In addition, we examined these priors' success in identifying the right determinants in simulated datasets.
The UIP performed better than the other 11 priors in the growth data, and in simulated data, and as measured by our preferred median CRPS scoring rule. The UIP together with the uniform model prior also performed better than the Mitchell–Beauchamp model prior with expected model size 7, which had previously been recommended by Sala-i-Martin et al. (2004). We view the UIP with the uniform model prior as a reasonable default prior and starting place, but our results also highlight that researchers should also assess other possibilities that may be more appropriate for their data and applications.
We have focused here on priors where π and g are fixed. A Bayesian alternative is to put prior distributions on π and g themselves and integrate them out. Ley and Steel (2009) advocated putting a prior distribution on π but their results did not show that this led to improved predictive performance, as we have seen. Liang et al. (2008) reviewed a range of parameter priors that put a prior on g and integrate it out (they called them mixtures of g-priors). They assessed predictive performance in one example using only the highest probability model under each prior rather than BMA, and reported only the MSE of prediction, and not any measure of the performance of the full predictive distribution. They concluded that the differences in MSE were not enough to suggest that the mixtures of g-priors performed better than the fixed g methods. It would be interesting to see a more complete assessment of these methods in terms of predictive performance.
In terms of economic impact, the UIP with uniform model prior identified more growth determinants than Fernández et al. (2001b), who used the same dataset. The additional regressors include Primary and Secondary Education, Size of Labor Force, Ethnolinguistic Fragmentation, Minging, Latin America, Colonies (British, French, Spanish), Civil Liberties, Non Equipment Investment, Black Market Premium, Outward Orientation and Fraction Speaking English and Hindu.
ACKNOWLEDGMENTS
We thank three anonymous referees, the handling editor (Steven Durlauf), Veronica Berrocal, Gernot Doppelhofer, Edward George, Tilmann Gneiting, Jennifer Hoeting, Andros Kourtellos, Andreas Leukert, Eduardo Ley, Chih Ming Tan, Arnold Zellner, and seminar participants at the Department of Statistics, University of Washington, and the 2009 Econometric Society meetings in San Francisco for valuable comments and discussions. We also thank Amanda Cox for her tireless support, advice, and programming, Drew Creal for excellent software programming, Tilmann Gneiting for kindly sharing his CPRS code for BMA applications, Eduardo Ley for sharing data, and Fred Nick at the University of Washington Center for Social Science Computation and Research for providing computing support. Eicher gratefully acknowledges financial support from the University of Washington Center for Statistics and the Social Sciences through a seed grant. Raftery's research was supported by NSF grants ATM 0724721 and IIS-0534094, by NIH grant HD054511 and by the Joint Ensemble Forecasting System (JEFS) under subcontract No. S06-47225 from the University Corporation for Atmospheric Research (UCAR). The views expressed in this study are the sole responsibility of the authors and should not be attributed to the International Monetary Fund, its Executive Board, or its management.




