How do subjective mortality beliefs affect the value of social security and the optimal claiming ages?
Abstract
Households that postpone claiming Social Security benefits are, in effect, making additional purchases of the Social Security annuity and acquiring valuable longevity insurance. This paper investigates the impact of plausible variations of subjective mortality beliefs on the value of delayed claiming and the optimal claiming ages of retired workers. Using the Health and Retirement Study data, we show that older individuals could, on average, predict their life expectancy correctly; however, the average variance of age of death calculated from subjective mortality tables is 6.2%–14.4% lower than that from cohort life tables. Using numerical optimization techniques, we further show that, theoretically, older households place a lower value on delaying claiming when they have greater confidence in their ability to forecast their age of death. But the magnitude of this effect is not large enough to change their optimal claiming ages, unless they hold extreme subjective mortality beliefs. As a result, we conclude that subjective mortality beliefs alone cannot explain the prevalence of early claiming behaviors.
1 INTRODUCTION
In the United States, Social Security provides benefits in the form of an inflation-indexed annuity. Retired workers can claim their benefits from age 62 to 70. Those who delay claiming receive an increase in monthly benefits with the delay being equivalent to purchasing an actuarially fairly priced annuity from the Social Security Administration (SSA). Although there are no significant gains or losses in expected present value terms, Coile et al. (2002) and Sun and Webb (2011) show that delayed claiming provides older households valuable longevity insurance against the risk of outliving their wealth. Assuming population average mortality and given plausible preference parameters, both studies find that rational households who claim early suffer substantial losses in expected utility terms and run the risk of low consumption in the event that they live an unexpected lengthy life. Contrary to theoretical predictions, data from the Health and Retirement Study (HRS) show that most households claim their benefits soon after becoming eligible, even when they have sufficient financial assets to postpone claiming.
One of the central predictions of the life-cycle model is that consumption, savings, and annuitization decisions are influenced by subjective mortality beliefs. These decisions should be influenced not only by how long individuals expect to live but also by the degree of uncertainty regarding individuals' age of death. At one extreme, an individual who can forecast his age of death with certainty will value an annuity at the present value of the income stream to his age of death. This is because he can decumulate unannuitized wealth over a period ending with his date of death. At the other extreme, an individual with the same life expectancy but who is highly uncertain as to his age of death will value an annuity considerably more than its expected present value because he will otherwise need to substantially reduce his consumption to guard against the risk of outliving his wealth.
In this paper, we investigate how plausible variations of subjective mortality beliefs affect the value of postponing claiming Social Security benefits and whether subjective mortality beliefs contribute to the prevalence of early claiming behaviors. First, we examine the characteristics of older individuals' subjective mortality beliefs. Previous literature, for instance Hurd & McGarry (1995, 2002), primarily focuses on whether older individuals are capable of forming unbiased estimates of their life expectancy. This paper further explores whether older individuals can accurately quantify the degree of uncertainty regarding their age of death. Using the HRS data, we recover older individuals' subjective mortality tables and calculate that older individuals could, on average, predict their life expectancy correctly (which is consistent with previous studies). However, they exhibit greater confidence in their ability to forecast their age of death, relative to estimates that assume they experience the population average mortality. The average variance of age of death calculated from the estimated subjective mortality tables is 6.2%–14.4% lower than that from the SSA cohort life tables, indicating that individuals likely possess private information about their relative mortality risk.
Second, by constructing a life-cycle optimization model and incorporating the estimated subjective mortality statistics, we investigate how plausible variations of subjective mortality rates influence the value of delaying claiming and the optimal claiming ages of retired workers. As in Coile et al. (2002) and Sun and Webb (2011), the analysis concentrates on calculating the theoretical optimal claiming behaviors.1 We show that the value of postponing claiming will be greater for individuals who are more uncertain as to their age of death. However, the magnitude of this effect is not large enough to change the optimal claiming ages of retired households, unless they exhibit extreme subjective mortality beliefs.
The remainder of the paper is organized as follows: Section 2 briefly outlines features of the US Social Security program and discusses relevant research. Section 3 presents patterns of older individuals' subjective mortality beliefs. Section 4 develops a life-cycle optimization model to explore the impact of plausible variations of subjective mortality beliefs on the theoretical optimal claiming behaviors of older households. Section 5 concludes.
2 POLICY BACKGROUND AND PREVIOUS RESEARCH
2.1 The US Social Security program
Single individuals can claim their retired worker benefits earned through their own contributions from age 62 to 70, subject to an earnings test.2 Those who claim benefits at their full retirement age (FRA) receive the primary insurance amount (PIA).3 Benefits are adjusted for those who claim before or after their FRA. Benefits are reduced by 5/9 of 1% for each month retired workers claim before their FRA up to 36 months, 5/12 of 1% thereafter, and are increased by 2/3 of 1% for each month retired workers claim after their FRA until age 70.4 At a 3% real interest rate, the increase in monthly benefits from age 62 to 70 is approximately actuarially fair for retired workers with population average mortality born after 1943 (Sass et al., 2007).
Married couples can claim two additional categories of Social Security benefits: spousal benefits and survivors' benefits. The spousal benefits can be claimed by the spouse of the retired worker after age 62, provided that the spousal benefits exceed the retired worker benefits based on the spouse's own earnings record, and given that the retired worker has already claimed. The spousal benefits are 50% of the retired worker's PIA if the spouse claimed at or after the FRA. The spousal benefits are subject to a reduction of 25/36 of 1% for each month claimed before the spouse's FRA, up to 36 months, 5/12 of 1% thereafter. The survivors' benefits equal 100% of the deceased spouse's retired worker benefits if claimed at or after the FRA of the living spouse, which can be greater or less than the PIA, depending on the initial claiming age of the deceased spouse. The benefits can be claimed as early as age 60 and the reductions vary with the birth cohort of the living spouse. The benefits are bounded by a floor of 71.5% of the deceased spouse's PIA if claimed before the FRA of the living spouse and 82.5% of the deceased spouse's PIA if claimed at or after the FRA of the living spouse. The reductions in spousal and survivors' benefits are also approximately actuarially fair for older workers with population average mortality (Sass et al., 2007).
2.2 Research on subjective mortality beliefs
All previous studies of subjective mortality beliefs focus on whether individuals could form unbiased estimates about their life expectancy and have not considered the degree of uncertainty surrounding their age of death. Hurd and McGarry (1995) analyze subjective survival probability estimates provided by participants in the 1992 wave of the HRS. They show these estimates aggregate to life table probabilities and covary with risk factors. Hurd and McGarry (2002) further show that the above beliefs are predictive of subsequent mortality over a 2-year time horizon and respond in the panel to the receipt of new information. Sondergeld et al. (2002) find that, on average, individuals approaching retirement mis-state life expectancy by only small amounts.5 In contrast, Elder (2007) finds that HRS participants are pessimistic about their chances of surviving to age 75 but optimistic about their chances of surviving to age 85 relative to the predictions of life tables. He finds that higher subjective survival probabilities are associated with households holding a larger proportion of their wealth in stocks. But this relationship does not hold for individuals who assess their survival probability at 100%, suggesting that these individuals may differ in some way from those whose responses are close to, but less than, 100%. Problems arise in the interpretation of focal point responses.6 Gan et al. (2005) propose a Bayesian updating methodology for recovering the individual's true underlying beliefs. Although their approach produces life tables that vary with individuals' responses, it is not self-evident that these tables better reflect individuals' true underlying beliefs than the raw responses.
2.3 Research on Social Security claiming decisions
As discussed above, the Social Security program is an actuarially fair system, but the expected present value calculations do not incorporate the value of longevity insurance provided by Social Security benefits. An extensive literature, for example, Mitchell et al. (1999) and Brown and Poterba (2000), shows that the value of an annuity substantially exceeds its money's worth, defined as the expected present value of the income stream, discounted by an interest rate and annual survival probabilities, divided by the premium paid. This is because households face an uncertain age of death. If they choose not to annuitize, they run the risk of outliving their wealth if they decumulate too rapidly or forgoing valuable consumption opportunities if they decumulate too slowly. Given plausible preference parameters, Coile et al. (2002) and Sun and Webb (2011) find that it is optimal for retired workers to postpone claiming for a number of years. Coile et al. (2002) show that the optimal claiming age for a hypothetical single male born in 1930 could be as late as age 65, depending on his wealth level. Sun and Webb (2011) calculate the optimal claiming ages for typical nonbudget-constrained married couples born in 1946 are between age 67 and 70. The above papers assume that individuals' annual mortality risk equals that predicted by annuitant or SSA cohort life tables. Brown (2003) and Sun and Webb (2011) show that although mortality rates vary significantly by socioeconomic status, they have little effect on annuity valuation. Although the average household in high mortality groups faces a smaller chance of surviving to advanced old age, it will still want to restrict current consumption to safeguard against that possibility, should it choose not to annuitize.
Several researchers have undertaken empirical analyses of Social Security claiming decisions. Hurd et al. (2004) find a small but significant relationship between the subjective mortality beliefs and the age of claiming, as do Coile et al. (2002). They show individuals with low probability of surviving to age 75 are more likely to make the joint decision of retiring and claiming Social Security benefits early. But the average delay is much less than theoretical calculations suggest is optimal. Recently, the structural framework has made significant advancements in explaining the early claiming behaviors. Gustman and Steinmeier (2005) estimate a structural model of Social Security claiming decisions and attribute the prevalence of early claiming behaviors to heterogeneity in rates of time preference. Benitez-Silva et al. (2007) attribute the prevalence of early claiming behaviors to uncertainty as to whether scheduled benefits will be paid. Gustman and Steinmeier (2015) show that claiming decisions are influenced by retired workers' beliefs regarding the sustainability of the Social Security program, the expected returns of financial assets, and the utility aggregation of married couples. Pashchenko and Porapakkarm (2023) show that the low demand for public annuity can be explained by the combination of bequest motives and impatience. Bairoliya and McKiernan (2022) find that claiming frictions, including Social Security marital rules, labor income and medical expenditure risks, misbeliefs in mortality rates and in institutional details, and bequest motives, together account for 78% of early claiming behaviors in the data.
3 SUBJECTIVE MORTALITY BELIEFS
3.1 Focal point responses
We investigate individuals' subjective mortality beliefs using the HRS data. The HRS is a national representative panel of older individuals first interviewed in 1992. Individuals have been reinterviewed every 2 years. Starting from the first wave, individuals have been asked to self-assess their probabilities of surviving to age 75 and 85. However, the responses suffer from focal point biases, with considerable bunching of responses at 0%, 50%, 100%, and so on. It is unclear how to understand these responses. Do individuals literally mean that they rate their survival probability at 0% or 100%, or somewhere close to these numbers? In 2008, individuals who gave focal point responses were asked follow-up questions designed to elicit information regarding their true underlying beliefs. We use the answers to investigate the nature and extent of focal point biases.
In 2008, individuals aged less than 65 in the HRS were again asked to self-assess the probabilities that they would live to age 75 and 85 (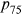 and
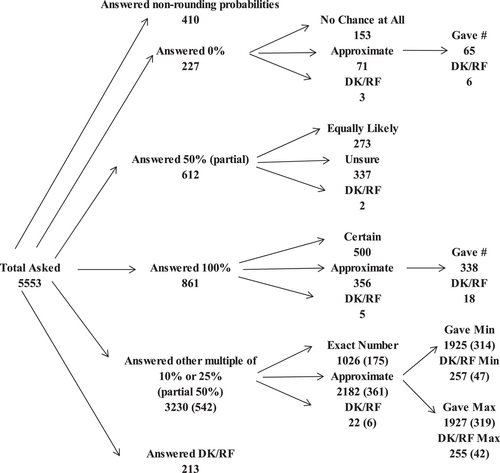
and 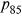 hereafter). As in previous waves, a substantial proportion of individuals provided focal point estimates of 0%, 50%, 100%, and so on. In contrast to previous waves, individuals were asked follow-up questions that were designed to test the degree of precision of their estimate. The series of questions are listed in Appendix A and Figure A1 of Appendix A summarizes the response patterns. Of the 5553 individuals who were asked the
hereafter). As in previous waves, a substantial proportion of individuals provided focal point estimates of 0%, 50%, 100%, and so on. In contrast to previous waves, individuals were asked follow-up questions that were designed to test the degree of precision of their estimate. The series of questions are listed in Appendix A and Figure A1 of Appendix A summarizes the response patterns. Of the 5553 individuals who were asked the 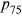 question, only 213 individuals (3.8%) either refused to answer or said that they did not know, 410 individuals (7.4%) gave a nonrounding probability, whereas 4930 individuals (88.8%) gave forecasts that were multiples of 10% or 25%, and were therefore potential focal point responses.
question, only 213 individuals (3.8%) either refused to answer or said that they did not know, 410 individuals (7.4%) gave a nonrounding probability, whereas 4930 individuals (88.8%) gave forecasts that were multiples of 10% or 25%, and were therefore potential focal point responses.
A total of 227 individuals answered that they had 0% chance of living to age 75 and 861 individuals said they were 100% sure they can survive to age 75. A total of 153 (67.4%) and 500 (58.1%) of them, respectively, stated that it was a precise estimate. A total of 1154 individuals answered they had a 50% chance of living to age 75. 448 (38.8%) of them stated that it meant equally likely that they would survive to age 75. Among those 2689 individuals who answered multiples of 10% or 25% but other than 0%, 50%, or 100%, 851 individuals (31.7%) stated it was an exact probability. So, individuals assessing 0% or 100% appear more confident of their forecasting abilities than those assessing other probabilities.
Individuals who answered 0% and 100% and said their forecast was an approximation were generally able to provide a more accurate estimate. The averages of the new estimates are 25.5% and 85.6%, respectively, considerably different than the original answers, suggesting that their original responses may not accurately reflect their true beliefs. Individuals who answered other multiples of 10% or 25% and said that their forecast was an approximation were asked to provide a range for their estimate. On average, the range length is 17.9% and the median of the range is 64.4%, exactly the same as the average of the original focal point forecasts of 64.4%. We interpret this as indicating that individuals attach a plausible degree of imprecision to their subjective mortality estimate.
The differences between the original estimates and the answers from the follow-up questions, especially for those who initially answered 0% or 100%, suggest the necessity of correcting for focal point biases before performing further calculations. Therefore, we update the answers of the 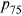 question to the more precise estimate if provided and to the median of the range if a range is provided in the follow-up questions.
question to the more precise estimate if provided and to the median of the range if a range is provided in the follow-up questions.
3.2 Recovering subjective mortality tables
Next, we estimate subjective mortality tables for each individual in the HRS sample, and calculate their self-assessed life expectancy and the variance of age of death. From the 5553 individuals, we drop 213 and 147 individuals who did not provide original forecasts for the 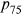 and
and 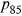 questions, respectively. We further drop 616 individuals who cannot provide a more precise estimate in the follow-up questions. We finally drop 358 individuals for whom
questions, respectively. We further drop 616 individuals who cannot provide a more precise estimate in the follow-up questions. We finally drop 358 individuals for whom 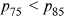 . This leaves a sample of 4219, of which 1653 are men and 2566 are women.7
. This leaves a sample of 4219, of which 1653 are men and 2566 are women.7
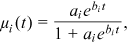 ()
()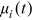 is individual i's subjective mortality rate at age
is individual i's subjective mortality rate at age 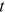 . Parameters
. Parameters 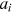 and
and  control how mortality rates change as individual
control how mortality rates change as individual 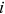 age. Using method of simulated moments, we estimate
age. Using method of simulated moments, we estimate  and
and 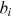 for each individual, so that the simulated probabilities of surviving to age 75 and 85 best match their self-reported probabilities in the data. We then simulate every individual's subjective mortality rates at all ages and calculate their life expectancy,
for each individual, so that the simulated probabilities of surviving to age 75 and 85 best match their self-reported probabilities in the data. We then simulate every individual's subjective mortality rates at all ages and calculate their life expectancy, 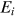 , and variance of age of death,
, and variance of age of death, 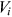 , conditional on attaining age 62, using the following formulas:
, conditional on attaining age 62, using the following formulas:
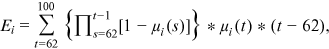 ()
()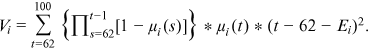 ()
()The patterns of subjective mortality beliefs of the HRS sample are presented in Tables 1 and 2, which compare the average and median life expectancy and variance of age of death calculated using the estimated subjective mortality rates and the objective mortality rates from the SSA cohort life tables, respectively.8 Conditional on being alive at age 62, we calculate the average subjective life expectancy is 21.7 years, slightly higher than the 21.6 years predicted by the cohort life tables, showing individuals could in general accurately predict their life expectancy. This is consistent with previous literature (Hurd & McGarry, 1995, 2002; Siegel et al., 2003). However, we show that the average variance of age of death calculated using the subjective mortality tables is 88.3 years2, 6.2% lower than the 94.2 years2 calculated using the objective mortality tables, indicating individuals predict their age of death with greater precision. The results hold for both men and women. The average subjective variances of age of death are 86.0 and 89.8 years2 for men and women, respectively, compared with the 90.5 and 96.5 years2 calculated using the cohort life tables. Additionally, the median subjective variance of age of death of the HRS sample is lower, at 76.1 years2, 20.9% lower than the median variance of age of death of 96.1 years2 calculated using the cohort life tables.
| Full sample | Clean sample | |||
|---|---|---|---|---|
| Life expectancy | Variance of age of death | Life expectancy | Variance of age of death | |
| All | ||||
| Predictions of subjective life tables | 21.7 | 88.3 | 21.8 | 80.6 |
| Predictions of SSA cohort life tables | 21.6 | 94.2 | 21.6 | 94.2 |
| N | 4219 | 2187 | ||
| Men | ||||
| Predictions of subjective life tables | 20.3 | 86.0 | 20.3 | 77.9 |
| Predictions of SSA cohort life tables | 19.5 | 90.5 | 19.6 | 90.5 |
| N | 1653 | 844 | ||
| Women | ||||
| Predictions of subjective life tables | 22.6 | 89.8 | 22.7 | 82.3 |
| Predictions of SSA cohort life tables | 22.9 | 96.5 | 22.9 | 96.5 |
| N | 2566 | 1343 | ||
- Note: Conditional on individuals' attaining age 62.
| Full sample | Clean sample | |||
|---|---|---|---|---|
| Life expectancy | Variance of age of death | Life expectancy | Variance of age of death | |
| All | ||||
| Predictions of subjective life tables | 22.5 | 76.1 | 22.5 | 57.6 |
| Predictions of SSA cohort life tables | 22.6 | 96.1 | 22.6 | 96.1 |
| N | 4219 | 2187 | ||
| Men | ||||
| Predictions of subjective life tables | 20.6 | 69.7 | 21.1 | 52.8 |
| Predictions of SSA cohort life tables | 19.5 | 90.4 | 19.5 | 90.4 |
| N | 1653 | 844 | ||
| Women | ||||
| Predictions of subjective life tables | 22.6 | 79.8 | 23.1 | 60.1 |
| Predictions of SSA cohort life tables | 22.8 | 96.6 | 22.8 | 96.6 |
| N | 2566 | 1343 | ||
- Note: Conditional on individuals' attaining age 62.
Because there is no follow-up  question, the focal point responses of the
question, the focal point responses of the  question may affect our results. We thus consider a clean sample which only consists of individuals who answered nonrounding probabilities and who answered multiples of 10% or 25% for the
question may affect our results. We thus consider a clean sample which only consists of individuals who answered nonrounding probabilities and who answered multiples of 10% or 25% for the  question and said it was an exact probability. These individuals provided a precise estimate for the
question and said it was an exact probability. These individuals provided a precise estimate for the 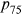 question and most likely also provided a precise estimate of the
question and most likely also provided a precise estimate of the 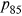 question.9 We show that individuals continue to predict their life expectancy accurately. The average and median subjective life expectancies are 21.8 and 22.5 years, respectively, compared with the 21.6 and 22.6 years calculated using objective mortality tables. However, the deviations of the subjective variance of age of death in the clean sample are larger than the full sample. We calculate the average and median subjective variance of the age of death of the clean sample are 80.6 and 57.6 years2 respectively, 14.4% and 40.1% lower than the 94.2 and 96.1 years2 calculated using the cohort life tables. The patterns again hold for both men and women. Thus, the results are sensitive to how to handle focal point responses.
question.9 We show that individuals continue to predict their life expectancy accurately. The average and median subjective life expectancies are 21.8 and 22.5 years, respectively, compared with the 21.6 and 22.6 years calculated using objective mortality tables. However, the deviations of the subjective variance of age of death in the clean sample are larger than the full sample. We calculate the average and median subjective variance of the age of death of the clean sample are 80.6 and 57.6 years2 respectively, 14.4% and 40.1% lower than the 94.2 and 96.1 years2 calculated using the cohort life tables. The patterns again hold for both men and women. Thus, the results are sensitive to how to handle focal point responses.
4 SOCIAL SECURITY CLAIMING DECISIONS
4.1 The life-cycle model
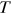 is set at 100. The individual maximizes its expected discounted lifetime utility as follows:
is set at 100. The individual maximizes its expected discounted lifetime utility as follows:
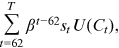 ()
()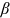 is the time discount factor.
is the time discount factor.  is the probability of the individual being alive at time
is the probability of the individual being alive at time 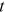 .
. 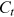 is the consumption. The utility function takes the common Constant Relative Risk Aversion (CRRA) form:
is the consumption. The utility function takes the common Constant Relative Risk Aversion (CRRA) form:
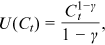 ()
()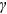 is the coefficient of risk aversion.
is the coefficient of risk aversion.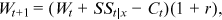 ()
()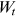 is the individual's nonannuitized financial wealth.
is the individual's nonannuitized financial wealth. 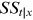 represents the Social Security benefits payable to the individual at time
represents the Social Security benefits payable to the individual at time 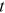 , conditional on claimed at age
, conditional on claimed at age 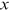 .
. 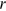 is the real interest rate. There is the usual nonnegative asset constraint, so that
is the real interest rate. There is the usual nonnegative asset constraint, so that 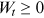 at all
at all 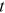 .
.In each period, the individual decides how much to consume and whether to claim Social Security benefits. The dynamic optimization problem is solved by backward induction. The baseline calculations assume the representative individual has population average mortality rates for the 1950 birth cohort from the SSA cohort life tables.11 The individual has a PIA of $2000.12 And as in Sun and Webb (2011), we endow the household with an amount of financial wealth equal to the EPV of Social Security benefits they would receive if claimed as soon as possible. This amount of financial wealth is sufficient to ensure that the household has sufficient financial assets to fund consumption from age 62 to 70, thereby mitigating the effect of liquidity constraint. We further assume the coefficient of risk aversion equals 3 which is in range as reported in the literature (Chetty, 2006). Finally, as is conventional in the annuity literature, both the real interest rate and the time discount rate are set at 3%.
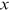 can be calculated as follows:
can be calculated as follows:
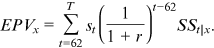 ()
()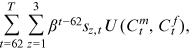 ()
()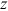 is the survival status. It equals 1 when both spouses are alive, 2 if only the husband is alive, and 3 if only the wife is alive.
is the survival status. It equals 1 when both spouses are alive, 2 if only the husband is alive, and 3 if only the wife is alive. 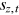 is the probability of the couple being in survival status
is the probability of the couple being in survival status 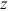 at time
at time 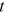 .
. 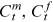 denote the consumption of the husband and the wife at time
denote the consumption of the husband and the wife at time 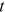 , respectively. We follow Brown and Poterba (2000) and assume that the married couple has an additive utility function of the following form:
, respectively. We follow Brown and Poterba (2000) and assume that the married couple has an additive utility function of the following form:
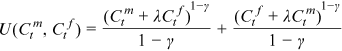 ()
()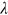 measures the jointness of the couple's consumption. When
measures the jointness of the couple's consumption. When 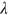 equals one, all consumption is joint. When
equals one, all consumption is joint. When  equals zero, none of the household's consumption is joint.
equals zero, none of the household's consumption is joint.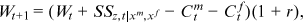 ()
()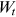 is the couple's joint financial wealth at time
is the couple's joint financial wealth at time 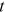 .
.  is the household's total Social Security benefits payable in survival state
is the household's total Social Security benefits payable in survival state 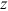 at time
at time 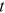 , conditional on the combination of ages at which the husband and the wife claimed benefits (
, conditional on the combination of ages at which the husband and the wife claimed benefits (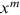 and
and 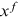 ). Again,
). Again, 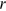 is the real return of a risk-free asset and there is the nonnegative asset constraint.
is the real return of a risk-free asset and there is the nonnegative asset constraint.In each period, the couple decide how much to consume, whether the husband should claim his Social Security retired worker benefits, and whether, conditional on the husband has claimed, the wife should claim her spousal benefits. Upon the death of the husband, spousal benefits are immediately replaced by survivor benefits. The optimal choices depend on their joint financial wealth and whether both or only one of the spouses is alive. We perform benchmark calculations for a single-earner couple and assume 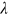 equals 0.5 as in Sun and Webb (2011). Both spouses are the same age with the population average mortality for the 1950 birth cohort in the baseline calculations. The husband has a PIA of $2000. We again endow the married couple with an amount of financial wealth equal to the EPV of Social Security benefits they would receive if claimed as soon as possible to rule out the effect of liquidity constraint. The rest of the parameters are the same as in the single's case.
equals 0.5 as in Sun and Webb (2011). Both spouses are the same age with the population average mortality for the 1950 birth cohort in the baseline calculations. The husband has a PIA of $2000. We again endow the married couple with an amount of financial wealth equal to the EPV of Social Security benefits they would receive if claimed as soon as possible to rule out the effect of liquidity constraint. The rest of the parameters are the same as in the single's case.
4.2 Recovering subjective mortality tables for the representative households
Using the same approach described in Section 3.2, we calculate the representative households' annual subjective mortality rates based on different numerical exercise assumptions. We first extract the objective mortality rates, given the representative household's gender and birth cohort, from the SSA cohort life tables, and calculate the population average life expectancy and variance of age of death, conditional on attaining age 62, based on Equations (2) and (3). We then estimate the representative household's parameters 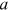 and
and 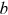 in Equation (1) using methods of simulated moments, so that the life expectancy and the variance of age of death calculated by simulated mortality rates best match the chosen life expectancy and variance of age of death, produced by population average mortality rates and adjusted as appropriate, that is,
in Equation (1) using methods of simulated moments, so that the life expectancy and the variance of age of death calculated by simulated mortality rates best match the chosen life expectancy and variance of age of death, produced by population average mortality rates and adjusted as appropriate, that is, 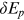 and
and 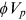 , where
, where 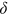 and
and 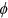 are adjustment factors based on proposed numerical experiments. We finally recover the representative individual's subjective mortality probabilities at each age using estimated parameters
are adjustment factors based on proposed numerical experiments. We finally recover the representative individual's subjective mortality probabilities at each age using estimated parameters 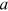 and
and 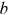 .
.
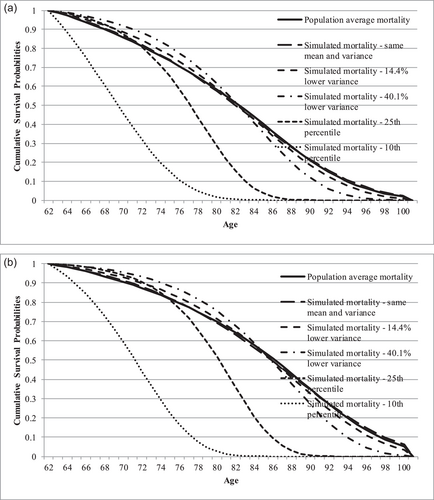
To illustrate, Figure 1a,b compare the cumulative survival probabilities of selected levels of life expectancy and variance of age of death, conditional on alive at age 62, for men and women, respectively. The solid curves are plotted using the population average mortality rates of men and women born in 1950. The long-dashed curves are calculated using the Thatcher et al. (2010) model simulated mortality rates by matching the life expectancy and the variance of age of death produced by above cohort life tables. Although there are only two parameters in the Thatcher et al. (2010) model, the two cumulative survival probabilities are matched fairly well. Additionally, in Section 3.2, we calculate from the HRS clean sample that, on average, individuals can correctly predict their life expectancy, but the average and median variance of age of death calculated using their subjective mortality tables are 14.4% and 40.1% lower than that calculated by the cohort life tables, respectively. Thus, the dashed and dash-dotted curves compare the cumulative survival probabilities predicted by the Thatcher et al. (2010) model with the same life expectancy but 14.4% and 40.1% lower variance of age of death. The curves are steeper, indicating individuals are more certain of their age of death, relative to individuals whose mortality risks equal that predicted by the cohort life tables. Finally, the short-dashed and dotted curves plot the cumulative survival probabilities for individuals whose subjective life expectancy and subjective variance of age of death are at the 25th and 10th percentiles of the respective distribution. Except for being steeper, the curves further demonstrate a noticeable leftward shift, suggesting that the subjective life expectancies are also lower than the estimates calculated using the cohort life tables.
4.3 Results
Tables 3 and 4 report SSEIs in expected present value terms and in expected utility terms for the representative single households, respectively. The upper panel of each table reports SSEIs for single male households and the lower panel presents the calculations for single female households. Our benchmark calculations reported in the first column assume individuals have population average mortality for the 1950 birth cohort from the SSA cohort life tables. Single men with population average mortality maximize their EPV of benefits by claiming at age 64 (the SSEI at age 64 is 1.000 indicating his Social Security benefits stream has the highest EPV if claimed at age 64). As women live longer than men, they place a higher value on delay and their optimal claiming age is 67. Claiming earlier than the ages does not result in substantial EPV losses because the benefit adjustment for early claiming is approximately actuarially fair. For example, if a single man claims at age 62, the earliest possible age, the SSEI is 1.001, indicating he would only require a 0.1% increase in his age 62 benefits to achieve the same EPV of benefits as that obtained by claiming at the optimal age of 64.
| Claim age | Benchmark | Variance—14.4% | Variance—40.1% | 25th percentile | 10th percentile |
|---|---|---|---|---|---|
| Single men | |||||
| 62 | 1.001 | 1.002 | 1.003 | 1.000 | 1.000 |
| 63 | 1.007 | 1.007 | 1.008 | 1.025 | 1.110 |
| 64 | 1.000 | 1.000 | 1.000 | 1.039 | 1.230 |
| 65 | 1.001 | 1.001 | 1.001 | 1.066 | 1.393 |
| 66 | 1.010 | 1.010 | 1.009 | 1.106 | 1.615 |
| 67 | 1.013 | 1.013 | 1.013 | 1.146 | 1.894 |
| 68 | 1.025 | 1.025 | 1.026 | 1.205 | 2.285 |
| 69 | 1.044 | 1.046 | 1.048 | 1.284 | 2.842 |
| 70 | 1.072 | 1.075 | 1.080 | 1.389 | 3.654 |
| Single women | |||||
| 62 | 1.032 | 1.033 | 1.035 | 1.000 | 1.000 |
| 63 | 1.030 | 1.031 | 1.032 | 1.014 | 1.079 |
| 64 | 1.015 | 1.015 | 1.016 | 1.015 | 1.159 |
| 65 | 1.007 | 1.007 | 1.007 | 1.028 | 1.271 |
| 66 | 1.007 | 1.006 | 1.006 | 1.050 | 1.424 |
| 67 | 1.000 | 1.000 | 1.000 | 1.070 | 1.612 |
| 68 | 1.001 | 1.001 | 1.002 | 1.103 | 1.876 |
| 69 | 1.009 | 1.010 | 1.011 | 1.150 | 2.251 |
| 70 | 1.024 | 1.026 | 1.028 | 1.214 | 2.793 |
- Note: The benchmark calculations assume individuals have population average mortality for the 1950 birth cohort from the Social Security Administration cohort life tables. In all calculations, individuals have a PIA of $2000. Both the real interest rate and the time discount factor are set at 3%.
| Claim age | Benchmark | Variance—14.4% | Variance—40.1% | 25th percentile | 10th percentile |
|---|---|---|---|---|---|
| Single men | |||||
| 62 | 1.141 | 1.130 | 1.108 | 1.019 | 1.000 |
| 63 | 1.121 | 1.111 | 1.092 | 1.018 | 1.026 |
| 64 | 1.086 | 1.078 | 1.062 | 1.004 | 1.048 |
| 65 | 1.059 | 1.053 | 1.041 | 1.000 | 1.097 |
| 66 | 1.041 | 1.037 | 1.027 | 1.006 | 1.208 |
| 67 | 1.018 | 1.015 | 1.009 | 1.011 | 1.707 |
| 68 | 1.004 | 1.003 | 1.000 | 1.032 | 3.243 |
| 69 | 1.000 | 1.000 | 1.000 | 1.078 | 7.100 |
| 70 | 1.008 | 1.009 | 1.012 | 1.267 | 17.977 |
| Single women | |||||
| 62 | 1.177 | 1.167 | 1.147 | 1.042 | 1.000 |
| 63 | 1.153 | 1.144 | 1.127 | 1.036 | 1.021 |
| 64 | 1.114 | 1.107 | 1.092 | 1.016 | 1.034 |
| 65 | 1.084 | 1.078 | 1.066 | 1.006 | 1.065 |
| 66 | 1.062 | 1.057 | 1.047 | 1.005 | 1.127 |
| 67 | 1.034 | 1.030 | 1.023 | 1.000 | 1.274 |
| 68 | 1.015 | 1.012 | 1.008 | 1.007 | 1.892 |
| 69 | 1.003 | 1.002 | 1.000 | 1.027 | 3.475 |
| 70 | 1.000 | 1.000 | 1.001 | 1.073 | 7.979 |
- Note: The benchmark calculations assume individuals have population average mortality for the 1950 birth cohort from the Social Security Administration cohort life tables. In all calculations, individuals have a PIA of $2000. Both the real interest rate and the time discount factor are set at 3%. The coefficient of risk aversion is 3.
However, at a coefficient of risk aversion of three, a single man maximizes his expected lifetime utility if he claims his Social Security benefits at age 69 (the SSEI at age 69 is 1.000 indicating he gets the highest expected discounted lifetime utility by claiming at age 69). Those who claim their Social Security benefits early receive lower expected discounted lifetime utility and run the risk of low consumption in the event they live an unexpectedly long time. They require their Social Security benefits to be increased each month to receive the same level of expected discounted lifetime utility as claiming at the optimal claiming age 69, reflecting the high value placed on the additional longevity insurance acquired as a result of delaying claiming. For example, a single man who claims at age 62 would require a 14.1% increase in his benefits to be as well off as he would be were he to delay until age 69. The same conclusion applies to single women. Because women usually live longer than men, they will place even higher value on delaying claiming. A single woman maximizes her expected lifetime utility by delaying claiming until age 70. If a single woman is forced to claim at age 62, she would require a 17.7% increase in her age 62 benefits to be as well off in EU terms.
We next consider how plausible variations of subjective mortality beliefs affect the value of postponing claiming Social Security benefits and the optimal claiming ages of retired workers, compared with the benchmark case. In Section 3.2, we find that the average subjective variance of age of death of the HRS participants is 6.2%–14.4% lower than that calculated from the SSA cohort life tables. Therefore, we start our experiments by decreasing the variance of age of death by 14.4%, while holding the life expectancy constant (the adjustment factors are: 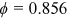 and
and 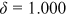 ). Columns 2 in Tables 3 and 4 show SSEIs of this numerical exercise. A 14.4% decrease in variance of age of death has almost no impact on the EPV of Social Security benefits. This is not surprising, because the primary concern of the EPV calculations is on life expectancy, which stays constant in the exercise. However, the exercise reduces the interquartile survival range by 1 and 2 years for men and women, respectively. It also decreases SSEIs in EU terms at all ages, indicating individuals place a lower value on delaying claiming as they are more certain about their age of death. The effect is small in magnitude. Single men and women claiming at age 62 would require 13.0% and 16.7% increase in benefits to be as well off in EU terms, a change of 1.1% and 1.0%, respectively, from the benchmark case. In addition, the optimal claiming ages stay the same at age 69 and 70 for single men and women, respectively.
). Columns 2 in Tables 3 and 4 show SSEIs of this numerical exercise. A 14.4% decrease in variance of age of death has almost no impact on the EPV of Social Security benefits. This is not surprising, because the primary concern of the EPV calculations is on life expectancy, which stays constant in the exercise. However, the exercise reduces the interquartile survival range by 1 and 2 years for men and women, respectively. It also decreases SSEIs in EU terms at all ages, indicating individuals place a lower value on delaying claiming as they are more certain about their age of death. The effect is small in magnitude. Single men and women claiming at age 62 would require 13.0% and 16.7% increase in benefits to be as well off in EU terms, a change of 1.1% and 1.0%, respectively, from the benchmark case. In addition, the optimal claiming ages stay the same at age 69 and 70 for single men and women, respectively.
In Section 3.2, we also demonstrate that the deviation between the median variances of age of death calculated using the subjective and objective mortality tables is larger, ranging from 20.9% to 40.1%. Therefore, we conducted a second numerical exercise by decreasing the variance of age of death of the representative households by 40.1% while keeping their life expectancy the same as the benchmark case (the adjustment factors are: 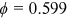 and
and 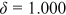 ). In this exercise, the interquartile survival range decreases by 3 years for men and 5 years for women compared to the benchmark case. Columns 3 of Tables 3 and 4 report the SSEIs in EPV terms and in EU terms, respectively. Again, the SSEIs in EPV terms barely change, indicating the variation in the variance of age of death has minimal impact on the EPV of benefits. The exercise has a larger effect on the SSEIs in EU terms. Decreasing the variance of age of death by 40.1% further reduces SSEIs at age 62 for men and women by 3.3 and 3.0 percentage points to 1.108 and 1.147, respectively. Additionally, it is now optimal for single men and women to claim their benefits 1 year early than the benchmark case at age 68 and 69, respectively.
). In this exercise, the interquartile survival range decreases by 3 years for men and 5 years for women compared to the benchmark case. Columns 3 of Tables 3 and 4 report the SSEIs in EPV terms and in EU terms, respectively. Again, the SSEIs in EPV terms barely change, indicating the variation in the variance of age of death has minimal impact on the EPV of benefits. The exercise has a larger effect on the SSEIs in EU terms. Decreasing the variance of age of death by 40.1% further reduces SSEIs at age 62 for men and women by 3.3 and 3.0 percentage points to 1.108 and 1.147, respectively. Additionally, it is now optimal for single men and women to claim their benefits 1 year early than the benchmark case at age 68 and 69, respectively.
To provide a more comprehensive understanding of how subjective mortality beliefs may theoretically shape older individuals' optimal claiming decisions, we conduct two additional numerical experiments, assuming that the representative households experience relatively extreme, yet plausible, subjective mortality beliefs. More specifically, we calculate the SSEIs and optimal claiming ages for individuals whose life expectancy and variance of age of death are both at the 25th or 10th percentile of the respective subjective mortality belief distributions.13 These individuals are pessimistic and fairly confident, but not certain, that they will not survive to advanced old ages. As discussed in the introduction, we expect that individuals who have extreme confidence on predicting their age of death are likely to attribute a limited value on postponing claiming Social Security. This is because they benefit much less from the additional longevity insurance that would otherwise protect them from the risk of outliving their wealth.
Conditional on attaining age 62, the subjective life expectancy for men at the 25th percentile of the subjective mortality belief distribution is 14.6 years. It is 28.4% lower than the average subjective life expectancy and 25.5% lower than the average life expectancy calculated using the cohort mortality tables. For women at the 25th percentile, their subjective life expectancy is 17.0 years, which is 25.2% lower than the average subjective life expectancy and 25.5% lower than the average objective life expectancy. The subjective variance of age of death for men and women at the 25th percentile is 26.3 and 27.3 years2, respectively. These values are 66.2% and 66.8% lower than the corresponding average subjective variance of age of death, and 70.9% and 71.7% lower than the corresponding average variance of age of death calculated using the cohort life tables, respectively. At the 10th percentile, the subjective life expectancy of men and women further reduces to 7.3 and 8.8 years, respectively, and the subjective variance of age of death further reduces to 16.4 and 16.7 years2, respectively.
We report the results in Columns 4 and 5 in Tables 3 and 4, respectively. Both shorter life expectancy and lower variance of age of death reduce incentives for individuals to delay claiming. At the 25th percentile, claiming immediately at age 62 becomes optimal for both men and women in EPV calculations. The costs of early claiming in EU terms are also lower. Single men maximize their expected discounted lifetime utility at age 65 and single women maximize their expected discounted lifetime utility at age 67, 4 and 3 years earlier than the benchmark case, respectively. Those who claimed at age 62 would require 1.9 % and 4.2% increase in benefits, respectively, to be as well off as he or she would be if claimed at the optimal ages, dropping from 14.1% and 17.7% in the benchmark calculations. At the 10th percentile, it further becomes optimal for both men and women to claim their Social Security benefits at age 62, the youngest plausible age, in both EPV and EU terms.
Next, we show how subjective mortality beliefs affect Social Security claiming decisions of married couples. We concentrate on explaining the SSEIs in expected utility terms.14 Our base case is a one-earner couple. Both the husband and the wife are at the same age with population average mortality for the 1950 birth cohort. The SSEIs are reported in the first panel in Table 5. We do not report values for infeasible combinations of claiming ages—those in which the wife's claiming age is less than that of her husband. For married couples with population average mortality, their expected discounted lifetime utility is maximized when both husband and wife claim at age 67. A husband and wife claiming at age 62 would require an 8.9% increase in benefits to be as well off in EU terms.
| Wife claim age | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Husband claim age | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| Benchmark | |||||||||
| 62 | 1.089 | 1.088 | 1.080 | 1.074 | 1.072 | 1.092 | 1.111 | 1.131 | 1.150 |
| 63 | 1.082 | 1.074 | 1.069 | 1.067 | 1.087 | 1.106 | 1.126 | 1.145 | |
| 64 | 1.051 | 1.046 | 1.044 | 1.063 | 1.082 | 1.100 | 1.119 | ||
| 65 | 1.023 | 1.021 | 1.039 | 1.057 | 1.075 | 1.093 | |||
| 66 | 1.004 | 1.022 | 1.039 | 1.057 | 1.074 | ||||
| 67 | 1.000 | 1.017 | 1.034 | 1.051 | |||||
| 68 | 1.001 | 1.018 | 1.034 | ||||||
| 69 | 1.008 | 1.024 | |||||||
| 70 | 1.020 | ||||||||
| Variance—14.4% | |||||||||
| 62 | 1.084 | 1.084 | 1.075 | 1.069 | 1.067 | 1.087 | 1.107 | 1.127 | 1.147 |
| 63 | 1.078 | 1.070 | 1.065 | 1.062 | 1.082 | 1.102 | 1.122 | 1.142 | |
| 64 | 1.047 | 1.042 | 1.040 | 1.060 | 1.079 | 1.098 | 1.117 | ||
| 65 | 1.021 | 1.018 | 1.037 | 1.056 | 1.075 | 1.093 | |||
| 66 | 1.002 | 1.021 | 1.039 | 1.057 | 1.075 | ||||
| 67 | 1.000 | 1.018 | 1.035 | 1.053 | |||||
| 68 | 1.003 | 1.020 | 1.037 | ||||||
| 69 | 1.011 | 1.028 | |||||||
| 70 | 1.025 | ||||||||
| Variance—40.1% | |||||||||
| 62 | 1.075 | 1.074 | 1.065 | 1.059 | 1.056 | 1.077 | 1.098 | 1.119 | 1.140 |
| 63 | 1.071 | 1.061 | 1.056 | 1.053 | 1.074 | 1.095 | 1.116 | 1.137 | |
| 64 | 1.041 | 1.036 | 1.033 | 1.054 | 1.074 | 1.094 | 1.115 | ||
| 65 | 1.016 | 1.014 | 1.034 | 1.053 | 1.073 | 1.093 | |||
| 66 | 1.000 | 1.019 | 1.039 | 1.058 | 1.077 | ||||
| 67 | 1.001 | 1.020 | 1.038 | 1.057 | |||||
| 68 | 1.007 | 1.026 | 1.044 | ||||||
| 69 | 1.019 | 1.038 | |||||||
| 70 | 1.037 | ||||||||
| 25th Percentile | |||||||||
| 62 | 1.011 | 1.015 | 1.011 | 1.012 | 1.016 | 1.041 | 1.067 | 1.093 | 1.119 |
| 63 | 1.021 | 1.017 | 1.018 | 1.022 | 1.048 | 1.075 | 1.101 | 1.128 | |
| 64 | 1.008 | 1.008 | 1.013 | 1.039 | 1.065 | 1.091 | 1.117 | ||
| 65 | 1.000 | 1.004 | 1.030 | 1.056 | 1.082 | 1.108 | |||
| 66 | 1.003 | 1.028 | 1.055 | 1.081 | 1.108 | ||||
| 67 | 1.024 | 1.051 | 1.077 | 1.104 | |||||
| 68 | 1.055 | 1.083 | 1.111 | ||||||
| 69 | 1.100 | 1.130 | |||||||
| 70 | 1.173 | ||||||||
| 10th Percentile | |||||||||
| 62 | 1.000 | 1.017 | 1.030 | 1.047 | 1.068 | 1.101 | 1.133 | 1.162 | 1.188 |
| 63 | 1.047 | 1.061 | 1.080 | 1.103 | 1.139 | 1.173 | 1.205 | 1.233 | |
| 64 | 1.075 | 1.096 | 1.120 | 1.159 | 1.196 | 1.230 | 1.260 | ||
| 65 | 1.117 | 1.144 | 1.186 | 1.228 | 1.266 | 1.304 | |||
| 66 | 1.184 | 1.236 | 1.289 | 1.341 | 1.384 | ||||
| 67 | 1.340 | 1.418 | 1.474 | 1.503 | |||||
| 68 | 1.810 | 1.816 | 1.820 | ||||||
| 69 | 2.773 | 2.685 | |||||||
| 70 | 4.391 | ||||||||
- Note: The benchmark calculations assume individuals have population average mortality for the 1950 birth cohort from the Social Security Administration cohort life tables. Husband and wife are assumed to be the same age. In all calculations, individuals have a PIA of $2000. Both the real interest rate and time discount factor are set at 3%. The coefficient of risk aversion is 3.
The second and third panels, respectively, assume that both the husband and wife have 14.4% and 40.1% lower variance of age of death, holding life expectancy constant. When decreasing the variance of age of death by 14.4%, the combination of claiming ages that maximizes the households’ expected discounted lifetime utility is identical to that of the benchmark case, but the required benefits increase if both spouses claim at age 62 reduces to 8.4%. When the variance of age of death is 40.1% lower than the benchmark case, the value of delaying claiming is further reduced and the optimal combination of claiming ages is 1 year early than the benchmark case.
The fourth and fifth panels show SSEIs of husband and wife that have both life expectancy and variance of age of death that lie at the 25th or 10th percentiles of the respective distributions. Again, both lower life expectancy and lower variance of age of death reduce the value of delaying claiming Social Security. At the 25th percentile, both spouses should claim at age 65 to maximize their expected discounted lifetime utility, 2 years earlier than the benchmark scenario. A married couple that both spouses claiming at age 62 would require a 1.1% increase in their benefits to be as well off as they would be if claimed at the optimal combination of claiming ages. At the 10th percentile, it further becomes optimal for the couple to claim as soon as becoming eligible.
4.4 Sensitivity analysis
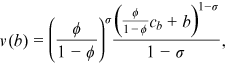 ()
()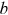 represents the amount of bequests left to heirs. The parameter
represents the amount of bequests left to heirs. The parameter 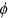 measures the strength of the individuals' bequest motives and the parameter
measures the strength of the individuals' bequest motives and the parameter 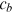 is a consumption floor below which households do not leave bequests. The two-parameter utility function of bequests in De Nardi et al. (2016) takes the following form:
is a consumption floor below which households do not leave bequests. The two-parameter utility function of bequests in De Nardi et al. (2016) takes the following form:
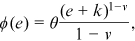 ()
()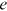 represents the estates. The parameter
represents the estates. The parameter 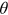 represents the bequest intensity and the parameter
represents the bequest intensity and the parameter 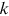 determines the curvature of the function. We take the parameter values directly from the two studies, so
determines the curvature of the function. We take the parameter values directly from the two studies, so 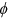 is 0.95 and
is 0.95 and 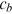 is 24.8 thousand dollars based on Lockwood (2018) and the two parameters
is 24.8 thousand dollars based on Lockwood (2018) and the two parameters 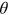 and
and 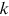 in De Nardi et al. (2016) are 39.7 and 13.0 thousand dollars, respectively.15
in De Nardi et al. (2016) are 39.7 and 13.0 thousand dollars, respectively.15We focus on explaining the results of single households which are reported in Table 6. Columns 1–3 assume individuals experience objective mortality rates. The variance of age of death is reduced by 14.4% (holding the life expectancy constant) in Columns 4–6. Under each mortality assumption, we compare SSEIs of three scenarios: no bequest motives, Lockwood (2018) bequest motives and De Nardi et al. (2016) bequest motives. We show that bequest motives significantly reduce retired workers' optimal claiming ages. Modeling bequest motives as in Lockwood (2018) would decrease the optimal claim ages of single men and women from ages 69 and 70 in the no bequest motives scenario to ages 65 and 67, respectively. The effect of bequest motives is smaller when using the parameter values in De Nardi et al. (2016). The optimal claiming age is age 67 for single male households and age 68 for single female households. The subjective uncertainty regarding individuals' age of death, however, again has little effect on the optimal claiming ages. In scenarios that accommodate both bequest motives and a 14.4% lower variance of age of death, the optimal claiming ages remain the same as in the scenarios that only incorporate the corresponding bequest motives.16
| Benchmark | Variance—14.4% | |||||
|---|---|---|---|---|---|---|
| Claim age | No bequest motive | Lockwood (2018) | De Nardi et al. (2016) | No Bequest Motive | Lockwood (2018) | De Nardi et al. (2016) |
| Single men | ||||||
| 62 | 1.141 | 1.019 | 1.060 | 1.130 | 1.018 | 1.055 |
| 63 | 1.121 | 1.018 | 1.050 | 1.111 | 1.017 | 1.046 |
| 64 | 1.086 | 1.004 | 1.026 | 1.078 | 1.004 | 1.023 |
| 65 | 1.059 | 1.000 | 1.012 | 1.053 | 1.000 | 1.010 |
| 66 | 1.041 | 1.004 | 1.007 | 1.037 | 1.005 | 1.006 |
| 67 | 1.018 | 1.005 | 1.000 | 1.015 | 1.006 | 1.000 |
| 68 | 1.004 | 1.016 | 1.006 | 1.003 | 1.018 | 1.006 |
| 69 | 1.000 | 1.039 | 1.028 | 1.000 | 1.041 | 1.029 |
| 70 | 1.008 | 1.073 | 1.075 | 1.009 | 1.076 | 1.076 |
| Single women | ||||||
| 62 | 1.177 | 1.053 | 1.100 | 1.167 | 1.052 | 1.095 |
| 63 | 1.153 | 1.046 | 1.085 | 1.144 | 1.045 | 1.081 |
| 64 | 1.114 | 1.025 | 1.055 | 1.107 | 1.024 | 1.052 |
| 65 | 1.084 | 1.013 | 1.034 | 1.078 | 1.012 | 1.032 |
| 66 | 1.062 | 1.009 | 1.022 | 1.057 | 1.009 | 1.021 |
| 67 | 1.034 | 1.000 | 1.006 | 1.030 | 1.000 | 1.005 |
| 68 | 1.015 | 1.000 | 1.000 | 1.012 | 1.001 | 1.000 |
| 69 | 1.003 | 1.010 | 1.005 | 1.002 | 1.010 | 1.006 |
| 70 | 1.000 | 1.028 | 1.025 | 1.000 | 1.029 | 1.025 |
- Note: The benchmark calculations assume individuals have population average mortality for the 1950 birth cohort from the Social Security Administration cohort life tables. In all calculations, individuals have a PIA of $2000. Both the real interest rate and the time discount factor are set at 3%. The coefficient of risk aversion is 3.
5 CONCLUSION
This paper presents the patterns of subjective mortality beliefs of older individuals and investigates how plausible variations of subjective mortality beliefs affect the value of delaying claiming Social Security benefits and the optimal claiming ages of retired workers. We conclude that, for plausible preference parameters, observed variations in subjective mortality beliefs on average have little effect on the theoretical optimal claiming ages. In order for claiming at age 62 to be optimal, households that are not liquidity-constrained would require their subjective mortality beliefs significantly deviate from the center of the distribution. More specifically, they would have to substantially over-estimate their mortality risk and be highly confident of their ability to forecast their age of death. Thus, we conclude that subjective mortality beliefs alone could not explain the prevalence of early claiming behaviors.
ACKNOWLEDGMENTS
The research reported herein was pursuant to a grant from the US Social Security Administration (SSA), funded as part of the Retirement Research Consortium (RRC). Tiantian Dai was also supported by the Program for Innovation Research in Central University of Finance and Economics. Wei Sun also received funding support by the Humanities and Social Sciences Research General Program of the Ministry of Education of China (Grant No. 22YJA790052).
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest.
ETHICS STATEMENT
Not applicable.
APPENDIX A
The HRS follow-up questions that are designed to test the degree of precision of subjective mortality beliefs are as follows:
Those who answered 100% were asked the following question:
When you say 100% chance, do you mean that you are certain you will live to 75 or beyond, or do you mean you see a large enough chance that 100 is a good approximation?
Those who answered that it was an approximation were then asked:
If you think there is a large chance that you will live to 75 or beyond, please give your best estimate of what that chance is.
Those who answered 0% were asked the following question:
When you say 0% chance, do you mean that you see no chance at all are certain you will live to 75 or beyond, or do you mean you see a large enough chance that zero is a good approximation?
Those who answered that it was an approximation were then asked:
If you think there is a small chance that you will live to 75 or beyond, please give your best estimate of what that chance is.
Individuals who answered 10, 20, 25, 30, 40, 60, 75, 80, or 90%, and a random assignment of those who answered 50% were asked:
When you said x% just now, did you mean this as an exact number or were you rounding or approximating?
Those who answered that it was an approximation were asked:
What range of numbers did you have in mind when you said x%?
The remainder of those answering 50% was asked:
Do you think that it is about equally likely that you will die before 75 as it is that you will live to 75 or beyond, or are you just unsure about the chances?
| Answered 0% | Answered 50% | Answered 100% | Answered oth. mul. of 10, 25% | |||||
|---|---|---|---|---|---|---|---|---|
| Then no chance at all | Then equally likely | Then certain | Then exact number | |||||
| Marginal effect | Standard error | Marginal effect | Standard error | Marginal effect | Standard error | Marginal effect | Standard error | |
| Math score scale of 0 to 4 | 0.014 | 0.033 | 0.009 | 0.020 | −0.002 | 0.017 | −0.007 | 0.008 |
| Math score missing | 0.204 | 0.093 | −0.033 | 0.113 | −0.012 | 0.082 | 0.012 | 0.046 |
| Log household income | −0.059* | 0.027 | 0.008 | 0.015 | −0.015 | 0.012 | −0.012* | 0.006 |
| Log financial wealth | 0.003 | 0.005 | 0.002 | 0.003 | −0.001 | 0.002 | 0.000 | 0.001 |
| age | −0.023** | 0.008 | −0.002 | 0.005 | −0.002 | 0.004 | 0.001 | 0.002 |
| Male | −0.029 | 0.073 | 0.028 | 0.048 | 0.012 | 0.040 | 0.033 | 0.019 |
| Married | −0.007 | 0.074 | 0.011 | 0.050 | −0.032 | 0.041 | 0.055** | 0.020 |
| Race | ||||||||
| Black | −0.078 | 0.106 | 0.024 | 0.068 | −0.063 | 0.046 | 0.065* | 0.029 |
| Hispanic | −0.109 | 0.102 | 0.092 | 0.073 | −0.051 | 0.066 | 0.078* | 0.032 |
| Education | ||||||||
| Less than high school | 0.088 | 0.085 | −0.022 | 0.074 | −0.083 | 0.061 | −0.007 | 0.032 |
| Some college | 0.020 | 0.085 | 0.099* | 0.047 | 0.004 | 0.041 | 0.009 | 0.020 |
| Smoke ever | −0.157 | 0.081 | 0.094 | 0.050 | 0.030 | 0.039 | −0.021 | 0.019 |
| Smoke now | 0.103 | 0.089 | −0.078 | 0.057 | −0.020 | 0.055 | 0.004 | 0.025 |
| Drink ever | −0.051 | 0.079 | 0.101* | 0.047 | 0.008 | 0.038 | 0.054** | 0.019 |
| Never do vigorous physical activity | 0.143 | 0.079 | 0.028 | 0.063 | 0.064 | 0.060 | −0.049 | 0.026 |
| Never do moderate physical activity | −0.022 | 0.110 | 0.024 | 0.093 | −0.038 | 0.101 | 0.024 | 0.043 |
| Never do light physical activity | 0.032 | 0.068 | −0.024 | 0.045 | −0.013 | 0.038 | −0.021 | 0.018 |
| Ever been diagnosed with | ||||||||
| High blood pressure | 0.071 | 0.076 | −0.018 | 0.048 | −0.033 | 0.038 | 0.010 | 0.018 |
| Diabetes | −0.054 | 0.080 | −0.058 | 0.056 | −0.065 | 0.052 | −0.027 | 0.023 |
| Cancer | −0.086 | 0.116 | −0.055 | 0.069 | −0.062 | 0.068 | 0.013 | 0.030 |
| Lung disease | −0.081 | 0.097 | 0.061 | 0.072 | −0.014 | 0.083 | 0.005 | 0.033 |
| Heart disease | 0.042 | 0.083 | 0.019 | 0.053 | −0.025 | 0.061 | −0.008 | 0.025 |
| Stroke | −0.080 | 0.128 | 0.059 | 0.102 | 0.023 | 0.102 | 0.007 | 0.045 |
| Arthritis | 0.221** | 0.079 | 0.037 | 0.046 | −0.097** | 0.037 | −0.011 | 0.018 |
| Obese | 0.072 | 0.068 | 0.009 | 0.046 | −0.017 | 0.039 | −0.022 | 0.019 |
| Number of words recalled-immedialy | 0.018 | 0.031 | 0.054* | 0.023 | 0.036* | 0.017 | −0.004 | 0.008 |
| Number of words recalled-delayed | −0.030 | 0.023 | −0.024 | 0.019 | −0.009 | 0.014 | 0.014* | 0.007 |
| N | 214 | 593 | 840 | 3117 | ||||
- Note: * and ** indicate that the coefficient is statistically significant at 5% and 1 % level, respectively.
REFERENCES
- 1 A more sophisticated approach to quantify the impact of subjective mortality beliefs on retired workers' Social Security claiming decisions would be to first estimate a structural model that captures the key characteristics of claiming behaviors in the data, then perform counterfactual experiments to examine the extent to which subjective mortality beliefs can change their decisions. In our specific case, however, we tend to think the benefit of estimating a structural model is limited. This is because we find that, on average, observed variations in subjective mortality beliefs have only a small effect on the theoretical optimal claiming ages, thus, it might be challenging to observe such an effect in the data.
- 2 For years before the FRA, benefits are reduced by one dollar for every two dollars earnings exceeding a limit. For the year that a worker attains his FRA, benefits are reduced by one dollar for every three dollars earnings exceeding a second limit. There is no earnings test after the FRA. After the worker attains his FRA, his benefits are actuarially adjusted to reflect benefits previously withheld.
- 3 The PIA is calculated by the earnings' history of retired workers. See Sass et al. (2007) for more details.
- 4 The numbers are for retired workers who were born at or after 1943. For those who were born before 1943, the increase in their benefits after the FRA, called the delayed retirement credit (DRC), is smaller and thus less than actuarially fair.
- 5 Their benchmark is the Annuity 2000 Basic Life Table. This table estimates the mortality risk of annuitants and yields lower mortality rates than the population life tables used by other researchers.
- 6 In 1992, individuals were asked to assess the chance they will “live to be 75 or more” on a scale of zero to 10 where zero means absolutely no chance and 10 means absolutely certain. In 1994 and subsequent waves, individuals aged less than 65 were asked to assess the “percent chance” they will live to 75 or more. Eighty-two percent of 1994 respondents provide probabilities that are multiples of 10% or 25%.
- 7 To avoid losing more individuals, we do not drop individuals when they provided the same answer for both the
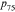 and
and 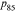 questions. Instead, we make an assumption that they gave a small range close to the reported probability. When both
questions. Instead, we make an assumption that they gave a small range close to the reported probability. When both 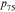 and
and 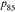 equal zero, we assume that the underlying beliefs are 5% and 1%. When both probabilities are 100, we assume that the underlying beliefs are 99% and 95%. We assume there is a 5% range around the estimate when
equal zero, we assume that the underlying beliefs are 5% and 1%. When both probabilities are 100, we assume that the underlying beliefs are 99% and 95%. We assume there is a 5% range around the estimate when 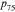 and
and 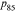 both equal some other probability.
both equal some other probability. - 8 We extract each individual's objective mortality rates from the SSA cohort life tables based on their gender and birth year.
- 9 We find that individuals who said that their estimate was precise and those who said that their answer was approximations are not systemically different, so the clean sample remains representative. We run four probit models, and the results are presented in Table A1 in Appendix A. The dependent variables take the value one if individuals stated that their response was precisely zero, 50, 100, and other multiples of 10% or 25%, respectively, and zero if they answered that their response was an approximation. We find that there are few consistent and significant differences in either socioeconomic characteristics or health-related variables between the two groups.
- 10 We do not attempt to fit our theoretical predictions to actual claiming behaviors in the data. We acknowledge the potential concern that our model, and models like ours, predict much higher levels of annuitization than observed.
- 11 1950 is the average birth year of the individuals in the HRS sample. The FRA is 66.
- 12 $2000 roughly equals the average retried worker benefits of $1834.80 in the United States in April, 2023. Website: https://www.ssa.gov/policy/docs/quickfacts/stat_snapshot/. In the numerical exercises without bequest motives, PIA is only a scaling factor, any arbitrary PIA will produce the same results.
- 13 There is a less than perfect correlation between the subjective life expectancy and the subjective variance of age of death. Among men and women, 60% and 61% have both subjective life expectancy and subjective variance of age of death above the 25th percentile, and 82% have both subjective life expectancy and subjective variance of age of death above the 10th percentile.
- 14 To keep the text compact, we choose not to report SSEIs in EPV terms for married couples. The results are available upon request.
- 15 The other preference parameters estimated in Lockwood (2018) and De Nardi et al. (2016) are fairly close to our choices. In our model, we assume the time discount factor is 0.97 and the coefficient of risk aversion is 3. In Lockwood (2018), the assumed time discount factor is 0.975 and the estimated risk averse coefficient is 2. In De Nardi et al. (2016), the estimated time discount factor and the risk averse coefficient are 0.994 and 2.83, respectively. This reinforces our confidence that directly taking parameter values from the two studies would not lead to significant deviations in the outcomes.
- 16 A noteworthy point to mention is that, the representative households have a PIA of $2000 in the calculations. In addition, when individuals enter the model, we further endow them with an amount of financial wealth that is equal to the expected present value of the Social Security benefits they would receive if they claimed at age 62 (approximately $275,000). Because bequest motives are modeled as luxury goods, the effect of bequest motives may depend on the wealth of the representative households. In the results that we are not reported, we check the SSEIs under the scenario where the income and financial assets of the representative households are both doubled. We find that the effect of bequest motives is larger for wealthier households; however, the lower variance of age of death still does not change the optimal claiming ages of the representative households.




