Trading rule discovery using technical analysis and a template matching technique for pattern recognition: Evidence from the Chinese stock market
Abstract
This paper examines the potential profit of bull flag trading rules in the Shanghai Stock Exchange Composite Index (SSE) using a template matching technique based on price pattern recognition. This paper fills a gap in the literature by applying a template matching technique for the recognition of bull flag patterns in the Shanghai Stock Exchange Composite Index (SSE) during the period of 1991–2021. To the best of our knowledge, no previous study has applied bull flag trading rules to the Chinese stock market. Our results indicate that bull flag trading rules can correctly predict the price movement direction of the index most of the time, achieving significantly positive excess profits. Moreover, shorter fitting windows and better quality of price fit values for lower holding periods are associated with better performance. This research may have relevant practical implications for investors who opt for this indicator in their asset allocation decisions.
1 INTRODUCTION
Technical analysis, also known as “charting,” is a discipline that aims to predict price evolution based on the recognition of archetypal graphical patterns in market price history (Lo et al., 2000; Zapranis & Tsinaslanidis, 2012a, 2012b). There are indications that technical analysis is one of the most popular methods of stock market forecasting among practitioners. For example, according to a survey conducted by Menkhoff (2010) among 692 fund managers in the United States, Germany, Switzerland, Italy, and Thailand, 87% of the respondents recognized the importance of technical analysis and 18% declared that it was their favorite method of market prediction. More recently, Bose et al. (2020) reviews evidence on the percentage of traders that use technical analysis mentioning that these percentages range from 27% to 90% depending in the market under scrutiny.
The detection of patterns in the time series of prices assumes that some price movements are significant for the future evolution of prices because they contribute to the formation of specific graphical patterns. This belief seems to be at odds with the efficient market hypothesis (EMH) proposed by Fama (1970). According to the weak version of the EMH, the current market price already contains in itself all that can be known about the future. Therefore, market data should not contain any discernable and exploitable patterns (Fama, 1970; Fama & Blume, 1966). In consequence, the finding that charting methods are of significant value for stock market prediction is problematic to the EMH.
Because the identification of price formations relies on the visual inspection of graphs, it is difficult to measure the performance of this feature of technical analysis through the application of statistical tests. As it is stated by Neftci (1991, p. 549), “[T]echnical analysis is a broad class of prediction rules with unknown statistical properties, developed by practitioners without reference to any formalism.”
The scarcity of studies on technical analysis based on pattern detection is highlighted in the literature reviews on the topic (Nazário et al., 2017; Park & Irwin, 2007; Shah et al., 2019). For example, Farias Nazário et al. (2017) verify that from the 85 papers under analysis, chart pattern detection was the least utilized method with only two examples. Therefore, according to Farias Nazário et al. (2017, p. 121), the methodologies based on “chart patterns should be prioritized in future studies.”
In this paper, we fill this gap in the literature by applying a template matching technique for the recognition of bull flag patterns in the Shanghai Stock Exchange Composite Index (SSE) during the period of 1991–2021. The template matching technique is a qualitative indicator that calculates fit values by using a chart for pattern recognition (Leigh, Purvis, et al., 2002b; Wang & Chan, 2007). A bull flag is a technical chart formation that resembles a flag of consolidation of prices within a narrow range followed by a sharp rise in the positive direction. The detection of this bull flag pattern in the time series of the SSE is thus understood to be a buy signal (Leigh et al., 2004; Leigh, Modani, et al., 2002; Leigh, Purvis, et al., 2002). Our paper contributes to the literature since, to the best of our knowledge, no previous study has applied bull flag trading rules to the Chinese mainland's stock market. Emerging markets are a particularly interesting setting for testing the efficiency of markets through studies on the profitability of technical analysis. However, papers that focus on these markets are still comparatively rare (Farias Nazário et al., 2017). Thus, our study also contributes to fill this gap in the literature. Moreover, the template matching technique is relatively recent and still little explored in academic research. Notice that, given the potential increase in market efficiency due to the investors' higher levels of financial literacy, simpler rules of technical analysis could be less useful in detecting patterns in asset prices. This argument justifies the use of more sophisticated techniques such as the matching template.
Our empirical results indicate that a trading approach based on the bull flag pattern is capable of yielding positive and significant annualized returns, especially for shorter holding periods, even after considering transaction costs. Bull flag trading rules have a buy signal success rate of around 80% for the various fitting windows, which is higher than those success rates resulting from the market-based strategy. These findings highlight the superior predictive power of technical analysis and the possibility of obtaining abnormal returns.
The remainder of the paper is organized as follows. Section 2 reviews the previous literature related to chart pattern detection. Section 3 describes the data and the methods employed in the empirical study. Section 4 discusses our results. Section 5 concludes.
2 LITERATURE REVIEW
Chart pattern studies test the profitability of visual chart patterns commonly used by technical analysts. Familiar chart patterns, whose names are derived from their shapes in bar charts, include flags, pennants, saucers, triangles, head-and-shoulders, tops and bottoms, and support and resistance levels. Most academic papers on technical analysis focus on general trading indicators such as those based on moving averages (see Farias Nazário et al., 2017, for a recent literature review on the topic). The studies that resort to charting pattern recognition methods are comparatively scarce (Farias Nazário et al., 2017).
In a seminal study, Levy (1971) provided evidence on the profitability of 32 “five-point chart patterns” for NYSE securities, including head-and-shoulders formations, triple tops and triple bottoms. His main finding is that none of the 32 patterns generates significantly greater than average profits for any holding period.
The studies by Neftci (1991), Brock et al. (1992), and Chang and Osler (1999) conducted in the 1990s are worth mentioning. Neftci (1991) shows that the method of technical analysis that capture the nonlinear nature of asset prices can improve forecasts generated via the Wiener–Kolmogorov prediction theory. Brock et al. (1992) examined the profitability of trading strategies based on resistance and support levels in the Dow Jones Index in the period 1897–1986. The result indicates that such buy and sell signals generated by the crossing of those price levels are informative. Chang and Osler (1999) assess the performance of head-and-shoulders patterns in the daily spot rates of six exchange rates against the US dollar during the period 1973–1994. Their main conclusion is that trading based on the chart pattern generates statistically significant returns for two of the exchange rates under study. The trading returns remain substantial even after considering transaction costs, interest differentials, and adjustments for risk.
Lo et al. (2000) conducted one of the most influential studies on the topic. The authors examined the usefulness of 10 well-known chart patterns in predicting NYSE/AMEX stock returns over the period 1962–1996 using a pattern detection algorithm derived from nonparametric kernel regressions. By comparing the unconditional empirical distribution of daily stock returns to the conditional distribution based on the technical formations under scrutiny, Lo et al. (2000) conclude that several indicators may have predictive power. Thus, the results raise the possibility that the identification of pattern formations can add value to the investment process.
Dawson and Steeley (2003) and Savin et al. (2007) resorted to modified versions of the algorithm of Lo et al. (2000) in their studies. Dawson and Steeley (2003) examine UK stock data to corroborate the conclusions of Lo et al. (2000) in support of the predictive ability of technical analysis. In spite of this, the informativeness of the chart patterns does not necessarily translate into trading profits. Savin et al. (2007) confirm that the application of the algorithm to the head-and-shoulders formation has substantial predictive power for US stock returns over periods of 1–3 months.
Zapranis and Tsinaslanidis (2012a) proposed a rule-based mechanism to identify horizontal support and resistance levels. The results generated with the application of the method to the stocks listed on NASDAQ and NYSE fail to generate excess returns in comparison with simple buy-and-hold strategies. Therefore, the findings are in general consistent with the EMH. In a follow-up study, Zapranis and Tsinaslanidis (2012b) examine the performance of a trading strategy based on the identification of saucers and resistance levels to seven US tech stocks. The authors report positive excess returns only in the first subperiods of examination (the 1990s) and note that the indications of positive returns can be eliminated by transaction costs.
Variations of a template matching technique are used by Leigh et al. (2004); Leigh, Modani, et al. (2002), Leigh, Purvis, et al. (2002), Wang and Chan (2007), Parracho et al. (2010), Cervelló-Royo et al. (2015), and Arévalo et al. (2017) to identify bull flag formations. For example, Leigh et al. (2002) applied template fitting processes to test a bull flag price pattern for the NYSE during the period 1981–1996. A 60-day history of price and volume was used to predict the evolution of prices in a 20-day horizon. The trading strategy is found to result in significantly higher price changes than a random selection of trading days. Subsequently, Leigh, Purvis, et al. (2002) and Leigh et al. (2004) extended the method proposed by Leigh, Modani, et al. (2002) to examine a bull flag volume pattern in the NYSE Composite Index. The main result is that better bull flag template volume fits are associated with higher profits in comparison to a buy-and-hold strategy.
Wang and Chan (2007) implemented a template matching technique based on the recognition of flag formations in the Nasdaq Composite Index (NASDAQ) and Taiwan Weighted Index (TWI). The empirical results indicate that all the technical trading rules correctly predicted the direction of changes in the NASDAQ and TWI. Moreover, better bull flag templated price fit is found to be associated with higher average returns.
Parracho et al. (2010) combined template matching with genetic algorithms to identify upward trends and the optimal values for the parameters on the S&P 500 stock data for the period 2005–2010. The results obtained indicate that the method outperforms the passive strategy in the case of the stock index and yields decent results for individual stocks. Also using a genetic algorithm, Leitão et al. (2016) developed a new approach (Symbolic Important Rules), which was tested with real data from the S&P500 index. Their results evidence the possibility to obtain a total return of 76.7% in the period 2011–2014, outperforming the total return of 61.9% obtained with the buy-and-hold strategy.
Cervelló-Royo et al. (2015) also examined the performance of a trading rule based on the identification of flag patterns. The study introduces two parameters (stop loss and take profit) to capture the dynamic nature of trading. The trading rule is applied to intraday data and also to opening and closing prices of stock indexes of the United States (Dow Jones Industrial Average), Germany (DAX), and the United Kingdom (FTSE). The results show that the trading rule drawing on the detection of flag patterns produces higher returns for the European than for the US index, which the authors attribute to the greater inefficiency of the European markets.
Arévalo et al. (2017) build their study on the template matching technique proposed initially by Cervelló-Royo et al. (2015) to recognize flag patterns in the data. The authors impose additional filters based on Exponential Moving Averages before considering the flag patterns as actionable for making trades. This approach is found to perform much better than the original strategy of Cervelló-Royo et al. (2015), resulting in higher profits and lower levels of risk.
In general, it is fair to conclude that, although the results of chart pattern studies vary depending on the patterns, markets, and sample periods under examination, they suggest that some chart patterns might be profitable in predicting the evolution of stock markets.
3 DATA AND METHODOLOGY
The present paper aims to evidence the potential profit of bull flag technical trading rules, using a template matching technique, in contrast to the average market returns for the emerging Chinese mainland's stock market—the Shanghai Stock Exchange Composite Index (SSE). This methodology has never been applied to a large emerging market, as the only available studies focus on the Chinese Taiwan's stock market (Chen & Chen, 2016; Wang & Chan, 2007).
Daily index values for the SEE were collected from the statistical database Refinitiv Datastream. The data ranges from February 1, 1991 to December 31, 2021, encompassing 31 years and totaling 7549 valid trading days (Figure 1). The time range analyzed is in line with most of the relevant literature (Chen & Chen, 2016; Leigh et al., 2002, 2004, 2008; Wang & Chan, 2007).
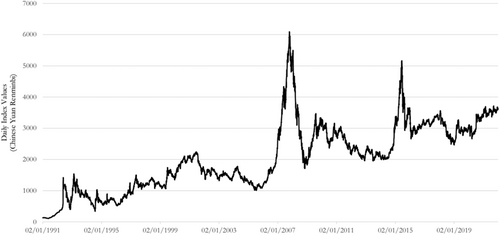
The present paper follows the methodology proposed by Wang and Chan (2007), which identifies the bull flag trough a pattern recognition technique, which is a graphic pattern used to detect buy signals. Figure 2 presents the template used by Wang and Chan (2007) as the main tool of the forecasting procedure.
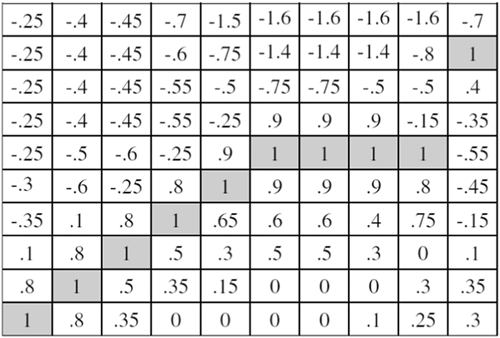
The numbers contained in the templates are weights that allow to define the bull flag pattern in the squares marked in gray. The calculation of these weights is done using a machine learning method based on artificial neural networks (Leigh et al., 2002). However, this is a process that involves a certain degree of arbitrariness as it depends on how the user conceives the image he wants to represent in the template (Zapranis & Tsinaslanidis, 2012b). In turn, the numbers that constitute the weights are extracted from the network and can be used for image characterization purposes. Furthermore, the higher the value assigned to a weight, the closer the template pixel is to the optimal representation of a bull flag. As can be observed in Figure 2, Wang and Chan (2007) first categorize a bull flag pattern transcribed in a template by an upward trend, as is possible to identify in the first five columns, then between columns six and nine a horizontal consolidation and, in the last column, the representation of an ascending breakout. According to the authors this template can reliably detect price increases, which are essential for the process of identifying a bull flag pattern.
With the template defined, it must then be combined with the information collected on the daily prices of the SSE index for several p trading day windows, p = {20, 40, 60, 80, 100, and 120}, to obtain fitting values (hereafter Fitk). The latter will serve as inputs for the application of conditional trading rules.
Furthermore, this type of analysis is subject to the possibility of nonsynchronous trading results, which is a measurement error that can cause overestimation of the returns of the securities being valued using observed data (Bessembinder & Chan, 1998; Scholes & Williams, 1977). However, this problem can easily be solved by adding 1 day lag to the time the transaction is made in relation to the buy signal, that is, the buy signal is followed by a day of delay before the transaction takes place (Wang & Chan, 2007). As a result, the calculation of Fitk, which assesses the goodness of fit between the bull flag matching template and the various trading windows with p trading days, will infer that each of the trading days is defined as K − 1 in the sample period.
For a given trading day k, if Fitk exceeds a trading threshold (T), the investor must buy on that same day, as the method already incorporates the 1-day lag, then hold the securities for q number of days, to sell them only afterward.
Finally, we compare the return generated by the trading rule (Equation 8), with the average market return (Equation 7) to assess whether the detection of bull flag patterns allow investors to obtain excessive profits.
4 RESULTS OF THE EMPIRICAL STUDY
4.1 Average return
Table 1 presents the average returns of the SEE index and the average returns yielded by the bull flag trading rule. These results vary depending on the length of fitting windows (p), holding periods (q) and threshold values (T) under consideration.
| Bull flag | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Market | Average return (%) | T = 0 | T = 1 | T = 2 | T = 3 | |||||
| p | q | N (buys) | Average return (%) | N (buys) | Average return (%) | N (buys) | Average return (%) | N (buys) | Average return (%) | |
| 20 | 20 | 1.58 | 5167 | 2.60 | 3785 | 3.75 | 2326 | 6.87 | 1381 | 9.76 |
| 20 | 40 | 3.33 | 5167 | 5.56 | 3785 | 7.80 | 2326 | 12.73 | 1381 | 16.66 |
| 20 | 60 | 5.13 | 5167 | 8.17 | 3785 | 10.65 | 2326 | 15.90 | 1381 | 21.27 |
| 20 | 80 | 6.84 | 5167 | 10.47 | 3785 | 13.57 | 2326 | 19.43 | 1381 | 27.18 |
| 20 | 100 | 8.65 | 5167 | 12.77 | 3785 | 16.20 | 2326 | 23.23 | 1381 | 33.37 |
| 40 | 20 | 1.58 | 5213 | 0.56 | 3603 | 0.94 | 2238 | 1.93 | 1338 | 3.13 |
| 40 | 40 | 3.33 | 5213 | 4.01 | 3603 | 6.55 | 2238 | 10.38 | 1338 | 13.52 |
| 40 | 60 | 5.13 | 5213 | 7.78 | 3603 | 12.18 | 2238 | 18.29 | 1338 | 24.04 |
| 40 | 80 | 6.84 | 5213 | 10.05 | 3603 | 15.33 | 2238 | 23.22 | 1338 | 31.20 |
| 40 | 100 | 8.65 | 5213 | 12.48 | 3603 | 18.09 | 2238 | 26.16 | 1338 | 35.26 |
| 60 | 20 | 1.58 | 5210 | 0.53 | 3529 | 1.23 | 2177 | 2.15 | 1190 | 3.33 |
| 60 | 40 | 3.33 | 5210 | 3.12 | 3529 | 5.45 | 2177 | 8.72 | 1190 | 12.30 |
| 60 | 60 | 5.13 | 5210 | 6.91 | 3529 | 11.62 | 2177 | 18.95 | 1190 | 28.41 |
| 60 | 80 | 6.84 | 5210 | 10.44 | 3529 | 17.35 | 2177 | 27.05 | 1190 | 40.02 |
| 60 | 100 | 8.65 | 5210 | 13.22 | 3529 | 21.07 | 2177 | 30.99 | 1190 | 46.06 |
| 80 | 20 | 1.58 | 5386 | 0.39 | 3846 | 0.42 | 2141 | 0.27 | 1266 | 0.37 |
| 80 | 40 | 3.33 | 5386 | 2.28 | 3846 | 2.85 | 2141 | 3.36 | 1266 | 4.02 |
| 80 | 60 | 5.13 | 5386 | 5.38 | 3846 | 6.75 | 2141 | 8.38 | 1266 | 10.79 |
| 80 | 80 | 6.84 | 5386 | 8.94 | 3846 | 11.55 | 2141 | 18.21 | 1266 | 24.28 |
| 80 | 100 | 8.65 | 5386 | 12.26 | 3846 | 16.35 | 2141 | 27.05 | 1266 | 37.39 |
| 100 | 20 | 1.58 | 5140 | 0.67 | 3553 | 1.30 | 2057 | 0.90 | 1182 | 2.37 |
| 100 | 40 | 3.33 | 5140 | 2.84 | 3553 | 4.33 | 2057 | 3.29 | 1182 | 6.42 |
| 100 | 60 | 5.13 | 5140 | 5.75 | 3553 | 8.21 | 2057 | 7.03 | 1182 | 11.68 |
| 100 | 80 | 6.84 | 5140 | 9.02 | 3553 | 12.57 | 2057 | 12.51 | 1182 | 19.82 |
| 100 | 100 | 8.65 | 5140 | 12.92 | 3553 | 18.53 | 2057 | 22.93 | 1182 | 32.64 |
| 120 | 20 | 1.58 | 4746 | 0.39 | 3405 | 0.12 | 1950 | 0.58 | 978 | 2.01 |
| 120 | 40 | 3.33 | 4746 | 1.53 | 3405 | 2.07 | 1950 | 3.84 | 978 | 6.58 |
| 120 | 60 | 5.13 | 4746 | 3.62 | 3405 | 5.44 | 1950 | 9.19 | 978 | 12.64 |
| 120 | 80 | 6.84 | 4746 | 6.55 | 3405 | 9.46 | 1950 | 15.35 | 978 | 20.95 |
| 120 | 100 | 8.65 | 4746 | 10.15 | 3405 | 14.69 | 1950 | 24.06 | 978 | 35.91 |
- Note: p represents the number of days in the fitting window, which can range from 20 to 120 days. Both trading strategies buy and hold for a q number of trading days in the horizon period, which can range from 20 to 100 days. T refers to the threshold implicit in the trading rules. N (buys) is the number of buy signals indicated by the trading rules. The market average return is the average daily profit generated from buying on every day. The bull flag average return is the trading rule average profit generated from buying on the days indicated by the rules.
The first columns of the table reflect the results of a strategy that buys the SSE index in all tradable days, a trading policy advocated by the EMH. The columns on the right present the returns of a trading strategy guided by bull flag trading rules. For both strategies, it is possible to identify that each fitting window may have allocated five different holding periods, q = {20, 40, 60, 80 and 100}. In general, the longer the holding period, regardless of the length of the fitting window, the higher the average return generated by a given strategy. For example, as far as the buy everyday strategy is concerned, it generates an average daily market return of 1.58% for a fitting window and a holding period of 20 days. On the other hand, under the same conditions, a trading policy based on the bull flag is able to generate an average return per buy signal of 9.76% for a T = 3, which corresponds to the best template price fit of this study. This specific trading rule (Fitk ≥ 3) delivered 1381 buy signals in a total of 7549 trading days.
Moreover, it is interesting to note that for the market-based strategy, each holding period corresponds to a single average return value, completely independent of the number of days chosen to compose the fitting window. This phenomenon can be explained by the intrinsic condition of the trading policy, which is to buy the index everyday, causing the fitting windows to be entirely composed of days in which an investment was made. Consequently, this neutralizes any effect on the return caused by varying the number of days each window covers. On the other hand, this same phenomenon is not observed when implementing the method based on technical analysis, as the buy signals are not triggered daily, but rather through a system of trading rules that integrate bull flag patterns. That is, bull flag returns are influenced by the quality of Fitk, which naturally incorporates the value chosen as the p-trading day fitting window, as explained in the previous section. Instead, the implementation of conditional trading rules is associated with another event, which is related to the empirical result that, commonly, for holding periods of shorter duration and small fitting windows, the greater the number of p-days in the fitting window, the lower the average returns.
The average bull flag returns are categorized according to different threshold levels and can take the values of T = {0, 1, 2, and 3}. A threshold value can be defined, in this case, as being a lower bound of a hypothetical Fitk measure from which conditional trading rules give a buy signal, that is, Bk = 1 if Fitk ≥ T and Bk = 0, otherwise. On this sense, the empirical findings show the existence of another event related to the fact that there is a direct and positive relationship between the values assumed as threshold and the returns obtained, so that the higher the value of T, the greater the average return. For example, for a p = 20 and q = 20, the bull flag average returns were 2.60%, 3.75%, 6.87%, and 9.76% for increasing T values, respectively. These results are in agreement with other studies carried out in emerging markets, such as the Chinese Taiwan's stock market (Wang & Chan, 2007). In fact, increasing the threshold value makes the required level of Fitk's quality also higher, which means that better degrees of template price fit lead trading rules to perform better, achieving higher average returns. On the contrary, the buy every day approach does not require the setting of any threshold as no condition prevents buying the index on any trading day.
It is also worth mentioning that each fitting window has an immutable number of days in which there was a buy indication, regardless of the holding period that can be chosen. This event occurs because each trading day is associated with a value of Fitk, and the purchase of the index is decided based on the relationship of Fitk's quality, on that trading day, with the threshold. Therefore, the number of days the investment is held has no impact on the quantity of signals captured by the trading rules. In addition, increasing the value assigned to the threshold causes the number of buy signals to decrease as higher Fitk volumes are required, but on the other hand, as mentioned earlier, it improves the performance of the bull flag. However, if the method used is supported by the EMH, the methodological process is simpler, since the number of trading days that make up the sample period is equal to the number of times the index is bought.
The results observed in Table 1 illustrate that, in general, bull flag conditional trading rules can validly predict changes in the direction of the SSE index values regardless of the fitting window. Indeed, as the number of p-trading days increases, bull flag average returns tend to deteriorate, generating values below market returns on some occasions, mainly for shorter holding periods. As an example, this occurs for a p = 100, q = 20 and T = 0, in which the return obtained by the bull flag was 0.67%, being lower than the associated market average return, which was 1.58%.
These results are similar to those obtained by Wang and Chan (2007) when testing TAIEX, although, in this case, there was no indication of observations with worse performance than the market. The observed differences between our results and those obtained by Wang and Chan (2007) for the Chinese Taiwan's market may be attributed to several factors. First, the analysis periods are different: Wang and Chan (2007) focused on the period 1971–2004, while our article examines the period 1991–2021. Second, although both the Chinese mainland's and the Chinese Taiwan's stock markets can be considered emerging markets, there are significant differences between them. One noteworthy distinction is that the Chinese mainland's stock market has a significant presence of state-owned enterprises, which can impact market dynamics and investor sentiment, while in Chinese Taiwan, the proportion of state-owned companies is relatively lower. Additionally, the accessibility of the two markets to foreign investors presents significant differences. Historically, the Chinese mainland's stock market has had restrictions on foreign investor participation, with certain limitations on foreign ownership and investment channels. In contrast, the Chinese Taiwan's stock market has been relatively more accessible to foreign investors.
As a consequence of these empirical findings and considering only average returns, an investor interested in buying the Chinese index should follow strategies focused on the search for investment opportunities based on short fitting windows. Likewise, in Leigh et al. (2004), the bull flag strategies applied to the NYSE index with the shortest fitting windows are those that record the highest average returns for positive window price changes during the period from 1981 to 1999. In addition, Wang and Chan (2007) argue that an approach that uses shorter fitting windows can enhance the performance of technical analysis when applied to the NASDAQ and TAIEX indexes.
4.2 Excess profit after trading costs
Table 2 presents detailed evidence on other profitability indicators of both trading strategies, in situations in which the investor chooses to use a 20-day fitting window and simultaneously the best available price fit values, which occur when Fitk ≥ 3.
| p | q | Market | Bull flag (T = 3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average return (%) | Annualized return (%) | Standard deviation | N (buys) | Average return (%) | Transaction cost (%) | Annualized return (%) | Standard deviation | Annualized excess profit (%) | ||
| 20 | 20 | 1.58 | 20.09 | 13.63 | 1381 | 9.76 | 4.88 | 123.93 | 16.14 | 103.83a |
| 20 | 40 | 3.33 | 21.14 | 21.37 | 1381 | 16.66 | 8.33 | 105.80 | 27.03 | 84.66a |
| 20 | 60 | 5.13 | 21.71 | 27.35 | 1381 | 21.27 | 10.64 | 90.06 | 35.85 | 68.35a |
| 20 | 80 | 6.84 | 21.72 | 31.36 | 1381 | 27.18 | 13.59 | 86.30 | 46.64 | 64.58a |
| 20 | 100 | 8.65 | 21.98 | 35.32 | 1381 | 33.37 | 16.69 | 84.76 | 56.10 | 62.78a |
- Note: p represents the number of days in the fitting window, in this case 20 days. Both trading strategies buy and hold for a q number of trading days in the horizon period, which can range from 20 to 100 days. The annualized excess profit is the difference between the annualized return achieved by the bull flag trading rules and the annualized return derived from the market strategy defined as buy on everyday. Both annualized returns and annualized excess profits are calculated based on the 254 trading days existing in a calendar year. The transaction cost corresponds to the theoretical value that the cost of an operation of a single transaction would need to have in order for it to be able to offset the gains generated by the bull flag trading strategy. The formula used for this purpose is as follows: Transaction Cost = .
- a Statistically significant at the 5% level.
- Source: own calculations.
The average daily return and the annualized return are two measures commonly used to infer the performance of a financial portfolio. However, in this case, it is necessary to make a distinction between the two. On the one hand, the average return is methodologically computed using a simple arithmetic average of the daily returns on the days indicated by the trading rules. Nonetheless, if one wants to retain some sort of conclusion regarding the performance of trading rules with different holding periods, it is important to resort to estimates expressed in annualized returns rather than average returns. In fact, this study is applied to an emerging market that has been expanding over the years. Thus, if we analyze only the average of the generated returns, it is quite natural that they are higher the longer the holding period. Thus, the annualized return calculates the average amount of money earned by a given investment on an annual basis that comprises 254 trading days and depends on the holding period of the assets. As a result, this measure allows the comparison of strategies based on trading rules with different holding periods (Wang & Chan, 2007). Henceforth, inferences about the performance of any trading approach are mainly supported by estimations of annualized returns.
The experimental results in Table 2 are circumscribed by 20-day fitting windows, as this is the only p capable of generating bull flag average returns higher than those of the buy everyday strategy, regardless of the holding period or threshold value, as seen in Table 1. Furthermore, due to the empirical fact highlighted above of better results in terms of bull flag performance for fitting windows with shorter days. In addition, the observations are restricted to the maximum threshold as the higher the value of T, the higher the average return yielded by the bull flag trading rule.
The empirical results show a positive and statistically significant annualized excess profit for all holding periods. These findings hold true even when considering the existence of transaction costs. This is an important aspect as it is a factor that makes the data analysis closer to reality. Indeed, the column in Table 2 referring to transaction cost relates to the theoretical value that the operating cost of a single transaction would need to have so that, in their entirety, the costs involved in buying and selling a given index on the days indicated by the trading rules, were able to offset the bull flag average gains. For example, for the bull flag average return with a trading rule that has a p = 20 and q = 20 to be offset by the associated transaction costs, the unit cost of a trading operation would have to be 4.88%. According to Leippold et al. (2022, p. 80), “25 bps might be a reasonable estimate of transaction cost in the Chinese mainland's stock market during normal times”. Thus, considering reasonable transaction costs, the bull flag approach continues to be profitable and with better results than the buy everyday strategy, since the theoretical costs indicated in Table 2 are shown to be fairly high.
The results displayed in Table 2 suggest that an increase in the holding period is associated with a decrease in excess profit. The bull flag annualized excess return when q = 20 was 103.83%, while for a q = 100 it was only 62.78%. So, based on this empirical observation, investors should hold index assets for the shortest possible time to maximize their possible gains, in this case, 20 days. In the literature, this trend is in agreement with the study by Wang and Chan (2007) for the NASDAQ and TAIEX Indices. However, according to Leigh et al. (2004), this investment policy is only viable when the market presents a positive window price change because if it is falling (usually connoted as a bear market), the opposite was true for the NYSE Index.
In this context, the standard deviation can be seen as a measure of investment risk as it determines the dispersion of the securities' returns around its average. Thus, the greater the movement of index values, the greater the market volatility, which increases the standard deviation. Relative to the Chinese index, the standard deviation associated with the bull flag is higher than that observed in the market for any q, but the average returns linked to trading rules are significantly higher. Thus, using the coefficient of variation that calculates an investment total risk per unit of return, it can be noticed that the underlying risk of the bull flag is lower than that of the buy everyday strategy, as shown in Table 3 (Reed et al., 2002).
| p | q | Coefficient of variation | |
|---|---|---|---|
| Market | Bull flag | ||
| 20 | 20 | 8.62 | 1.65 |
| 20 | 40 | 6.42 | 1.62 |
| 20 | 60 | 5.33 | 1.69 |
| 20 | 80 | 4.58 | 1.72 |
| 20 | 100 | 4.08 | 1.68 |
- Note: p represents the number of days in the fitting window, in this case, 20 days. Both trading strategies buy and hold for a q number of trading days in the horizon period, which can range from 20 to 100 days.
Considering the variable referring to excess profits, and compared to other studies, it were obtained higher excess profits in the SSE index than in the emerging market of Chinese Taiwan analyzed by Wang and Chan (2007).
4.3 Market timing
The empirical results presented in Table 2 indicate that buy signals derived from bull flag patterns and captured by conditional trading rules generate the best performance when p = 20, q = 20, and Fitk ≥ 3. Interestingly, among the displayed data, this is the observation where the annualized excess profit is maximum and, at the same time, the standard deviation is minimum. As in the previous section, this section is intended to provide additional detailed information on the performance of the aforementioned trading strategies, under the same conditions. In particular, it investigates the forecasting ability related to changes in the direction of the stock index series as shown in Table 4.
| p | q | Market | Bull flag (T = 3) | ||||
|---|---|---|---|---|---|---|---|
| N (buys) | N (r > 0) | Ratio (%) | N (buys) | N (r > 0) | Ratio (%) | ||
| 20 | 20 | 7549 | 3948 | 52.30 | 1381 | 1124 | 81.39 |
| 20 | 40 | 7549 | 3905 | 51.73 | 1381 | 1132 | 81.97 |
| 20 | 60 | 7549 | 3947 | 52.29 | 1381 | 1093 | 79.15 |
| 20 | 80 | 7549 | 4030 | 53.38 | 1381 | 1096 | 79.36 |
| 20 | 100 | 7549 | 4148 | 54.95 | 1381 | 1079 | 78.13 |
- Note: p represents the number of days in the fitting window, in this case, 20 days. Both trading strategies buy and hold for a q number of trading days in the horizon period, which can range from 20 to 100 days. N (r > 0) symbolizes the number of buy signals that subsequently translated into positive returns. Ratio corresponds to the fraction of N (r > 0) divided by N(buys).
- Source: Own calculations.
The statistics in Table 4, more specifically those attributed to the variable designated as Ratio, indicate the percentage of success allocated to the forecasting power of technical analysis by comparing predictions about changes in the direction of the index values, that is, whether the market will continue to rise or, instead, will have a decline in the future. This indicator is thus expressed by the number of buy signals that resulted in positive returns, in relation to subsequent actual changes in the market. Empirically, it is possible to observe that this quotient varies between 78.13% and 81.97%. In addition, these values are higher than those recorded by the buy everyday strategy, regardless of the holding period. As a result, based on these results, the bull flag strategy can accurately predict the movement of market prices, promptly signaling opportunities for price increases. This mechanism, in turn, improves the return associated with its investments, outperforming the market strategy.
As previously mentioned, for a p = 20 and Fitk ≥ 3, the bull flag achieves its best performance when q = 20. In this case, in relation to the fraction of buys that resulted in a return greater than zero, this quotient is maximum when q = 40. However, it should also be noted that the existing figures for q = 20 and q = 40 are very close, which reinforces the results presented in Table 2. Likewise, Wang and Chan (2007) argue that technical analysis structured in bull flag conditional trading rules has an effectively higher degree of prediction than a buy everyday approach. Furthermore, the ratio between the number of buys with a positive return and the total number of buys reaches its maximum at 66.02% for the emerging market of Chinese Taiwan when q = 20 and 73.27% for the NASDAQ when q = 100 (Wang & Chan, 2007).
4.4 Robustness of empirical results for several nonoverlapping subperiods
The main objective of this section is to test the robustness of the results expressed in Table 2, particularly, the trading rule that had the best performance. To this end, the overall sample period is divided into five nonoverlapping subperiods of equivalent duration for the SSE index. Subsequently, in Table 5, these time horizons are investigated individually in terms of their average and annualized returns. Consequently, this information makes it possible to assess whether the bull flag's performance is due to the good results of a certain subperiod or if, on the contrary, it is explained by a generalized trend.
| p | q | Subperiod | Market | Bull flag (T = 3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N(buys) | Average return (%) | Annualized return (%) | Standard deviation | N(buys) | Average return (%) | Annualized return (%) | Standard deviation | Annualized excess profit (%) | ||||
| 20 | 20 | 1 | 1510 | 5.01 | 63.61 | 26.24 | 375 | 19.33 | 245.50 | 25.57 | 181.90 | (0.0000)a |
| 20 | 20 | 2 | 1510 | 0.96 | 12.24 | 7.63 | 253 | 6.16 | 78.20 | 8.73 | 65.96 | (0.0000)a |
| 20 | 20 | 3 | 1510 | 1.45 | 18.45 | 9.39 | 305 | 9.50 | 120.68 | 8.14 | 102.24 | (0.0000)a |
| 20 | 20 | 4 | 1510 | 0.32 | 4.00 | 7.41 | 220 | 5.86 | 74.45 | 8.79 | 70.45 | (0.0000)a |
| 20 | 20 | 5 | 1509 | 0.23 | 2.98 | 6.78 | 228 | 2.11 | 26.78 | 4.33 | 23.80 | (0.0000)a |
- Note: p represents the number of days in the fitting window, in this case, 20 days. Both trading strategies buy and hold for a q number of trading days in the horizon period, in this case 20 days. The five subperiods defined for the SSE are 01/02/1991 to 30/12/1996, 31/12/1996 to 24/04/2003, 25/04/2003 to 17/07/2009, 20/07/2009 to 12/10/2015, and 13/10/2015 to 31/12/2021. The annualized excess profit is the difference between the annualized return achieved by the bull flag trading rules and the annualized return derived from the market strategy defined as buy on everyday. Both annualized returns and annualized excess profits are calculated based on the 254 trading days existing in a calendar year.
- a 5% significance level assigned to t tests.
- Source: Own calculations.
The five subperiods defined for the SSE are 01/02/1991 to 30/12/1996, 31/12/1996 to 24/04/2003, 25/04/2003 to 17/07/2009, 20/07/2009 to 12/10/2015, and 13/10/2015 to 31/12/2021. For all these subperiods, the empirical results inherent to the bull flag trading rule, characterized by a 20-day fitting window, 20-day holding period and maximum threshold, show positive average and annualized returns. It is also noteworthy that the returns from the buy everyday strategy are positive for all time intervals but on a much smaller scale.
According to Table 5, technical analysis achieves positive and significant annualized excess profits for the five subperiods of each index, relative to the market's trading strategy. Therefore, these results are statistically consistent with the data presented in Table 2, reinforcing its robustness. In fact, the excess profit found for this trading rule is the result of a greater predictive power translated during the entire sample period, an result that does not change when the investigation is carried out considering nonoverlapping subperiods. In addition, it is noted that subperiods with a better level of performance, related to higher annualized returns, are linked to a greater number of buy signals detected by the trading rules.
4.5 Performance of the “buying run” approach
According to Leigh et al. (2004), the empirical results presented in Tables 2 and 5 may be incorrect. It is argued that the statistical computation of applied significance tests is more likely to calculate probabilities that represent lower bounds rather than what those values might truly be. To this end, the authors identify two assumptions in the decision-making process with inconsistent dependencies regarding the use of the t-test as a mechanism to calculate the significance of the difference between the average returns of both strategies for all trading rules. First, the fact that the commitment to buy at the beginning of the next trading day is established after the market has closed on the previous day and, finally, the circumstance that the price change to any fitting window of p-days after a trading day is closely related to that same change for the next trading day. Consequently, to establish an upper bound, this article also suggests using probabilities measured through t-tests that only incorporate the first trading day of each buying run. This means that the remaining buy signals arising from the bull flag-conditioned trading rules are completely ignored. In fact, buy recommendations normally occur during consecutive days, which gives rise to a concept called buying runs.
Table 6 reveals the bull flag performance adjusted to the concept of buying runs for a 20-day fitting window and Fitk ≥ 3. At this point, instead of the quantity of buy signals, only the number of buying runs that can be identified during the whole period under analysis is measured. For instance, there were 111 trading days that culminated in consecutive index purchases. Note also that the average run length is approximately 11 days. Furthermore, with the exception of the 20-day holding period, trading rules are capable of generating positive average returns for both indices and, in particular, it appears that the annualized return is higher the smaller the holding period associated with it. In turn, when compared with a market approach, the bull flag manages to produce significant annualized excess profits in four out of five observations. For a q = 20, there is an insignificant loss of performance of technical analysis relative to the buy everyday strategy of −7.99%. Thus, in general the empirical results presented in this section corroborate the result expressed in Tables 2 and 5, where trading rules seem to perform better than the market strategy, even in situations where buying runs are considered.
| p | q | N (runs) | First day of run only | |||
|---|---|---|---|---|---|---|
| Average run length | Average return (%) | Annualized return (%) | Excess profit | |||
| 20 | 20 | 111 | 11.01 | 0.95 | 12.10 | −7.99 (0.5344) |
| 20 | 40 | 111 | 11.01 | 9.73 | 61.77 | 40.63 (0.0190)a |
| 20 | 60 | 111 | 11.01 | 11.29 | 47.80 | 26.09 (0.0423)a |
| 20 | 80 | 111 | 11.01 | 12.88 | 40.89 | 19.17 (0.0297)a |
| 20 | 100 | 111 | 11.01 | 14.72 | 37.40 | 15.42 (0.0306)a |
- Note: The statistics referring to the first day of run only are calculated considering just the first day of each run, completely ignoring the remaining trading days. N(runs) corresponds to the number of runs. The annualized excess profit is the difference between the First day of run only annualized return achieved by the bull flag trading rules and the annualized return derived from the market strategy defined as buy on everyday. Both annualized returns and annualized excess profits are calculated based on the 254 trading days existing in a calendar year.
- a 5% significance level assigned to t tests.
- Source: Own calculations.
In the literature, when bull flag trading rules are conditioned to situations of buying runs on the Chinese Taiwan's stock market, technical analysis has shown to be an instrument with “great forecasting power” (Wang & Chan, 2007, p. 314). For instance, considering buying runs with an average run length of roughly 4 days, the excess return from the bull flag when q = 20 was 22.74% and with q = 40 it was 13.93% for the TAIEX. On the contrary, for both the NASDAQ and the NYSE, bull flag trading rules often produce insignificant excess profits when only buying runs are considered (Leigh et al., 2004; Wang & Chan, 2007).
5 CONCLUSION
Technical analysis is one of the most popular methods of predicting stock price movements. This paper examines for the first time the potential profit of bull flag trading rules in the Shanghai Stock Exchange Composite Index using a template matching technique based on price pattern recognition. Our sample covers the period 1991–2021. The experimental results support the idea that technical analysis based on the bull flag pattern has the ability to correctly predict changes in the direction of the SSE index values for almost all trading rules. In fact, bull flag trading rules have a buy signal success rate of around 80% for the various fitting windows, which is higher than those success rates resulting from the market-based strategy. In comparison with the buy everyday strategy, the bull flag achieved statistically significant annualized excess profits of greater magnitude for smaller fitting windows in conjunction with holding periods of shorter duration, even after considering transaction costs. Investments in the SSE are subjected to a higher level of risk, but the returns achieved are found to more than compensate for that added risk. Moreover, the excess profit elicited by the bull flag signal depends on the value assigned to the threshold: the higher the quality of the template price fit, the better the strategy's performance for lower holding periods. For example, for a 20-day fitting window and holding period, a trading strategy based on the bull flag signal generates an annualized excess profit of 103.83% over the standard approach.
The evidence presented in this paper suggests that technical analysis can be seen as an asset management approach that provides incremental information based on price patterns resulting from past trading activity. Indeed, these methods seem to be useful to identify important investment opportunities in terms of an investor's asset allocation process. In this regard, our results seem difficult to reconcile with the EMH.
One limitation concerning our empirical research should be mentioned. According to Zapranis and Tsinaslanidis (2012b), the execution of a template-matching technique commonly involves a certain degree of subjectivity. This occurs because to identify any pattern in prices, it is necessary to previously define each of the weights contained in the template grid, a process that is often done arbitrarily. In spite of this, Zapranis and Tsinaslanidis (2012b) argue that the subjective nature of technical analysis should not prevent researchers from assessing the validity of the investment process.
One future development of the present paper could be the comparison of the results using another major Chinese mainland's stock index. For instance, since the Shenzhen Stock Exchange has more private companies in new economy sectors (such as information technology and healthcare) than the Shanghai Stock Exchange, which is dominated by larger, state-owned companies, examining the potential of the use of bull flag patterns to predict price movement direction in that market would provide a valuable comparison.
Considering the limited number of academic papers that focus on the performance of qualitative technical indicators, it may be interesting for future research to continue to pay attention to this topic. For example, other templates or variations of the bull flag pattern can be used to investigate technical analysis in developed and emerging markets.
AUTHOR CONTRIBUTIONS
Júlio Lobão: conceptualization; formal analysis; methodology; project administration; supervision; writing—review and editing. Luís Pacheco: validation; writing—review and editing. António Fernandes: formal analysis; investigation; methodology; writing—original draft.
ACKNOWLEDGMENTS
This research has been financed by Portuguese public funds through FCT—Fundação para a Ciência e a Tecnologia, I. P., in the framework of the project with references UIDB/04105/2020 and UIDB/05105/2020.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest.
ETHICS STATEMENT
None declared.




