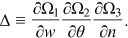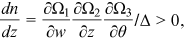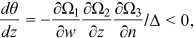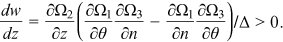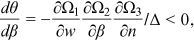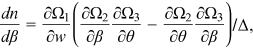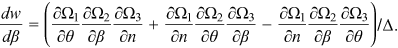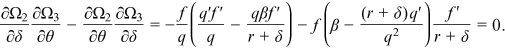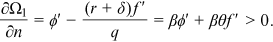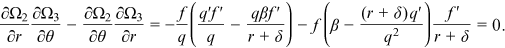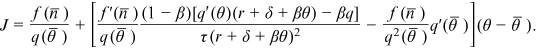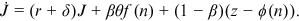Search, technology choice, and unemployment
Abstract
Technology variations among countries account for a significant part of their income differences. In this paper, a firm's technology choice is embedded in a search theoretic framework for unemployment. More advanced technology is assumed to have a higher setup cost, but it is more productive. The model is tractable and the following results are derived analytically. An increase in the unemployment benefit leads to an increase in the equilibrium wage rate, giving an incentive to firms to choose a more advanced technology. Thus, this result regarding unemployment insurance in models with wage posting carries through with Nash bargaining as well. As a consequence, the equilibrium unemployment rate increases. Furthermore, an increase in the bargaining power of workers increases the unemployment rate but has an ambiguous impact on the equilibrium level of technology and the wage rate. Finally, an increase in the exogenous job separation rate or the interest rate increases the unemployment rate and decreases the wage rate but does not affect the equilibrium level of technology.
1 INTRODUCTION
The issue of the appropriate choice of production technology is common for firms facing different market sizes and endowments of resources. Young (1928) argued that the size of the American market was bigger than that of Britain. These led American firms to choose mass production technologies, which may not have been profitable in Britain. Differences in technology choice among countries have significant implications. For example, Comin and Hobijn (2010) study the diffusion of 15 technologies for 166 countries and find that cross-country variation in technologies is responsible for more than one quarter of per capita cross-country income differences. When firms choose among different technologies, they frequently face the tradeoff between fixed and marginal costs of production. Here are two examples of this tradeoff. First, Prendergast (1990) studies empirical regularities concerning technology choices in several industries. He finds that marginal costs of production of firms decrease when firms adopt technologies with higher levels of fixed costs. Second, one of the most important innovations in the transportation sector in the 20th century is the adoption of containers. Before the adoption of containers, longshoremen conducted loading and unloading of goods. Containerization is a technology with much higher fixed costs (shown in specially designed container ports, container ships, and cranes) but much lower marginal costs of production.
However, the potential impact of technology on unemployment has been a largely contentious issue in the economics literature. One strand argues that the adoption of labor-saving technologies displaces workers resulting in higher unemployment. The view of higher unemployment as the outcome of new technologies used in the production process is commonly referred to as “technological unemployment.” Critics of this view argue that firms' savings from lower production costs caused by new technologies are passed on to the consumers in the form of lower prices. In turn, the demand for products adjusts quickly to these prices prompting firms to increase production without destroying jobs. For example, Autor and Salomons (2018) show that while innovations reduce labor demand directly, indirect effects (own-industry output effects; cross-industry input–output effects; between-industry shifts; and final demand effects) actually increase labor demand. Overall, technological innovations need not reduce aggregate labor demand.
Our theoretical results are consistent with the view of unemployment as technology-induced. Autor et al. (2003) document the reduction in the labor input of routine manual and cognitive tasks due to computerization in US industries between 1960 and 1998. Similarly, Goos et al. (2014) show that recent technological change in 16 Western European countries over the period 1993–2010 is biased toward replacing labor in routine tasks. In addition, Morin (2015) studies the effects of cheaper electricity in the US labor market during the Great Depression. The author finds that firms adjusted to this labor-saving technology by decreasing employment instead of increasing their output production.
The search model developed by Peter Diamond, Dale Mortensen, Christopher Pissarides, and others provides an elegant approach to explaining the existence of equilibrium unemployment based on microfoundations. This model has been used as a workhorse to address various issues such as employment fluctuation in business cycles, coordination failure in macroeconomics (Diamond, 1982), and the impact of opening to international trade on a country's unemployment.1 To the best of our knowledge, technology choice has not been incorporated into search-type models.
This paper contributes to the literature by introducing technology choice by firms into the search model of unemployment of Pissarides (2000). This extension to the benchmark search model is useful in providing more detailed modeling of firm behavior. In our framework, when a firm creates a vacancy, it chooses from a set of different technologies. Technology with a higher setup cost is more productive. The tractability of the model allows us to show analytically that an increase in the unemployment benefit leads to an increase in the equilibrium wage rate. This provides an incentive to firms to choose a more advanced technology. This, in turn, results in the equilibrium unemployment rate increasing. Furthermore, an increase in the bargaining power of workers increases the unemployment rate. However, the impact on the equilibrium level of technology is ambiguous because an increase in the bargaining power of a worker reduces a firm's surplus from job creation but makes it easier to find a match.
Interestingly, a change in the exogenous job separation rate does not affect the equilibrium level of technology. The reason for this result is as follows. There are two effects when the exogenous job separation rate changes: a direct effect from the change in the marginal unemployment benefit and an indirect effect on the possibility of finding a match through labor market tightness. Since the two effects work in opposite directions and they cancel out each other in equilibrium, the equilibrium level of technology does not change with the exogenous job separation rate. Similarly, a change in the interest rate does not affect the equilibrium level of technology.
The above results are broadly supported by empirical evidence. For instance, the positive association in our model between automation and wages is consistent with the empirical results of Graetz and Michaels (2018) who analyze the impact of industrial robots using data on a large panel of industries in 17 countries from 1993 to 2007. The authors find that the increased use of robots in the production process has a positive and statistically significant effect on average wages. In terms of our predicted increase in the unemployment rate, Graetz and Michaels's (2018) estimation results suggest that while the reduction in total employment is not significant, the use of robots reduced the hours of both low and middle-skilled workers.
Hagedorn et al. (2013) develop a new econometric methodology to measure the effect of changes in the unemployment benefit on the job creation decisions by firms during the Great Recession. The empirical results of these authors are consistent with the theoretical predictions of our model: higher unemployment benefits raise equilibrium wages leading to a significant reduction in job vacancy creation, a contraction in employment, and a rise in the unemployment rate.
On the other hand, the bargaining power of workers can be readily identified with labor unions. While the Canadian and US economies are similar, Partridge (2001) finds that lower US unionization is important in explaining greater relative unemployment rates in Canada in the 1990s. Pantuosco et al. (2001) use a panel of 48 US states for the 1978–1994 period to estimate the effects of unions on the labor market. The estimated effects of these authors agree with the prediction of our model that an increase in the bargaining power of workers raises the unemployment rate. However, this paper does not deal with the issue of technology adoption. Furthermore, the effect of unions on the wage rate is positive while in our case it is ambiguous.
The effect of trade unions on technological innovation is the subject of the paper by Menezes-Filho and Reenen (2003). In addition to reviewing the theoretical literature on this topic, these authors also survey several empirical studies. The estimated effects for North America appear to be statistically significant and negative on a consistent basis, while unions do not appear to have any impact on technological innovation in Europe. In our view, the lack of a uniformly strong result in one direction or the other in empirical work lends support to the theoretical ambiguity that arises in our model.
Relative to the benchmark search model of Pissarides (2000), while some results generalize to the incorporation of the choice of technology, others turn out to be ambiguous in our model. For example, while an increase in the bargaining power of a worker increases the wage rate in Pissarides (2000), the impact is ambiguous in our model.
In the literature on search and unemployment, Pissarides (1984) has studied a model in which workers can choose search intensity and firms can choose the level of job advertising. There are some significant differences between his model and ours. First, in his model, wage determination is not studied. The author is mainly interested in showing that there is no market wage rate that is socially efficient. In our model, the wage rate is determined through Nash bargaining. We are mainly interested in studying the impact of technology choice on the wage rate and the unemployment rate. Second, in his model, when a firm chooses a higher level of advertising, the rate for a firm to find a match increases, but the output of a firm does not change. In our model, if a firm spends more on maintaining a vacancy, the rate for a firm to find a match is not directly affected and the output of a firm increases. Pissarides (1985) conducts comparative studies on the impact of a simultaneous change in the setup cost of a firm and output of a worker. In this model, we make this simultaneous change a choice variable and, thus, endogenously determined. Acemoglu and Shimer (2000a) have studied a stimulating model in which firms choose their capital stock. One difference between their model and ours is that in their framework wages are not negotiated between a firm and a worker through Nash bargaining as in the present model. Instead, wages are posted by firms that endogenize bargaining power. These authors are mainly interested in addressing the issue of whether the market outcome is socially efficient. Thus, the focus of their work is significantly different from ours. We show that the result in Acemoglu and Shimer (2000b) regarding unemployment insurance carries through with Nash bargaining and without even assuming risk aversion.
In Ramsey and Watson (1997), like in the prisoner's dilemma, both firms and workers have incentives to provide “low effort” even though “high effort” will be beneficial to them. The firm chooses its technology and the tradeoff it faces is as follows: a higher level of investment is costly but makes the contract more robust to negative shocks. A firm may choose a less durable contract when the possibility of a bad state is low. Their efficiency wage setup is different from the search framework used here.
The paper is organized as follows. Section 2 describes the model and establishes the steady-state equilibrium conditions. Section 3 conducts comparative statics to explore the properties of the steady state. Section 4 studies short-run dynamics around the steady state. Finally, Section 5 discusses some generalizations and extensions of the model, and concludes.
2 THE MODEL
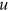 . There is an unlimited supply of potential firms. Firms decide whether to create vacancies. The vacancy rate is
. There is an unlimited supply of potential firms. Firms decide whether to create vacancies. The vacancy rate is 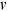 . The ratio between the unemployment rate and the vacancy rate is called labor-market tightness:
. The ratio between the unemployment rate and the vacancy rate is called labor-market tightness:
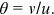
Unemployed workers and vacancies are matched through a matching function. The rate at which vacant jobs become filled is 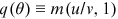 . Thus,
. Thus, 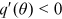 . Following Pissarides (2000), the elasticity of
. Following Pissarides (2000), the elasticity of 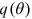 is assumed to be a number between 0 and −1.
is assumed to be a number between 0 and −1.
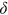 . Let a dot over a variable denote its time derivative. With unemployment increasing at the rate of
. Let a dot over a variable denote its time derivative. With unemployment increasing at the rate of  and the new employment rate rising by
and the new employment rate rising by 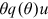 , the evolution of the unemployment rate is as follows:
, the evolution of the unemployment rate is as follows:
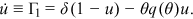 ()
()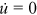 . Therefore, it follows from Equation (1) that the steady-state unemployment rate is given by
. Therefore, it follows from Equation (1) that the steady-state unemployment rate is given by
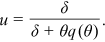 ()
()For a firm considering creating a vacancy, like Zhou (2004, 2009, 2011, 2013, 2021), Gong and Zhou (2014), and Ma et al. (2015), there are different technologies indexed by a positive number  . If a firm chooses technology
. If a firm chooses technology 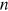 , it incurs a fixed cost
, it incurs a fixed cost 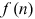 per unit of time. The value of a job's output is
per unit of time. The value of a job's output is 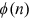 . More advanced technology has a higher setup cost but is more productive. That is,
. More advanced technology has a higher setup cost but is more productive. That is, 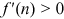 and
and 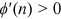 . To make sure the second-order condition for a firm's optimal choice of technology is satisfied, we also assume that
. To make sure the second-order condition for a firm's optimal choice of technology is satisfied, we also assume that 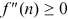 and
and 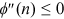 .
.
 . The present discounted value of expected profit from an occupied job is denoted by
. The present discounted value of expected profit from an occupied job is denoted by 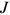 . The present discounted value of expected profit from a vacant job is
. The present discounted value of expected profit from a vacant job is 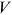 . The asset equation for a vacancy is given by
. The asset equation for a vacancy is given by
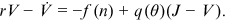 ()
()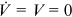 , we have
, we have
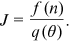 ()
()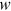 and the job yields return
and the job yields return 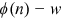 . When a job experiences an adverse shock, it leads to a loss of
. When a job experiences an adverse shock, it leads to a loss of 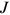 . Thus, the asset equation for a firm with a worker is
. Thus, the asset equation for a firm with a worker is
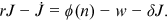 ()
() and
and  denote the present-discounted value of the expected income stream of an unemployed and an employed worker, respectively. When unemployed, a worker's return is equal to
denote the present-discounted value of the expected income stream of an unemployed and an employed worker, respectively. When unemployed, a worker's return is equal to  . This return can be interpreted as an unemployment benefit or the benefit from enjoying leisure. The asset equation for an unemployed worker is
. This return can be interpreted as an unemployment benefit or the benefit from enjoying leisure. The asset equation for an unemployed worker is
 ()
()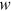 and the asset equation is
and the asset equation is
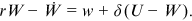 ()
()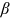 , which is a constant between zero and one. As in the literature, this means that
, which is a constant between zero and one. As in the literature, this means that 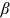 percent of the joint surplus created from a match between a worker and a firm goes to the worker. With the outside option
percent of the joint surplus created from a match between a worker and a firm goes to the worker. With the outside option 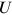 for the worker and
for the worker and 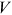 for the firm, the joint surplus is
for the firm, the joint surplus is 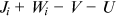 . Here, subscript
. Here, subscript 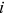 refers to a worker. Thus, Nash bargaining yields
refers to a worker. Thus, Nash bargaining yields
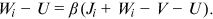 ()
()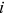 . Plugging Equation (11) into Equation (10) yields the following equation for the wage rate:
. Plugging Equation (11) into Equation (10) yields the following equation for the wage rate:
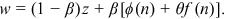 ()
()Our Equation (12) is similar to equation (1.20) in Pissarides (2000, p. 17) and the interpretation is similar. The average hiring cost for an unemployed worker is 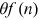 and this term enters the wage equation because workers will be rewarded for the saving of hiring costs that a firm enjoys when a job match is formed.
and this term enters the wage equation because workers will be rewarded for the saving of hiring costs that a firm enjoys when a job match is formed.
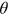 as given and chooses technology
as given and chooses technology 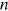 to maximize its expected value. From the above equation, the first-order condition for a firm's optimal choice of
to maximize its expected value. From the above equation, the first-order condition for a firm's optimal choice of  is
is
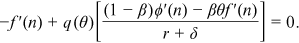 ()
()In Equation (14), when a firm chooses its technology, it recognizes that this choice will affect the wage of a worker. From Equation (12), the wage rate increases with the level of technology. That is, a firm's incentive to choose a more advanced technology is smaller because a portion of the gains from higher productivity will go to the worker.
In a steady state, variables do not change over time. In this long-run equilibrium, Equations (2), (6), (12), and (14) form a system of four equations defining four variables 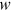 ,
, 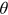 ,
, 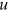 , and
, and 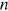 as functions of exogenous parameters. For this set of four variables, while
as functions of exogenous parameters. For this set of four variables, while 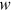 and
and 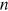 are choice variables and can jump over time,
are choice variables and can jump over time, 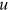 will evolve only gradually according to Equation (1). Since
will evolve only gradually according to Equation (1). Since 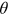 is a ratio involving
is a ratio involving 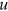 , labor market tightness
, labor market tightness 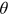 is also a state variable.
is also a state variable.
3 STEADY-STATE
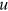 separately from the other variables, we can focus on the system of Equations (6), (12), and (14) defining three endogenous variables
separately from the other variables, we can focus on the system of Equations (6), (12), and (14) defining three endogenous variables 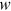 ,
, 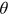 , and
, and 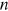 as functions of exogenous parameters.3
as functions of exogenous parameters.3
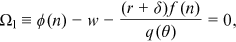 ()
()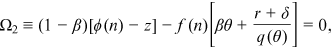 ()
()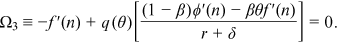 ()
()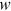 ,
, 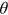 ,
, 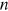 ,
, 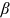 ,
, 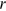 ,
, 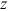 , and
, and 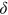 yields4
yields4
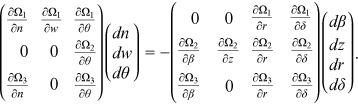 ()
()Partial differentiation of Equations (15a)–(15c) yields 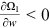 ,
, 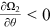 , and
, and 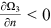 . Therefore,
. Therefore,  . With
. With 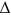 being nonsingular, it follows that a unique steady state exists. With existence and uniqueness established, we now explore the properties of the steady state.
being nonsingular, it follows that a unique steady state exists. With existence and uniqueness established, we now explore the properties of the steady state.
When the unemployment benefits increases, the opportunity cost for a worker from being employed rises. The following proposition studies the impact of a change in the unemployment benefit on technology choice and the labor market.
Proposition 1.An increase in the unemployment benefit leads a firm to choose a more advanced technology and labor-market tightness declines. Both the wage rate and the unemployment rate increase.
With 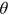 decreasing and the elasticity of
decreasing and the elasticity of 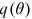 being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases as
being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases as 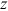 increases. □
increases. □
The intuition behind Proposition 1 is as follows. When the unemployment benefits increase, the value of the outside option for a worker becomes higher. Through Nash bargaining, the wage rate increases higher. When the wage rate is higher, a firm chooses naturally a more advanced technology to save on its labor cost. This reduces the amount of vacancies created and the equilibrium unemployment rate increases. The results here that the wage rate increases and labor-market tightness declines are consistent with those in Pissarides (2000, p. 21). However, the effect on production technology is new.
In their theoretical model, Acemoglu and Shimer (1999) have established a very interesting result that a higher unemployment benefit makes risk-averse workers more interested in higher-paying jobs which induce firms to create more productive employment opportunities for them. Acemoglu and Shimer (2000b) have demonstrated that “unemployment insurance increases labor productivity by encouraging workers to seek higher productivity jobs, and by encouraging firms to create those jobs.” Note that although our model does not yield any results on social welfare, Acemoglu and Shimer (2000b) further show quantitatively that a higher unemployment insurance benefit in the United States would generate higher social welfare. We view the results of our Proposition 1 as complementary to the results of these authors since we show that their result regarding unemployment insurance is robust to our alternative setup with Nash bargaining.
The bargaining power of workers could be affected by labor legislation which can adjust the generosity of the unemployment benefit and, thus, enhance the bargaining power of workers. When the bargaining power of the worker increases, the bargaining power of the firm decreases correspondingly. The following proposition studies the impact of a change in the bargaining power of workers on endogenous variables.
Proposition 2.An increase in the bargaining power of workers reduces labor-market tightness and increases the unemployment rate. However, the impact on the level of technology and the wage rate is ambiguous.
Since the sign of 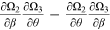 is ambiguous, the sign of
is ambiguous, the sign of  is ambiguous. Furthermore, since the sign of
is ambiguous. Furthermore, since the sign of 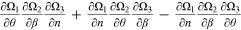 is ambiguous, the sign of
is ambiguous, the sign of 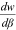 is ambiguous as well. Finally, with
is ambiguous as well. Finally, with 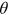 decreasing and the elasticity of
decreasing and the elasticity of 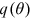 being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases. □
being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases. □
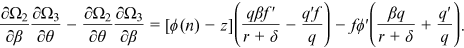
Thus, if 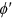 is sufficiently large (i.e., the productivity of a worker increases at a relatively fast rate with the level of technology),
is sufficiently large (i.e., the productivity of a worker increases at a relatively fast rate with the level of technology), 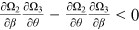 . In this case,
. In this case, 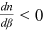 and the sign of
and the sign of 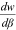 is ambiguous. In contrast, if
is ambiguous. In contrast, if 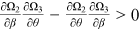 , then
, then 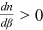 and
and 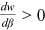 .
.
The intuition behind Proposition 2 is as follows. When a worker's bargaining power increases, the firm's surplus becomes lower. This reduces the firm's incentive to create a vacancy. Therefore, in aggregate, the number of vacancies created and labor-market tightness both decline. From Equation (15c), other things equal, there is a negative relationship between the level of technology and labor market tightness. When a worker's bargaining power increases, there are two channels affecting the level of technology chosen by a firm. First, since the benefit to the firm from choosing a more advanced technology decreases, the direct channel is that the firm tends to choose a less advanced technology. Second, through labor market tightness, the indirect channel is that the firm tends to choose a more advanced technology because it is now easier to find a match.
The two effects work in opposite directions. Without additional structure, the impact of an increase in the bargaining power of a worker on the equilibrium level of technology is ambiguous. Since the wage rate is affected by the level of technology, the impact of an increase in the bargaining power of a worker on the equilibrium wage rate is also ambiguous. On the other hand, if the equilibrium level of technology increases with a worker's bargaining power, Equation (17) implies that the direct effect of an increase in the bargaining power on the wage rate and the indirect effect through technology choice work on the same direction and the equilibrium wage rate increases. Here the result that an increase in the bargaining power of workers has an ambiguous impact on the wage rate is different from that in Pissarides (2000, p. 21) where the wage rate unambiguously increases with a worker's bargaining power. The reason for this difference is that the incorporation of the choice of technology leads to one additional effect which is absent in Pissarides.
The exogenous job separation rate can be affected by economy-wide shocks, such as the eruption of COVID-19 which could increase this rate. When the level of the exogenous job separation rate increases, the labor market becomes less efficient. The following proposition studies the impact of a change in the exogenous job separation rate on the endogenous variables of the model.
Proposition 3.An increase in the exogenous job separation rate decreases labor-market tightness and the unemployment rate increases. The equilibrium level of technology does not change and the wage rate declines.
Proof.An application of Cramer's rule to (16) yields
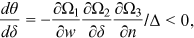
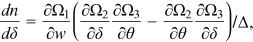
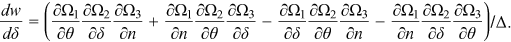
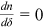 . Since
. Since 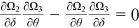 , it follows that
, it follows that
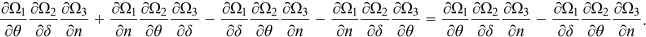
Furthermore, from Equations (15a) and (15b), 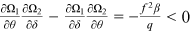 , thus
, thus 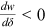 . Finally, with
. Finally, with 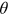 decreasing and the elasticity of
decreasing and the elasticity of 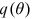 being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases. Also, there is a direct effect of an increase in
being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases. Also, there is a direct effect of an increase in 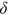 on the unemployment rate. Both effects work in the same direction increasing the unemployment rate. □
on the unemployment rate. Both effects work in the same direction increasing the unemployment rate. □
The intuition behind Proposition 3 is as follows. When the exogenous job separation rate increases, the expected job duration decreases, and the value of a job to the firm declines. This reduces a firm's incentive to create a vacancy and, as a consequence, labor-market tightness declines. When the job separation rate rises, there are two channels affecting the equilibrium level of technology. First, since the expected job duration is shorter and thus the marginal benefit of choosing a more advanced technology decreases, the direct channel is that a firm tends to choose a less advanced technology. Second, through labor market tightness, the indirect channel is that a firm tends to choose a more advanced technology since it is easier to find a match. Overall, the two effects cancel out each other and the level of technology does not change. When the equilibrium level of technology does not change, the impact of an increase in the exogenous job separation rate on the wage rate is then the same as in Pissarides (2000).
Finally, when the interest rate rises, an individual discounts the future at a lower rate. The following proposition studies the impact of a change in the interest rate on the endogenous variables of the model.
Proposition 4.An increase in the interest rate decreases labor-market tightness and the unemployment rate rises. Furthermore, the equilibrium level of technology does not change and the wage rate decreases.
Proof.An application of Cramer's rule to (16) yields
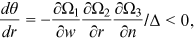
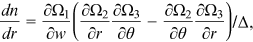
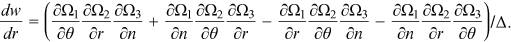
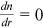 . Since
. Since 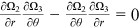 , it follows that
, it follows that
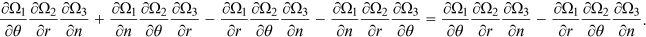
From Equations (15a) and (15b), 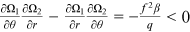 , thus
, thus 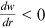 . Furthermore, with
. Furthermore, with  decreasing and the elasticity of
decreasing and the elasticity of 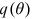 being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases. □
being a number between 0 and −1, it follows from Equation (2) that the unemployment rate increases. □
The intuition behind Proposition 4 is as follows. The impact of a change in the interest rate is similar to that of a change in the exogenous job separation rate. When the interest rate increases, this reduces the number of vacancies created, and the unemployment rate increases. Like the above discussion, the equilibrium level of technology does not change and the equilibrium wage rate decreases.
4 SHORT-RUN DYNAMICS
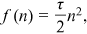 ()
()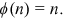 ()
()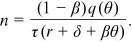 ()
()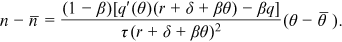 ()
()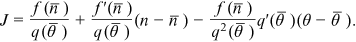 ()
()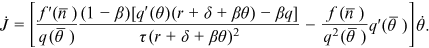 ()
()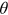 and
and 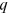 are evaluated at their steady-state values. From the above equation, we can derive the following equation defining the evolution of labor-market tightness:
are evaluated at their steady-state values. From the above equation, we can derive the following equation defining the evolution of labor-market tightness:
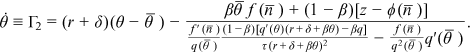 ()
()The following proposition studies the stability of the steady state.
Proposition 5.The steady state is a saddle point.
Proof.Equations (1) and (25) form a system of two equations defining the evolution of two variables 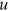 and
and 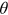 .
.
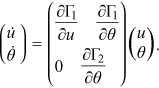 ()
()From partial differentiation of Equations (1) and (25), it is clear that 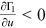 ,
, 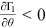 , and
, and 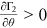 . Since the determinant of the coefficient matrix of system (26) is negative, this system is saddle-point stable. □
. Since the determinant of the coefficient matrix of system (26) is negative, this system is saddle-point stable. □
The result in Proposition 5 that the steady state is a saddle point is similar to that in Pissarides (2000, chap. 1). When there is a shock to the steady state, labor market tightness will immediately reach its new steady state value, while the unemployment rate will adjust gradually according to Equation (3) to its new steady state value. The phase diagram is shown in Figure 1.
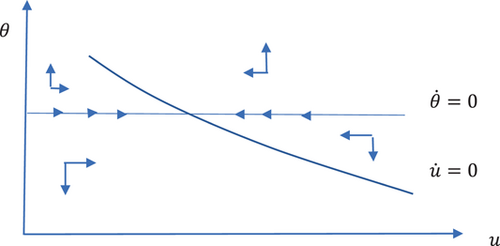
5 CONCLUSION
Technology variations play a significant role in explaining cross-country income differences. In this simple model, we have studied the impact of incorporating the choice of technology into a search theory framework for unemployment. We have derived the following results for the steady state. An increase in the unemployment benefit increases the wage rate and the unemployment rate and leads a firm to choose a more advanced technology. An increase in the bargaining power of workers increases the unemployment rate but has an ambiguous effect on the equilibrium level of technology and the wage rate. Furthermore, an increase in the exogenous job separation rate or the interest rate increases the unemployment rate and decreases the wage rate. Interestingly, the equilibrium level of technology does not change with the exogenous job separation rate or the interest rate.
There are some interesting generalizations and potential extensions to the model. First, in our framework, job destruction is exogenous. It will be useful to incorporate endogenous job destruction into the model. Second, wage rigidity is frequently observed in real-world economies. One interesting avenue for future research is to study the choice of technology under competitive search. This extension can reduce the high degree of flexibility of the wage rate. Third, technology choice in this model is captured as the tradeoff between productivity and fixed cost, which does not depend on any characteristics of firms. By introducing some sort of firm heterogeneities such as size or age heterogeneity, technology choices would depend on the current status of firms. A firm's technology is frequently positively associated with its level of output. To allow differences in firms' output, firms could engage in oligopolistic competition. It is likely that a firm with a higher level of output will choose technology with a higher fixed cost because this cost can be spread to a higher level of output, thus causing the average cost to be lower. Fourth, a fruitful generalization of this model is to make the job separation rate endogenous. Then, the impact of labor protection laws, such as the easiness or cost related to firing workers in the United States versus Europe and China, on the unemployment rate can be addressed.
Finally, one interesting research question is how automation, robots, or capital adoption impacts the labor market. To address this kind of question, Acemoglu and Restrepo (2018) consider different types of tasks (routine vs. nonroutine) and labor (high skill vs. low skill, abstract skill vs. routine skill). They classify technologies into different types, some of which substitute for labor while others serve as complements to it. Following their lead, labor market heterogeneity can be incorporated into our model. Thus, the implications of technology choice on the unemployment rate may vary across different labor markets.
AUTHOR CONTRIBUTIONS
Constantine Angyridis: Conceptualization; Formal analysis; Investigation; Writing – original draft; Writing – review & editing. Haiwen Zhou: Conceptualization; Formal analysis; Investigation; Methodology; Writing – original draft; Writing – review & editing.
ACKNOWLEDGMENT
We thank Kevin X. Huang, Wen Lei, and two anonymous reviewers for their insightful suggestions on our paper. The usual disclaimer applies.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
ETHICS STATEMENT
The authors declare ethics for conducting research are followed.
REFERENCES
- 1 See Mortensen and Pissarides (1999) and Albrecht (2011) for surveys of this line of literature.
- 2 Elsby and Michaels (2013) have studied a model with endogenous job destruction. In their model, productivity shocks may lead to job destruction. Firms may have decreasing returns to scale, and this makes bargaining in a search setting challenging to analyze.
- 3 Equation (15b) is derived from combining Equation (12) with (15a).
- 4 Equation (15c) is used to show that
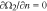 .
.



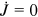 . Plugging the value of
. Plugging the value of 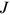 from Equation (
from Equation (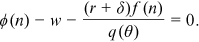
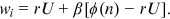
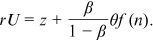
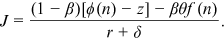
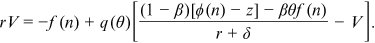
 denote the determinant of the coefficient matrix of endogenous variables in (
denote the determinant of the coefficient matrix of endogenous variables in (