Inequality and poverty in Spain: Insights from a regional convergence analysis
Abstract
We study the dynamics of inequality and poverty across 17 Spanish regions during 2008–2021. Through a club convergence approach, the results show noticeable differences in both indicators, income inequality (S80/S20) and poverty rate: two clubs are endogenously derived from inequality, while the analysis of the poverty was conducted in four clubs. In addition, the results are complemented with the outcomes for the GDP per capita, where more heterogeneity is detected, with three clubs, but with six divergent regions. The ordered logit model allows to identify the driving factors of such clubs. Finally, policy implications are discussed: the findings recommend the need for specific public policies to address regional differences in terms of economic and social growth also considering the trajectories—convergence or divergence—in inequality and poverty and their determining factors.
1 INTRODUCTION
Inequality and poverty are two major issues in the economic literature. The distribution of income (and wealth) and the percentage of the population under certain income levels have attracted attention from theoretical and empirical perspectives. Undoubtedly, high inequality and poverty in a society can be associated with social instability and may perpetuate over time.
The theoretical relationship between convergence, inequality, and poverty has been widely discussed in the economic literature. The convergence theory predicts that regions or countries with lower income levels will grow faster than those with higher income levels, which in turn will lead to a decline in income inequality. However, some studies have found that convergence does not always lead to a reduction in inequality and, therefore, not necessarily to a reduction in poverty.
One of the first studies to address this relationship was the seminal work of Kuznets (1955), who argued that convergence could occur as economies develop, but that this process could be hindered by inequality. Subsequently, Solow (1956) and Swan (1956) developed growth models that incorporated convergence and inequality.
Other authors, such as Li and Zo (1998), analyzed the relationship between inequality and economic growth,1 finding that inequality can have negative effects on growth. Aghion et al. (1999) and Barro (2000) argued that convergence may be more likely in countries with appropriate policies to foster economic growth and reduce inequality. Furthermore, Ravallion (1995) did not find evidence of such a relationship from the developing countries in the 1980s. The growth elasticity of poverty reduction was also investigated by Bourguignon (2003) and Beck et al. (2007) who reviewed the importance of the financial system for the poor. Finally, Balasubramanian et al. (2023) addressed the multidimensional poverty of 91 low and middle-income countries between 1990 and 2018, concluding that a 10% increase in GDP decreased multidimensional poverty by 4%–5%.
Also interestingly, Ravallion (1997) analyzed inequality and poverty, concluding that at any positive rate of growth, the higher the initial inequality, the lower the rate at which income-poverty falls. In addition, Banerjee and Duflo (2003) found that reducing inequality can be an effective way to reduce poverty. Perugini and Martino (2008) analyzed the relationship between inequality and growth in Europe, concluding that inequality can have negative effects on long-term growth. Other interesting studies on these topics are provided by Ravallion (2001), Lopez and Servén (2006), Kraay and Raddatz (2007), and Chen and Ravallion (2010).
Overall, the literature shows that the theoretically sound relationship connecting convergence, inequality, and poverty is an important concern in economics today. In theory, economic convergence should reduce inequality between countries or regions, as lagging economies should grow faster than more advanced economies. However, in practice, economic convergence does not always translate into reduced inequality, as the benefits of economic growth can be concentrated in the upper strata of the society, widening the gap between the rich and the poor. Indeed, if no measures are taken to ensure that economic growth is inclusive, economic convergence may even increase poverty and social exclusion, as the most vulnerable groups in society may be left behind in the process of economic development.
In this regard, some studies have proposed specific policies to reduce inequality and foster convergence. For example, Aghion et al. (1999) suggest that investment in education and technology can reduce the gap between rich and poor countries. Banerjee and Duflo (2003) propose income transfer policies and access to basic services to reduce poverty and inequality, and others, such as Berg and Ostry (2017) recommend that fiscal and regulatory policies can help reduce the income gap and improve income distribution.
Within this context, the convergence (or divergence, and its patterns) of inequality and poverty is an interesting issue in the literature. As is review in Section 2, while some studies are devoted to the convergence on inequality, with different approaches and mixed results, the issue of poverty has not been addressed from a convergence perspective to date.
Hence, this paper addresses the convergence of income inequality and poverty across Spanish regions in the recent years. The case of Spain is interesting for several reasons. First, this country presents a high (income) inequality and poverty rate. Specifically, according to the latest data available for the UE from Eurostat, in 2021, Spain presented a Gini index of 33.0, only after Bulgaria, Latvia, Lithuania, and Romania, with an average of 30.1 for the European Union (EU). Similarly, the risk of poverty or social exclusion was 27.8, only exceeded by Romania, Bulgaria, and Greece, while that rate was 21.7 in the EU. In this context, it should be remarked that both indicators were high in Spain also before the pandemic, although the country experienced the largest decrease of GDP in 2020—and will not even recover its pre-crisis level until late 2023 or early 2024—second, Spain is a highly decentralized country, where the regional levels of government have powers in spending and revenue issues, with potential impact on income distribution and poverty rates. Additionally, there are noticeable differences in inequality and poverty among the Spanish regions, as we will examine later.
Specifically, we analyse the convergence of (income) inequality and poverty across Spanish regions through a club convergence approach (Phillips & Sul, 2007 and 2009). This approach has been widely employed in several areas, as income and growth (Sofi et al., 2023), house prices (Holmes et al., 2011; Holmes et al., 2019), R&D (Blanco et al., 2020b; Delgado et al., 2024), CO2 emissions (Apergis & Payne, 2017), eco-innovation (Costantini et al., 2023), taxation (Delgado et al., 2022) or fiscal decentralization (Blanco et al., 2020a). A recent great survey can be found in Tomal (2023), analyzing 370 empirical papers mainly in economics, ecology, energy, finance, and health.
We consider the period 2008–2021, available data for the Spanish regions. In consequence, we cover the onset of the Great Recession and the various stages, thereafter, also including the pandemic (2020) and the year after (2021), with the beginning of the Next Generation funds (750,000 million euros for the recovery of the EU in 2021–2026). Therefore, this paper contributes with the first study of (club) convergence of inequality and poverty jointly, and to the scarce literature on poverty convergence reviewed in Section 2. In addition, to the best of our knowledge, this is also the first attempt to analyze the convergence of inequality, or poverty, for Spain,2 with the special features commented above. Furthermore, several stakeholders will benefit from the results achieved in this research, especially policymakers and individuals (households), because of the critical nature of inequality and poverty issues and the possibility of evaluating the performance of the (regional) political representatives taking into account the evolution of these magnitudes.
The rest of the paper is organized as follows. Section 2 briefly reviews the literature on inequality and poverty convergence. Section 3 describes the methodology, based on club convergence, while Section 4 reports the data, the main results—from club convergence and the ordered logit model—and discussion. Finally, Section 5 concludes the paper.
2 LITERATURE REVIEW
We review the literature on inequality and poverty convergence. To this end, we separate studies about each issue, and also according to the territories analyzed.
2.1 Inequality
Starting with Benabou (1996), who analyzed several samples with a beta convergence approach, and concluded convergence, other studies focusing on a sample of countries also concluded beta convergence, namely Ravallion (2003) and Bleaney and Nishiyama (2003) Suárez-Arbesú et al. (2023), through the methodology of the club convergence approach, analyzed the case of EU countries, spanning the period 2007–2018, and concluded the presence of four clubs—with four divergent countries—, while they identified economic openness, public intervention and education as the main drivers of inequality reduction.
Focusing on other areas, Ranjbar et al. (2014) studied the African countries with panel stationarity tests with breaks and documented that most countries diverged from the United States.
In another group of studies, focusing on the US states, Panizza (2001) and Lin and Huang (2011) also deduced beta convergence, while Lin and Huang (2012) found convergence through panel stationarity tests with breaks for the period 1916–2005, and Ezcurra and Pascual (2009) from a nonparametric approach over the period 1969–1999. In contrast, Ho (2015) did not find any convergence through a panel unit roots approach in the period 1916–2012. Finally, Apergis et al. (2018), considering several periods, employed the club convergence analysis and provided evidence of mixed results.
In the case of the regional level, Ezcurra and Pascual (2005) showed convergence from EU regions (1993–1998) through density functions, while Tian et al. (2016) evaluated convergence across certain Chinese provinces (1978–2013) through club convergence, identifying only two clubs. Their results indicated that within-club inequality decreased, but between-club disparity widened in the period. Furthermore, Mendonza-Velázquez et al. (2019) studied the Mexican states (1940–2010) employing an Euclidian measure with mixed results; their results are in line with Ivanovski et al. (2020) for the Australian states (1942–2013). In addition, Kacou (2022) examined the African regions over the period 1992–2012, deriving multiple equilibria and identifying the determining factors of the clubs. Finally, at the local level of government, Gomes (2007) analyzed the Brazilian municipalities. He reported the presence of convergence, while he also detected certain differences across regions.
Thus, we also intend to fill the gap in the literature in terms of empirical work on income convergence among Spanish regions.
2.2 Poverty
As stated above, the poverty has been scarcely analyzed through a convergence approach to date. Although not under the convergence approach used in this study, Crespo-Cuaresma et al. (2022) investigated the relationship between a country's economic growth and the poverty rate, concluding that the presence of poverty convergence depends on the speed of convergence of average income in relation to other parameters.
In addition, in a related work, Ravallion (2012) claimed that two stylized facts in economic development, namely the advantage of backwardness and the advantage of growth, while under the assumption that the processes for growth and poverty reduction do not depend on the initial poverty level, would lead to poverty convergence. However, analyzing data for 90 developing countries, his findings highlighted the presence of low or no sign of such type of convergence. This scarce literature on poverty convergence, as stated previously, justifies the convenience and contribution of the present study.
Again, there is a lack of empirical work on the convergence of poverty in the Spanish regions.
3 METHODOLOGY
Finally, Phillips and Sul (2009) propose a merge procedure to solve the potential overestimation of the clubs achieved in the first stage.
4 DATA AND RESULTS
4.1 Data
We use data for the Spanish regions, spanning the period 2008–2021. Specifically, we use the ratio S8020 as an indicator of inequality, and the poverty rate. Both measures are provided by INE—Instituto Nacional de Estadística- and they are available online.3 Data for other inequality measures, as Gini coefficient, Theil index, or the proposal of Palma and Stiglitz (2016), are not available directly from INE for the Spanish regions during a large period for this type of analysis. With regard to the quintile share ratio, it should be noted that it is less vulnerable to extreme values and also considered a larger part of the distribution than other ratios as 9010.
Table 1 reports the descriptive statistics, including the study of the well-known sigma convergence through the coefficient of variation (CV) along time, depicted in Figure 1, also incorporating the GDP per capita to enrich the analysis. The joint analysis of (income) inequality, poverty and per capita income allows us to have a more complete view of the situation of each territory.
| 2008 | 2014 | 2021 | |
|---|---|---|---|
| Inequality (S8020) | |||
| Mean (unweighted) | 5.10 | 6.20 | 5.60 |
| SD | 0.54 | 1.03 | 0.88 |
| C.V. | 0.1076 | 0.1670 | 0.1564 |
| Min. | 4.2 | 4.8 | 4.8 |
| Max. | 6 | 8.9 | 8.2 |
| Range | 1.8 | 4.1 | 3.4 |
| N. obs. | 17 | 17 | 17 |
| Poverty rate | |||
| Mean (unweighted) | 19.10 | 21.30 | 20.50 |
| SD | 7.89 | 8.10 | 7.02 |
| C.V. | 0.4125 | 0.3798 | 0.3423 |
| Min. | 5.9 | 10.2 | 9.80 |
| Max. | 35.3 | 37.2 | 32.30 |
| Range | 29.4 | 27.00 | 22.50 |
| N. obs. | 17 | 17 | 17 |
| GDPpc | |||
| Mean (unweighted) | 23,965.8 | 21,971.7 | 25,047.6 |
| SD | 4547.42 | 4645.47 | 4978.39 |
| C.V. | 0.1897 | 0.2114 | 0.1988 |
| Min. | 16,632.9 | 15,274.2 | 18,906.0 |
| Max. | 32,155.0 | 30,610.0 | 34,821.0 |
| Range | 15,522.1 | 15,335.8 | 15,915.0 |
| N. obs. | 17 | 17 | 17 |
- Source: INE and own elaboration.
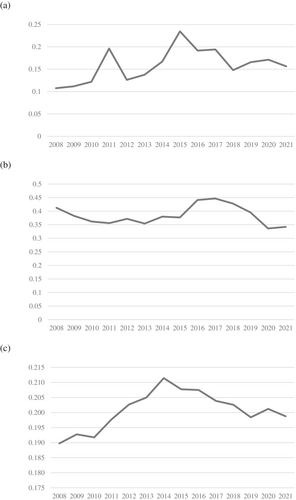
Source: Own elaboration
.Comparing the situation in 2008, before the Great Recession, and 2021, after the pandemic crisis—although its effects extended beyond that year—, we observe opposite results for inequality and poverty. In this way, while a sigma convergence is achieved for poverty, a clear sigma divergence is detected for inequality. This may be true because a reduction in poverty rates does not imply a reduction in the gap between rich and poor, but it may be that policies across the Spanish regions have reduced poverty rates, but not in all cases, leading to the reduction in inequality. In the context of the pandemic, this can be explained by the fact that on the one hand, the social policies carried out by both the national and regional governments cushioned the impact of the crisis on some of the poorest individuals, while on the other hand, the richest percentage of the population managed to maintain their income, and in some cases, even to increase it.
As inequality and poverty are two different but related phenomenon, the evolution, determinants, and policies against them are not always the same. The fight against poverty has traditionally supported in strengthening economic growth, increasing equality, or both. Considering the regional convergence approach of this paper, it should be also noted that the inequality and poverty, in the country as a whole, have experienced the evolution reflected in Figure 2, where different stages are certainly identified.
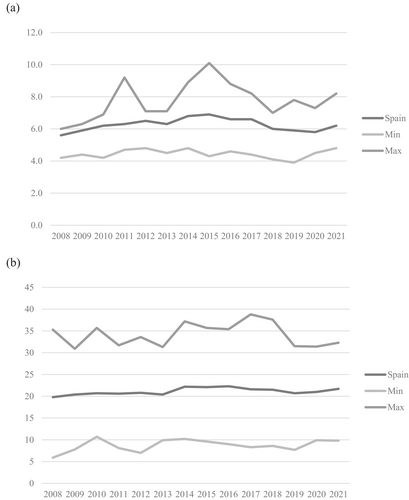
Source: INE and own elaboration
.If we look at the GDP per capita, the evolution is more similar to the inequality case, with a clear sigma divergence until 2014, and then sigma convergence, which stopped in 2020, and concluded in 2021, with a CV 4.75% greater than that in 2008.4 The two periods of divergence coincide with the last two crises and their consequences, that is, the economic crisis of 2008 and the pandemic crisis of COVID-19.
After evaluating these results for the entire sample, the club convergence approach will allow us to investigate the evolution of each region or a cluster of regions, identifying common trends, as well as divergent cases. In addition, the ordered logit model will permit the identification of the determining factors of the clusters.
4.2 Club convergence results
The findings5 of the club convergence are reported in Table 2 and mapped in Figure 3, including the evolution of the averages for each club –and divergent regions- in Figure 4.
| Club | Regions | |||
|---|---|---|---|---|
| (a) Inequality | ||||
| Full sample | −28.5197a | −1.2483 (0.0438) | ||
| Club 1 | Andalucía, Asturias, Islas Baleares, Castilla—La Mancha, Cataluña, C. Valenciana, Galicia, Madrid | 0.9066 | 0.2176 (0.2400) | 0.1088 |
| Club 2 | Aragón, Cantabria, Castilla y León, Extremadura, Navarra, País Vasco, La Rioja | 1.6034 | 0.2244 (0.1400) | 0.1122 |
| Divergence | Islas Canarias, Murcia | |||
| (b) Poverty | ||||
| Full sample | −49.1963a | −0.9308 (0.0189) | ||
| Club 1 | Andalucía, Extremadura | 13.9967 | 1.9307 (0.1379) | 0.9654 |
| Club 2 | Asturias, Canarias, Castilla—La Mancha, C. Valenciana, Murcia | 2.3110 | 0.3098 (0.1340) | 0.1549 |
| Club 3 | Aragón, Islas Baleares, Cantabria, Castilla y León, Cataluña, Madrid | 6.3000 | 0.9770 (0.1551) | 0.4885 |
| Club 4 | Navarra, País Vasco, La Rioja | 3.7136 | 0.4159 (0.1120) | 0.2080 |
| Divergence | Galicia | |||
| (c) GDPpc | ||||
| Full sample | −41.2295 | −0.9093 (0.0221) | −0.4547 | |
| Club 1 | Cataluña, Navarra | 2.1609 | 0.1845 (0.0854) | 0.0923 |
| Club 2 | Cantabria, Castilla y León, Galicia, Islas Baleares | 2.8209 | 0.4646 (0.1647) | 0.2323 |
| Club 3 | Andalucía, Canarias, Castilla—La Mancha, Extremadura, Murcia | 2.5569 | 0.1294 (0.0506) | 0.0647 |
| Divergence | Aragón, Asturias, C. Valenciana, Madrid, País Vasco, La Rioja |
- a Indicates rejection of the null hypothesis of convergence at the 5% level.
- Source: Own elaboration.
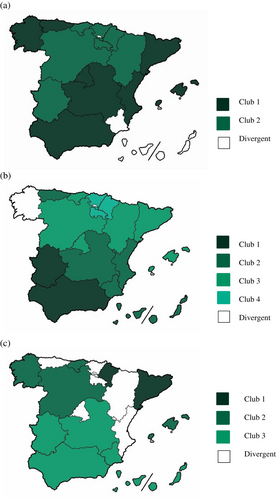
Source: Own elaboration
. [Colour figure can be viewed at wileyonlinelibrary.com]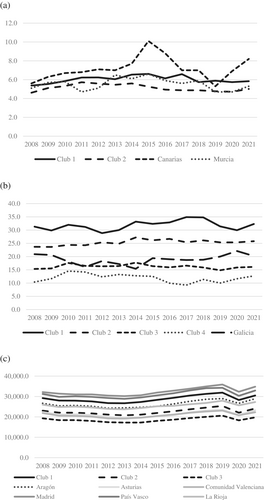
Source: Own elaboration
.As a general result, a higher fragmentation is reached in poverty, where the procedure endogenously identifies four clubs, plus a divergent case. However, in the income perspective, the 17 Spanish regions are arranged into only two clusters, with two divergent regions.
More specifically, in the case of inequality convergence, two clubs, comprising 7–8 regions, are arranged, while Islas Canarias and Murcia are divergent territories; Islas Canarias is the region with the largest inequality in Spain. It should also be remarked that among the four richest regions, Cataluña and Madrid are classified into club 1—higher inequality, while Navarra and País Vasco appear in club 2—lower inequality. Both clubs present relative convergence with small coefficients (0.1088 and 0.1122, respectively).
When we analyze the poverty convergence, club 1, contains Andalucía and Extremadura with a coefficient (α) of 0.97, near of absolute convergence—convergence in level. Those two regions are precisely the poorest territories (GDPpc) in Spain. On the other extreme, focusing again on the four richest territories, Cataluña and Madrid are located into club 3, and País Vasco and Navarra in club 4. In this case, the divergent region is Galicia.
Considering the territorial reality in Spain and the regional financing system, and specifically regarding the four richest regions, it should be remarked that Navarra and País Vasco have a system more beneficial for them, the so-called formal way, while the rest of the territories, including Madrid and Cataluña, are under the common system, where those richest regions must contribute more intensively to regional solidarity.
The results for the GDP per capita indicate the presence of three clubs and six divergent regions. Above the first club, comprised by Cataluña and Navarra, two territories emerge: Madrid and País Vasco. Other two autonomous communities are located between the first two clubs, namely Aragón and La Rioja. Finally, Asturias and C. Valenciana are identified before the last club.
Considering the three indicators, inequality, poverty, and per capita income, it should be remarked that the southern region of Andalucía is classified in club 1 for inequality and poverty, and club 3 in per capita income. As stated below in Table 3, this region exhibits the largest unemployment rate in the period. The other Spanish region with the lowest per capita income, Extremadura, appears in club 3 in that dimension, and accompanies Andalucía in club 1 in poverty, but integrates into club 2 in income inequality.
| A. Inequality | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | Club Ineq | Inequality | Poverty | GDPpc | Invest | Unemp | Structure | HumCap | Openness | Public | Foreign | Rural |
| Canarias | Div | 1 | 3 | 13 | 16 | 2 | 11 | 14 | 15 | 13 | 4 | 13 |
| Balears, Illes | 1 | 2 | 8 | 7 | 6 | 7 | 16 | 15 | 17 | 12 | 1 | 12 |
| Andalucía | 1 | 3 | 2 | 16 | 10 | 1 | 3 | 12 | 10 | 15 | 11 | 7 |
| Madrid | 1 | 4 | 13 | 1 | 5 | 12 | 17 | 2 | 9 | 17 | 6 | 17 |
| Comunitat Valenciana | 1 | 5 | 6 | 12 | 14 | 6 | 10 | 11 | 7 | 14 | 3 | 14 |
| Castilla—La Mancha | 1 | 6 | 5 | 15 | 2 | 4 | 1 | 16 | 14 | 9 | 9 | 2 |
| Cataluña | 1 | 7 | 15 | 4 | 13 | 9 | 14 | 6 | 2 | 7 | 5 | 15 |
| Asturias | 1 | 8 | 12 | 10 | 12 | 8 | 13 | 4 | 12 | 6 | 15 | 9 |
| Murcia | Div | 9 | 4 | 14 | 3 | 5 | 8 | 13 | 3 | 16 | 2 | 11 |
| Extremadura | 2 | 10 | 1 | 17 | 8 | 3 | 2 | 17 | 16 | 3 | 17 | 1 |
| Rioja, La | 2 | 11 | 11 | 6 | 1 | 15 | 4 | 7 | 13 | 5 | 7 | 8 |
| País Vasco | 2 | 12 | 16 | 2 | 17 | 17 | 15 | 1 | 5 | 2 | 13 | 16 |
| Cantabria | 2 | 13 | 10 | 9 | 15 | 14 | 12 | 5 | 11 | 4 | 14 | 10 |
| Galicia | 1 | 14 | 7 | 11 | 11 | 10 | 6 | 10 | 4 | 10 | 16 | 6 |
| Castilla y León | 2 | 15 | 9 | 8 | 7 | 11 | 7 | 9 | 8 | 11 | 12 | 3 |
| Aragón | 2 | 16 | 14 | 5 | 4 | 13 | 5 | 8 | 6 | 8 | 8 | 4 |
| Navarra | 2 | 17 | 17 | 3 | 9 | 16 | 9 | 3 | 1 | 1 | 10 | 5 |
| Correlation with inequality | 0.4804 | −0.3235 | −0.0907 | 0.6912 | −0.2574 | −0.4142 | −0.5172 | −0.6152 | 0.5270 | −0.4779 | ||
| B. Poverty | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | Club Pov | Poverty | Inequality | GDPpc | Invest | Unemp | Structure | HumCap | Openness | Public | Foreign | Rural |
| Extremadura | 1 | 1 | 10 | 17 | 8 | 3 | 2 | 17 | 16 | 3 | 17 | 1 |
| Andalucía | 1 | 2 | 3 | 16 | 10 | 1 | 3 | 12 | 10 | 15 | 11 | 7 |
| Canarias | 2 | 3 | 1 | 13 | 16 | 2 | 11 | 14 | 15 | 13 | 4 | 13 |
| Murcia | 2 | 4 | 9 | 14 | 3 | 5 | 8 | 13 | 3 | 16 | 2 | 11 |
| Castilla—La Mancha | 2 | 5 | 6 | 15 | 2 | 4 | 1 | 16 | 14 | 9 | 9 | 2 |
| Comunitat Valenciana | 2 | 6 | 5 | 12 | 14 | 6 | 10 | 11 | 7 | 14 | 3 | 14 |
| Galicia | Div | 7 | 14 | 11 | 11 | 10 | 6 | 10 | 4 | 10 | 16 | 6 |
| Balears, Illes | 3 | 8 | 2 | 7 | 6 | 7 | 16 | 15 | 17 | 12 | 1 | 12 |
| Castilla y León | 3 | 9 | 15 | 8 | 7 | 11 | 7 | 9 | 8 | 11 | 12 | 3 |
| Cantabria | 3 | 10 | 13 | 9 | 15 | 14 | 12 | 5 | 11 | 4 | 14 | 10 |
| Rioja, La | 4 | 11 | 11 | 6 | 1 | 15 | 4 | 7 | 13 | 5 | 7 | 8 |
| Asturias | 2 | 12 | 8 | 10 | 12 | 8 | 13 | 4 | 12 | 6 | 15 | 9 |
| Madrid | 3 | 13 | 4 | 1 | 5 | 12 | 17 | 2 | 9 | 17 | 6 | 17 |
| Aragón | 3 | 14 | 16 | 5 | 4 | 13 | 5 | 8 | 6 | 8 | 8 | 4 |
| Cataluña | 3 | 15 | 7 | 4 | 13 | 9 | 14 | 6 | 2 | 7 | 5 | 15 |
| País Vasco | 4 | 16 | 12 | 2 | 17 | 17 | 15 | 1 | 5 | 2 | 13 | 16 |
| Navarra | 4 | 17 | 17 | 3 | 9 | 16 | 9 | 3 | 1 | 1 | 10 | 5 |
| Correlation with poverty | 0.4804 | −0.9289 | 0.0956 | 0.8652 | 0.5098 | −0.8701 | −0.5172 | −0.4730 | 0.0319 | 0.2917 | ||
- Note: Ranked 1-highest to 17-lowest.
- Source: Own elaboration.
It should be noted that the merge procedure proposed by Phillips and Sul (2009) does not lead to changes in our initial results exposed in Table 2. Specifically, the proposal does not conclude club fusions in inequality and GDP per capita. In terms of poverty, the procedure could lead to a fusion of club 1 and club 2, but with α = −0.0481, maintaining the initial clustering in this case.
- GDP per capita.
- Investment as percentage of GDP.
- Unemployment rate.
- Economic structure: percentage of primary sector in GDP.
- Human capital/education: percentage of population with tertiary education.
- Openness: sum of exports and imports as percentage of GDP.
- Public sector: per capita public expenditure.
- Foreign: foreigners as percentage of total population.
- Rural: rural population as percentage of total population.
The rank correlations between inequality or poverty and those variables indicate potential relationships. First, it should be noted that the rank correlation between inequality and poverty is relatively high, 0.48. With regard to inequality, noticeable positive rank correlations are identified with unemployment and foreigners, while negative correlations are found for the size of the public sector, economic openness, and rural. In the case of poverty, we detect important positive rank correlations for unemployment and structure, and negative correlations with GDP per capita, human capital, economic openness, and the size of the public sector.
Therefore, in the next section, we perform an ordered logit model with these variables to identify the driving factors of the clubs. However, a review of the empirical literature about the determinants of inequality and poverty among Spanish regions is useful before the analysis. Thus, in addition to the mentioned paper about the inequality of opportunity in Spain (Cabrera et al., 2021), and also other references to Spain as a whole (Ayala, 1994; Ayala et al., 2021; Ayllón, 2013; Campoy-Muñoz et al., 2022; Cantó, 2002; de la Escosura, 2008; Gradín, 2021; Pijoan-Mas & Sánchez-Marcos, 2010), few papers have addressed to date the evolution and determinants of inequality and poverty in the Spanish regions.
Ayala and Jurado (2011) concluded that the improvement derived from economic growth in the long-term for lower income percentiles was not uniform across regions, and also found limited possibilities for poverty reduction in the lower-income territories. In Ayala et al. (2017) the poverty and the business cycle are examined. In this context, they stated that unemployment has a positive impact on severe poverty, but inflation has a negative one. Finally, Palomino et al. (2023) analyzed the COVID-19 shock on inequality and poverty in Spanish regions. They concluded that the compensating measures through public expenditure made it possible to soften the impact on poverty and (wages) inequality but warn of a possible erosion of regional cohesion in the country.
4.3 Ordered logit model
- GDP per capita initial (2008)8: mixed
- GDP per capita: mixed
- Investment: mixed
- Unemployment rate: positive (−)
- Economic structure: mixed, mostly positive (−)
- Human capital-percentage of population with tertiary education: negative (+)
- Openness: mixed, mostly negative (+)
- Public sector: negative (+)
- Foreign: mixed, mostly positive (−)
- Rural: mixed, mostly positive (−)
In addition, although inequality and poverty are different phenomena, our assumption is that those signs are a priori similar for both indicators.
The results are summarized in Table 4. As general outcomes, the results for income inequality illustrate the relevance of all these variables, except human capital and investment. In the case of poverty, we have found no significant effects for investment, openness, and foreign.
| A. Inequality | |
|---|---|
| Variable | Estimation |
| GDPpc0 | 0.002754*** (0.000563) |
| GDPpc | −0.000998*** (0.000303) |
| Invest | −0.106066 (0.071944) |
| Unempl | 0.224899** (0.099199) |
| Structure | 0.446303* (0.233721) |
| HumCap | −0.144831 (0.121454) |
| Openness | −0.120270*** (0.034259) |
| Public | 0.004250*** (0.000997) |
| Foreign | −0.845532*** (0.198180) |
| Rural | 0.237228*** (0.064594) |
| LR χ2 (10) = 184.21 (prob > χ2 = 0.0000) | |
| Pseudo R2 = 0.6348 | |
| Log-likelihood = −52.9879 | |
| Obs. = 210 | |
| B. Poverty | |
|---|---|
| Variable | Estimation |
| GDPpc0 | 0.003042*** (0.000412) |
| GDPpc | −0.001257*** (0.000232) |
| Invest | 0.030284 (0.057718) |
| Unempl | −0.285917*** (0.075639) |
| Structure | 1.073829*** (0.216338) |
| HumCap | −0.129938* (0.077340) |
| Openness | −0.019310 (0.015656) |
| Public | 0.002434*** (0.000522) |
| Foreign | −0.071160 (0.081417) |
| Rural | −0.076417** (0.036587) |
| LR χ2 (10) = 405.30 (prob > χ2 = 0.0000) | |
| Pseudo R2 = 0.6932 | |
| Log-likelihood = −89.6916 | |
| Obs. = 224 | |
- Note: ***, **, and * indicate significance at 1%, 5%, and 10%, respectively. Standard errors in parentheses. Club 1 indicates the highest inequality (poverty).
- Source: Own elaboration.
4.3.1 Inequality
More specifically, in the inequality case, although the results are not statistically significant for human capital and investment, we find a positive effect (− sign) for GDP per capita, in line with part of the literature, given that the results for this variable are mixed. In other words, an increase in per capita income illustrates that the regions move into lower inequality clubs. In the case of Spain, as stated previously, it should be remarked that there is a large distance between regions, ranging from 18,906 to 34,821 euros in 2021.
As expected, the effect reached for unemployment is negative (+ sign); therefore, an increase in unemployment moves the regions to higher clubs, indicating a rise in inequality across the Spanish regions. Again, it is important to highlight that the data on unemployment varies intensely across Spanish regions: in 2021, from 9.8% in País Vasco to 23.2% in Islas Canarias. Additionally, the high rate of unemployment of Spain, both in the EU and OECD contexts, surely explain, to a large extent, the high levels of inequality (and poverty) in the country. Thus, the design of better employment policies must be one of the main objectives of the Spanish public sector next years.
The economic structure, considering the percentage of the primary sector in GDP, appears with a significant and negative impact (+ sign) on inequality. Thus, a higher participation rate of the primary sector in GDP moves the clubs to a higher club, indicating higher levels of inequality. This clearly indicates the Spanish policymakers should emphasize strengthening other forms of production, mostly through other sectors.
Regarding the human capital, as stated above, our results indicate that it is not statistically significant, although the expected impact is positive (− sign), indicating that improved levels of human capital led to lower inequality clubs and convergence is getting easier.
The economic openness appears with a significant and positive effect (− sign), showing that higher levels of openness move the region to lower clubs characterized by lower inequality. The findings corroborate certain previous studies that have identified similar results, as Roine et al. (2009) who document the presence of non-significant evidence for this variable.
As expected, the public sector size effect is significant and negative (+ sign), highlighting that higher sizes of the public sector move the regions to higher convergence clubs that support higher inequality. In fact, following Eurostat, the government expenditure of Spain was 50.0% of GDP, and according to the classification of the public expenditure by function, COFOG, the social protection expenditure represented the 20.3% of GDP in Spain.
In addition, the foreign people appear with a positive effect (− sign) as expected, but the rural population with a negative impact (+ sign). In other words, higher levels of foreign people across the Spanish regions move those regions to lower convergence clubs, indicating lower inequality, as the contribution of these people is clearly on the positive side. At the same time, a higher percentage of the rural areas across regions contributes negatively to convergence since increases the probability these regions to move to higher convergence clubs that display higher inequality levels.
4.3.2 Poverty
With respect to poverty, besides the mentioned no significance of investment (as in inequality), openness and foreign, most results are in line with the achieved for the income inequality, evidencing again that inequality and poverty are two different but related issues.
In this case, our results indicate significant and positive effects (− sign) for GDP per capita unemployment, human capital, and rural. By contrast, the findings support the presence of negative effects (+ sign) in the cases of economic structure and public sector size.
In the case of unemployment, there exists a positive impact (− sign), providing support to the fact that lower levels of unemployment lead the regions to lower convergence clubs characterized by lower poverty.
Regarding human capital, our results support the argument that propose education as one major instrument to fight poverty. Its effect is shown to be positive (− sign), since improved human capital pushes the regions to lower convergence clubs that display lower poverty levels.
On the other hand, in terms of GDP, we can observe that the higher the GDP, the higher the probability of belonging to lower convergence clubs, which are defined as lower poverty clubs.
Finally, in terms of the role of the primary sector in the poverty process, it has a negative impact (+ sign) on poverty, since the positive sign highlights that a greater size of the primary sector in GDP worsens the probability a regio to move to lower poverty clubs. Similarly, the same result seems to hold for the case of the public sector. By contrast, the opposite holds for the variables of foreign people and the rural areas.
4.4 Discussion
The study of the convergence and (income) inequality and poverty for the Spanish regions allows us to identify common patterns and divergent trajectories during the recent years. Convergence refers to the reduction of differences between regions in terms of income and economic growth. In this sense, the analysis of convergence shows that some regions in Spain have achieved greater economic growth and a greater reduction in poverty in recent years, while other regions have experienced stagnation or even a decline in their growth trends.
By contrast, income and poverty inequality are important factors to consider in this analysis, as they can both affect the ability of regions to achieve higher growth rates. In that sense, the study of inequality shows that in some Spanish regions the gap between the richest and the poorest has widened, which may be holding back their capacity for economic growth and poverty reduction.
Our results point out large disparities across Spanish regions in this period, evidencing the need for an improved regional policy. The islands, Islas Canarias and Baleares, and Andalucía—the most populous Spanish region—lead the income inequality ranking, while Extremadura, Andalucía, and Islas Canarias are at the top of the poverty ranking. As stated above, precisely Andalucía and Extremadura have the lowest per capita income in 2008–2021. In the other extreme, Navarra, a floral region in financing terms, has the lowest inequality and poverty in the average of the period. This territory is a leader in economic openness and size of the public sector and has the lowest unemployment rate together with País Vasco.
These results are clearly of general interest for policymakers because inequality and poverty are core issues in the economy, but also in the society. The analysis of these clubs and their determining factors should also be interesting in specific policies, namely regional growth policies or within the dichotomy urban versus rural. Our results are also appealing for individuals, as the population should be aware of certain details about the current conditions of the territory and the public policies associated with political representatives in each region. More specifically, given that the divergence results across the Spanish regions highlight that these regions are characterized by differences in their total factor productivity and there is the need to speed up a process of technological catch-up primarily through educational investments. These implications call for more analysis, looking at the effects of specific interventions and channels either through domestic funds, or through European Cohesion funds for which individuals can clearly benefit. Such potential convergence mechanisms and channels could be education, income support, wage policies, funding support for specific sectors, and other socioeconomic macro, sectoral, or regional policies. Finally, individuals can benefit from inequality and poverty convergence if institutional quality is also improved across regions. In particular, a stronger control of corruption, rules of law, and government effectiveness can lead to better convergence patterns across Spanish regions, given that national and regional governments characterized by high institutional quality are more able to provide a better transparent framework to compete and increase productivity.
Overall, the findings recommend the need for specific public policies to address regional differences in terms of economic and social growth. For example, regions that are experiencing greater convergence and poverty reduction may require different policies than regions that are experiencing a divergent trajectory.
In the case of Spain, this could involve implementing policies that encourage economic growth in poorer regions, promoting investments in infrastructure, and fostering job creation patterns. It would be also necessary to address income inequality and poverty through redistributive policies that ensure that the benefits of economic growth are distributed more equitably.
5 CONCLUSIONS
We analyzed the convergence (or divergence) of income inequality and poverty rate across the Spanish regions over the period 2008–2021. In an initial sigma convergence analysis to complete the descriptive view of the regions as a whole during this period, we observed opposite patterns for inequality and poverty, finding sigma divergence and sigma convergence, respectively. In addition, the same analysis for the GDP per capita exposed more similarity with inequality.
The club convergence analysis by Phillips and Sul (2007, 2009) provided evidence for certain heterogeneity in these variables, rejecting in all cases the full convergence hypothesis. As a general result, a higher fragmentation was reached in poverty, where the procedure endogenously identified four clubs, plus a divergent case. However, in terms of income, the 17 Spanish regions were arranged into only two clusters, with two divergent regions. The analysis for the GDP per capita identified three clubs, but six divergent autonomous regions.
When the drivers of club membership were researched, the analysis performed an ordered logit model estimation considering as determinants GDP per capita, investment, unemployment rate, economic structure, human capital, economic openness, public sector, foreign population, and rural population. The results for the inequality documented the relevance of all these variables except human capital and investment. In the case of poverty, we have found no significant effects for investment, openness, and foreign.
The results achieved in this study are beneficial not only for policymakers, but also for households, as they can acknowledge and evaluate the evolution of these indicators, as well as the performance of the political parties in their jurisdictions.
With regard to the limitations of our analysis, it should be remarked that the analysis used as inequality measure the S80/S20, because other measures, namely the Gini index, the Atkinson & Theil index or the Palma-ratio, were not available for all regions within the period under consideration.
Finally, as potential extensions of this study, it will be interesting to repeat the analysis in a few years in the future when new data will be available so as to better identify the effects of the recent pandemic and the current high inflation epoch on this convergence, and when the Next Generation funds devoted to the recovery and resilience of the EU will have been spent on those regions. It should be remarked that Spain is one of the countries most benefited from these funds, along with Italy. The fair and efficient use of these funds will be assessed by the European institutions, especially considering that the financing is carried out with the issuance of joint debt in the very long term. Undoubtedly, inequality and poverty are critical phenomena for the progress and stability of the entire society, especially in Spain, a country characterized by high levels in both dimensions.
ACKNOWLEDGMENTS
We are grateful to the editor and the anonymous reviewers for their comments and suggestions. The usual disclaimer applies.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest.
ENDNOTES
- 1 In another interesting study, Karakotsios et al. (2020) analyze the relationship between income inequality, taxation and economic freedom for 58 countries in the period 1995–2016. The results exhibit a trade-off between economic freedom and income equality.
- 2 Interestingly, Cabrera et al. (2021) study the inequality of opportunity in Spain. These authors conclude that opportunity inequality represents 44 per cent of overall inequality.
- 3 See https://www.ine.es/jaxi/Tabla.htm?path=/t00/ICV/dim1/l0/&file=11401_2.px&L=0 for inequality and https://www.ine.es/jaxiT3/Tabla.htm?t=9963 for poverty.
- 4 The coefficient of correlation between the GDP per capita and inequality is 0.6340, while between the GDP per capita and poverty is only 0.1469.
- 5 These results have been obtained using Stata. See Du (2017) for implementing the club convergence in Stata.
- 6 The divergent regions have been excluded from this analysis (inequality: Canarias and Murcia; poverty: Galicia).
- 7 It should be noted that, to avoid this contradiction, the estimation can be performed assigning the value 1 to the last club (lowest inequality or poverty), but we decided to maintain the ordering from the club convergence approach to better identify the clubs.
- 8 Following the suggestion raised by one of the referees, we have also included the GDP per capita at the beginning of the sample.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available in INE at https://www.ine.es/jaxi/Tabla.htm?path=/t00/ICV/dim1/l0/&fil. These data were derived from the following resources available in the public domain: - INE, https://www.ine.es/jaxi/Tabla.htm?path=/t00/ICV/dim1/l0/&fil - INE, https://www.ine.es/jaxiT3/Tabla.htm?t=9963.




