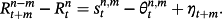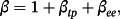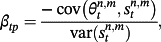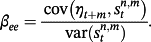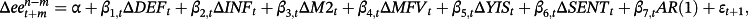Expectation hypothesis and term structure anomaly
Abstract
Campbell and Shiller (1991) find the presence of term structure anomaly, in which the slope of the term structure predicts inconsistently to the change in yield of longer term bonds over the life of shorter term bonds during 1952–1987. Focusing on the post Campbell and Shiller period, our findings suggest that the anomaly is not only attributed to term premia but also relates to expectation errors. We found that macroeconomic surprises and irrationality from investors' behaviour are important determinants of time-varying expectation errors. These factors are capable of explaining the rejection of the expectation hypothesis and the U.S. term structure anomaly in long-term securities.
1 INTRODUCTION
The expectation hypothesis (EH) of the term structure of interest rates, one of the best known theories in financial economics, postulates that the spread between long-term and short-term interest rates is capable of explaining or even predicting changes in interest rates. That is, a positive (negative) yield spread between long-term and short-term interest rates predicts a rising (declining) interest rates. Conventional EH theory regards the spread as a forecast of changes in interest rates and applies it to interpret shifts in the yield curve. Campbell and Shiller (1991) use U.S. Treasury bill/bond rates ranging from 1-month rates to 10-year rate in the period of 1952 and 1987 and find that prediction is opposite to the expectation theory of term structure of interest rates. This phenomenon contradicts EH theory and hence is called a “term structure anomaly” in this study.
Numerous studies investigated the causes of this term structure anomaly. We summarize the literature here to outline the potential determinants. The first links to the time-varying term premia (Jongen, Verschoor, & Wolff, 2011; Mankiw & Miron, 1986; Mankiw & Summers, 1984). Holding default-free bonds with long-term maturities in one's portfolio may not be the same as holding short-term default-free bonds because the latter strategy incurs uncertainty of return for the second bond. Even when accounting for time-varying term premia, prior studies still struggle with the presence of the U.S. anomaly. Backus, Gregory, and Zin (1989) find that variations in the risk premium are insufficient to explain related results, and a similar claim has been proposed by Froot and Frankel (1989) in the forward exchange market. Froot (1989) finds that the time-varying term premia explanation is exclusively plausible only for short-term securities, but it plays a minor role in instruments with longer durations.
Peso problem also contributes to the term structure anomaly or the failure of EH. Peso problems relate to the sample moments that do not coincide with the population moments. Specially, this reflects the fact that the Fed's policy innovations can induce economic agents to revise their expectations, because the available information set is different from that observed in the past. This change, in turn, causes forecast errors of interest rates in small samples (Bekaert & Hodrick, 2001; Ederington & Huang, 1995; Lewis, 1989; Mankiw & Summers, 1984).
The last source arises from the agents who trade irrationally and hence impact asset prices and returns. More recent studies, such as Baker and Wurgler (2006), utilize interim advances in behavioural finance theory to provide sharper tests of sentiment effects. De Long, Shleifer, Summers, and Waldmann (1990) indicate that prices and returns are set by rational arbitragers who face limits to arbitrage and irrational investors who are prone to exogenous sentimental. As identified by Shleifer and Vishny (1997), arbitrageurs use funds from investors to conduct arbitrage activities and hence face pressure from investors to liquidate their portfolio in a short horizon. As a result, prices may not always stay on the corresponding fundamental values. Under such circumstance, mispricing arises from either sentiment or a limit to arbitrage or their combination.
Certainly, irrationality about the bullishness and bearishness of future interest rates or macroeconomics variables has a deterministic role on changes in interest rates or bond prices. Shefrin (2008, chapter 20) indicates that heterogeneous beliefs of representative investors can inject more volatility to long-term than short-term rates. Therefore, Shiller (1979) finds that long-term rates are too volatile to be consistent with what the model expects. Once arbitrage is restrictive, arbitrageurs are unable to substitute long-term bonds to short-term bonds, and subsequently, bond prices and future interest rates tend to deviate from the equilibrium level. As a consequence, we will see a systematic expectation error between ex post realized rate and expected future rate.
This paper contributes to propose alternative explanations of the term structure anomaly and the rejection of EH in the post Campbell–Shiller period. Using U.S. Treasury bond yields for the period from 1987 to 2010, we examine whether irrationality proxied by investors' bullishness or bearishness and other factors jointly define time-varying expectation errors and consequently resulted in the term structure anomaly. To do so, the coefficient of the Campbell–Shiller equation is decomposed into term premia and the expectation error, which benefits our understanding on relative contributions to the failure of the EH and term structure anomaly. Further, we distil the irrational part from the expectation errors to reveal its relationship with investors' bullishness and bearishness and thus judge its contribution and significance to the term structure anomaly.
Results show that the rejection of EH and the term structure anomaly appears in long-term securities exclusively. We find that term premia dominates the coefficients of the Campbell–Shiller equation and appears to be one of major factors on term structure anomaly for long-term bonds. Rational factors account for the expectation errors more than irrational factors do. Investor sentiment, a proxy of irrationality, is significantly related to expectation errors for many cases at 5%. Irrationality partly contributes to the rejection of the EH, whereas term premia contributes more to the term structure anomaly for long-term bonds.
This study complements to previous works that have identified the relationship between irrationality and the EH. For example, Shiller (1979) finds that long rates are too volatile to be consistent with the linear expectations model. Froot (1989) finds that the expectation of short-term instruments systematically underreacts to the short-term rates, whereas the expectations of long-term instruments tend to overreact to the long-term rates. The finding of Shiller (1979) and Froot (1989) may be explained by Shefrin (2008, chapter 20) who states that the heterogeneous beliefs of representative investors inject different levels of volatility into long-term and short-term rates, thus damaging the validity of the EH. This injection may be driven by the irrational behaviour of investors. Similarly, Ederington and Huang (1995) point out that the failure of EH is caused by agents' varying perceptions of the weights of short and long rates in the market. Because agents may be irrational, the expected future rate may diverge from expectations about the spread of long and short rates.
This study differs from Bulkley, Harris, and Nawosah (2015) who investigate whether behaviour biases explain the rejections of the EH of the term structure of interest rates in many ways. They found the expectation errors conforming to some patterns of behaviour biases. However, they do not consider components identified by past literature affecting the term structure anomaly. Additionally, they do not follow the conventional approach developed by past literature used to measure the expected future rate such as survey data or trading prices. Instead, they use the rates implied from term structure of interest rates, and hence, the essence of expectation error may not be exactly consistent with a well-accepted definition (see Cavaglia, Verschoor, & Wolff, 1994; Froot, 1989; Jongen et al., 2011). Finally, they have not yet considered the determinants of time-varying expectation errors, which are critical to affect term structure anomaly. In this study, we attempt to complement the work of Bulkley et al. (2015) and go further by providing a clearer picture for the term structure anomaly. Recently, Chen and Chiang (2017) study time-varying term premium using U.S. interest rate data and found that investor sentiment and macroeconomic surprises are the main driving force. However, this paper studies the relationship between expectation errors of U.S. interest rates and behaviour issues.
The paper is organized as follows. Section 2 examines the unbiased validity of EH using the Campbell–Shiller equation. Section 3 derives the components attributable to term premia and expectation errors contained in the EH, and then the expectation error is separated into rational and irrational parts. In Section 4, we explore the determinants of expectation error. Then conclusions are provided in the final section.
2 CAMPBELL AND SHILLER EQUATION
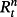 , and the yield of a shorter term m period,
, and the yield of a shorter term m period,
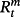 , under the rational expectation can simply be written as the following:
, under the rational expectation can simply be written as the following:
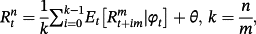 (1)
(1)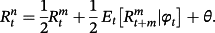 (2)
(2)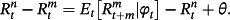 (3)
(3)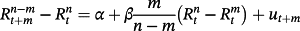 (4)
(4)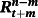 is the ex post realized rate at time t + m for the period n–m. In this case, n/m is not necessarily an integer. According to rational expectations (Muth, 1961), ut + m is the forecast error at time t + m assuming to be orthogonal with the information available at time t. We test the null hypothesis of β = 1 to examine whether there is an unbiased predictor of future changes in interest rate when using any combinations of the spread. The Newey and West (1987) procedure is applied to get rid of the problem arising from overlapping data.
is the ex post realized rate at time t + m for the period n–m. In this case, n/m is not necessarily an integer. According to rational expectations (Muth, 1961), ut + m is the forecast error at time t + m assuming to be orthogonal with the information available at time t. We test the null hypothesis of β = 1 to examine whether there is an unbiased predictor of future changes in interest rate when using any combinations of the spread. The Newey and West (1987) procedure is applied to get rid of the problem arising from overlapping data.Using the Treasury rates with various combinations of n and m in the period between 1952 and 1971, Campbell and Shiller (1991) find that the coefficients are negative in most cases, indicating that the spread between long-term and short-term yields predicts an opposing movement of future interest rate. The results are apparently against the EH and have become a puzzle for researchers, hence stimulating further discussions.
Table 1 presents the estimates of the regression model using Equation 4 where the monthly U.S. zero-coupon bond yields for the period between March 1987 and December 2010 have been employed. 1 We find that the hypothesis of β = 1 is rejected for all cases at the conventional significance level, except for some cases in m = 12, indicating that the EH of the term structure is not held for most of the cases. Asymptotic standard errors, which have been corrected for heteroskedasticity and equation error overlap, in the manner of Newey and West (1987), almost show that the coefficients of β are insignificant, suggesting that the slope of the term structure fails to predict the change in interest rates, particularly for the short-term forecast horizon. For m = 12 and 24, the short end of the term structure shows a superior predictive ability for the movement of interest rates.
| n–m (months) | ||||||
|---|---|---|---|---|---|---|
| m (months) | 3 | 6 | 12 | 24 | 60 | 120 |
| 3 | 0.228 | 0.282 | 0.178 | −0.039 | −1.112 | −0.985 |
| (0.294) | (0.232) | (0.186) | (0.096) | (1.132) | (0.804) | |
| (0.256) | (0.202) | (0.144) | (0.105) | (1.065) | (0.836) | |
| 6 | −0.098 | −0.061 | 0.198 | −0.149 | −0.962 | −0.938 |
| (0.185) | (0.532) | (0.365) | (0.275) | (0.865) | (0.743) | |
| (0.097) | (0.400) | (0.338) | (0.217) | (0.849) | (0.712) | |
| 12 | 0.496 | 1.093 | 0.715 | 0.329 | −0.376 | −0.879 |
| (0.207) | (0.172) | (0.169) | (0.141) | (0.713) | (0.712) | |
| (0.183) | (0.114) | (0.168) | (0.122) | (0.675) | (0.665) | |
| 24 | 1.951 | 1.936 | 1.722 | 1.456 | 0.559 | −0.321 |
| (0.370) | (0.313) | (0.297) | (0.170) | (0.196) | (0.400) | |
| (0.338) | (0.228) | (0.249) | (0.134) | (0.123) | (0.368) | |
- Note. This table shows the regression coefficient and upper and lower standard errors (in parenthesis) are computed under the assumption of homoskedasticity, using Newey and West (1987), which takes account of heteroskedasticity. Constant terms (not shown) are included in all regressions. All rates are U.S. zero-coupon bond yields obtained from Datastream for the period March 1987 and December 2010. Under the null hypothesis that the expectations hypothesis holds and that expectations are Muth rational, β = 1 and the error term ut + m is a pure random innovations.
Equation 4 may be incorrectly estimated because the regression results do not consider possible structural breaks during the sample period. The Chow test rejects the null hypothesis of no structural break and detects a break in August 2007. It is well known that the subprimed crisis began in the United States and spread around the globe. Before that period, 10-year Treasury bond rate is greater than 3-month Treasury bill rate, but they become opposite after that period. At best, we shall use structural break model that may yield better estimates. However, the period after August 2007 contains only small sample (less than 3 years); the estimate using full sample without considering structural break model is not likely to alter our results.
By investigating the period between 1952 and 1987, Campbell and Shiller (1991) find an opposing direction when forecasting the yield changes of long-term discount bonds over the life of short-term discount bonds, which is referred to as a “term structure anomaly.” Table 1 shows that the anomaly has almost vanished during the latter period in comparison with the period studied by Campbell and Shiller (1991). However, the anomaly still remains on short forecast horizons (m = 3 and 6) and the long end of the term structure (n–m > 24). So far, previous works have related the term structure anomaly to the time-varying term premium (Jongen et al., 2011) or peso problems (Bekaert, Hodrick, & Marshall, 2001; Chen, Kuo, & Chiang, 2014; Jardet, 2008; Lewis, 1991). However, this study addresses it from the other angle. We proceed the decomposition in Equation 1, the term premium component and the expectation error component, and evaluate their contributions to the anomaly in the following section.
3 TERM PREMIA AND EXPECTATION ERROR
3.1 Decomposition of term structure anomaly
The results are in accordance with Campbell and Shiller (1991). We now turn our attention to the post Campbell–Shiller period and find that, although the spread provides a right direction of the prediction, support on the EH is still hard to achieve throughout the subsample. To study the cause, we provide a procedure to decompose the β coefficients in Equation 4.
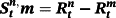 and
and
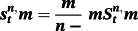 . Then after rewriting Equation 4, we obtain Equation 5:
. Then after rewriting Equation 4, we obtain Equation 5:
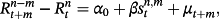 (5)
(5)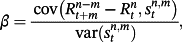 (6)
(6)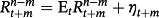 and ηt + m is the expectation error term, which assumes a random number under rational expectation. Then the left-hand side of Equation 5 can be specified as
and ηt + m is the expectation error term, which assumes a random number under rational expectation. Then the left-hand side of Equation 5 can be specified as
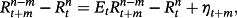 (7)
(7)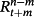 at time t + m for the period n–m. In addition, we know that the term premium,
at time t + m for the period n–m. In addition, we know that the term premium,
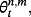 is defined as the difference between the spread and expected future spot rate at time t for the period between n and m,
1
is defined as the difference between the spread and expected future spot rate at time t for the period between n and m,
1
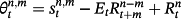 . Hence,
. Hence,
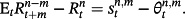 (8)
(8)The subscript tp denotes the term premium, equal to
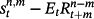 where the subscript ee is the expectation error, defined as
where the subscript ee is the expectation error, defined as
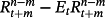 . Note that the beta decomposition is based on spreads rather than the forward premiums used by Froot (1989).
. Note that the beta decomposition is based on spreads rather than the forward premiums used by Froot (1989).
3.2 Expected future interest rates
To compute the term premium and expectation errors, expected future Treasury yields is required in advance either from survey data or from market trading price. Survey data are now widely available. 2 Froot (1989), Cavaglia et al. (1994), and Jongen et al. (2011) use survey data to calculate the survey term premium. However, using exchange-traded Eurodollar futures rates as alternatives is promising for several reasons. First, Eurodollar futures contracts are traded with an average of 2 million contracts per day during the examined period. Thus, the volumes of these contracts are far greater than Treasury futures contracts. With active trading activity, the Eurodollar futures rates represent market assessments of future interest rates. Second, in contrast to survey data, market participants in futures contracts trade assets by risking their financial wealth based on their views of rates. These rates are determined in very timely fashion and altered frequently. Third, although Eurodollar futures run parallel to Treasury bond futures, they are considered to show a mirror image of future Treasury yields. Yet they do not encounter the problems of delivery options and on-the-run or off-the-run bond. Quarterly maturing Eurodollar futures contracts are traded up to 40 quarter series contracts at the same time, reaching maturity of up to 10 years. The compounding rates implicit in the roll-over effect allow market participants to manage short- and long-term exposures, and build expectations of future interest rates. For these reasons, they are better candidates for expected future Treasury yields than Treasury futures contracts.
To obtain expected future Treasury yield from Eurodollar futures rates, a parallel adjustment is necessary to remove the additional risk. The risk relates to the spread of interbank rate over Treasury yield with the same maturity. We use the adjusted Eurodollar futures rate for computing term premium and expectations error, by applying a roll-over strategy to compute compounding rates for other maturities and forecast horizons. The procedure is described in Appendix B.
Table 2 reports the estimates for decomposed coefficients of term premia, βtp, and expectation error, βee, with different forecast horizons and instruments for the period between March 1987 and December 2010. We have two findings given the evidence. First, βtp and βee (m = 3 only) increase as n gets greater. Because the n period rate is a simple average of the current and expected future-period rates up to n–m periods in the future, plus a term premium (Campbell & Shiller, 1991), holding a combination of m period bonds and m–n period bonds leads to a greater excess return if n is longer. When m (forecast horizon) increases, βtp gets smaller, whereas βee becomes greater.
| Component attributable to term premium (βtp) | Component attributable to expectation error (βee) | |||||||
|---|---|---|---|---|---|---|---|---|
| n–m/m | 3 | 6 | 12 | 24 | 3 | 6 | 12 | 24 |
| 3 | −0.835 | −0.433 | −0.923 | 0.222 | 0.063 | −0.273 | 0.419 | 0.729 |
| 6 | −0.923 | −0.821 | −0.777 | 0.188 | 0.205 | −0.240 | 0.870 | 0.748 |
| 12 | −1.406 | −0.684 | −1.003 | −0.041 | 0.584 | −0.118 | 0.718 | 0.763 |
| 24 | −2.685 | −1.295 | −1.560 | −0.325 | 1.646 | 0.146 | 0.889 | 0.781 |
| 60 | −7.118 | −2.664 | −1.984 | −0.605 | 5.006 | 0.702 | 0.608 | 0.164 |
| 120 | −8.068 | −4.293 | −3.326 | −1.413 | 6.083 | 2.355 | 1.447 | 0.092 |
- Note. This table shows the betas of the term premium and expectation error, which are computed from Equations 9 and 10, respectively, using the monthly zero-coupon bond yield from March 1987 to December 2010. The subscript tp of β denotes the term premium, whereas the subscript ee of β denotes the expectation error. The expected future rates are obtained from the Eurodollar futures rates based on the procedure described in Appendix B.
Table 2 also reveals the relative dominance between the time-varying term premium and the expectation error across different forecast horizons. For short-term forecast horizon, such as m = 3 or 6, the coefficients of term premium are greater than the coefficients of expectation errors in terms of absolute magnitude, showing that the former predominates the expectation of the term structure. In the case of m = 12, the dominance becomes weaker or even reverse in the case of m = 24. The disjunctive dominance between shorter-term and longer-term forecast horizon reveals the relative contribution of the term premium and the expectation error. Hence, we conclude that the term premium is a more important determinant for short forecast horizons, whereas the expectation error plays a greater role in the long forecast horizon.
It is worthwhile to note that Froot (1989) decomposed the coefficient of forward premium (forward rate minus short term rate), whereas in Table 2, the coefficient is split based on the spread between the long rate and short rate. In line with Froot (1989), we find that the coefficients of term premia have a tendency towards a negative sign, whereas the coefficients of time-varying expectation errors become more positive across forecast horizons. This pattern is consistent to that in Froot (1989), which shows that coefficients of term premia appear to decrease as n increases. For example, when m = 3 and n–m = 3, βtp in Table 2 is −0.835, but it is −0.835 (−0.835*3/3) when using a forward premium. However, for the same m, when n–m = 60 and 120, βtp are −7.11 and −8.06, but they become −0.36 (−7.11*3/60) and −0.20 (−8.06*3/120) based on a forward premium. The pattern is also repeated in the results of m = 6, 12, and 24. Hence, results of βtp for various m and n are consistent with the finding of Froot.
The second fact that emerges from Table 2 is that the level of expectation error appears to increase across the forecast horizons. For a long forecast horizon, such as m = 24 months, the component attributable to the expectation error is much greater than the component associated with the term premium. Thus, for long-term forecast horizons, the expectation error dominates the EH and deviates more from the null hypothesis of β = 1 than those of short-term forecast horizons. It is plausible that long-term forecasts yield greater uncertainty and thus produce greater forecast error than short-term forecasts, whereas term premia is less sensitive to forecast horizon. Hence, for long-term forecast horizons, expectation errors are more critical for explaining the failure of the EH. However, for short-term forecast horizons, term premia are more important.
To give an example of the relative values of term premia and expectation errors, Table 3 shows the statistics of term premium and expectation errors for the forecast horizon of 3 months. One can see that the absolute mean value increases as the maturity of the instrument increases, except for the maturity of 60 months. Again, the standard deviation column shows that term premia are more stable than expectation errors. Table 3 also shows that there are high levels of autocorrelation, though the degree of autocorrelation decreases as the lag increases. To take a 3-month forecast horizon for a 60-month rate as an example, the first and second lags are 0.91 and 0.83, respectively, but the result is significantly reduce to −0.04 when the lag reaches to 50. The persistence of expectation errors may be caused by either the overlapped data or measurement errors. Thus, the claim for rejecting the rational expectation seems insufficient in this stage.
| Autocorrelations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n–m | Mean | Dev* | Skew | Kurt | r1 | r2 | r3 | r10 | r50 | |
| Term premia | 3 | 0.06 | 0.25 | 1.91 | 8.77 | 0.65 | 0.41 | 0.36 | 0.28 | −0.03 |
| 6 | 0.22 | 0.23 | 1.39 | 6.00 | 0.67 | 0.40 | 0.31 | 0.19 | −0.05 | |
| 12 | 0.39 | 0.28 | 0.21 | 3.15 | 0.75 | 0.57 | 0.47 | 0.27 | 0.04 | |
| 24 | 0.40 | 0.43 | 0.24 | 2.63 | 0.87 | 0.77 | 0.70 | 0.43 | −0.13 | |
| 60 | 0.12 | 0.71 | 0.59 | 3.04 | 0.91 | 0.83 | 0.77 | 0.35 | −0.04 | |
| 120 | −0.62 | 1.05 | 0.30 | 3.20 | 0.89 | 0.80 | 0.74 | 0.30 | 0.10 | |
| Expectation error | 3 | −0.18 | 0.39 | −0.81 | 4.96 | 0.63 | 0.35 | 0.09 | 0.12 | 0.06 |
| 6 | −0.09 | 0.47 | −0.62 | 4.83 | 0.69 | 0.39 | 0.12 | 0.15 | 0.03 | |
| 12 | 0.19 | 0.57 | −0.19 | 3.78 | 0.72 | 0.39 | 0.10 | 0.12 | 0.03 | |
| 24 | 0.23 | 0.72 | 0.04 | 2.81 | 0.75 | 0.45 | 0.17 | 0.15 | −0.02 | |
| 60 | 0.02 | 0.93 | 0.25 | 2.88 | 0.80 | 0.55 | 0.34 | 0.19 | −0.03 | |
| 120 | −0.69 | 1.22 | 0.12 | 2.92 | 0.84 | 0.66 | 0.52 | 0.22 | 0.07 | |
- Note. The term premium is computed from the difference between the spread and expected future rate
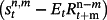 , whereas the expectation error is defined as the ex post realized rate minus the expected future rate (
, whereas the expectation error is defined as the ex post realized rate minus the expected future rate (
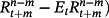 . The expected future rate is obtained from the Eurodollar futures rate from the period between March 1987 and December 2010. Appendix B shows how to match the forecast horizon and maturity of the zero-coupon bond yield using Eurodollar futures rate.
. The expected future rate is obtained from the Eurodollar futures rate from the period between March 1987 and December 2010. Appendix B shows how to match the forecast horizon and maturity of the zero-coupon bond yield using Eurodollar futures rate. - * This indicates standard deviation.
We need to examine further whether the persistent expectation errors in Table 3 contain irrational components that systematically create positive or negative errors, that is, the positive error existed in this month has not yet been modified for the next months. This systematic expectation error is repeated for all four forecast horizons and for the rates with different maturities, though we only provide the rates with 3-month forecast horizon. More interestingly, the evidence for the rates with the maturities longer than 24 months is more striking than those of shorter maturities, implying that rates with longer maturities render greater systematic expectation errors. It would be of interest to understand whether these findings relate to the term structure anomaly observed in the Campbell and Shiller equation. As pointed out above, the rational component is part of the expectation error. Therefore, we have to figure this component out and control it if we hope to understand the existence of irrationality. We further discuss this issue in the following section.
3.3 Decomposition of expectation errors
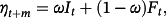 (14)
(14) (15)
(15)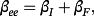 (16)
(16)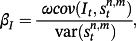 (17)
(17)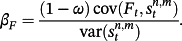 (18)
(18)4 IRRATIONALITY AND EXPECTATION ERROR
One of the objectives of this study is to study whether irrationality during the post Campbell–Shiller period can explain the term structure anomaly. We found that term premia contributes more to the failure of the EH than the expectation error for the short end of the term structure, but for the long end of the term structure, expectation error dominates. To specify which part of the expectation errors is more critical in term structure anomaly and leads to a rejection of EH for the long end of the term structure, we proceed to explore the determinants of time-varying expectation errors.
As mentioned above, the expectation errors are decomposed into rational and irrational components. Three streams of previous literature explain the sources of rational factors. The first stream of rational variables includes the variables governed by peso problems (Bekaert et al., 2001; Evans, 1996; Jardet, 2008) and learning behaviour (Lewis, 1989). Peso problems arise from infrequent discrete shifts in economic determinants causing asset price behaviour to differ from conventional rational expectation. It is reasonable to assume that experience leads market participants to rationally predict future interest rates. When rare events occur, their expectations about future interest rates generate expectation errors. The learning behaviour of market participants also creates expectation errors because they gradually absorb and adjust their expectation when the rare events occur.
Second, expectation errors can arise from prediction of rates using equilibrium interest rate models, such as Vasicek (1977) or Cox, Ingersoll, and Ross (1985) models, which are formulated with assumptions of economic variables, and derive a process for short-term interest rates. Inconsistency between the assumptions behind these models, in regard to what economic variables evolve and the actual movement of the variables, could cause incorrect estimation of future interest rates. When these models are adopted for estimating future interest rates, systematic expectation errors between ex post realized rate and expected future interest rates may be generated.
The third stream of literature relates to incorrect estimation of macroeconomic variables where certain variables govern the interest rate changes. As pointed by Bartolini, Bertola, and Prati (2002); Benkert (2004); and Deuskar, Gupta, and Subrahmanyam (2008), default spread, inflation, money supply, and yield spread affect interest rate movements. Unexpected changes or shocks in inflation, for example, can create erroneous estimations in interest rates. Fama (2006) discusses the phenomenon of downward movement for U.S. 1-year interest rates for the period between 1981 and 2004, as the result of permanent shocks. Certainly, an unexpected change in interest rates may arise from the phenomenon of peso problem, the learning behaviour of market participant, incorrect model estimation, and so on.
Apart from rational variables, irrational components can impact expectation errors, for example, when investors trade fixed-income securities by extrapolating the trend or predict continuity of interest rates. Trend-chasing investors typically produce continuous errors across time, often resulting in persistently high number of correlated lags.
To obtain a suitable proxy for rational variables including peso problems, investor learning behaviour, and incorrect estimation of macroeconomic variables, we use the so-called macroeconomic surprises, defined as a vector of the unexpected relevant macroeconomic variables. There are three reasons that these surprise variables capture all rational variables. First, because macroeconomic variables are directly linked to interest rate movements, uncertain movements in these variables are bound to create an expectation error. In particular, uncertainty about economic variables is likely to disturb the probability distribution of interest rates that investors use to form their expectations when making financial decisions.
Second, information about the new stochastic process for interest rates is limited and/or may be revealed gradually, because agents learn about interest rate processes only from past information, and the ex post distribution may not agree with the ex ante distribution even based on rational expectations. With limited information available to agents, it is assumed that peso problems, learning behaviour, and incorrect estimation of economic variables are closely tied to the unexpected components of macroeconomic variables. In fact, unobserved regime changes or policy innovations can lead to surprises in macroeconomic fundamentals. Therefore, peso problems can be examined by testing their significance in relation to surprises resulting from macroeconomic variables.
Following Bartolini et al. (2002), Benkert (2004), and Deuskar et al. (2008), we use default spread, inflation, money supply, and yield spread as economic variables. Default spread (DEF) is obtained from the difference between 3-month LIBOR and Treasury bill rate, the so-called TED spread. This spread is often used as an indicator of market default in practice. Inflation (INF) affects the rate change in the way that higher inflation triggers higher nominal interest rates. Money supply (M2) is often used by central banks to control circulation of currency and inflation. This is done by changing interest rates. The yield spread (YIS), obtained from the difference between 5-year and 1-year rates, represents the market forecast of future interest rates.
Specifically, the ARIMA model is employed to estimate unpredictable (or unexpected) components from the time series of each economic variable. The estimated residuals for each variable and their corresponding standard deviations from the ARIMA model can be used to form the “surprise” series. The ARIMA model depicts the dynamics of a variable and explains its evolution based on its own lags and the lags of the other related variables. This feature is in accordance with a dynamic learning behaviour in that historical information is generally used to predict future interest rate movements. We therefore use the ARIMA model to remove serial correlated components, which do not impact expectation error, and to calculate residuals as macroeconomic surprises. First, each variable is differenced to account for nonstationarity. Second, based on the correlogram of each variable, the lag of the AR and/or MA component is determined and then the ARIMA model is run to generate a residual series for the surprise variable.
To measure the irrational variables, we follow Brown and Cliff (2004) and Baker and Wurgler (2006). Brown and Cliff (2004) provide a list of direct and indirect sources of sentiment proxies. The former is obtained from surveys, and the latter is derived from market trading activities. The direct sentiment proxies considered in this study are AAII, the Michigan consumer index, and the survey data from MarketVane. Another sentiment proxy is the monthly Baker and Wurgler Sentiment Index (Baker). Appendix B provides a description of these sentiment indices.
The indirect measures of sentiment proxies are mainly obtained from derivatives markets. Trading information in futures and options markets is considered as forward looking of market movement because market participants trade derivatives and risk their wealth based on their assessments of future price movement. First, put/call volume ratio (PCratio) obtained from Eurodollar options is considered as a bearish (bullish) indicator of Eurodollar futures (3-month Libor rate). Second, Commodities Futures Trading Commission (CFTC) reports the long/short volume for futures contracts traded in the United States. The net position in the 13-week Treasury bill on noncommercial traders is used as a proxy for institutional sentiment (INSTIT) and activity by small traders is used as a proxy for individual sentiment (INDIVD).
To remove nonsentiment-related component from each proxy, we follow Baker and Wurgler (2006) by constructing a common component, the first principal component from principal component analysis (PCA), from all variables. 1 By applying the PCA, we construct a composite sentiment index comprising the (a) AAII bearish percentage, (b) Michigan consumer index, (c) the bullish consensus for Eurodollar futures, (d) Baker and Wurgler Sentiment Index, (e) Eurodollar put/call volume ratio, (f) net long/short volume for noncommercial traders, and (g) net long/short volume for small traders.
Table 4 displays the regression results from time series of interest rate data for 3- and 6-month forecast horizons, whereas Table 5 shows those with 12- and 24-month forecast horizons. Note that each regression includes the AR(1) component to control for serial correlation in the expectation errors, which may boost the coefficient and affect subsequent inference of our results. As can be seen, all equations show various scales of significance for macroeconomic surprises and sentiment variables. The R2 values are between 0.20 and 0.60, where the higher the forecast horizon the higher the value of R2.
| m | n–m | ΔDEF | ΔINF | ΔM2 | ΔYIS | ΔSENT | AR(1) | R2 |
|---|---|---|---|---|---|---|---|---|
| 3 | 3 | 0.247** (0.10) | −0.208** (0.09) | 21.5*** (6.07) | −0.232*** (0.08) | −0.034*** (0.01) | −0.026* (0.02) | 0.23 |
| 6 | 0.286*** (0.09) | −0.192* (0.10) | 21.76*** (7.39) | −0.217** (0.09) | −0.075** (0.03) | −0.027 (0.02) | 0.19 | |
| 12 | 0.275** (0.11) | −0.213* (0.12) | 19.198** (7.98) | −0.312*** (0.10) | −0.045** (0.02) | −0.03 (0.02) | 0.22 | |
| 24 | 0.323** (0.13) | −0.226* (0.12) | 21.23** (8.92) | −0.529*** (0.11) | −0.077** (0.04) | −0.033 (0.03) | 0.21 | |
| 60 | 1.354*** (0.17) | −0.324** (0.16) | 24.286* (12.71) | −0.855*** (0.10) | −0.176*** (0.04) | −0.062* (0.04) | 0.43 | |
| 120 | 1.935*** (0.19) | −0.305* (0.16) | 10.733 (14.80) | −1.128*** (0.14) | −0.106*** (0.03) | −0.081* (0.04) | 0.55 | |
| 6 | 3 | 0.405** (0.16) | −0.088 (0.10) | 20.585*** (7.47) | −0.593*** (0.09) | −0.046 (0.15) | −0.031 (0.03) | 0.28 |
| 6 | 0.421*** (0.16) | −0.112 (0.11) | 21.269** (8.34) | −0.538*** (0.09) | −0.255** (0.11) | −0.034 (0.03) | 0.26 | |
| 12 | 0.406** (0.17) | −0.108 (0.12) | 20.104** (9.30) | −0.655*** (0.09) | 0.119*** (0.04) | −0.036 (0.03) | 0.27 | |
| 24 | 0.61*** (0.23) | −0.113 (0.12) | 18.217* (9.96) | −0.823*** (0.10) | 0.048** (0.02) | −0.023 (0.03) | 0.34 | |
| 60 | 1.567*** (0.14) | −0.136 (0.16) | 25.041** (12.38) | −1.109*** (0.09) | −0.589*** (0.15) | −0.089** (0.04) | 0.57 | |
| 120 | 1.871*** (0.17) | −0.414** (0.20) | 15.009 (16.04) | −1.274*** (0.16) | −0.497** (0.24) | −0.123** (0.05) | 0.41 |
- Note. The following equation is run:
- where Δ is the change operator applying to a variable under investigation;
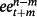 is the expectation error, obtained from the zero coupon yield for the period of n–m traded at time t + m less the expected future rate. The expected future rate is obtained from the Eurodollar futures rate using interpolation basis. DEFt is the default spread on date t, proxied by the difference between 3-month LIBOR and 3-month Treasury bill rate on date t; INFt is the inflation rate; M2t is the money supply figure on date t; YISt is the yield spread on date t, representing the difference between 5- and 1-year zero coupon rate; SENTt is the sentiment proxy on date t obtained from the procedure described in the text. All variables are obtained from the difference of the value to account for nonstationary series. Then each variable is obtained from the residual after removing the AR or MA component. The values in parentheses are the Newey and West (1987) standard error.
is the expectation error, obtained from the zero coupon yield for the period of n–m traded at time t + m less the expected future rate. The expected future rate is obtained from the Eurodollar futures rate using interpolation basis. DEFt is the default spread on date t, proxied by the difference between 3-month LIBOR and 3-month Treasury bill rate on date t; INFt is the inflation rate; M2t is the money supply figure on date t; YISt is the yield spread on date t, representing the difference between 5- and 1-year zero coupon rate; SENTt is the sentiment proxy on date t obtained from the procedure described in the text. All variables are obtained from the difference of the value to account for nonstationary series. Then each variable is obtained from the residual after removing the AR or MA component. The values in parentheses are the Newey and West (1987) standard error. - *** Significance at 1% level.
- ** Significance at 5% level.
- * Significance at 10% level.
| m | n–m | ΔDEF | ΔINF | ΔM2 | ΔYIS | ΔSENT | AR(1) | R2 |
|---|---|---|---|---|---|---|---|---|
| 12 | 3 | 0.388*** (0.15) | −0.098 (0.09) | 25.306*** (8.26) | −0.611*** (0.09) | −0.261** (0.13) | −0.032 (0.03) | 0.30 |
| 6 | 0.364*** (0.14) | −0.105 (0.10) | 23.435*** (7.98) | −0.578*** (0.10) | −0.218* (0.13) | −0.029 (0.03) | 0.25 | |
| 12 | 0.437*** (0.16) | −0.108 (0.09) | 24.536*** (8.44) | −0.699*** (0.10) | −0.247 (0.18) | −0.035 (0.03) | 0.28 | |
| 24 | 0.602*** (0.20) | −0.127 (0.09) | 20.587** (9.38) | −0.791*** (0.12) | −0.542** (0.23) | −0.029 (0.03) | 0.30 | |
| 60 | 1.403*** (0.19) | −0.103 (0.12) | 26.218** (12.81) | −1.083*** (0.14) | −0.497* (0.28) | −0.083* (0.04) | 0.49 | |
| 120 | 1.592*** (0.28) | −0.105 (0.13) | 24.586 (15.38) | −1.326*** (0.17) | −0.538* (0.29) | −0.082* (0.05) | 0.51 | |
| 24 | 3 | 0.787*** (0.12) | −0.226*** (0.07) | 6.651 (6.09) | −0.776*** (0.07) | −0.269* (0.16) | −0.052 (0.04) | 0.18 |
| 6 | 0.908*** (0.11) | −0.196** (0.08) | 0.406 (6.53) | −0.81*** (0.08) | −0.281* (0.15) | −0.028 (0.03) | 0.51 | |
| 12 | 0.964*** (0.11) | −0.191** (0.09) | −9.696 (7.28) | −0.891*** (0.09) | −0.402** (0.17) | −0.02 (0.03) | 0.51 | |
| 24 | 1.044*** (0.09) | −0.14 (0.10) | −19.105** (7.74) | −0.97*** (0.10) | −0.372** (0.17) | −0.014 (0.04) | 0.54 | |
| 60 | 1.505*** (0.15) | −0.224* (0.13) | −9.423 (10.23) | −1.06*** (0.13) | −0.457** (0.23) | −0.062 (0.04) | 0.52 | |
| 120 | 1.753*** (0.17) | −0.256* (0.14) | −5.943 (12.66) | −1.213*** (0.15) | −0.024** (0.01) | −0.066* (0.04) | 0.55 |
- Note. See the note in Table 4.
- *** Significance at 1% level.
- ** Significance at 5% level.
- * Significance at 10% level.
Default spread and yield spread surprises are significant for nearly all cases at the 1% level. Default spread is negatively related to time-varying expectation errors whereas yield spread is positively related. As we know, default spread is an acceptable measure of the aggregate liquidity variable as well as the default risk of constituent banks in U.S. dollar fixing. Incorrect estimation of this variable can affect the estimation of general interest rate level. However, yield spread is an indicator of economic conditions as well as the direction of expected future interest rates. Hence, an erroneous prediction of yield spread leads to invalid expectations about future interest rates, contributing to expectation errors.
The inflation and M2 surprises series generally follow a certain trend. Because money supply variable is strongly tied to inflation, our results show that they are not joint significantly related to expectation errors. Once the money supply surprise variable is significant, this variable absorbs the forecast power of inflation surprise, resulting in insignificance. Conversely, when the inflation surprise variable dominates, the money supply variable loses its influence. The argument is supported by the correlation ranging from −0.74 to −0.85.
Irrational variables proxied by selected sentiment variables show convincing results. First, the R2 value on average increases by 2% when the equation includes sentiment variables (not reported). Particularly, long-term rates coupled with long-term forecast horizons tend to produce higher R2 values than other cases. Second, the sentiment index appears to be significant for most cases including short-term forecast horizons in Table 4 and long-term forecast horizons (particularly 24 month) in Table 5. A negative coefficient indicates that a bullishness consensus in expected future rate spurs the expected future rate, producing negative expectation errors. The ex post realized rate is consequently less than the expected future rates. Conversely, a bearishness consensus may trigger a decline in the expected future rate, which causes the ex post realized rate to surpass the expected future rates and results in a positive expectation error.
Irrespective of forecast horizons, expectation errors for long-term securities appear to be governed more by investor sentiment than short-term securities, as evidenced the consistent significance of securities with 60- and 120-month maturities. One possible interpretation is that long-term securities prices are more sensitive to change in interest rates than short-term prices and hence are more likely to be affected by irrational investor sentiment. Another interpretation relates to Fama (2006) who indicates that swings of spot rates for short-term forecast horizons are driven by slow mean reversion, but spot rates for long-term forecast horizons are driven by permanent shocks to the long-term expected spot rate. As seen in Tables 4 and 5, even short- or long-term changes of spot rates are affected by several series of macroeconomic surprises. When surprises occur, irrational investor behaviour also affects expectation errors, leading to a predictive divergence from the slope of the term structure. Long-term securities, however, are more vulnerable to these shocks and are more closely related to investor behaviour.
5 CONCLUSIONS
Unbiased predictors of long and short rate spread have been rejected overwhelmingly by previous studies. Based on various maturities of U.S. Treasury yields and forecast horizons, Campbell and Shiller (1991) show that long–short rate spreads provide an opposing forecasts of spot rates. This phenomenon is referred to as a term structure anomaly or puzzle in this study. Prior works suggest that this anomaly is attributable to term premia, peso problems, or investor learning behaviour. Looking at the post Campbell–Shiller period of U.S. Treasury yields from 3 months to 10 years, and forecast horizons from 3 months to 2 years, the anomaly does not appear to be as serious as before, when focusing on short-term forecast horizons and the long end of the term structure.
This study provides new insight from Bulkley et al. (2015) explaining the term structure anomaly and the failure of the EH. We found that the failure of the EH for the short end of the term structure is driven mainly by term premia. However, for the long end of the term structure, time-varying expectation errors primarily cause the failure. Across forecast horizons, expectation error tends to dominate the failure of the EH. Consistent with Fama (2006), diverging forecasts to the future spot rate and the long–short rates are attributable not only to the presence of term premia but also to the macroeconomic surprises (shocks) across forecast horizons. This study especially points out the deterministic role of investor's irrational behaviour on the term structure anomaly during the post Campbell–Shiller period.
APPENDIX A.
DATA
This study uses monthly U.S. zero-coupon bond yields from March 1987 to December 2010, obtained from Datastream. These yields are computed continuously and compounded on an annual basis. To conduct this study, monthly frequency of 3, 6, 12, 24, 60, and 120 months of yields with forecast horizons of 3, 6, 12, and 24 months are selected. Although U.S. zero-coupon bond yields are available from 1961, we use the selected period to match the availability of expected future rate, which is Eurodollar futures rate. This historical zero-coupon bond yield can also be found on the website of the U.S. central bank, Federal Reserve. -8 U.S. zero-coupon bonds of yields actively traded noninflation-indexed issues are adjusted for constant maturity.
APPENDIX B.
PROCEDURES FOR COMPUTING EXPECTED FUTURE RATE
Eurodollar futures contracts are traded in the Chicago Mercantile Exchange with maturity up to 10 years and based on the underlying asset of the 3-month LIBOR rate. Consistent with the notation used above, in this case, m (the time to maturity) is from the closest 3 months up until 10 years with 3 months in between, and n–m is 3 months, which is the period of the LIBOR rate. In order to test the expectation hypothesis, m (forecast horizon) should be adjusted to be 3, 6, 12, or 24 months, and n–m should be 3, 6, 12, 24, 50, or 120 months for the period of the zero-coupon bond yield.
The following procedures are implemented. First, Eurodollar futures rates are computed from the Eurodollar futures prices with the equation of 100-Eurodollar futures price. Second, we deduct the risk spread from the Eurodollar futures rate where the spread is computed from the 3-month LIBOR rate minus 3-month Treasury bill rate. When Eurodollar futures are traded on date t, the Eurodollar futures are mature on date t + m. The spread should be computed on date t + m, that is, both rates starts on date t + m and terminates in 3 months. Third, each day, interpolation technique is applied for each contract to adjust m (day to maturity) to be a sequence of 3 months until 120 months. Then, each day, consecutive contracts are computed linearly to let n–m be 3, 6, 12, 24, 60, or 120 months. For example, on date t, if we want m to be 6 months and n–m to be 12 months, the Eurodollar futures rates with 6-month maturity (m = 6), together with three consecutive contracts (m = 9, 12, and 15), are used to compute the rate with n–m equal 12 months. This procedure is implemented each day to compute the Eurodollar futures rate with desired m and n–m until the end of the sample period. Then monthly observations of rates taken from the beginning of the month are used to test the EH.
APPENDIX C.
DESCRIPTION OF SENTIMENT PROXIES
This appendix describes several direct sentiment proxies. The AAII surveys individual investors weekly in respect to their outlooks, asking them to state whether they believe that over the next 6 months, the stock market will be bullish, bearish, or neutral. The AAII sentiment index is defined as the ratio of bullish responses to bearish responses. Another sentiment proxy is the monthly Baker and Wurgler Sentiment Index (Baker). Baker and Wurgler (2006) constructed first principal component from six sentiment proxies and their lags. This index is commonly used because it removes idiosyncratic and nonsentiment-related components, and it can determine the lead–lag relationships of those variables. A further appealing property is that it levels out the extreme observations that may be biased and thus affect the inference. The third sentiment is the monthly index of Consumer Sentiment (CS) collected by the University of Michigan based on a survey of households' perceptions about current and future financial conditions. The main objective of creating this index is to judge the consumer's level of optimism/pessimism by assessing near-time consumer attitudes about the business climate or gauging economic expectations of consumer saving and spending behaviour. Monthly forecasts of commodity market returns collected by Market Vane are an alleged bullish predictor of futures market behaviour that is derived by tracking buy and sell recommendations.
REFERENCES
- 1 The data used in this study are described in Appendix A.
- 1 The EH implies that the spread is a term premium, plus an optimal forecast of changes in future interest rate (Campbell & Shiller, 1991, p. 497).
- 2 Bulkley et al. (2015) use the rates obtained from term structure of interest rates as expected future rates to calculate expectation errors. Then they found the pattern of expectation errors conforming to specific behaviour biases.
- 0 Peso problems arise whenever the ex post frequencies of states within the sample differ substantially from their ex ante probabilities and where these deviations distort econometric inference (Evans, 1996). When a peso problem is present, the sample moments calculated from the available data do not coincide with the population moments that rational agents would have used when making their decisions.
- 1 To be consistent with other macroeconomic variables, each sentiment proxy is differenced and then PCA is implemented to extract the common component.
- -8 Please see the website of U.S. Federal Reserve website for the zero-coupon: http://www.federalreserve.gov/releases/h15/data.htm