In 2007, the USEPA issued its “Framework for Metals Risk Assessment.” The framework provides technical guidance to risk assessors and regulators when performing human health and environmental risk assessments of metals. This article focuses on advances in the science including assessing bioavailability in aquatic ecosystems, short- and long-term fate of metals in aquatic ecosystems, and advances in risk assessment of metals in sediments. Notable advances have occurred in the development of bioavailability models for assessing toxicity as a function of water chemistry in freshwater ecosystems. The biotic ligand model (BLM), the multiple linear regression model, and multimetal BLM now exist for most of the common mono- and divalent metals. Species sensitivity distributions for many metals exist, making it possible for many jurisdictions to develop or update their water quality criteria or guidelines. The understanding of the fate of metals in the environment has undergone significant scrutiny over the past 20 years. Transport and toxicity models have evolved including the Unit World Model allowing for estimation of concentrations of metals in various compartments as a function of loading and time. There has been significant focus on the transformation of metals in sediments into forms that are less bioavailable and on understanding conditions that result in resolubilization or redistribution of metals in and from sediments. Methods for spiking sediments have advanced such that the resulting chemistry in the laboratory mimics that in natural systems. Sediment bioavailability models are emerging including models that allow for prediction of toxicity in sediments for copper and nickel. Biodynamic models have been developed for several organisms and many metals. The models allow for estimates of transport of metals from sediments to organisms via their diet as well as their water exposure. All these advances expand the tool set available to risk assessors. Integr Environ Assess Manag 2024;20:924–951. © 2023 The Authors. Integrated Environmental Assessment and Management published by Wiley Periodicals LLC on behalf of Society of Environmental Toxicology & Chemistry (SETAC).

INTRODUCTION

In 2007, the USEPA issued its “Framework for Metals Risk Assessment” (Fairbrother et al., 2007; USEPA, 2007a). The document is intended to provide technical guidance to risk assessors and regulators when performing human health and environmental risk assessments of metals. The guidance pertains to a broad suite of assessments performed by the Environmental Protection Agency (USEPA) including site assessments under Superfund and chemical reviews under the Toxic Substances Control Act (TSCA) for new and existing substances. The USEPA Metals Framework document has not been updated since 2007, and there have been several advances in the science related to aquatic assessments that are now available for risk assessors in all fields of assessment. Metals possess properties that are uniquely different from organic compounds. Many metals are essential for the survival and growth of animals and/or plants, and are mainly regulated by active transport systems; moreover, their accumulation by biota as measured by bioaccumulation or bioconcentration factors is inversely related to exposure concentration (McGeer et al., 2003; Menzie et al., 2009). Since 2007, important advances in the science of risk assessment for metals have occurred, and the USEPA document no longer presents the latest scientific findings and modeling approaches in some key areas relevant to metals.

The goal of this article is to review the recent scientific findings related to metals risk assessment and suggest areas where the USEPA Metals Framework could be updated to reflect the latest science. We focus on four areas that are primarily associated with freshwater ecosystems:

(1)
bioavailability of metals in aquatic systems;
(2)
biodynamic models for assessing bioaccumulation;
(3)
fate of metals in aquatic ecosystems; and
(4)
evaluation of metal toxicity in sediments.

METHODS

The approach used to develop the findings of this article was to review the existing information in the USEPA Metals Framework Document and to supplement this by conducting literature searches from 2000 to present, evaluating review articles and interviews with key authors about their publications, and by evaluating aquatic toxicity models through hands-on use.

(1)
Bioavailability of metals in aquatic systems—Our literature review focused on available bioavailability models for predicting toxicity of metals to aquatic organisms in freshwater ecosystems. The review includes extensive assessment of modifying factors of toxicity as a function of water chemistry and types of models currently available.
(2)
Biodynamic models for assessing bioaccumulation—These models have been used to study the relative contribution of metals in water and food to different types of organisms and describe the kinetics of metal bioaccumulation processes over time.
(3)
Fate of metals in aquatic ecosystems—Here, we focused on these advances in understanding and modeling fate processes for metals. Advances in transformation and/or dissolution, loss from the water column, application of the Unit World Model (UWM) to estimate metal fate, and fate following resuspension are discussed.
(4)
Evaluation of metal toxicity in sediments—Significant advances in the science of assessing metal toxicity in sediments have occurred with new models, sediment toxicity testing methods with spiked sediments, and interpretation of results.

BIOAVAILABILITY OF METALS IN AQUATIC SYSTEMS

Metal toxicity to aquatic life is well documented and it is known that toxicity varies as a function of water chemistry, as much as 50–100-fold due to differences in testing laboratory conditions related to pH, hardness, dissolved organic carbon (DOC), and other ions in solution. Metal bioavailability is defined as an index of the rate and extent to which the metal reaches the site of toxic action (Adams et al., 2020). The science of metal bioavailability has advanced to the point where several types of bioavailability models are available with varying levels of complexity and sophistication. This has led to renewed emphasis on nuances between protectiveness versus predictiveness and ease of use (Adams et al., 2020).

In the last two decades, regulatory use of bioavailability models in the determination of water quality standards and guidelines has increasingly grown in acceptance and application (Australian and New Zealand Governments and Australian State and Territory Governments, 2018; European Union, 2013; USEPA, 2007b).

To date, the USEPA (2007b) has developed its water quality criteria for copper using the biotic ligand model (BLM) (Paquin et al., 2002); Canada has, likewise, used the BLM for its water quality guideline for copper (Environment and Climate Change Canada [ECCC], 2021). The USEPA used acute data with an acute to chronic ratio, whereas Canada used only chronic data and a BLM version based on chronic data.
Recently, the USEPA has used a multiple linear regression (MLR) model for calculating water quality criteria for aluminum (USEPA, 2018).
Canada has adopted water quality guidelines for lead and zinc (ECCC, 2020) using an MLR approach.

Empirically based MLR models have mechanistic foundations similar to BLMs but utilize simple equations to predict metal toxicity on a species-specific basis (Brix et al., 2017; Brix, DeForest, et al., 2020). This is the result of renewed interest in the development of easy-to-use empirical models to supplement the BLMs to predict metal bioavailability and derive protective values for aquatic life. The predictive capacity of empirical bioavailability models is based on toxicity-modifying factors (TMFs) such as pH, DOC, and hardness.

Key considerations in the design and selection of a model include ease of use, model fit to the range of TMFs for the ecosystem of interest, goodness-of-fit to existing toxicity data sets, and robust agreement of the model to measured toxicity values. When developing a new toxicity model, it should be able to detect nonlinear responses to TMFs, should demonstrate inclusion of the key TMFs, and be applicable to a broad array of species (Garman et al., 2020).

Models specifically used for regulatory purposes should be selected based on their ability to meet performance criteria as specified through a model-validation process (Brix, 2019, Brix, DeForest, et al., 2020; Garman et al., 2020; Van Genderen et al., 2020; Schlekat et al., 2020). Model validation generally involves an assessment of a model's appropriateness, relevance, and accuracy (Garman et al., 2020). Models should be validated to a level to fit a specific purpose. Understanding the advantages and limitations by considering the tradeoffs between ease of use versus complexity allows for selection of the most appropriate model.

Toxicity-modifying factors

Toxicity of metals depends on many factors including the intrinsic properties of the individual metal and its chemical speciation, and the duration, magnitude, and route of exposure. The toxic responses to metals by aquatic organisms are poorly predicted using total metal concentrations. Noted exceptions to this are aluminum and iron, where laboratory toxicity studies for these two metals indicate that toxicity correlates with total metal and not dissolved metal because the formation of the metal hydroxides and their precipitates limits the amount of metal in the dissolved form. However, the metal hydroxide complexes that form in solution and eventually precipitate are bioavailable, and their toxicity is affected by TMFs, thus allowing their toxicity to be modeled. For most other metals, while dissolved metal concentration is a better predictor of toxicity than total metal concentration, bioavailable metal concentration is the most accurate predictor of toxicity. Metal bioavailability is a function of many TMFs that affect the speciation, bioavailability, and toxicity of metals. These factors include pH, water hardness (primarily Ca and Mg ions), alkalinity, temperature, sodium, chloride, fluoride, suspended solids, and DOC. However, the TMFs that have been shown to have the strongest influence on toxicity in terms of empirical bioavailability models are pH, hardness, and DOC (Adams et al., 2020).

Toxicity-modifying factors can affect the bioavailability of metals in different ways, subsequently affecting the physiological responses of aquatic organisms (Meyer et al., 2007). One way is by metal ions competing for binding sites on organism respiratory membranes with other key ligands (e.g., competition from H⁺ and hardness cations, particularly Ca²⁺ and Mg²⁺) and binding to DOC. Different metals respond differently to the effects of various TMFs. This is due to metal-specific intrinsic properties such as speciation and is dependent on the type and strength of bonds (ionic or covalent) formed with the binding sites.

One of the factors for which the influence on toxicity can vary greatly from metal to metal is pH. The mechanisms by which pH can affect metal bioavailability include changes in speciation and solubility and by H⁺ ion competitive interactions between the metal and biotic ligands. When pH declines below 7, many metals become more soluble and dissociate, releasing free metal ions to a greater extent. For example, aluminum (Al) at pH 5 occurs almost exclusively as Al⁺⁺⁺. As pH increases above pH 7, many metals form complexes with hydroxides and carbonates. These forms are frequently less soluble and therefore less toxic. However, increasing the pH can increase the toxicity of metals to algae due to reduced proton competition. In marine waters, which typically have a pH of ~8, metals such as Al, iron (Fe), and lead (Pb) form hydroxide and carbonate, respectively, and rapidly precipitate, resulting in very low concentrations of the metals in marine waters. Key TMFs by metal are summarized in Table 1 adapted and expanded from the US Environmental Protection Agency (2022).

Table 1. Metal toxicity-modifying factors and their importance

Metal	Importance of modifying factor	References	Important modifying factors
Metal	Importance of modifying factor	References	Hardness	pH	DOC
Aluminum	Hardness moderately modifies Al toxicity; pH is critical; toxicity is greatest at low pH (5) and elevated pH (>8.5) pH; DOC consistently reduces Al toxicity. Solubility minimum around pH 6.0.	DeForest et al. (2018), DeForest, Brix, et al. (2020)	X	X X X	X
Cadmium	Hardness regressions predict acute and chronic toxicity in natural waters; pH effects are weak; and the threshold for a DOC effect appears to be >5 mg/L.	Clifford and McGeer (2010), Mebane et al. (2008), Niyogi et al. (2008), USEPA (2016)	X X X	X	X
Cobalt	Hardness is important and pH moderately affects gill uptake, with uptake increasing with increasing pH up to 8.7. DOC has a small effect.	Borgmann et al. (2005), Diamond et al. (1990), Stubblefield et al. (2020)	X X	X	X
Copper freshwater	DOC has a strong binding affinity to Cu and significantly reduces Cu toxicity. pH shift from acid to alkaline reduces the toxicity of Cu (larger LC50)—the opposite is also true. Hardness is a small factor in natural waters on a chronic basis but important on an acute basis.	Cusimano et al. (1986), Erickson et al. (1996), Markich et al. (2005), Welsh et al. (2000)	X	X X	X X X
Copper marine	Increasing DOC and salinity tend to reduce Cu toxicity in marine and estuarine waters. In marine waters, pH is stable (~8.0) and Ca and other ions are constant; hence, DOC is the driving factor.	Arnold (2009), Grosell et al. (2007)			X X X
Iron	DOC is the most important variable for fish, Daphnia, and algae. A DOC increase in low-pH waters (5.9–6.4) results in a 10-fold reduction in algal toxicity. Ceriodaphnia dubia was influenced by DOC, but not by pH. Algae were not affected by hardness. Algae are affected by phosphorus (P) and iron precipitation of P.	Arbildua et al. (2016), Brix et al. (2023), Cardwell et al. (2023)	X	X	X X X
Lead	DOC has a strong effect on the bioavailability and toxicity of Pb; pH has a moderate effect. Hardness becomes more important when DOC is low (Mebane et al., 2012).	DeForest et al. (2017)	X	X	X X X
Nickel	Ni toxicity tends to moderately decrease as hardness and DOC increase; pH has an inconsistent influence on toxicity (Croteau et al., 2021; Santore et al., 2021).	Croteau et al. (2021), Santore et al. (2021)	X		X
Silver	Ni binds strongly to particles, sediments, and reduced sulfides in solution. DOC significantly reduces toxicity, but pH and hardness influences may be inconsistent. Ni BLM is an acute BLM.	Naddy et al. (2018)			X
Zinc	Hardness has a strong influence on Zn toxicity, decreasing toxicity with increasing hardness; fish toxicity increases with increasing pH, but the relationship may be inconsistent in other taxa. DOC reduces Zn toxicity, but some studies suggest a nonlinear relationship, with a threshold of 10 mg/L DOC required to substantially reduce toxicity.	Bringolf et al. (2006), Canadian Council of Ministers of the Environment (CCME) (2018), Clifford and McGeer (2009), De Schamphelaere and Janssen (2004), Hyne et al. (2005), Ivey et al. (2019), Mebane et al. (2012)	X X X	X X	X

Abbreviations: BLM, biotic ligand model; DOC, dissolved organic carbon.
Source: Adapted from the USEPA (2022).

Toxicity-modifying factors other than DOC, pH, and hardness have been evaluated and incorporated, to some extent, in BLM models. Temperature is a factor that has been evaluated for aluminum, and the kinetics underlying aluminum bioavailability has a strong dependency on temperature (Santore et al., 2018). Existing data for other metals such as nickel, copper, and zinc do not show the same magnitude of correlations between temperature and chronic toxicity (Pereira et al., 2017). However, temperature effects on toxicity have not been thoroughly evaluated. To some extent, this is the result of standardized tests that prescribe a given temperature for a test species. Aluminum also appears to be influenced to some degree by fluoride (Santore et al., 2018). Particulate organic carbon (POC) in suspended solids is also an important TMF due to the sorption of metals to POC. When considered, POC is frequently treated like DOC, or the binding strength to solids is estimated by the soil to particle distribution coefficient (K_d). Sodium is another important TMF due to competition at metal binding sites on the respiratory membrane (i.e., gill) of the organism and because of the need for freshwater aquatic organisms to conserve sodium. While not the focus of this article, anions such as phosphate, nitrate, and sulfate are important TMFs for the oxyanions (arsenate, selenate, molybdate, vanadate, uranate).

Bioavailability models

A variety of methods to account for the relative bioavailability of metals in aquatic systems have been developed including hardness adjustment, water–effect ratio, Free Ion Activity Model, BLM (Paquin et al., 2002), and MLRs (Adams et al., 2020). At the time of the issuance of the USEPA Metals Framework in 2007, the acute copper and silver BLM models were available. The USEPA adopted the BLM for its water quality criteria document for copper (USEPA, 2007b). The approach was based on using an acute copper BLM with an extensive amount of acute data and a calculation of chronic effects using an acute to chronic ratio for copper. This is the only US water quality criteria document in which the BLM approach is applied. Subsequently, Canada adopted a chronic BLM for its national copper guideline (Canadian Council of Ministers of the Environment [CCME], 2021), and the European Union (EU) has adopted a bioavailability-based nickel Annual Average Environmental Quality Standard (EQS) under the Water Framework Directive (European Commission [EC], 2011). Finally, the updated USEPA aluminum water quality criteria document has adopted a chronic MLR approach in the derivation of the criteria (USEPA, 2018) based on DeForest et al. (2018) and Deforest, Brix, et al. (2021).

Biotic ligand models are based on the principle that toxicity occurs by accumulation of the metal-bound exchange surface of the organism. MacRae (1994) first demonstrated this approach by measuring copper metal accumulation on fish gills in acute studies as a function of water chemistry. The BLM approach successfully combines the influences of speciation (e.g., free metal ion, DOC complexation) and cationic competition (e.g., K⁺, Na⁺, Ca²⁺, Mg²⁺) to predict metal accumulation and toxicity to aquatic organisms (Adams et al., 2020).

Most BLMs are models with a single set of binding constants and other parameters that are applied in a consistent manner to the acute and/or chronic toxicity data (Brix, DeForest, et al., 2020). The model, in theory, is only adjusted for differences in metal sensitivity among species for a given endpoint and exposure duration. Consequently, adjustments are made to the sensitivity parameter (i.e., LA50-lethal accumulation for 50%), rather than two independent models, to deal with both the acute and chronic toxicity.

A common misconception is that there is one BLM for each metal that can be used for all species to account for either bioavailability differences in water chemistry in which the organisms were tested or to develop a threshold for effects in each water body. However, experience has demonstrated that not all organisms respond the same way to water chemistry changes, especially pH. For example, algae often respond differently than fish and invertebrates—with toxicity decreasing (lower EC values) at higher pH values rather than at lower pH levels. This has necessitated the need to develop BLMs specific to a given group(s) of organisms (Mebane et al., 2020). To normalize a given data set to a standard set of water chemistry conditions, separate BLM calculations may be needed for different groups of organisms. A list of BLMs by metal and the organism groups to which they apply is provided in Table 2 (expanded from the USEPA, 2022). To simplify things, the various software packages typically have multiple models in one computer package, allowing for calculations for algae, invertebrates, fish, and occasionally plants and amphibians.

Table 2. MLRs for predicting metal toxicity to aquatic organisms

Metal	MLR model	Equation
Aluminum	The Akaike information criterion (AIC) and the Bayesian information criterion (BIC) were used to determine which combination of terms resulted in the most parsimonious models for predicting EC20s for each species. Pseudokirchneriella subcapitata and Pimephales promelas EC20s were based on the AIC and BIC; Ceriodaphnia dubia was based on AIC. All three models included interaction terms. The USEPA (2018) approach did not use the interaction terms. No acute model was developed.	P. subcapitata: Al ln(EC20) = −61:952 + 1:678 ln[DOC] + 17:019 × pH + 4:007 × ln[H] − 1:020 × pH2 − 0:204 × (ln[DOC] × pH) − 0:556 × (ln[H] × pH). C. dubia: Al ln(EC20) = -41:026 + 0.525 × ln[DOC] + 11:282 × pH + 2:201 × ln[H] − 0:663 × pH2 − 0:264 × (ln [H] × pH). P. promelas: Al ln(EC20) = −14:029 + 0:503 × ln[DOC] + 3:131 × pH + 3.443 × ln[H] − 0.494 × (ln[H] × pH) DeForest et al. (2018).
Copper	Pooled model. Following USEPA guidelines for WQC development, species data were then combined to develop a linear model with pooled slopes for each independent parameter (i.e., DOC, pH, and hardness) and species-specific intercepts using analysis of covariance.	Acute: Exp(0.700 × ln(DOC) + 0.579 × ln(Hard) + 0.778 × pH − 6.738). Chronic: Exp(0.855 × ln(DOC) + 0.221 × ln(Hard) + 0.216 × pH − 1.402). Brix et al. (2021).
Lead	A pooled chronic model was developed using C. dubia and L. stagnalis to represent invertebrates and a species-specific P. promelas model to represent fish. A separate chronic MLR model was also developed for an alga (Raphidocelis subcapitata).	Acute: CMC (μg Pb/L) = exp(0.776 × ln(DOC) + 0.437 × ln(Hard) + 0.445 × pH − 1.150); DeForest, Tear, et al. (2020). Chronic: C. dubia = exp(0.865 × ln(DOC) + 0.131 × ln(Hard) + 0.206 × pH + 0.921). Chronic: L. stagnalis = exp(0.865 × ln(DOC) + 0.131 × ln(Hard) + 0.206 × pH – 1.109). Chronic: P. promelas = exp(0.433 × ln(DOC) + 1.428 × ln(Hard) + 0.146); DeForest, Tear, et al. (2020).
	A pooled MLR lead model with data for five different species, with DOC and a hardness variable R² value of 0.72, is currently used in Canada (ECCC, 2020)	FWQG = exp(0.514[ln(DOC)] + 0.214[ln(Hardness)] + 0.4152).
Nickel	Acute model = pooled stepwise regression model with only DOC and hardness. Chronic model: Pooled all group stepwise regression that produced the same model results whether interactions were considered and whether AIC and BIC were used. The model selected included only hardness and DOC.	Acute: ECx (μ_g/L) = e0.454 × ln (hardness) + 0.084 × ln(DOC) + intercept. Chronic: ECx (μ_g/L) = e0.471 × ln (hardness) + 0.147 × ln(DOC) + intercept Croteau et al. (2021).
	Pooled Daphnia model used to standardize toxicity values for all species with acute data to common water chemistry. The Oncorhynchus mykiss model (hardness and pH) was used to standardize chronic toxicity values for all species to common water chemistry.	Acute: EC50 = exp[ln(EC50meas) – 0.240(ln[DOCmeas] − ln[DOCtarget]) − 0.833(ln[hardmeas] − ln[hardtarget])]. Chronic: EC10 = exp[ln(EC10meas) − 0.995(ln[hardnessmeas] − ln[hardnesstarget]) + 0.847(pHmeas − pHtarget)] CCME (2018).
Zinc	Pooled model. Following USEPA guidelines for WQC development, the species data were combined to develop a linear model with pooled slopes for each independent parameter (i.e., DOC, pH, and hardness) and species-specific intercepts using analysis of covariance.	CWQG = exp(0.995[ln(hardness)] − 0.847[pH] + 4.932). De Schamphelaere and Janssen (2004).

Abbreviations: BLM, biotic ligand model; DOC, dissolved organic carbon; MLR, multiple linear regression; WQC, water quality criteria.
Source: Expanded from the USEPA (2022).

Recently, “user-friendly” bioavailability tools and/or models have been developed. These models generally only require DOC, pH, and hardness as input parameters compared with BLMs, require less training, and allow for rapid assessment of large data sets (Peters et al., 2011). These models have been used for rapid assessments and to determine compliance with EU EQS.

Examples of user-friendly models include Bio-met, PNEC-pro, and MBAT:

(1)
Bio-met bioavailability tool, Ver 2.3—this is a “look-up table”—developed by Arche Consulting, WCA Environment (2014).
(2)
PNECPro, Ver 6—this an “algorithm”-based tool in MS Excel format developed by Deltares in the Netherlands.
(3)
M-BAT, Ver 31—an “algorithm”-based tool in MS Excel developed by WCA Environment (Water Framework Directive—UK Technical Advisory Group, 2014).

One barrier to the use of BLMs is the technical complexity of the approach, in addition to the transparency of the algorithms, and the large number of water chemistry parameters required (USEPA, 2022). An alternative approach, the MLR model approach, has recently been developed for many cationic metals. These models have begun to replace BLMs due to their ease of use and access in an excel format (Peters et al., 2011; USEPA, 2018). The approach is similar to existing toxicity adjustments for hardness that pool data across species (USEPA, 1985). Multiple linear regression models fit toxicity responses to several variables, usually pH, DOC, and hardness, but other variables can be modeled. Multiple linear regression models frequently pool the toxicity data to provide a single model for multiple species; however, they may be developed for a single species. For example, Brix et al. (2017) indicated that for copper, they followed USEPA (1985) guidelines for calculating a hardness adjustment equation, where the species data were combined to develop a linear model with pooled slopes for each independent parameter (i.e., DOC, pH, and hardness) and species-specific intercepts using analysis of covariance.

Early use of MLRs for describing the effects of water chemistry on metal toxicity occurred in the 1980s (Erickson et al., 1987a, 1987b). More recently, MLRs were developed for lead (Esbaugh et al., 2011, 2012) and copper (Brix et al., 2017)—the latter using a single equation based on the pooling of data across species. The Brix et al. (2017) paper helped establish the fundamental principles used in the development of MLRs for subsequent models as they published the first multispecies MLR for copper in a framework suitable for use in setting environmental quality standards. Subsequently, MLR models for aluminum, lead, nickel, and zinc have been developed (Croteau et al., 2021; DeForest, Tear, et al., 2020; Santore et al., 2018; Peters et al., 2011; CCME, 2020; DeForest et al., 2023, respectively).

Ambient water quality criteria for metals, and most chemicals, are developed from species sensitivity distributions (SSDs), with the 5th percentile of the SSD typically used to define the criterion. Multiple linear regression models that predict metals toxicity as a function of key TMFs (namely, DOC, hardness, and pH) can be used to normalize the SSD and the resulting criterion to site-specific conditions. Multiple linear regression-based criteria may be derived from a single pooled model that is applied to all species in the SSD or the criteria may be derived from two or more MLR models (e.g., an invertebrate MLR model may be applied to invertebrates and a fish MLR model may be applied to fish). If a pooled MLR model is selected for criteria development, the MLR-based criteria can be expressed as a single equation (analogous to the USEPA's hardness-based criteria). If two or more MLR models are selected for criteria development, the TMF slope coefficients are applied to their respective species in the SSD. For the latter case, the MLR-based criterion cannot be reduced to a single MLR equation. Rather, the MLR models are used to update the SSD, and the associated 5th percentile, for the TMF conditions of interest. The use of two or more MLR models to develop criteria is conceptually more complex, but simple Excel-based tools can be developed to automate the process.

A mixture of pooled MLR criteria equations and species-specific MLR equations is presented in Table 2. A single pooled equation is presented when it exists for a given metal (see copper, lead [acute only], nickel, and zinc equations). For aluminum and lead (chronic only), species-specific equations are provided for normalizing the invertebrate and fish toxicity values to a common TMF condition. In these cases, the TMF slope coefficients in the equations would be used to adjust the toxicity values for other species in the SSD. For the chronic lead model, note that a pooled Ceriodaphnia dubia and Lymnaea stagnalis MLR model was recommended for invertebrates. Multiple linear regression models for both species are shown in Table 2, but note that the TMF slope coefficients are the same and only the intercept differs. The intercepts reflect differences in the sensitivity of these two species to lead; however, to be clear, only the TMF slope coefficients from the pooled model are necessary for adjusting the SSD to the TMF conditions of interest (it is not necessary to calculate the intercept for each species in the SSD).

As noted, once a single pooled MLR equation or multiple MLR equations are used to adjust the SSD to the TMF conditions of interest, the 5th percentile of the SSD is typically used to derive the criterion. In the United States, the statistical approach of Erickson and Stephan (1988) is used to calculate the 5th percentile. The regression analysis is typically driven by the four most sensitive genera in the sensitivity distribution. Depending on the sample size, the 5th percentile may be interpolated among the four most sensitive genera or extrapolated below the most sensitive genera. The approach uses a triangular distribution that represents a censored statistical approach that improves estimation of the lower tail with the assumption that the shape of the whole distribution is uncertain. User-friendly Excel programs are used to calculate the 5th percentile or site-specific criterion with only the need for site-specific DOC, pH, and hardness data.

The main disadvantage of MLRs is that they do not explicitly model metals speciation or the binding affinity of the metal for the biotic ligand receptor within the model, but instead are based on empirical observations. Biotic ligand models can help to inform the mechanistic underpinnings of the MLRs.

Model validation

The use of bioavailability models for regulatory purposes should be contingent on meeting performance criteria as specified through a model-validation process (Garman et al., 2020). Garman et al. (2020) identified three types of validation: (1) auto-validation, (2) independent validation, and (3) cross-species validation. Auto-validation is an evaluation of how well the model describes the toxicity data set from which the model was calibrated. Independent validation is an evaluation of how well the model developed from one toxicity data set predicts toxicity in another data set. Cross-species validation evaluates the ability of a model developed for one or more species to predict toxicity for a species that is not in the model.

Brix, DeForest, et al. (2020) and Garman et al. (2020) provide a general approach for model validation. From this general approach, that of Brix et al. (2021), who compared the copper BLM with the copper MLR model, the following four performance evaluations are recommended: (1) Develop a 1:1 plot of observed versus predicted effect concentrations (ECx). Include a diagonal trend line denoting a 1:1 agreement, with corresponding lines indicating a factor of ±2 agreement, and provide the model (adjusted) R² (Figure 1). (2) Evaluate model residuals of observed versus predicted values to identify systematic biases in the model predictions (e.g., underprediction of toxicity at lower observed ECx values and overprediction of toxicity at higher ECx values). Residuals should be evaluated for all TMFs considered in the model (DOC, pH, hardness) to identify the parameter(s) responsible for any observed patterns in residuals. (3) Develop cumulative probability distributions (CPDs) of observed and/or predicted ECx values and factor-of-agreement plots to expand on information in the 1:1 plot. (4) Develop a comparative CPD using the geometric mean of all toxicity values for a species without bioavailability adjustment. These plots provide a visual comparison of the two data sets characterizing the percentage of data that are over- or underpredicted by the models as well as a simple way to evaluate the percentage of toxicity predictions that are within a given factor of agreement.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Comparative 1:1 plots of the pooled acute Cu multiple linear regression model and the biotic ligand model using auto-validation data sets for *Daphnia magna*. Solid line = line of perfect agreement between observed and predicted median effect concentrations. Dashed lines indicate a factor of ±2. BLM, biotic ligand model; LC50, median lethal concentration; MLR, multiple linear regression; RFx,2.0, percentage of data within a factor of 2 using the slope rating formula. *Source*: Adapted from Brix et al. (2021)

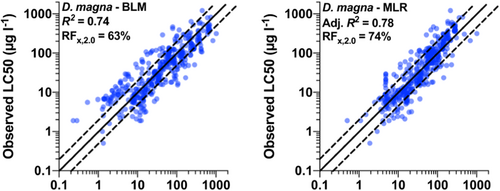
Comparative performance of BLM and MLR models

The USEPA signed a Cooperative Research and Development Agreement (CRADA) with eight metals associations (Aluminum Association, Aluminum REACH Consortium, Cobalt Institute, International Copper Association, Copper Development Association, International Lead Association, International Zinc Association, NiPERA Inc.) in December 2017. The Agency's goal was to engage external technical experts from the metals associations to develop a modeling approach to predict the bioavailability and toxicity of metals in aquatic environments under a range of common water chemistry conditions. The results of the CRADA efforts are summarized here and by the USEPA (2022).

A key part of the initial phase of the CRADA was to make a head-to-head comparison of the BLM with the MLR model for two metals with chronic data (i.e., copper and aluminum), with subsequent comparisons of BLMs with MLR models for lead and nickel. Copper and aluminum were selected because there were existing bioavailability models for both metals and chronic data. Copper represents a metal with a large toxicity data set and aluminum with a much smaller toxicity data set. Brix, Tear, et al. (2020) and Brix et al. (2021) compared the BLM and MLR models applied to the aluminum and copper data sets. The goal of the comparison was to evaluate the bioavailability model performance and to determine how the BLM and MLR model results compare.

As a general conclusion, both models worked well for both metals. They observed that the chronic Al MLR model performs substantially better than the Al BLM across a range of metrics. However, there were substantial differences between models in the resulting water quality criteria as a function of water chemistry. It was to be expected that the Al MLR would fit the data set somewhat better than the BLM as the MLR model was built using the same data set used to establish the USEPA water quality criteria (USEPA, 2018). For copper, Brix et al. (2021) found that the acute Cu MLR and BLM performances were quite comparable, although there were differences in performance on a species-specific basis and in the resulting water quality criteria as a function of water chemistry. The chronic Cu MLR performed distinctly better than the chronic BLM. Observed differences in performance were due to the smaller effects of hardness and pH on chronic Cu toxicity compared with acute Cu toxicity. These differences were captured in the chronic MLR model but not the chronic BLM, which adjusts only for differences in organism sensitivity. A question that usually arises is as follows: when there are different water quality criteria predicted by two models, which is more accurate? One way to assess this is to examine the fit of the model to the toxicity data at the lower end of the SSD. As new models are developed, Brix et al. (2021) recommend development of both modeling approaches because they provide useful comparative insights into the strengths, limitations, and predictive capabilities of each model.

Multimetal BLMs (mBLM)

The recognition that metals in aquatic ecosystems usually occur as metal mixtures has led to the development of bioavailability models that are designed to predict the toxicity of the mixture as a function of water chemistry. The same concepts built into the BLM lend themselves to the development of models that predict toxicity of multiple metals acting upon receptor sites. In general, based on interactions between the dissolved metal and various ligands in solution, BLMs calculate metal concentration at a biotic ligand (e.g., fish gill) and predict toxicity. In the past, approaches to assessing metal mixtures have focused on evaluating whether the metals are additive, less than additive, or more than additive (Meyer et al., 2015; Vijver et al., 2011). To assist with the development of models for metal mixtures, a modeling evaluation project was initiated (Van Genderen et al., 2015). Four separate research groups developed multimetal models and utilized the model to predict toxicity for several data sets (Farley & Meyer, 2015a).

The four models developed for the project were used to develop a single streamlined multimetal model (Farley & Meyer, 2015b), demonstrating that predictions of toxicity due to metal mixtures can be predicted. Santore and Ryan (2015) developed a multimetal, multiple binding site version of the BLM (i.e., mBLM). The model can predict toxicity using dissolved metal as well as mBLM normalized bioavailable metal. Individual BLMs for cadmium, copper, lead, and zinc were combined to develop the mBLM to predict the toxicities of mixtures of these four metals. The mBLM is an advancement from single-metal BLMs in that it considers the influence of the interactions of metals of cadmium, copper, lead, and zinc as well as aluminum and iron with various aqueous ligands.

For given data sets, the toxicity predictions indicate that mixtures are slightly more than additive, whereas on an mBLM normalized basis, the mixtures are additive or slightly less than additive. The difference is because the mBLM accounts for the interaction of the metals with the ligands in solution and adjusts for bioavailability.

While multimetal models now exist, they have primarily been used in risk assessments or to assist in research projects as opposed to regulatory applications such as water quality standards. The mBLM has recently been used to assess toxicity of metal mixtures in sediment porewaters (Santore et al., 2022). The authors used this model to help determine the suitability of metal porewater measurements obtained by dialysis (peepers) versus centrifugation.

Use of bioavailability models in risk assessment and other applications

The BLM and MLR models are most frequently associated with the development of water quality criteria or guidelines; however, there are other potential uses including risk assessments, effluent permitting, evaluation of impaired water bodies, and assessment of stormwaters. Risk assessment, either retrospective or prospective, frequently requires the assessment of metal concentrations in water bodies associated with contaminated sites, acid mine drainage, or pesticide runoff. For example, arsenic (cotton) and copper (grapes) have been used as pesticides with unintentional runoff to local waterbodies. Metals are associated with multiple superfund sites, producing surface and groundwater contributions to nearby steams. These models are useful in assisting with risk determinations.

Under the US Clean Water Act (2002), section 303d, each of the states is required to identify water bodies that do not meet the established water quality standards for the respective state. A mass loading study is then required, and steps are to be taken to bring the water body into compliance. The 303d determinations are frequently based on total metal or dissolved metal in-stream concentrations. Bioavailability models assist in the determination of the extent, if any, of the exceedance of the water quality standard and in the mass loading allocation. These models have also found use in assessing metals in stormwater and receiving waters with the potential to impact fish populations. For example, this has been demonstrated in assessing the potential for Cu to impair olfactory sensory detection (Meyer & Adams, 2010; Meyer & DeForest, 2018) in surface waters. Another example is the use of the BLM to identify concentrations of Cu in Panther Creek, Idaho, below the Blackbird mine that would allow for the recovery of fish populations in the Panther Creek after installation of a lime treatment system to control acid mine drainage (Mebane et al., 2015).

BIODYNAMIC MODELS FOR ASSESSING BIOACCUMULATION

Biodynamic (bioaccumulation) modeling was only briefly covered in the USEPA Metals Framework in 2007. The approach has evolved, many more metals and organisms have been tested, methods have been developed to identify cellular locations of metals, and efforts have been made to use the approach to assess toxicity in addition to bioaccumulation. Biodynamic modeling describes the uptake, distribution, and elimination of a substance over time (Ashauer & Escher, 2010). This is in contrast to equilibrium-based models, such as the BLM, which assume that reaction rates or conditions remain constant over time, and that assume the exposure route is primarily water. Biodynamic modeling provides a means of assessing metal accumulation via various pathways including both water and diet. The biodynamic approach also provides a means to assess the metal variability in tissue among species (Luoma & Rainbow, 2005). This approach utilizes data on assimilation efficiencies of metals from the diet as well as species-specific accumulation and elimination kinetics. Biodynamic modeling allows for identification of the key route(s) of exposure and for comparison among species (Stewart et al., 2004).

In general, the biodynamic modeling approach has not been used to predict toxicity. However, there has been an effort to link the biodynamic modeling approach to toxicity by Buchwalter et al. (2007) and Khan et al. (2015). The models have also been used to compare the bioaccumulation of several metals in freshwater and marine invertebrates using a one-compartment approach and two uptake routes, that is, water and diet (Luoma & Rainbow (2005). Their results demonstrated the applicability of the approach and explained the large differences in metal tissue concentrations in terms of differences in uptake and elimination rates and the relative importance of water and diet as sources of metal. The dynamic modeling approach has also been used to model metal transfer from one trophic level to another and to predict metal accumulation in food webs (Van Campenhout et al., 2009; Rainbow et al., 2009).

While kinetics of uptake and bioaccumulation are key features in metal risk assessment, whole-body or specific organ concentrations are not necessarily predictive of metal toxicity. For instance, the critical body residue concept works for some species but not for others and is most applicable to mercury and selenium (Adams et al., 2011). The general lack of correlation of tissue accumulation with toxicity is explained by the fact that once inside the organism, a metal enters a biological system in which metals bind with different biological ligands and can be stored in inert pools (Gao et al., 2015). Additionally, the lack of observed toxicity in biodynamic studies is due to short-term studies (e.g., on the order of hours, not days) and are designed to assess the kinetics of uptake (and depuration) via dietary and water exposure; they are not designed to solicit toxic responses. Techniques have been developed to identify metals in biologically active or metabolically available pools and inactive or detoxified pools using tissue and subcellular fractionation techniques (Liao et al., 2011; Wallace & Lopez, 1997). This information on accumulation of metals in sensitive and less sensitive pools can be incorporated into biodynamic models to allow for the overall disposition of the metal in an organism. Metal toxicity occurs when the binding or accumulation of a metal to one or more key biotic ligands reaches a critical threshold. Selenium is the classic example because fish and amphibians preferentially deposit selenium in their ovaries, resulting in deformed embryos when the concentrations are sufficiently high (Chapman et al., 2010).

As mentioned, there are limited examples of toxic effects reported with the development of biodynamic models. One example where the experimental design allowed for toxicity as well as bioaccumulation assessment was conducted with copper sorbed to hydrous iron oxide (Cain et al., 2016). The experimental design used copper particle concentrations that spanned nearly a factor of 1000. Results showed that copper influx and ingestion rates decreased as copper concentrations increased above 10⁴ nmol/g. This was accompanied by lysosomal destabilization and lysosomal membrane damage.

Other examples of biodynamic modeling of metals include the bioaccumulation of arsenic and zinc by polychaetes (Casado-Martinez et al., 2009; Rainbow & Luoma, 2011, respectively); bioaccumulation of lead by a freshwater amphipod (Urien et al., 2015); uptake of cadmium by a freshwater bivalve (Pyganodon grandis) (Cooper et al., 2010); biodynamic understanding of mercury accumulation (Wang, 2012); and bioaccumulation of arsenic and silver by caddisfly larvae (Awrahman et al., 2015).

Kinetic approaches can also be used when performing measurements of metal concentrations and potential bioavailability. For instance, diffusive gradients in thin films (DGT) and Chelex columns can be used to assess metals in water and sediments when the rate-determining step is diffusion of the metal from the complex at the membrane, rather than uptake into the organism, as may be the case with chronic exposure to low metals concentrations (Gillmore et al., 2020).

Overall, biodynamic modeling can be a useful approach to understand and predict the uptake rates and accumulation of metals in aquatic organisms and inform the exposure assessment. Compared with aqueous bioavailability models (BLM/MLR), it requires more detailed information for parameterization. The coupling of metal uptake and accumulation to toxicity requires further research to fully exploit the power of the dynamic modeling approach and potentially adapt it to the development of toxicity and water quality criteria.

FATE OF METALS IN AQUATIC ECOSYSTEMS

The USEPA Framework for Metals Risk Assessment discussed in detail factors associated with metal speciation, sorption, complexation, precipitation, and the importance of pH and redox. In the years since the issuance of the USEPA Framework, there have been advances in the science related to the fate of metals in aquatic environments, particularly with regard to measuring metal dissolution and/or transformation and modeling the fate, transport, and resuspension of metals. Models have emerged that allow for integrating the processes that determine metal loss from the water column and the ultimate fate in sediments. Here, we focus on these advances in understanding and modeling fate processes for metals. In the context of risk assessment, understanding the fate of metals in aquatic ecosystems allows for improved exposure assessments in the water and sediment compartments and can be used to inform the linkages to be selected in the conceptual model.

Transformation–dissolution

For proper exposure assessment, an understanding of the solubility of metal substances is needed. A common misunderstanding in assessing the risk of metals is to assume that they are infinitely soluble and/or 100% bioavailable. Toxicity tests usually use soluble metal salts to determine the toxicity of the metal. However, metals released into the environment frequently are rarely in that form. This is especially true for contaminated sites near mining, smelting, and refining operations. The transformation–dissolution protocol (TDPs) was developed to provide the means to help determine whether a metal of interest will go into solution and the rate and extent to which that will occur. In aquatic environments, massive metals and sparingly soluble metal compounds dissolve at different rates depending on the intrinsic properties of the metal and the environmental water chemistry. The rate and extent of dissolution are critical to understanding the rate of metal ions' release in solution. Data generated from the TDP tests (concentration of metal in solution) can be compared with ecotoxicity reference values to determine the short- and long-term potential aquatic hazard of the metal-bearing substance for both hazard classification and risk assessment purposes.

Efforts began in the late 1990s as part of the Organization for Economic Co-Operation and Development (OECD, 2001) to develop a globally harmonized system of classification and labeling and to develop a reliable method for measuring metal dissolution. This led to the development of a TDP (Skeaff & King, 1997). The protocol was adopted by OECD and included in Annex 10 of the United Nations Globally Harmonized System of Classification and Labeling of Chemicals (United Nations [UN], 2005). The method is now used worldwide for assessing metal and metal alloys transformation. With the passage of the EU regulations dealing with the Registration, Evaluation, Authorization and Restrictions of Chemicals (REACH) in 2006, there was a need for risk assessment to be performed for substances produced and/or imported over 1 ton. Hence, most metals have been subjected to a TDP evaluation. Thus, there are data in the REACH metal dossiers on common metal substances. The TDP approach requires that a standard means of assessing the extent of dissolution be developed and related to the mass of the material placed in solution. The testing approach utilizes an aqueous medium simulating natural surface water and testing at pH of 6, 7, and 8 for periods of 1–28 days, with the testing solution being constantly mixed at 100 rpm. It is now recognized that the best approach to interpreting the dissolution data is to base the calculation on the surface area of the metal being tested rather than on the mass of material placed in solution (Skeaff et al., 2000). Surface area is an intrinsic property of a metal and has a much greater influence on the resulting dissolution than the mass of the metal being tested.

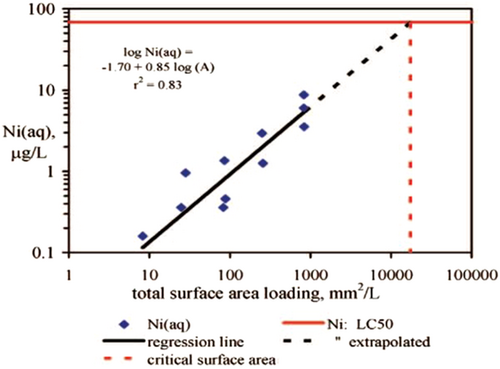
The outcome of the TDP testing is frequently used to determine the environmental hazard classification of a metal substance according to the UNGHS, where the concentration in solution after 7 or 28 days is used to determine whether the solution will be acute or chronically toxic to fish, invertebrates, or algae. In Figure 2, it can be seen that the nickel alloy being tested does not dissolve sufficiently to cause acute toxicity to aquatic organisms. In this example, one can also calculate the critical surface area needed to release sufficient nickel to cause acute toxicity. This allows for a calculation of the surface area and/or particle size required to result in sufficient ions in solution to cause toxicity.

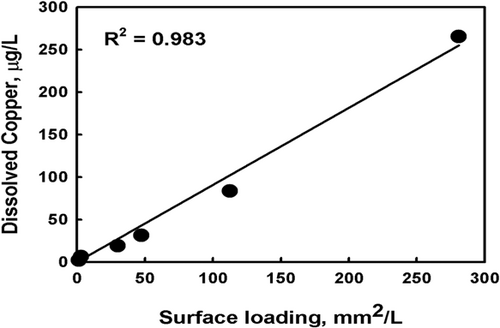
Another example of measuring dissolution as a function of surface area using a copper wire was demonstrated by Rodriguez et al. (2007) (Supporting Information: Figure S-1). It was observed that abrasion needed to be avoided in the test to avoid elevated concentrations of copper in solution; therefore, plastic wheels were used that suspended the copper wire. The surface area of the wire was measured and used to calculate the extent of dissolution (Figure 3), resulting in a linear relationship. In contrast, if one were to plot dissolution as a function of loading, the relationship would be curvilinear, indicating that loading by itself cannot account for dissolution. Thus, it is possible to maintain the loading (mass) constant and achieve different amounts of metal in solution if the surface areas are different. This is critical to understanding the dissolution of sparingly soluble metals.

Loss from the water column

The principal advancements in the science since USEPA published its Framework for Metal Risk Assessment in 2007 have been in areas of understanding of rate processes in aquatic ecosystems affecting metal bioavailability, speciation changes, sorption kinetics, and the ability to integrate these processes in a predictive model that includes both the water column and the sediments. In this section, a brief review of recent developments regarding metal loss from the water column is provided.

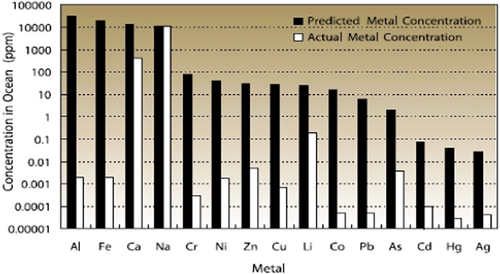
Metal loss from the water column is a natural process that reflects transport to sediments via sorption to particulate and/or biological matter. Metals are continually being lost from the water column by transport to the sediments in all aquatic ecosystems (Adams, 2020). This process has been depicted by calculating the loss of metals in the ocean (Figure 4). Metals are continually carried to the ocean, and one might expect the concentrations to increase over time. However, it has been shown that for metals other than sodium, they are continuously being transported to the sediments and the resulting concentrations are much lower than would be predicted if they were infinitely soluble—by a factor of 10 000 or more (Di Toro, Allen, et al., 2001).

The rate of transport of metals to the ocean floor is slow in relation to the depth of the ocean, on the order of a few meters per day. However, in shallow marine ecosystems such as estuaries or in freshwater ecosystems, a transport rate of 1–2 m/day can be significant in terms of a removal mechanism and reduction in exposure for water column organisms. Detailed studies with several metals (e.g., Cu, Ni, Zn, Pb, Ag) indicate that they are very particle reactive, with strong affinities for suspended solids, Fe oxides, sulfides, organic ligands, and algae (Danner et al., 2015; Moffett & DuPont, 2007; Rossi & Jamet, 2008; Stumm & Morgan, 1996).

Multiple processes are interacting to reduce exposure in both the water column and the sediment compartments. These include sorption to particles as well as iron and manganese oxyhydroxides and subsequent settling, binding with acid-volatile sulfides (AVS), changes in speciation to less reactive forms, covalent bonding with other elements, burial, resuspension, and re-oxidation. Each of these processes is rate limited by the intrinsic properties of the specific metal, and ecosystem-specific water and sediment chemistry. These factors, and the fact that it is known that free metal ions (toxic form of common metals) are very reactive (seconds to minutes) with various inorganic and organic ligands, have led to the development of the UWM. This model integrates the above-mentioned fate processes and allows for estimation of exposure concentrations in various environmental compartments in aquatic ecosystems.

The UWM concept (Adams & Chapman, 2006) was developed to model these rate processes and allow for estimates of exposure both in the water column and in the sediments (Supporting Information: Figure S-2). This is somewhat analogous to the development of the BLM, in that both models allow for assessment of competing binding phases (MFs) and ultimate exposure of the metal to various aquatic organisms. The Tableau Input Coupled Kinetics Equilibrium Transport (Ticket) UWM (Farley et al., 2011) “is based on a computation that allows for simultaneous consideration of dissolved and particulate phase transport; metal complexation to organic matter and inorganic ligands; precipitation of metal hydroxides, carbonates, and sulfides and competitive interactions of metals and major cations with biotic ligands. It includes a simplified description of biogeochemical cycling of organic carbon and sulfur; and dissolution kinetics for metal powders, massives, and other solid forms.” The model has been applied in several lake scenarios and a generalized lake in the Sudbury area of the Canadian Shield to demonstrate the overall cycling of metals in lakes and the nonlinear effects of chemical speciation on metal responses. The model can be used in conjunction with the BLM (overlying water and porewater) and be used to calculate a loading rate (critical load) to a water body that will exceed a threshold for effects.

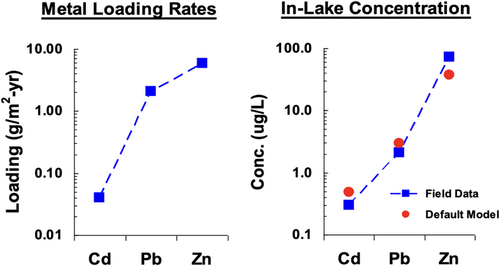
The UWM applied to the Canadian Shield Lake calculated critical loads for Cu, Ni, Pb, and Zn ranging from 2.5 to 39.0 g metal/m²-year. These critical loads were a factor of 10 or more higher than those for organic compounds (e.g., lindane, DDT, and PAHs), thus indicating a lower degree of concern for the metals as opposed to the selected organic compounds. Farley et al. (2009) have also used the UWM to calculate response to loading in Lake Coeur d'Alene as a verification of the model (Supporting Information: Figure S-3). The results of the estimated surface water concentrations are in good agreement with the measured values (Figure 5).

The UWM has been applied in risk assessment scenarios for surface waters in Europe and considered as a possible addition to or replacement for the EUSES model currently used for REACH risk assessments (EC, 2004). In support of the use of the UWM for European risk assessments, a project was completed to define 16 of the parameters used in the UWM (e.g., pH, DOC, Ca, Mn, etc.) and their relevant ranges representing their natural occurrence in EU surface waters along with median, average, 10th, and 90th percentiles (Vercaigne et al., 2013).

The two models are available at the following web addresses:

TICKET Unit World Model—A modeling framework for metal… (https://www.unitworldmodel.net/).
https://echa.europa.eu/en/support/dossier-submission-tools/download-euses

Rate of loss

The rate at which metals are lost from the water column in aquatic ecosystems has been the focus of several recent publications by Burton et al. (2019), Huntsman et al. (2019), Rader et al. (2019), and Adams (2020). Classification of substances for protection of the aquatic environment under the UNGHS or EU Classification, Labeling and Packaging regulations is based on aquatic chronic toxicity and can be modified by biodegradability. Substances that are rapidly degraded (rapid loss) present a low risk to the aquatic environment. Rapid loss for organic compounds is measured using a standard ready biodegradability test. For metals, it has been argued that rapid loss from the water column, sediment burial, transformation into insoluble forms, followed by mineralization is equivalent, that is, exposure is reduced or eliminated. The debate has centered on the rate of loss from the water column and the extent to which the metals are permanently lost to sediments. The relevance to risk assessment is that loss from the water column reduces the exposure concentration to organisms living in this compartment.

To evaluate the potential for a metal to undergo rapid loss from the water column, we consider the following: (1) the intrinsic properties of the metal that determine its fate in aquatic systems; (2) available field and/or laboratory studies that assess the fate of dissolved metal ions in aquatic systems; and (3) application of a laboratory test protocol to assess metal removal and/or remobilization under standardized conditions (i.e., ETRP) to gain insight into the physicochemical processes that influence metal fate.

Intrinsic properties and metal fate

Intrinsic properties of a chemical substance are those that influence its behavior and that are typically independent of concentration. Classic examples are number of protons and neutrons, valence states, chemical speciation, and sorption to ligands. The intrinsic properties of metals such as copper, lead, silver, and zinc cause them to react in the environment in ways that influence their bioavailability and fate. Copper, mercury, and silver, for example, interact strongly with various functional groups present in dissolved and POC as well as iron and manganese oxyhydroxides and sulfide. Since metal ions are electron donors, they can bind to electron receptors within various ligands. Metal atoms are Lewis acids since they donate electrons to the central metal (coordination with the metal ion as opposed to the anion—the Lewis base). This is an intrinsic property of the metal (Burton et al., 2019).

Changes in speciation can increase or reduce bioavailability (Di Toro, Allen, et al., 2001). Key changes in speciation occur through metal complexation, sorption, and precipitation reactions, Rader et al. (2019). These changes require the formation or breaking of bonds. This contrasts with organic molecules, which sorb to particles or DOC. Sorption occurs by means of weak van der Waals forces (Schwarzenbach et al., 1993). Hence, the organic molecule remains unchanged.

Metal precipitation can be an important factor in controlling environmental exposures. The chemistry of aluminum, iron manganese, and tin represent examples of metals that rapidly transform into metal hydroxides in freshwater ecosystems (in a pH range of 6–8.5) and rapidly precipitate from the water column and are transported to sediments, where they react with other ligands. These precipitation reactions can occur in minutes to hours depending upon pH, temperature, and other factors. In marine systems, it is well known that concentrations of lead in the water column as well as aluminum and iron are controlled by precipitation reactions.

Metals are frequently categorized as hard or soft metals, indicating their reaction with oxygen and nitrogen (hard metals, such as aluminum, cobalt, chromium, iron, manganese, strontium) or with sulfur (soft metals, i.e., copper, cadmium, mercury, silver). The soft metals are those that readily react with sulfur and are associated with AVSs found in sediments. “Soft” (e.g., Cu, Cd) and “borderline” metal ions (e.g., Zn, Ni, Co) exchange oxygen-containing ligands for sulfur, where they are sequestered via various mechanisms including adsorption, inclusion, metal-exchange, and co-precipitation (Rickard, 2012). Over time, these metals become incorporated into pyritic minerals, which are resistant to further transformation (Huerta-Diaz et al., 1993, 1998; Morse & Luther, 1999). “Hard” metal ions remain bonded to oxygen-containing ligands and remain adsorbed to mineral surfaces, particulate organic matter, or precipitate as amorphous oxides, hydroxides, and carbonates. Over time, these metals age into even more insoluble forms or become incorporated into mineral crystalline structures and are frequently associated with insoluble iron and manganese oxyhydroxides along with aluminum and iron silicates.

Understanding the chemistry of metal ions in solution requires a detailed analysis of chemical speciation of each metal and affinity for the ligands present. Knowledge of speciation is necessary to understand the chemical form present with respect to valence state(s) and activity of the metal and the potential of the free metal ion to interact with various ligands in solution or suspension. Likewise, stability constants are fundamental to understanding and predicting the behavior of metal ions in the environment. The equilibrium constant involving the formation of a metal complex from the aquo-metal ion and a simple ligand is a standard measure of the effectiveness of the ligand in coordinating (combining) with the metal ions. Stability constants are frequently expressed as logarithms and express the strength of the metal ligand.

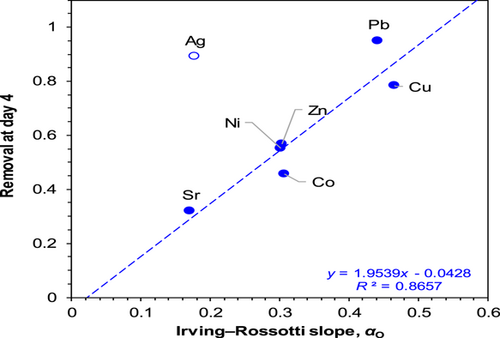
Carbonaro et al. (2007), Carbonaro et al. (2011), and Atalay et al. (2013) have developed linear free-energy relationships to describe bonding of metal ions to ligands containing oxygen donor atoms, the same groups that are responsible for metal partitioning in the water column. A single metal-specific parameter, α_O (the Irving–Rossotti slope), indicates the extent to which a given metal bonds preferentially to negatively charged oxygen donor atoms relative to the proton (Irving & Rossotti, 1956). The magnitude of metal loss from the water column is strongly correlated to the magnitude of the Irving–Rossotti slope. This is because metals bind with select components of particulate matter in lakes (e.g., humic acids, fulvic acids, and metal oxides) through negatively charged oxygen donor atoms (Dzombak & Morel, 1990; Tipping & Hurley, 2002). This relationship was assessed experimentally using an adaptation of the TDP with several metals in a 4-day experiment (Huntsman et al., 2019). This is discussed further in the section on resuspension. The data show that there is a linear relationship between the Irving–Rossotti slope (α_O) and the extent of loss from the water column (Figure 6). Silver appears to be an outlier and may be explained by its strong affinity for ligands other than oxygen such as sulfur including reduced sulfur groups (Bell & Kramer, 1999; Smith et al., 2002). The relationship in Figure 6 indicates that metal removal is related to the relative preference of a metal for oxygen donor atoms (i.e., the Irving–Rossotti slope).

Field and laboratory data on rate of loss

Assessment of exposure is fundamental to assessing the risk of toxicity to exposed organisms. Reactions of metals with their environment result in both loss of the metal from the water column and resolubilization under some circumstances. Understanding the dominant vector and metal fate processes controlling exposure is central to exposure assessment. Recent reviews of papers reporting loss of metals from aquatic ecosystems (Burton et al., 2019; Huntsman et al., 2019; Mebane et al., 2015; Rader et al., 2019) all indicate that there is rapid and substantial loss of metals from the water column following releases.

Numerous studies have demonstrated metal removal in surface waters for most of the common metals. Burton et al. (2019) and Rader et al. (2019) reviewed 20+ publications related to metal loss from the water column. Here, we briefly summarize the literature pertaining to rate and loss of metals in various ecosystems as well as estimates using the UWM with supporting field data for select examples. The experiments performed by Diamond et al. (1990) using mesocosms placed in a lake assessed the behavior of several metals in the same mesocosms. They observed the following half-times (i.e., the time at which the concentration has decreased by 50%, average of the two mesocosms, in days): cobalt (4.35), tin (9.45), iron (10.8), mercury (14.45), zinc (17.6), arsenic (19.2), and cesium (22.65). The rate of loss was correlated with sorption to particles and settling (Supporting Information: Figure S-4).

A review of removal rates for copper in several lakes and mesocosms (Rader et al., 2019) indicates that the half-life removal times for copper are typically on the order of 2–15 days (Table 3). In one experiment in which the addition of copper was continuous, the half-life was calculated as 76.2 days. This experiment is interesting in that, with the continuous addition of copper (i.e., flow-through system), approximately 50% of the copper is lost from the water column at steady state (Di Toro, Kavvadas, et al., 2001; Rader et al., 2019; Supporting Information: Figure S-5).

Table 3. Experimental measures of removal rates of copper from natural lakes and ponds

Ecosystem	Measurement	% Removal (days)	50% removal time (days)	70% removal time (days)	Author
Cazenovia Lake	Total copper	34%–68% (23)	2.0–9.6	14–> 23	Effler et al. (1980)
Lake Matthews	Total copper	62% (9.4)	15.6	27.2	Haughey et al. (2000)
Lake Courtille	Dissolved copper	80% (22)	9.0	15.6	van Hullebusch et al. (2002)
Saint Germain les Belles	Dissolved copper	75% (9)	4.1	7.1	van Hullebusch, Chatenet, Deluchat, Chazal, Froissard, Botineau, et al. (2003); van Hullebusch, Chatenet, Deluchat, Chazal, Froissard, Lens, et al. (2003)
Catfish ponds	Total copper		0.48	0.84	Liu et al. (2006)
Microcosms–Fraunhofer	Dissolved copper		1.4–3.7	2.4–6.3	Schäfers (2001)
Novosibirskoye Mesocosms	Total copper	86%–95% (19)	4.5–8.7	7.8–15.1	Smolyakov, Ryzhikh, Bortnikova, et al. (2010); Smolyakov, Ryzhikh, and Romanov (2010)
Lake Baldegg Limno-corals	Dissolved copper		76.2	130	Gächter (1979)

Source: Adapted from Rader et al. (2019) and Burton et al. (2019).

The UWM has been used to demonstrate metal removal with remobilization potential in a lake ecosystem simulation for copper (Cu), zinc (Zn), lead (Pb), nickel (Ni), cobalt (Co), cadmium (Cd), and aluminum (Al) (Mutch Associates, 2012). The model calculations were based on use of the same model parameters (e.g., DOC, pH Ca, Mg, etc.) as the EUSES model and with initial metal concentrations of 29, 76.3, 120, and 136 µg/L. Starting concentrations were based on acute or chronic toxicity thresholds (Mutch, 2013). The data are presented as the fraction of the original concentration [C(t)/C_T(0)] remaining as a function of time plotted on the y-axis. A fraction remaining of 0.3 corresponds to a 30% remaining or 70% removal. Time to 70% removal following a single spike to the model ecosystem for Cu, Ni, Pb, and Zn ranges from 2 to 5.5 days in (Supporting Information: Figure S-6). In contrast, the data for barium (not shown) indicate almost no loss from the water column over 28 days unless the starting concentration exceeded the saturation point and the metal precipitated.

While single-metal releases into the environment are rare, the data shown here indicate that the ability now exists to model metal exposure concentrations and predict exposure outcomes under a variety of natural conditions by changing the input parameters to the model to simulate metal fate at a site of interest. This approach provides a step change in the science related to exposure assessment for metals.

Assessment of metals following sediment resuspension (remobilization)

The potential for metal remobilization from sediments is a key issue to be considered in risk assessments. This should be considered both in terms of the short term and longer time periods. In the short term, several factors may influence exposure including the fact that some small fraction of particulate phase-bound metals may not be permanently sequestered in the bottom sediments (Kalnejais et al., 2007). The burrowing activity of organisms, hydrologically related events (e.g., increased flow rate, storm events), or occasional human activities (e.g., dredging, seabed mining) are all processes that could cause sediments resuspension. During these processes, previously redox-stratified sediments will mix with oxygenated overlying water, thereby altering metal sediment–water partitioning and speciation (Simpson & Batley, 2003). Additionally, seasonally induced changes in redox/zones can have a pronounced influence on the chemical phase distribution. For example, in winter, oxygen penetration in the sediment is deemed to affect deeper layers, while lake turnover in the spring and fall will influence the oxygen content at the sediment surface layer. However, following these events, there is a redistribution of metals to various binding phases and a reset of steady-state conditions. The amount of metal mass that is perturbed is always a small fraction of the total. Therefore, a short-term increase in exposure occurs that may be significant depending upon the mass of metal in the sediments and extent of the perturbation. However, toxicity does not appear to be the norm following short-term resuspension events as the metals are rapidly sorbed to oxyhydroxide surfaces.

Huntsman et al. (2019) developed a method for determining the loss of metals from the water column using a modification and/or extension to the TDP known as the Environmental Transformation and Removal Protocol (ETRP). This method measures metal removal from the water column via interactions with dissolved and suspended particles to nonavailable forms and potential for metals to reenter the water column following a resuspension event. The ETRP quantifies the rate of environmental transformation of dissolved metal species into nonavailable forms and the transport of metals into sediments. The ETRP follows as an extension to the TDP, which calls for the addition of three loadings of a metal-bearing substance into an aquatic medium, with agitation, followed by the evaluation of metal concentrations in solution over a 28-day period. To evaluate removal potential, 10 g of sediment is placed in 1-L Schott–Duran flasks with an aquatic solution spiked with dissolved metal, followed by a period of rapid mixing, and then settling. The rapid mixing is meant to mimic a resuspension event, although this vigorous mixing in the laboratory would likely produce a worst-case scenario. The rate of loss is calculated by comparing metal concentrations at the beginning and end of the test. In Huntsman et al. (2019), three different sediment substrates were tested at pH values of 6, 7, and 8 to evaluate the effect of pH and sediment characteristics on metal loss for several metals including silver, copper, lead, zinc, cobalt, nickel, and strontium. The results show that silver, copper, lead, zinc, and, to a lesser extent, nickel and cobalt were rapidly and substantially reduced in the water column. Conversely, strontium concentrations declined at a slow rate.

Several studies have investigated the chemical composition and changes that occur when sedimentary metal phases are suspended in oxygenated water (Fetters et al., 2016; Kalnejais et al., 2007, 2010, 2015). Sulfides are thermodynamically unstable in oxidizing environments, leading to a potential initial release of metals to the dissolved phase (De Jonge et al., 2012; Kalnejais et al., 2007; Simpson et al., 2012). However, the released trace metals are in turn strongly scavenged by iron and manganese oxide phases so that precipitation of these oxides close to the sediment–water interface can lead to an enriched layer of trace metals close to the sediment–water interface (Sutherland et al., 2007). Costello et al. (2015, 2016) indicated that copper and nickel released during CuS and NiS oxidation were not lost from the sediment but were instead retained by other solid-phase ligands, likely organic matter and Fe and Mn oxides. The relative importance of these opposing processes will ultimately determine the net effect on trace metal bioavailability.

In summary, Fetters et al. (2016) showed that short-term resuspension of sediments resulted in limited metal mobilization that was sediment and metal specific. Xie et al. (2015, 2019) showed that zinc was moderately released only after two days of vigorous resuspension. Burton et al. (2015) concluded that while increases in toxicity were observed in some laboratory studies, most resuspension events, laboratory or field, are nontoxic due to the short duration of the exposures.

The binding of metals to sediments over the long term is typically not reversible, because metals are sequestered to stable forms or buried at depth, which means that they will not be released into the porewater of the active biological zone (Cappuyns & Swennen, 2006). In this regard, adsorption time is a factor to be considered in the distribution and partitioning of metals. The prolonged aging of metals in sediment or soils has been demonstrated to be a major factor in determining their availability: the exchangeable and carbonate fractions decrease, while the refractory fractions (organic and mineral phases) increase (Guo et al., 2011; Jones et al., 2008; Peng et al., 2009; Zhong et al., 2012). For example, aging (fixation) can redistribute the adsorbed metals to the interior of sorption sites of organic and mineral substrates and as such increase retention of metals (Cappuyns & Swennen, 2006). Fixation of metals takes place by the slow diffusion of metals into Fe hydroxides and hydrous oxides of Al and Mn (Trivedi & Axe, 2000), clay minerals (Ma & Uren, 1998), and by diffusion or coprecipitation in carbonates (Nakhone & Young, 1993).

At a steady state, the input of a metal via sedimentation and the output via resuspension will reach an equilibrium. As metals are being transported to deeper sediment layers, they will be less prone to resuspension. The burial process and the increasing irreversible binding of the metals into the sediment matrix control metal exposure in the long term. The conditions in which organisms are most vulnerable to metal exposure are as follows:

(1)
recent release (spill) resulting in a significant increase in concentration in the water and sediment;
(2)
continuous release (effluent) that exceeds the assimilative capacity of the ecosystem, such as has occurred at mining sites due to elevated concentrations in the effluent or acid mine drainage; and
(3)
substantial change in the pH of the ecosystem such as might occur following an acid spill or changes following prolonged acid rain deposition.

In examples 1 and 2 above, the key issue is that the mass loading has exceeded the ability of the ecosystem to respond on a short-term basis. Once management of the release occurs, the ecosystem will reach a steady state and most of the metal will be sequestered and become nonavailable to organisms. Regarding #3 above, Schindler et al. (1980) evaluated the effects of acidification on mobilization of metals from sediments in a 10 m (dia) enclosure in a freshwater lake (#223) in Ontario. The pH was reduced from 6.7–6.8 to 5.7 and 5.1 (one enclosure each). Aluminum, iron, manganese, and zinc were released from the sediments, with subsequent redistribution back to the sediments. Radiotracers showed that the acidification slowed the loss of manganese and zinc, while losses of barium, cesium, selenium, and vanadium to sediments were more rapid under acid conditions. While acidification results in an initial release of metals, over a longer period, the metals are transported to sediments through partitioning to suspended solids.

An example of system recovery was reported by Mebane et al. (2015) for Panther Creek, Idaho, following massive releases of copper, arsenic, and cobalt due to mining operations in the 1930s–1960s era. Efforts to restore water quality began in 1995, and by 2002, copper levels had been reduced by about 90%. Full recovery of salmonid populations occurred within about 10 years after the onset of restoration efforts and about four years after the USEPA chronic copper criteria had mostly been met. Shorthead Sculpin (Cottus confusus) numbers recovered within four years after their first arrival at a site. Benthic macroinvertebrate biomass increased, reaching about 70%–90% of the reference. The key to success was the implementation of a treatment plant to remove metals from acid mine drainage and hence, mass load reduction. This occurred despite the significant concentrations of metals remaining in the sediments.

EVALUATION OF METAL TOXICITY IN SEDIMENTS

Sediment assessment tools have advanced since the issuance of the Metals Framework in 2007. There has been considerable effort to improve sediment spiking procedures, identify appropriate aging periods, and develop models to assess or predict metals toxicity in sediments. These improvements are reviewed along with background information leading to these developments.

Numerous studies have demonstrated that dry weight concentrations of total recoverable metals in sediments cannot be used to predict toxicity across sediments of differing characteristics. Considering that most sediment risk assessments begin with such measurements, this is disconcerting and has led to various approaches for assessing metals in sediments. One of the early methods for assessing sediments was the Apparent Effects Threshold (AET) method (Barrick et al., 1988). Under the AET approach, empirical field and laboratory data are used to identify concentrations of chemicals above which there were always effects. The AET method, while providing an approach for many organics and metals, was limited because it could not provide direct causality for observed effects to a specific chemical since the toxicity tests were based on field samples that included many chemicals. This led to the development of weight of evidence approaches evaluating metal chemistry, toxicity, and field evidence using benthic community studies referred to as the “Triad Approach” (Chapman, 1996). Weight of evidence approaches were later improved with a better definition of lines of evidence and decision criteria (Hope & Clarkson, 2014; Hull & Swanson, 2006). Several approaches were developed from laboratory toxicity studies performed with field-collected sediments with the goal of developing sediment quality guidelines (SQGs) as indicators of benthic effects in the field and for remedial action decisions for sediments. These SQGs are usually defined as concentrations of single contaminants in sediments (mg/kg dry weight) below which toxicity is rarely observed and above which toxicity is frequently observed (Long & MacDonald, 1998; Long et al., 1995; MacDonald et al., 1996, 2000). These methods, like the AET method, lack definitive evidence of causality due to co-occurring contaminants, but have been widely used. Additionally, logistic regression modeling has been used to match sediment toxicity and chemistry data (Field et al., 1999, 2002), and field-based SSDs have been proposed as a tool for sediment risk assessment (Kwok et al., 2008; Roman et al., 2005).

While these approaches have merit, there has been considerable effort to develop an approach that defines a metal concentration that is either nontoxic or toxic (safe–not safe). In the mid-1990s, studies on the presence of AVS in anoxic sediments demonstrated an amazing ability to control the bioavailability of common divalent metals. Numerous studies (>100) demonstrated a lack of toxicity when AVS exceeded the sum of the simultaneously extracted metals (SEMs) (Ankley, 1996; Ankley et al., 1996; Di Toro, Allen, et al., 2001). This approach was improved upon using sediment interstitial water measurements compared with toxicity results from water-only exposure toxicity tests with benthic organisms (Berry et al., 1996). This was based on a long-standing premise that toxicity of contaminants to benthic organisms is primarily due to desorption into interstitial water (Adams et al., 1984). Di Toro et al. (2005) developed a sediment version of the aqueous BLM in which sediment porewater toxicity could be predicted for cadmium, copper, nickel, lead, and zinc using POC as a replacement for DOC. The model requires pH measurement of the porewater and uses the SEM procedure for metal measurements that are normalized to the sediment OC and uses the BLM to assess possible toxicity of the sediment porewater.

This addition to the AVS-SEM model allowed for estimates of when sediment would be toxic as opposed to identifying nontoxic sediments. This was the state of the science at the time the USEPA's Metals Framework document was issued (USEPA, 2007a). These concepts have been widely used and remain valid; however, these methods are (1) not predictive and (2) do not address sediments that are oxic or where AVS is low and <SEM. Since the issuance of the USEPA Framework for Metals Risk Assessment (USEPA, 2007a), approaches have been developed for spiking sediments and aging sediments for consideration of phases other than AVS including oxyhydroxides and suspended solids, for development of species sensitivity (SSD) curves for benthic invertebrates allowing for predictive models, for sediment toxicity assessment, and for application of the mBLM in assessing sediment porewater metal concentrations.

Sediment toxicity models: Copper

The toxicity of copper to benthic organisms has been evaluated in 106 chronic toxicity tests for six different organisms, that is, amphipods Hyalella azteca (25 individual no-observed effet concentration [NOEC] values) and Gammarus pulex (six individual NOEC values), oligochaetes Tubifex tubifex (39 individual NOEC values) and Lumbriculus variegatus (three individual NOEC values), insect Chironomus riparius (27 individual NOEC values), and insect Hexagenia (six NOEC values) (Cu-VRAR, 2008). A total number of 11 types of sediments were tested, grouped into artificial sediments with a range of OC and AVS concentrations; natural sediments with low AVS concentrations; or natural sediments with high AVS concentrations.

Copper was spiked into the sediment–water system as CuCl₂·2H₂0, placed into test vessels, and were stabilized and/or equilibrated for 8–11 days before test initiation. According to Simpson et al. (2004), equilibration of Cu-spiked sediments occurs within 10–15 days. The water renewal regime was two to three times a week and porewater and overlying water were sampled to assess dissolved copper. The observed NOEC values ranged between 18.3 and >3158 mg/kg dry weight (min–max value) without correcting for bioavailability. The distribution of AVS and OC in selected toxicity data varied between 0.05 and 58.6 mmol/kg dry weight and 0.5% and 24.8%, respectively (Supporting Information: Figure S-7).

A high degree of variability was observed in the effect levels, which is attributed to the variation observed in the AVS-OC sediment characteristics presented above. To assess the data, an MLR model was used. The resulting model had an adjusted R² of 0.81, indicating that both OC and AVS had a significant positive effect on the NOEC. Organic carbon has the largest effect on the log10(NOEC) value, which is apparent from its slope (i.e., 0.112). The AVS slope (0.044) indicated a less pronounced effect, which is not surprising since AVS is more suited as a model to predict the absence of toxicity and not the onset of toxicity. The interaction term between OC and AVS is negative, indicating that the positive effect on the log10(NOEC) of each was lower if the other was also high. The model parameters and output of the model (observed versus predicted values are shown in Table 4 (Supporting Information: Figure S-8). Most of the toxicity thresholds for all species showed a clear relationship with OC and/or AVS/OC and the model predicts the relationship quite well.

Table 4. Results of linear regression analysis (endpoint: growth/biomass) for the pooled copper sediment; data set for Tubifex tubifex, Hyalella azteca, Lumbriculus variegatus, Chironomus riparius, and Gammarus pulex (n = 37)

	Estimate	Std. error	t Value	p Value
Intercept	1.543	0.075	20.565	<2e−16***
OC	0.112	0.015	7.632	8.74e−09***
AVS	0.044	0.010	4.615	5.71e−05***
OC:AVS	−0.003	0.000	−6.301	3.99e−07***

Abbreviations: AVS, acid-volatile sulfides; OC, organic carbon.
***p < 0.05.
Source: Adapted from Cu-VRAR (2008).

A separate analysis was undertaken to investigate only the relationship between NOEC values and OC, based on sediments in tests that contained no AVS, but that contained a gradient in OC. This analysis confirmed the positive relationship between the toxicity values and the OC content of the sediment (Supporting Information: Figure S-9) for all species (n = 14). Most sediments in this set of tests had a narrow OC range (i.e., 1%–3%). For each species, only one sediment was tested at a significantly higher OC concentration (i.e., 9.8%). This approach was undertaken to accommodate assessments in which the sediment AVS is low and/or where regulatory bodies recommend the use of a worst case (most conservative) scenario.

The above analysis clearly shows that both AVS and OC have a significant effect on the observed copper toxicity levels for all test species in freshwater sediments. Taking these bioavailability factors into account reduces intraspecies variability to a large extent, resulting in more robust sediment quality assessment values and the ability to predict toxicity as a function of sediment chemistry.

In addition to the above models for copper, Simpson et al. (2011) developed a copper model to predict toxicity to marine sediment organisms based on binding to OC in the <65 μm particles size category. They concluded that adequate protection for all benthic organisms is expected for an OC-normalized copper concentration of 3.5 mg Cu/g OC in the <63 µm sediment fraction. For short-term exposures, the equivalent acute guideline is 11 mg Cu/g OC.

Sediment toxicity models: Nickel

Bioavailability-based models have been published for nickel in sediments (Schlekat et al., 2015; Vangheluwe et al., 2013). The approaches applied are based upon laboratory toxicity studies with a large number of species. This allows for the creation of SSDs and corrections in the species responses observed for different sediments based on the development of equilibrium partitioning-based bioavailability models.

A sediment testing program was established that utilized extensive laboratory testing, followed by field verification of laboratory findings regarding nickel toxicity to benthic organisms. The laboratory program was designed to address three objectives: (1) evaluate various sediment spiking methods to ensure that the laboratory sediments reflect real-world chemistry conditions; (2) generate a reliable and expanded benthic data set using 10 benthic species in sediments with low and high nickel binding capacity; and (3) examine sediment bioavailability relationships for OC, AVS, Fe, Mn, and cation exchange capacity (CEC) (Schlekat et al., 2015; Vangheluwe et al., 2013). Additionally, six nickel-spiked sediments were deployed in the field to examine benthic colonization. The test results were used to develop SSDs and bioavailability models for sediments with differing chemistries.

Vangheluwe et al. (2013) utilized eight field-collected sediments for nickel sediment toxicity tests with a range of chemical parameters. Ten benthic species were tested using spiked sediments following the spiking and equilibration procedure described by Brumbaugh et al. (2013) (see the next section). The data were also used to develop bioavailability models based on EC20 values. The data were used to develop chronic SSSs for the different sediment chemistries (Supporting Information: Figure S-10). The natural sediment (Spring River MO) with the lowest AVS and total organic carbon (TOC) was used to derive a reasonable worst-case PNEC for nickel.

The bioavailability models developed by Vangheluwe et al. (2013) used stepwise MLR analysis. The models were based on AVS, TOC, pH, Fe, and Mn (mg/kg dry wt), CEC (Meq/100 g), sand (%), silt (%), and clay (%) (Table 5). The approach allowed for the development of toxicity thresholds (EC20 and HC5 values, that is, hazard concentration at the 5th percentile species) using AVS, total recoverable Fe, TOC, and CEC.

Table 5. Nickel sediment bioavailability models developed by species and sediment parameter

Species	Model	R²	Intercept (SE)	Slope (SE)
	AVS based
Hyalella azteca	Log EC20 total Ni (mg/kg dry wt) = 2.65 + 0.492 log AVS (µmol/g dry wt.)	0.74	2.65 (0.11)	0.492 (0.11)
Gammarus pseudolimnaeus	Log EC20 total Ni (mg/kg dry wt) = 2.8 + 0.358 log AVS (µmol/g dry wt.)	0.62	2.8 (0.13)	0.358 (0.13)
Hexagenia sp.	Log EC20 total Ni (mg/kg dry wt) = 2.35 + 0.175 log AVS (µmol/g dry wt.)	0.59a (p = 0.07)	2.35 (0.06)	0.175 (0.07)a
	TOC based
H. azteca	Log EC20 total Ni (mg/kg dry wt) = 2.81 + 0.513 log OC (%)	0.59	2.81 (0.11)	0.513 (0.17)
G. pseudolimnaeus	Log EC20 total Ni (mg/kg dry wt) = 2.81 + 0.557 log OC (%)	0.79	2.81 (0.09)	0.557 (0.13)
Hexagenia sp.	Log EC20 total Ni (mg/kg dry wt) = 2.40 + 0.164 log OC (%)	0.29a (p = 0.26)	2.40 (0.07)	0.164 (0.13)
	Fe based
H. azteca	Log EC20 total Ni (mg/kg dry wt) = − 0.54 + 0.854 log Fe (mg/kg dry wt.)	0.62	−0.54 (1.15)a	0.854 (0.27)
G. pseudolimnaeus	Log EC20 total Ni (mg/kg dry wt) = 0.31 + 0.666 log Fe (mg/kg dry wt.)	0.68	0.31 (0.87)a	0.666 (0.20)
Hexagenia sp.	Log EC20 total Ni (mg/kg dry wt) = 0.75 + 0.418 log Fe (mg/kg dry wt.)	0.79	0.75 (0.45)a	0.418 (0.11)
	CEC based
H. azteca	Log EC20 total Ni (mg/kg dry wt) = 2.11 + 0.783 log CEC (meq/100 g)	0.59	2.11(0.32)	0.783 (0.26)
G. pseudolimnaeus	Log EC20 total Ni (mg/kg dry wt) = 2.28 + 0.679 log CEC (meq/100 g)	0.68	2.28 (0.26)	0.679 (0.26)
Hexagenia sp.	Log EC20 total Ni (mg/kg dry wt) = 2.20 + 0.0.244 log CEC (meq/100 g)	0.36a (p = 0.21)	2.2 (0.20)	0.244 (0.16)

Abbreviations: AVS, acid-volatile sulfides; CEC, cation exchange capacity; OC, organic carbon; TOC, total organic carbon.
^a Nonsignificant.
Source: Adapted from Vangheluwe et al. (2013).

The effects data set for nickel with 10 benthic species is the largest sediment data set for any metal and is representative of several feeding strategies and exposure routes. However, there is a lack of guidance on what is an adequate sediment database of benthic invertebrates for the development of an SSD and PNEC. The USEPA (1985) recommends eight families for water column species. This is currently not possible due to a lack of suitable test methods. Vangheluwe et al. (2013) recommended that different exposure conditions and feeding behavior of sediment organisms be the guiding principle related to organism selection.

Based on the experience of the aforementioned nickel testing program, the authors proposed an overarching approach to assessing risk associated with metals in sediment based on (1) laboratory-based sediment toxicity testing; (2) development of bioavailability models; (3) determination of effects thresholds; and (4) field validation (Supporting Information: Figure S-11).

In summary, the nickel and copper sediment assessment programs discussed have advanced the science of sediment risk assessments for freshwater organisms by developing regression models that can be used to predict toxicity as a function of AVS and OC (copper) and AVS and Fe (nickel). The models have been applied to SSDs for benthic organisms and to field-collected sediments. It has been demonstrated that variability in toxicity responses can be reduced by applying bioavailability corrections to the sediment toxicity data. This is analogous to the approach that USEPA uses for water quality criteria for copper and aluminum (USEPA, 2007b, 2018). While this represents an advancement in predicting metals toxicity in sediments, the use of MLR models has not advanced to the same level for sediments as for the aqueous environment. For example, the models for copper and iron have not yet integrated AVS, OC, Fe, and Mn into a single regression model. However, it is fair to point out that the UWM accomplishes that integration and allows for calculation of a concentration in sediment or the water column that is toxic or nontoxic. It is not, however, a single equation that can be performed using a spreadsheet and thus has not been widely used.

Spiking and aging

Borgmann et al. (2001), Vandegehuchte et al. (2007), and Costello et al. (2011) have shown that sediment samples spiked with metals for laboratory toxicity tests produce significantly different results (greater toxicity) when the tests are conducted shortly after spiking versus aging the samples for several weeks. It is now widely recognized that toxicity tests with unaged sediments provide overly conservative results due to increased metal concentration in the porewater. Costello et al. (2016) showed that when sediments high in nickel (Raisin River, MI) were delivered to the laboratory, they were initially toxic to Hyalella azteca due to oxidation of AVS caused by oxygen ingress to the sediments during sediment transport, but over 10 days, they became nontoxic as the porewater nickel concentrations declined. The goal in laboratory testing is to achieve metal concentrations in sediments with distribution between dissolved and solid phases that resemble those measured in field-collected sediments (Brumbaugh et al., 2013; Costello et al., 2016; Simpson & Batley, 2003; Simpson et al., 2004). Thus, there is a need to use sediments in toxicity tests that reflect the bioavailability of those in natural waters. The literature is replete with studies in which sediments are collected, delivered to the laboratory, mixed and spiked (or not), and evaluated for toxicity by placing organisms in the test chambers without proper characterization of the sediment and without determining the redox and AVS of the test system relative to the natural conditions.

Relative to natural sediment that has an oxidized surface layer, homogenized and equilibrated sediment placed into test chambers presumably has greater concentrations of reduced ligands (e.g., AVS) and decreased oxidized ligand concentrations (e.g., Fe oxides) near the sediment–water interface (Costello et al., 2016). Reduced sulfur (measured as AVS) is unstable in the presence of O_2, and in homogenized sediment, AVS is rapidly oxidized within the surface 1 cm (Costello et al., 2015; De Jonge et al., 2012; Simpson et al., 2012). A decline in AVS concentration in surface sediment during aging will change metal bioavailability. Oxidation of reduced sulfur and/or metal sulfides results in a nonequilibrium condition for metal binding and a change to sorption to other ligands, with a potential release of metal into the dissolved phase. There can be a loss of oxidized ligands (e.g., Fe and Mn oxides) during homogenization of sediment, especially if the pH has been lowered due to addition of the metal.

For Ni, there is evidence that toxicity and speciation are strongly correlated to Fe and Mn oxide concentrations (Costello et al., 2011). Simpson and Batley (2003) reported that Zn release rates increased rather than decreased from sediments, upon exposure to more oxygenated waters, indicating that oxygen penetration into the sediments did not increase sufficiently to cause oxidation of pore-water Fe(II) to Fe(III) with formation of the hydroxide and sorption of released Zn. The increased rate of Zn release from the sediments was attributed to the slow oxidation of Zn sulfide phases present in the surface sediments (0–2 cm). The competing rates between Zn sulfide dissolution and Ferric hydroxide sorption of Zn control the concentration of zinc in the porewater. Thermodynamics predict that sulfide oxidation should occur in preference to Fe(II) oxidation.

Simpson et al. (2004) demonstrated that sediments spiked with nickel required a relatively long time for equilibration (i.e., 70 days) as compared with 15, 40, and 45 days for Cu, Zn, and Cd, respectively. Brumbaugh et al. (2013) confirmed the need for an extended aging period (10 weeks) for nickel, and Hutchins et al. (2007) demonstrated this for copper. Zhong et al. (2012) demonstrated the need for a two-month aging period by extracting ⁶⁵Cu-spiked sediments and extracting them with digestive fluid mimicking deposit feeders. An additional refinement in sediment spiking procedures is to neutralize the sediments after spiking to adjust downward pH shifts that occur using NaOH (Simpson et al., 2004). The pH shift results from metal hydrolysis and the fact that the stock solutions used for spiking are typically acidic to keep the metal in solution. Hydrolysis lowers pH, resulting in competition of solid-phase binding sites between H+ and Me+, allowing for the release of increased concentrations of metals into the porewater. A similar approach has been developed for spiking soils and has been the basis for developing laboratory to field correction factors for several metals (Smolders et al., 2009). Sediment aging after pH adjustment allows for a redistribution of metal between binding phases, incorporation into the particle matrix, and a change in metal speciation to less labile forms of the metal. It also allows for reestablishment of preexisting redox conditions, formation of AVS, and achievement of a steady state of metal concentrations between the porewater and the sediment. The latter is critical to enable comparison with effects occurring in natural sediments at a given site.

Brumbaugh et al. (2013) recommend the following spiking procedure: Use of an indirect (two-step) spiking approach as proposed by Hutchins et al. (2007), which utilizes adjustment of pH via the addition of NaOH at a 2:1 ratio to the spiked metal during preparation of “super-spikes.” This is followed by a four-week equilibration period in the spiking jars, after which the spiked sediment is mixed and equilibrated with incremental portions of unspiked sediment to achieve the desired test concentrations. The procedures are performed under nitrogen to prevent oxygen ingress. This approach was effective in producing consistent pH values and other chemical characteristics across spiking levels. When spiking Ni into sediment having high AVS and high organic matter, a total equilibration period of at least 10 weeks is recommended because of the slow reaction kinetics of Ni with AVS.

Additional studies that summarize methods for spiking sediments with metals have been published by Simpson et al. (2004), Zhong et al. (2012), Besser et al. (2011, 2013), Simpson and Batley (2016), and Hartford et al. (2022).

Sediment porewater measurement and assessment (mBLM)

There has been considerable discussion regarding how to reliably collect sediment porewater (interstitial water) for metals beginning back in the 1980s. Four approaches that have frequently been used include dialysis, centrifugation, pressurized squeezing, and vacuum extraction. Dialysis (collection by a passive sample across a membrane, often referred to as peepers) is often thought of as the gold standard. This method is the least susceptible of the methods to cross-contamination with suspended solids and eliminates oxygen ingression into the sediment from sample handling. It frequently provides the lowest metal concentrations. Samples collected with peepers require a minimum of a week of equilibration and provide a very small amount of porewater (i.e., <5 mL), which limits the ability to conduct toxicity tests, and only some analytical methods and equipment can analyze metals in volumes this small. Centrifugation has the advantage that the samples can be processed within minutes after collection, large volumes of water can be produced, and many samples can be processed rapidly. The disadvantage is that there can be a change in speciation and loss of metal when the samples are exposed to oxygen.

Judd et al. (2021) and Santore et al. (2022) reviewed several large data sets in which toxicity studies were conducted, and porewater metal concentrations were measured using peepers and centrifugation. The results indicate that metal concentrations are generally higher in centrifugation-collected porewater, the results are more variable than metals concentrations measured by peepers, and that toxicity correlated best with the peeper metal concentrations (Supporting Information: Figure S-12).

Santore et al. (2022) (companion paper to Judd et al. (2021) used the multimetal BLM to predict toxicity of porewater metals to Hyalella azteca in 184 samples of paired survival with excess SEM (i.e., SEM-AVS). The aim of the paper was to use toxicity results to support a conclusion as to the use of centrifugation versus peepers for sediment assessment. The prediction was significantly more accurate using peeper porewater measurements than centrifugation using H. azeteca (Supporting Information: Figure S-13). Their analysis showed that when SEM exceeds the AVS, toxicity is generally expected and becomes more prevalent as the excess SEM increases. Their data also demonstrate a reduction in toxicity when the porewater is normalized to organic carbon content. The mBLM assessment using peeper data provided the most accurate prediction of toxicity for the highest number of samples. Santore et al. (2022) concluded that peepers provide a better measure of toxicity potential, but that centrifugation is acceptable for collecting samples for DOC, pH, and soluble metal ions such as calcium and sodium, and the two methods could be used in tandem.

Interpreting sediment toxicity tests

A workshop sponsored by the European Chemicals Agency (ECHA) identified several recent scientific advances as well as areas where guidance in assessing sediment toxicity data is lacking (European Chemicals Agency, 2014). One such area relates to how to interpret the results of laboratory sediment toxicity tests in terms of determining whether the toxicity is due to the sediment, the porewater, or overlying water in the test chamber. This problem exists for tests with spiked sediments and field-collected sediments when the tests are conducted using a static design versus tests conducted where the water exchange in the test chambers is insufficient to maintain the contaminant in the overlying water below the aqueous toxic effect concentration. In this circumstance, there is a high probability that the porewater contaminant concentration is the same as the overlying water concentration. The problem is further compounded by the fact that, unless the sediments were properly aged before introducing the organisms, the porewater concentration will be higher than what is observed in the field. This leads to the conclusion that the laboratory tests are biased on the high side and are often not representative of field conditions.

The solution to this problem is the following: (1) Age the sediment appropriately such that the porewater reflects the field conditions. This usually takes a period several weeks, or it requires core samples to be collected and kept under nitrogen until they are tested. (2) Perform the test using a flow-through test system (or multiple water replacements) so that the concentration of the contaminant(s) is maintained below the concentration causing toxicity due to aqueous exposure (no sediment). The approach used by Adams et al. (1984) demonstrated this for kepone by conducting static and flowthrough tests along with water-only exposure tests. They demonstrated that the toxic effects could be expected to occur only if the chemical concentration is high enough in the sediments such that the equilibrium interstitial water concentration reached by desorption is equal to or higher than the concentration demonstrated to cause effects in a water-only exposure test. This allowed for calculation of the kepone sediment concentration that produced a porewater concentration that was toxic. Adams et al. (1984) demonstrated that kepone sorbed to food (i.e., no kepone in water or sediment) did not cause toxicity at the highest level tested. If the concern is that the chemical may exert toxicity via ingestion, it is critical to maintain the overlying water below the aqueous effect level and to measure the porewater concentrations during the experiment. Without these additional measures, it cannot be determined as to which is the route of exposure and what sediment metal concentration causes effects. Lack of proper aging for the test sediments and improper spiking procedures also lead to results that are not comparable to field conditions (see the section on sediment spiking and aging).

CONCLUSION

The science associated with assessing metals in the environment has advanced over the past 15 years since the USEPA Metals Framework was published in 2007. Notable advances have been made in the development of bioavailability models for assessing toxicity as a function of water chemistry in freshwater ecosystems. Biotic ligand model and MLR models now exist for most of the common mono- and divalent metals. Additionally, with the aid of the EU REACH regulations, aquatic toxicity databases were developed or significantly expanded for most of the common metals. This has allowed for the development of SSDs for these metals and made it possible for many jurisdictions to develop or update their water quality criteria or guidelines.

The understanding of the fate of metals in the environment has undergone significant scrutiny over the past 20 years or more. It is now clear that the ultimate fate of metals in aquatic ecosystems is the sediment compartment. The rate and extent to which metals are transported to sediments have been extensively studied in both the laboratory and in natural systems. Transport and toxicity models have evolved, and models such as the UWM allow for estimating concentrations of metals in various compartments as a function of loading and time. Additionally, there has been significant focus on the transformation of metals in sediments into forms that are less bioavailable and to understanding conditions that result in re-solubilization or redistribution of metals in and from sediments.

Assessment of metal bioavailability of metals in sediments has been extensive. Methods for spiking sediments have been developed such that the resulting chemistry in the laboratory mimics that in natural systems. Sediment bioavailability models are emerging. The complexity of the sediment chemistry and the lack of toxicity test methods for sediment have limited the scope of the sediment bioavailability models. Nevertheless, models that allow for prediction of when sediments are nontoxic have advanced, and models that allow for prediction of sediment toxicity are emerging. Models for copper and nickel are two examples. These models take advantage of MLR approaches analogous to those used for the aqueous environment, making use of chemistry parameters including AVS, OC, Fe, Mn, and CEC. This is an area that still needs further development.

Biodynamic models have been developed for several organisms and many metals. The key parameters such as uptake and depuration rate constants as well as bioavailability of the metal in the food have been developed for several species. This allows for estimates of transport of metals from sediments to organisms via their diet in addition to water exposure. Sediments that are judged to be nontoxic using toxicity tests or infauna studies may still allow for contaminants to be transported through the food chain. This concern is particularly true for substances that are highly bioaccumulative (typically organics and metallo-organics such as methyl mercury and selenium in some cases).

As the science continues to develop, the tool set available to environmental risk assessors has expanded significantly over the past 15 years. Emphasis on usability and fit for purpose continues to drive the development of models and approaches for use in both the scientific and regulatory arenas.

AUTHOR CONTRIBUTION

William J. Adams: Conceptualization; data curation; formal analysis; funding acquisition; investigation; project administration; writing—original draft. Emily R. Garman: Data curation; investigation; methodology; writing—review and editing.

ACKNOWLEDGMENT

William J. Adams acknowledges financial support to develop this work from the North American Metals Council (NAMC). Emily R. Garman received no compensation for her efforts in developing the manuscript.

CONFLICT OF INTEREST

Both authors acknowledge that they work for the metals industry, but indicate that the views expressed here are those of the authors and not the organizations for which they work.

Open Research

DATA AVAILABILITY STATEMENT

The supplemental data and all data in the article are available from the corresponding author William J. Adams at [email protected].

Supporting Information

REFERENCES

Adams, W. J. (2020). Rapid loss of copper from the water column. Environmental Toxicology and Chemistry, 39(4), 737–738.
10.1002/etc.4665
CAS PubMed Web of Science® Google Scholar
Adams, W. J., Blust, R., Borgmann, U., Brix, K. V., DeForest, D. K., Green, A. S., Meyer, J., McGeer, J. C., Paquin, P., Rainbow, P., & Wood, C. (2011). Utility of tissue residues for predicting effects of metals on aquatic organisms. Integrated Environmental Assessment and Management, 7(1), 75–79.
10.1002/ieam.108
CAS PubMed Google Scholar
Adams, W. J., Blust, R., Dwyer, R., Mount, D., Nordheim, E., Rodriguez, E., & Spry, D. (2020). Bioavailability assessment of metals in freshwater environments: A historical review. Environmental Toxicology and Chemistry, 39(1), 48–59.
10.1002/etc.4558
CAS PubMed Web of Science® Google Scholar
Adams, W. J., & Chapman, P. M. (2006). Assessing the hazard of metals and inorganic metal substances in aquatic and terrestrial systems. SETAC Pellston Workshop May 2003, SETAC Press.
Google Scholar
Adams, W. J., Kimerle, R. A., & Mosher, R. G. (1984). Aquatic safety assessment of chemicals sorbed to sediment. In R. D. Cardwell, R. Purdy, & R. C. Bahner (Eds.), Proceedings of the Seventh Annual ASTM Aquatic Toxicology Symposium (Vol. 854, pp. 429–453). Special Technical Publication STP.
Google Scholar
Ankley, G. T. (1996). Evaluation of metal/acid-volatile sulfide relationship2 in the prediction of metal bioaccumulation by benthic macroinvertebrates. Environmental Toxicology and Chemistry, 15(12), 2138–2146.
10.1002/etc.5620151209
CAS Web of Science® Google Scholar
Ankley, G. T., Di Toro, D. M., Hansen, D. J., & Berry, W. J. (1996). Technical basis for deriving sediment quality criteria for metals. Environmental Toxicology and Chemistry, 15(12), 2056–2066.
10.1002/etc.5620151202
CAS Web of Science® Google Scholar
Arche Consulting & WCA Environment. (2014). A systematic comparison of user-friendly tools used to estimate the bioavailability of copper, nickel and zinc in the aquatic environment of Europe. A report prepared for NiPERA, ECI, IZA.
Google Scholar
Arnold, R. (2009). Effects of dissolved organic carbnon on copper toxicity: implications for saltwater copper toxicity. Integrated Environmental Assessment and Management, 1(1), 34–39.
10.1897/IEAM_2004a-002b.1
Google Scholar
Ashauer, R., & Escher, B. I. (2010). Advantages of toxicokinetic and toxicodynamic modelling in aquatic ecotoxicology and risk assessment. Journal of Environmental Monitoring, 12, 2056–2061.
10.1039/c0em00234h
CAS PubMed Web of Science® Google Scholar
Atalay, Y. B., Di Toro, D. M., & Carbonaro, R. F. (2013). Estimation of stability constants for metal–ligand complexes containing neutral nitrogen donor atoms with applications to natural organic matter. Geochimica et Cosmochimica Acta, 122, 464–477.
10.1016/j.gca.2013.08.030
CAS Web of Science® Google Scholar
Australian and New Zealand Governments and Australian State and Territory Governments. (2018). Australian and New Zealand guidelines for fresh and marine water quality. Retrieved October 21, 2022. https://www.waterquality.gov.au/guidelines/anz-fresh-marine
Google Scholar
Awrahman, Z., Rainbow, P. S., Smith, B. D., Khan, F. R., Bury, N. R., & Fialkowski, W. (2015). Bioaccumulation of arsenic and silver by the caddisfly larvae Hydropsyche siltalai and H. pellucidula: A biodynamic modelling approach. Aquatic Toxicology, 161, 196–207.
10.1016/j.aquatox.2015.01.004
CAS PubMed Web of Science® Google Scholar
Barrick, R., Becker, S., Pastorok, R., Brown, L., & Beller, H. (1988). Sediment quality values refinement: 1988 update and evaluation of Puget Sound AET. Prepared by PTI Environmental Services for Environmental Protection Agency.
Google Scholar
Bell, R. A., & Kramer, J. R. (1999). Structural chemistry and geochemistry of silver–sulfur compounds: Critical review. Environmental Toxicology and Chemistry, 18, 9–22.
10.1002/etc.5620180103
CAS PubMed Web of Science® Google Scholar
Berry, W. J., Hansen, D. J., Mahony, J. D., Robson, D. L., Di Toro, D. M., Shipley, B. P., Rogers, B., Corbin, J. M., & Boothman, W. S. (1996). Predicting the toxicity of metal-spiked laboratory sediments using acid-volatile sulfide and interstitial water normalizations. Environmental Toxicology and Chemistry, 15(12), 2067–2079.
10.1002/etc.5620151203
CAS Web of Science® Google Scholar
Besser, J. M., Brumbaugh, W. G., Ingersoll, G. I., Ivey, C. D., Kunz, J. L., Kemble, N. E., Schlekat, C. E., & Garman, E. R. (2013). Chronic toxicity of nickel spiked freshwater sediments: Variation in toxicity among eight invertebrate taxa and eight sediments. Environmental Toxicology and Chemistry, 32, 2495–2506.
10.1002/etc.2271
CAS PubMed Web of Science® Google Scholar
Besser, J. M., Brumbaugh, W. G., Kemble, N. E., Ivey, C. D., Kunz, J. L., Ingersoll, C. G., & Rudel, D. (2011). Toxicity of nickel-spiked freshwater sediments to benthic invertebrates—Spiking methodology, species sensitivity, and nickel bioavailability (US Geological Survey Scientific Investigations Report 2011–5225). 53pp.
Google Scholar
Borgmann, U., Neron, R., & Norwood, W. (2001). Quantification of bioavailable nickel in sediments and toxic thresholds to Hyalella azteca. Environmental Pollution, 111, 189–198.
10.1016/S0269-7491(00)00076-2
CAS PubMed Web of Science® Google Scholar
Borgmann, U., Couillard, Y., Doyle, P., & Dixon, D. G. (2005). Toxicity of sixty-three metals and metalloids to Hyalella azteca at two levels of water hardness. Environmental Toxicology and Chemistry, 24(3), 641–652.
10.1897/04-177R.1
CAS PubMed Web of Science® Google Scholar
Bringolf, R. B., Morris, B. A., Boese, C. J., Santore, R. C., Allen, H. E., & Meyer, J. S. (2006). Influence of dissolved organic matter on acute toxicity of zinc to larval fathead minnows (Pimephales promelas). Archives of Environmental Contamination and Toxicology, 51, 438–444.
10.1007/s00244-005-0088-6
CAS PubMed Web of Science® Google Scholar
Brix, K. V., DeForest, D. K., Tear, L., Grosell, M., & Adams, W. J. (2017). Use of multiple linear regression models for setting water quality criteria for copper: A complementary approach to the biotic ligand model. Environmental Science and Technology, 51, 5182–5192.
10.1021/acs.est.6b05533
CAS PubMed Web of Science® Google Scholar
Brix, K. V., DeForest, D. K., Tear, L., Peijnenburg, W., Peters, A., Middleton, E. T., & Erickson, R. (2019). Development of empirical bioavailability models for metals. Environmental Toxicology and Chemistry, 39(1), 85–100.
10.1002/etc.4570
Web of Science® Google Scholar
Brix, K. V., DeForest, D. K., Tear, L., Peijnenburg, W., Peters, A., Middleton, E. T., & Erickson, R. (2020). Development of empirical bioavailability models for metals. Environmental Toxicology and Chemistry, 39, 85–100.
10.1002/etc.4570
CAS PubMed Web of Science® Google Scholar
Brix, K. V., Tear, L., DeForest, D. K., & Adams, W. J. (2023). Development of multiple linear regression models for predicting chronic iron toxicity to aquatic organisms. Environmental Toxicology and Chemistry, 42(6), 1386–1400.
10.1002/etc.5623
CAS PubMed Web of Science® Google Scholar
Brix, K. V., Tear, L., Santore, R. C., Croteau, K., & DeForest, D. K. (2020). Comparative performance of multiple linear regression and biotic ligand models for estimating the bioavailability of aluminum and copper. Technical Report prepared for Aluminum Association; Aluminum REACH Consortium; International Copper Association; Copper Development Association.
Google Scholar
Brix, K. V., Tear, L., Santore, R. C., Croteau, K., & DeForest, D. K. (2021). Comparative performance of multiple linear regression and biotic ligand models for estimating the bioavailability of copper in freshwater. Environmental Toxicology and Chemistry, 40(6), 1649–1661.
10.1002/etc.5012
CAS PubMed Web of Science® Google Scholar
Brumbaugh, W. G., Besser, J. M., Ingersoll, C. G., May, T. W., Ivey, C. D., Schlekat, C. E., & Rogevich-Garman, E. (2013). Nickel partitioning during chronic laboratory toxicity tests with eight different spiked freshwater sediments: Toward more environmentally realistic testing conditions. Environmental Toxicology and Chemistry, 32, 2482–2494.
10.1002/etc.2272
CAS PubMed Web of Science® Google Scholar
Buchwalter, D. B., Cain, D. J., Clements, W. H., & Luoma, S. N. (2007). Using biodynamic models to reconcile differences between laboratory toxicity tests and field biomonitoring with aquatic insects. Environmental Science and Technology, 41, 4821–4828.
10.1021/es070464y
CAS PubMed Web of Science® Google Scholar
Burton, G. A., Farley, K. J., Rader, K., Carbonaro, R. F., & Gallani, J. (2015). Predicting the fate and effects of resuspended metal contaminated sediments (Strategic Environmental Research and Development Program (SERDP) Project ER-1746). Department of Defense.
Google Scholar
Burton, Jr., G. A., Hudson, M. L., Huntsman, P., Carbonaro, R. F., Rader, K. J., Waeterschoot, H., Baken, S., & Garman, E. (2019). Weight-of-evidence approach for assessing removal of metals from the water column for chronic environmental hazard classification. Environmental Toxicology and Chemistry, 38, 1839–1849. https://doi.org/10.1002/etc.4470
10.1002/etc.4470
CAS PubMed Web of Science® Google Scholar
Cain, D. J., Croteau, M. N., Fuller, C. C., & Ringwood, A. H. (2016). Dietary uptake of copper sorbed to hydrous iron oxide is linked to cellular toxicity and feeding inhibition in a benthic grazer. Environmental Science and Technology, 50, 1552–1560.
10.1021/acs.est.5b04755
CAS PubMed Web of Science® Google Scholar
Canadian Council of Ministers of the Environment (CCME). (2018). Scientific criteria document for the development of the Canadian water quality guidelines for the protection of aquatic life: Zinc.
Google Scholar
Canadian Council of Ministers of the Environment (CCME). (2020). Scientific criteria document for the development of the Canadian water quality guidelines for the protection of aquatic life.
Google Scholar
Canadian Council of Ministers of the Environment (CCME). (2021). Federal environmental quality guidelines: Copper.
Google Scholar
Cappuyns, V., & Swennen, R. (2006). Comparison of metal release from recent and aged Fe-rich sediments. Geoderma, 137, 242–251.
10.1016/j.geoderma.2006.08.013
CAS Web of Science® Google Scholar
Carbonaro, R. F., Atalay, Y. B., & Di Toro, D. M. (2011). Linear free energy relationships for metal–ligand complexation: Bidentate binding to negatively-charged oxygen donor atoms. Geochimica et Cosmochimica Acta, 75, 2499–2511.
10.1016/j.gca.2011.02.027
CAS PubMed Web of Science® Google Scholar
Carbonaro, R. F., & Di Toro, D. M. (2007). Linear free energy relationships for metal–ligand complexation: Monodentate binding to negatively-charged oxygen donor atoms. Geochimica et Cosmochimica Acta, 71, 3958–3968.
10.1016/j.gca.2007.06.005
CAS Web of Science® Google Scholar
Cardwell, A. S., Rodriguez, P. H., Stubblefield, W. A., DeForest, D. K., & Adams, W. J. (2023). Chronic toxicity of iron to aquatic organisms under variable pH, hardness and dissolved organic carbon conditions. Environmental Toxicology and Chemistry, 42(6), 1371–1385.
10.1002/etc.5627
CAS PubMed Web of Science® Google Scholar
Casado-Martinez, C. M., Smith, B. D., DelValls, A., & Luoma, S. N. (2009). Biodynamic modelling and the prediction of accumulated trace metal concentrations in the polychaete Arenicola marina. Environmental Pollution, 157, 2743–2750.
10.1016/j.envpol.2009.04.032
CAS PubMed Web of Science® Google Scholar
Chapman, P. M. (1996). Presentation and interpretation of Sediment Quality Triad data. Ecotoxicology, 15, 327–339.
10.1007/BF00119054
Google Scholar
Chapman, P. M., Adams, W. J., Brooks, M. L., Delos, C. G., Luoma, S. N., Maher, W. A., Ohlendorf, H. M., Presser, T. S., & Bradshaw, P. (2010). Ecological assessment of selenium in the aquatic environment. SETAC Press.
10.1201/EBK1439826775
Google Scholar
Clean Water Act, as amended (33 U.S.C.” Code of Federal Regulations, title 40 (2002): 694–697. https://www.govinfo.gov/app/details/CFR-2002-title40-vol1/CFR-2002-title40-vol1-part35-subpart320
Google Scholar
Clifford, M., & McGeer, J. C. (2009). Development of a biotic ligand model to predict the acute toxicity of zinc to Daphnia pulex in soft waters. Aquatic Toxicology, 91(1), 26–32.
10.1016/j.aquatox.2008.09.016
CAS PubMed Web of Science® Google Scholar
Clifford, M., & McGeer, J. C. (2010). Development of a biotic ligand model to predict the acute toxicity of cadmium to Daphnia pulex. Aquatic Toxicology, 98(1), 1–7. https://doi.org/10.1016/j.aquatox.2010.01.001
10.1016/j.aquatox.2010.01.001
CAS PubMed Web of Science® Google Scholar
Cooper, S., Hare, L., & Campbell, P. G. C. (2010). Modelling cadmium uptake from water and food by the freshwater bilvalve (Pyganodon grandis). Canadian Journal of Fisheries and Aquatic Sciences, 67(11), 1874–1888.
10.1139/F10-103
CAS Web of Science® Google Scholar
Costello, D. M., Burton, G. A., Hammerschmidt, C. R., Rogevich, E. C., & Schlekat, C. E. (2011). Nickel phase partitioning and toxicity in field-deployed sediments. Environmental Science and Technology, 45, 5798–5805.
10.1021/es104373h
CAS PubMed Web of Science® Google Scholar
Costello, D. M., Hammerschmidt, C. R., & Burton, G. A. (2015). Copper sediment toxicity and partitioning during oxidation in a flow-through flume. Environmental Science and Technology, 49, 6926–6933.
10.1021/acs.est.5b00147
CAS PubMed Web of Science® Google Scholar
Costello, D. M., Hammerschmidt, C. R., & Burton, G. A. (2016). Nickel Partitioning and toxicity in sediment during aging: Variation in toxicity related to stability of metal partitioning. Environmental Science and Technology, 50(20), 11337–11345.
10.1021/acs.est.6b04033
CAS PubMed Web of Science® Google Scholar
Croteau, K., Ryan, A. C., Santore, R., DeForest, D., Schlekat, C., Middleton, E., & Garman, E. (2021). Comparison of multiple linear regression and biotic ligand models to predict the toxicity of nickel to aquatic freshwater organisms. Environmental Toxicology and Chemistry, 40(8), 2189–2205. https://doi.org/10.1002/etc.5063
10.1002/etc.5063
CAS PubMed Web of Science® Google Scholar
Cu-VRAR. (2008). Voluntary Risk Assessment Report (VRAR) of copper, copper sulphate pentahydrate, copper(I)oxide, copper(II)oxide, dicopper chloride trihydroxide. http://echa.europa.eu/nl/copper-voluntary-risk-assessment-reports
Google Scholar
Danner, K. M., Hammerschmidt, C. R., Costello, D. M., & Burton, Jr., G. A. (2015). Copper and nickel partitioning with nanoscale goethite under variable aquatic conditions. Environmental Toxicology and Chemistry, 34, 1705–1710. https://doi.org/10.1002/etc.297
10.1002/etc.2977
CAS PubMed Web of Science® Google Scholar
DeForest, D., Brix, K., Tear, L., & Adams, W. (2018). Multiple linear regression models for predicting chronic aluminum toxicity to freshwater organisms and developing water quality criteria. Environmental Toxicology and Chemistry, 37(1), 80–90.
10.1002/etc.3922
CAS PubMed Web of Science® Google Scholar
DeForest, D., Brix, K., Tear, L., Cardwell, A., Stubblefield, W., Nordheim, E., & Adams, W. (2020). Updated multiple linear regression models for predicting chronic aluminum toxicity to freshwater aquatic organisms and developing water quality guidelines. Environmental Toxicology and Chemistry, 39(9), 1724–1736.
10.1002/etc.4796
CAS PubMed Web of Science® Google Scholar
DeForest, D. K., Ryan, A. C., Tear, L. M., & Brix, K. V. (2023). Comparison of multiple linear regression and biotic ligand models for predicting acute and chronic zinc toxicity to freshwater organisms. Environmental Toxicology and Chemistry, 42(2), 393–413. https://doi.org/10.1002/etc.5529
10.1002/etc.5529
CAS PubMed Web of Science® Google Scholar
DeForest, D. K., Santore, R. C., Ryan, A. C., Church, B. G., Chowdhury, M. J., & Brix, K. V. (2017). Development of biotic ligand model–based freshwater aquatic life criteria for lead following US Environmental Protection Agency guidelines. Environmental Toxicology and Chemistry, 36(11), 2965–2973. https://doi.org/10.1002/etc.3861
10.1002/etc.3861
CAS PubMed Web of Science® Google Scholar
DeForest, D., Tear, L., & Brix, K. V. (2020). Comparison of multiple linear regression models and biotic ligand models for predicting acute and chronic lead toxicity to aquatic organisms. Windward and EcoTox report to International Lead Association (ILA).
Google Scholar
De Jonge, M., Teuchies, J., Meire, P., Blust, R., & Bervoets, L. (2012). The impact of increased oxygen conditions on metal-contaminated sediments part I: Effects on redox status, sediment geochemistry and metal bioavailability. Water Research, 46, 2205–2214.
10.1016/j.watres.2012.01.052
CAS PubMed Web of Science® Google Scholar
De Schamphelaere, K. A. C., & Janssen, C. R. (2004). Bioavailability and chronic toxicity of zinc to juvenile rainbow trout (Oncorhynchus mykiss): Comparison with other fish species and development of a biotic ligand model. Environmental Science and Technology, 38, 6201–6209.
10.1021/es049720m
CAS PubMed Web of Science® Google Scholar
Diamond, M. L., Mackay, D., Cornett, R. J., & Chant, L. A. (1990). A model of the exchange of inorganic chemicals between water and sediments. Environmental Science and Technology, 24, 713–722.
10.1021/es00075a016
CAS Web of Science® Google Scholar
Dzombak, D. A., & Morel, F. M. (1990). Surface complexation modeling. Hydrous ferric oxide. Wiley-Interscience.
Google Scholar
Effler, S. W., Litten, S., Field, S. D., Tong-Ngork, T., Hale, F., Meyer, M., & Quirk, M. (1980). Whole lake responses to low level copper sulfate treatment. Water Research, 14, 1489–1499.
10.1016/0043-1354(80)90015-9
CAS Web of Science® Google Scholar
Environment and Climate Change Canada (ECCC). 2020. Canadian Environmental Protection Act, 1999 Federal Environmental Quality Guidelines – Lead. National Guidelines and Standards Office, Environment and Climate Change Canada, 351 Saint Joseph Boulevard, Gatineau, QC K1A 0H3, Canada.
Google Scholar
Environment and Climate Change Canada (ECCC). (2021). Canadian Environmental Protection Act, 1999 Federal Environmental Quality Guidelines—Copper. National Guidelines and Standards Office, Environment and Climate Change Canada.
Google Scholar
Erickson, R. J., Benoit, D. A., & Mattson, V. R. (1987a, August 30–September 4). Effects of physical and chemical parameters of test water on acute toxicity of copper to larval fathead minnows. American Chemical Society.
Google Scholar
Erickson, R. J., Benoit, D. A., & Mattson, V. R. (1987b). A prototype toxicity factors model for site-specific water quality criteria. US Environmental Protection Agency.
Google Scholar
Erickson, R. J., Benoit, D. A., Mattson, V. R., Nelson, H. P, Jr, & Leonard, E. N. (1996). The effects of water chemistry on the toxicity of copper to fathead minnows. Environmental Toxicology and Chemistry, 15, 181–193.
10.1002/etc.5620150217
CAS Web of Science® Google Scholar
Erickson, R., & Stephan, C. (1988). Calculation of the final acute value for water quality criteria for aquatic organisms (EPA 600/3-88/018 (NTIS PB88214994)). U.S. Environmental Protection Agency.
Google Scholar
European Chemicals Agency. (2014). Principles for environmental risk assessment of the sediment compartment. In: Proceedings of the Topical Scientific Workshop; 2013 7–8 May; Helsinki, Finland (ECHA-14-R-13-EN). European Chemicals Bureau.
Google Scholar
European Commission (EC). (2004). European Union system for the evaluation of substances 2.0 (EUSES) (RIVM Report 601900005). Prepared for the European Chemicals Bureau by the National Institute of Public Health and the Environment.
Google Scholar
European Commission (EC). (2011). Nickel EQS dossier. Prepared by the sub-group on review of the priority substances list (under working group E of the common implementation strategy for the Water Framework Directive).
Google Scholar
European Union. (2013). Directive 2013/39/EU of the European Parliament and of the Council. OJL, 226, 1–17.
Google Scholar
Esbaugh, A. J., Brix, K. V., Mager, E. M., & Grosell, M. (2011). Multi-linear regression models predict the effects of water chemistry on acute lead toxicity to Ceriodaphnia dubia and Pimephales promelas. Comparative Biochemistry and Physiology Part C: Toxicology and Pharmacology, 154, 137–145.
10.1016/j.cbpc.2011.04.006
CAS PubMed Web of Science® Google Scholar
Esbaugh, A. J., Brix, K. V., Mager, E. M., De Schamphelaere, K. A. C., & Grosell, M. (2012). Multi-linear regression analysis, preliminary biotic ligand modeling, and cross species comparison of the effects of water chemistry on chronic lead toxicity in invertebrates. Comparative Biochemistry and Physiology. C: Comparative Pharmacology and Toxicology, 155, 423–431.
10.1016/j.cbpc.2011.11.005
CAS PubMed Web of Science® Google Scholar
Fairbrother, A., Wentzel, R., Sappington, K., & Wood, W. (2007). Framework for metals risk assessment. Ecotoxicology and Environmental Safety, 68, 145–227.
10.1016/j.ecoenv.2007.03.015
CAS PubMed Web of Science® Google Scholar
Farley, K. J., Carbonaro, R. F., Fanelli, C. J., Costanzo, R., Rader, K. J., & Di Toro, D. M. (2011). TICKET-UWM: A coupled kinetic, equilibrium, and transport screening model for metals in lakes. Environmental Toxicology and Chemistry, 30, 1278–1287.
10.1002/etc.518
CAS PubMed Web of Science® Google Scholar
Farley, K. J., Carbonaro, R. F., Rader, K. J., Fanelli, C., Miglino, A. N. (2009) Model evaluations for sediment clean-up targets and TMDLs for metals. Presentation at the Fifth International Conference on Remediation of Contaminated Sediments, Jacksonville, FL, USA.
Google Scholar
Farley, K. J., & Meyer, J. S. (2015a). Metal Mixtures Modeling Evaluation Project: 2. Comparative evaluation of four modeling approaches. Environmental Toxicology and Chemistry, 34(4), 741–753.
10.1002/etc.2820
CAS PubMed Web of Science® Google Scholar
Farley, K. J., & Meyer, J. S. (2015b). Metal Mixtures Modeling Evaluation Project: 3. Lessons learned and steps forward. Environmental Toxicology and Chemistry, 34(4), 821–832.
10.1002/etc.2837
CAS PubMed Web of Science® Google Scholar
Fetters, K. J., Costello, D. M., Hammerschmidt, C. R., & Burton, Jr., G. A. (2016). Toxicological effects of short-term resuspension of metal-contaminated freshwater and marine sediments. Environmental Toxicology and Chemistry, 35(3), 676–686.
10.1002/etc.3225
CAS PubMed Web of Science® Google Scholar
Field, L. J., MacDonald, D. D., Norton, S. B., Ingersoll, C. G., Severn, C. G., Smorong, D., & Lindskoog, R. (2002). Predicting amphipod toxicity from sediment chemistry using logistic regression models. Environmental Toxicology and Chemistry, 21, 1993–2005.
10.1002/etc.5620210929
CAS PubMed Web of Science® Google Scholar
Field, L. J., MacDonald, D. D., Norton, S. B., Severn, C. G., & Ingersoll, C. G. (1999). Evaluating sediment chemistry and toxicity data using logistic regression modeling. Environmental Toxicology and Chemistry, 18, 1311–1322.
10.1002/etc.5620180634
CAS Web of Science® Google Scholar
Gächter, R. (1979). MELIMEX, an experimental heavy metal pollution study: Goals, experimental design and major findings. Schweizerische Zeitschriftfür Hydrologie, 41, 169–176.
Web of Science® Google Scholar
Gao, Y., Feng, J., & Zhu, L. (2015). Prediction of acute toxicity of cadmium and lead to zebrafish larvae by using a refined toxicokinetic–toxicodynamic model. Aquatic Toxicology, 169, 37–45.
10.1016/j.aquatox.2015.09.005
CAS PubMed Web of Science® Google Scholar
Garman, E. R., Meyer, J. S., Bergeron, C. M., Blewett, T. A., Clements, W. H., Elias, M. C., Farley, K. J., Gissi, F., & Ryan, A. C. (2020). Validation of bioavailability-based toxicity models for metals. Environmental Toxicology and Chemistry, 39, 101–117.
10.1002/etc.4563
CAS PubMed Web of Science® Google Scholar
Gillmore, M., Price, G., Golding, L., Stauber, J., Adams, M., Simpson, S., Smith, R., & Jolley, D. (2020). The diffusive gradients in thin films (DGT) technique predicts sediment nickel toxicity to the amphipod, Melita plumulosa. Environmental Toxicology and Chemistry, 40, 1266–1278. https://doi.org/10.1002/etc.4971
10.1002/etc.4971
Web of Science® Google Scholar
Grosell, M., Blanchard, J., Brix, K. V., & Gerdes, R. (2007). Physiology is pivotal for interactions bwtween salanity and acute copper toxicity to fish and invertebrates. Aquatic Toxicology, 84, 162–172.
10.1016/j.aquatox.2007.03.026
CAS PubMed Web of Science® Google Scholar
Guo, G., Yuan, T., Wang, W., Li, D., & Wang, J. (2011). Effect of aging on bioavailability of copper on the fluvo aquic soil. International Journal of Environmental Science and Technology, 8, 715–722.
10.1007/BF03326256
CAS Web of Science® Google Scholar
Hartford, A. J., Simpson, S. L., Humphrey, C. L., Parry, D. L., Kumar, A., Chandler, L., Stauber, J., & van Dam, R. A. (2022). Sediment spiking and equilibration procedures to achieve partitioning of uranium similar to contamination in tropical wetlands near a mine site. Environmental Pollution, 295, 118673.
10.1016/j.envpol.2021.118673
PubMed Web of Science® Google Scholar
Haughey, M. A., Anderson, M. A., Whitney, R. D., Taylor, W. D., & Losee, R. F. (2000). Forms and fate of Cu in a source drinking water reservoir following CuSo₄ treatment. Water Research, 34, 3440–3452.
10.1016/S0043-1354(00)00054-3
CAS Web of Science® Google Scholar
Hope, B., & Clarkson, J. R. (2014). A strategy for using weight of evidence methods in ecological risk assessments. Human and Ecological Risk Assessment, 20, 290–315.
10.1080/10807039.2013.781849
CAS Web of Science® Google Scholar
Hull, R. N., & Swanson, S. (2006). Sequential Analysis of Lines of Evidence - an advanced weight-of-evidence approach for ecological risk assessment. Integrated Environmental Assessment and Management, 2, 302–311.
10.1002/ieam.5630020401
PubMed Web of Science® Google Scholar
Huerta-Diaz, M. A., Carignan, R., & Tessier, A. (1993). Measurement of trace metals associated with acid volatile sulfides and pyrite in organic freshwater sediments. Environmental Science and Technology, 27, 2367–2372.
10.1021/es00048a009
CAS Web of Science® Google Scholar
Huerta-Diaz, M. A., Tessier, A., & Carignan, R. (1998). Geochemistry of trace metals associated with reduced sulfur in freshwater sediments. Applied Geochemistry, 13, 213–233.
10.1016/S0883-2927(97)00060-7
CAS Web of Science® Google Scholar
van Hullebusch, E., Chatenet, P., Deluchat, V., Chazal, P. M., Froissard, D., Botineau, M., Ghestem, A., & Baudu, M. (2003). Copper accumulation in a reservoir ecosystem following copper sulfate treatment (St. Germain les Belles, France). Water, Air, and Soil Pollution, 150, 3–22.
10.1023/A:1026148914108
Web of Science® Google Scholar
van Hullebusch, E., Chatenet, P., Deluchat, V., Chazal, P. M., Froissard, D., Lens, P. N. L., & Baudu, M. (2003). Fate and forms of Cu in a reservoir ecosystem following copper sulfate treatment (Saint Germain les Belles, France). Journal de Physique IV: Proceedings, 107, 1333–1336.
Google Scholar
van Hullebusch, E., Deluchat, V., Chazal, P. M., & Baudu, M. (2002). Environmental impact of two successive chemical treatments in a small shallow eu- trophied lake: Part II. Case of copper sulfate. Environmental Pollution, 120, 627–634.
10.1016/S0269-7491(02)00191-4
PubMed Web of Science® Google Scholar
Huntsman, P., Beaudoin, R., Rader, K. J., Carbonaro, R. F., Burton, Jr., G. A., Hudson, M., Baken, S., Garman, E., & Waeterschoot, H. (2019). Method development for determining the removal of metals from the water column under transformation/dissolution conditions for chronic hazard classification. Environmental Toxicology and Chemistry, 38, 2032–2042. https://doi.org/10.1002/etc.4471
10.1002/etc.4471
CAS PubMed Web of Science® Google Scholar
Hutchins, C. M., Teasdale, P. R., Lee, S. Y., & Simpson, S. L. (2007). Influence of sediment metal spiking procedures on copper bioavailability and toxicity in the estuarine bivalve Indoaustriella lamprelli. Environmental Toxicology and Chemistry, 28, 1885–1892.
10.1897/08-469.1
Web of Science® Google Scholar
Hyne, R. V., Pablo, F., Julli, M., & Markich, S. J. (2005). Influence of water chemistry on the acute toxicity of copper and zinc to the cladoceran Ceriodaphnia dubial. Environmental Toxicology and Chemistry, 24(7), 1667–1675.
10.1897/04-497R.1
CAS PubMed Web of Science® Google Scholar
Irving, H. M. N. H., & Rossotti, H. (1956). Some relationships among stabilities on metal complexes. Acta Chemica Scandinavica, 10, 72–93.
10.3891/acta.chem.scand.10-0072
CAS Web of Science® Google Scholar
Jones, R. P., Hassan, S. M., & Rodgers, Jr., J. H. (2008). Influence of contact duration on sediment-associated copper fractionation and bioavailability. Ecotoxicology and Environmental Safety, 71, 104–116.
10.1016/j.ecoenv.2007.09.004
CAS PubMed Web of Science® Google Scholar
Judd, N. L., Toll, J. E., McPeek, K., Baldwin, A., Bergquist, B., Tobiason, K., DeForest, D. K., & Santore, R. C. (2021). Collection and use of porewater data from bioassay studies for understanding exposure to bioavailable metals. Integrated Environmental Assessment and Management, 18(5), 1321–1234.
Web of Science® Google Scholar
Khan, F. R., Paul, K. B., Dybowska, A. D., Valsami-Jones, E., Lead, J. R., Stone, V., & Fernandes, T. F. (2015). Accumulation dynamics and acute toxicity of silver nanoparticles to Daphnia magna and Lumbriculus variegatus: Implications for metal modeling approaches. Environmental Science and Technology, 49, 4389–4397.
10.1021/es506124x
CAS PubMed Web of Science® Google Scholar
Kalnejais, L. H., Martin, W. R., & Bothner, M. H. (2010). The release of dissolved nutrients and metals from coastal sediments due to resuspension. Marine Chemistry, 121, 224–235.
10.1016/j.marchem.2010.05.002
CAS Web of Science® Google Scholar
Kalnejais, L. H., Martin, W. R., & Bothner, M. H. (2015). Porewater dynamics of silver, lead and copper in coastal sediments and implications for benthic metal fluxes. Science of the Total Environment, 517, 178–194.
10.1016/j.scitotenv.2015.02.011
CAS PubMed Web of Science® Google Scholar
Kalnejais, L. H., Martin, W. R., Signell, R. P., & Bothner, M. H. (2007). Role of sediment resuspension in the remobilization of particulate-phase metals from coastal sediments. Environmental Science and Technology, 41, 2282–2288.
10.1021/es061770z
CAS PubMed Web of Science® Google Scholar
Kwok, K. W., Bjorgesaeter, A., Leung, K. M., Lui, G. C. S., Gray, J. S., Shin, P. K., & Lam, P. K. (2008). Deriving site-specific sediment quality guidelines for Hong Kong marine environments using field-based species sensitivity distributions. Environmental Toxicology and Chemistry, 27, 226–234.
10.1897/07-078.1
CAS PubMed Web of Science® Google Scholar
Liao, C. M., Yun, R., & Chen, W. Y. (2011). Subcellular portioning links BLM-based toxicokinetics for assessing cadmium toxicity to rainbow trout. Environmental Toxicology, 26, 600–609.
10.1002/tox.20584
CAS PubMed Web of Science® Google Scholar
Liu, R., Zhao, D., & Barnett, M. (2006). Fate and transport of copper applied in channel catfish ponds. Water, Air, and Soil Pollution, 176, 139–162.
10.1007/s11270-006-9155-5
CAS Web of Science® Google Scholar
Long, E. R., & MacDonald, D. D. (1998). Recommended use of empirically derived sediment quality guidelines for marine and estuarine ecosystems. Human and Ecological Risk Assessment, 4, 1019–1039.
10.1080/10807039891284956
Web of Science® Google Scholar
Long, E. R., MacDonald, D. D., Smith, S. L., & Calder, F. D. (1995). Incidence of adverse biological effects within ranges of chemical concentrations in marine and estuarine sediments. Environmental Management, 19, 81–97.
10.1007/BF02472006
PubMed Web of Science® Google Scholar
Luoma, S. N., & Rainbow, P. S. (2005). Why is metal bioaccumulation so variable? Biodynamics as a unifying concept. Environmental Science and Technology, 39, 1921–1931.
10.1021/es048947e
CAS PubMed Web of Science® Google Scholar
Ma, Y. B., & Uren, N. C. (1998). Dehydration, diffusion and entrapment of Zn in bentonite. Clays and Clay Minerals, 46, 132–138.
10.1346/CCMN.1998.0460202
CAS Web of Science® Google Scholar
MacDonald, D. D., Carr, R. S., Calder, F. D., Long, E. R., & Ingersoll, C. G. (1996). Development and evaluation of sediment quality guidelines for Florida coastal waters. Ecotoxicology, 5, 253–278.
10.1007/BF00118995
CAS PubMed Web of Science® Google Scholar
MacDonald, D. D., Ingersoll, C. G., & Berger, T. (2000). Development and evaluation of consensus-based sediment quality guidelines for freshwater ecosystems. Archives of Environmental Contamination and Toxicology, 39, 20–31.
10.1007/s002440010075
CAS PubMed Web of Science® Google Scholar
MacRae, R. K. (1994). The copper binding affinity of rainbow trout (Oncorhynchus mykiss) and brook trout (Salvelinus fontinalis) gills [MSc thesis, Department of Zoology and Physiology, University of Wyoming].
Google Scholar
Markich, S. J., Batley, G. E., Stauber, J. L., Rogers, N. J., Apte, S. C., Hyne, R. V., Bowles, K. C., Wilde, K. L., & Creighton, N. M. (2005). Hardness corrections for copper are inappropriate for protecting sensitive freshwater biota. Chemosphere, 60, 1–8.
10.1016/j.chemosphere.2004.12.005
CAS PubMed Web of Science® Google Scholar
McGeer, J. C., Brix, K. V., DeForest, D. K., Brigham, S. I., Skeaff, J. M., Adams, W. J., & Green, A. (2003). Bioconcentration factor for the hazard identification of metals in the aquatic environment: A flawed criterion? Environmental Toxicology and Chemistry, 22(5), 1017–1037.
10.1002/etc.5620220509
CAS PubMed Web of Science® Google Scholar
Mebane, C. A., Chowdhury, J. M., De Schamphelaere, K. A. C., Lofts, S., Paquin, P. R., Santore, R. C., & Wood, C. M. (2020). Metal bioavailability models: Current status, lessons learned, considerations for regulatory use, and the path forward. Environmental Toxicology and Chemistry, 39(1), 118–130.
10.1002/etc.4560
PubMed Web of Science® Google Scholar
Mebane, C. A., Dillon, F. S., & Hennessy, D. P. (2012). Acute toxicity of cadmiu, lead, zinc and their mixtures to stream-resident fish and invertebrates. Environmental Toxicology and Chemistry, 3(6), 1334–1348.
10.1002/etc.1820
Google Scholar
Mebane, C. A., Eakins, R. J., Fraser, B. G., & Adams, W. J. (2015). Recovery of a mining-damaged stream ecosystem. Elementa Science of the Anthropocene, 3, 42. https://doi.org/10.12952/journal.elementa.000042
10.12952/journal.elementa.000042
Web of Science® Google Scholar
Mebane, C. A., Hennessy, D. P., & Dillon, F. S. (2008). Developing acute-to chronic toxicity ratios for lead, cadmium, and zinc using rainbow trout, a mayfly, and a midge. Water, Air, and Soil Pollution, 188, 41–66.
10.1007/s11270-007-9524-8
CAS Web of Science® Google Scholar
Menzie, C. A., Zicardi, L. M., Lowney, Y. W., Fairbrother, A., Scott, S. S., Tsuji, J. S., Hamai, D., Proctor, D., Henry, E., Steave, H. S., Kierski, M. W., Mcardle, M. E., & Yost, L. J. (2009). Importance of considering the framework principles in risk assessment for metals. Environmental Science and Technology, 43, 8478–8482.
10.1021/es9006405
CAS PubMed Web of Science® Google Scholar
Meyer, J., & Adams, W. (2010). Relationship between biotic ligand model-based water quality criteria and avoidance and olfactory responses to copper by fish. Environmental Toxicology and Chemistry, 29(9), 2096–2103.
10.1002/etc.254
CAS PubMed Web of Science® Google Scholar
Meyer, J., & DeForest, D. K. (2018). Protectiveness of Cu water quality criteria against impairment of behavior and chemo/mechanosensory responses: An update. Environmental Toxicology and Chemistry, 37(5), 1260–1279.
10.1002/etc.4096
CAS PubMed Web of Science® Google Scholar
Meyer, J. S., Clearwater, S. J., Doser, T. A., Rogaczewski, M. J., & Hansen, J. A. (2007). Effects of water chemistry on bioavailability and toxicity of waterborne cadmium, copper, nickel, lead, and zinc to freshwater organisms (p. 352). Society of Environmental Toxicology and Chemistry (SETAC).
Google Scholar
Meyer, J. S., Farley, K. J., & Garman, E. R (2015). Metal Mixtures Modeling Evaluation Project: 1. Technical background. Environmental Toxicology and Chemistry, 34(4), 726–740.
10.1002/etc.2792
CAS PubMed Web of Science® Google Scholar
Moffett, J. W., & DuPont, C. (2007). Cu complexation by organic ligands in the sub-arctic NW Pacific and Bering Sea. Deep-Sea Research I, 54, 586–595.
10.1016/j.dsr.2006.12.013
CAS Web of Science® Google Scholar
Morse, J. W., & Luther, G. W. (1999). Chemical influences on trace metal-sulfide interactions in anoxic sediments. Geochimica et Cosmochimica Acta, 63, 3373–3378.
10.1016/S0016-7037(99)00258-6
CAS Web of Science® Google Scholar
Mutch Associates. (2012). Metal Classification using a unit world model (TICKET-UWM). Prepared for the Aluminium REACH Consortium, European Aluminium Association, Brussels, Belgium.
Google Scholar
Naddy, R. B., Gorsuch, J. W., Rehner, A. B., McNermey, G. R., Bell, R. A., & Kramer, J. R. (2018). Chronic toxicity of silver nitrate to Ceriodaphnia dubia and Daphnia magna, and potential mitigating factors. Aquatic Toxicology, 84(1), 1–10.
10.1016/j.aquatox.2007.03.022
Google Scholar
Nakhone, N. L., & Young, S. D. (1993). The significance of (radio-) labile cadmium pools in soil. Environmental Pollution, 82(1), 73–77.
10.1016/0269-7491(93)90164-J
CAS PubMed Web of Science® Google Scholar
Niyogi, S., Kent, R., & Wood, C. M. (2008). Effects of water chemistry variables on gill binding and acute toxicity of cadmium in rainbow trout (Oncorhynchus mykiss): A biotic ligand model (BLM) approach. Comparative Biochemistry and Physiology Part C: Toxicology & Pharmacology, 148(4), 305–314. https://doi.org/10.1016/j.cbpc.2008.05.015
10.1016/j.cbpc.2008.05.015
CAS PubMed Web of Science® Google Scholar
Organisation for Economic Co-operation and Development. (2001). Guidance document on transformation/dissolution of metals and metal compounds in aqueous media (Series on Testing and Assessment No. 29. ENV/JM/MON 9).
Google Scholar
Paquin, P. R., Gorsuch, J. W., Apte, S., Batley, G. E., Bowles, K. C., Campbell, P. G. C., Delos, C. G., Di Toro, D. M., Dwyer, R. L., Galvez, F., Gensemer, R. W., Goss, G. G., Hogstrand, C., Janssen, C. R., McGeer, J. C., Naddy, R. B., Playle, R. C., Santore, R. C., Schneider, U., … Wu, K. B. (2002). The biotic ligand model: A historical overview. Comparative Biochemistry and Physiology. Toxicology & Pharmacology: CBP, 133, 3–35.
10.1016/S1532-0456(02)00112-6
PubMed Web of Science® Google Scholar
Peng, J. F., Song, Y. H., Yuan, P., Cui, X. Y., & Qiu, G. L. (2009). The remediation of heavy metals contaminated sediment. Journal of Hazardous Materials, 161, 633–640.
10.1016/j.jhazmat.2008.04.061
CAS PubMed Web of Science® Google Scholar
Pereira, C. M. S., Deruytter, D., Blust, R., & De Schamphelaere, K. A. C. (2017). Effect of temperature on chronic toxicity of copper, zinc, and nickel to Daphnia magna. Environmental Toxicology and Chemistry, 36, 1909–1916. https://doi.org/10.1002/etc.3714
10.1002/etc.3714
CAS PubMed Web of Science® Google Scholar
Peters, A., Lofts, S., Merrington, G., Brown, B., Stubblefield, W., & Harlow, K. (2011). Development of biotic ligand models for chronic manganese toxicity to fish, invertebrates, and algae. Environmental Toxicology and Chemistry, 30(11), 2407–2415.
10.1002/etc.643
CAS PubMed Web of Science® Google Scholar
Peters, A., Merrington, G., Delbeke, K., & de Schamphelaere, K. A. C. (2011). Regulatory consideration of bioavailability for metals: Simplification of input parameters for the chronic copper biotic ligand model. Integrated Environmental Assessment and Management, 7, 437–444.
10.1002/ieam.159
CAS PubMed Google Scholar
Rader, K. J., Carbonaro, R. F., van Hullebusch, E. D., Baken, S., & Delbeke, K. (2019). The fate of copper added to surface water: Field, laboratory, and modeling studies. Environmental Toxicology and Chemistry, 38, 1386–1399. https://doi.org/10.1002/etc.4440
10.1002/etc.4440
CAS PubMed Web of Science® Google Scholar
Rainbow, P. S., & Luoma, S. N. (2011). Metal toxicity, uptake and bioaccumulation in aquatic invertebrates – Modelling zinc in crustaceans. Aquatic Toxicology, 105(3–4), 455–465.
10.1016/j.aquatox.2011.08.001
CAS PubMed Web of Science® Google Scholar
Rainbow, P. S., Smith, B. D., & Luoma, S. N. (2009). Biodynamic modelling and the prediction of Ag, Cd and Zn accumulation from solution and sediment by the polychaete Nereis diversicolor. Marine Ecology Progress Series, 390, 145–155.
10.3354/meps08218
CAS Web of Science® Google Scholar
Rickard, D. (2012). Sulfidic sediments and sedimentary rocks. Elsevier.
Google Scholar
Rodriguez, P. H., Adams, W., & Delbeke, K. (2007). Methodology for aquatic hazard classification for metal massive forms: The copper case. In D. Rodier & W. Adams (Eds.), Sustainable Development, HS&E, and Recycling, Proceedings of the Sixth International Copper-Cobre Conference, Volume VI, Toronto, Ontario. Canadian Mining, Metallurgy and Petroleum. www.metsoc.org
Google Scholar
Roman, Y. E., De Schamphelaere, K. A. C., Nguyen, L. T. H., & Janssen, C. R. (2005). Chronic toxicity of copper to five benthic species in laboratory-formulated sediment: Sensitivity comparison and preliminary risk assessment. Science of the Total Environment, 387, 128–140.
10.1016/j.scitotenv.2007.06.023
Web of Science® Google Scholar
Rossi, N., & Jamet, J. M. (2008). In situ heavy metals (copper, lead and cadmium) in different plankton compartments and suspended particulate matter in two coupled Mediterranean coastal ecosystems (Toulon Bay, France). Marine Pollution Bulletin, 56(11), 1862–1870. https://doi.org/10.1016/j.marpolbul.2008.07.018
10.1016/j.marpolbul.2008.07.018
CAS PubMed Web of Science® Google Scholar
Santore, R., Kroglund, F., Teien, H.-C., Ryan, A., Rodriguez, R., Stubblefield, W., Adams, W., & Nordheim, E. (2018). Development and application of a biotic ligand model for predicting the toxicity of dissolved and precipitated aluminum. Environmental Toxicology and Chemistry, 37(1), 70–79.
10.1002/etc.4020
CAS PubMed Web of Science® Google Scholar
Santore, R. C., Croteau, K., Ryan, A. C., Schlekat, C., Middleton, E., & Garman, E. (2021). A review of water quality factors that affect nickel bioavailability to aquatic organisms: Refinement of the biotic ligand model for nickel in acute and chronic exposures. Environmental Toxicology and Chemistry, 40(8), 2121–2134. https://doi.org/10.1002/etc.5109
10.1002/etc.5109
CAS PubMed Web of Science® Google Scholar
Santore, R. C., & Ryan, A. C. (2015). Development and application of a multimetal multibiotic ligand model for assessing aquatic toxicity of metal mixtures. Environmental Toxicology and Chemistry, 34(4), 777–787.
10.1002/etc.2869
CAS PubMed Web of Science® Google Scholar
Santore, R. C., Toll, J. E., DeForest, D. K., Croteau, K., Shaw, A., Bergquist, B., McPeek, K., Tobiason, K., & Judd, N. L. (2022). Refining our understanding of metal bioavailability in sediments using information from porewater: Application of a multi-metal BLM as an extension of the equilibrium partitioning sediment benchmarks. Integrated Environmental Assessment and Management, 18(5), 1321–1234.
10.1002/ieam.4572
Web of Science® Google Scholar
Schäfers, C. (2001). Community level study with copper in aquatic micro-cosms. Fraunhofer Institute for Molecular Biology and Applied Ecology (IME).
Google Scholar
Schindler, D. W., Wagemann, R., Cook, R. B., Ruszcynki, T., & Prokopowich, J. (1980). Experimental acidification of Lake 223, experimental lakes area: Background data and the first three years of acidification. Canadian journal of Fisheries and Aquatic Sciences, 37(3), 12–24. https://doi.org/10.1139/f80-048
10.1139/f80-048
Web of Science® Google Scholar
Schlekat, C. E., Garman, E. R., Vangheluwe, M. L. U., & Burton, G. A. (2015). Development of a bioavailability-based risk assessment approach for nickel in freshwater sediments. Integrated Environmental Assessment and Management, 12(4), 735–746.
10.1002/ieam.1720
Web of Science® Google Scholar
Schlekat, C., Stubblefield, W., & Gallagher, K. (2020). State of the science on metal bioavailability modeling: Introduction to the outcome of a Society of Environmental Toxicology and Chemistry Technical Workshop. Environmental Toxicology and Chemistry, 39, 42–47.
10.1002/etc.4561
CAS PubMed Web of Science® Google Scholar
Schwarzenbach, R. P., Gschwend, P. M., & Imboden, D. M. (1993). Environmental organic chemistry. Wiley-Interscience.
Google Scholar
Simpson, S. L., Angel, B. M., & Jolley, D. F. (2004). Metal equilibration in laboratory-contaminated (spiked) sediments used for the development of whole-sediment toxicity tests. Chemosphere, 54, 597–609.
10.1016/j.chemosphere.2003.08.007
CAS PubMed Web of Science® Google Scholar
Simpson, S. L., & Batley, G. E. (2003). Disturbances to metal partitioning during toxicity testing of iron (II)-rich estuarine pore waters and whole sediments. Environmental Toxicology and Chemistry, 22(2), 424–432.
10.1002/etc.5620220225
CAS PubMed Web of Science® Google Scholar
Simpson, S. L., & Batley, G. E. (2016). Sediment quality assessment: A practical guide. CSIRO Publishing.
10.1071/9781486303854
Google Scholar
Simpson, S. L., Batley, G. E., Hamilton, I. L., & Spadaro, D. L. (2011). Guidelines for copper in sediments with varying properties. Chemosphere, 85, 1487–1495.
10.1016/j.chemosphere.2011.08.044
CAS PubMed Web of Science® Google Scholar
Simpson, S. L., Ward, D., Strom, D., & Jolley, D. F. (2012). Oxidation of acid-volatile sulfide in surface sediments increases the release and toxicity of copper to the benthic amphipod Melita plumulosa. Chemosphere, 88, 953–961.
10.1016/j.chemosphere.2012.03.026
CAS PubMed Web of Science® Google Scholar
Skeaff, J., & King, P. (1997). Development of a protocol for measuring the rate and extent of transformations of metals and sparingly soluble metal compounds in aqueous media. Phase I, tasks 3 and 4: Study of pH and of particle size/surface area (Division Report 97-71(CR)). Mining and Mineral Sciences Laboratories, CAN- MET, Natural Resources Canada.
Google Scholar
Skeaff, J., Delbeke, K., Van Assche, F., & Conard, B. (2000). A critical surface area concept for acute hazard classification of relatively insoluble metal-containing powders in aquatic environments. Environmental Toxicology and Chemistry, 19, 1681–1691.
10.1002/etc.5620190627
CAS Web of Science® Google Scholar
Smith, D. S., Bell, R. A., & Kramer, J. R. (2002). Metal speciation in natural waters with emphasis on reduced sulfur groups as strong metal binding sites. Comparative Biochemistry and Physiology. Toxicology & Pharmacology: CBP, 133, 65–74.
10.1016/S1532-0456(02)00108-4
PubMed Web of Science® Google Scholar
Smolders, E., Oorts, K., Van Sprang, P., Schoeters, I., Janssen, C. R., McGrath, S. P., & McLaughlin, M. J. (2009). Toxicity of trace metals in soil as affected by soil type and aging after contamination: Using calibrated bioavailability models to set ecological soil standards. Environmental Toxicology and Chemistry, 28(8), 1633–1642.
10.1897/08-592.1
CAS PubMed Web of Science® Google Scholar
Smolyakov, B. S., Ryzhikh, A. P., Bortnikova, S. B., Saeva, O. P., & Chernova, N. Y. (2010). Behavior of metals (Cu, Zn and Cd) in the initial stage of water system contamination: Effect of pH and suspended particles. Applied Geochemistry, 25, 1153–1161.
10.1016/j.apgeochem.2010.05.001
CAS Web of Science® Google Scholar
Smolyakov, B. S., Ryzhikh, A. P., & Romanov, R. E. (2010). The fate of Cu, Zn, and Cd in the initial stage of water system contamination: The effect of phyto-plankton activity. Journal of Hazardous Materials, 184, 819–825.
10.1016/j.jhazmat.2010.08.115
CAS PubMed Web of Science® Google Scholar
Stewart, A. R., Luoma, S. N., Schlekat, S. C., Doblin, M. A., & Hieb, K. A. (2004). Food web pathway determines selenium biomagnification in aquatic organisms. Environmental Science and Technology, 38, 4519–4526.
10.1021/es0499647
CAS PubMed Web of Science® Google Scholar
Stubblefield, W. A., Van Genderen, E., Cardwell, A. S., Heijerick, D. G., Janssen, C. R., & DevSchamphelaere, K. A. C. (2020). Acute and chronic toxicity of cobalt to freshwater organisms: Using a species sensitivity distribution approach to establish international water quality standards. Environmental Science and Technology, 39(4), 799–811.
10.1002/etc.4662
CAS Google Scholar
Sutherland, T. F., Petersen, S. A., Levings, C. D., & Martin, A. J. (2007). Distinguishing between natural and aquaculture-derived sediment concentrations of heavy metals in the Broughton Archipelago, British Columbia. Marine Pollution Bulletin, 54, 1451–1460.
10.1016/j.marpolbul.2007.05.010
CAS PubMed Web of Science® Google Scholar
Stumm, W., & Morgan, J. J. (1996). Aquatic chemistry: Chemical equilibria and rates in natural waters ( 3rd ed.). John Wiley & Sons.
Google Scholar
Tipping, E., & Hurley, M. A. (2002). A unifying model of cation binding by humic substances. Geochimica et Cosmochimica Acta, 56(10), 3627–3641.
10.1016/0016-7037(92)90158-F
Google Scholar
Di Toro, D. M., Allen, H. E., Bergman, H. L., Meyer, J. S., Paquin, P. R., & Santore, R. C. (2001). Biotic ligand model of the acute toxicity of metals. 1. Technical basis. Environmental Toxicology and Chemistry, 20, 2383–2396.
10.1002/etc.5620201034
CAS PubMed Web of Science® Google Scholar
Di Toro, D. M., Kavvadas, C. D., Mathew, R., Paquin, P. R., & Winfield, R. P. (2001). The persistence and availability of metals in aquatic environments. International Council on Metals and the Environment.
Google Scholar
Di Toro, D. M., McGrath, J. A., Hansen, D. J., Berry, W. J., Paquin, P. R., Rooni, M., Kuen, B. W., & Santore, R. C. (2005). Predicting sediment metal toxicity using a sediment biotic ligand model: Methodology and initial application. Environmental Toxicology and Chemistry, 24(10), 2410–2427.
10.1897/04-413R.1
CAS PubMed Web of Science® Google Scholar
Trivedi, P., & Axe, L. (2000). Modeling Cd and Zn sorption to hydrous metal oxides. Environmental Science and Technology, 34, 2215–2223.
10.1021/es991110c
CAS Web of Science® Google Scholar
Urien, U., Uher, E., Billoir, O., Geffard, L. C., Fechner, L., & Lebrun, J. D. (2015). A biodynamic model predicting water-borne lead bioaccumulation in Gammarus pules: Influence of water chemistry and in situ validation. Environmental Pollution, 203, 22–30.
10.1016/j.envpol.2015.03.045
CAS PubMed Web of Science® Google Scholar
United Nations (UN). (2005). The globally harmonized system of classification and labelling of chemicals (ST/SG/AC.10/30/Rev. 1). Retrieved February 14, 2007, from: www.unece.org/trans/danger/publi/ghs/ghs_rev01/01files_e.html
Google Scholar
USEPA. (1985). Guidelines for deriving numerical national water quality criteria for the protection of aquatic organisms and their uses (PB85-227049). US Environmental Protection Agency, National Technical Information Service.
Google Scholar
USEPA. (2007a). Framework for metals risk assessment (EPA 120/R-07/001). WWW.EPA.gov.osa
Google Scholar
USEPA. (2007b). Aquatic life ambient freshwater quality criteria—Copper (EPA-822-R-07-001).
Google Scholar
USEPA. (2016). Aquatic life ambient water quality criteria - Cadmium (EPA-820-R-16-002). EPA Office of Water, Washington, DC.
Google Scholar
USEPA. (2018). Final aquatic life ambient water quality criteria for aluminum 2018 (EPA-822-R-18-001).
Google Scholar
USEPA. (2022). Metals Cooperative Research and Development Agreement (CRADA) phase I report: Development of an overarching bioavailability modeling approach to support US EPA's Aquatic Life Water Quality Criteria for Metals (EPA-822-R-22-001). EPA Office of Water.
Google Scholar
Van Campenhout, K., Bervoets, L., Redeker, E. S., & Blust, R. (2009). A kinetic model for the relative contribution of waterborne and dietary cadmium and zinc in the common carp (Cyprinus carpio). Environmental Toxicology and Chemistry, 28, 209–219.
10.1897/08-136.1
CAS PubMed Web of Science® Google Scholar
Vandegehuchte, M., Roman, Y., Nguyen, L., Janssen, C., & De Schamphelaere, K. (2007). Toxicological availability of nickel to the benthic oligochaete Lumbriculus variegatus. Environment International, 33, 736–742.
10.1016/j.envint.2007.02.006
CAS PubMed Web of Science® Google Scholar
Van Genderen, E., Adams, W., Dwyer, R., Garman, E., & Gorsuch, J. (2015). Modeling and interpreting biological effects of mixtures in the environment: Introduction to the metal mixture modeling evaluation project. Environmental Toxicology and Chemistry, 34(4), 721–725.
10.1002/etc.2750
CAS PubMed Web of Science® Google Scholar
Van Genderen, E., Stauber, J. L., Delos, C., Eignor, D., Gensemer, R. W., McGeer, J., Merrington, G., & Whitehouse, P. (2020). Derivation and application of thresholds for metals using bioavailability-based approaches. Environmental Toxicology and Chemistry, 39, 118–130.
10.1002/etc.4559
CAS PubMed Web of Science® Google Scholar
Vangheluwe, M. L. U., Verdonck, F. A. M., Besser, J. M., Brumbaugh, W. G., Ingersoll, C. G., Schlekat, C. E., & Garman, E. R. (2013). Improving sediment quality guidelines for nickel: Development and application of predictive bioavailability models to assess chronic toxicity of nickel in freshwater sediments. Environmental Toxicology and Chemistry, 32, 2507–2519.
10.1002/etc.2373
CAS PubMed Web of Science® Google Scholar
Vercaigne, I., Heijerick, D., & Vangheluwe, M. (2013). Unit world model—Overview of available data on relevant environmental parameters. ARCHE Company report.
Google Scholar
Vijver, M. G., Elliott, E. G., Peijnenburg, W. J. G. M., & De Snoo, G. R. (2011). Response predictions for organisms water-exposed to metal mixtures: A meta-analysis. Environmental Toxicology and Chemistry, 30, 1482–1487.
10.1002/etc.499
CAS PubMed Web of Science® Google Scholar
Wallace, W. G., & Lopez, G. R. (1997). Bioavailability of biologically sequestered cadmium and the implications of metal detoxification. Marine Ecology Progress Series, 147, 149–157.
10.3354/meps147149
CAS Web of Science® Google Scholar
Wang, W. X. (2012). Biodynamic understanding of mercury accumulation in marine and freshwater fish. Advances in Environmental Sciences, 1(1), 15–35.
CAS Google Scholar
Water Framework Directive—UK Technical Advisory Group. (2014). Metal bioavailability assessment tool.
Google Scholar
Welsh, P., Lipton, J., Chapman, G., & Podrabsky, T. L. (2000). Relative importance of calcium and magnesium in hardness-based modification of copper toxicity. Environmental Toxicology and Chemistry, 19, 1624–1631.
10.1002/etc.5620190620
CAS Web of Science® Google Scholar
Xie, M., Alsine, M. A., Yuen, J., Packman, A., & Gaillard, J. F. (2019). Effects of resuspension on the mobility and chemical speciation of zinc in contaminated sediments. Journal of Hazardous Materials, 365, 300–308.
10.1016/j.jhazmat.2018.10.043
Google Scholar
Xie, M., Brooke, A. J., Da Silva-Cadoux, C., Fetters, K. J., Burton, Jr., G. A., Gaillard, J.-F., & Packman, A. I. (2015). Coupled effects of hydrodynamics and biogeochemistry on Zn mobility and speciation in highly dynamic contaminated sediments. Environmental Science and Technology, 49, 5346–5353.
10.1021/acs.est.5b00416
CAS PubMed Web of Science® Google Scholar
Zhong, H., Kraemer, L., & Evans, D. (2012). Effects of aging on the digestive solubilization of Cu from sediments. Environmental Pollution, 164, 195–203.
10.1016/j.envpol.2012.01.045
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume20, Issue4

July 2024

Pages 924-951

Recommended updates to the USEPA Framework for Metals Risk Assessment: Aquatic ecosystems

Abstract