1 Introduction

Solid-state thermoelectric coolers [1] (TEC), which operate on the Peltier effect, can be used in the fields of temperature stabilizing of 5G optical communication chips [2-7], the cooling of infrared detection chips [2, 8], and so on. The cooling power and the maximum temperature difference (ΔT_max) between the hot and cold sides of TECs are significantly dependent on the device configuration and the figure of merit, zT, of constituted thermoelectric materials. The zT value is estimated by the formula zT = S²T/ρ(κ_E + κ_L), where S is the Seebeck coefficient, T is the absolute temperature, ρ is the electrical resistivity, and κ_E and κ_L represent the electronic and lattice components of the thermal conductivity, respectively. For thermoelectric cooling applications, high thermoelectric performance near or below room temperature is highly desired.

Basically, the thermoelectric figure of merit is a function solely of the parameter β, which is proportional to ~T(μ/κ_L)(m*/m_e)^3/2 [9, 10], where μ is carrier mobility, m* is the density of state effective mass. Seeking high carrier mobility and low lattice thermal conductivity is necessary for achieving high thermoelectric cooling performance. This is evidenced in classical low temperature materials which have intrinsic high mobility along a specific direction due to anisotropic band structure and low lattice thermal conductivity in another direction like Bi₂Te₃ [11, 12], Bi_1−xSb_x [13], and Mg₃(Bi,Sb)₂ alloys [14, 15]. The lattice thermal conductivity near room temperature can be minimized toward the theoretical limit by various strategies, including the introduction of various defects [16-19]. However, the mobility is inevitably seriously deteriorated especially in low temperature range due to the unexpected scatter mechanism such as ionized centers [20] or grain boundaries [21, 22], which makes it troublesome to get a high zT value in the low temperature range.

MgAgSb [23-26] is considered as a promising candidate for thermoelectric cooling due to superior p-type thermoelectric performance and abundant element availability on Earth. It crystallizes in a rocksalt-type structure above 693 K and transforms into tetragonal α-phase below 563 K after twice phase transitions [27]. The distortion of Mg-Sb sublattice [28, 29] and loosely bonded [30] Ag⁺ makes α-MgAgSb own intrinsically low and greatly suppressed lattice thermal conductivity in the low temperature range. Besides, α-MgAgSb displays a high power factor ~20 W/cm-K [23, 31] near room temperature, which is comparable to or superior to some traditionally high-performance thermoelectrics, such as Mg₃(Bi,Sb)₂ [32], IV–VI compounds [33-36] due to the highly degenerate band structure with N_v ~ 8 [37]. All the above make α-MgAgSb one of the top candidates for future thermoelectric cooling. Nevertheless, due to the high defects concentration in the matrix, the carriers are greatly scattered at low temperatures, and previous works like Li [38], Na [39], Ca [40], Yb [41] doping at Mg site, Pb, Sn, Bi [40] doping at Sb site [42], Cu [42] at the Ag site all lead to decrease of carrier mobility, making it hard to optimize selective scattering of carriers and phonons at low temperature.

Noted that the intrinsic defects can be adjusted and is an effective way to manipulate the transport of carriers and phonons by changing the chemical bond circumstances of the lattice, as happened in PbSe [43], GeTe [9], PbTe [44], and Cu₃SbSe₄ [45]. Previous DFT calculations have found that among all the intrinsic defects in α-MgAgSb, Mg-Ag anti-sites have the lowest formation energy [46], apart from Ag vacancies, but rare works have concentrated on the manipulation of such defects, especially for thermoelectric cooling. As Mg is easy to evaporate, the low formation energy of Mg-Ag anti-site defect would make Ag atoms occupy Mg sites in the matrix, thus reducing the Ag precipitation. This would greatly weaken the scattering of carriers by the Ag secondary phase and increase the carrier mobility. Therefore, promoting the formation of Mg-Ag anti-sites is beneficial for improving the thermoelectric properties of α-MgAgSb in the low-temperature range.

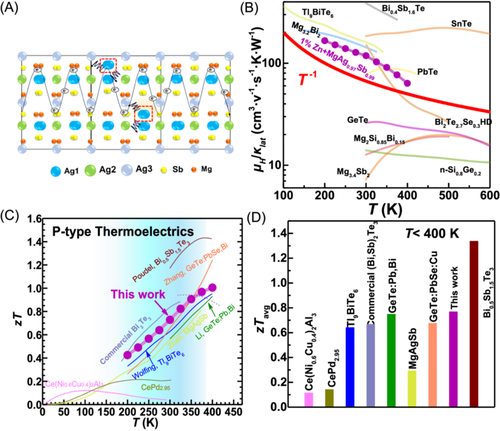
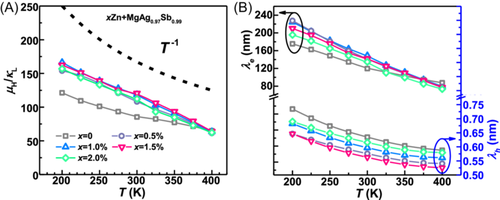
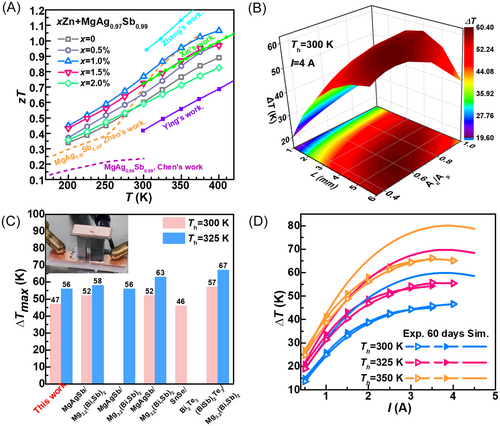
Besides, Zn doping is introduced for carrier concentration reduction, and the DFT calculation is carried out for the influence of Mg-Ag anti-site defects formation. It is found that Zn doping would significantly decrease the formation energy and promote the formation of Mg-Ag anti-site. This leads to an obvious increase in sample purity and carrier mobility of the samples. Besides, in the experiment, we found that the high concentration of defects forms a staggered coherent nanostructure that retains the same lattice as the intrinsic α-MgAgSb; thus, the transport tunnel of the original crystal lattice is scarcely affected. Therefore, the temperature-dependent Hall carrier mobility still follows the trend of T^−1.5 when the temperature is down to ~200 K. Meanwhile, the fluctuation of lattice atom arrangement leads to large strains between the crystals and greatly scatter phonons, resulting in different scattering mechanism for carriers and phonon in the matrix, as schematically illustrated in Figure 1A. The suppression of lattice thermal conductivity and undepressed carrier mobility makes the ratio of μ_H/κ_L follows the temperature dependence of T⁻¹ as shown in Figure 1B, indicating distinctive scattering mechanism for carriers and phonons in α-MgAgSb between 200 and 400 K. Due to the separately scattering of carriers and phonons, a high zT value of ~0.45 at 200 K, and an average figure of merit ~0.75 between 200 and 400 K is achieved for 1% Zn-doped α-MgAgSb in this study, which displays a significant advantage, especially between 200 and 300 K (Figure 1C,D) compared to other reported high-performance low-temperature thermoelectric materials. The unit couple thermoelectric device α-MgAgSb/Bi₂Te₃ exhibits a temperature difference of 46 K at 300 K and 56 K at 325 K, indicating α-MgAgSb is a promising thermoelectric material for thermoelectric cooling applications.

2 Results and Discussion

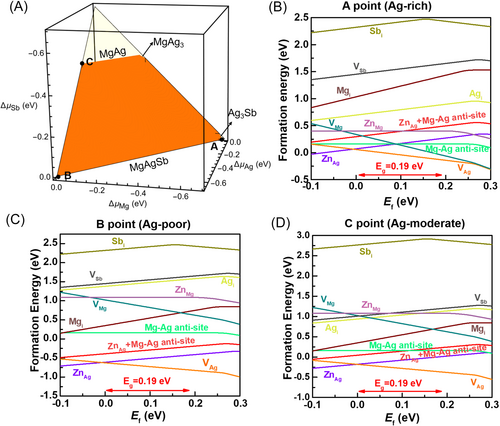
In this study, the samples are synthesized by a two-step preparation process involving melting, ball milling, and annealing to ensure the stable state of all samples. The detailed procedures are outlined in the experiment part of the Supporting Information. Figure S1 shows the room-temperature powder XRD patterns and the lattice parameters of samples xZn + MgAg_0.97Sb_0.99 (0 ≤ x ≤ 0.03). The matrix is identified as α-MgAgSb until the emergence of Sb and Ag₃Sb second phases, which occurs when Zn content increases to 2%. The precipitation of these second phases is attributed to the narrow composition range. According to the formation enthalpies of α-MgAgSb and other possible second phases, the chemical potential area of α-MgAgSb is formed marked with orange in the three-dimensional (µ_Ag, µ_Mg, µ_Sb) diagram (Figure 2A), and µ_Ag, µ_Mg, µ_Sb represent the chemical potential for Ag, Mg, and Sb, respectively. The three critical points A, B, and C represent Ag-rich, Ag-poor, and Ag-moderate conditions, where Ag₃Sb, Mg₃Sb₂, and MgAg second phase appears when the elemental chemical potential exceeds these points, respectively. Details of the calculation can be found in the Supporting Information. On the other hand, as Ag atoms fill in the distorted hexahedrons constructed by Mg-Sb sublattice, the weak Mg-Sb bonds and relatively small radius of hexahedrons make larger size Ag unstable [54] and easy to veer off from the original site. The Ag vacancies in the lattice contribute to p-type carrier concentration and lead to the formation of Ag-rich second phases within the matrix, as observed by SEM images (Figure S2A). This is consistent with the result of DFT calculation, which indicates that, for all Ag-rich (Figure 2B), Ag-poor (Figure 2C), and Ag-moderate (Figure 2D) conditions, Ag vacancies (V_Ag) have the lowest formation energy (calculation details are provided in the Supporting Information). The labels V_Ag, V_Mg, V_Sb in Figure 2B–D represent the formation energies of Ag vacancy, Mg vacancy, and Sb vacancy; Ag_i, Mg_i, Sb_i represent the formation energies of intestinal Ag, intestinal Mg and intestinal Sb; Mg-Ag anti-site represent the formation energies of Mg-Ag anti-site; Zn_Mg and Zn_Ag represent the formation energies of Zn taking the Ag site and Mg site, respectively. This is also identical to the previous result [46]. Furthermore, according to the calculations for aforementioned conditions, Mg-Ag anti-site defects possess the second-lowest formation energy, closely behind V_Ag. As Mg atoms are easily volatilized, it is reasonable to hypothesize that the unstable Ag atoms easily occupy the left Mg vacancy, and the original Mg-Ag-Sb lattice will become an Ag-Ag-Sb lattice. Notably, the intrinsic Ag-Mg anti-site point defects can also be effectively manipulated by Zn doping. It is found that for Ag-poor and Ag-moderate conditions, the formation energy of Mg-Ag anti-site is lowered with Zn doping, which would promote the formation of Mg-Ag anti-site defects, and reduce the Ag precipitation second phase in the matrix (Figure S2B). By Zn doping, additional defects are formed, which are expected to greatly scatter phonons. Besides, it is shown in Figure 2B,C that, Zn_Ag defects have the lowest formation energy for p-type α-MgAgSb for all Ag-poor, Ag-moderate, and Ag-rich conditions, meaning that Zn tends to take Ag site in the lattice. Overall, the carrier concentration comes from both the intrinsic Ag vacancies and the left Mg vacancies because of the evaporation of Mg atoms. The occupation of Ag at Mg site and Zn at Ag site both provides one electron and tunes the carrier concentration.

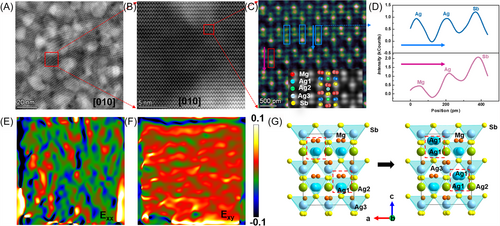
The Mg-Ag anti-site defects result in a structural transformation from the original Mg-Ag-Sb chain to Ag-Ag-Sb arrangement within the matrix. This transformation was investigated using aberration-corrected transmission electron microscopy (TEM) for sample Zn_0.01MgAg_0.97Sb_0.99. The atomic structure of the sample along [010] zone axis was revealed using high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM). The image contrast was proportional to the square of the atomic number; thus, Mg shows the darkest contrast compared with Ag, and Sb shows the brightest contrast. As displayed in Figure 3A,B and Figure S3A, the matrix comprises alternating dark and white contrast areas, indicating the different composition in these zones. It's worth noting that the staggered dark and bright areas share the same set lattice structure with the normal areas, with no impurity phase observed even in the magnified zone (Figure S3B) and in the diffraction pattern obtained by Fourier transform. Further investigation of the atomic configuration in the light zones revealed a high concentration of Ag-Ag-Sb configuration, in contrast to the original Mg-Ag-Sb configuration (Figure 3C,D). These observations evidenced the existence of Mg-Ag anti-site defect. The extremely similar lattice in these two regions has a minimal influence on carrier transport across the entire measured temperature range. However, the staggered structure significantly enhances the lattice anharmonicity at the borders, inducing strain redistribution around the lattice. Analysis of high-resolution TEM (HRTEM) images via geometric phase analysis (GPA) (Figure 3E,F) revealed large strains around the staggered zones in the matrix, which could act as nanoscale scatter centers for phonons transport.

The electrical performance of both intrinsic and Zn-doped samples is clearly illustrated in Figure 4. Specifically, Figure 4A–C individually depict the temperature-dependent Seebeck coefficient, resistivity, and power factor within the range of 200–400 K for xZn + MgAg_0.97Sb_0.99 (0 ≤ x ≤ 0.02) samples studied in this study. As temperature rises, both the Seebeck coefficient and resistivity exhibit an increase, indicative of degenerate semiconductor behavior. It is discussed that both of Zn/Ag substation and the occupation of Ag at Mg site provide one extra electron. Consequently, the carrier concentration decreases with increased Zn doping, but it increases again when the doping amount reaches saturation at x = 1.5% (Figure 4A) due to the appearance of metallic Ag₃Sb second phase. Corresponding to these variations in carrier concentration, the Seebeck coefficient and resistivity initially increase with Zn-doping but decline when x ≥ 1.5%.

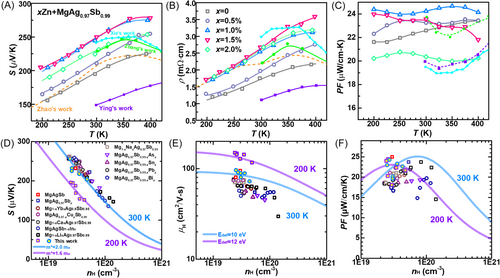
To estimate the optimal electrical property, Figure 4C–F presents the Hall carrier concentration-dependent Seebeck coefficient, Hall mobility, and the resultant power factor data for the samples in this study, alongside reported results for comparison [38-42, 59]. The solid blue and purple lines represent the predicted result at 200 and 300 K, respectively, based on the single parabolic band model assuming phonon-to-phonon scattering as the dominant scattering mechanism evidenced by T^−1.5 temperature dependence in Figure 4B. The density of state effective mass, m_d*, and deformation potential, E_def, is taken as ~1.7 m_e and ~12 eV at 200 K (purple line), and m_d* is ~2.0 m_e, E_def is ~10 eV (blue line) at 300 K. It is seen in Figure 4D that the experiment data for Zn-doped samples align closely with the solid lines for both 300 K and 200 K, and are in line with the reported results, indicating the m_d* remains unchanged for Zn-doped samples in this study. Given that the valence band edge of α-MgAgSb is primarily contributed by Mg-s and Ag-d orbitals, DFT calculation is conducted to access the impact of Zn doping and Mg-Ag anti-sites on the band structure. As displayed in Figure S5, the valence band edge remains unaltered in all scenarios involving Mg-Zn anti-site, Zn doping combined with Mg-Zn anti-site, compared to intrinsic α-MgAgSb, which are consistent with the findings in Figure 4D. Compared with previous reported data [38-42, 58, 59], the Hall mobility in this study is obviously increased (Figure S4A) and is comparable to the recently reported value [23] obtained by excluding the grain boundary scattering. The resultant carrier concentration-dependent power factor is derived as shown in Figure 4F. The optimal carrier concentration for maximizing the power factor is predicted to be ~3 × 10¹⁹cm⁻³ at 200 K and ~8 × 10¹⁹cm⁻³ at 300 K, which conforms to the trend of n_opt ∝ m_d*T^3/2. By Zn doping, the carrier concentration falls within the optimal range at 200 K, making the material more suitable for low-temperature applications and a peak power factor ~24 μW/cm-K is achieved. However, at 300 K, the intrinsic sample exhibits the highest value due to its highest carrier concentration.

The differential scattering mechanism of carriers and phonons is illuminated by the temperature-dependent Hall mobility (Figure S4B) and lattice thermal conductivity (Figure S7B). The lattice thermal conductivity is estimated by subtracting the electronic part from the total thermal conductivity, κ_L = κ−LTσ, where L is Lorentz number determined by SPB model. As temperature decreases, the Hall mobility increases, exhibiting a T^−1.5 temperature dependence, which suggests that acoustic phonon scattering is the dominant mechanism. Conversely, the increase in lattice thermal conductivity follows a T^−0.5 dependence, deviating from the traditional phonon-phonon scattering process (T⁻¹ dependence). The anti-site defects of Mg-Ag lead to a staggered Ag-Ag-Sb structure within the matrix at nanoscale. Together with the soft crystalline sublattices resulting from the weak bonding of Mg-Sb, low-frequency phonons undergo significant scattering, leading to a notable suppression of lattice thermal conductivity. Due to the different temperature dependences of Hall mobility and lattice thermal conductivity, the Hall mobility to lattice thermal conductivity ratio approximately follows a T⁻¹ dependence within the measured temperature range (Figure 5A), highlighting the distinctive scattering mechanism at low temperatures. To further validate the electrical and thermal transport properties in α-MgAgSb, the temperature-dependent mean free length of carriers and phonons are calculated and presented in Figure 5B. The calculation details are provided in the Supporting Information. It is obvious that carriers possess a significantly larger mean free length than phonons, and the values for phonons are comparable to the lattice parameters of the crystal, which effectively impacts the transport of phonons.

The electrical property is much improved because of the increased carrier mobility and optimized carrier concentration by Mg-Ag anti-site manipulation. But it is clearly seen that (Figure S7B) the lattice thermal conductivity in this study is about 20% higher than reported samples prepared by two-step balling process [23, 57], which is also consistent with the previous melting method result [58]. The observed difference in lattice thermal conductivity for samples prepared by melting and balling process can be rationally explained by microstructural differences. As clearly demonstrated in our work and previous reports, the lower lattice thermal conductivity of melt-processed materials originates from the much fine grain size, which scatter phonons greatly, especially. At last, a high zT value of 0.45 at 200 K, 0.76 at 300 K, and an average value of 0.75 between 200 and 300 K is obtained in this study by 1% Zn-doping (Figure 6A). Based on the high thermoelectric performance near room temperature, a single pair thermoelectric device comprised by α-MgAgSb and commercial n-type Bi₂Te₃ is prepared with the geometry size optimized by COMSOL simulation (Figure 6B). In this study, Ag is adopted as a resist layer and is prepared by one-step hot press which is evidenced as an effective way for MgAgSb device [64]. The device displays 47 K temperature difference at 300 K and 56 K temperature difference at 325 K (Figure 6C). The lower cooling temperature difference may be caused by the higher contact resistivity as the legs are soldered to electrode without transition barrier layer directly without transition barrier layer. Higher cooling ability will be achieved if the contact resistivity is reduced by introducing Ohmic interlayer. Although the experiment cooling temperature difference is lower than the predicted level due to the relatively large contact resistivity, the device shows high reliability (Figure 6D). It is seen that after 60 days of annealing in air, the cooling temperature difference nearly unchanged, indicating the promising application potential.

3 Summary

In conclusion, the investigation in this study experimentally revealed that intrinsic Ag vacancies and Ag-Mg anti-site defects coexist in the α-MgAgSb. These anti-site defects provide lattice sites for precipitated Ag, depressing the formation of Ag second phase in the matrix and enhancing carrier mobility. Importantly, the anti-site defect areas share the same lattice set with the normal regions, and the carrier mobility is not impacted while the phonons are scattered greatly. This different scattering mechanism for carriers and phonons leads to a T⁻¹ temperature dependence of mobility to lattice thermal conductivity ratio, which is beneficial for low temperature thermoelectric property. Zn doping in this study further reduces the Mg-Ag anti-site defect energy and improves the carrier mobility due to the decreased Ag-rich second phase in the matirx. Furthermore, Zn doping tunes the carrier concentration to an optimal level for α-MgAgSb at 200 K. Consequently, a zT value of ~0.45 at 200 K, and an average figure of merit ~0.75 between 200 and 400 K is achieved for 1% Zn-doped α-MgAgSb in this study, comparable to other high-performance low-temperature thermoelectric materials. And the α-MgAgSb/Bi₂Te₃ unit couple obtained a temperature difference of 47 K at 300 K and 56 K at 325 K, which is repeatable even after 60 days, demonstrating the promising thermoelectric cooling ability of the obtained materials.

Conflicts of Interest

The authors declare no conflicts of interest.