Multimodal water age distributions and the challenge of complex hydrological landscapes
Funding information: École Polytechnique Fédérale de Lausanne; Fonds National de la Recherche Luxembourg, Grant/Award Numbers: FNR/CORE/C14/SR/8353440/STORE-AGE, FNR/CORE/C17/SR/11702136/EFFECT
Abstract
Travel time distributions (TTDs) are concise descriptions of transport processes in catchments based on water ages, and they are particularly efficient as lumped hydrological models to simulate tracers in outflows. Past studies have approximated catchment TTDs with unimodal probability distribution functions (pdf) and have successfully simulated tracers in outflows with those. However, intricate flow paths and contrasting water velocities observed in complex hydrological systems may generate multimodal age distributions. This study explores the occurrence of multimodal age distributions in hydrological systems and investigates the consequences of multimodality for tracer transport. Lumped models based on TTDs of varying complexity (unimodal and multimodal) are used to simulate tracers in the discharge of hydrological systems under well-known conditions. Specifically, we simulate tracer data from a controlled lysimeter irrigation experiment showing a multimodal response and we provide results from a virtual catchment-scale experiment testing the ability of a unimodal age distribution to simulate a known and more complex multimodal age system. Models are based on composite StorAge Selection functions, defined as weighted sums of pdfs, which allow a straightforward implementation of uni- or multi-modal age distributions while accounting for unsteady conditions. These two experiments show that simple unimodal models provide satisfactory simulations of a given tracer, but they fail in reproducing processes occurring at different temporal scales. Multimodal distributions, instead, can better capture the detailed dynamics embedded in the observations. We conclude that experimental knowledge of flow paths and the systematic use of data from multiple, independent tracers can be used to validate the assumption of water age unimodality. Multimodal age distributions are more likely to emerge in landscapes where the distributions of flow path lengths and/or water velocities are themselves multimodal. In general, age multimodality may not be particularly pronounced and detectable, unless comparable amounts of water with contrasting ages reach a given outflow.
1 INTRODUCTION
The representation of hydrological systems in mathematical terms is a challenging task that deals with the complexity of the natural environment (Bras, 2015; Clark et al., 2017; Dooge, 1986). Spatially implicit mathematical descriptions (e.g., lumped models) are widely used because they prove suitable to summarise hydrological processes at different scales (Hrachowitz & Clark, 2017). Transfer functions that relate system inputs to system outputs by an integral operation are particularly widespread in hydrology, notably for problems like flow and solute response of a catchment to precipitation events. Although the flow and solute responses are mathematically formulated with transfer functions in an almost identical way, the meaning of these functions is contrasting (Botter, Bertuzzo, & Rinaldo, 2010). The flow response deals with the celerity of pressure propagation, while the solute response deals with the velocity of water parcels within a catchment (Kirchner, Feng, & Neal, 2000; McDonnell & Beven, 2014).
Transfer functions are typically modelled as probability distribution functions (pdf) whose shape is assumed a priori and the relevant parameters are calibrated to available data. When focusing on the hydrological response of a catchment to an impulse input, the transfer function is termed instantaneous unit hydrograph (IUH) and its functional form is often assumed to be a gamma, lognormal or Weibull distribution. In some cases the shape of the IUH can be obtained starting from measurable properties of the landscape, such as its geomorphologic structure (Rinaldo, Marani, & Rigon, 1991; Rodriguez-Iturbe & Valdes, 1979). This type of unit hydrographs can have complex and multimodal shapes that originate from the geomorphological complexity of a catchment. Tracer hydrology focuses on the variations in the concentrations of non-ideal tracers like solutes (e.g., chloride) or ideal tracers like constituents of the water molecule (e.g., 2H) that are transported with water. The transfer functions that are relevant to tracers (ideal or not) are termed travel (or transit) time distributions (TTD). These describe the time that water molecules take to move through a hydrological control volume (i.e., water ages in outflows) and they are used to relate tracer inputs (e.g., stable isotopes or chloride in precipitation) to tracer outputs (e.g., stable isotopes or chloride in discharge and evapotranspiration). Many studies employing TTDs as models of catchment transport have successfully simulated tracer concentrations in discharge by calibrating TTDs to tracer data under the assumption of steady-state flow conditions (see McGuire & McDonnell, 2006; Soulsby, Birkel, Geris, & Tetzlaff, 2015). TTDs are often assumed to be gamma-distributed because this shape is consistent with the spectral signatures of measured solute time series (Kirchner et al., 2000; Kirchner & Neal, 2013). Alternatively, various TTD shapes can be obtained by solving the advection–dispersion equation under different boundary conditions (Kreft & Zuber, 1978). These TTDs have been employed in groundwater systems with specific aquifer configurations (Małoszewski & Zuber, 1982). A comprehensive review of steady-state TTDs was provided by Leray, Engdahl, Massoudieh, Bresciani, and McCallum (2016), who illustrated the physical meaning and mathematical derivation of several TTD shapes.
If the assumption of steady-state flow conditions is removed (Botter et al., 2010; Botter, Bertuzzo, & Rinaldo, 2011), the resulting non-stationary TTDs are expected to have complex and irregular shapes even when the transport processes are simple (e.g., complete mixing). In transient hydrological conditions, the shape of non-steady TTDs cannot be assumed a priori, but StorAge Selection (SAS) functions (Botter et al., 2011; Harman, 2015; Rinaldo et al., 2015; van der Velde, Torfs, van der Zee, & Uijlenhoet, 2012) can be used to derive unsteady TTDs (also to derive steady-state TTDs in the particular case of steady flow conditions; Berghuijs & Kirchner, 2017). SAS functions can take different mathematical forms and have usually been assumed to be beta distributions (van der Velde et al., 2012; Visser et al., 2019), power functions (Benettin et al., 2017; Queloz et al., 2015) or gamma distributions (Harman, 2015; Wilusz, Harman, & Ball, 2017). The resulting unsteady TTDs display various peaks corresponding to the variability of the hydrological fluxes (i.e., precipitation or discharge). These TTDs may be called ‘instantaneous’ because they change at every moment due to temporal changes in water fluxes or to internal changes in the configuration of flow paths to the outlet (Kim et al., 2016). Yet, when ‘instantaneous’ TTDs are averaged out to obtain an average (or marginal) TTD, simple shapes emerge (Benettin, Soulsby, et al., 2017; Remondi, Kirchner, Burlando, & Fatichi, 2018; van der Velde et al., 2015) and suggest that it is still possible to approximate transport processes in a catchment with a single (marginal) TTD.
Whether TTDs are derived by direct calibration to data, by averaging unsteady TTDs starting from SAS functions, or by solving simplified fluid equations, their shape is often found/assumed to have a single mode. This seems to suggest that integrating a large number of contrasting flow paths results, on average, in a seamless distribution of transit times. But should we expect TTDs to always have simple shapes in the real world? And what processes can possibly give rise to multimodality in the TTD? Hydrological landscapes transport water inputs over a wide range of distances and in highly heterogeneous media with variable wetness conditions. It is unlikely that the existing plethora of transport processes always results in age distributions without multiple distinct and meaningful peaks. In fact, many studies (see Section 2) proposed to use multimodal age distributions in various hydrological systems for a number of physical reasons.
The problem of inferring the true shape of TTDs is made difficult by a major experimental issue: we cannot measure TTDs in catchments. TTDs can only be measured through tracer mass breakthrough curves, which is feasible in controlled systems like lysimeters (Pütz et al., 2016) or small experimental hillslopes (Kendall, McDonnell, & Gu, 2001; Kim et al., 2016; Rodhe, Nyberg, & Bishop, 1996; Volkmann et al., 2018). At the catchment scale, TTDs can only be deduced indirectly through aggregated tracer information in inflows and outflows (Kirchner, 2016). In other words, hypotheses about the TTDs (e.g., functional form and parameters) cannot be tested by comparing the assumed TTDs to actual measurements of water ages, but only by comparing the tracer simulation associated with the assumed TTD to the tracer observations. The task of deducing TTDs in catchments is often transformed into a model calibration problem and this may overlook parts of the TTDs accounting for a range of transport processes not immediately visible in the tracer data (Figure 1). Until we are able to measure the true shape of an age distribution through a large-scale tracer experiment, research efforts are needed to assess the consequences of over-simplified age distributions. This is particularly important as TTDs are seen as a way to simulate solute chemistry and bridge previously disconnected fields of environmental modelling (Hrachowitz et al., 2016).
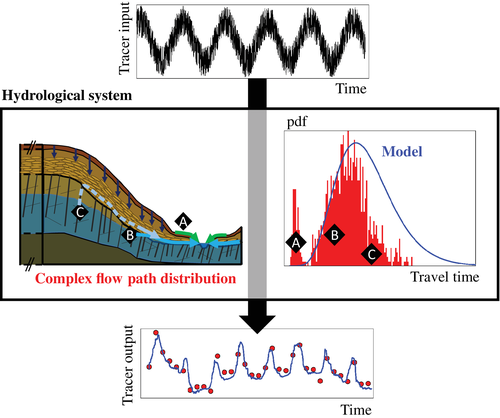
We first provide a reasonable definition of multimodality in the context of time-variable hydrological fluxes. Then, this study explores the occurrence of multimodal age distributions in hydrological systems and investigates the potential of lumped transport models to account for the causes and for the consequences of multimodality in tracer transport. We aim to clarify when we should expect to observe multimodal distributions in a hydrological system and what is the effect of not accounting for this multimodality.
The remainder of the article is organised as follows: Section 2 reviews previous studies that reported multimodal TTD behaviour. Section 3 reports the methodology to simulate tracer transport using TTDs and SAS functions. Section 4 provides modelling results for a lysimeter tracer experiment characterised by a bimodal tracer breakthrough curve, while Section 5 looks into the potential consequences of simplifying a multimodal TTD with a unimodal TTD by means of a catchment-scale virtual tracer experiment. A discussion of the results (Section 6) and a summary of the conclusions (Section 7) close the article.
2 ACKNOWLEDGING THE MULTIMODALITY OF WATER AGE DISTRIBUTIONS
In various hydrological systems, TTDs are assumed to follow steady-state models such as the piston flow, the exponential and the dispersive models, or combinations of them (Małoszewski & Zuber, 1982). These analytical distributions work well in many catchments (McGuire & McDonnell, 2006; Stewart, Morgenstern, & McDonnell, 2010), where the tracers used to infer them are sampled at lower frequencies (mostly weekly to monthly). However, only strong assumptions about the system boundary conditions and its internal transport mechanisms (Leray et al., 2016; Małoszewski & Zuber, 1982) can lead to such unimodal distributions. Multimodal and irregular shapes of TTDs are instead found with physically based transport models, even in steady-state conditions (Engdahl & Maxwell, 2014; Goderniaux, Davy, Bresciani, de Dreuzy, & Le Borgne, 2013).
A number of studies advocated the use of multimodal TTDs in the context of steady-state (Leray et al., 2016, p. 78, and citations below). At different scales, contrasts in water velocities or in flow path lengths may generate multimodal TTDs. Contrasting flow path lengths can for example come from: stream channel morphological features (Haggerty, Wondzell, & Johnson, 2002; Ward, Schmadel, & Wondzell, 2018), competing recharge areas to a groundwater well (Cirpka et al., 2007; Massoudieh, Sharifi, & Solomon, 2012; Visser, Broers, Purtschert, Sültenfuß, & de Jonge, 2013), different sources of surface water or groundwater (Duy et al., 2019; Stolp et al., 2010) or shallow and local vs. deep and regional subsurface flows (Goderniaux et al., 2013; Solomon, Genereux, Plummer, & Busenberg, 2010; Wilusz, Harman, Ball, Maxwell, & Buda, 2020). Contrasting water velocities can originate from: preferential flow in soil macropores (Jackisch et al., 2017; Klaus, Zehe, Elsner, Külls, & McDonnell, 2013; Scaini et al., 2017; Utermann, Kladivko, & Jury, 1990; White, Dyson, Haigh, Jury, & Sposito, 1986), heterogeneous rock permeability (Desbarats, 1990; Eberts, Böhlke, Kauffman, & Jurgens, 2012; Ritzi et al., 2000; Weissmann, Zhang, LaBolle, & Fogg, 2002) or conduit flow bypassing rock matrix flow in karst geologies (Long & Putnam, 2009).
In unsteady conditions, multiple peaks can be found in TTDs because of dynamic hydrological fluxes (Botter et al., 2010; vander Velde et al., 2012). However, clusters of peaks in the TTD can be related to different major transport processes to an outlet. van der Velde, de Rooij, Rozemeijer, van Geer, & Broers (2010, Figure 6) found time-varying discharge TTDs with two distinct groups of peaks, the first one being intermittent and associated with tile drainage of the root zone storage (younger water) and the second being permanent and associated with slower groundwater flows in the subsurface. Recent numerical experiments on real or virtual hydrological systems (Danesh-Yazdi, Klaus, Condon, & Maxwell, 2018; Kaandorp, de Louw, van der Velde, & Broers, 2018; Remondi et al., 2018; Yang, Heidbüchel, Musolff, Reinstorf, & Fleckenstein, 2018) showed that, even if SAS functions simplify the shapes of the age distributions compared with TTDs, they may not be described well by unimodal distributions. Rodriguez and Klaus (2019) used high frequency (i.e., sub-daily) stable isotopes in precipitation and discharge over 2 years and found that the SAS function in a slate catchment with complex flow paths may contain several peaks consistent with experimentally identified discharge generation processes.
There is an emerging perception that TTDs in hydrological systems are complex and may be multimodal for reasons other than time-varying hydrological fluxes. However, studies that supported TTD multimodality had only little or no tracer data to constrain model predictions and to validate the simulated TTD shapes. Thus, the existence of high-quality data is crucial to advance our knowledge of TTD shapes. The recent improvements in 2H and 18O measurement techniques (Gupta, Noone, Galewsky, Sweeney, & Vaughn, 2009; Lis, Wassenaar, & Hendry, 2008) and sampling methods (Berman, Gupta, Gabrielli, Garland, & McDonnell, 2009; Herbstritt, Gralher, & Weiler, 2019; Koehler & Wassenaar, 2011; Munksgaard, Wurster, & Bird, 2011; Pangle, Klaus, Berman, Gupta, & McDonnell, 2013) allowed a considerable increase in the tracer record lengths up to several decades (Hrachowitz et al., 2009; IAEA, 2019; IAEA and WMO, 2019; Pfister et al., 2017) and in the resolution of tracer data up to minutes (von Freyberg, Studer, & Kirchner, 2017). This has made the detection of the entire shape of the TTDs more feasible than in the past. High-frequency tracer observations can now constrain the left-hand part of TTDs representing the short (e.g., hours to days) and intermediate (e.g., weeks) transport time scales (Rodriguez & Klaus, 2019), while long records of tracers can constrain the right-hand tail of TTDs associated with long transport time scales (e.g., months to years, Rodriguez, Pfister, Zehe, & Klaus, 2019; Neal et al., 2011). Tracer time series that span several years at high resolution (von Freyberg, Studer, Rinderer, & Kirchner, 2018) will pave the way for the detailed investigation of water flow paths and their influence on TTDs.
3 SIMULATIONS OF TRACER CONCENTRATIONS THROUGH SAS FUNCTIONS
We focus on the multimodality of the discharge TTD, seen as the TTD of all the water draining to a single outlet like streamflow, as opposed to the TTD of the evapotranspiration flux. Thus, the terminology ‘TTD’ or ‘SAS function’ will always refer to discharge unless specified otherwise.
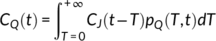 (1)
(1)For non-ideal tracers such as solutes undergoing chemical reactions, the changes in concentration since the tracer entrance into the system need to be accounted for. Assuming that these changes are a direct function of water age T allows using Equation 1 to simulate non-ideal tracers in outflows as well (Maher, 2011; Rinaldo & Marani, 1987). In such a case,
C
J(t − T) is replaced by
C
S(T, t), i.e., the tracer concentration of water in storage with age T at time t. For atmospheric tracers that are introduced through precipitation and decay with age such as tritium (Stewart et al., 2010; Visser et al., 2019), the following relationship can be implemented: 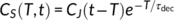 , where τdec is a kinetic (decay) constant (e.g., 17.77 years for tritium). For geogenic reactive tracers like silicon and sodium (Benettin et al., 2015; Clymans et al., 2013; Hornberger, Scanlon, & Raffensperger, 2001; Johnson, Likens, Bormann, & Pierce, 1968; Maher, 2010), where the input is typically tracer-free and tracer concentration can increase with age towards some limiting concentration Clim, the storage concentration takes the form:
, where τdec is a kinetic (decay) constant (e.g., 17.77 years for tritium). For geogenic reactive tracers like silicon and sodium (Benettin et al., 2015; Clymans et al., 2013; Hornberger, Scanlon, & Raffensperger, 2001; Johnson, Likens, Bormann, & Pierce, 1968; Maher, 2010), where the input is typically tracer-free and tracer concentration can increase with age towards some limiting concentration Clim, the storage concentration takes the form: 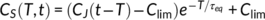 , where τ
eq is a kinetic constant (e.g., 1 year). Tracer concentrations in storage can also increase because of specific removal of tracer-free water by ET (evapoconcentration). The resulting effect on
C
S(T, t) is explained in detail by Queloz, Carraro, et al. (2015) and can be formulated through an evapoconcentration parameter α, where α = 0 represents pure evapoconcentration and α = 1 represents fully conservative tracer behaviour (Bertuzzo, Thomet, Botter, & Rinaldo, 2013).
, where τ
eq is a kinetic constant (e.g., 1 year). Tracer concentrations in storage can also increase because of specific removal of tracer-free water by ET (evapoconcentration). The resulting effect on
C
S(T, t) is explained in detail by Queloz, Carraro, et al. (2015) and can be formulated through an evapoconcentration parameter α, where α = 0 represents pure evapoconcentration and α = 1 represents fully conservative tracer behaviour (Bertuzzo, Thomet, Botter, & Rinaldo, 2013).
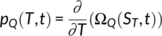 (2)
(2)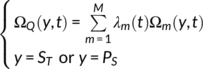 (3)
(3)The M functions λ m(t) are time-varying weights summing to 1 to ensure mass conservation. In this study, we used constant weights, but they can be parameterised to change with various hydrological quantities such as precipitation intensities, storage, or storage variations (Rodriguez & Klaus, 2019). Each weight λ m(t) defines the relative volumetric contribution of the component Ω m(y, t) to the considered outflow [here discharge Q(t)] at time t. Ω m(y, t) is a probability distribution function of the variable y = P S or y = S T associated with a contribution (labelled with m) of water ages to the outflow. This contribution can be a given hydrological process (Wilusz et al., 2020) or a spatial end-member (e.g., soil water) having a particular age range (e.g., young water for overland flow). In this study, we assumed that the Ω m(y, t) do not explicitly depend on t. They can nevertheless be explicitly dependent on time t to include the effect of a time-varying age selection for each component and to increase the overall temporal variability of the SAS function (Wilusz et al., 2020). Note that even a SAS function with no explicit dependence on t allows simulations of time-varying TTDs. This differs from previous similar formulations of composite TTDs that were at steady state (Leray et al., 2016). Composite SAS functions can be defined the same way in non-cumulative form. To test our results for a larger number of SAS shapes, we used SAS functions defined both over the age-ranked storage (Section 5) and over its normalised form (Section 4).
4 MULTIMODALITY IN A LYSIMETER-SCALE EXPERIMENT
Small-scale (~2 m) experimental setups like lysimeters (Pütz et al., 2016) are currently the only hydrological system where TTDs can be measured by labelling individual precipitation events. While tracer experiments in lysimeters often resulted in substantial single-mode tracer breakthrough curves (BTC) (Groh et al., 2018; Stumpp, Nützmann, Maciejewski, & Maloszewski, 2009), the experiment by Queloz et al. (2015) is one rare example showing a clear bimodal behaviour with two distinct peaks in the BTC.
4.1 Data and methods
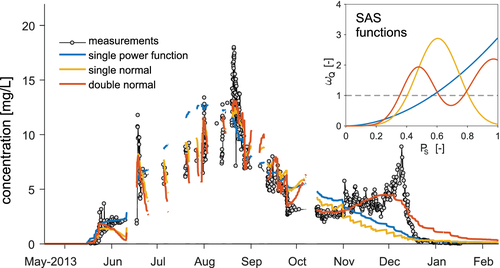
Extensive information about the experiment including hydrological and tracer data can be found in Queloz, Bertuzzo, et al. (2015). In brief, the experiment was carried out at EPFL campus (CH) between 2013 and 2014 in a large (2.5 m-depth, 1.2 m2-diameter) vegetated lysimeter. The experiment was forced by controlled, non-stationary irrigation. Two small willow trees planted within the lysimeter triggered intense evapotranspiration fluxes that regularly exceeded 30 mm/day during warm summer days. Flow from the bottom drainage was discontinuous, with peaks following irrigation and no flow during dry days (Figure 2). A number of five fluorobenzoate (FBA) tracers were applied in Spring 2013 and showed different recoveries. We focus here on the tracer that had the most conservative behaviour (2,6-DFBA, 60% recovery). The tracer arrived at the bottom of the lysimeter over two distinct timescales that resulted in two different major peaks with duration of weeks to months (Figure 2). It is worth to recall here that the TTD is the normalised mass breakthrough curve (MBTC) and not the concentration breakthrough curve (CBTC). The MBTC is influenced by the variability of the hydrological fluxes and would resemble the drainage time series, with multiple individual peaks corresponding to high flow events. Yet, the CBTC better reveals the two longer-lasting peaks and we consider those as representative of contrasting transport processes occurring within the lysimeter. The major of the two peaks occurred through the summer (roughly 3 months after application) when flow was very discontinuous, while the other peak occurred at the beginning of the winter (roughly 6 months after application), when evapotranspiration became significantly lower. Although the second peak is smaller in magnitude compared with the first peak, it drained more tracer mass because flows were higher.
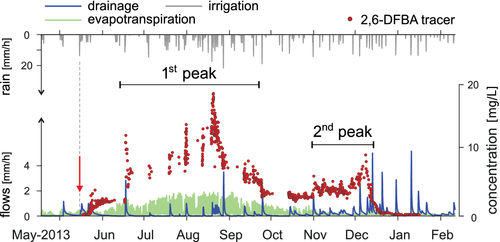
Tracer transport for this experiment was previously modelled by (Queloz, Carraro, et al., 2015), who used an approach based on SAS functions and conceptualised the lysimeter as two systems in series: the unsaturated soil (modelled through a power-function SAS) and the saturated gravel filter (modelled as a fully mixed compartment). In this study, we use one single control volume for the entire lysimeter system (unsaturated and saturated) and we test a new functional shape for the SAS function Ω
Q(P
S). We introduce the truncated normal SAS function 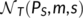 (formula in S1.1), which has two parameters: m, corresponding to the mode of the distribution and s, which is proportional to the standard deviation of the distribution. Depending on the value of the parameters, the normal SAS function can be bell-shaped or not. Note that even a symmetric SAS function does not imply that the resulting TTDs are symmetric. As the parameters of the normal SAS function are strongly related to the function mode, it is an appealing candidate to explore multimodality. Thus, we generated a composite SAS function as the linear combination of two normal SAS functions (see section S1.1). The composite function allows for two distinct peaks and has a total of five calibration parameters (two for each normal distribution and one for the partitioning). For comparison, we also used a single normally distributed SAS function (two parameters) and a power-function (one parameter) for Ω
Q. The SAS function for the ET flux (Ω
ET) is assumed in all cases to be a uniform distribution over the younger storage fraction defined by the parameter u, as proposed by Harman (2015). The model further assumes that the tracer is conservative but only partially taken up by vegetation, through a parameter α ≤ 1 (see Section 3). This partial uptake of the FBA tracer by the willow trees in the lysimeter was revealed by Queloz, Bertuzzo, et al. (2015) who found small amounts of tracer in plant tissues, and whose breakthrough curves were not described well either by an absence of vegetation uptake, or by a complete vegetation uptake of the tracer. The simulation was run using tran-SAS (Benettin & Bertuzzo, 2018) and calibrated to measured tracer data through the DREAM
ZS algorithm (ter Braak & Vrugt, 2008; Vrugt et al., 2009). Calibration was based on the assumption that residuals were independent and normally distributed. Further details on the model and calibration setup can be found in Section S2. For each of the three tested SAS models, the best parameter combination (Table S1) was retained to obtain the instantaneous TTDs and compute the marginal TTD.
(formula in S1.1), which has two parameters: m, corresponding to the mode of the distribution and s, which is proportional to the standard deviation of the distribution. Depending on the value of the parameters, the normal SAS function can be bell-shaped or not. Note that even a symmetric SAS function does not imply that the resulting TTDs are symmetric. As the parameters of the normal SAS function are strongly related to the function mode, it is an appealing candidate to explore multimodality. Thus, we generated a composite SAS function as the linear combination of two normal SAS functions (see section S1.1). The composite function allows for two distinct peaks and has a total of five calibration parameters (two for each normal distribution and one for the partitioning). For comparison, we also used a single normally distributed SAS function (two parameters) and a power-function (one parameter) for Ω
Q. The SAS function for the ET flux (Ω
ET) is assumed in all cases to be a uniform distribution over the younger storage fraction defined by the parameter u, as proposed by Harman (2015). The model further assumes that the tracer is conservative but only partially taken up by vegetation, through a parameter α ≤ 1 (see Section 3). This partial uptake of the FBA tracer by the willow trees in the lysimeter was revealed by Queloz, Bertuzzo, et al. (2015) who found small amounts of tracer in plant tissues, and whose breakthrough curves were not described well either by an absence of vegetation uptake, or by a complete vegetation uptake of the tracer. The simulation was run using tran-SAS (Benettin & Bertuzzo, 2018) and calibrated to measured tracer data through the DREAM
ZS algorithm (ter Braak & Vrugt, 2008; Vrugt et al., 2009). Calibration was based on the assumption that residuals were independent and normally distributed. Further details on the model and calibration setup can be found in Section S2. For each of the three tested SAS models, the best parameter combination (Table S1) was retained to obtain the instantaneous TTDs and compute the marginal TTD.
4.2 Results
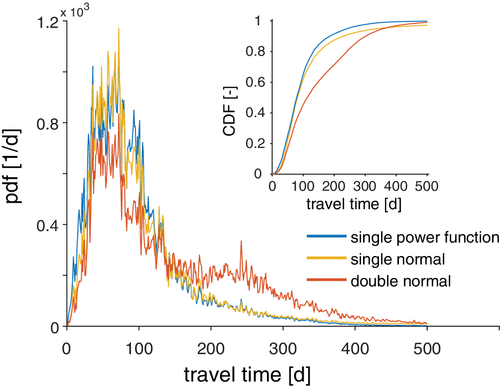
The results of the tracer breakthrough simulations are shown in Figure 3 together with their corresponding SAS function Ω Q. Breakthrough curves are discontinuous because of the frequent absence of flow during the dry summer months. The three curves all match the beginning of the early breakthrough in mid-May 2013. This 1-month delay since tracer application is obtained through SAS functions that, in all cases (see Figure 3 inset), are almost null up to P S = 0.2, meaning that drainage does not comprise the 20% younger soil waters. The three simulations are also fairly similar at reproducing the first wide peak from June to October, with the power-function simulation less-variable and slightly higher than the tracer peak, but overall broadly comparable with measurements. The main difference occurs upon the second peak, which is entirely missed by the simpler models while it is captured by the double normal SAS function. The higher accuracy obviously comes at a cost (five SAS parameters instead of 1 or 2) but, besides a much better performance (see additional analyses in Section S2), the double normal model is more appropriate because it allows expressing the multimodality of the data. As a result, model errors are symmetric and much less correlated than in the other cases (Figure S2 and Table S2). The marginal TTDs resulting from the three models are illustrated in Figure 4. As expected, the marginal TTD resulting from the multimodal SAS function has two distinct peaks: the first at 90–100 days and the second at 200–250 days. By contrast, the marginal TTDs resulting from other SAS functions have a single and higher peak at 90–100 days and underestimate the older water contribution in the right tail of the distribution. These simulations ultimately tell us that in all cases, water found at the bottom drainage is representative of the older water stored in the lysimeter (Figure 3, inset). However, two major transport mechanisms emerge from the data and the simulations: some water is relatively fast and it is able to percolate during the dry summer season (c.f. first peak of the CBTC), likely due to the occasional activation of preferential pathways; the rest of the tracer mass moves with the matrix flow and takes more than twice as much to reach the lysimeter bottom (c.f. second peak of the CBTC).
5 MULTIMODALITY IN A VIRTUAL, CATCHMENT-SCALE EXPERIMENT
The tracer breakthrough experiment shown in Section 4 cannot be easily applied at larger scales (e.g., hillslopes, catchments). Thus, the applicability of these results and the validity of these conclusions at larger scales require a numerical experiment.
5.1 Methods
- A virtual pesticide (e.g., Atrazine) with a short kinetic (decay) constant τdec = 50 days (<0.5 MTT, Table 1), applied as a single pulse C0 = 50 mg/L during a 100 mm precipitation event over 1 day.
- Nitrate (
 ), with a long-term input of 60 mg/L, then linearly decreasing from 60 mg/L to 0 in 150 days (≃0.5 MTT, Table 1).
), with a long-term input of 60 mg/L, then linearly decreasing from 60 mg/L to 0 in 150 days (≃0.5 MTT, Table 1). - A weathering product (e.g., silicon) with a long kinetic constant τ eq = 550 days (≃2 MTT, Table 1) and limit concentration Clim = 200 mg/L.
| Ω ref | Ω Q | |
|---|---|---|
| (true multimodal gamma) | (calibrated unimodal gamma) | |
| MTT [years] | 0.81 | 1.22 |
| MdTT [years] | 0.72 | 0.94 |
| F(T < 2 days) [%] | 0.049 | 0.00 |
| F(T < 7 days) [%] | 0.47 | 0.00 |
| F(T < 31 days) [%] | 6.5 | 0.023 |
| F( T< τdec = 50 days) [%] | 8.7 | 0.15 |
| F yw(T < 73 days) [%] | 10 | 0.82 |
| F(T < 2 τdec = 100 days) [%] | 13 | 2.5 |
| F(T < 3 τdec = 150 days) [%] | 20 | 8.7 |
| F(T < 365 days) [%] | 73 | 55 |
| F( T< τ eq = 550 days) [%] | 90 | 77 |
| F(T < 2 τ eq = 1,100 days) [%] | 99 | 95 |
| F(T < 3,000 days) [%] | ≃ 100 | 99.7 |
- Abbreviations: MdTT, median travel time; MTT, mean travel time.
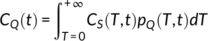 (4)
(4)where C S(T, t) has a different expression depending on the considered solute (Section 3, and SI, section S3). These additional tracers have Damköhler numbers between roughly 0.5 and 6 for the considered catchment (ratio of MTT to kinetic constant, see Oldham, Farrow, & Peiffer, 2013; Maher & Chamberlain, 2014; Ameli et al., 2017), representing from reaction-limited to transport-limited tracer dynamics, respectively. The pesticide, with a low Damköhler number, will thus be highly sensitive to the accuracy of the model in rapidly transporting water to the outlet. Conversely, the weathering product, with a high Damköhler number, will be highly sensitive to the accuracy of the model in retaining water for a long time in storage until it nearly reaches chemical equilibrium.
5.2 Results
The unimodal gamma-distributed Ω Q simulated the observed stream δ2H well, with a Nash-Sutcliffe Efficiency of NSE = 0.89 (Figure 5a). The model only failed to reproduce some of the rapid δ2H responses, especially at the beginning of wetter periods. The corresponding calibrated Ω Q is similar to the old water component Ω2 of the SAS function Ωref (Figure 5). As such, it clearly neglects the young water component Ω1 ( S T ≲ 200 mm), and it overestimates the old water fractions ( S T ≳ 600 mm) compared with Ω2. This is also visible in the corresponding marginal TTDs (average TTD over 100 years) (Figure 6), which have the largest differences over both younger ( T ≲ 0.2 year) and older ( T ≳ 1 year) water components. The observed differences between Ωref and Ω Q did not have a large influence on the simulations of the stream δ2H. To assess the consequences of those differences for other tracers, we compared the simulations from those two models for the three additional solutes in the stream. The observed differences between the unimodal Ω Q calibrated to δ2H and the bimodal Ω ref are well reflected in the simulations of these three tracers. Because of the mismatch in old water fractions ( T ≳ 1 year, Figure 6), Ω Q constantly overestimates the concentration in weathering product (Figure 5b). The mismatch in intermediate ages (0.25 ≲ T ≲ 1 year) results in a slower middle-term response of Ω Q to a change in the nitrate input (Figure 5c), with a 6 months delay to return to concentrations below the WHO guideline of 50 mg/L and about 2 years more to return to nitrate-free water. Finally, without a young water component ( T ≲ 0.2 years), the unimodal Ω Q does not simulate the quick pesticide breakthrough (Figure 5d) nor does it simulate a long-term response because of the quick decay of the pesticide (τdec = 50 days). The differences in water age between the two models are quantified through some statistics of the marginal age distributions (Table 1). The unimodal Ω Q results in a much larger mean travel time (MTT) (explaining the delay in middle-term response in nitrate), in a fraction of water younger than τdec 58 times lower, and in a higher fraction (13% more) of water older than τ eq.
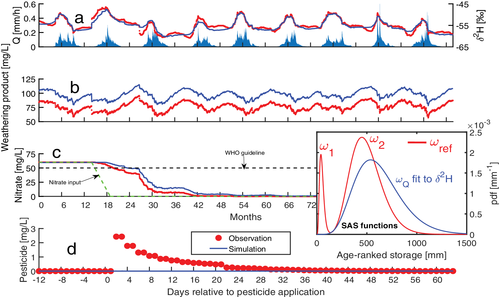
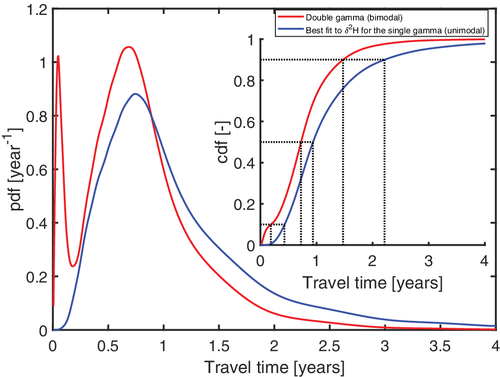
These results show that, despite the ability to simulate the observed δ2H, the calibrated unimodal Ω Q fails to simulate other tracers. Overall, we can expect that a deviation of a model (here Ω Q) from the ‘truth’ (usually unknown, but here Ωref) around a given age T will create a mismatch for all tracers whose stored concentrations vary with a time scale close to T. For instance, the unimodal approximation is reliable only for travel times close to 1 year (Figure 6, the curves cross around T = 1 year). δ2H in storage depends on the δ2H of precipitation, which essentially varies over a whole year. Thus, the unimodal approximation matches the time scale of δ2H dynamics, and the simulations of δ2H in the stream are accurate. For all the other solutes, the large differences between the unimodal approximation and the true age description exactly correspond to the time scales of the tracer dynamics in storage, and the simulations are wrong.
6 DISCUSSION
6.1 Relevance of water age multimodality for tracers
Our results confirm the ability of age-based lumped models to simulate tracer dynamics in discharge. Unimodal SAS functions only had one or two parameters but they provided satisfactory simulations with good performance measures. This is because they managed to capture the average tracer dynamics (e.g., as seen through a moving average) resulting from the range of travel times that characterises the majority of the discharge. For the lysimeter, 50% of the water left via the bottom drainage in less than 100 days, which is captured by the power function and the single normal function well enough (Figure 4). For the virtual catchment, 50% of the water left via discharge in less than 1 year, which is captured by the single gamma distribution well enough (Figure 6). Detailed characteristics of the tracer observations such as flashy responses associated with small discharge volumes (e.g., short-term dynamics within each peak in Figure 3, months 24–30, 12–16, and 52–56 in Figure 5), or secondary peaks (Oct–Jan in Figure 3) do not need to be reproduced to obtain satisfactory values of the standard objective functions used for calibration. Yet, these detailed characteristics represent transport processes acting at different time scales and they can be highly informative on the deficiencies of a too simple model. They could also be used as ‘soft data’ (Seibert & McDonnell, 2002) along with experimental knowledge to justify the selection of more complex age models accounting for more hydrological processes (as in Rodriguez & Klaus, 2019).
Composite SAS functions increased model complexity but in return gave more accurate process representation. For instance, the double normal model applied to the lysimeter experiment (Section 4) was able to capture the two main timescales at which the tracer was transported through the lysimeter, while the simpler models underestimated the impact of longer transit times (Figures 3 and 4). In some cases, the increase in performance could be insufficient to justify the use of additional parameters. For example, for the catchment-scale virtual experiment, the performance in δ2H of the single gamma model does not motivate the use of a more complex model. This highlights that a single tracer measured in inflows and outflows may not allow the identification of all peaks of the TTDs. Furthermore, the virtual catchment experiment showed that the simpler model, although efficient enough in reproducing δ2H, essentially failed to simulate the three other tracers. The unimodal approximation neglected the short term response of the catchment, it delayed the middle term response, and it overestimated the long-term response. This shows that simulations of solute chemistry require an accurate estimation of the TTDs that goes beyond conservative tracer input–output relationships, and that accounts for the potential multiple modes of transport associated with different age fractions (Benettin et al., 2017). On the other hand, this also means that stream chemistry data (Neal et al., 2013) and new available tracers (Abbott et al., 2016; Hissler, Stille, Guignard, Iffly, & Pfister, 2014; Pfister et al., 2017; Visser et al., 2019) can be used to validate TTDs deduced from a conservative tracer input–output relationship (Guillet et al., 2019). Overall, these results highlight the need for new methods that do not calibrate TTDs using tracer input–output relationships but instead measure the TTDs directly, such as (Kim et al., 2016; Kirchner, 2019).
Several characteristics shared by the two hydrological systems described in Sections 4 and 5 made the comparison between unimodal and multimodal models possible. Contrary to previous studies on the shape of TTDs and SAS functions, our work was not impacted by large unknowns such as total storage (Birkel, Soulsby, & Tetzlaff, 2011; Rodriguez, McGuire, & Klaus, 2018) and unknown past inputs and initial conditions (Hrachowitz, Soulsby, Tetzlaff, & Malcolm, 2011). In addition, there was no uncertainty related to hydrological and tracer data regarding the spatial homogeneity of inputs, the calculations of ET, the limited tracer sampling frequency (Hrachowitz et al., 2011; Kirchner, Feng, Neal, & Robson, 2004; Stockinger et al., 2016) and record length (McGuire & McDonnell, 2006). In addition, we avoided using several common modelling assumptions that may have a noticeable impact on the inferred age distributions. These assumptions include the no-flow boundaries defining the control volume to ensure the closure of the mass balance (related to the calculation of actual ET and/or deep water losses), and the ages of water used by ET. van der Velde et al. (2015) and Ali, Fiori, and Russo (2014) showed that the ET flux and its TTD influence the TTD of discharge. Further research is needed to improve our understanding of the role of the water ages abstracted by ET on the shapes of the discharge TTD (via the effect of Ω ET on S T or P S hence p Q).
6.2 Interpretations of the water age uni- or multi-modality
To understand the possible reasons for the multimodal character of TTDs not simply caused by time-varying inflows and outflows, it may useful to see the travel time T of an individual water parcel from a Lagrangian point of view (i.e., following the water parcel on its journey). The travel time can be expressed as T = L/v, where L is the total length of the flow path taken by that particle (from entry into the system to exit), and v is the harmonic mean of Lagrangian velocities of that parcel along the considered flow path of length L (see SI, section S4). The harmonic mean of velocities is used to obtain an average that appropriately summarises the entire history of Lagrangian velocities along the flow path in a single measure. We use this particular point of view as a simplification that helps us focusing on the role of flow path lengths and velocities in shaping the TTD, whereas potentially more complex Lagrangian representations of water transport are possible (Berkowitz, Cortis, Dentz, & Scher, 2006; Botter, Bertuzzo, Bellin, & Rinaldo, 2005; Cvetkovic, Carstens, Selroos, & Destouni, 2012; Davies, Beven, Rodhe, Nyberg, & Bishop, 2013; Sternagel, Loritz, Wilcke, & Zehe, 2019; Zehe & Jackisch, 2016). Using a similar approach, Kirchner, Feng, and Neal (2001) calculated the shape of TTDs for theoretical catchment geometries corresponding to various distributions of L [called width function w(x), with x the distance to the stream]. Seeing both L and v as random variables makes the TTD a ratio distribution (Rinaldo, Vodel, Rigon, & Rodriguez-Iturbe, 1995). Ratio distributions generally do not have simple analytical expressions (Curtiss, 1941), meaning that the shape of the TTDs can be complex, with potentially many peaks and often a heavy tail. In particular, if the distributions of L and v are multimodal for various physical reasons (see Section 2), it can be expected that the TTD is multimodal as well (see Figure 7, note, however, the implicit assumption of independence between L and v). This has been recently observed in a catchment in Switzerland where the extension and the contraction of the flow network for different wetness conditions creates complex patterns of flow paths leading to multimodal TTDs (assuming a constant, homogeneous velocity field) (van Meerveld, Kirchner, Vis, Assendelft, & Seibert, 2019). In reality, the shape of TTDs will depend on the relationship between L and v. In catchments, it can be expected that the location of a given input will determine L, but also v. For instance, in heterogeneous media, dispersion causes the distribution of v to broaden and flatten with increasing L (Le Borgne, de Dreuzy, Davy, & Bour, 2007). This can be interpreted as an increased probability with time that the advective velocity of a water particle has changed along its transport (e.g., as in Davies et al., 2013; Scaini, Amvrosiadi, Hissler, Pfister, & Beven, 2019; Zehe & Jackisch, 2016). Therefore, L and v are probably not independent, making the TTD, as the pdf of their ratio, difficult to estimate a priori (Curtiss, 1941). Consequently, even a complete knowledge of the distributions of L and v may not allow to determine the TTD as it was done in Figure 7 by assuming that L and v are independent.
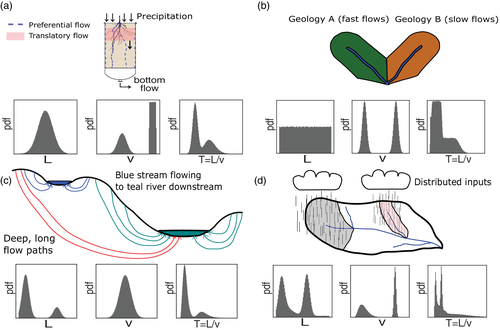
At large scales (e.g., hillslope, catchment), L can be much larger than the scale of the heterogeneous properties of the porous media (i.e., different pore sizes, macropore network, rocks, roots, etc.). As a result, dispersion is strong and the differences in travel time T between the water particles coming from different parts of the catchment (with different L) can be attenuated. This may explain the general validity of unimodal TTDs in catchments (McGuire & McDonnell, 2006). For instance, Kirchner et al. (2001) found that low Péclet numbers (i.e., advection ≪ dispersion) are needed to explain the gamma shape of TTDs suggested by the spectral slopes of stream chemistry. At smaller scales, L can be small compared with the scale of heterogeneities (i.e., advection ≫ dispersion) such that the TTDs are more likely to be multimodal. For example, preferential flow in soils can cause a strongly bimodal distribution for v. In the lysimeter at EPFL (Section 4), flow paths are mostly vertical and the transport distance is probably narrowly distributed around L = 2.5 m (the depth of the soil column). The multimodal TTDs obtained in the lysimeter are thus due to contrasting velocities coming from preferential flow vs. matrix flow in the lysimeter (Figure 7a), which was clearly identified from comparisons of tracers measured in soil water vs. discharge (Benettin, Queloz, Bensimon, McDonnell, & Rinaldo, 2019). The importance of preferential flow in soils for catchment-scale TTDs may be difficult to evaluate. Glaser, Jackisch, Hopp, and Klaus (2019) showed in the Weierbach catchment (Luxembourg) that rainfall-runoff simulations were not improved by modelling vertical preferential flow at the catchment scale, using the soil preferential flow parameters deduced from plot-scale tracer breakthrough experiments. However, non-uniform lateral flow (similar to lateral preferential flow) appeared to be an important mechanism for discharge generation in this catchment, and it could be implemented in the model by using a highly conductive horizontal soil layer (Glaser et al., 2019). Different conclusions regarding preferential flow were found by van Schaik et al. (2014), who highlighted its non-negligible role for runoff simulations during extreme rainfall events in a semi-arid catchment in Spain. This suggests that preferential flow has an influence on a catchment TTD only if it provides sufficient volumes of water to the outlet.
Our results suggest that different hydrological processes generate multimodal TTDs only if these processes result in contrasting water ages and provide comparable volumes of water. For instance, if surface runoff reaches the stream in 1 hour, there may be no detectable peak in the TTD around T = 1 hour if 99% of discharge is generated by subsurface stormflow having water of at least 1 week of age. Similarly, if two recharge areas to a groundwater well provide similar water ages, the TTD of the well will be unimodal regardless of the sizes of each recharging area. Composite SAS functions provide an intuitive mathematical representation: multiple peaks are observed in the marginal TTDs if the different probability distribution functions summed together in the SAS function are far from each other in the age domain (T, P S, or S T), and if they are associated with weights λ (Equations S3 and S6) that are comparable (e.g., 25% and 75%).
6.3 Process knowledge and the shape of composite SAS functions
The characteristics (number of peaks, peak amplitudes, and age ranges) of multimodal age distributions can be deduced from experimental knowledge of hydrological processes and are useful to test hypotheses about these processes (Rodriguez & Klaus, 2019). In this case, a step-wise increase in the complexity of the age distributions may allow a better understanding of the complexity of the hydrological system enciphered in the tracer data. For instance, one may start with an age component for young water after detecting surface runoff in the catchment and mapping its extent from manual survey and/or aerial images. The characteristics of this age component may then be deduced from GIS analysis, using initially simple assumptions of flow paths and water velocities (c.f., van Meerveld et al., 2019). Spectral slopes of stream chemistry suggest that a gamma distribution with a shape parameter k < 1 may be an appropriate candidate for this young water component (Kirchner et al., 2000). However, a uniform distribution on a small age range may perform well for tracer simulations, and may avoid numerical issues due to the asymptote at age 0 of the gamma distribution with k < 1 (Rodriguez & Klaus, 2019). Older water components may then be deduced from estimates of soil water storage and age (based for instance on soil moisture measurements, hydraulic turnover time) and hydrogeological knowledge of the aquifer (no-flow boundaries, hydraulic conductivity, groundwater depth) for the groundwater component. The functional form of older components may be chosen among popular functions, such as the power function (Benettin, Soulsby, et al., 2017; Queloz, Carraro, et al., 2015) or the beta distribution (Danesh-Yazdi, Botter, & Foufoula-Georgiou, 2017; Kaandorp et al., 2018; van der Velde et al., 2015; Yang et al., 2018) to use P S as a variable. The uniform distribution or the gamma distribution (Harman, 2015; Rodriguez & Klaus, 2019; Smith, Tetzlaff, & Soulsby, 2018) may be chosen to use S T instead, which may reduce the uncertainties related to the usually unknown total storage.
On the other hand, composite SAS functions may more easily lead to over-parameterization and the related parameter uncertainties (hence age uncertainties) compared with simpler models. In some cases, it may not be possible to conclude that age multimodality exists in the investigated hydrological system (even if it is true) because the available data does not justify the use of more complex models (c.f., for the virtual catchment when considering only δ2H). This may happen in particular when the employed tracer data is at insufficient resolution or when its record length is too short to reveal the influence of contrasting water age contributions to the outlet. Furthermore, lumped models based on water ages often do not allow identifying hydrological processes on their own due to the ‘compression’ of information about the hydrological system. This compression is the consequence of the current inability of mathematical models to perfectly reflect all the perceptual information contained in process knowledge. A given composite TTD or SAS function can correspond to many configurations of processes (c.f., Figure 7a,c). This means that the details on the various hydrological processes aggregating to catchment response cannot be derived from water ages alone. Only precise knowledge of potential water flow paths or velocities (such as for the EPFL lysimeter or Biosphere 2 hillslope) may allow such inductive reasoning. Alternatively, such inferences may be possible by linking parts of the TTDs or SAS functions (e.g., components and age ranges) inferred from one tracer to different end-members and spatial contributions identified from other independent tracers. This could be done by sampling more than just catchment inputs (precipitation) and outputs (e.g., streamflow), and by using numerous tracers in End Member Mixing Analysis (Christophersen, Neal, Hooper, Vogt, & Andersen, 1990; Correa et al., 2017; Martinez-Carreras et al., 2015), or by using Bayesian Mixing (Evaristo et al., 2019; Parnell et al., 2013; Zhang, Evaristo, Li, Si, & McDonnell, 2017) when the number of tracers is limited.
6.4 Modelling complex hydrological systems with complex age distributions
The composite TTDs (Leray et al., 2016) and the composite SAS functions proposed in this study (see also Rodriguez & Klaus, 2019) have the ability to embed a larger variety of processes compared with traditional lumped models, but they are still analytical approximations of potentially more complex distributions. Shape-free distributions are more flexible and could better represent the range of transport processes in hydrological systems. Shape-free distributions can be determined from time series analyses (Turner & Macpherson, 1990), by deconvoluting the tracer output signal (Cirpka et al., 2007; Gooseff et al., 2011; Luo & Cirpka, 2008; McCallum, Engdahl, Ginn, & Cook, 2014), from Bayesian inference using several tracers (Massoudieh et al., 2012; Massoudieh, Visser, Sharifi, & Broers, 2014), or from multilinear regression analysis (Kirchner, 2019). However, these methods require a large number of tracers (Massoudieh et al., 2014), or tracer time series that are well conditioned for numerical reasons (Kirchner, 2019), and the resulting solutions can be highly non-unique (McCallum et al., 2014). Eventually, analytical solutions can perform better than shape-free solutions in some cases (Massoudieh et al., 2014). Composite TTDs and SAS functions could thus offer a good balance between model parsimony and sufficient representation of the relevant processes at the scale of interest, which is precisely the aim of lumped models.
Spatially explicit models allow a detailed representation of flow paths and transport media properties. These suggest that complex SAS functions and TTD shapes emerge from specific flow paths (Kaandorp et al., 2018; Pangle et al., 2017; Wilusz et al., 2020; Yang et al., 2018) or from various conductivity (or velocity) distributions in the system (Danesh-Yazdi et al., 2018; Davies et al., 2013). Distributed models also allow linking water sources to travel times, providing complementary spatial information that cannot be visualised in lumped models (Sayama & McDonnell, 2009; van Huijgevoort, Tetzlaff, Sutanudjaja, & Soulsby, 2016). However, these models usually require more detailed initial and boundary conditions (Delavau, Stadnyk, & Holmes, 2017; Jing et al., 2019), which get more uncertain at larger scales. In addition, these models are more computationally expensive than their lumped counterparts, and thus require efficient parallelised numerical solutions (Maxwell, Condon, Danesh-Yazdi, & Bearup, 2018). While we often do not have the means to validate the age results from these models, they are useful to explore the possible complexities of the age distributions and relate them to the dominant hydrological processes (Wilusz et al., 2020). This is especially true as these models can much better represent the small-scale mechanisms leading to the observed hydrological processes compared with lumped models, provided that sufficient experimental data is available to characterise well the associated small-scale heterogeneities. In particular, this means that contrary to lumped models, spatially explicit models allow identifying which hydrological processes may lead to complex TTDs and SAS functions.
7 CONCLUSIONS
Simple TTDs with mainly one peak (or mode) have been prevalent in the last decades because more elaborate models were not needed to obtain a satisfactory tracer simulation. Nevertheless, multimodal TTDs can better describe how different groups of water ages emerge at the outlet of a catchment because of complex flow paths and water velocity distributions. Recent tracer and numerical experiments (including the two examples presented here) show that TTDs with multiple peaks can better simulate the detailed tracer dynamics observed in high-resolution tracer measurements. Moreover, using the TTDs for water chemistry simulations can expose the flaws of a too simple TTD model that underestimates/overestimates large portions of the age distribution with implications for tracer concentrations. Our work highlights that, in various hydrological systems, TTDs are likely to be multimodal because of contrasts in flowpath length or velocity (or both). We provided examples of situations where multimodal TTDs are not simply caused by the dynamics of hydrological fluxes. Multimodality can occur due to: preferential flows in soils, heterogeneity of the catchment geological substratum, deep subsurface flows beyond catchment topographical boundaries, and distributed precipitation over large catchments. Different hydrological processes providing comparable volumes of waters with contrasting ages to an outlet will likely result in multimodal TTDs.
ACKNOWLEDGEMENTS
PB thanks ENAC school at EPFL for financial support. NBR (FNR/CORE/C14/SR/8353440/STORE-AGE) and JK (FNR/CORE/C17/SR/11702136/EFFECT) thank the Luxembourg National Research Fund.
Open Research
DATA AVAILABILITY STATEMENT
The codes and data used in this study are available on Zenodo (Virtual catchment: http://doi.org/10.5281/zenodo.3686582 and Lysimeter: http://doi.org/10.5281/zenodo.3686596). The mathematical and numerical approaches are very similar to tran-SAS (Benettin & Bertuzzo, 2018). We recommend new users to start with tran-SAS and to define the customized SAS functions they need, following one of the initial SAS function template files.




