2.1 Participants

Thirty healthy right-handed volunteers (15 females; age 22–26 years; mean age 24 years) participated in the study. The sample size was estimated based on a medium effect size of $$$ f=0.25 $$$ (Cohen 1992) at $$$ \alpha =0.05 $$$ for a $$$ 2\times 6 $$$ repeated measures analysis of variance (rmANOVA) that examined both interaction effects and main effects, assuming a conservative correlation of 0.5 among the 6 levels of repeated measures (Potvin and Schutz 2000). According to G*Power 3.1 (Faul et al. 2007), a minimum sample size of 20 is required to achieve statistical power of $$$ 1-\beta >0.8 $$$. Considering potential data exclusions, we ultimately recruited 30 participants, a common sample size used in behavioral research (Brysbaert 2019), which also aligns with a previous functional neuroimaging study on longitudinal motor training in healthy populations with 5 training sessions (Choi et al. 2020).

Participants were recruited through online advertisements among postgraduate students majoring in computer science and technology. They were naive to the study's purpose and had no prior knowledge of psychology or neuroscience research. Their familiarity with computer interface and gamified digital environment ensured similar levels of baseline skills and higher learning rates, while also enhancing participant retention and sustained engagement over the 5-day training period. Inclusion criteria were: (1) normal or corrected-to-normal vision, (2) no history of psychiatric and/or neurological disorder, (3) no history of motor impairments and/or sensory-motor deficits, (4) right handedness, as assessed by Edinburgh Handedness Inventory (Oldfield 1971) with a criterion of laterality quotient $$$ >60 $$$, (5) no severe discomfort or complications associated with wearing head-mounted neuroimaging devices. The study was approved by Ethics Committee of Department of Psychology of Sun Yat-sen University (2020-0515-0140) and completed in accordance with the Declaration of Helsinki. All participants gave written informed consent and were compensated CNY 200, plus a bonus up to CNY 150 depending on performance.

2.2 Experimental Design

2.2.2 Procedures

Each participant visited the laboratory for 5 consecutive days and completed 5 experimental sessions (1 Session/Day) (Figure 1A). The 5-day training period, which corresponds to a fast learning stage, was chosen based on a prior test of 12 consecutive training sessions, where the participant (author X.L.) exhibited rapid performance improvements within the first 5 sessions (see Figure S1). We used a block-design continuous target tracking task, consisting of 6 conditions with different difficulty levels, labeled from L1 (easiest) to L6 (hardest). Different difficulty conditions were presented in separate blocks and counterbalanced across participants within each session. Within each block, after an initial 15 s fixation period, participants performed 5 repetitions of a 15 s tracking task, each interleaved with a 15 s fixation period, resulting in a total duration of 165 s per block (Figure 1B). In total, participants completed 30 trials (6 Difficulty levels × 5 Repetitions) during each session.

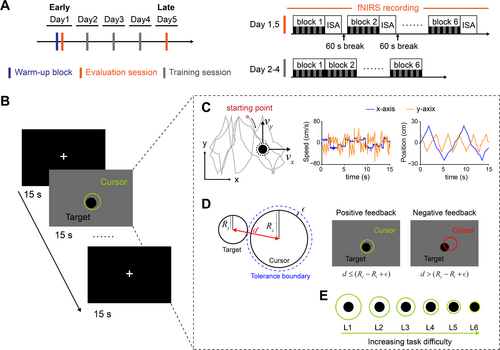
The experiment includes 2 evaluation sessions and 3 training sessions. For familiarization, participants completed a warm-up block consisting of 6 trials, with each difficulty level presented once in a pseudorandom order. During the evaluation sessions (Day 1 and Day 5), fNIRS signals were recorded throughout the entire experimental period to evaluate the task-related neural activation patterns in the early (Day 1) and late (Day 5) stages of motor learning. After each block, participants provided a rating of their subjective workload level, as defined by a 5-point (5–excessive, 4–high, 3–comfortable, 2–relaxed, 1–under utilized) instantaneous self-assessment (ISA) rating scale (Tattersall and Foord 1996). There was no time limit for this assessment. Here, we chose the ISA rating because it provides a fast response method that allows for continuous monitoring of changes in subjective workload across different experimental blocks. Following the ISA rating, participants took a 60 s inter-block break, during which a countdown timer was displayed in the center of the screen, before the next block began. During the training sessions (Day 2–4), participants only performed the main tasks without fNIRS recordings and ISA ratings. They could take a break after each block until they clicked a button to proceed.

For incentivization, a ranking list based on the overall success rate of each participant was displayed at the end of each session. Participants were informed that, after all participants had completed the experiment, the top three performers in the experiment would receive an additional bonus.

2.2.3 Continuous Target Tracking Task

The experimental task was generated using Unity3D software (version 5.6.5f1). Participants used a joystick (new T16000 FCS, Thrustmaster) with their right hand to control a circle (the cursor) and track the movement of a black disc (the target) in a two-dimensional (2D) plane as closely as possible. During the task, participants could freely gaze at any location on the screen, with no constraints on fixation points.

The target movement patterns were manipulated by varying their speed over time in the horizontal (x-axis) and vertical (y-axis) directions, following unpredictable trajectories (see Supporting Information for more details). Figure 1C shows a representative trajectory of the target movements within a single trial, as well as the changes in speed and position over time in both the x- and y-axes (with the origin at the center of the screen). In our experiment, target trajectories were identical within each block but varied across blocks, sessions, and participants. The x- and y-coordinates of the target and cursor positions were recorded throughout the 6 experimental sessions as behavioral data.

Reward feedback based on tracking performance was given by changing the cursor color: it turned green (positive feedback) when the target was within the cursor's boundary; otherwise, it turned red (negative feedback). Let $$$ {R}_c $$$ and $$$ {R}_t $$$ be the radii of the cursor and target, respectively. We defined a tolerance boundary as an extension of $$$ {R}_c $$$ by a tolerance of $$$ \upvarepsilon $$$. To judge whether the target is within the cursor's boundary, we compared the distance, $$$ d $$$, between the center of the target and cursor and a threshold given by $$$ {R}_c-{R}_t+\upvarepsilon $$$ (Figure 1D):

$$$$ {\displaystyle \begin{array}{l}d\le \left({R}_c-{R}_t+\upvarepsilon \right),\kern1em \mathrm{Positive}\kern0.5em \mathrm{feedback};\\ {}d>\left({R}_c-{R}_t+\upvarepsilon \right),\kern1em \mathrm{Negative}\kern0.5em \mathrm{feedback},\end{array}} $$$$(1)

The task difficulty was manipulated by varying the cursor size (as illustrated in Figure 1E, reducing cursor size $$$ {R}_c $$$ increased task difficulty), quantified by task index of difficulty

$$$$ \mathrm{ID}=-{\log}_2\left(\frac{R_c-{R}_t+\upvarepsilon}{2{R}_t}\right), $$$$(2)

We set $$$ {R}_t=1.5 $$$ cm and $$$ \upvarepsilon =3 $$$ mm as fixed parameters throughout the whole experiment, so ID was solely dependent on $$$ {R}_c\in \left\{\mathrm{2.5,2.0,1.8,1.5,1.3,1}\right\}\cdot {R}_t $$$. According to Equation (2), ID corresponding to each task difficulty level was $$$ \mathrm{ID}\in \left\{\mathrm{0.23,0.74,1.00,1.51,2.00,3.32}\right\} $$$ (from L1 to L6).

2.2.3.1 fNIRS Data Acquisition

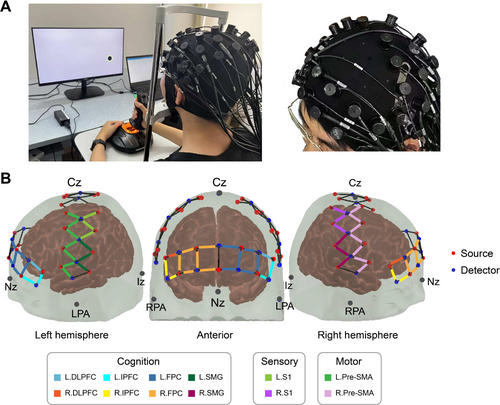
Cerebral hemodynamic signals were recorded by a commercial continuous-wave fNIRS device (Nirsmart, Danyang Huichuang Medical Equipment). The system uses two-wavelength (740 nm and 850 nm) light-emitting diode (LED) as light sources, with a sample rate of 10 Hz. A total of 23 sources and 15 detectors created 47 long-separation channels with a source-detector distance of 3 cm. The fNIRS cap was symmetrically positioned on the participant's head, aligning Cz to the intersection of the sagittal and coronal planes. The cap was then adjusted according to the international 10–20 system (Klem 1999)—with special marks on the cap—to ensure alignment with anatomical landmarks. To ensure consistent placement, participants performed a simple hand-grasping task before fNIRS recordings, verifying activation in contralateral sensorimotor areas (S1 and Pre-SMA).

To determine the spatial locations of the channels, we used a Patriot 3D Digitizer (Polhemus, USA) to collect the anatomical locations of all the optodes and 5 reference landmarks (Cz, Nz, Iz, LPA, and RPA). The channel locations were then converted to the Montreal Neurological Institute (MNI) coordinates using the NIRS-SPM toolbox (Ye et al. 2009). As illustrated in Figure 2, we selected 12 ROIs in the frontoparietal areas based on the Talairach Daemon labeled Brodmann area (BA) (Lancaster et al. 2000), which are associated with three different brain functions, including cognition areas: Dorsolateral prefrontal cortex (DLPFC, BA–46), inferior prefrontal cortex (IPFC, BA–47), frontopolar cortex (FPC, BA–10), and supramarginal gyrus (SMG, BA–40); sensory areas: Primary somatosensory cortex (S1, BA–1, 2, 3); and motor areas: Pre-motor and supplementary motor area (Pre-SMA, BA–6).

2.3 Data Analysis

2.4 Statistics

We performed statistical analysis using Matlab (version R2020b), JASP (version 0.18.1) and R (version 4.3.1). Statistical analyses focused on behavioral and neural results in the early and late stages to examine learning effects on load-dependent patterns in behavioral performance and neural representation following longitudinal motor training. For all the group level analyses, outliers were identified based on the ‘3 sigma’ rule—data points that exceed three SD from the mean.

Firstly, we examined the effect of learning stage and difficulty level on behavioral outcomes, by applying 2 (Learning stage: Early, Late) × 6 (Difficulty level: L1, L2, L3, L4, L5, L6) two-way rmANOVA on the three different behavioral measures: SR, ER, and VAR, with paired t-test for post hoc analysis. Normality was assessed using the Shapiro–Wilk test, and sphericity was evaluated using Mauchly's test. When normality or sphericity assumptions were violated, we employed a permutation-based rmANOVA ($$$ {10}^5 $$$ permutations) and performed Wilcoxon signed-rank tests for post hoc analysis. To control for multiple comparisons, Bonferroni correction was applied in post hoc analysis. We also examined the relationship between the two measures of task load (objective: ID; subjective: ISA) and their associations with three behavioral measures (SR, ER, and VAR) at individual level using Spearman's rank correlation coefficients. Subsequently, we applied paired t-test at group level to compare correlation coefficients between the early and late stages. For all paired comparisons between the early and late stages, participants with missing data in either stage were excluded.

Next, we examined learning-induced plastic changes in neural activity after longitudinal motor training, collapsing data across different load levels within each stage of learning. First, we compared the differential cortical activation (i.e., beta values) in the early and late stages using paired t-test. To assess the relationship between behavioral and neural changes, we conducted partial Pearson correlation between $$$ \Delta \mathrm{Beta}\kern0.5em \left({\mathrm{Beta}}_{\mathrm{late}}-{\mathrm{Beta}}_{\mathrm{early}}\right) $$$ and $$$ \Delta \mathrm{Behavior}\kern0.5em \left({\mathrm{Behavior}}_{\mathrm{late}}-{\mathrm{Behavior}}_{\mathrm{early}}\right) $$$, controlling baseline activation ($$$ {\mathrm{Beta}}_{\mathrm{early}} $$$) and behavior ($$$ {\mathrm{Behavior}}_{\mathrm{early}} $$$) as covariates. Additionally, we applied Pearson correlation analysis to examine whether task-related cortical activation predicts individual behavioral outcomes at different learning stages. These analyses were performed separately for each ROI and behavioral measure (ER, VAR, and SR).

Lastly, we explored the effect of motor learning on load-dependent cortical activation patterns. First, we tested whether the relationship between cortical activation and task load (either ID or ISA) was better characterized by a linear or quadratic model using LMM. This analysis was conducted for each ROI separately to explore region-specific effects. If one ROI was found to exhibit different load-dependent patterns in the early and late stages, we performed a moderation analysis to determine whether motor learning affected these changes. Details on the model comparison between linear and quadratic models and the moderation analysis are provided in the Supporting Information.

All data are presented as mean ± SEM (standard error of the mean), unless otherwise indicated. P-values were adjusted across 12 ROIs using Benjamini and Hochberg false discovery rate (FDR) procedure (Benjamini and Hochberg 1995). Raw p-values are denoted by $$$ p $$$, and adjusted p-values after FDR correction are denoted by $$$ {q}_{\left(\mathrm{FDR}\right)} $$$. Statistical significance level was set at 0.05. Effect sizes were estimated by partial eta-squared values ($$$ {\eta}_p^2 $$$).

3.1 Effective Motor Skill Learning as Training Progressed

It is evident that participants successfully learned the tracking task. As illustrated by the target and cursor trajectories of one representative participant, the participant's hand (i.e., cursor) movements followed the target movements more accurately after training, and the cursor trajectories became more consistent across trials within each block (Figure 3A). Despite the overnight declines in behavioral performance, participants exhibited continuous improvement in tracking performance as learning progressed, indicated by the increasing success rate and decreasing tracking error (i.e., RMSE) across trials (Figure 3B). It should be noted that, because we used a within-subject experimental design, the observed improvement in behavioral performance after training reflects an aggregated learning effect across all difficulty levels.

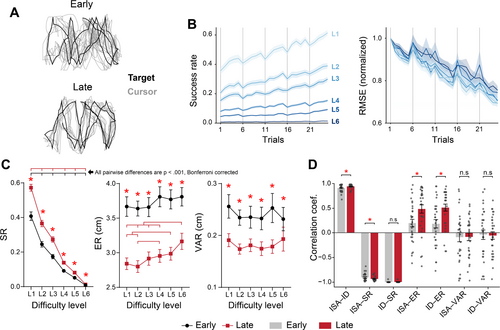
To further examine the effects of difficulty level and learning stage on behavioral performance, we conducted 2 (Learning stage: Early, Late) × 6 (Difficulty level: L1, L2, L3, L4, L5, L6) two-way rmANOVA on each of the behavioral measures: SR, ER, and VAR. Interaction effect between learning stage and difficulty level was significant only for SR ($$$ {F}_{\mathrm{5,145}}=47.05,\kern0.5em p<0.001,\kern0.5em {\eta}_p^2=0.62 $$$, permutation-based rmANOVA). Main effect of learning stage was significant for all three behavioral measures (SR: $$$ {F}_{1,29}=371.13,\kern0.5em p<0.001,\kern0.5em {\eta}_p^2=0.93 $$$, permutation-based rmANOVA; ER: $$$ {F}_{1,27}=261.17,\kern0.5em p<0.001,\kern0.5em {\eta}_p^2=0.91 $$$, rmANOVA; VAR: $$$ {F}_{1,29}=30.29,\kern0.5em p<0.001,\kern0.5em {\eta}_p^2=0.51 $$$, permutation-based rmANOVA). Main effect of difficulty level was significant for SR ($$$ {F}_{\mathrm{5,145}}=453.15,\kern0.5em p<0.001,\kern0.5em {\eta}_p^2=0.94 $$$, permutation-based rmANOVA) and ER ($$$ {F}_{\mathrm{5,135}}=7.80,\kern0.5em p<0.001,\kern0.5em {\eta}_p^2=0.22 $$$, rmANOVA).

Post hoc analyses revealed significant increase in SR (all $$$ p<0.001 $$$), and decrease in ER (all $$$ p<0.001 $$$) and VAR (all $$$ p<0.039 $$$) after learning, regardless of difficulty level. In both the early and late stages, significant differences were found in all pairwise comparisons between difficulty levels for SR (all $$$ p<0.001 $$$, Bonferroni corrected), while SR decreased with increasing difficulty levels. By contrast, significant difference between difficulty levels was found ER only in the late stage ($$$ p<0.05 $$$, Bonferroni corrected, for pairs: L1–L5, L1–L6, L2–L4, L2–L5, L2–L6, L3–L6, and L4–L6) (Figure 3C). Notably, differences in behavioral performance across difficulty levels emerged only found in the late stage, where performance declined at high difficulty levels, as indicated by increased ER (i.e., reduced tracking accuracy).

3.2 Relationship Between Task Load and Behavior

In our experiment, we used two different measures to quantify task load: an objective evaluation based on task ID, as defined by Equation (2), and a subjective evaluation of workload using the ISA scale. We investigated the relationship between these two task load measures and examined their associations with behavioral performance at the individual level. For all participants, ISA was positively correlated with ID (all $$$ rho>0.676 $$$, Spearman correlation), and this correlation was stronger in the late stage ($$$ {t}_{29}=2.436,\kern0.5em p=0.021 $$$, paired t-test), suggesting a monotonic mapping from objective task load to subjective workload. Then, we performed separate correlation analysis for all possible pairs between any of the task load and behavioral measures. The strongest correlation was found for the relationship between ISA/ID and SR (ISA–SR: all $$$ rho<-0.676 $$$; ID–SR: all $$$ rho<0.-943 $$$, Spearman correlation). More specifically, the magnitude of the correlation between ISA and SR was stronger in the late stage ($$$ {t}_{29}=-2.133,\kern0.5em p=0.042 $$$, paired t-test), while no significant difference was found in the correlation between ID and SR correlation ($$$ {t}_{29}=0.571,\kern0.5em p=0.573 $$$, paired t-test). Although the correlations between ISA/ID and ER were weaker and exhibited large inter-individual variability, these associations were strengthened after training (ISA–ER: $$$ {t}_{29}=2.338,\kern0.5em p=0.027 $$$; ID–ER: $$$ {t}_{29}=2.867,\kern0.5em p=0.008 $$$, paired t-test). In contrast, there was no clear association between ISA/ID and VAR (Figure 3D). This suggests that task load primarily regulated reward outcomes rather than absolute movement accuracy and consistency across trials.

3.3 Learning-Induced Changes in Cortical Activation and Brain-Behavior Relationships

We first performed ROI-wise analysis comparing the early versus late task-related cortical activation (i.e., beta value). To focus on the overall learning effect after training, beta values were collapsed across different difficulty levels. Significant difference was only observed in R.IPFC, showing increased cortical activation in the late stage ($$$ {t}_{143}=3.406,\kern0.5em {q}_{\left(\mathrm{FDR}\right)}=0.010 $$$, paired t-test) (Figure 4A, see Figure S3 for the comparisons of all ROIs).

In the following analysis, we examined whether and how cortical activation was associated with behavioral performance, as well as the learning-induced changes in these associations. To this end, we conducted separate correlation analysis between beta value and each of the behavioral measures. The results revealed consistent negative correlation between beta value and ER, indicating that participants with higher cortical activation exhibited lower tracking error (i.e., better performance), regardless of ROIs and stages of learning. The overall correlation between beta value and ER was strengthened after training (Early: mean $$$ r=-0.197 $$$; Late: mean $$$ r=-0.299 $$$, Pearson correlation). Specifically, significant correlation was observed in both stages of learning, while these correlations were stronger and more widespread in the late stage (Figure 5A, Table S2).

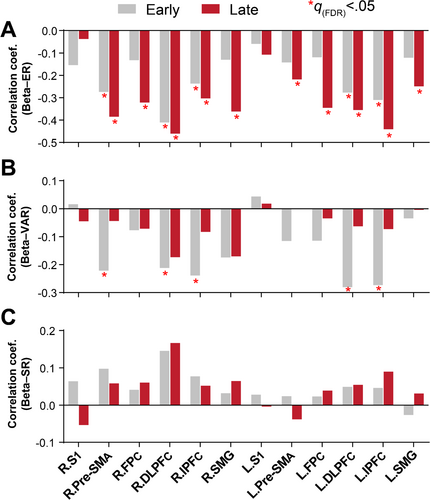
On the contrary, correlation between beta value and VAR decreased after training (Early: mean $$$ r=-0.140 $$$; Late: mean $$$ r=-0.062 $$$, Pearson correlation), with significant correlation observed only in the early stage. Additionally, the overall strength of the Beta–VAR correlation was weaker compared to the Beta–ER correlation (Figure 5B, Table S3). However, there was no clear association between beta value and SR in any of the ROIs or stages of learning (Figure 5C, Table S4). We further conduced separate correlation analyses at each difficulty level (see results in Figure S5). Significant correlations were only found for the Beta–ER and Beta–SR relationships in the late stages, particularly at low difficulty levels (L1-L3). Also, we examined the relationship between cortical activation and each of the task load measures (i.e., ISA or ID), while no significant correlation was found in any of the ROIs or stages (all $$$ \mid rho\mid <0.113,\kern0.5em {q}_{\left(\mathrm{FDR}\right)}>0.741 $$$, Spearman correlation; Tables S5 and S6).

We further tested whether changes in cortical activation is associated with changes in behavioral outcomes. To control the effect of baseline activation and behavior, we calculated the partial Pearson correlation between changes in cortical activation ($$$ \Delta \mathrm{Beta} $$$) and changes in any of the behavioral measures ($$$ \Delta $$$ ER, $$$ \Delta $$$ VAR, or $$$ \Delta $$$ SR), with cortical activation and behavior in the early stage as covariates. All the changes were calculated as the differences between late and early learning stages (Late—Early). Significant correlation was only found in the relationship between $$$ \Delta $$$ Beta and $$$ \Delta $$$ ER in L.IPFC ($$$ r=-0.246,{q}_{\mathrm{FDR}}=0.043 $$$, partial Pearson correlation). As shown in Figure 4B, nearly all the observations exhibited reduced tracking error after training ($$$ \Delta \mathrm{ER}<0 $$$). The negative correlation between $$$ \Delta $$$ Beta and $$$ \Delta $$$ ER indicates that greater change in activation, specifically increased beta value after training, was associated with greater behavioral improvement (i.e., reduced tracking error). In other words, individuals who had greater increases in activation after training exhibited more performance improvement.

3.4 Load-Dependent Cortical Activation Patterns

Next, we examined whether the relationship between cortical activation (i.e., beta value) and task load (i.e., ID/ISA) was better characterized by the linear or the quadratic models, and explored whether and how motor learning modulated these load-dependent cortical activation patterns. To estimate the within-subject effect, we used LMM to fit individual beta values, controlling inter-individual variability by including random slope and intercept for each individual. For the Beta–ID relationship, evidence of inverted-U patterns was observed in L.Pre-SMA in the late stage ($$$ \Delta \mathrm{AIC}=8.378,\kern0.5em {\chi}^2(1)=10.378,\kern0.5em {q}_{\left(\mathrm{FDR}\right)}=0.015 $$$, Figure 6A, see individual fits in Figure S7), while no substantial evidence favoring the quadratic model was found in the early stage (all $$$ {q}_{\left(\mathrm{FDR}\right)}>0.934 $$$). To further confirm the changes in the load-dependent activation pattern at different stages were driven by learning, we conducted subsequent moderation analysis. Results revealed that introducing interaction terms (Stage × Load and Stage × Load²) significantly improved goodness-of-fit over a reduced model without the interaction in L.Pre-SMA ($$$ \Delta \mathrm{AIC}=4.527,\kern0.5em {\chi}^2(2)=8.527,\kern0.5em p=0.014 $$$).

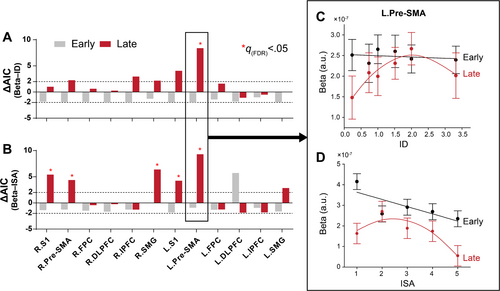
Similar analyses were conduced to estimate the Beta–ISA relationship. Consistent with the results for Beta–ID relationship, no evidence favoring the quadratic model in the early stage (all $$$ {q}_{\left(\mathrm{FDR}\right)}>0.056 $$$). In the late stage, inverted-U pattern was found in multiple regions including L.Pre-SMA ($$$ \Delta \mathrm{AIC}=10.332,\kern0.5em {\chi}^2(1)=12.332,\kern0.5em {q}_{\left(\mathrm{FDR}\right)}=0.005 $$$), R.S1 ($$$ \Delta \mathrm{AIC}=5.141,\kern0.5em {\chi}^2(1)=7.141,\kern0.5em {q}_{\left(\mathrm{FDR}\right)}=0.031 $$$) and R.SMG ($$$ \Delta \mathrm{AIC}=5.097,\kern0.5em {\chi}^2(1)=7.097,\kern0.5em {q}_{\left(\mathrm{FDR}\right)}=0.031 $$$). However, only L.Pre-SMA survived after subsequent analysis of the moderation effect of learning stage ($$$ \Delta \mathrm{AIC}=10.050,\kern0.5em {\chi}^2(2)=14.050,\kern0.5em p=0.001 $$$) (Figure 6B, see individual fits in Figure S8). Together, these results consistently indicated that an inverted-U pattern of load-dependent activation was more prominent after training, as this pattern was only observed in the late stage. Moreover, the learning-induced changes from a linear to an inverted-U shape relationship was most evident in the left (contralateral) Pre-SMA.

To demonstrate the changes in load-dependent activation pattern more clearly, we visualized the relationship between group-averaged cortical activation and task load in L.Pre-SMA. For both the Beta–ID and Beta–ISA relationships, the load-dependent activation pattern exhibited clear changes across learning stages (Figure 6C,D), shifting from a linear to an inverted-U relationship after learning (see Supporting Information for model comparison and moderation analysis). Notably, these changes were primarily driven by reduced activation at extreme load levels (i.e., the highest and lowest ID/ISA), while activation remained relatively stable at moderate load levels, where cortical activation peaked—at ID = 2.0 (i.e., difficulty level L5) for objective measure and ISA = 2 for subjective measure of task load.

4.1 Functional Roles of IPFC in Motor Learning

Motor learning can be characterized by an improvement in performance with repeated practice, which is associated with the development of executive function—a top-down process that enables people to achieve specific goals (Hallett and Grafman 1997; Diamond 2013; Cristofori et al. 2019). In our experiment, participants were incentivized to ‘catch’ the target, keeping the target inside the cursor so the cursor would turn green. To achieve this goal, they needed to track the target trajectories as close as possible. The improvement in tracking accuracy (i.e., reduced tracking error) after learning was accompanied by increased activation in the right IPFC, while individuals with greater behavioral improvements exhibited greater degree of increased activation in the left IPFC (Figure 4). The plastic changes in IPFC after learning may be attributed to enhanced ability in inhibitory control (Coxon et al. 2016; Jaffard et al. 2008; Rubia et al. 2003; Hampshire et al. 2010; Aron et al. 2014; Swick et al. 2008; Gavazzi et al. 2019)—inhibiting the unsuccessful tracking movements and reinforcing the successful ones (Laureiro-Martínez et al. 2015; Iwasaki et al. 2024). Additionally, improved inhibitory control may be linked to the exploration-exploitation tradeoff during motor learning (Dhawale et al. 2017; Krakauer et al. 2019), shifting towards an exploitation-dominated strategy in the late stage, as indicated by the reduced trial-to-trial variability following learning (Figure 3C).

Interestingly, the IPFC exhibited lateralized effects between the left and right hemisphere. While the right IPFC showed a group-level increase in activation after learning, the left IPFC activation was more closely associated with individual differences in performance improvement. This asymmetry may reflect functional specialization, as the right inferior frontal gyrus (IFG) is thought to be specialized for inhibition (Aron et al. 2014), whereas the left IFG appears to be more involved in the early development of inhibitory control (Gavazzi et al. 2019). This distinction may make the left IFG particularly sensitive to individual differences in performance improvement during learning. To our knowledge, our work is the first to demonstrate such dissociation between the left and right IPFC within a single motor learning task. However, further research is needed to elucidate the lateralized contributions of the IPFC to motor inhibition.

4.2 Task Load Regulates Reward Rather Than Behavioral Performance

In the current study, we adopted two measures of task load: objective (i.e., ID) and subjective measures (i.e., ISA). The latter reflects participants' metacognitive ability to distinguish between ‘easy’ and ‘hard’ tasks and to monitor task performance (Petrusic and Cloutier 1992; Fleming 2024). The strong positive correlation between ID and ISA (all $$$ rho>0.676 $$$, Spearman correlation) suggests a monotonic mapping between objective task load and subjective workload. Note that both ID and ISA shows similar patterns in their correlation to behavioral outcomes, being stronger to success rate (an indicator of reward) but weaker to tracking error (a measure of behavioral performance) (Figure 3C). In our task, increasing ID (i.e., decreasing cursor size) raised the required tracking accuracy to receive positive feedback, thereby reducing reward rate. Participants may have used reward rate to infer their metacognitive judgement of ISA, leading to higher ISA as ID increased. Moreover, the strengthened correlations between task load and both success rate and tracking error after learning suggest enhanced metacognitive ability in the late stage.

Notably, our findings revealed a dissociation between the effects of task load on reward and behavioral performance. As shown in Figure 3C, increasing difficulty level significantly reduced the success rate (less reward) in both early and late learning stages. However, despite this decline in success rate, tracking error remained stable across difficulty levels in the early stage. In contrast, differences in tracking error across difficulty levels emerged in the late stage, with higher tracking error at high difficulty levels. We speculate that participants initially adopted an exploration-dominated strategy, engaging in greater motor exploration to facilitate subsequent learning (Uehara et al. 2019). As a result, behavioral performance was less sensitive to reward in the early stage.

4.3 Brain Tracks Behavioral Performance but Not Task Load or Reward

Our results revealed strong correlations between cortical activation and behavioral performance (i.e., tracking error), showing consistently negative correlation across all ROIs, and these correlations were strengthened after training (Figure 5A). The negative correlation seems to be contradictory to our previous work on a continuous tracking task with very low task difficulty, where tracking error and cortical activation was positively correlated (Wang et al. 2023). In that earlier study, high performers exhibited low cortical activation, suggesting they required fewer neural resources to achieve better performance. This apparent contradiction may be explained by the influence of task difficulty on neural efficiency. Neubauer and Fink (2009) described a similar pattern, where high performers exhibit lower neural activity (more efficient) compared with low performers in easy tasks but demonstrate the opposite trend under high task difficulty. They argued that high performers do not fully utilize their neural capacity in easy tasks, which allows them to ‘save energy’ and engage greater neural resources to meet the demands of more challenging tasks. In contrast, low performers require more neural resources (less efficient) in easy task, and may fail to further engage neural resources when facing very difficulty tasks.

However, no significant association was found between cortical activation and task load or success rate. Note that success rate served as a proxy for rewards, which in turn reflected objective task load (ID) and informs subjective workload (ISA). Given this, we speculate that during reward-based learning, the brain may prioritize monitoring performance rather than task load or reward. The absence of a linear association between cortical activation and task load suggests that brain dynamics during motor learning may be more complex than a simple linear resource allocation model, potentially involving nonlinear mechanisms that regulate neural adaptation to increasing task load.

4.4 Motor Learning Induces an Inverted-U Load-Dependent Pattern in the Contralateral Pre-SMA

We observed robust evidence of learning-induced changes in the load-dependent activation pattern, leading to the emergence of an inverted-U pattern in the late stage, particularly evident in the left (contralateral) Pre-SMA (Figure 6). Prior work has identified Pre-SMA as part of the capacity-limited system involved in maintaining and manipulating information for working memory (Van Snellenberg et al. 2015). The reduced activation in the contralateral Pre-SMA at high loads may arise not only from the limit of information capacity of the human motor system, but also from the limit of working memory capacity, as working memory capacity is closely related to visuomotor performance (Bo and Seidler 2009; Seidler et al. 2012; Anguera et al. 2010). Our findings further support the close interaction between the working memory and sensorimotor system.

Note that the reduced activation at high loads was accompanied by a decline in behavioral performance (i.e., increased tracking error, Figure 3C) in the late stage, indicating a possible connection between cortical activation and task performance in high difficulty tasks. The declined performance may correspond to the right side of the Yerkes-Dodson curve, which describes an inverted-U shaped relationship between arousal and performance. According to this theory, arousal—a mental state that is critical for regulating information processing and voluntary movement control (Garcia-Rill et al. 2016; Bortoletto et al. 2011)—initially enhances performance as it increases but eventually impairs performance once it exceeds an optimal level. In our experiment, the overall task difficulty was extremely high, suggesting that the task loads may have exceeded the optimal arousal level. Therefore, as task difficulty increased, the increased arousal was likely to have caused the deterioration in performance. Given the functional role of Pre-SMA in adapting to different levels of task loads (Schubotz and von Cramon 2003; Kimberley et al. 2008), it is plausible that arousal levels mediated its activation. This may result in the reduced activation at high loads, ultimately leading to the decline in behavioral performance.

Group level analysis provides an intuitive understanding of how learning alters the load-dependent activation pattern in the left Pre-SMA. The emergence of the inverted-U pattern in the late stage appears to be driven by reduced activity at the lowest and highest loads after learning (Figure 6C,D). The overall reduced activation in premotor areas might be associated with motor automaticity with practice (Poldrack et al. 2005), as practice could facilitate the transition from deliberate (more cognitive demanding) to automatic action (Huberdeau et al. 2019). Additionally, in the early stage, we observed decreasing cortical activation as subjective workload (ISA) increased, a pattern that may correspond to the right side of the inverted-U shape curve. In contrast, in the late stage, the activation peak of the inverted U-curve appeared at a moderate workload level (ISA = 2). We speculate that this right shift towards higher loads of the activation peak may reflect an enhanced capacity after training, a phenomenon similar to what has been observed in working memory training tasks (Iordan et al. 2020).

Interestingly, we did not observe inverted-U patterns in prefrontal areas that are closely related to cognitive control (Kane and Engle 2002), which have been shown to exhibit reliable inverted-U patterns in working memory tasks. This is consistent with the findings in a previous fNIRS study using a continuous force control task, where inverted-U patterns were only observed in lower-level networks such as sensorimotor and visual areas, rather than in the prefrontal cortex (Zheng et al. 2021). The absence of an inverted-U pattern in prefrontal areas may be attributed to the different paradigms. In continuous movement control tasks requiring rapid responses, the limited time available restricts the use of cognitively demanding strategies, such as deliberate planning. As a result, the reduced activation at high loads (the right side of the inverted-U curve), typically associated with capacity limits or overload, may be less prominent. In contrast, discrete motor tasks, which allow more time for planning, may better activate cognitive control processes. Therefore, future work comparing the load-dependent effects between discrete and continuous motor tasks would provide more valuable insights into these differences. Nevertheless, it is also possible that the use of fNIRS limited the sensitivity to detect such subtle patterns in prefrontal regions, while previous findings identifying such patterns mainly used fMRI. Simultaneous fNIRS-fMRI recordings in future research could consolidate our understanding of these region-specific effects.