1 INTRODUCTION

Cerebral cortex folds during its development in most mammalian brains (Rakic 2009, Sun and Hevner 2014). It has been widely reported that normal cortical growth and folding patterns are crucial for normal brain function since abnormality in cortical folding induced by aberrant or interrupted neuronal development has been related to many brain function malformations, cognitive deficits, and mental disorders (Richman et al. 1974, Clark 2001, Molko et al. 2003, Gaitanis and Walsh 2004, Rakic 2004, Nakamura et al. 2007, Cykowski et al. 2008, Shim et al. 2009, Barkovich et al. 2012, Stutterd and Leventer 2014, Fernández et al. 2016, Di Donato et al. 2017). Therefore, it has long been a wide interest in estimating a precise and consistent mapping of brain anatomy to cyto- and myelo- architectures, and functional activities (Zilles and Palomero-Gallagher 2001).

However, the high variability of cortical folding patterns presents huge challenges for estimating the brain anatomy-function relationship. Even the primary sulci and gyri, which can be consistently identified in all the healthy individuals and have a clear relation to major function areas, were demonstrated to not align very well with boundaries of a finer functional/cytoarchitectonic subdivision (Rademacher et al. 1993, Zilles et al. 1997, Roland and Zilles 1998, Amunts et al. 2000, Hasnain et al. 2001, Morosan et al. 2001, Eickhoff et al. 2006, Fischl et al. 2008, Hinds et al. 2008, Frost and Goebel 2012), let alone the secondary/tertiary gyri and sulci for which it is even difficult to find anatomical cross-individual correspondence due to their huge variability (Ono et al. 1990).

Therefore, the identification of cortical landmarks that bear higher anatomical cross-individual consistency and more consistent relation to functional areas at a finer resolution than the coarse-resolution folding patterns, such as gyri and sulci (Jiang et al. 2021) could improve the accuracy of anatomy-function mapping (Lohmann et al. 2008).

In fact, many cortical landmarks have been found and demonstrated to satisfy these requirements. In sulcal regions, it has been demonstrated that the sulcal patterns become more consistent at increasing depths (Le Goualher et al. 1999, Lohmann et al. 1999). The locally deepest sulcal foci, also known as sulcal pits, could be the first putative cortical folds present at the fetal stage (Im et al. 2017). Their location and geometry are relatively stable across individuals and change least as the brain develops (Lohmann et al. 2008, Im et al. 2010, Im et al. 2011, Meng et al. 2014). The invariance was further associated with the regulative effects of genetic control (McKay et al. 2013, Le Guen et al. 2018). Importantly, the presence/absence of sulcal pits has been demonstrated to relate to brain function and cognition. For example, the hemispheric asymmetries of sulcal pits distribution and frequency on superior temporal sulcus were related to the lateralization of language function in human brains in both infant and adult groups (Im et al. 2010). The presence of sulcal pit in the left posterior inferior frontal sulcus and the right posterior inferior temporal sulcus is related to verbal intelligence (Im et al. 2011). The number of sulcal pits in the left posterior inferior frontal sulcus and the right posterior inferior temporal sulcus was positively related to average IQ (Im et al. 2013). Also, sulcal patterns on postnatal brains with cerebral malformation are significantly different from normal templates regarding the location and depth (Im et al. 2017).

Despite these insightful and promising findings in sulcal regions, few studies were found to identify whether there are similar cortical landmarks in gyral system. In fact, gyri and sulci develop simultaneously in the same cortical regions. For example, sylvian fissure and insular gyrus develop at 10 ~ 15 gestation week (GW), and the central sulcus that develops at 20 ~ 23 GW is followed by the development of precentral gyrus and postcentral gyrus at 24–27 GW (Chi et al. 1977, Welker 1990, Zilles et al. 1997, Blanton et al. 2001, White et al. 2010). Importantly, the presence/absence of a gyrus could also be related to brain function or even cognitive capacity. For example, it was reported that adults whose left lateral occipitotemporal sulcus were interrupted by the gyrus in the posterior portion had better reading fluency than those having a continuous one (Cachia et al. 2018). In this sense, we intuitively wonder whether a cortical landmark, as a possible counterpart of a sulcal pit, can be found in gyral regions.

To this end, we defined gyral peaks as the locally highest points along gyral crests, developed a computational method for extracting gyral peaks, and examined their spatial distribution, longitudinal variation, and relationship to structural connectivity parcellation based on a longitudinal neuroimaging of the rhesus macaque brains dataset (Young et al. 2017). Fewer inter-individual and temporal variabilities in cortical folding of macaque brains than those of human brains could assist us to estimate the spatiotemporal alignment of cortical folds (including gyral peaks in this work) across subjects and/or ages, and the mapping of structural/functional architectures to gyral peaks, with higher accuracy. In this dataset, we investigated whether gyral peaks are spatially consistent across individuals and ages; whether they bear identifiable anatomical, structural connective and functional features compared to other gyral regions; and how are they related to sulcal pits. In all these respects, we considered that the gyral peaks, the locally highest points of a gyral crest, are the significant gyral landmarks.

2 METHODS

2.3 Gyral height and gyral peaks

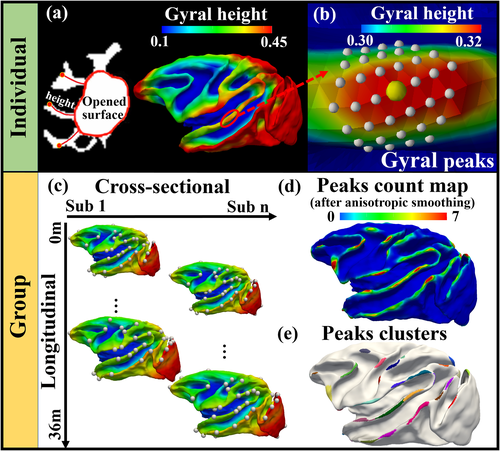
As shown in Figure 1a-b, gyral height and gyral peaks were defined in an individual surface. We used morphological opening operations with a spherical structuring element of radius 6 mm in the WM map to yield the “opened surface” (the red closed curves in Figure 1a), which is “a deep white matter surface resembling a primitive unfolded or lissencephalic brain” as described in Lohmann et al. (2008). Discussion on the selection of radius as well as the selection on different ages is present in section 3.1 and Supplemental Materials (Figure S2 and related texts). To measure the height of a vertex on the white matter surface, we adopted the algorithm named the adaptive distance transform (ADT) (Jin et al. 2013) to compute the length of the shortest path that is within white matter from the vertex to the opened surface (curves in gyri in Figure 1a). In this way, we obtained the gyral height surface map (right panel of Figure 1a). For the convenience of analyses across subjects, we normalize the height to [0, 1]. We defined the vertex with local maximal gyral height value in 9-order ring neighbors (radius is about 2.34 mm) as a gyral peak center (the yellow bubble in Figure 1b). The X-order ring neighbors of a vertex include the vertices that are X-steps away on the triangular mesh. For ease of analysis in the following steps (such as cross-subject smoothing), a gyral peak is defined as the peak center and its local neighbors (vertices within a 3-order ring highlighted by white dots in Figure 1b). It is noted that identification of local height maxima is not impacted by the normalization of height (to [0, 1]).

3 RESULTS

3.2 Spatial distribution of gyral peaks

Figure 2a shows the detected gyral peaks in the individual space of a randomly selected subject. The group-wise peak count map on the template subject was shown in Figure 2b. It is observed that the gyral peaks extracted from all subjects over ages are not scattered on the template but yield a Gaussian distribution in terms of peak count on the template, with the furthest distance of the 95% confidence interval boundaries from the possible centers as 0.95 ± 0.61 mm, on average. Also, the distribution patterns of the distance of two neighboring peaks are similar across subjects (Pearson's r = 0.86 ± 0.14, details are referred to section 5.1 in Supplemental Materials). The gyral peak clusters by applying a watershed algorithm to the count map were shown in Figure 2c. The left and right hemispheres have 39 and 37 clusters, respectively. The count map was further validated via bootstrapping statistics. One-hundred bootstrapping tests yield count maps that have Pearson's r = 0.99 ± 0.15, on average (details are referred to section 5.2 in the Supplemental Materials). The spatial distributions and peak count of most clusters show hemispherical symmetry with four exceptions, including postcentral gyrus, inferior temporal gyrus and visual cortex on the left hemisphere and hippocampal fissure on the right hemisphere (framed by red in Figure 2c). The symmetry was supported by the results that the Dice ratio between clusters on the right hemispheres and those mirror-flipped ones from the left hemisphere is 0.53 ± 0.17, in terms of surface area; and the asymmetry index (AI) (Greve et al. 2013) between left–right clusters defined as: AI = (L-R)/(L + R), in terms of count density, is 0.16 ± 7.28 × 10⁻². Details are referred to section 6 in Supplemental Materials. Since peaks with higher count values are those more consistently found across subjects and ages, we investigated whether the consistency is relevant to anatomical and structural measures in the following analyses, by classifying peaks into the more consistent ones (defined as “major peaks”, black indices in Figure 2c) and the less consistent ones (“minor peaks”, blue indices). We calculated the sum of peak counts in each cluster and arranged them in descending order. Major peak clusters account for 75% counts, leaving the others as minor ones. The left hemisphere has 26 major gyral peaks and 13 minor gyral peaks. The right hemisphere has 25 major gyral peaks and 12 minor gyral peaks. From each gyral peak cluster, we selected the vertex with the highest count as the location of the group-wise gyral peak (Figure 2d).

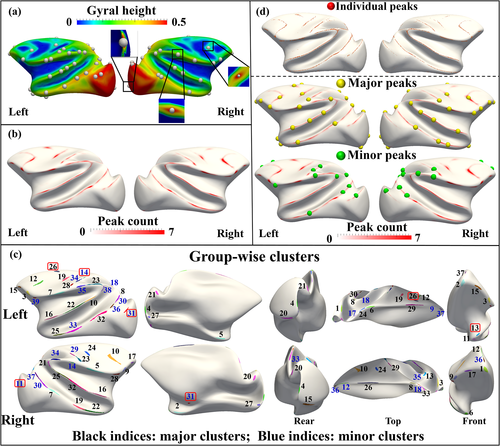
Finally, to investigate the consistency of major peaks and minor peaks between individuals, we take all major peaks as a group and compute the ratio of the present major peak for the i^th individual as follows: r_i = n_i/n, where n_i denotes the number of the present major peak on the i^th individual and n is the number of major peaks the individual is supposed to have (left hemisphere: n = 26; right hemisphere: n = 25). A similar ratio was also computed for the minor peak group for the i^th individual (13 left minor peaks and 12 right ones are expected). The standard deviation (as well as the mean) of the ratios across individuals are LH (left hemisphere): 0.75 ± 0.08, RH (right hemisphere): 0.75 ± 0.06 for major peaks, and LH: 0.32 ± 0.12, RH: 0.30 ± 0.13 for minor peaks. It is seen that major peaks have less standard deviation than minor peaks, demonstrating the higher cross-individual consistency of major peaks.

3.3 Comparison across ages

The cluster of gyral peaks obtained on four age groups (0-6 months, 7-15 months, 16-24 months, and 28-36 months) were shown in Figure 3. It is noted that we used the same template in Figure 2 to present the results for ease of comparison. The correspondences of the clusters across age groups were estimated by the overlap ratio between the age-specific cluster map in Figure 3 and the all-age cluster map in Figure 2d which is also shown in the top row of Figure 3 as a reference.

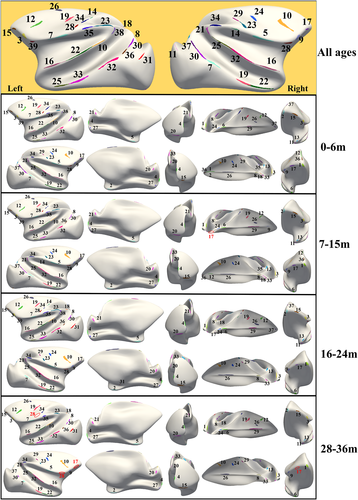
In general, the consistency regarding the spatial distribution of the gyral peak clusters across ages is observed in Figure 3, suggesting that the positions of gyral peaks were considerably independent of the dynamic cortex development, such as tangential cortical expansion and radial height increase. It is noted that a few clusters on the all-age map are not found in one or two age groups (highlighted by red indices and circles in Figure 3).

3.4 Anatomical and structural attributes of gyral peaks

In this section, we firstly investigated the anatomical and structural features of the more consistent gyral peaks, major peaks in sections 3.4.1 and 3.4.2. Minor peaks, the less consistent ones, were compared with major ones in section 3.4.3.

3.4.1 Anatomical features

We computed anatomical measures, including cortical thickness and mean curvature, of major gyral peaks at different age groups. Vertices of the same number of peaks were randomly selected and have these anatomical measures computed as well. Random tests were repeated 10,000 times to provide the chance line. Two strategies of random selection were used: 1) random selection on the whole cortex and 2) random selection on gyral crests (curvature>0.5). The mean (±standard deviation) values were reported in Table 1. In general, whether compared to random selection on the whole cortex or gyral crests, major gyral peaks have significantly (p < .05 for all) greater thicker cortex and larger curvature.

TABLE 1. Anatomical measures of major gyral peaks across ages. Means (±SD) of these measures as well as those on random tests (1$\times$ 10⁴ times) were reported. These random tests provide a null hypothesis distribution to test the significance of the means from major gyral peaks. Recall that the height was normalized to [0, 1]

		Age 1	Age 2	Age 3	Age 4
Cortical Thickness (mm)
Major	L	1.34 ± 0.25	1.23 ± 0.26	1.17 ± 0.26	1.15 ± 0.26
	R	1.30 ± 0.23	1.20 ± 0.23	1.15 ± 0.23	1.11 ± 0.24
Random Whole Cortex	L	0.95 ± 0.06	0.89 ± 0.06	0.87 ± 0.06	0.85 ± 0.06
	R	0.93 ± 0.06	0.86 ± 0.06	0.85 ± 0.06	0.84 ± 0.06
Random Gyral Crest	L	1.12 ± 0.09	1.04 ± 0.09	0.87 ± 0.06	0.96 ± 0.09
	R	1.10 ± 0.09	1.02 ± 0.09	0.98 ± 0.09	0.95 ± 0.09
Mean Curvature (mm−1)
Major	L	0.99 ± 0.24	0.94 ± 0.22	0.93 ± 0.23	0.94 ± 0.24
	R	0.98 ± 0.22	0.92 ± 0.21	0.90 ± 0.22	0.91 ± 0.22
Random Whole Cortex	L	0.04 ± 0.05 0.04 ± 0.05	0.04 ± 0.05 0.04 ± 0.05	0.04 ± 0.05	0.03 ± 0.05
	R			0.04 ± 0.05	0.03 ± 0.05
Random Gyral Crest	L	0.67 ± 0.07	0.66 ± 0.07	0.67 ± 0.07	0.65 ± 0.07
	R	0.70 ± 0.08	0.68 ± 0.07	0.69 ± 0.07	0.68 ± 0.08

It is important to note that the significant difference mentioned above is found for all four age groups. The longitudinal comparison reveals that the cortical thickness (L: −17.76 ± 9.72%; R: −15.41 ± 8.48%) and curvature (L: −4.22 ± 9.89%; R: −7.33 ± 11.26%) decreases.

3.4.2 Structural wiring patterns

As a reference, the mean nodal metrics averaged over random tests on the cortex and gyral crests within each age group were reported in the first and second groups in each subfigure of Figure 4, respectively. The mean metrics averaged over major gyral peak nodes are in the third group. On average, major gyral peaks have significantly (p < .05, with betweenness of the first age group as the only one exception) higher metric values than the means on the whole brain and gyral crests. In addition, major gyral peaks' graph metrics increase across ages, except for efficiency that changes less.

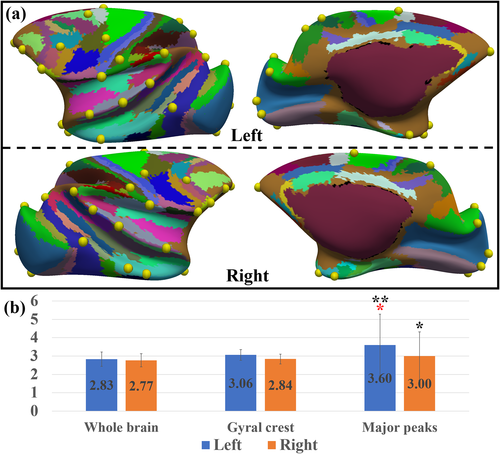
Finally, we computed the number of different cortical areas in the LVE atlas that are found in the neighbor of a gyral peak. Since many cortical areas in this atlas were suggested to coincide with those in brain functional regions (Lewis and Van Essen 2000), we posited that more cortical areas found around a gyral peak indicate that it might be engaged with more brain functions. It is observed in Figure 5a that gyral peaks are usually found on the borders of cortical areas. These peaks have more cortical areas (L: 3.60 ± 1.68, R: 3.00 ± 1.32) found around their neighborhood (7-order ring neighborhood, r ≈ 1.84 mm) compared to randomly selected vertices on either the whole cortex or the gyral crest (Figure 5b), while the peak–crest difference is not significant on the right hemisphere.

3.4.3 Measures on minor peaks

Compared with major peaks, minor peaks are relatively less consistent regarding group-wise peak count and have relatively lower curvature but thicker cortex (Table 2). The difference is not significant for all (p > .05).

TABLE 2. Anatomical measures of minor gyral peaks across ages. Means (±SD) of these measures were reported. The height was normalized to [0, 1]

	Age1	Age2	Age3	Age4
Cortical Thickness (mm)
L	1.42 ± 0.19	1.30 ± 0.20	1.23 ± 0.20	1.22 ± 0.20
R	1.30 ± 0.37	1.17 ± 0.35	1.13 ± 0.32	1.07 ± 0.32
Mean Curvature(mm−1)
L	0.98 ± 0.27	0.90 ± 0.21	0.90 ± 0.21	0.89 ± 0.18
R	0.97 ± 0.36	0.87 ± 0.28	0.85 ± 0.26	0.84 ± 0.23

Minor peaks' cortical thickness decreases with higher amplitude (L: −18.15 ± 6.37%; R: −17.05 ± 5.38%, p < .05 for both hemispheres). Curvature decreases with higher amplitude (L: −9.83 ± 11.87%; R: −15.99 ± 10.43%, p < .05 for both hemispheres).

Minor peaks have slightly higher graph metric values than those of random tests on whole-brain and gyral crest. However, the difference is not consistently significant, especially for peak-crest comparison. Minor peaks have slightly more cortical areas in their neighbor (L: 3.42 ± 1.51, R: 3.38 ± 1.19) than both random tests, but there is no significant difference between major peaks and minor peaks. Details are referred to Figures S12, S13 of Supplemental Materials.

3.5 Spatial patterning of gyral peaks

3.5.1 Gyral peaks vs. gyral hinges

In our previous works, we defined another group of gyral landmarks (Li et al. 2010), termed gyral hinges, which reside on the crossings of gyri from multiple directions (see examples in Figure S14). Gyral hinges were found to have the thickest cortices, the strongest long-range axonal connections, the most pronounced connectivity diversity, and the most aggregative functional profiles, composing the majority of the cortico-cortical structural connective network's “core” (Li et al. 2010, Yu et al. 2013, Chen et al. 2014, Jiang et al. 2015, Li et al. 2017, Ge et al. 2018, Zhang et al. 2020). It is noted that gyral hinges in Figure 6a are the ones consistent across subjects and ages using a similar pipeline for gyral peak detection. Since gyral peaks were also defined on gyri, we compared the positions of all gyral peaks and gyral hinges and found that some peaks are overlapped with hinges (if the distance is less than 9-order ring neighborhood, r ≈ 2.34 mm and a peak is only assigned to a hinge. Note that the distance between two neighboring gyral crests is 5.70 ± 0.65 mm on the template surface. Therefore, a peak is not likely being overlapped with a hinge on another gyrus), highlighted by yellow bubbles (overlapped peaks, hereafter). Among these overlapped peaks, more major gyral peaks (64.71%) were found than minor ones (40.00%).

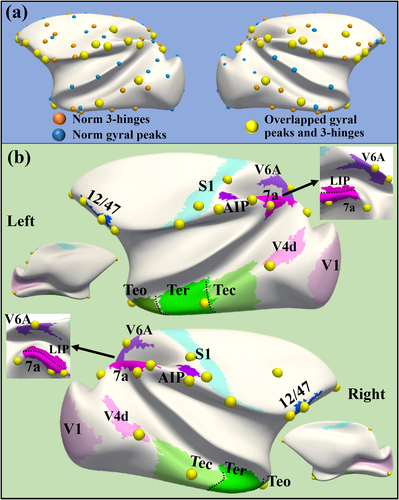
It is found that these overlapped peaks are spatially close to brain regions on visual and auditory pathways, including a trans-modal auditory responsive area (12/47) (Romanski 2007), visual areas (V1, V4, V6A, LIP, 7a, and AIP on dorsal pathway, and Teo, Ter, and Tec on ventral pathway (Freud et al. 2016), as well as the regions in a primary cortex: S1. This result might suggest that these overlapped peaks are spatially placed on a global cortical gradient between the trans-modal cortex and unimodal cortex (Huntenburg et al. 2018). It is noted that there is only one exception, the gyral peak in the frontal pole, which is not close to any of these functional regions.

3.5.2 Gyral peaks vs. Sulcal pits

It was reported in Lohmann et al. (2008) that sulcal pits form prominent chains stretching from the anterior pole to the posterior pole. The general arrangement of those chains follows the alignment of the lateral ventricle. Such sulcal pit chains were reproduced in macaque brains (yellow bubbles and curves in Figure 7). These sulcal pits are the ones consistent across subjects and ages using asimilar pipeline for gyral peak detection in this work.

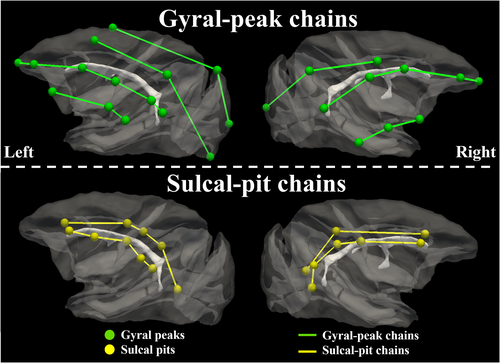
We found that gyral peaks form three chains (green bubbles and curves) of the same orientation as sulcal-pit chains (yellow bubbles and curves). The arrangement of both gyral peak chains and sulcal pit chains all follow the alignment of the lateral ventricle.

We further applied the computational finite element model to investigate the spatial relationship between gyral peaks and sulcal pits. For the details of the computational model check Figure S16 and related texts in Supplemental Materials. In general, we constructed a double-layer cubic model (Figure S16), where the top layer as the cortex grows faster than the bottom layer as the core to mimic the folding process. According to differential tangential growth theory, the cortex as the outer layer of the developing brain grows faster than the core as the inner layer (Richman et al. 1974, Razavi et al. 2015). After a certain amount of growth of the cortex, mechanical instability occurs in the model, and consequently folds form on the cortex (Figure S17). We run 30 models with different initial small perturbations on the surface of the cortex while other parameters were kept the same to have meaningful statistical data. In a real brain, this perturbation could stem from the variation in curvature or heterogeneous growth on distant sites of the brain (Zhang et al. 2016). Initial perturbation in each model was applied as random and small displacements on the nodes of the cortex's surface. The amplitude of the displacements was 0.01 of the cortex thickness (Chavoshnejad et al. 2021). Figure 8 shows the top views of 4 of the 30 models after suppressing the cortex layer.

We found that 42.64 ± 4.20 sulcal pits and 67.11 ± 3.50 gyral peaks were identified in these computational models. The count ratio of gyral peak to sulcal pit is 1.63 ± 0.22, on average. In contrast, the average numbers of sulcal pits, gyral peaks and the ratio are 20.73 ± 3.10, 21.01 ± 2.15 and 0.97 ± 0.16 in macaque brains, respectively. These results suggest that the initial shape could roughly determine the ratio between peaks and pits, since the ratio remains relatively consistent across perturbations in computational models, and cross-subject and -age variabilities in macaque brains. Also, we empirically identified chains of sulcal pits and gyral peaks which spatially alternate with each other, in the same way as those on macaque brains (Figure 7), suggesting that the emergence of sulcal pits and gyral peaks, as well as their chains, might not be independent of each other.

4 CONCLUSION AND DISCUSSION

In this work, we defined gyral landmarks, termed gyral peaks, which are the local highest regions on gyri. We studied 156 MRI scans of 32 macaque monkeys with ages ranging from 0 to 36 months and detected 39 and 37 gyral peaks on the left and right hemispheres. We found that: (1) gyral peaks are spatially consistent across individuals; (2) the spatially consistent distributions of gyral peaks are relatively stable during the first 3 years; (3) compared to vertices in other gyral regions, gyral peaks have a thicker cortex and greater mean curvature; (4) the nodal graph metrics on gyral peaks in a dMRI derived structural network, including degree, strength, betweenness, and efficiency, are significantly higher than other nodes including those on gyral crests; (5) gyral peaks are on the borders of structural connectivity parcellations, possibly indicating gyral peaks are involved in more brain functional activities than other brain regions; (6) the gyral peaks overlapping with gyral hinges are distributed on S1 and visual and auditory pathways; (7) gyral peaks form chains and their arrangement follows the alignment of the lateral ventricle in the same way as sulcal pits.

We found that the regularity of gyral peaks is related to the distribution of anatomical and structure wiring features. Major peaks, with higher inter-individual regularity, thinner cortex, and higher curvature compared with minor peaks with lower inter-individual regularity. The longitudinal variation trends of major peaks and minor ones are different in these anatomical and structure measures (see the results in Table 1, Table 2, and Figure 4). Thicker cortex of gyral peaks, compared with one of the other cortical regions including other gyral regions, could be associated with their sharper gyral shapes and stronger axonal connections found in our work, which needs further investigation. The less consistency of minor peaks, most of which are found in temporal lobe, parietal lobe, and frontal lobe, could be explained by the trajectory of development differed across cortical region, where occipital cortex reaches its volume peak at 13 weeks of age and exhibits a continuous decline afterward while the frontal, temporal, and parietal lobes show the protracted growth (Scott et al. 2016). In this sense, ontogenetic factors or the order of development could play a role with later developing lobes, yielding secondary/tertiary cortical folding, including the minor peaks in this work, and being more variable than earlier ones (Fischl et al. 2008).

By comparing our gyral peak related findings with those for sulcal pits in previous reports, we found that they shared similar characteristics in many perspectives. The spatial arrangement of sulcal pits was suggested to be regular across humans in spite of huge cross-subject cortical folding variabilities (Im et al. 2010). Such consistency was also found to be present at term birth and persists in later years in spite of the dramatic expansion of the cortex and deepening of sulci (Meng et al. 2014). In our work, gyral peaks exhibit similar cross-subject and longitudinal consistency. Although the cortical folding topology of macaque brains is less variable across subjects and ages, our findings suggest a possibility that these gyral landmarks as well as their spatiotemporal consistency can be found in human brains, which is our next research aim. In addition, the arrangement of sulcal pits forms chains, and the arrangement of the sulcal pit chains seem to follow the alignment of the lateral ventricles (Lohmann et al. 2008). The arrangement of gyral peaks forming similar chains interweaved by sulcal pit chains is shown in both brains (Figure 7) and simulation experiments (Figure 8). These findings suggest that gyral peaks and sulcal pits could be produced simultaneously, and might fundamentally be subjected to a related genetic influence.

It is interesting to find that there are overlaps between gyral hinges and gyral peaks. From the mechanical point of view, due to the elasticity and plasticity of brain tissues, gyri and sulci could be the results of the cortical wave development when the outer cortical layer expands faster than the inner one (Bayly et al. 2013). In this sense, gyral hinges could be the results of the interplay of waves from two orientations, since their anatomical appearance is the crossings of gyri from more than two directions. On the other hand, because gyral peaks are the highest cortical locations, they are also expected to be at the locations where peaks of two waves meet and superimpose on each other. Therefore, it is not surprising to find a widely distributed overlap between gyral peaks and gyral hinges, since they could be intrinsically produced by the same mechanical mechanisms (Bayly et al. 2013, Razavi et al. 2015, 2017). However, gyral peaks and hinges do not entirely overlap with each other. Some gyral hinges do not reside on the local maxima of gyral height while some gyral peaks do not reside on the crossing of two gyri. This inconsistency suggests that instability of cortical development (Thoma et al. 2005), usually caused by the faster expansion of the outer layers of the cortex, could not be the only factor to shape the anatomical morphology of cortical folds. Denser fibers connected to gyral hinges reported in our previous work (Ge et al. 2018) could be one of the other factors, in that tension was found along with the orientation of axons (Van Essen 1997, Xu et al. 2010) such that the height of a gyral hinge could be restricted by stronger axonal tension. On the other hand, the elasticity and plasticity of brain tissues as well as degenerative neuronal processes during brain development, such as synaptic pruning (Neniskyte and Gross 2017), possibly lead to the degeneration of some cortical folds, including gyral peaks. One example is “pli de passage” (Gratiolet 1854, Régis et al. 2005, Parent 2014, Mangin et al. 2019), which are pairwise gyri buried in the depth of sulci. In a small group of brains, a continuous gyrus was found to replace the “pli de passage” to literally divide one sulcus into two shorter ones (Régis et al. 2005, Mangin et al. 2019). In this sense, the gyral peaks found on a continuous gyrus and not overlapped with gyral hinges (not on a crossing of gyri from two directions), could be programmed to be crossings of waves at first, but the gyrus from one wave might degenerate for some reasons at last. Based on these discussions above, gyral peaks overlapped by gyral hinges are the “perfect” gyral cortical folds superimposed by two cortical waves in that they reside on gyri crossings and local height maxima at the same time. More interestingly, these landmarks were found on visual and auditory pathways. Since these pathways exhibit a functional gradient from unimodal regions to trans-modal ones, these anatomical landmarks could offer new insights for the proto-map of the large-scale gradients of brain functions, which were demonstrated to be in line with developmental and genetic gradients on the cortex (Huth et al. 2016, Margulies et al. 2016, Baldassano et al. 2017, Huntenburg et al. 2017, Huntenburg et al. 2018). The timing of cortical development could also be an important factor. It seems that the overlapped landmarks with the closest distance (less than 1 mm) to cortical area borders are more on the higher-order cortex than the normal ones, probably due to that the higher-order cortex has more complicated morphology and develops later than unimodal ones (Sydnor et al. 2021), such that the interplay of folding waves from two orientations yielding the crossings of gyri might account for the higher coincidence between peaks and hinges in these regions.

When relating gyral peaks with structural connective graph metrics, we found that gyral peaks have a higher nodal degree, strength, betweenness, and efficiency in contrast to the mean values on the whole brain and gyral crests, suggesting that they could behave more like hubs of the structural network (Bassett and Bullmore 2006, Bullmore and Sporns 2009, He and Evans 2010). Also, these metrics (except for efficiency) on major gyral peaks increase across ages. It has been reported that the long-range axons and the core of the structural network are present at birth (Dubois et al. 2008, Li et al. 2015, Batalle et al. 2018). In this sense, these results suggest that the role of major gyral peaks as hubs at birth might not be as pronounced as that in adulthood, particularly when compared to other gyral regions. In addition, most gyral peaks are found on the boundary of LVE cortical areas (Figure 5). This finding suggests that gyral peaks could be engaged with more brain functions. Or, they are simply on the borders of these cortical regions, belonging to none of them. Low spatial resolution of macro-scale brain function imaging techniques, such as the functional MRI, may not be able to reveal the functional role of gyral peaks, since the volumetric voxel where a gyral peak resides could cover the multiple functional units such that their activities are blended in one functional signal, making it difficult to determine whether the complex signal of a gyral peak is a result of a blending of multiple sources or reflects its signal-integration nature.

We compared the peak/pit results on macaque brains and those on simulation models. The ratio on macaque brains is around 1 and slightly increases across age groups (age group #1: 0.95 ± 0.16; age group #2: 0.94 ± 0.16; age group #3: 1.00 ± 0.17; age group #4: 1.04 ± 0.12), but the increase is not significant (all neighboring age group difference does not pass t-tests, p-value>.05). This ratio is in line with our empirical hypothesis that peaks and pits could alternate with each other on macaque brains. The slight increase in the peak/pit ratio suggests that the postnatal development of gyri and sulci might not be synchronous. In our recent work (Li et al. 2022), we found on the same dataset that the cortical area expansion is faster on gyral crests than that on sulcal fundi while the depth shrinks faster on sulcal fundi than that on gyral crests. In this sense, it is hypothesized that gyri might develop later or longer than sulci during the postnatal stage, resulting in a slight increase in peak/pit ratio. Also, the simulation model yields more convoluted gyro-sulcal patterns and a higher peak/pit ratio than the less convoluted macaque cortex. It is thus inferred that the growing complexity of cortical morphology might impose more impact on gyri than sulci. A more concrete investigation of these hypotheses is needed in the future on a prenatal dataset and a multi-species dataset.From the perspective of peak/pit development, it seems that the principal directions of gyri and sulci present a meridian/parallel organization (Toro and Burnod 2003, Régis et al. 2005, Clouchoux et al. 2010, Auzias et al. 2013), which was suggested to result from the principal curvatures of the smooth cortical surface (Tallinen et al. 2016). The periodicity of both sulcal pits and gyral peaks was observed on this organization, which could coincide with gyro-sulcal wavelength. In this sense, sulcal pits and gyral peaks could be the accumulative local minima and maxima where multiple waves superimpose on each other.

Since many deep sulcal pits that are consistent across subjects and invariant across ages were suggested to be the earliest cortical folds (Im et al. 2010), gyral peaks, as morphologically dual patterns, might also appear earlier than other gyral regions. Also, like sulcal pits, higher gyral peaks might also be in place earlier than shallower ones. This postulation deserves further in-depth investigation on the cortex during its fetal stages.

The spatial and temporal coupling between gyral peaks and sulcal pits could be elicited by multiple neuronal processes and associated bio-mechanics. For example, neuron proliferation and migration could be modular in OSVZ, leading to modularized prosperity of neurons in the cortical plate (Stahl et al. 2013). Cortex plate modules with higher neuron popularity were suggested to bulge, making the neighboring modules with neurons less populated buried. Such regionalized proliferation and migration patterns were suggested to give rise to conventional wavy gyro-sulcal patterns. As mentioned above, the landscape of the cortex could be the superimposition of waves of multiple orientations. It is intuitive to postulate that peaks, as maxima of superimposition, might be the region with the highest neuron population, while pits might have the least neuron popularity. Axonogenesis was also suggested to correlate with gyrification (White et al. 2010). In our previous work (He et al. 2021), we suggested that gyral hinges might be coupled with denser and longer axons and possibly more neurons in the cortex to send and receive axonal outputs and inputs. Since gyral hinges are largely overlapped with gyral peaks (Figure 6 in this work), we postulate that gyral peaks could also be connected by denser axons than other gyral regions. On the other hand, co-occurrence of plis de passage gyri and U-shape fibers was suggested in Garcia et al. (2021), while the co-occurrence of plis de passage gyri and sulcal pits wasreported (Mangin et al. 2019) as well. Taken together, it could be possible that U-shape fiber bundles connecting two plis de passage gyri on two neighboring gyri might take the “deepest” U-turn at sulcal pits. Even though the close relationship between axonogenesis and gyrification was partially supported by the synchronous timing of the emergence of white matter connections and cortical folds (Chi et al. 1977, Huang et al. 2009, White et al. 2010, Takahashi et al. 2012, Dubois et al. 2014, Razavi et al. 2017), the causality between them is still in debate (Garcia et al. 2021). Nevertheless, there still seems to be a consensus that different folding patterns are associated with different axonal wiring patterns. Other development processes, such as the development of intermediate the zone and subplate (Kriegstein et al. 2006, Budday et al. 2015, Duque et al. 2016) and the formation of connections in subcortical tissue (Dehay et al. 2001, Vue et al. 2013, Gamberini et al. 2016, Garcia and Buffalo 2020), were also suggested to contribute to gyrification and worth further attention.

In summary, our definitions and findings of gyral peaks, as well as the relationship between their regularity and multiple anatomical/structural measures provide new clues to explore the neuronal mechanisms of gyrification, such as neurogenesis, migration, axonogenesis, gliogenesis, and myelinogenesis (Chi et al. 1977, Smart et al. 2002, Huang et al. 2009, Takahashi et al. 2010, White et al. 2010, Takahashi et al. 2012, Betizeau et al. 2013, Borrell and Götz 2014, Dubois et al. 2014, Florio and Huttner 2014, Lewitus et al. 2014, Taverna et al. 2014, Hagemeyer et al. 2017, Rash et al. 2019), the underlying genetic mechanisms (Stahl et al. 2013, De Juan Romero and Borrell 2015, Richiardi et al. 2015, Zeng et al. 2015, Krienen et al. 2016) as well as the anatomy-function relationship (Rademacher et al. 1993, Fischl et al. 2008).

CONFLICT OF INTEREST

The authors declare that they have no conflict of interest