Differential spatial patterns of structural connectivity of amygdala nuclei with orbitofrontal cortex
Funding information: National Institute of General Medical Sciences, Grant/Award Number: P20GM103653; NIH Blueprint for Neuroscience Research, Grant/Award Number: 1U54MH091657; University of Delaware Research Foundation
Abstract
The orbitofrontal cortex (OFC)-amygdala circuit is critical to goal-directed behavior, learning, and valuation. However, our understanding of the OFC-amygdala connections that support these emergent processes is hampered by our reliance on the primate literature and insufficient knowledge regarding the connectivity patterns between regions of OFC and amygdala nuclei, each of which is differentially involved in these processes in humans. Thus, we examined structural connectivity between different OFC regions and four amygdala nuclei in healthy adults (n = 1,053) using diffusion-based anatomical networks and probabilistic tractography in four conceptually distinct ways. First, we identified the OFC regions that connect with each nucleus. Second, we identified the OFC regions that were more likely to connect with a given nucleus than the others. Finally, we developed probabilistic and rank-order maps of OFC (one for each nucleus) based upon the likelihood of each OFC voxel exhibiting preferential connectivity with each nucleus and the relative density of connectivity between each OFC voxel and each nucleus, respectively. The first analyses revealed that the connections of each nucleus spanned all of OFC, reflecting widespread overall amygdala linkage with OFC. Analysis of preferential connectivity and probabilistic and rank-order maps of OFC converged to reveal differential patterns of connectivity between OFC and each nucleus. Present findings illustrate the importance of accounting for spatial specificity when examining links between OFC and amygdala. This fine-grained examination of OFC-amygdala connectivity can be applied to understand how such connectivity patterns support a range of emergent functions including affective and motivational processes.
1 INTRODUCTION
The orbitofrontal cortex (OFC) and the amygdala form a circuit that is centrally involved in initiating and maintaining goal-directed behavior toward motivationally significant outcomes (Elliott, Dolan, & Frith, 2000; Sharpe & Schoenbaum, 2016). Critically, the OFC and amygdala engage in complementary functions subserving goal-directed behavior: the amygdala is thought to learn stimulus-outcome associations and encode the value of the outcome predicted by a stimulus, whereas the OFC forms networks of associations between such stimuli and the outcomes they predict (Sharpe & Schoenbaum, 2016). Together, the OFC and amygdala facilitate the prediction of the potential outcome value associated with a behavior, given the current context. Additionally, the OFC and amygdala jointly contribute to conditioned reinforcement resulting in the maintenance of a behavior over time without immediate reinforcement (Roberts, Reekie, & Braesicke, 2007).
Given their importance in maintaining goal-directed behavior through associative learning, it is no surprise that coordinated activity of the OFC and amygdala is crucial for supporting memory, emotional, and motivational processes (Rolls, 2013; Zald et al., 2014). For example, a meta-analysis demonstrated consistent functional connectivity between medial OFC, amygdala, and hippocampus during memory tasks (Zald et al., 2014). Furthermore, coupling between the OFC and amygdala is associated with individual differences in self-control and emotion regulation (Crane, Gorka, Phan, & Childs, 2018; Lee, Heller, van Reekum, Nelson, & Davidson, 2012). This circuit has also been implicated in several forms of pathology, including obsessive–compulsive disorder (Paul et al., 2018), depression (Zheng et al., 2018), and anxiety (Kim et al., 2011).
Due to the critical importance of the OFC-amygdala circuit, much research has focused on understanding how they interact. However, methodological limitations have restricted human research in this area largely to using functional connectivity (i.e., via fMRI), and thus only a few studies have inferred structural connectivity (i.e., via diffusion-weighted imaging [dMRI]). Consequently, much of our knowledge regarding anatomical connections between the OFC and amygdala is drawn from the animal literature. Tract-tracing studies in primates have demonstrated reciprocal anatomical connectivity between the OFC and amygdala, with the densest amygdalar projections arriving in posterior, medial, and lateral OFC (Carmichael & Price, 1995). Human studies using fMRI and dMRI largely corroborate these findings. For example, a meta-analysis of OFC functional connectivity in humans found consistent links between amygdala and both medial and lateral divisions of OFC, with amygdala showing preferential connectivity with medial OFC (Zald et al., 2014). In a study employing dMRI in humans, Bracht et al. (2009) identified a pathway connecting the OFC and amygdala through the uncinate fasciculus, a long-range white matter bundle that connects the anterior temporal lobe (e.g., amygdala, hippocampus) with anterior/inferior prefrontal cortex (e.g., OFC, frontal pole). Thus, there is limited, but convergent, evidence for direct structural connections between the OFC and amygdala from human and primate studies.
Unfortunately, past work in humans utilizing structural approaches to investigate OFC-amygdala connectivity has almost uniformly treated amygdala as a single homogeneous structure. However, amygdala is a collection of nuclei known to have different functions and patterns of connectivity (McDonald, 1998). There are several ways to classify amygdala nuclei, but common models distinguish between basolateral (i.e., lateral, basal, and accessory basal), superficial cortex-like (i.e., cortical, peri-amygdaloid cortex), and centromedial (i.e., central and medial) nuclei (McDonald, 1998). Note that the peri-amygdaloid cortex discussed in the rodent literature is equivalent to the cortico-amygdaloid transition area (CAT) in humans (Saygin et al., 2017). Again, differential connectivity patterns of these nuclei have primarily been investigated in animals, including primates. For example, animal work indicates that basolateral amygdala exhibits projections throughout the OFC, with particularly dense projections to posterior and medial OFC, whereas superficial cortex-like amygdala exhibits connectivity primarily with posterior OFC (Carmichael & Price, 1995). These divergent connectivity patterns appear to support distinct functions of these nuclei. For example, animal research suggests that basolateral amygdala is involved in forming associations between objects and their current value (Baxter & Murray, 2002), whereas the superficial cortex-like areas are involved in providing emotional context for stimulus associations (Fudge, de Campo, & Becoats, 2012; Fudge & Tucker, 2009).
In addition to spatial variance in amygdala, animal work suggests that connections between the OFC and amygdala also vary by the area of OFC examined (Carmichael & Price, 1995; Cavada, Company, Tejedor, Cruz-Rizzolo, & Reinoso-Suarez, 2000; Ghashghaei & Barbas, 2002; McDonald, 1998). As with the amygdala nuclei, differential patterns of connectivity across areas of OFC likely support different functions (Zald et al., 2014). Evidence from both the human and animal literatures suggests the existence of both medial-lateral and anterior–posterior gradients in OFC function (Elliott et al., 2000; Murray, Moylan, Saleem, Basile, & Turchi, 2015; Zald et al., 2014). In particular, the medial-lateral gradient appears to reflect reward vs. punishment valuation, with medial OFC activated when decisions must be made on the basis of reward value and lateral OFC activated when a prepotent response must be inhibited in order to avoid punishment (Elliott et al., 2000; O'Doherty, Kringelbach, Rolls, Hornak, & Andrews, 2001). In contrast, the anterior–posterior gradient appears to reflect pre- versus post-goal valuation, with anterior OFC needed for goal-selection based on stored value and posterior OFC needed for updating stored values based on the outcome of goal attainment (Murray et al., 2015). Given this human and animal evidence of spatial specificity in the functions of both amygdala and OFC, along with animal evidence of distinct connectivity patterns, it is likely that connectivity with each amygdala nucleus varies spatially across OFC, and that this variation contributes meaningfully to the different functions supported by these regions.
Similar to the work described above for whole-amygdala connectivity, past human work examining the connectivity patterns of amygdala nuclei with OFC has relied on functional connectivity, and only three studies to date have examined OFC-amygdala structural connectivity (Abivardi & Bach, 2017; Bach, Behrens, Garrido, Weiskopf, & Dolan, 2011; Grèzes, Valabrègue, Gholipour, & Chevallier, 2014). Unfortunately, this work is limited in the inferences that can be drawn regarding spatial specificity in both amygdala and OFC. For example, Bach et al. (2011) parcellated amygdala into only two subregions, corresponding to deep and superficial nuclei, based on its connections with temporal pole and lateral OFC, which does not allow for spatial specificity in the OFC regions identified and leaves the majority of OFC unexamined. Abivardi and Bach (2017) divided amygdala again into only two subregions, using the same procedure as their previous study, and observed some differences in OFC connectivity with the two amygdala subregions. However, as these authors noted, these findings are confounded by the fact that OFC was used to define the clusters in the first place. In addition, although connectivity with the amygdala subregions was performed voxel-wise, statistical analyses were performed only on entire regions, again limiting potential OFC spatial specificity. Although Grèzes et al. (2014) examined three amygdala subregions (centromedial, basolateral, and superficial), their findings did not provide any spatial specificity in OFC, given that they examined connectivity with OFC as a whole. Thus, structural connectivity between amygdala nuclei and different regions of OFC has yet to be characterized in humans.
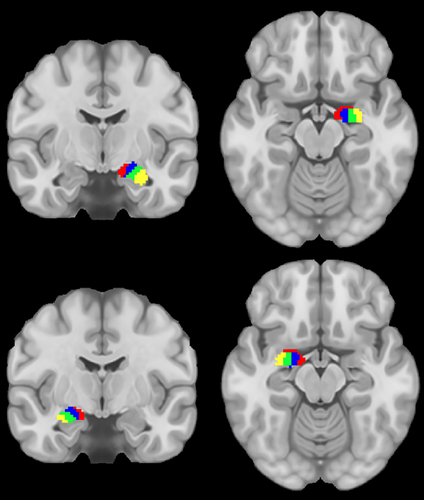
The present study addressed these gaps by characterizing structural connectivity between amygdala nuclei and OFC in a large sample (n = 1,053) of healthy young adults. Structural connectivity was derived from high-definition dMRI using probabilistic tractography. We investigated the connectivity of four amygdala nuclei: lateral (La), basal (Ba), accessory basal (AB), and the CAT. These nuclei were chosen as they are the largest divisions in FreeSurfer's amygdala atlas (Saygin et al., 2017), and thus they were likely to be the most reliably segmented across participants and have the most reliable signals, given that more voxels entered into determining connectivity (Figure 1).
To develop a comprehensive picture of OFC connectivity with amygdala nuclei, we examined connections in four conceptually distinct ways. First, connectivity between each voxel in the OFC and each amygdala nucleus was examined to identify OFC areas connected with each amygdala nucleus. Second, connectivity between each voxel in the OFC and each (individual) amygdala nucleus was compared to connectivity between that OFC voxel and the average of the other three amygdala nuclei. This identified regions of OFC that were preferentially connected to each amygdala nucleus (relative to connectivity with overall amygdala), which may be useful for inferring functional differences related to such spatial specificity. Third, probabilistic maps of OFC (one for each amygdala nucleus) were created based upon the likelihood of each OFC voxel exhibiting preferential connectivity with each nucleus. Each OFC voxel in a given map reflects the probability (across all participants) that this voxel is more connected to a given nucleus than to the other three nuclei. A limitation of this method is that only the nucleus with the highest connectivity is reflected in these maps, which results in the loss of a substantial amount of information about connectivity patterns. Thus, our fourth analysis created rank-order maps of OFC (one for each amygdala nucleus) based upon the relative density of connectivity between each OFC voxel and each nucleus. In essence, the first analysis simply identified the existence of connections between regions of OFC and each amygdala nucleus, the second analysis identified the patterns of preferential patterns of connectivity for each nucleus, and the third and fourth provided spatial atlases of OFC.
In summary, there is limited direct evidence of structural connectivity between the OFC and amygdala in humans. Further, structural connectivity between the OFC and amygdala nuclei in humans has yet to be characterized. Because connectivity between the OFC and amygdala is critical to maintaining goal-directed behavior, forming and updating learned associations, and encoding the value of stimuli or behavioral responses, and given evidence that particular amygdala nuclei and areas of OFC are differentially involved in these processes (e.g., BLA and forming associations between objects and their current value), it is critical to understand the precise pattern of connections between different regions of OFC and different amygdala nuclei. Such an understanding has the potential to provide insight into the functions supported by these nuclei and how pathological processes may emerge from connectivity between the OFC and amygdala nuclei.
2 METHODS
2.1 Participants
We used data collected from 1,053 healthy participants (mean age = 28.75, SD = 3.68; female = 571 [54.2%]; White = 799 [75.9%], Black = 148 [14.1%], Asian/Pacific = 63 [6.0%], American Indian/Alaskan = 2 [0.2%], Multiple = 26 [2.5%], Hispanic/Latino = 88 [8.4%], Not reported = 15 [1.4%]) as part of the Human Connectome Project (HCP; RRID:SCR_003490). Briefly, the HCP offers a database of anonymous structural, diffusion, and functional MRI for connectomics research purposes (Van Essen et al., 2013). We conducted secondary analysis on de-identified open access data after agreeing to the HCP Open Access Data Use Terms. Informed consent, including consent to share de-identified data, was acquired by the HCP and approved by the Washington University institutional review board.
2.2 MRI acquisition
Structural and diffusion-weighted data were acquired on a modified 3 T Skyra System (Siemens) using a 32-channel coil. A T1-weighted structural image was acquired (TR = 2,400 ms; TE = 2.14 ms; TI = 1,000 ms; flip angle = 8°; voxel size = .7 × 7 × 7 mm) (Uǧurbil et al., 2013). Diffusion acquisition involved a spin-echo multiband EPI with 270 diffusion-weighted directions (TR = 5,520 ms; TE = 89.5 ms; flip angle = 78°; refocusing flip angle = 160°; voxel size = 1.25 × 1.25 × 1.25 mm; multiband factor = 3; b-values = 1,000, 2000, 3,000 s/mm2) (Sotiropoulos et al., 2013; Uǧurbil et al., 2013).
2.3 HCP MRI preprocessing
All imaging data passed HCP quality assurance (Marcus et al., 2013) and were run (by HCP) through several standardized preprocessing pipelines. Our use of this (standardized) preprocessed data allow for greater methodological transparency and replicability across studies. Structural T1-weighted images first underwent gradient distortion and bias field correction. Next, T1 images were run through FreeSurfer (RRID:SCR_001847) to obtain a participant-specific subcortical segmentation, delineation of the cortical mantle, and segmentation of a white matter mask (Fischl, 2012). Lastly, T1 images were registered to both standard MNI and diffusion space. Diffusion data were run through an HCP pipeline in FSL (RRID:SCR_002823) to normalize b0 image intensity across runs and to correct for EPI and eddy-current induced distortions, gradient-nonlinearities, and participant motion (Glasser et al., 2013; Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012). Next, diffusion data was processed by FSL's bedpostx, which creates the files necessary for performing probabilistic tractography (Hernández et al., 2013).
2.4 Connectivity atlas
We used the participant-specific Destrieux cortical parcellation (Destrieux, Fischl, Dale, & Halgren, 2010) in conjunction with the participant-specific subcortical segmentation, both obtained via FreeSurfer (Fischl et al., 2002). In addition, we segmented the amygdala nuclei via FreeSurfer's hippocampal subfields and amygdala nuclei module using both T1- and T2-weighted images (Saygin et al., 2017). An OFC ROI was created by merging together orbital gyri, gyrus rectus, and lateral, medial, and orbital sulci ROIs from the cortical parcellation. Although there is some debate about whether gyrus rectus should be considered part of OFC (Rudebeck & Rich, 2018), including it in our analyses did not impact examination of other areas, and thus we chose to be inclusive in order to facilitate comparisons with prior research that similarly defines OFC (e.g., Liu, Qin, Qi, Jiang, & Yu, 2015; Mavrogiorgou et al., 2017; Petrides & Mackey, 2006; Zald et al., 2014). FreeSurfer ROIs representing white matter were combined to create a white matter mask for use in tractography. Segmentation of the amygdala resulted in nine ROIs. However, only the basal (Ba), accessory basal (AB), lateral (La), and CAT nuclei of amygdala were used in the present study, as these were the largest nuclei and thus most likely to be reliably segmented across participants.
2.5 Calculation of connectivity
Interregional white matter connectivity was estimated using probabilistic tractography (Behrens, Berg, Jbabdi, Rushworth, & Woolrich, 2007) via FSL's probtrackx2, which infers the orientation of a tract by repeatedly sampling from the estimated diffusion fiber orientations calculated in bedpostx. A distribution of the tract's path from each voxel using these estimates is then built. Multiple tracts are sampled from each voxel, building a connectivity distribution for that voxel. Estimated connectivity between two regions is then equal to the probability of a tract starting at the seed region and going through the target region (Behrens et al., 2003). Thus, probabilistic tractography was used to estimate the streamline count between pairs of ROIs, which covaries with both the number of axons connecting two regions and the microstructural integrity of those axons (Jbabdi & Johansen-Berg, 2011).
To obtain these estimates of interregional white matter connectivity (i.e., streamlines) between the OFC and the amygdala nuclei, tractography was performed from the OFC ROI to each amygdala nucleus ROI. In order to determine which regions of the OFC were more likely to be connected to each amygdala nucleus (over and above general amygdala connectivity), we compared OFC connectivity with a single nucleus to OFC connectivity with the average of the three other nuclei (based on tractography performed with all four nuclei as potential targets of streamlines sampled from OFC voxels). This strategy of comparing against the three remaining nuclei, rather than the sum of all four nuclei (i.e., including the nucleus currently under examination), was chosen because adding the signal from the ROI under investigation would only lower the likelihood of finding specificity, without any added benefit. In other words, controlling for the connectivity of CAT when trying to identify patterns of connectivity specific to CAT does not address any potential confounds.
Tractography was performed once per hemisphere, with all four nuclei as different targets and OFC as the seed. Connectivity was calculated separately for right and left hemispheres, because the relatively few contralateral (vs. ipsilateral) amygdalar connections are known from tracing studies to be light and mimic the much denser ipsilateral connections (McDonald, 1998). Five thousand sample tracts were generated from the center of each OFC voxel, and only tracts that (a) reached a target amygdala ROI and (b) passed through white matter were retained. This resulted in one image per amygdala target, per participant, with each value in that image indicating the number of sample tracts sent out from each voxel of OFC that reached that target.
Although all streamlines were required to pass through white matter, this did not address the possibility of indirect connections. Thus, in a subset of participants (n = 95), probabilistic tractography was rerun in probtrackx with the “-avoid” flag and an exclusion mask to suppress indirect connections between amygdala and OFC. Specifically, to create an exclusion mask for each participant we (a) binarized the (participant-specific) FreeSurfer cortical/subcortical masks, (b) subtracted the seed, target, and waypoint (i.e., amygdala, OFC, white matter) masks, and eroded this mask via a 3 mm cube kernel. Erosion was done to account for potential small misregistrations of the atlas/segmentation errors. Lastly, the exclusion mask used in FSL's XTRACT to track the uncinate fasciculus, which connects amygdala and OFC, was added and the result binarized. In other words, the exclusion mask contained everything in the brain except the amygdala, OFC, and white matter. Thus, the use of these exclusion masks would prevent streamlines that entered thalamus, striatum, or non-OFC cortical areas, for example, from counting as connecting amygdala and OFC. The inclusion of the uncinate fasciculus exclusion mask ensured that our exclusion mask was consistent with that used in standardized protocols to segment the white matter pathway connecting amygdala and OFC. Importantly, this method of creating exclusion masks is similar to, or more conservative than, that used in other studies employing probabilistic tractography (e.g., Abivardi & Bach, 2017; Barbagallo et al., 2017; Berndt et al., 2019; Findlater, Mazerolle, Pike, & Dukelow, 2019; Lehmann et al., 2019; Wan et al., 2019; Wong et al., 2018), and much more conservative than the one used in FSL's XTRACT (Warrington et al., 2020).
In the left hemisphere, using an exclusion mask resulted in 103% of the number of streamlines calculated without an exclusion mask, and this increase reflects the probabilistic nature of the tractography and sampling of voxel-wise orientations from the bedpostx distributions. In other words, the results for the left hemisphere were essentially unchanged by adding the exclusion mask, and thus the majority of the streamlines observed in our main analyses appear to be direct.
In the right hemisphere, using an exclusion mask resulted in 73% of the number of streamlines calculated without an exclusion mask. As above, this reduction may partly be due to the probabilistic nature of the analyses. However, it also appears possible that some of the tracts found in our main analyses were indirect, although the majority remain direct and thus these analyses remain valid. The cause of the hemispheric differences is unclear. Of course, this may accurately reflect underlying anatomical differences, although we were unable to locate any evidence of this in the literature. Another possible explanation is differential accuracy of the FreeSurfer segmentation across hemispheres. For example, uncinate fasciculus is known to pass through the narrow band of white matter between insula and putamen, and thus overestimation of the size of insula and/or putamen could block valid streamlines. To account for this possibility, we performed erosion of the exclusion mask, but this may not have been adequate. Overall, the use of exclusion masks supports the inference that our main results reflect direct connections between amygdala and OFC, particularly in the left hemisphere.
Because the four amygdala nuclei differed substantially in size from each other, comparisons between nuclei would be biased in favor of larger nuclei. Specifically, larger nuclei contain more voxels within which streamlines could terminate, and thus there is a greater likelihood of streamlines connecting to that nucleus. To be clear, we are not asserting that the streamline counts themselves are biased, as larger amygdala nuclei may in fact have more axonal connections with OFC. Rather, the comparisons between ROIs would be biased due to ROI size. To account for this, the total number of streamlines between a particular OFC voxel and a particular amygdala nucleus was divided by the total number of voxels in the amygdala target ROI, consistent with similar studies in this area (e.g., Abivardi & Bach, 2017). Although we entered OFC as the seed ROI and the amygdala nuclei as the target ROIs, dMRI cannot detect directionality, and thus we can make no inferences regarding the contribution of projections from OFC to amygdala versus amygdala to OFC to the streamline counts. Connectivity maps were then warped into MNI152 nonlinear sixth generation standard space to facilitate between-subject comparisons. Connectivity maps were then used to (a) identify connections between OFC regions and amygdala nuclei, (b) compare maps between amygdala nuclei, (c) calculate probabilistic OFC maps of preferential connectivity with amygdala nuclei, and (d) calculate rank-order OFC maps of relative density of connectivity among amygdala nuclei.
2.6 OFC classification
In order to classify areas of OFC based upon connectivity patterns with different amygdala nuclei, connectivity maps from OFC to each amygdala nucleus were input into FSL's “find_the_biggest” function (Behrens et al., 2003). This function operates on the output of tractography performed with multiple target ROIs (e.g., amygdala nuclei) and a single seed (e.g., OFC) and performs hard segmentation of the seed based upon its connections with the target ROIs. Thus, each voxel of OFC was labeled with the amygdala nucleus demonstrating the highest connection probability to that voxel. As mentioned above, the participant-level tractography results used in this analysis were first divided by the total number of voxels in that participant's target (i.e., amygdala nucleus) ROI to address bias resulting from difference in size among the nuclei. The resultant participant-level OFC segmentation was warped into standard space using nearest neighbor interpolation (Andersson, Jenkinson, & Smith, 2007) to facilitate classification of OFC areas.
2.7 Data analysis
2.7.1 Identification of connections between OFC regions and amygdala nuclei
To identify OFC voxels that receive projections from each nucleus, we performed nonparametric (5,000 repetitions) 1-sample t-tests on the normalized streamlines connecting a given nucleus to OFC using FSL's randomize tool. Although between-nuclei comparisons were not computed in this analysis, we used the normalized values for consistency across analyses. Importantly, this normalization (i.e., dividing streamlines by ROI size) does not impact the results of this analysis, as all values within an analysis were normalized by the same value (i.e., it is a linear transformation). For each voxel in OFC, we tested whether, across all participants, there were a significant number of streamlines connected to the given nucleus. These tests allowed us to identify which areas of OFC are significantly connected with each amygdala ROI. Significance was determined via permutation tests using threshold-free cluster enhancement (TFCE) and controlling for family-wise error (FWE) (Winkler, Ridgway, Webster, Smith, & Nichols, 2014). TFCE increases the sensitivity of analyses (vs. voxelwise thresholding), while minimizing the problems associated with using a hard (and arbitrary) cluster-defining threshold (Smith & Nichols, 2009). Lastly, MNI coordinates of the max value (i.e., largest test statistic) and center of gravity for significant clusters (p's < .05) for each nucleus were identified. To characterize the location of clusters, we identified the Destrieux atlas ROI in which these coordinates were located (Destrieux et al., 2010).
2.7.2 Between-amygdala nuclei comparisons of connections with OFC
We next identified clusters of OFC that exhibited more connections with one nucleus than the other three nuclei. In particular, for each OFC voxel, we used paired t tests to compare the streamlines for a single nucleus to the streamlines for the combined ROI consisting of the other three nuclei. Note that, as described above, the difference in ROI size between a single nucleus and the combination of the other three nuclei was accounted for, and thus did not bias analyses. Unlike the 1-sample tests described above, which simply identified the connectivity pattern of each nucleus, these paired tests allowed us to identify which areas of OFC were preferentially connected to a particular amygdala nucleus (relative to general amygdala connectivity). As above, FSL's randomize and TFCE were used (5,000 repetitions) and MNI coordinates for the max value and center of gravity for each cluster were identified.
2.7.3 Probabilistic OFC maps of preferential connectivity with amygdala nuclei
In order to obtain spatial atlases of OFC for each amygdala nucleus, we used the output of FSL's “find_the_biggest” function, which classifies each OFC voxel by the amygdala nucleus that demonstrated the highest probability of connection to that OFC voxel within each participant. This method was used instead of simple connectivity between OFC and amygdala nuclei because each nucleus demonstrated (at least weak) widespread connectivity across OFC, making probabilistic maps of simple connectivity of little informational value. In contrast, preferential connectivity is less widespread, and thus would be of greater utility. Although the previous set of analyses also provided insight into preferential connectivity, the probabilistic maps provided additional information because they were based on simple dominance of connectivity—for each participant, each OFC voxel was labeled with the nucleus that had the strongest connectivity. Therefore, these analyses provide insight into the likelihood that a given OFC voxel shows the highest connectivity with each amygdala nucleus. Participant-level classifications of each OFC voxel were then used to obtain, for each amygdala nucleus, probabilistic maps of OFC (i.e., allowing a voxel to be associated with more than one label) based on the likelihood of an OFC voxel demonstrating connectivity to a given nucleus across all participants. For each amygdala nucleus and for each OFC voxel, the number of participants with the label corresponding to the given amygdala nucleus was divided by the entire sample size (i.e., 1,053). Thus, we obtained four probabilistic maps of OFC indicating the likelihood of each OFC voxel demonstrating preferential connectivity with a given amygdala nucleus. The maps were then characterized by identifying which Destrieux atlas ROIs overlapped with the area with the highest probability.
2.7.4 Rank-order OFC maps of connectivity with amygdala nuclei
Because FSL's “find_the_biggest” function employs a “winner-takes-all” approach, information other than which nucleus exhibited the largest number of streamlines was ignored. To compensate for this weakness, a second set of OFC spatial atlases was computed based on the rank-order of connectivity with each amygdala nucleus. Specifically, for each participant, amygdala nuclei were rank ordered within each OFC voxel based on the number of streamlines between that voxel and each nucleus. These values were used to compute 4 OFC maps (one for each amygdala nucleus) per participant, with values reflecting the rank order for that nucleus. Group-level rank-order maps were then obtained by calculating the modal rank (across participants) for each OFC voxel in each amygdala nucleus map. Specifically, for each amygdala nucleus, the modal rank value across all participants was calculated for each voxel and used to create the group-level rank-order map. Thus, the value for each voxel in the group-level maps reflects the most common rank for that nucleus across participants. These maps were then characterized by identifying, for each rank, which Destrieux atlas ROIs overlapped with the identified OFC area.
3 RESULTS
We calculated the volume of each amygdala nucleus and the percentage of the whole amygdala that each nucleus comprised, per hemisphere. In the left hemisphere La was the largest (mean = 698.69 voxels, SD = 83.57, 36.57%), followed by Ba (mean = 480.55 voxels, SD = 60.14, 25.15%), AB (mean = 288.08 voxels, SD = 35.9, 15.08%), and CAT (mean = 206.22 voxels, SD = 26.19, 10.79%). In the right hemisphere La was again largest (mean = 731.12 voxels, SD = 86, 37.24%), followed by Ba (mean = 491.8 voxels, SD = 57.88, 25.05%), AB (mean = 289.83 voxels, SD = 34.15, 14.76%), and CAT (mean = 200.05 voxels, SD = 23.77, 10.19%; see Table 1 for all other volumes).
| Nucleus | Mean | SD | Percentage of whole amygdala |
|---|---|---|---|
| Left lateral nucleus (La) | 698.69 | 83.57 | 36.57 |
| Left basal nucleus (Ba) | 480.55 | 60.14 | 25.15 |
| Left accessory basal nucleus (AB) | 288.08 | 35.90 | 15.08 |
| Left cortico-amygdaloid transition (CAT) | 206.22 | 26.19 | 10.79 |
| Left anterior amygdaloid area | 63.18 | 8.80 | 3.31 |
| Left central nucleus | 57.71 | 10.30 | 3.02 |
| Left paralaminar nucleus | 57.25 | 7.35 | 3.00 |
| Left medial nucleus | 27.68 | 6.77 | 1.45 |
| Left cortical nucleus | 31.13 | 5.26 | 1.63 |
| Left whole amygdala | 1,910.49 | 221.91 | 100.00 |
| Right lateral nucleus (La) | 731.12 | 86.00 | 37.24 |
| Right basal nucleus (Ba) | 491.80 | 57.88 | 25.05 |
| Right accessory basal nucleus (AB) | 289.83 | 34.15 | 14.76 |
| Right cortico-amygdaloid transition (CAT) | 200.05 | 23.77 | 10.19 |
| Right anterior amygdaloid area | 68.24 | 9.14 | 3.48 |
| Right central nucleus | 65.59 | 10.39 | 3.34 |
| Right paralaminar nucleus | 56.61 | 6.84 | 2.88 |
| Right medial nucleus | 29.80 | 6.66 | 1.52 |
| Right cortical nucleus | 30.36 | 5.46 | 1.55 |
| Right whole amygdala | 1,963.39 | 216.52 | 100.00 |
3.1 Identification of OFC regions receiving projections from amygdala nuclei
Using probabilistic tractography, we examined OFC-amygdala nucleus connectivity. The relative number of streamlines, normalized for nucleus ROI size, reflects the probability that a connection between OFC and a given amygdala nucleus exists. In our first set of analyses, we performed tractography between OFC and each amygdala nucleus, and then identified clusters for each nucleus that were consistent across all participants. In both hemispheres and across all nuclei, the clusters spanned the entirety of the OFC and the center of gravity of connectivity was in anterior middle OFC, in the orbital sulcus corresponding to lateral BA 11. There was some differentiation in the area of OFC with the largest effect size (indicated by the largest test statistic): OFC connectivity with all left nuclei and right Ba and La nuclei had a maximum in the anterior lateral orbital gyri corresponding to rostral anterior BA 47 and OFC connectivity with right AB and CAT had a maximum in the posterior orbital gyri corresponding to superior BA 47 and (all p's < .0002 after controlling for FWE; see Table 2). Due to all clusters spanning the entirety of the OFC, Figure 2 illustrates the locations of the centers of gravity and maximum test statistics. In order to gain insight into the overall connectivity between OFC and each nucleus, we also calculated mean connectivity (across OFC voxels) for each nucleus and participant (after normalization for ROI size as described), and then calculated with mean/SD of these values across participants. In the left hemisphere, mean connectivity of CAT was the largest (mean = 0.044, SD = 0.032) followed by AB (mean = 0.036, SD = 0.022), La (mean = 0.034, SD = 0.021), and Ba (mean = 0.029, SD = 0.019). In the right hemisphere, mean connectivity of La was the largest (mean = 0.044, SD = 0.024) followed by CAT (mean = 0.041, SD = 0.053), AB (mean = 0.036, SD = 0.022) and Ba (mean = 0.029, SD = 0.019).
| Nucleus | # of voxels | Max | Max x | Max y | Max z | FreeSurfer label | COG x | COG y | COG z | FreeSurfer label |
|---|---|---|---|---|---|---|---|---|---|---|
| Left lateral nucleus (La) | 8,137 | 30.8 | −42 | 46 | −16 | Orbital gyri | −26.3 | 38.7 | −14.0 | Orbital sulcus |
| Left basal nucleus (Ba) | 8,123 | 30.9 | −42 | 46 | −16 | Orbital gyri | −26.5 | 38.9 | −14.0 | Orbital sulcus |
| Left accessory basal nucleus (AB) | 8,242 | 28.9 | −42 | 48 | −14 | Orbital gyri | −26.7 | 38.9 | −13.9 | Orbital sulcus |
| Left cortico-amygdaloid transition (CAT) | 7,899 | 26.5 | −38 | 38 | −16 | Orbital sulcus/gyri | −26.5 | 39.1 | −14.1 | Orbital sulcus |
| Right lateral nucleus (La) | 8,127 | 29.2 | 44 | 52 | −8 | Orbital gyri | 28.2 | 37.9 | −14.1 | Orbital sulcus |
| Right basal nucleus (Ba) | 7,961 | 29.5 | 44 | 50 | −12 | Orbital gyri | 28.1 | 38.6 | −14.1 | Orbital sulcus |
| Right accessory basal nucleus (AB) | 7,912 | 29.3 | 38 | 22 | −12 | Orbital gyri | 28.6 | 38.8 | −13.9 | Orbital sulcus |
| Right cortico-amygdaloid transition (CAT) | 7,650 | 25.4 | 36 | 22 | −12 | Orbital gyri | 28.8 | 38.8 | −13.9 | Orbital sulcus |
- Note: Coordinates given in MNI coordinates (mm). Max = coordinates of voxel with largest test statistic. COG = coordinates of Center of Gravity voxel (weighted average of the coordinates by the intensities within the cluster).

3.2 Between-amygdala nuclei comparison of projections to OFC
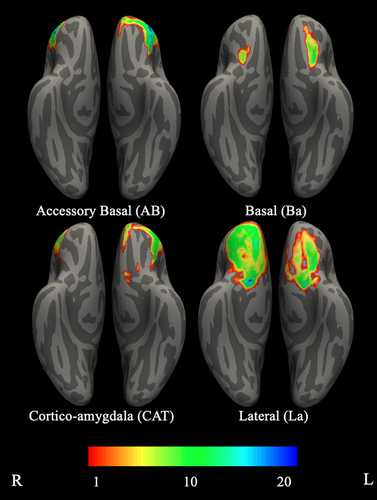
Next, we examined preferential connectivity of OFC with a given amygdala nucleus, relative to OFC connectivity with the remaining three nuclei. Thus, the clusters identified reflect areas of OFC where the estimate of connections between OFC and a given amygdala nucleus (e.g., AB) is greater than those of the average of the three other nuclei (e.g., Ba, La, CAT), normalized for size differences. In the left hemisphere, we found that preferential OFC connectivity with AB and CAT spanned anterior-medial and lateral (anterior and posterior) areas of OFC. In addition, CAT connectivity formed a second cluster covering posterior-medial OFC. Preferential OFC connectivity with Ba spanned primarily middle OFC, extending into portions of posterior OFC, and preferential connectivity with La spanned middle and posterior OFC. In the right hemisphere, OFC connectivity with AB and CAT spanned anterior-lateral OFC. OFC connectivity with Ba concentrated in a small area of posterior-middle OFC, and connectivity with La spanned the entirety of OFC, but centered on medial OFC (all p's < .0002 after controlling for FWE; see Table 3, Figure 3).
| Nucleus | # of voxels | Max | Max x | Max y | Max z | FreeSurfer label | COG x | COG y | COG z | FreeSurfer label |
|---|---|---|---|---|---|---|---|---|---|---|
| Left lateral nucleus (La) | 1,518 | 16.6 | −22 | 4 | −14 | Orbital gyri | −20.1 | 21.2 | −19.3 | Orbital sulcus |
| Left basal nucleus (Ba) | 530 | 13.1 | −24 | 12 | −26 | Orbital gyri | −23.8 | 22.7 | −21.1 | Orbital gyri |
| Left accessory basal nucleus (AB) | 3,145 | 22.2 | −42 | 36 | −18 | Orbital gyri | −35.3 | 45.7 | −10.5 | Orbital gyri |
| Left cortico-amygdaloid transition (CAT) | 2,825 | 14.9 | −38 | 20 | −14 | Orbital gyri | −34.1 | 45.0 | −10.3 | Orbital gyri |
| Left cortico-amygdaloid transition (CAT) | 63 | 8.9 | −8 | 8 | −20 | Gyrus rectus | −7.9 | 12.9 | −22.1 | Gyrus rectus |
| Right lateral nucleus (La) | 4,292 | 19.5 | 12 | 8 | −16 | Medial orbital | 20.3 | 36.6 | −17.8 | Orbital sulcus |
| Right basal nucleus (Ba) | 131 | 8.6 | 24 | 16 | −24 | Orbital gyri | 22.8 | 17.5 | −23.1 | Orbital gyri |
| Right accessory basal nucleus (AB) | 1,591 | 19.1 | 46 | 48 | −8 | Orbital gyri | 44.6 | 44.4 | −6.8 | Orbital gyri |
| Right cortico-amygdaloid transition (CAT) | 1,134 | 11.2 | 46 | 46 | −8 | Orbital gyri | 44.8 | 43.8 | −5.9 | Lateral orbital |
- Note: Coordinates given in MNI coordinates (mm). Max = coordinates of voxel with largest test statistic. COG = coordinates of Center of Gravity voxel (weighted average of the coordinates by the intensities within the cluster).
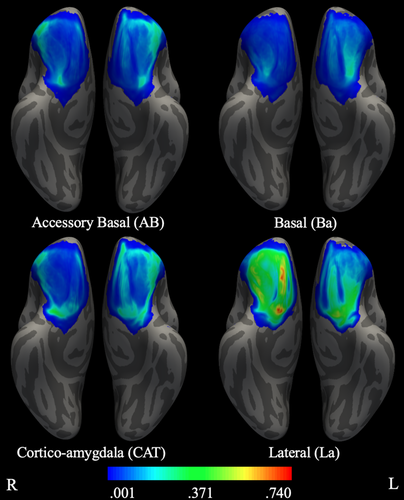
3.3 Probabilistic OFC maps of preferential connectivity with amygdala nuclei
We examined connectivity between OFC and amygdala nuclei, using connectivity-based seed classification (Behrens, Johansen-Berg, et al., 2003). At the individual participant level, each voxel in OFC was classified according to the amygdala nuclei that showed the highest probability of connection. Next, four maps were created across participants (one for each amygdala nucleus), with each OFC voxel in a given map reflecting the probability that it was labeled with the amygdala nucleus of interest. Thus, each voxel in a given amygdala nucleus map reflects the probability that the given nucleus exhibits greater connectivity with that voxel than did any of the other three nuclei. For this analysis, there were 2,986 voxels labeled in the left OFC and 3,117 voxels labeled in the right OFC.
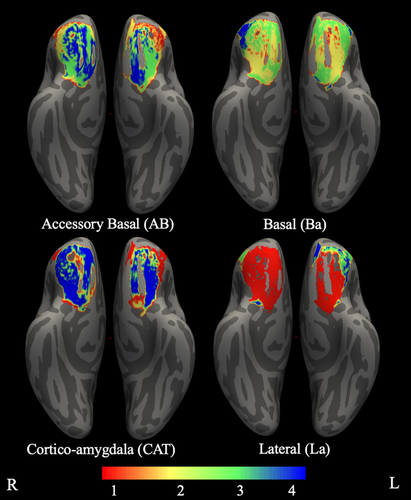
In both hemispheres, all four probabilistic maps spanned all OFC ROIs (i.e., orbital gyri and sulcus, rectal gyrus, medial, and lateral orbital). The area of OFC with the highest probability of demonstrating preferential connectivity with AB, Ba, and CAT was located in orbital gyri and the area for La was located in medial orbital. In the left hemisphere, OFC connectivity with AB spanned anterior and lateral OFC and OFC connectivity with Ba spanned posterior-middle OFC. OFC connectivity with CAT and La spread widely over OFC. Specifically, CAT connectivity spanned lateral OFC, anterior lateral and middle portions of the orbital sulcus and gyrus, and a medial area of gyrus rectus. La connectivity spanned posterior medial OFC, middle portions of the orbital sulcus, the posterior orbital gyri, and gyrus rectus. In the right hemisphere, OFC connectivity with AB and CAT spanned anterior and posterior lateral OFC. OFC connectivity with Ba spanned posterior-middle OFC and OFC connectivity with La spanned the majority of OFC, including the orbital sulcus, the posterior and middle and lateral anterior portions of the orbital gyri, medial OFC, and the gyrus rectus (see Table 4, Figure 4).
| Nucleus | Probability range | Probability mean | FreeSurfer label at maximal probability |
|---|---|---|---|
| Left lateral nucleus (La) | .539–.001 | .065 | Medial orbital |
| Left basal nucleus (Ba) | .267–.001 | .035 | Orbital gyri |
| Left accessory basal nucleus (AB) | .360–.001 | .058 | Orbital gyri |
| Left cortico-amygdaloid transition (CAT) | .384–.001 | .070 | Orbital gyri |
| Right lateral nucleus (La) | .742–.001 | .121 | Medial orbital |
| Right basal nucleus (Ba) | .201–.001 | .023 | Orbital gyri |
| Right accessory basal nucleus (AB) | .363–.001 | .050 | Orbital gyri |
| Right cortico-amygdaloid transition (CAT) | .387–.001 | .050 | Orbital gyri |
- Note: Probability range: maximum and minimum probabilities of participants demonstrating connectivity between OFC and an amygdala nucleus. Probability mean: mean probability of participants demonstrating connectivity between OFC and an amygdala nucleus.
3.4 Rank-order OFC maps of preferential connectivity with amygdala nuclei
Lastly, we examined connectivity between OFC and amygdala nuclei by rank-ordering the amygdala nuclei within each OFC voxel based on the level of connectivity between that OFC voxel and each amygdala nucleus (see Table 5, Figure 5). In both hemispheres La exhibited the greatest connectivity with OFC as a whole, as evidenced by the majority of highest-ranked OFC voxels in the La map across orbital gyri and sulcus, medial lateral gyrus, and gyrus rectus. In the left hemisphere, AB exhibited some of the highest ranked connectivity with OFC in the anterior lateral area. Two opposing trends emerged across rank of connectivity between amygdala nuclei and areas of OFC. For posterior and middle OFC, rank-order of connectivity decreased from lateral to medial amygdala (i.e., rank of La > Ba > AB > CAT). In contrast, for lateral-anterior OFC, rank-order of connectivity decreased from medial to lateral amygdala. In the left hemisphere, this pattern was exactly opposite of that seen for posterior and middle OFC (i.e., rank of CAT > AB > Ba > La), whereas the pattern for right lateral-anterior OFC was slightly different (i.e., CAT > AB > La > Ba). Overall, results from this analysis were consistent with the probabilistic maps.
| Rank 1 | Rank 2 | Rank 3 | Rank 4 | Total | |
|---|---|---|---|---|---|
| Left lateral nucleus (La) | |||||
| Orbital gyri | 239 (28%) | 6 (1%) | 154 (18%) | 93 (11%) | 492 (57%) |
| Orbital sulcus | 79 (9%) | 7 (1%) | 43 (5%) | 16 (2%) | 145 (17%) |
| Lateral orbital | 0 (0%) | 0 (0%) | 15 (2%) | 0 (0%) | 15 (2%) |
| Medial orbital | 85 (10%) | 0 (0%) | 0 (0%) | 0 (0%) | 85 (10%) |
| Gyrus rectus | 51 (6%) | 0 (0%) | 3 (0%) | 69 (8%) | 123 (14%) |
| Total | 454 (53%) | 13 (2%) | 215 (25%) | 178 (21%) | 860 (100%) |
| Left basal nucleus (Ba) | |||||
| Orbital gyri | 0 (0%) | 197 (22%) | 260 (30%) | 41 (5%) | 498 (57%) |
| Orbital sulcus | 0 (0%) | 66 (8%) | 85 (10%) | 0 (0%) | 151 (17%) |
| Lateral orbital | 0 (0%) | 0 (0%) | 11 (1%) | 5 (1%) | 16 (2%) |
| Medial orbital | 0 (0%) | 33 (4%) | 45 (5%) | 0 (0%) | 78 (9%) |
| Gyrus rectus | 0 (0%) | 1 (0%) | 131 (15%) | 1 (0%) | 133 (15%) |
| Total | 0 (0%) | 297 (34%) | 532 (61%) | 47 (5%) | 876 (100%) |
| Left accessory basal nucleus (AB) | |||||
| Orbital gyri | 97 (11%) | 171 (20%) | 137 (16%) | 96 (11%) | 501 (58%) |
| Orbital sulcus | 35 (4%) | 33 (4%) | 40 (5%) | 37 (4%) | 145 (17%) |
| Lateral orbital | 0 (0%) | 16 (2%) | 0 (0%) | 0 (0%) | 16 (2%) |
| Medial orbital | 0 (0%) | 1 (0%) | 15 (2%) | 63 (7%) | 79 (9%) |
| Gyrus rectus | 4 (0%) | 81 (9%) | 0 (0%) | 44 (5%) | 129 (15%) |
| Total | 136 (16%) | 302 (35%) | 192 (22%) | 240 (28%) | 870 (100%) |
| Left cortico-amygdaloid transition (CAT) | |||||
| Orbital gyri | 246 (29%) | 0 (0%) | 0 (0%) | 248 (29%) | 494 (58%) |
| Orbital sulcus | 44 (5%) | 0 (0%) | 0 (0%) | 106 (12%) | 150 (17%) |
| Lateral orbital | 19 (2%) | 0 (0%) | 0 (0%) | 0 (0%) | 19 (2%) |
| Medial orbital | 20 (2%) | 8 (1%) | 0 (0%) | 46 (5%) | 74 (9%) |
| Gyrus rectus | 103 (12%) | 5 (1%) | 0 (0%) | 14 (2%) | 122 (14%) |
| Total | 432 (50%) | 13 (2%) | 0 (0%) | 414 (48%) | 859 (100%) |
| Right lateral nucleus (La) | |||||
| Orbital gyri | 584 (49%) | 0 (0%) | 92 (8%) | 6 (1%) | 682 (57%) |
| Orbital sulcus | 220 (18%) | 0 (0%) | 0 (0%) | 0 (0%) | 220 (18%) |
| Lateral orbital | 0 (0%) | 0 (0%) | 11 (1%) | 0 (0%) | 11 (1%) |
| Medial orbital | 114 (10%) | 0 (0%) | 0 (0%) | 1 (0%) | 115 (10%) |
| Gyrus rectus | 170 (14%) | 0 (0%) | 0 (0%) | 0 (0%) | 170 (14%) |
| Total | 1,088 (91%) | 0 (0%) | 103 (9%) | 7 (1%) | 1,198 (100%) |
| Right basal nucleus (Ba) | |||||
| Orbital gyri | 0 (0%) | 191 (17%) | 253 (23%) | 206 (18%) | 650 (58%) |
| Orbital sulcus | 0 (0%) | 72 (6%) | 116 (10%) | 9 (1%) | 197 (18%) |
| Lateral orbital | 0 (0%) | 0 (0%) | 1 (0%) | 13 (1%) | 14 (1%) |
| Medial orbital | 0 (0%) | 69 (6%) | 46 (4%) | 0 (0%) | 115 (10%) |
| Gyrus rectus | 0 (0%) | 9 (1%) | 134 (12%) | 0 (0%) | 143 (13%) |
| Total | 0 (0%) | 341 (30%) | 550 (49%) | 228 (20%) | 1,119 (100%) |
| Right accessory basal nucleus (AB) | |||||
| Orbital gyri | 67 (6%) | 209 (18%) | 151 (13%) | 235 (21%) | 662 (59%) |
| Orbital sulcus | 0 (0%) | 18 (2%) | 35 (3%) | 148 (13%) | 201 (18%) |
| Lateral orbital | 7 (1%) | 6 (1%) | 0 (0%) | 0 (0%) | 13 (1%) |
| Medial orbital | 0 (0%) | 2 (0%) | 51 (5%) | 61 (5%) | 114 (10%) |
| Gyrus rectus | 0 (0%) | 35 (3%) | 9 (1%) | 96 (8%) | 140 (12%) |
| Total | 74 (7%) | 270 (24%) | 246 (22%) | 540 (48%) | 1,130 (100%) |
| Right cortico-amygdaloid transition (CAT) | |||||
| Orbital gyri | 97 (9%) | 72 (7%) | 0 (0%) | 448 (42%) | 617 (58%) |
| Orbital sulcus | 0 (0%) | 21 (2%) | 0 (0%) | 168 (16%) | 189 (18%) |
| Lateral orbital | 13 (1%) | 0 (0%) | 0 (0%) | 0 (0%) | 13 (1%) |
| Medial orbital | 2 (0%) | 12 (1%) | 0 (0%) | 98 (9%) | 112 (11%) |
| Gyrus rectus | 0 (0%) | 57 (5%) | 0 (0%) | 67 (6%) | 124 (12%) |
| Total | 112 (11%) | 162 (15%) | 0 (0%) | 781 (74%) | 1,055 (100%) |
- Note: For each amygdala nucleus and OFC region, the number of voxels with a given rank (highest rank = 1) are provided. The percentage of the number of voxels in a given OFC region and of a particular rank out of the total number of voxels in OFC exhibiting connectivity with a particular nucleus are given in parentheses in order to illustrate the how the rank of connectivity between amygdala and OFC varies by amygdala nucleus and OFC region.
4 DISCUSSION
The goal of the study was to advance our understanding of human OFC-amygdala connectivity by elucidating the patterns of connections between different regions of the OFC and amygdala nuclei. In characterizing connectivity between the OFC and amygdala nuclei, our results provide direct evidence of the structural connections that likely support the different emergent functions of the OFC-amygdala circuit, including those related to memory, emotion, and motivation. In order to fully illustrate different aspects of this connectivity, we employed several strategies to characterize the patterns of structural connections between the OFC and amygdala nuclei using automatic segmentation of amygdala nuclei (Saygin et al., 2017), dMRI, and probabilistic tractography (Hernández et al., 2013). Specifically, we first identified which OFC areas were connected with each amygdala nucleus, independent of the other nuclei, by examining connectivity between each OFC voxel and each amygdala nucleus. Second, we identified patterns of preferential connectivity for each nucleus by comparing OFC connectivity with one nucleus to average OFC connectivity with the other three amygdala nuclei. This revealed which regions of OFC were more highly connected with a particular amygdala nucleus, relative to overall OFC connectivity with amygdala. Third, we calculated probabilistic maps of OFC based upon the likelihood of preferential connectivity with each amygdala nuclei.
Simple OFC connectivity with each amygdala nucleus, independent of the other nuclei, spanned the entirety of the OFC for all nuclei. Additionally, within hemisphere, all nuclei had approximately the same center of gravity of connectivity values in the OFC. In the left hemisphere, OFC connectivity with La, Ba, and AB and, in the right hemisphere, OFC connectivity with AB and CAT and with Ba and La had similar locations for the maximum test statistic. This set of findings reflects the similarity of overall amygdala connectivity but does not address the potential specificity of amygdala nuclei connections with OFC, thus spurring us to conduct additional analyses. These three approaches assayed preferential OFC connectivity for each amygdala nucleus, and differences in the connectivity patterns of the four amygdala nuclei with OFC were found across these approaches. Overall, La demonstrated the strongest and widest connections to the OFC in both hemispheres. Although not directly compared, La appeared to dominate connectivity to a greater extent in the right hemisphere, whereas connectivity in the left hemisphere was concentrated in middle and posterior OFC. CAT and AB demonstrated more restricted patterns of connectivity, primarily with anterior and lateral areas of OFC. Ba demonstrated the most restricted pattern, with connections concentrated in posterior-middle OFC. As seen in Figures 3 and 4, AB and CAT and, to a lesser extent, Ba and La, overlap in their preferential connectivity patterns, with AB/CAT overlapping in anterior and lateral OFC and Ba/La overlapping in posterior-middle OFC. At first glance, it may seem strange to see overlapping spatial patterns in analyses of preferential connectivity. However, this can occur because the connectivity of each individual amygdala nucleus was compared to the average connectivity of the other three nuclei. Thus, connectivity profiles of two nuclei can overlap, and yet the profile of each of those nuclei can still be significantly different from the average of the other three nuclei. This is evident in the largely overlapping spatial connectivity patterns of AB and CAT (see Figures 3 and 4) which does diverge strongly from those associated with La and Ba. Thus, the pattern averaged across CAT, La, and Ba will be quite different from AB. Furthermore, as seen in Figure 1, AB and CAT are adjacent to each other, as are Ba and La. Thus, it is reasonable for nuclei physically near each to demonstrate similar connectivity patterns and those located farther away to demonstrate distinct connectivity patterns. This pattern of spatially dependent findings is consistent with the topographic organization of many human neural connections (Thivierge & Marcus, 2007) and with the topographic organization of OFC—amygdala connections in primates (McDonald, 1998). Overall, present findings demonstrate differential patterns of OFC connectivity across the four amygdala nuclei.
Our findings generally converge with analogous investigations carried out in animals. Non-human primate studies using tract-tracing methodology have found that overall, amygdala projections terminate predominately in lateral OFC (Cavada et al., 2000). Conversely, OFC projections to amygdala terminate predominately in La and AB (Aggleton, Burton, & Passingham, 1980) and are densest from posterior OFC (Ghashghaei & Barbas, 2002). Specifically, Ba and AB project throughout the OFC and AB and La project most strongly to posterior and medial OFC (Carmichael & Price, 1995). Interestingly, although the animal literature has found Ba to have some of the densest connections with OFC (Carmichael & Price, 1995; Cavada et al., 2000), the present study found that Ba showed the most spatially restricted pattern of connectivity (Figure 3), at least when examining preferential connectivity (i.e., relative to the other three nuclei). Of note, one of the few studies that examined structural connectivity between amygdala nuclei and OFC in humans found that centrocortical nucleus (e.g., centro-medial and cortical nuclei), compared with basolateral nucleus, exhibited greater connection strength to frontal cortex, including the orbital gyri (Abivardi & Bach, 2017). Thus, our findings are consistent with available evidence in humans, although they diverge from those in the animal literature. This discrepancy was not due to differences in the spatial distribution of connectivity, because the mean level of Ba connectivity was the smallest of the four nuclei. In other words, it could have been the case that Ba had the same (or even greater) overall level of connectivity with OFC, but it was more spatially widespread and thus did not emerge in the analyses of preferential connectivity. However, this could not be the case, given that Ba also showed the smallest overall levels of connectivity. Additionally, to test if normalization by ROI size impacted the observed connectivity of Ba, we repeated analyses using the total number of streamlines (not divided by ROI size). However, the observed pattern of Ba connectivity was not more expansive than in the reported analyses. Thus, divergence between the animal literature and our findings in humans may be due to differences in methodology. Limitations of tractography methods using dMRI include the inability to measure the density of connections directly or the directionality of connections. In contrast, directionality can be inferred from tracer studies, which have found that the OFC projects more widely to amygdala (i.e., projecting to more regions of amygdala) than the amygdala to OFC (i.e., fewer regions of amygdala project to OFC) (Cavada et al., 2000). Due to the inability of dMRI to measure directionality of connections, the regions of amygdala with reciprocal connections could be represented similarly to those with dense projections to the OFC. With dMRI tractography, we are unable to differentiate between areas of OFC receiving and sending amygdala projections. Given this, and the asymmetry in connections sent and received by the OFC with amygdala nuclei, the apparent strength of Ba connections with the OFC may be diminished by the comparative strength of reciprocal connections between the OFC and the other nuclei. Furthermore, Ba, La, and AB nuclei are often combined into the basolateral complex in other studies, which would obscure the differences in connectivity patterns we found for Ba, La, and AB.
In addition, present findings suggest that CAT connects preferentially with anterior-lateral OFC in both hemispheres, as well as medial and posterior OFC in the left hemisphere. This partially diverges from the animal literature, which suggests that the peri-amygdala cortex (PAC), the primate equivalent of CAT (Saygin et al., 2017), connects primarily with posterior OFC and, to a lesser extent, medial OFC (Carmichael & Price, 1995). However, some studies in both the primate and human literature amygdala define CAT as a transitional zone encompassing portions of Ba, the paralaminar nucleus, and the PAC, as distinct from the PAC proper (Crosby & Humphrey, 1941; Fudge & Tucker, 2009; Sims & Williams, 1990). Thus, given heterogeneous definitions of CAT, and the lack of connectivity studies directly investigating CAT (as compared to PAC or a vaguely defined “transition area”), it is not surprising that our results do not align with those of the primate PAC.
Our finding that patterns of connectivity varied by both OFC region and amygdala nucleus has implications for functions thought to be supported by connectivity between these regions. For example, our finding that La demonstrates strong and consistent (across participants) connections with medial and posterior OFC suggests that these connections may support the involvement of this OFC area in making decisions based on reward value (Elliott et al., 2000) and updating the value of outcomes based upon information (Murray et al., 2015), along with the involvement of La in associating objects with value (Baxter & Murray, 2002). Additionally, the similar structural connectivity patterns found for CAT and AB suggests that these nuclei may support similar functions to each other. Furthermore, given that structural connections support functional connectivity (Horn, Ostwald, Reisert, & Blankenburg, 2014), our findings can provide insight into how the patterns of functional connectivity between these regions emerge. Thus, our findings illustrate the importance of examining specific amygdala nuclei in order to consider the potentially different or similar (in the case of CAT and AB) influences of individual amygdala nuclei on emergent functions. The increased specificity of structural evidence of OFC-amygdala connectivity provided by the present results can be applied widely to studies investigating such connectivity in a variety of contexts from learning and motivation (Roberts et al., 2007; Sharpe & Schoenbaum, 2016) to affective processes (Lee et al., 2012; Rolls, 2013). An advantage of the current study was the use of high-quality dMRI data with sufficient resolution to segment amygdala into its nuclei. However, this is not always possible due to equipment constraints and participant compliance. Thus, our creation of probabilistic and rank order maps of OFC based upon the likelihood of amygdala nuclei demonstrating the greatest probability of connecting to a given OFC voxel and the relative level of connectivity that amygdala nuclei exhibit with a given OFC voxel, respectively, will allow for inferences regarding the role of individual amygdala nuclei when examining OFC, even when segmentation of amygdala is not feasible.
4.1 Strengths and limitations
The present study benefited from a number of strengths, including an extremely large sample size (n = 1,053), multi-shell diffusion acquisition with a large number of directions (n = 270), which provided unparalleled accuracy in tractography, and examination of amygdala nuclei. Several limitations must also be considered. Although we used the best methods currently available, present findings are dependent on the connectivity algorithms used, and thus, it is possible that systematic biases remain. In addition, only four of the nine amygdala nuclei segmented in the FreeSurfer atlas were examined due to the small size and likely low reliability of accurate segmentation of the additional five nuclei. However, the probabilistic and rank order maps of OFC with each amygdala nuclei introduced herein can be used to examine the connections of OFC and amygdala in a more fine-grained manner, including on the topics of emotional and motivational processes. Lastly, although we propose that the different connectivity patterns of the four amygdala nuclei investigated may relate to different psychological processes, we do not directly test this, and this will be a promising avenue for future work.
5 CONCLUSION
This report represents an advance in our knowledge of OFC connections with amygdala nuclei in humans. For individual amygdala nuclei, we delineated their connectivity patterns with OFC and evaluated the comparative strength of these connectivity patterns (relative to the other nuclei examined) that were highly convergent with OFC-amygdala nuclei connections identified in nonhuman primate studies. However, our results did differ from these histological studies in a few ways. Thus, caution should be taken in extrapolating findings from studies with differing methodologies (e.g., histological) and nomenclature (e.g., PAC and CAT) to human studies utilizing dMRI and probabilistic tractography when making inferences about differential patterns of connectivity between areas of OFC and amygdala nuclei. Regardless, these findings, and resultant probabilistic and rank order maps of OFC, provide insight into human OFC-amygdala connectivity that will facilitate investigating functional implications of OFC-amygdala connectivity and the tools to examine OFC-amygdala connectivity in a fine-grained manner. In summary, present findings expand our current understanding of OFC-amygdala circuit by delineating the connectivity profiles of OFC with amygdala nuclei.
Open Research
DATA AVAILABILITY STATEMENT
Data included in this manuscript were obtained from the Human Connectome Project (Young Adult), publicly available at https://www.humanconnectome.org/study/hcp-young-adult. Probabilistic and rank-order atlases derived from the HCP data are available on the last author's website (https://sites.udel.edu/jmsp/tools_data/).