Separate neural representations of prediction error valence and surprise: Evidence from an fMRI meta-analysis
Funding information: Biotechnology and Biological Sciences Research Council (BBSRC), Grant/Award Number: BB/J015393/1–2 (M.G.P.); Economic and Social Research Council (ESRC), Grant/Award Number: ES/L012995/1 (M.G.P.)
Abstract
Learning occurs when an outcome differs from expectations, generating a reward prediction error signal (RPE). The RPE signal has been hypothesized to simultaneously embody the valence of an outcome (better or worse than expected) and its surprise (how far from expectations). Nonetheless, growing evidence suggests that separate representations of the two RPE components exist in the human brain. Meta-analyses provide an opportunity to test this hypothesis and directly probe the extent to which the valence and surprise of the error signal are encoded in separate or overlapping networks. We carried out several meta-analyses on a large set of fMRI studies investigating the neural basis of RPE, locked at decision outcome. We identified two valence learning systems by pooling studies searching for differential neural activity in response to categorical positive-versus-negative outcomes. The first valence network (negative > positive) involved areas regulating alertness and switching behaviours such as the midcingulate cortex, the thalamus and the dorsolateral prefrontal cortex whereas the second valence network (positive > negative) encompassed regions of the human reward circuitry such as the ventral striatum and the ventromedial prefrontal cortex. We also found evidence of a largely distinct surprise-encoding network including the anterior cingulate cortex, anterior insula and dorsal striatum. Together with recent animal and electrophysiological evidence this meta-analysis points to a sequential and distributed encoding of different components of the RPE signal, with potentially distinct functional roles.
1 INTRODUCTION
Effective decision-making depends upon accurate outcome representations associated with potential choices. These representations can be defined through reinforcement learning (RL) (Rescorla & Wagner, 1972; Sutton, 1998), a modelling framework that uses the reward prediction error (RPE), the difference between actual and expected outcomes, as a learning signal to update future outcome expectations. In this framework, RPE is a signed quantity and learning is driven by two separate components of the RPE signal: its valence (i.e., the sign of the RPE, representing whether an outcome is better [+] or worse [−] than expected) and its surprise (i.e., the modulus of the RPE, representing the degree [high or low] of deviation from expectations). Whereas the valence informs an agent whether to reinforce or extinguish a certain behaviour (Fouragnan, Retzler, Mullinger, & Philiastides, 2015; Fouragnan, Queirazza, Retzler, Mullinger, & Philiastides, 2017; Frank, Seeberger, & O'reilly, 2004), the surprise component determines the extent to which the strength of association between outcome and expectations needs to be adjusted (Collins & Frank, 2016; Niv et al., 2015; den Ouden, Kok, & de Lange, 2012).
This modelling framework has received considerable attention in neuroscience since the early 90s when animal neurophysiological studies identified dopaminergic neurons in the midbrain, in particular in the ventral tegmental area (VTA), the substantia nigra pars compacta (SNc) and reticulata (SNr), whose tonic response profile appears to simultaneously capture both components of the RPE signal outlined above (Montague, Dayan, & Sejnowski, 1996; Schultz, Apicella, & Ljungberg, 1993; Schultz, Dayan, & Montague, 1997). Specifically, these neurons show anticipatory increase and suppression of their tonic activity in response to positive and negative RPE, respectively. While the anticipatory increase is proportional to the magnitude of positive RPE, the magnitude of negative RPE is encoded by the duration of the basal tonic suppression.
This discovery was a breakthrough in the field of learning and decision making and has continued to be influential in the field over the past two and a half decades (see Schultz, 2016a; Schultz, 2016b for a review). As a result, this neurophysiological work has strongly motivated human functional magnetic resonance imaging (fMRI) research to identify the corresponding macroscopic blood-oxygen-level-dependent (BOLD) pattern of the signed RPE. This pattern of activity was expected to be such that the strength of the BOLD would proceed from high positive RPEs > low positive RPEs > low negative RPEs > high negative RPEs. More specifically, studies have employed a model-based fMRI approach, whereby different types of reinforcement-learning models are first fitted to subjects’ behaviour to yield parametric predictors for signed RPE against which fMRI data are subsequently regressed (Daw, Gershman, Seymour, Dayan, & Dolan, 2011; Fouragnan et al., 2013; Gläscher, Daw, Dayan, & O'Doherty, 2010; O'Doherty et al., 2004; O'Doherty, Hampton, & Kim, 2007; Queirazza, Fouragnan, Steele, Cavanagh, & Philiastides, 2017).
These fMRI studies have employed different algorithms to derive the signed RPE, ranging from the simple formulation of the temporal difference learning algorithm to incorporating action learning, notably using the Q-learning and SARSA (‘state, action, reward, state and action’) algorithms (Schonberg et al., 2010; Seymour, Daw, Dayan, Singer, & Dolan, 2007; Tanaka et al., 2006). According to qualitative reviews of this previous findings (O'Doherty et al., 2007) as well as quantitative, coordinate-based meta-analyses of these studies, the regions correlating with the different formulations of signed RPE have been found to be predominantly subcortical, including the striatum and amygdala, with some cortical regions, such as the ventromedial prefrontal cortex and the cingulate cortex also reported (Bartra, McGuire, & Kable, 2013; Garrison, Erdeniz, & Done, 2013; Liu, Hairston, Schrier, & Fan, 2011). Additionally, substantial effort has been undertaken to identify how different types of outcomes (primary rewards such as food, or secondary rewards such as monetary outcomes) can modulate the signed RPE in the same regions and the extent to which it can be considered a domain-general, common currency signal (Sescousse, Caldú, Segura, & Dreher, 2013).
While using trial-by-trial estimates of signed RPE from reinforcement-learning models has provided an enormously productive framework for understanding learning and decision-making, a growing number of studies have also discussed the complementary role of surprise, namely the unsigned RPE, which can also be estimated at the single-trial level. These include, but are not limited to, the use of trial-by-trial estimates of the modulus of RPE or Bayesian surprise according to Bayesian learning theory (Hayden, Heilbronner, Pearson, & Platt, 2011; Iglesias et al., 2013). Additionally, human electroencephalography (EEG) studies, attempting to offer a temporal account of the cortical dynamics associated with RPE processing, did not find a systematic monotonic response profile consistent with a single RPE representation but instead offered evidence suggestive of separate representations for valence and surprise at the macroscopic level of responses recorded on the scalp. Specifically, multiple recent EEG studies combining model-based RPE estimates with single-trial analysis of the EEG revealed an early outcome stage reflecting a purely categorical valence signal and a later processing stage reflecting separate representations for valence and surprise (Fouragnan et al., 2015, 2017; Philiastides, Biele, Vavatzanidis, Kazzer, & Heekeren, 2010b). These later valence and surprise signals appeared in spatially distinct but temporally overlapping neural signatures.
These findings suggest that, in addition to the fully monotonic firing pattern of midbrain neurons, there exist individual representations for valence and surprise, potentially subserving different functional roles during reward-based learning (e.g., approach–avoidance behaviour and the speed of learning via varying degrees of attentional engagement, respectively). Here, we conducted an fMRI meta-analysis to more directly explore the possibility that there exist separate neuronal representations encoding valence and surprise promoting reward learning in humans. We discuss the findings of our work in the context of recent reports from animal neurophysiology and human neuroimaging experiments that provide evidence toward a distributed coding of the different facets of the RPE signal (Brischoux, Chakraborty, Brierley, & Ungless, 2009; Fouragnan et al., 2015, 2017; Matsumoto & Hikosaka, 2009).
2 MATERIALS AND METHODS
2.1 Literature search
We selected fMRI studies using the Pubmed database (http://www.ncbi.nlm.nih.gov/pubmed) with the following search keywords: ‘(fMRI OR neuroimaging) AND (prediction error OR reward OR surprise)’ along with three initial filters preselecting studies in which participants were human adults of over 19 years of age and excluding reviews. This initial selection resulted in 724 candidates for inclusion to which a further 64 articles were added from existing in-house reference libraries. Note that previous meta-analyses used the terms ‘prediction error’ or ‘reward’ but we are the first to include ‘surprise’ in our systematic search for relevant articles (Bartra et al., 2013; Garrison et al., 2013; Sescousse et al., 2013).
Abstracts from the 788 candidate-articles identified were then evaluated for inclusion in the corpus according to the following criteria. We required studies of healthy human adults, reporting changes in BOLD as a function of three different components of RPE: the categorical valence, surprise and signed RPE, including statistical comparisons either in the form of binary contrasts or continuous parametric analyses. Because the main objective of the present meta-analysis is to examine the neural coding of RPE processing at decision outcome, we also imposed the restriction that fMRI analyses were time-locked to the presentation of outcomes (feedback). We used studies involving outcomes consisting of abstract points, monetary payoffs, consumable liquids and arousing pictures but excluded articles in which outcomes consisted of social feedback. We also required that studies used functional brain imaging and did not use pharmacological interventions and ensured that the reported coordinates were either in Montreal Neurological Institute (MNI) or Talairach space. Finally, we excluded articles in which results were derived from region of interest (ROI) since our meta-analytic statistical methods assume that foci are randomly distributed in the whole brain under the null hypothesis. After applying these constraints our meta-analysis comprised 102 publications with a total of 2',316 participants, 144 contrasts and 991 activation foci. The number of participants per study ranged from 8 to 66 (median = 24, interquartile range [IQR] = 7).
2.2 Study categorization
The goal of this meta-analysis was to separately categorize studies along the three components of RPE, locked at time of outcome, in order to: (1) identify the extent to which there exist distinct neural representations for valence and surprise and (2) identify whether the neural correlates of the signed RPE simply intersect those of valence and surprise (possibly due to colinearities across these components) or appear as unique clusters of activation reflecting the true combined influence of the two measures.
To group the relevant articles according to the three main RPE components we used the following definitions: (1) valence represents the sign of the RPE and as such it is positive when an outcome is better than expected and negative when worse than expected, (2) surprise represents the absolute degree of deviation from expectations and is treated as an unsigned quantity and (3) signed RPE simultaneously reflects the influence of both valence and surprise and appears as a fully signed parametric signal. According to these definitions, we identified several fMRI statistical analyses conducted in the original studies that fall under each of the three RPE components (Table 1). The main assumptions of these fMRI analyses, with regard to the BOLD signal as a function of each RPE component, are presented schematically in Figure 1.
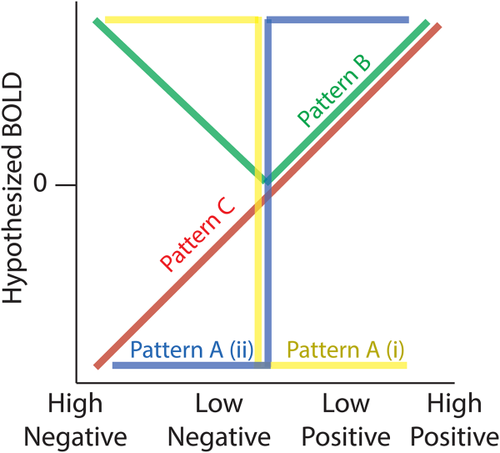
Hypothesized profiles for BOLD responses as function of the three RPE components. Pattern A (i and ii) describe the two categorical valence responses (yellow and blue colours indicate (i) responses being greater for negative compared with positive outcomes [NEG > POS] and (ii) responses being greater for positive compared with negative outcomes [POS > NEG]). Pattern B captures surprise effects with greater responses for higher outcome deviations from expectations, independent of the sign (valence) of the RPE. Pattern C shows a monotonically increasing response profile consistent with a signed RPE representation [Color figure can be viewed at wileyonlinelibrary.com]
| Statistical comparisons | Number | Total | Reference |
|---|---|---|---|
|
Valence Pattern A i (NEG>POS) |
32 | (de Bruijn, de Lange, Cramon, & Ullsperger, 2009; Daniel et al., 2011; Demos, Heatherton, & Kelley, 2012; van Duijvenvoorde et al., 2014; Elward, Vilberg, & Rugg, 2015; Ferdinand & Opitz, 2014; Fouragnan et al., 2015; Gläscher, Hampton, & O'Doherty, 2009; Haruno et al., 2004; Häusler, Oroz Artigas, Trautner, & Weber, 2016; Jocham et al., 2016; Kahnt, Heinzle, Park, & Haynes, 2010; Katahira et al., 2015; Klein-Flügge, Hunt, Bach, Dolan, & Behrens, 2011; Klein-Flügge et al., 2011; Knutson, Westdorp, Kaiser, & Hommer, 2000; Knutson, Adams, Fong, & Hommer, 2001; Koch et al., 2008; Leknes, Lee, Berna, Andersson, & Tracey, 2011; Losecaat Vermeer, Boksem, & G Sanfey, 2014; Marsh et al., 2010; Mattfeld, Gluck, & Stark, 2011; Noonan, Mars, & Rushworth, 2011; O'Doherty, Kringelbach, Rolls, Hornak, & Andrews, 2001; O'Doherty, Critchley, Deichmann, & Dolan, 2003; Rodriguez, 2009; Rolls, Grabenhorst, & Parris, 2008; Scholl et al., 2015; Seymour et al., 2007; Spicer et al., 2007; Spoormaker et al., 2011; Ullsperger & Cramon, 2003; Yacubian et al., 2006) | |
| Negative > Positive | 19 | ||
| Negative > No outcomes | 9 | ||
| Negative correlation with a regressor defining valence RPE (with a binary modulation whereby positive RPE = 1, and negative RPE = −1) | 4 | ||
|
Valence Pattern A ii (POS>NEG) |
33 | (Amiez, Sallet, Procyk, & Petrides, 2012; Aron et al., 2004; Bickel, Pitcock, Yi, & Angtuaco, 2009; de Bruijn et al., 2009; Canessa et al., 2013; Daniel et al., 2011; van Duijvenvoorde et al., 2014; Elliott, Friston, & Dolan, 2000; Ernst et al., 2004; Forster & Brown, 2011; Fouragnan et al., 2015; Fujiwara, Tobler, Taira, Iijima, & Tsutsui, 2009; Häusler et al., 2016; Hester, Barre, Murphy, Silk, & Mattingley, 2008; Hester, Murphy, Brown, & Skilleter, 2010; Jocham et al., 2016; Katahira et al., 2015; Knutson et al., 2000; Knutson et al., 2001; Knutson et al., 2001; Kurniawan, Guitart-Masip, Dayan, & Dolan, 2013; Losecaat Vermeer et al., 2014; Luking, Luby, & Barch, 2014; Paschke et al., 2015; Sarinopoulos et al., 2010; Scholl et al., 2015; Schonberg et al., 2010; Seymour et al., 2007; Späti et al., 2014; Spoormaker et al., 2011; Ullsperger & Cramon, 2003) | |
| Positive > Negative | 18 | ||
| Positive > No outcomes | 9 | ||
| Positive correlation with a regressor defining valence RPE (with a binary modulation whereby positive RPE = 1, and negative RPE = −1) | 6 | ||
|
Surprise Pattern B |
41 | (Allen et al., 2016; Amado et al., 2016; Amiez et al., 2012; Boll, Gamer, Gluth, Finsterbusch, & Büchel, 2013; Browning, Holmes, Murphy, Goodwin, & Harmer, 2010; Chumbley et al., 2014; Daw et al., 2011; Dreher, 2013; Ferdinand & Opitz, 2014; Forster & Brown, 2011; Fouragnan et al., 2015; Fouragnan et al., 2017; Fujiwara et al., 2009; Ide et al., 2013; Iglesias et al., 2013; Jensen et al., 2007; Knutson et al., 2001; Kotz, Dengler, & Wittfoth, 2015; Leong, Radulescu, Daniel, DeWoskin, & Niv, 2017; Losecaat Vermeer et al., 2014; Manza et al., 2016; McClure, Berns, & Montague, 2003; Metereau & Dreher, 2013; Metereau & Dreher, 2015; Meyniel & Dehaene, 2017; Nieuwenhuis, Slagter, von Geusau, Heslenfeld, & Holroyd, 2005; O'Reilly et al., 2013; den Ouden et al., 2012; Poudel, Innes, & Jones, 2013; Rodriguez, 2009; Rohe, Weber, & Fliessbach, 2012; Rohe & Noppeney, 2015; Rohe & Noppeney, 2015; Rolls et al., 2008; Schwartenbeck, FitzGerald, & Dolan, 2016; Silvetti & Verguts, 2012; Tobia, Gläscher, & Sommer, 2016; Watanabe, Sakagami, & Haruno, 2013; Wunderlich et al., 2009; Wunderlich, Symmonds, Bossaerts, & Dolan, 2011; Yacubian et al., 2006; Zalla et al., 2000; Zhang, Mano, Ganesh, Robbins, & Seymour, 2016) | |
| Unsigned RPE (‘RL surprise’) | 12 | ||
| Unsigned Bayesian RPE (‘Volatility’, ‘Bayesian surprise’) | 13 | ||
| Positive and Negative outcomes > No or low outcomes | 9 | ||
| ‘Associability’ term of the Pearce et Hall model | 2 | ||
| Parametric changes in magnitude of surprising positive RPE (unsigned) | 3 | ||
| Parametric changes in magnitude of surprising negative RPE (unsigned) | 2 | ||
|
Signed RPE Pattern C |
38 | (Abler, Walter, Erk, Kammerer, & Spitzer, 2006; Behrens et al., 2007; van den Bos, Cohen, Kahnt, & Crone, 2012; Cohen & Ranganath, 2007; Daw et al., 2011; Delgado et al., 2000; Delgado, 2007; Diederen et al., 2017; Diuk, Tsai, Wallis, Botvinick, & Niv, 2013; Dunne, D'Souza, & O'Doherty, 2016; Gläscher et al., 2010; Guo et al., 2016; Hare, O'Doherty, Camerer, Schultz, & Rangel, 2008; Ide et al., 2013; Katahira et al., 2015; Leong et al., 2017; Li & Zhang, 2006; Lin, Adolphs, & Rangel, 2012; Mattfeld et al., 2011; McClure et al., 2003; Metereau & Dreher, 2013; Metereau & Dreher, 2015; O'Doherty et al., 2003; Pessiglione, Seymour, Flandin, Dolan, & Frith, 2006; Pessiglione et al., 2008; Ribas-Fernandes et al., 2011; Rolls et al., 2008; Schlagenhauf et al., 2013; Schonberg et al., 2010; Scimeca, Katzman, & Badre, 2016; Seymour et al., 2007; Takemura, Samejima, Vogels, Sakagami, & Okuda, 2011; Tanaka et al., 2004; Tanaka et al., 2006; Valentin & O'Doherty, 2009; Watanabe et al., 2013; Wunderlich et al., 2011) | |
| Signed RPE (from model-free RL models) | 16 | ||
| Signed RPE (from model-based RL models) | 8 | ||
| Signed Bayesian RPE | 10 | ||
|
High positive RPEs > low positive RPEs > low negative RPEs > high negative RPEs |
4 |
For the valence components, the literature has looked at neural responses which vary categorically along positive-negative axes, as represented in patterns A (i) and (ii) of Figure 1. We therefore extracted activations exhibiting a relative BOLD signal increase for negative relative to positive outcomes (NEG > POS: pattern A [i]) and greater BOLD for positive relative to negative outcomes (POS > NEG: pattern A [ii]), respectively. We considered six types of fMRI statistical comparisons which reported coordinate results from either: (1) a contrast associated with negative > positive outcomes, (2) a contrast associated with negative > no outcomes, (3) a negative correlation with a trial-by-trial regressor modulated by [+1] for positive outcomes and [−1] for negative outcomes, (4) the positive correlation with the regressor described in (3), (5) a contrast associated with positive > negative outcomes and (6) a contrast associated with positive > no outcomes. We grouped results from contrasts 1–3 (i.e., NEG > POS) and contrasts 3–6 (i.e., POS > NEG) to capture regions yielding greater BOLD activity for negative relative to positive outcomes and a greater activity for positive relative to negative outcomes, respectively (Table 1).
While the fMRI literature on RPE processing has produced a large amount of theoretical and empirical evidence for the valence and the signed RPE components, comparatively little has been done to directly investigate surprise as a separate component. Fewer studies have used fMRI regressors that were parametrically modulated by trial-to-trial changes in surprise using the unsigned RPE (Fouragnan et al., 2017; Hayden et al., 2011; Iglesias et al., 2013). These studies used the terms ‘surprise’, ‘unsigned RPE’ or outcome ‘salience’ to refer to the mathematical modulus of RPE from computational learning models. In addition to these articles, our literature search has revealed a number of other measures (see below), which are highly correlated with outcome surprise, as defined by learning theory. We therefore used these measures as proxies of surprise to gain insights into the spatial extent of the relevant neural responses and the degree to which they overlap with those associated with valence.
Specifically, a recent line of research has investigated the neural basis of ‘Bayesian surprise’ or ‘volatility’, computed as the direct modulus of Bayesian predictive error (Ide, Shenoy, Yu, & Li, 2013; Iglesias et al., 2013; Mathys et al., 2014; O'Reilly et al., 2013) which corresponds to the absolute difference between categorical outcomes and the probabilistic expectation of these outcomes, estimated using Bayesian inference. In the framework of Bayesian learning, the absolute Bayesian RPE plays an important role in learning from rapid changes in behavioural exploration (Courville, Daw, & Touretzky, 2006). Finally, other studies used the term ‘associability’ which is a parameter in the Pearce-Hall model (Hall & Pearce, 1979; Pearce & Hall, 1980) defined as the degree of divergence between an actual outcome and the original expectation (e.g., the associative strength between a choice and an outcome - we note that in the RL framework, associability can also refer to the learning rate). It is clear from these reports that there is a lack of consistent terminology to refer to unsigned RPE, which emphasizes the need for a more unified framework for studying RPE processing.
To test for consistencies in the neuronal responses across these different reports, and provide initial support for a unified representation of surprise, we grouped fMRI analyses which reported outcome-locked activations resulting from: (1) a positive correlation with a trial-by-trial regressor of the modulus (unsigned) RPE resulting from RL models across both positive and negative outcomes (‘surprise’ or ‘unsigned RPE’), (2) a positive correlation with a trial-by-trial regressor of the unsigned RPE resulting from Bayesian modelling (‘Bayesian Surprise’ or ‘volatility’), (3) a positive correlation with a trial-by-trial regressor of the free parameter of the Pearce-Hall model (‘associability’ term), (4) a contrast associated with (high positive outcomes and high negative outcomes) > (low positive outcomes and low negative outcomes OR no outcomes), (5) a positive correlation with a parametric regressor of surprising positive RPE alone and (6) a positive correlation with a parametric regressor of surprising negative RPE alone (Table 1). Figure 1 illustrates the hypothesized pattern of BOLD signal predicted by these contrasts (pattern B), exhibiting a V-shaped response profile that is maximal for both highly surprising negative and positive RPEs. Despite possible subtle differences in the definition of these measures we expected that only foci consistently correlating with deviations from reward expectations would be revealed in this analysis.
One reason the surprise component has not been looked at closely in isolation is because the literature has focused primarily on signed RPE representations instead. This approach was motivated by neurophysiology experiments showing monotonic responses as a function of both valence and surprise and by a theoretical framework suggesting that learning is driven by a single signed RPE representation. To identify the spatial extent of these representations we also looked at fMRI data reporting positive correlations with signed RPE (negative correlation were discarded). Specifically, we combined four types of fMRI analyses, which estimated trial-by-trial signed RPE from different computational models. We used fMRI reports from (1) model-free and (2) model-based RL methods. Model-free methods include Markov Chain Monte Carlo and temporal difference methods (Samson, Frank, & Fellous, 2010; Seymour et al., 2007). Model-based methods include dynamic programming and certainty equivalent methods (Daw, Niv, & Dayan, 2005; Doya, Samejima, Katagiri, & Kawato, 2002). More on these algorithms can be found in the review by (Kaelbling, Littman, & Moore, 1996). We also included continuous parametric analyses using trial-by-trial signed RPE from (3) Bayesian RL framework described above (Iglesias et al., 2013; Mathys et al., 2014; den Ouden et al., 2012). Finally, our analysis for signed RPE also contained one type of parametric analysis that employed fixed RPE values (not estimated from RL models) ranked on a scale such that (4) high positive RPEs > low positive RPEs > low negative RPEs > high negative RPEs (Table 1). Figure 1 illustrates the hypothesized pattern of BOLD signal predicted by these contrasts (pattern C) and it is assumed to increase linearly as a function of signed RPE.
Crucially, we note that an issue requiring closer scrutiny pertains to the difficulty in disambiguating the signed RPE pattern of activity from those associated with valence and surprise. Specifically, pattern C (signed RPE) is generally highly correlated with pattern A (ii), (POS > NEG valence) and in studies in which only positive RPEs are considered, pattern C (signed RPE) and pattern B (surprise) are perfectly correlated. Nonetheless, comparing clusters of activations across the three RPE components could potentially reveal whether or not there exist unique clusters of activations associated with signed RPE.
2.3 Activation likelihood estimation analysis
We conducted the meta-analysis using the GingerALE software (version 2.3.6) (Eickhoff et al., 2009) that employs a revised (and rectified; Eickhoff, Laird, Fox, Lancaster, & Fox, 2017) version of the activation likelihood estimation (ALE) algorithm (Laird et al., 2005; Turkeltaub, Eden, Jones, & Zeffiro, 2002), which identifies common areas of activation across studies. This method performs coordinate based meta-analysis which considers each reported foci as a 3D Gaussian probability distribution, centred at the coordinates provided by each study reflecting the spatial uncertainty associated with each reported set of coordinates. Note that each contrast provided to the ALE algorithm is treated as a separate experiment. The probabilities distributions are then combined to create a modelled activation map, namely an ALE map for that contrast. Studies are weighted according to the number of subjects they contain by adjusting the full width at half maximum of the Gaussian distributions. The convergence of results across the whole brain is obtained by computing the union of all resulting voxel-wise ALE scores. To distinguish meaningful convergence from random noise, statistics are computed by comparing ALE scores with an empirical null-distribution representing a random spatial association between studies. To infer true convergence, a random-effect inference is applied to capitalize on the differences between studies rather than between foci within a particular study. The null-hypothesis is modelled by randomly sampling voxels from each of the ALE maps from which the union is obtained. The ALE maps are assessed against the null distribution using a cluster level threshold of specific p values. Contrast analyses between categories of the entire dataset are determined by ALE subtraction method, including a correction for differences in sample size between the categories.
Here, we manually extracted all coordinates from the studies shown in Table 1 and entered them into separate files for each of the three RPE components in preparation for the ALE analyses. Any studies that provided coordinates in Talairach space were converted into MNI space by the Matlab (MathWorks, Natick, Massachusetts) function tal2mni in the fieldtrip toolbox (Oostenveld, Fries, Maris, & Schoffelen, 2011). We conducted ALE analyses for each of the three components of RPE individually. Along the valence component, we looked at both patterns A (i) and A (ii) in Figure 1 (i.e., to identify activations for negative > positive RPE and vice versa, respectively). Accordingly, we ran separate ALE analyses for each of the two patterns. In addition, we performed two conjunction analyses—one between the valence and surprise components to investigate our hypothesis of largely separate neural representations and another between all three RPE components to identify regions that simultaneously encode these representations. Subsequently, we also performed all possible pairwise contrast analyses between the three patterns (A, B and C), using the individual maps associated with each pattern.
A total of 402 foci from 66 contrasts were used with 262 foci from 31 contrasts for Pattern A (i) revealing BOLD patterns greater for negative than positive outcomes and 205 from 35 contrasts for Pattern A (ii) (e.g., the opposite contrast). For the surprise (Pattern B) and signed RPE (Pattern C) analyses, we applied individual ALE analyses, with 284 foci from 40 contrasts for surprise and 240 foci from 38 contrasts for signed RPE. Overall, the number of contrasts used for each separate outcome component was large enough (>30) to allow sufficient power for the required statistical tests (Eickhoff & Etkin, 2016). Finally, we transformed the resulting ALE maps from the Colins MNI individual brain space (Colin27_T1_seg_MNI) to the MNI normalized brain space (MNI ICBM152 template) by applying an affine transformation using the FSL flirt program (Jenkinson, Bannister, Brady, & Smith, 2002), prior to overlaying onto the canonical MNI template for visualization.
3 RESULTS
All coordinates used for the following ALE analyses were collated from fMRI studies in which the components of RPE have been regressed onto BOLD activity time-locked to outcome presentation. We report ALE maps with clusters surviving the False Discovery Rate (FDR) yielding two p value thresholds. The most conservative FDR correction yields a p value with no assumptions about how the data is correlated (FRN), and the least conservative FDR correction assumes independence or positive dependence (FID) with p < .05 and a minimum volume clustering value of 50 mm3. Note that, using a cluster-level family-wise error (FWE) correction implemented with a cluster-extent threshold of p < .05 and a cluster-forming threshold of p < .001 revealed virtually identical results (compared with FRN) (Eickhoff et al., 2017) as per previous reports (Garrison, Done, & Simons, 2017). For all tables presenting ALE cluster results, the size of each cluster is provided in mm3 along with the associated MNI coordinates and maximum ALE score. The ALE score indicates the relative effect size for each peak voxel within each ALE analysis.
3.1 Outcome valence
The first two ALE analyses were conducted to identify regions in which BOLD signals correlate with outcome valence. Specifically, we looked at activations that yielded greater BOLD for negative relative to positive outcomes (NEG > POS; pattern A [i] in Figure 1) and greater BOLD for negative relative to positive outcomes (POS > NEG; pattern A [ii] in Figure 1), respectively. Accordingly, we considered all fMRI studies, which assumed BOLD responses varying categorically along a positive-negative axis for outcome valence.
The findings of the two valence ALE analyses are shown in Figure 2. The resulting maps revealed a highly distributed network of brain activations encompassing several cortical regions and sub-cortical structures. More precisely, NEG > POS valence clusters were found in a network encompassing the anterior and dorsal part of the mid-cingulate cortex (aMCC and dMCC) including the pre supplementary motor area (pre-SMA), the bilateral anterior and middle insular cortex (aINS, mINS), the bilateral dorsolateral prefrontal cortex (dlPFC), the bilateral thalamus, right amygdala, left inferior parietal lobule (IPL) and the habenula.
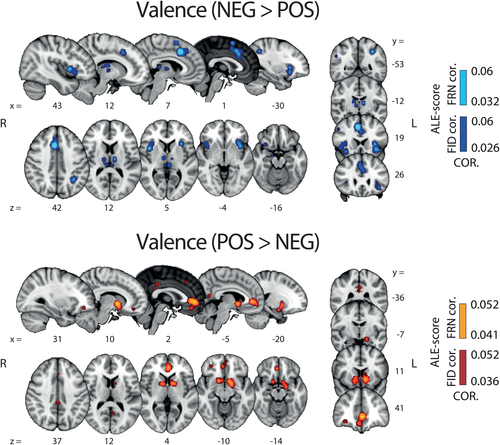
Results of whole-brain ALE analysis along the valence component. Overlays of brain areas activated by correlations with NEG > POS (blue) and POS > NEG (orange) (Pattern A [i] and [ii], respectively; Figure 1) (p values corrected with FDR-ID [FID] and FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3). Representative slices are shown with MNI coordinates given below each image [Color figure can be viewed at wileyonlinelibrary.com]
POS > NEG valence clusters were found in the bilateral ventral striatum (vSTR), the ventromedial prefrontal cortex (vmPFC), the posterior part of the cingulate cortex (PCC), as well as the ventrolateral orbitofrontal cortex (vlOFC). At a lower threshold (uncorrected p value of .001), we also found the midbrain as part of this network, encompassing the VTA, which is commonly associated with the delivery of reward (D'Ardenne, McClure, Nystrom, & Cohen, 2008). Table 2 contains the complete list of regions, coordinates and statistics of these two ALE analyses.
| Region | R/L | x | y | z | Cluster size | ALE score |
|---|---|---|---|---|---|---|
| Pattern A (i) NEG > POS | ||||||
| Dorsomedial cingulate cortex (dMCC) | R | 2 | 24 | 36 | 12,712 | 0.051 |
| Anterior insula (aINS) | R | 32 | 24 | −2 | 6,120 | 0.062 |
| – | L | −32 | 22 | −4 | 4,880 | 0.056 |
| Pallidum | R | 12 | 8 | 4 | 3,360 | 0.04 |
| – | L | −14 | 6 | 2 | 2,520 | 0.029 |
| Middle frontal gyrus | R | 38 | 4 | 32 | 3,152 | 0.029 |
| – | R | 30 | 10 | 56 | 488 | 0.021 |
| – | L | −28 | 12 | 60 | 104 | 0.019 |
| Inferior parietal lobule (IPL) | R | 40 | −48 | 42 | 2,416 | 0.039 |
| – | L | −38 | −48 | 42 | 2,216 | 0.043 |
| Middle temporal gyrus (MTG) | R | 60 | −28 | −6 | 1,192 | 0.031 |
| Amygdala | R | 18 | −6 | −12 | 704 | 0.024 |
| Thalamus | L | −12 | −12 | 10 | 624 | 0.025 |
| – | L | −6 | −26 | 8 | 280 | 0.023 |
| Habenula | R | 2 | −20 | −18 | 312 | 0.022 |
| Dorsolateral prefrontal cortex (dlPFC) | L | −44 | 28 | 32 | 360 | 0.020 |
| – | R | 40 | 34 | 30 | 344 | 0.020 |
| Fusiform area | L | −40 | −62 | −10 | 272 | 0.023 |
| Precentral cortex | L | −52 | 0 | 34 | 256 | 0.021 |
| Dorsomedial orbitofrontal cortex (dmOFC) | R | 38 | 58 | −2 | 192 | 0.020 |
| Dorsomedial prefrontal cortex (dmPFC) | R | 20 | 50 | 4 | 120 | 0.018 |
| Superior temporal sulcus | R | 58 | −42 | 22 | 120 | 0.017 |
| Pattern A (ii) (POS > NEG) | ||||||
| Ventral striatum (vSTR) | L | −12 | 8 | −4 | 4,880 | 0.052 |
| – | R | 8 | 8 | −2 | 2,880 | 0.038 |
| Ventromedial prefrontal cortex (vmPFC) | L | −2 | 42 | 0 | 3,416 | 0.037 |
| Posterior cingulate cortex (PCC) | L | 0 | −32 | 36 | 240 | 0.016 |
| – | L | 0 | −36 | 26 | 88 | 0.014 |
| Ventrolateral OFC (vlOFC) | R | 32 | 44 | −10 | 144 | 0.015 |
| Dorsomedial prefrontal cortex (dmPFC) | L | −6 | −56 | 14 | 96 | 0.016 |
| Medial prefrontal cortex (mPFC) | L | −2 | 46 | 20 | 88 | 0.014 |
3.2 Surprise
FMRI investigations of RPE have focused primarily on the valence components while neglecting potential contributions from possible separate representations along the surprise component, defined as the degree by which outcomes deviate from expectations and mathematically expressed as the modulus of RPE. A major goal of this work was to explore the possibility that there exist largely separate neuronal representations encoding surprise. To this end, we conducted a new ALE analysis in which the few empirical fMRI studies making use of the surprise from RL models were combined with other fMRI measures correlated with the surprise as defined by RL models (Table 1).
Figure 3 shows the areas in which BOLD signal correlated with surprise. We found evidence for activations in a distributed network encompassing the aMCC, dMCC, the pre-SMA the bilateral dorsal striatum (dSTR), the bilateral aINS, the MTG and the midbrain. Crucially, this activation map shows that the neural network associated with surprise is largely distinct from that of valence. This finding provides initial support for the notion that these two RPE components are encoded in separate brain areas and, as such, they might be contributing individually to promote learning. The full results of the surprise ALE analysis are also summarized in Table 3.
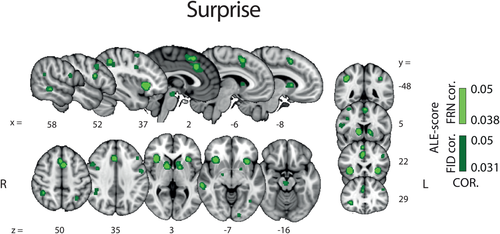
Results of the whole brain ALE analysis for the surprise component of RPE (pattern B, Figure 1). Overlay of brain areas activated by all analyses representing direct or indirect measures of the surprise component of RPE (p values corrected with FDR-ID [FID] and FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3). Representative slices are shown with MNI coordinates given below each image [Color figure can be viewed at wileyonlinelibrary.com]
| Region | R/L | x | y | z | Cluster size | ALE score |
|---|---|---|---|---|---|---|
| Anterior mid-cingulate cortex (aMCC) | R | 4 | 24 | 34 | 4072 | 0.029 |
| Anterior insula (aINS) | R | 32 | 24 | −4 | 2496 | 0.050 |
| – | L | −32 | 20 | −4 | 1544 | 0.038 |
| Inferior parietal lobule (IPL) | R | 40 | −46 | 42 | 1672 | 0.033 |
| – | L | −40 | −48 | 42 | 568 | 0.025 |
| Dorsal striatum (dSTR) | R | 12 | 8 | 4 | 1400 | 0.034 |
| – | L | −14 | 10 | 2 | 1216 | 0.021 |
| Middle temporal gyrus (MTG) | R | 60 | −28 | −8 | 648 | 0.022 |
| Lateral inferior frontal cortex | R | 52 | 10 | 18 | 488 | 0.025 |
| Lateral central frontal gyrus | L | −44 | 26 | 30 | 392 | 0.019 |
| Precentral gyrus | R | 48 | 12 | 34 | 360 | 0.019 |
| – | L | −52 | 0 | 34 | 224 | 0.020 |
| Midbrain | R | 2 | −20 | −18 | 304 | 0.021 |
| Dorsal mid-cingulate cortex (dMCC) | R | 12 | 14 | 42 | 224 | 0.019 |
| Hippocampus | R | 20 | −6 | −10 | 160 | 0.018 |
| Fusiform gyrus | L | −40 | −60 | −10 | 112 | 0.017 |
| Mid occipital pole | L | −16 | −90 | −6 | 112 | 0.016 |
| Superior temporal sulcus | R | 60 | −40 | 20 | 64 | 0.015 |
3.3 Valence and surprise conjunction and contrast analyses
The activation maps for valence (NEG > POS and POS > NEG) and surprise ALE analyses conducted above revealed little overlap between the spatial representations of these two RPE components. To formally quantify the degree of overlap between the valence and surprise networks, we next ran a conjunction analysis between the two components. The statistical map resulting from this conjunction analysis and the two separate statistical maps of valence and surprise (as already reported in Figures 2 and 3) are overlaid in Figure 4.
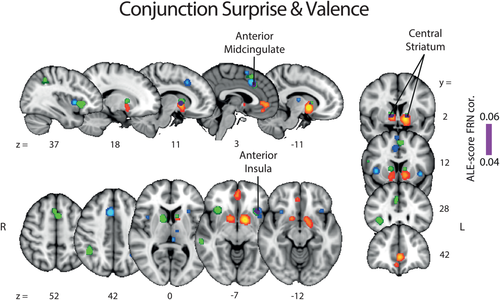
Results of the ALE conjunction analysis between valence and surprise (purple). The regions identified earlier with separate ALE analyses along the valence (NEG > POS: blue, POS > NEG: orange) and surprise (green) components are shown for comparison purposes. The p values were corrected with FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3 for the initial maps. Representative slices are shown with MNI coordinates given bellow each image [Color figure can be viewed at wileyonlinelibrary.com]
Contrast analyses were conducted for each possible pairing between any dimensions of valence (POS > NEG [positive]; NEG > POS [negative] and POS + NEG [all valence]) and surprise. These analyses allowed us to identify the areas that were unique and specific to each individual outcome and RPE-related component. The positive valence (pattern A [ii]) minus surprise (pattern B) contrast revealed two main clusters in the vSTR and vmPFC whereas the reverse contrast revealed a network of clusters including preSMA, aINS and MTG. Contrasting negative valence (pattern A [i]) and surprise also exposed separate networks of areas for each subtraction. Specifically, this contrast revealed a network encompassing the thalamus, the habenula, the right mINS and the dMCC, whereas the reverse contrast showed clusters in the dorsal portion of the STR and the dlPFC. The statistical maps resulting from these contrast analyses are presented in Figure 5.
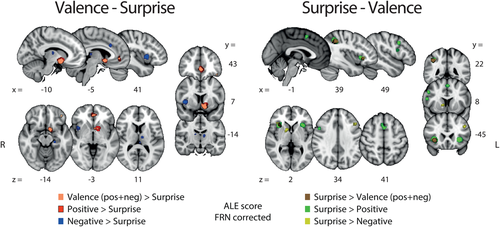
Results of the ALE contrast analyses for [valence – surprise] (left panel) and [surprise – valence]. The p values were corrected with FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3 for the initial maps. Representative slices are shown with MNI coordinates given bellow each image [Color figure can be viewed at wileyonlinelibrary.com]
3.4 Signed RPE
A major goal of this work was to investigate the spatial profile of the signed RPE component and to scrutinise more closely the extent to which it overlaps with the separate representations identified for valence (NEG > POS and POS > NEG) and surprise. The fMRI-RPE literature has focused on this component largely due to neurophysiological evidence suggesting that RPE-like learning is driven by a single, theoretically unified representation of both POS > NEG valence and surprise (Table 1).
Results from this ALE analysis revealed very few unique activations for signed RPE compared with valence and surprise. Instead, brain areas identified in this analysis overlapped mostly with areas appearing in the POS > NEG valence component and, to a lesser extent, surprise (Figure 6). Specifically, a large overlap between signed RPE and the POS > NEG valence component was found in the STR and a smaller one in the vmPFC. Similarly, areas appearing in the singed RPE analysis that overlapped with the surprise component were also found, albeit only in small clusters comprising the aMCC and dorsal STR. Taken together, these findings emphasize the potential collinearities between the BOLD predictors used to identify neural representations associated with the three RPE components and highlight the need for developing a methodology for properly disentangling their individual contributions ( Tables 4-7).
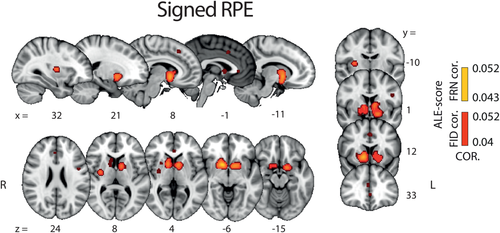
Results of whole brain ALE analysis for signed RPE. Overlay of brain areas activated by positive correlation with signed RPE (p values corrected with FDR-ID [FID] and FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3). Representative slices are shown with MNI coordinates given bellow each image [Color figure can be viewed at wileyonlinelibrary.com]
| Region | R/L | x | y | z | Clustersize | ALE score |
|---|---|---|---|---|---|---|
| Striatum (STR) | R | 12 | 6 | 4 | 1082 | 0.031 |
| – | L | −12 | 12 | 4 | 376 | 0.021 |
| Anterior insula (aINS) | L | −32 | 20 | −6 | 453 | 0.018 |
| Anterior mid-cingulatecortex (aMCC) | R | 3 | 22 | 37 | 221 | 0.014 |
| Inferior parietal lobule | L | 40 | −46 | 42 | 327 | 0.014 |
| Region | R/L | x | y | z | Cluster size | ALE score |
|---|---|---|---|---|---|---|
| Valence vs. surprise | ||||||
| Ventral striatum (vSTR) | L | −10 | 8 | −10 | 1,096 | 3.29 |
| Ventromedial prefrontal cortex (vmPFC) | L | −2 | 44 | 0 | 256 | 3.29 |
| Positive vs. surprise | ||||||
| Ventral striatum (vSTR) | L | −12 | −8 | −8 | 1,872 | 3.29 |
| Ventromedial prefrontal cortex (vmPFC) | R | 0 | 46 | 0 | 512 | 3.29 |
| Ventral striatum (vSTR) | R | 8 | 8 | −6 | 168 | 3.29 |
| Negative vs. surprise | ||||||
| Middle insula (mINS) | R | 40 | 10 | 2 | 544 | 3.29 |
| Mid cingulate Cortex (MCC) | R | 6 | 20 | 42 | 144 | 3.29 |
| Surprise vs. valence | ||||||
| Anterior insula (aINS) | R | 32 | 24 | −4 | 1,224 | 3.29 |
| Anterior insula (aINS) | L | −32 | 20 | −2 | 112 | 3.29 |
| Ventral tegmental area (VTA) | L | −6 | −16 | −10 | 96 | 3.29 |
| Ventral tegmental area (VTA) | R | 2 | −20 | −16 | 72 | 3.29 |
| Occipital lobe | R | 24 | −80 | −6 | 72 | 3.29 |
| Surprise vs. positive | ||||||
| Anterior insula (aINS) | R | 32 | 22 | −2 | 1,648 | 3.29 |
| Middle temporal gyrus (MTG) | R | 40 | −46 | 42 | 1,184 | 3.29 |
| Anterior insula (aINS) | L | −32 | 22 | −2 | 1,016 | 3.29 |
| Inferior Frontal Gyrus | R | 52 | 10 | 18 | 184 | 3.29 |
| Supplementary motor area (SMA) | L | −2 | 12 | 52 | 160 | 3.29 |
| Surprise vs. negative | ||||||
| Angular gyrus | R | 40 | −46 | 40 | 248 | 3.29 |
| Anterior insula (aINS) | R | 32 | 28 | −6 | 80 | 3.29 |
| Dorsal striatum (dSTR) | R | 12 | 10 | 2 | 56 | 3.29 |
| Region | R/L | x | y | z | Cluster size | ALE score |
|---|---|---|---|---|---|---|
| Striatum (STR) (encompasses left and right hemispheres) | R | 12 | 10 | −4 | 10888 | 0.053 |
| Putamen | R | 30 | −6 | 8 | 688 | 0.024 |
| Anterior mid-cingulate cortex (aMCC) | R | 6 | 26 | 46 | 160 | 0.018 |
| – | L | −2 | 14 | 40 | 120 | 0.016 |
| Anterior cingulate cortex (ACC) | R | 4 | 36 | 20 | 112 | 0.017 |
| Ventromedial prefrontal (vmPFC) | L | 0 | 34 | 0 | 64 | 0.015 |
| Lateral inferior frontal gyrus (lIFC) | L | −46 | 4 | 24 | 64 | 0.016 |
| Region | R/L | x | y | z | Cluster size | ALE score |
|---|---|---|---|---|---|---|
| Positive—signed RPE | ||||||
| Ventromedial prefrontal cortex (vmPFC) | R | 2 | 44 | −15 | 160 | 3.29 |
| Signed RPE—positive | ||||||
| No significant | ||||||
| Negative—signed RPE | ||||||
| Middle insula (mINS) | R | 40 | 12 | 0 | 528 | 3.29 |
| Dorsal middle cingulate cortex (dMCC) | R | 6 | 22 | 36 | 208 | 3.29 |
| Middle insula (mINS) | L | −38 | 18 | −4 | 184 | 3.29 |
| Habenula | L | −2 | −26 | 8 | 168 | 2.58 |
| Thalamus | R | 8 | −10 | 5 | 96 | 2.58 |
| Signed RPE—negative | ||||||
| Ventral striatum (vSTR) | R | 10 | 10 | −6 | 2208 | 3.29 |
| Valence—signed RPE | ||||||
| Ventromedial prefrontal cortex (vmPFC) | R | 2 | 44 | −12 | 760 | 3.29 |
| Middle insula (mINS) | R | 40 | 12 | 2 | 568 | 2.58 |
| Dorsal middle cingulate cortex (dMCC) | R | 6 | 24 | 38 | 480 | 2.58 |
| Signed RPE—valence | ||||||
| Ventral striatum (vSTR) | R | 12 | 16 | −2 | 184 | 3.29 |
| Surprise—signed RPE | ||||||
| Anterior insula (aINS) | L | −34 | 22 | 0 | 704 | 3.29 |
| Anterior midcingulate cortex (aMCC) | R | 0 | 14 | 52 | 136 | 3.29 |
| Pre supplementary motor area (preSMA) | R | 0 | 14 | 52 | 136 | 3.29 |
| Anterior insula (aINS) | R | 38 | 18 | −2 | 88 | 3.29 |
| Signed RPE—surprise | ||||||
| Ventral striatum (vSTR) | L | −10 | 8 | −10 | 904 | 3.29 |
| Ventral striatum (vSTR) | R | 12 | 14 | −3 | 192 | 3.29 |
| Ventral striatum (vSTR) | R | 4 | 6 | −6 | 72 | 3.29 |
3.5 Putting it all together
Subsequently, to formally test for the overlap between all three RPE components and identify potential regions integrating valence and surprise either into a signed RPE representation or a linear superposition of the two signals (Fouragnan et al., 2017), we performed a conjunction analysis between the valence (pattern A), the surprise (pattern B) and signed RPE (pattern C) signals. We summarize our conjunction results in Figure 7, which revealed a major overlap between all activations associated with signed RPE and each of the other two RPE representations in the central part of the STR. Thus, one possibility is that the STR meets the requirement that a full monotonic representation of the error signal also simultaneously encodes valence and surprise, as per our last ALE analysis.
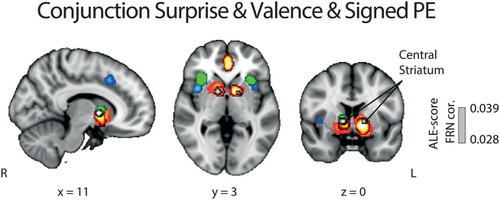
Results of the ALE conjunction analysis for all components of RPE. Overlay of brain areas individually activated by (1) valence (orange), (2) surprise (green), and (3) signed RPE (red), with p values corrected with FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3 for the initial maps. Importantly, the overlap between the three analyses, shown in white, also corresponds to the only cluster found for the ALE conjunction analysis between valence/surprise vs. signed RPE. MNI coordinates are given below each image [Color figure can be viewed at wileyonlinelibrary.com]
Another possibility is that the overlap between all outcome components outcomes in the STR is arising, at least in part, due to collinearities across the different outcome representations, particularly between the positive categorical nature of outcome valence (pattern A [ii]) and the signed RPE. To formally test this hypothesis, we performed a new series of contrast analyses between signed RPE and all dimensions of categorical valence and surprise. Particularly, we performed contrast analyses between patterns C-A(i), C-A(ii), C-A and C-B (and vice versa). The results are summarized in Figure 8. Intriguingly, we did not find any area unique to signed RPE when looking at each of the individual comparisons of signed RPE with the other three patterns. In fact, when comparing signed RPE to positive valence (pattern A [ii]), no clusters were found to be significantly different than those found with the categorical outcome valence (POS > NEG). Conversely, the STR was found for all the other signed RPE comparisons (signed RPE > negative; signed RPE > surprise). Finally, the unique network related to negative valence (pattern A [i]) was found in the dMCC, thalamus and mINS, the unique cluster related to positive valence was found in the vmPFC and the unique network related to surprise was found in the aMCC, preSMA and the aINS.
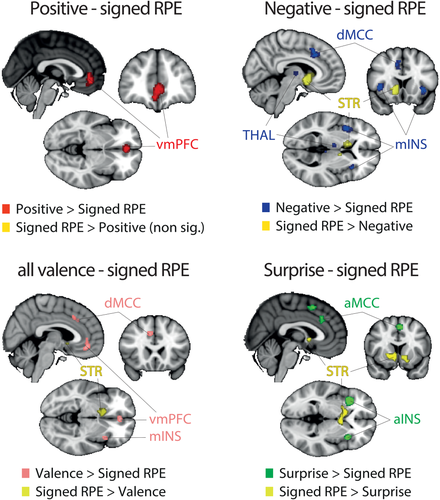
Results of the ALE contrast analyses for [signed RPE – positive valence] (left panel), [signed RPE – negative valence] (middle panel) and [signed RPE – (positive + negative valence)] (right panel). The p values were corrected with FDR-pN [FRN] < .05 and a minimum cluster volume of 50 mm3 for the initial maps. Representative slices are shown with MNI coordinates given bellow each image [Color figure can be viewed at wileyonlinelibrary.com]
4 DISCUSSION
In this fMRI meta-analysis work, we demonstrated that reward learning in humans involves separate neuronal signatures of RPE, comprising distinct representations for valence and surprise. Together with recent neurophysiological and EEG evidence (including studies using simultaneous EEG and fMRI), these findings point to a potentially sequential and distributed encoding of different RPE components with potentially functionally distinct roles.
4.1 Valence networks
The ALE analyses related to valence revealed two distributed set of activations correlating with both pattern A (i) and (ii) in Figure 1. Foci for which the BOLD signal was greater for negative than positive outcomes showed significant clustering in a large network of areas including the thalamus, the aMCC and dMCC, the aINS, mINS and the dlPFC. Conversely, foci for which the BOLD signal was greater for positive than negative outcomes showed significant clusters in a separate network including vmPFC, vSTR, PCC and vlOFC. These findings clearly suggest the presence of multiple systems responding to the categorical nature of valence which supports the notion that separate valuation systems shape learning in the human brain (Fiorillo, 2013; Fouragnan et al., 2013), although their functional role remains debated. More specifically, the debate focuses on the number and exact nature of the neural systems assigning value to decision outcomes and driving behaviours that are evolutionarily appropriate in response to changes in the environment.
A first theory describes two distinct valence systems invoking two orthogonal axes of decision-making: alertness (involving the implementation of action) and learning (including the updates of value expectations for future avoidance and approach behaviours). In this framework, the first system is thought to monitor on-going activity and interrupt it when needed to trigger switching behaviours (e.g., following negative RPEs). In contrast, the second system uses both negative and positive RPE values for decreasing or increasing internal value representations associated with decisions to ultimately drive avoidance and approach learning, respectively (Boureau & Dayan, 2011; Cools, Nakamura, & Daw, 2011; Elliot, 2006; Fiorillo, 2013; Fouragnan et al., 2015; Gray & McNaughton, 2003; Guitart-Masip et al., 2012).
A second (not mutually exclusive) proposition supports the idea that there are at least two separate systems responsible for aversive and appetitive reinforcements such that punishments and rewards are encoded separately (i.e., a punishment space and a reward space; Morrens, 2014). This proposition was developed on the basis of neurophysiological evidence showing that different types of neurons exhibit differential activity in response to punishing vs. non-punishing outcomes and rewarding versus non-rewarding outcomes, respectively (Fiorillo, Tobler, & Schultz, 2003; Fiorillo, 2013; Schultz, Apicella, Scarnati, & Ljungberg, 1992; Schultz, 1998). In this second theory, the punishment space is responsible for avoidance behaviours as well as avoidance learning and the reward space is responsible for approach behaviours and approach learning.
It is noteworthy that our meta-analysis on itself cannot directly distinguish between the two theories because the results do not reveal whether the relevant activations respond exclusively to either positive or negative outcomes or are modulated by both outcomes in opposite directions. This distinction is critical because the former response profile would suggest the presence of separate approach and avoidance systems that might not necessarily be linked to the learning processes as such, while the latter might point to both up- and down-regulation of activity consistent with learning and updating of reward expectations. Nonetheless, the meta-analysis results suggest that two main networks process valence. The network encompassing aINS, aMCC, thalamus and dlPFC could regulate on-going activity and alertness or could represent the punishment space in accordance to the first and the second theories, respectively. Conversely, the network of regions encompassing the vmPFC, vSTR, PCC and vlOFC could represent the learning system depicted in the first theory or could represent the reward space depicted in the second theory. Further research is required to tease apart the roles of these systems, especially by investigating their precise response profiles in the appetitive (where rewarding and non-rewarding outcomes are manipulated) and in a true aversive (where punishing and non-punishing outcomes are manipulated) domains, respectively.
4.2 Surprise network
Emerging evidence indicates that the brain encodes the unsigned RPE signal (surprise), which alerts the organism of relative deviations from expectations, regardless of the outcome value. However, to date, only few articles have modelled surprise as such to search for independent neural representations, with the exception of recent neurophysiological developments (Brischoux et al., 2009; Matsumoto & Hikosaka, 2009), recent EEG work (Philiastides et al., 2010b; Yeung & Sanfey, 2004) and an increasing number of fMRI studies (Fouragnan et al., 2017; Gläscher et al., 2010; Li & Daw, 2011; Metereau & Dreher, 2013). Nevertheless, other fMRI studies used variables highly correlated with surprise that can be employed as proxies (Behrens, Woolrich, Walton, & Rushworth, 2007; Iglesias et al., 2013; Nassar et al., 2012; den Ouden et al., 2012; Yu & Dayan, 2005). These studies share the assumption that the corresponding BOLD response profile is maximal for high positive and high negative RPE and minimal for no RPE, resembling a V-shape, as illustrated with pattern B in Figure 1. By combining these fMRI results into a single ALE-analysis, we expose for the first time the network associated with surprise while stressing the need for a common lexicon for this learning component to guide subsequent research in the field.
The surprise ALE-analysis revealed a large network including cortical and sub-cortical areas such as aMCC, bilateral aINS, dSTR and midbrain, that differed majoritarily from those of valence processing although small overlaps were found between the two components at the junction of ventral and dorsal STR, in left aINS and aMCC. Importantly, the role of surprise is still a subject of debate. Some studies propose that this network encodes the saliency of an outcome or how much a stimulus stands out from others (Litt, Plassmann, Shiv, & Rangel, 2011; Zink, Pagnoni, Martin-Skurski, Chappelow, & Berns, 2004). As such, the surprise system could be considered as a key attentional mechanism that enables an organism to focus its limited perceptual and cognitive resources on the most pertinent subset of the available sensory data, similarly to the attentional mechanism used to guide decisions in the case of salient stimuli (Kahnt & Tobler, 2013). Consistent with a role in attention regulation, representations of such signal have been found in lower-level visual areas (Serences, 2008), lateral intraparietal cortex (Huettel, Stowe, Gordon, Warner, & Platt, 2006; Kahnt & Tobler, 2013) and areas involved in visual and motor preparation such as the supplementary motor area (Wunderlich, Rangel, & O'Doherty, 2009) or the supplementary eye field (Middlebrooks & Sommer, 2012; So & Stuphorn, 2012).
In contrast, it has also been suggested that a surprise system can independently monitor unexpected information and act as a learning signal that allows better predictions of upcoming events, and help plan appropriate behavioural adjustments (Dayan & Balleine, 2002; Fouragnan et al., 2017; Kolling, Behrens, Mars, & Rushworth, 2012; Wittmann et al., 2016). In particular, some studies suggest that the aINS receives information related to surprise and direct modulation from the dSTR providing crucial information for behavioural adjustment (Menon & Levitin, 2005). Along these lines, the surprise signal also captures the essence of a learning signal that the brain needs to compute to maintain a homeostatic state (Friston, Kilner, & Harrison, 2006; Friston, 2009). Practically, this means that the brain elaborates internal predictions about sensory input and updates them according to surprise, a process that can be formulated as generalized Bayesian filtering or predictive coding in the brain. Finally, still in the framework of learning, some authors argue that surprise can also be considered as a signal predicting the level of risk associated with a future decision outcome, and thus reflect a risk RPE (Fiorillo et al., 2003; Preuschoff, Quartz, & Bossaerts, 2008; Rudorf, Preuschoff, & Weber, 2012).
4.3 Neuromodulatory pathways encoding multicomponent RPE signals
Supporting the idea of separate neural systems for valence and surprise, recent electrophysiological work has revealed both signals existing in neighbouring groups of neurons. The first study of this kind observed the response of dopaminergic neurons in ventral and dorsal areas of the SNc and reported two categories of dopamine neurons (Matsumoto & Hikosaka, 2009). Some dopamine neurons increase their phasic firing activity in response to valence while others responded only to the changes in unsigned RPE, regardless of the valence component. The latter population of neurons was located more dorsolaterally in the SNc, whilst the neurons encoding valence were located more ventromedially, including the VTA. Interestingly, the dorsolateral SNc projects mainly to the dorsal STR, whereas the ventral SNc and VTA project to the ventral STR, which matches the results of our last conjunction analysis (Figure 7). We found that the only region that encodes the full monotonic representation of the RPE as well as the separate valence and surprise components of RPE seems to be the central part of the STR as shown in Figure 7. This result aligns with the assumption that this region receives direct projections from the midbrain dopaminergic neurons encoding a fully monotonic signed RPE signal (Schultz et al., 1997). Additionally, the meta-analysis also revealed that both the valence (POS > NEG) and surprise networks include activity in the midbrain, confirming this hypothesis.
It is important to note that identifying neural activity associated with valence and surprise signals is challenging because in many experimental paradigms both components are highly correlated. For example, when positive RPE are manipulated in isolation, valence (POS > NEG) strongly correlates with surprise. Additionally, whether positive or negative, an unexpected outcome attracts more attention, leads to higher levels of emotional arousal and involves higher levels of motor preparation compared with no RPE (Matsumoto & Hikosaka, 2009; Maunsell, 2004; Roesch & Olson, 2004). Consequently, to disentangle these signals, one needs to design tasks in which the level of valence and surprise can independently be controlled and decoupled (Kahnt, 2017; Kahnt & Tobler, 2013) or capitalize on the variability of physiologically derived responses (i.e., endogenous variability) associated with valence and surprise (Fouragnan et al., 2015; Fouragnan et al., 2017; Pisauro, Fouragnan, Retzler, & Philiastides, 2017).
It is important to note that since the problem of collinearity and functional specificity of some brain regions is already present in single studies, it will inevitably be carried over to studies performing conjunction meta-analyses. Virtually every experimental design engages a large number of cognitive operations and, thereby, activates functional neural networks that may be irrelevant to a particular regressor (psychological construct) of interest. For example in our study, regions related to outcome valence and surprise might share variance with outcome confidence (Gherman & Philiastides, 2015; Gherman & Philiastides, 2017; Lebreton, Abitbol, Daunizeau, & Pessiglione, 2015; Philiastides, Heekeren, & Sajda, 2014). Despite this general limitation and the difficulty of interpreting conjunction results, aggregating results across a large number of experiments allows one to expose convergence of findings across studies and increasing the generalizability of the conclusions. In particular, this meta-analysis, capitalizing on both individual maps of activations as well as contrasts between different outcome components, points to a distributed encoding of valence and surprise, with potentially distinct functional roles.
4.4 Temporally specific components of RPE processing
The presence of separate RPE-related neural systems raises the question of how these systems unfold in time. Capitalizing on the high temporal resolution of EEG, three recent studies using simultaneous EEG-fMRI have started to shed light on the spatiotemporal characterisation of the RPE components. First, these studies have revealed two temporally specific EEG components discriminating between positive and negative RPEs peaking around 220 and 300 ms, respectively, largely consistent with the timing of the feedback-related negativity and feedback-related positivity ERP components (Cohen, Elger, & Ranganath, 2007; Hajcak, Moser, Holroyd, & Simons, 2006; Yeung & Sanfey, 2004). Additionally, the studies also revealed a late unsigned RPE component which overlaps temporally with the late valence signal (Philiastides et al., 2010b) but appears in a largely separate and distributed neural network (Fouragnan et al., 2017).
Based on these previous studies and the current meta-analysis, we propose that the early and late EEG valence components might reflect the separate contributions of the two networks of areas found for the ALE-valence analyses. This proposal assumes that an early network processes mainly negative RPEs in order to initiate a fast alertness response in the presence of negative outcomes. Conversely, a later network—associated with the brain's reward circuitry—is modulated by both positive and negative RPEs, consistent with a role in approach/avoidance learning and value updating (Philiastides, Biele, & Heekeren, 2010a). We also propose that the surprise network unfolds near simultaneously with the late valence component and thus influences learning through largely distinct spatial representations of the two outcomes signals, which happen to form a composite signal in overlapping areas (Fouragnan et al., 2017).
4.5 Full representation of a monotonic signed RPE signal
To examine the spatial profile of a true monotonic signed RPE representation in the human brain, we pooled results from fMRI studies, which hypothesized that RPE-like learning is driven by a simultaneous representation of both categorical valence and surprise. These fMRI studies are based on the influential assumption that BOLD signal increases monotonically as a function of signed RPE, as illustrated in pattern C (Figure 1), equivalent to the teaching signal that is predicted in the Rescorla–Wagner model of RL (Rescorla & Wagner, 1972). Additionally, we combined the valence and surprise networks and subsequently compared it with the signed RPE to test the requirement that the signed RPE simultaneous encodes both components. This conjunction analysis revealed that the only brain region that seems to encode a true monotonic signal is the STR in the basal ganglia, which could explain why such a signal is not tractable with EEG recordings as highlighted earlier. This result confirms the long standing view that the BOLD activity in STR mirrors the dopaminergic signalling of the mesolimbic neurons (Delgado, Nystrom, Fissell, Noll, & Fiez, 2000; Haber, Kunishio, Mizobuchi, & Lynd-Balta, 1995; O'Doherty et al., 2004; Pagnoni, Zink, Montague, & Berns, 2002) that fully encode the RL prediction error signal of the Rescorla–Wagner rule (Ikemoto, 2007; Schultz et al., 1992).
Nonetheless, the ALE contrast analyses between valence (the positive correlation with pattern A [ii]) and signed RPE revealed no significant activation, whereas the reverse contrast revealed a denser cluster of activity in vmPFC for valence than signed RPE. Given the evidence presented above that the signed RPE may only be encoded in the STR, we suggest that this result may arise due to collinearities between valence and signed RPE or surprise and signed RPE. More precisely, a parametric predictor for signed RPE would be positively correlated with the contrast positive > negative outcomes whereas the signed RPE and surprise would be perfectly correlated in the positive (appetitive) domain.
5 CONCLUSION
In conclusion, the current meta-analysis points to a framework whereby heterogeneous signals are involved in RPE processing. The proposal of a temporally distinct and spatially distributed representation of valence and surprise is open to debate and many questions remain about how these signals interact and how they correspond to the computations made in the brain. For example, it is currently unclear whether valence and surprise encoding occur before the computation of the signed RPE, or whether these three computations are performed in parallel. Nevertheless the taxonomy proposed is conceptually useful because it breaks down the learning and valuation processes into testable components and organizes the RPE literature in terms of the computations that are potentially involved. It will require additional experiments to validate the current proposal and to better understand the complexity of RPE processing.
ACKNOWLEDGMENTS
We thank Dr. Andrea Pisauro, Dr. Miriam Klein-Flugge and Dr. Jacqueline Scholl for helpful comments on the manuscript.




