Optimal design for nonlinear estimation of the hemodynamic response function
Abstract
Subject-specific hemodynamic response functions (HRFs) have been recommended to capture variation in the form of the hemodynamic response between subjects (Aguirre et al., [ 1998]: Neuroimage 8:360–369). The purpose of this article is to find optimal designs for estimation of subject-specific parameters for the double gamma HRF. As the double gamma function is a nonlinear function of its parameters, optimal design theory for nonlinear models is employed in this article. The double gamma function is linearized by a Taylor approximation and the maximin criterion is used to handle dependency of the D-optimal design on the expansion point of the Taylor approximation. A realistic range of double gamma HRF parameters is used for the expansion point of the Taylor approximation. Furthermore, a genetic algorithm (GA) (Kao et al., [ 2009]: Neuroimage 44:849–856) is applied to find locally optimal designs for the different expansion points and the maximin design chosen from the locally optimal designs is compared to maximin designs obtained by m-sequences, blocked designs, designs with constant interstimulus interval (ISI) and random event-related designs. The maximin design obtained by the GA is most efficient. Random event-related designs chosen from several generated designs and m-sequences have a high efficiency, while blocked designs and designs with a constant ISI have a low efficiency compared to the maximin GA design. Hum Brain Mapp, 2011. © 2011 Wiley-Liss, Inc.
INTRODUCTION
The hemodynamic response function (HRF) describes the functional magnetic resonance imaging (fMRI) signal change to one short stimulus based on the blood oxygen level-dependent contrast [Logothetis and Wandell, 2004]. Most statistical analyses of fMRI experiments are based on a general linear model where one specific shape for the HRF for all subjects and voxels is assumed, e.g., the canonical double gamma function with fixed parameter values [Friston et al., 1998]. However, it is well established that the HRF varies per subject [Aguirre et al., 1998; Boynton et al., 1996; Zarahn et al., 1997] and brain region [Handwerker et al., 2004; Miezin et al., 2000; Zarahn et al., 1997]. For this reason, Aguirre et al. (1998) suggested to handle the variability of the HRF by applying subject-specific HRFs. Region-specific functions might also be justified but in general the variability has been found to be more expressed between subjects than between regions in one subject [Handwerker et al., 2004]. Using a more accurate model for the HRF by allowing variability between subjects increases sensitivity [Aguirre et al., 1998]. In the following we will focus on subject-specific HRFs, while our methods and results can equally be applied to determine optimal designs for nonlinear estimation of region-specific HRF parameters.
Handwerker et al. ( 2004) compared the use of a subject-specific HRF to a canonical HRF with regard to false negatives, t-values and misestimation of the amplitude of the HRF. They showed that the subject-specific HRF performed better than the canonical HRF. Although differences between subject-specific and canonical HRF were small, they were statistically significant and will especially be relevant for cross-subject analyses. Acknowledging the relevance and importance of using subject-specific HRFs, the optimal design for estimation of such a HRF has to be found. The purpose of this article is to find the optimal design for nonlinear estimation of the parameters of the double gamma function which is a common model for the HRF and provides a good fit to the general form of the HRF.
A first experiment with one stimulus type can be performed to estimate the subject-specific HRF independently of subsequent experiments. From this first experiment, activated voxels or brain regions can be identified by fitting a general linear model based on a Fourier basis set or finite impulse response (FIR) basis set and corrected for multiple comparisons and dependence across voxels [Handwerker et al., 2004]. Furthermore, the HRF can be estimated nonlinearly from the identified voxels or brain regions. The subject-specific HRF can then be employed in fMRI data analyses for subsequent experiments with the same subject and more stimulus types, as variability across scan sessions has been proven to be minor [Aguirre et al., 1998]. Despite the fact that additional scanning time is necessary to firstly derive a subject-specific HRF, Handwerker et al. (2004) showed that if the fit of the canonical HRF is poor a subject-specific HRF will be beneficial.
Besides using subject-specific HRF, several other methods to capture variability of the HRF have been applied. Fourier basis sets [Josephs et al., 1997], splines [Crellin et al., 1998] and FIR sets [Ollinger et al., 2001a] are flexible in modeling the shape of the hemodynamic response, but are less parsimonious and provide less powerful tests than a double gamma function [Henson and Friston, 2007]. The interpretation of the parameters of these sets is also less direct than with a derived subject-specific double gamma function where only one parameter reflecting the amplitude of the HRF has to be estimated. Goutte et al. (2000) extend the approach of HRF estimation based on FIR sets by assuming a Gaussian prior on the FIR coefficients. This forces the HRF to be smooth and reduces the risk of ill determined parameters and overfitted models [Goutte et al., 2000].
Another approach to handle variability of the hemodynamic response from the standard form is the use of the canonical HRF plus partial derivatives [Friston et al., 1998]. The partial derivatives with respect to time and dispersion can capture small derivations from the canonical form. However, the amount of deviations that can be captured are small, i.e., up to 1 s in peak latency [Lindquist et al., 2009]. Subject-specific HRFs could capture more variability. Lindquist and Wager (2007) proposed a HRF model based on the superposition of three inverse logit functions and showed that by using their model parameter estimates of response height, delay and width are more independent of each other than with other common HRF models. Furthermore, deconvolution analysis, e.g., via a Wiener filter [Glover, 1999], can be used to estimate the HRF but deconvolution analysis is a noisy process and the deconvolution parameters must be chosen carefully [Glover, 1999]. Apart from the HRFs models mentioned so far, several other models [Buxton et al, 2004; Ciuciu et al., 2003; Rajapakse et al., 1998; Woolrich et al., 2004] have been proposed with their own advantages and disadvantages. Further details of other HRFs models, comparisons between models and the relevance of precise HRF estimation can be found in Lindquist and Wager (2007). The focus in this article is on using subject-specific parameters for the double gamma HRF which can be estimated from a nonlinear model by a nonlinear iterative least squares fitting algorithm, e.g., the Levenberg-Marquardt algorithm which uses a first order Taylor approximation [Handwerker et al., 2004; Lindquist and Wager, 2007; Miezin et al., 2000].
Optimal design for estimation of the HRF by means of a nonlinear model has not been considered yet. Previous research on optimal design for fMRI experiments has focused on optimizing detection power and estimation efficiency [Birn et al., 2002; Buračas and Boynton, 2002; Dale, 1999; Liu et al., 2001]. Detection power assumes a fixed shape of the HRF with known HRF parameters and refers to the power of a design to detect task-specific activation of brain regions whereas estimation efficiency refers to the efficiency of a design to estimate the HRF based on a linear model with a binary design matrix indicating stimulus presentations at certain time points [Dale, 1999; Henson and Friston, 2007; Liu et al., 2001]. Several designs, e.g., m-sequences [Buračas and Boynton, 2002], random event-related designs [Friston et al., 1999; Hagberg et al., 2001], blocked designs, and optimal designs generated by genetic algorithms (GAs) [Kao et al., 2009; Wager and Nichols, 2003] have been studied and applied to increase detection power and estimation efficiency. In this article, these commonly used designs are applied to find an optimal design for nonlinear estimation of the double gamma function parameters, and a thorough and balanced comparison of the efficiency of these various designs is provided. By means of the GA, optimal designs can be obtained without previous specialization of the design properties. Because the design space of all possible fMRI designs is enormous [Buračas and Boynton, 2002], this algorithm is useful to provide an efficient search within the design space [Kao et al., 2009]. It is known that blocked designs are optimal for detection power, whereas rapid event-related designs with randomized interstimulus intervals are optimal for estimation efficiency based on linear models [Birn et al., 2002; Liu and Frank, 2004; Liu, 2004]. However, not any randomly generated rapid event-related design achieves high estimation efficiency [Buračas and Boynton, 2002], and the GA provides more efficient designs than a random search in the design space [Wager and Nichols, 2003]. Our results show that a mixture of a blocked design and a rapid event-related design will be most efficient for the nonlinear model but that rapid event-related designs can also be very efficient for the nonlinear model.
To calculate the efficiency of a given design, e.g., an m-sequence, a Taylor approximation of first order is applied to linearize the model with respect to the unknown parameters of the HRF [Atkinson et al., 2007]. Based on the linearized model, the covariance matrix of the generalized least squares (GLS) estimator can be calculated for a given expansion point of the Taylor approximation. The D-optimality criterion is then considered to determine the optimal design which minimizes the determinant of the covariance matrix of the GLS estimators for the linearized model. The determinant of the GLS estimator is proportional to the area of the confidence ellipsoid for the estimator. Thus, minimizing the determinant leads to a minimized confidence ellipsoid. However, for the Taylor approximation an expansion point is needed. The optimal design may then depend on the expansion point and is thus locally optimal. To handle local optimality, a range for HRF parameters describing commonly observed shapes of the HRF was chosen from literature [Aguirre et al., 1998; de Zwaart et al., 2005; Glover, 1999; Handwerker et al., 2004; Le et al., 2001] and a maximin approach [Atkinson et al., 2007] was applied. The D-optimality criterion and the maximin criterion will be explained in the following theory section section.
THEORY
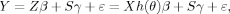 (1)
(1)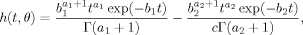 (2)
(2)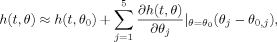 (3)
(3)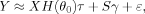 (4)
(4)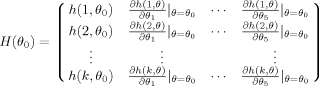 (5)
(5)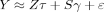 (6)
(6)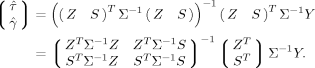 (7)
(7)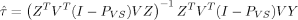 (8)
(8)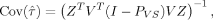 (9)
(9)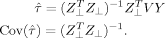 (10)
(10)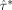 is equal to the determinant of the covariance matrix of
is equal to the determinant of the covariance matrix of
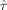 , while this equality is not guaranteed for the A-optimality criterion. Therefore, we focused on the D-optimality criterion. The following criterion based on D-optimality was applied
, while this equality is not guaranteed for the A-optimality criterion. Therefore, we focused on the D-optimality criterion. The following criterion based on D-optimality was applied
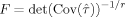 (11)
(11)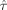 ). The higher F is, the better the design is.
). The higher F is, the better the design is.Because the matrix H(θ0) depends on the expansion point θ0, the obtained optimal design for a given value of θ0 is locally optimal. To handle the problem of local optimality the maximin criterion was applied for all designs ξ1 in the design space Ξ and all parameters θ0 in the parameter space θ. Here, the parameter space was the set of all considered values for the expansion point θ0 and is further described in the section on the parameter space for the expansion point. The maximin criterion was applied for each design type (m-sequences, blocked designs etc.) separately. Thus, each design type had its own design space which was the set consisting of all considered designs for this design type. The parameter space however remained the same for all design types. The design space for the GA consisted of all locally optimal designs obtained by the GA as described in the section on design types. Furthermore, the section on design types presents the design spaces for the other design types studied in this article, such as m-sequences, blocked designs and rapid event-related designs.
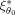 . The relative efficiency of a locally optimal design ξ1 versus the locally optimal design
. The relative efficiency of a locally optimal design ξ1 versus the locally optimal design
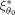 is given by
is given by
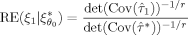 (12)
(12)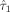 and
and
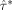 being the GLS estimators obtained by designs ξ1 and
being the GLS estimators obtained by designs ξ1 and
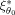 at the expansion point θ0. The covariance matrices of the GLS estimators Cov(
at the expansion point θ0. The covariance matrices of the GLS estimators Cov(
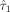 ) and Cov(
) and Cov(
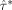 ) given by Eq.
(9) depend on their respective designs since the matrix X in Z = XH(θ0) differs per design. The relative efficiency of the design ξ1 versus the design
) given by Eq.
(9) depend on their respective designs since the matrix X in Z = XH(θ0) differs per design. The relative efficiency of the design ξ1 versus the design
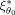 in Eq.
(12) depends on the expansion point θ0 because firstly the design ξ1 is compared to the locally optimal design
in Eq.
(12) depends on the expansion point θ0 because firstly the design ξ1 is compared to the locally optimal design
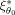 for the expansion point θ0 and secondly the GLS estimators obtained by the designs ξ1 and
for the expansion point θ0 and secondly the GLS estimators obtained by the designs ξ1 and
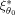 are both evaluated at the expansion point θ0. The relative efficiency in Eq.
(12) is a measure between 0 and 1 with a relative efficiency RE(ξ1|
are both evaluated at the expansion point θ0. The relative efficiency in Eq.
(12) is a measure between 0 and 1 with a relative efficiency RE(ξ1|
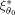 ) of almost 0 for the design ξ1 versus the design
) of almost 0 for the design ξ1 versus the design
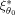 meaning that the design ξ1 is very inefficient compared to the locally optimal design
meaning that the design ξ1 is very inefficient compared to the locally optimal design
 at the expansion point θ0. A relative efficiency close to 1 indicates that the design ξ1 is almost as efficient as the locally optimal design
at the expansion point θ0. A relative efficiency close to 1 indicates that the design ξ1 is almost as efficient as the locally optimal design
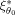 .
. of this design ξ1 over all expansion points θ0 in the parameter space θ, i.e., against all locally optimal designs
of this design ξ1 over all expansion points θ0 in the parameter space θ, i.e., against all locally optimal designs
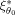 , is its worst relative efficiency. The maximin design MMD thus achieves the best-worst case for the relative efficiencies as it has the maximum minimum relative efficiency over all locally optimal designs ξ1 in the design space Ξ:
, is its worst relative efficiency. The maximin design MMD thus achieves the best-worst case for the relative efficiencies as it has the maximum minimum relative efficiency over all locally optimal designs ξ1 in the design space Ξ:
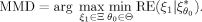 (13)
(13)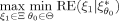 is high, the maximin design is very efficient versus the locally optimal designs at all parameter values in the parameter space.
is high, the maximin design is very efficient versus the locally optimal designs at all parameter values in the parameter space.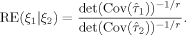 (14)
(14)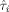 (i = 1,2) is the GLS estimator for the design ξi and depends on the design matrix belonging to design ξi. Using the model in Eq.
(6), the relative efficiency in Eq. (14) depends on the expansion point θ0. The inverse of the relative efficiency gives the number of times that design ξ1 has to be repeated to be as efficient as the design ξ2.
(i = 1,2) is the GLS estimator for the design ξi and depends on the design matrix belonging to design ξi. Using the model in Eq.
(6), the relative efficiency in Eq. (14) depends on the expansion point θ0. The inverse of the relative efficiency gives the number of times that design ξ1 has to be repeated to be as efficient as the design ξ2.METHODS
The GA was used to find locally optimal designs for the simultaneous nonlinear estimation of the parameters a1, b1, c, a2 and b2 for the double gamma function. From the locally optimal designs obtained by the GA (with one locally optimal design per considered expansion point of the Taylor approximation) the maximin design MMDGA was chosen. Furthermore, we obtained maximin designs from different specific design types which are commonly applied or known to be efficient, i.e., m-sequences, event-related designs with fixed ISI, blocked designs and rapid event-related designs with a geometric or uniform distribution for the ISI.
Parameter Space for Expansion Point
The expansion point for the Taylor approximation was varied in a1, b1, c, a2 and b2. Note that while the estimation of the amplitude parameter β is also optimized by maximizing Eq. (11), the locally optimal designs are not dependent on the value for β, but only on the expansion point θ0. Thus, only the HRF parameters a1, b1, c, a2 and b2 are varied for determination of the locally optimal designs. Parameter a1 had values 4.8, 5, 5.2, b1 was varied from 0.9 to 1.3 in steps of 0.1, c was varied between 4 and 8 in steps of 1 and a2 had values 14.5, 15 and 15.5. The parameter b2 was equal to 0.9, 1 or 1.1 for a2 = 14.5, equal to 0.9, 1, 1.1 or 1.3 for a2 = 15 and equal to 0.9, 1, 1.1 or 1.3 for a2 = 15.5. For each expansion point, the GA by Kao et al. ( 2009) was applied to find the locally optimal design which maximizes Eq. (11). The MATLAB code of Kao et al. (2009) was adapted to use the linearized model in Eq. (4). This resulted in 825 locally optimal designs from which the maximin design (MMDGA) was ascertained. The applied MATLAB code is available on request from the first author.
The chosen range for parameter values was obtained from the literature showing that the time to peak (TTP = a1/b1) of the HRF can lie between 3 s and 7 s [Aguirre et al.,
1998; de Zwaart et al., 2005; Handwerker et al., 2004; Le et al., 2001] while the canonical values for the double gamma function are a1 = 5 and b1 = 1. The full width at half maximum (FWHM) of the first gamma function, given by
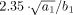 , was found to lie in the interval [3 s, 6 s] [Bandettini and Cox,
2000; de Zwaart et al., 2005; Glover, 1999; Le et al., 2001]. The time to undershoot (TTU = a2/b2) was found to vary between 9 s and 18 s for real data [Aguirre et al., 1998; Friston et al., 2002; Handwerker et al., 2004] and simulations [Woolrich et al., 2004; Penny et al., 2004]. The FWHM of the undershoot was assumed to be in the interval 7 s to 11 s because the canonical HRF with a1 = 5, b1 = 1, c = 6, a2 = 15 and b2 = 1 has a FWHM of 9.10 s for the second gamma function. To reduce computation time we restricted the parameters to the values as given above which satisfy the conditions for TTP, TTU and FWHM of both gamma functions. Furthermore, the parameter steps were based on the results of a regression analysis which was performed to study the influence of the parameters on the accuracy of the Taylor approximation. Concluding from the results of the regression analysis, we chose smaller steps for a1 and b1 than for a2 and b2. As a result, the modeled range of the time to peak is [3.69, 5.78], the modeled FWHM of the peak is [3.96, 5.95], the modeled range of the time to undershoot is [11.92, 17.22] and the modeled FWHM of the undershoot is [7.12, 10.28]. In Figure 1 the range of the HRFs given by the parameter space is presented. The values for a1 and b1 in Figure 1a and the values for a2 and b2 in Figure 1b were chosen so that the minima and maxima of the TTP, TTU and the FWHMs for the first and second gamma function were obtained.
, was found to lie in the interval [3 s, 6 s] [Bandettini and Cox,
2000; de Zwaart et al., 2005; Glover, 1999; Le et al., 2001]. The time to undershoot (TTU = a2/b2) was found to vary between 9 s and 18 s for real data [Aguirre et al., 1998; Friston et al., 2002; Handwerker et al., 2004] and simulations [Woolrich et al., 2004; Penny et al., 2004]. The FWHM of the undershoot was assumed to be in the interval 7 s to 11 s because the canonical HRF with a1 = 5, b1 = 1, c = 6, a2 = 15 and b2 = 1 has a FWHM of 9.10 s for the second gamma function. To reduce computation time we restricted the parameters to the values as given above which satisfy the conditions for TTP, TTU and FWHM of both gamma functions. Furthermore, the parameter steps were based on the results of a regression analysis which was performed to study the influence of the parameters on the accuracy of the Taylor approximation. Concluding from the results of the regression analysis, we chose smaller steps for a1 and b1 than for a2 and b2. As a result, the modeled range of the time to peak is [3.69, 5.78], the modeled FWHM of the peak is [3.96, 5.95], the modeled range of the time to undershoot is [11.92, 17.22] and the modeled FWHM of the undershoot is [7.12, 10.28]. In Figure 1 the range of the HRFs given by the parameter space is presented. The values for a1 and b1 in Figure 1a and the values for a2 and b2 in Figure 1b were chosen so that the minima and maxima of the TTP, TTU and the FWHMs for the first and second gamma function were obtained.
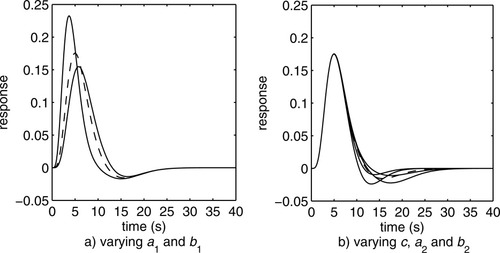
Range of hemodynamic response functions captured by expansion points in the parameter space. In Figure 1a the hemodynamic response functions for a1 = 4.8, b1 = 1.3 and a1 = 5.2, b1 = 0.9 are shown by the solid lines (c, a2 and b2 are fixed to c = 6, a2 = 15 and b2 = 1). In Figure 1b the hemodynamic response functions for a2 = 15.5, b2 = 0.9, c = 4 or 8 and a2 = 15.5, b2 = 1.3, c = 4 or 8 are shown by the solid lines (a1 and b1 are fixed to a1 = 5 and b1 = 1). The dashed lines in Figure 1a and Figure 1b present the canonical hemodynamic response function (a1 = 5, b1 = 1, c = 6, a2 = 15, b2 = 1).
Design Types
The GA was applied for Q=1 stimulus type, N=128 events (including null events) and an autocorrelation ρ = 0.3 within a first order autoregressive (AR1) error ε [Kao et al., 2009; Maus et al., 2010] so that the matrix Σ in Eq. (1) has the form of an AR1 covariance matrix. The number of events refers here to the total number of events for the design and is a sum of the number of null events and number of stimulus trials. The exact number of null events or stimulus trials differed for each considered design. Furthermore, the following factors were considered: ISI=2.5 s (here, minimum time between two consecutive stimulus events) and TR=2 s. This results in an effective sampling interval of dT=0.5 s for the HRF [Josephs et al., 1997; Miezin et al., 2000] and in the number of time points T = 160. For the nuisance matrix S, a second order Legendre polynomial was assumed. The HRF and its derivatives were calculated over a length of 40 s so that k = 40/dT+1 = 81. The algorithm parameters were G (size of population)=20, q (percentage of mutation)=1%, I (number of immigrants)=4 and Mg (number of generations)=10,000 [Kao et al., 2009]. The nonalgorithmic parameters Q, N, ρ and TR given above were also applied for the other design types and the minimum ISI was always chosen to be 2.5 s.
The maximin design MMDm was chosen from all possible 18 m-sequences for 128 events (including null events) and for one stimulus type. Strictly speaking, the m-sequence lengths were 127 events but one null event was added at the sequence end to achieve stimulus frequency equal to 0.5. Note that the stimulus frequencies in this article are determined on the “event design sequences” with N=128 events and not on the “scan design sequences” with T=160 time points as due to the minimum ISI of 2.5 s and the TR of 2 s not all stimulus events occurred at a scan. Furthermore, the maximin design MMDCI from several constant ISI designs and the maximin design MMDB from several blocked designs were chosen. Constant ISIs from 2.5 s, 5 s, …, 17.5 s, 20 s and blocked designs with block length of 10 s, 12.5 s, …, 27.5 s, 30 s and 60 s were considered. The blocked designs started with a stimulus block followed by a rest block of same length. Some block lengths resulted in remaining time points at the end of the time series. These remaining time points were either filled completely with rest events or completely with stimulus events. In total, 18 blocked designs were considered. All constant ISI designs and blocked designs were assumed to have a total number of events (including null events) of 128.
Additionally, maximin designs from random event-related designs were chosen. Commonly applied and proven to be efficient are a uniform or geometric distribution for the ISI [Biancardi et al., 2004; Hagberg et al., 2001; Liu et al., 2001; Ollinger et al., 2001b]. The maximin design MMDgeo was chosen out of realizations of designs with a geometric distribution for ISI. Such a distribution can be described by three parameters: ISImin which gives the smallest possible time between two events, p which models the probability of the number of time points between two events and ISIstep which is the step of ISIs. The random variable X which represents the number of ISI steps until the next stimulus event has probability P(X = x) = (1 − p)x p. The random variable ISI is given by ISImin + X . ISIstep. The 27 applied parameter sets for the geometric distribution are presented in Table I.
| ISImin (s) | ISIstep (s) | p | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 2.5 | 2.5 | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | G9 |
| 5.0 | 2.5 | G10 | G11 | G12 | G13 | G14 | G15 | G16 | G17 | G18 |
| 5.0 | 5.0 | G19 | G20 | G21 | G22 | G23 | G24 | G25 | G26 | G27 |
- Design G5 is the maximin design.
Each parameter set refers to a single design and we computed 200 realizations of each design so that 5400 sequences (27 designs) were obtained. The maximin design and the maximin design sequence were chosen in a two-step procedure.
In the first step, the maximin design and its parameter set were determined. The first step included determination of the locally optimal sequences from the 5400 sequences (one locally optimal design per expansion point), calculation of the relative efficiencies of all sequences against the locally optimal sequences and calculation of the minimum relative efficiency of each sequence. Finally, for each design the average minimum relative efficiency over all 200 realizations was calculated. The design with highest mean minimum relative efficiency is the maximin design. Averaging was performed to find a maximin design which generally results in sequences with high minimum relative efficiencies instead of finding a maximin design with by coincidence one highly efficient sequence.
In the second step, one design sequence was chosen from the realizations of the maximin design to be the maximin design sequence. The second step consisted of determination of the locally optimal sequences among the 200 sequences, calculation of the relative efficiencies and minimum relative efficiencies. The stimulus sequence with highest minimum relative efficiency among the 200 sequences was chosen to be the maximin design sequence.
Following the same two-step procedure as for the geometric distribution, the maximin design MMDuni was chosen out of 13 designs with a uniform distribution for ISI. 400 realizations of each design were performed so that 5200 sequences in total were obtained. According to the two-step procedure, the maximin design sequence was chosen out of the 400 realizations of the maximin design. The applied ISIs for the uniform designs are indicated in Table II.
| ISI (s) | Designs | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | U10 | U11 | U12 | U13 | |
| 2.5 | x | x | x | x | x | x | x | ||||||
| 5.0 | x | x | x | x | x | x | x | x | x | x | x | ||
| 7.5 | x | x | x | x | x | x | x | x | x | x | x | ||
| 10.0 | x | x | x | x | x | x | x | x | x | x | |||
| 12.5 | x | x | x | x | x | x | x | x | |||||
| 15.0 | x | x | x | x | x | x | |||||||
| 17.5 | x | x | x | ||||||||||
| 20.0 | x | ||||||||||||
- Design U6 is the maximin design.
Computation times for the different maximin designs under linearity were measured on a computer with Intel Core i7 processor, 2.67 GHz and 6.00 GB RAM. To model nonlinearity, we assumed a reduction in amplitude of 30% for an ISI of 2.5 s [Huettel and McCarthy, 2000] and of 21% for an ISI of 5 s [Miezin et al., 2000] within the design matrix X. Using the same design types, parameter sets and the same two-step procedure as described for linearity, maximin designs under the assumption of nonlinearity were obtained. We will refer to these designs as MMDGANL, MMDmNL, MMDCINL, MMDBNL, MMDgeoNL and MMDuniNL.
RESULTS
The maximin design MMDGA obtained from the GA, proved to be most efficient in comparison to the other maximin designs (MMDm, MMDCI, MMDB, MMDgeo and MMDuni) obtained under the assumption of linearity of the HRF. Likewise, the maximin design MMDGANL was most efficient under the assumption of nonlinearity of the HRF. Therefore, we restrict our design comparison in the following sections to the pairwise comparison of the maximin designs obtained by the GA to the maximin designs obtained by m-sequences, constant ISI designs, blocked designs, designs with geometric or uniform distribution for ISI under the assumption of linearity or nonlinearity.
The minimum relative efficiency of the maximin designs within their own design type and the range of relative efficiencies against the MMDGA or MMDGANL over the expansion points are given in Tables III and IV. Furthermore, the relative efficiencies of each maximin design from the specific design types against the maximin design MMDGA are illustrated in Figure 2. Note that the calculation of the relative efficiencies against MMDGA and MMDGANL in Figure 2, Tables III and IV is based on Eq. (14) and not on the by Eq. (12) calculated relative efficiencies, which were used to determine the maximin design from the locally optimal designs of each design type.
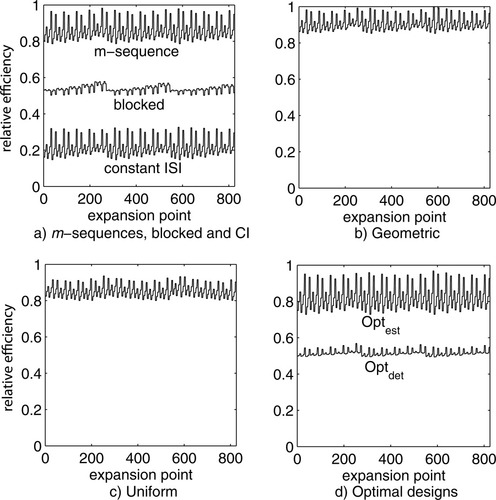
Relative efficiency of maximin designs based on different design types and optimal designs versus MMDGA . CI = constant ISI.
| Mean BL (s) | Mean ISI (s) | Frequency | min RE | RE versus MMDGA | Computation time | ||
|---|---|---|---|---|---|---|---|
| Genetic algorithm | 0 | 7.16 | 4.88 | 0.49 | 0.93 | 1.00 | 45.83 h |
| A | 7.39 | 0.51 | |||||
| m-sequence | 0 | 4.85 | 4.96 | 0.50 | 0.99 | 0.79–0.98 | 18 s |
| A | 5.00 | 0.50 | |||||
| Blocked | 0 | 25.00 | 4.74 | 0.47 | 0.89 | 0.50–0.58 | 18 s |
| A | 24.29 | 0.53 | |||||
| Constant ISI | 0 | 15.28 | 17.50 | 0.86 | 0.95 | 0.15–0.33 | 8 s |
| A | 2.50 | 0.14 | |||||
| Geometric | 0 | 4.83 | 4.53 | 0.45 | 0.97 (step 1), | 0.85–1.00 | 642 s (all steps) |
| A | 6.03 | 0.55 | 0.99 (step 2) | ||||
| Uniform | 0 | 7.05 | 6.35 | 0.62 | 0.95 (step 1), | 0.80–0.94 | 629 s (all steps) |
| A | 4.54 | 0.38 | 0.9976 (step 2) |
- Computation times were determined on a computer with Intel Core i7 processor, 2.67 GHz and 6.00 GB RAM.
| Mean BL (s) | Mean ISI (s) | Frequency | min RE | RE versus MMDGANL | ||
|---|---|---|---|---|---|---|
| Genetic algorithm | 0 | 6.16 | 5.43 | 0.54 | 0.95 | 1.00 |
| A | 5.27 | 0.46 | ||||
| m-sequence | 0 | 4.85 | 4.96 | 0.50 | 0.99 | 0.84–0.98 |
| A | 5.00 | 0.50 | ||||
| Blocked | 0 | 22.50 | 4.96 | 0.49 | 0.91 | 0.49–0.55 |
| A | 20.31 | 0.51 | ||||
| Constant ISI | 0 | 15.28 | 17.50 | 0.86 | 0.95 | 0.23–0.44 |
| A | 2.50 | 0.14 | ||||
| Geometric | 0 | 6.72 | 6.38 | 0.61 | 0.97 (step 1), | 0.89–0.98 |
| A | 4.31 | 0.39 | 0.9955 (step 2) | |||
| Uniform | 0 | 7.12 | 5.71 | 0.58 | 0.96 (step 1), | 0.84–0.93 |
| A | 5.40 | 0.42 | 0.9954 (step 2) |
After the presentation of the results for the different maximin designs, the maximin design MMDGA is compared in the section on optimal designs to the optimal design for HRF estimation, using a linear model with the stimulus convolution matrix as design matrix, and to the optimal design for detection of task-related activation, using a linear model where the regressors are obtained by multiplication of the stimulus convolution matrix with the sampled HRF. The latter design will be called the optimal design for detection power whereas the former design will be called the optimal design for estimation efficiency. The corresponding models will be named detection power model or estimation efficiency model. These comparisons are interesting for evaluation of the efficiency loss when the model and optimality criterion do not match with the ultimate data analysis of an fMRI design. Linearity of the HRF was assumed for the calculation of both designs which were obtained by applying the original code for the GA of Kao et al. ( 2009). More details are given in the section on optimal designs.
Linearity of HRF
The maximin design MMDGA presented in Figure 3a is a mixture of a blocked and a rapid event-related design, as it contains task and null blocks while other parts of the design sequence have an event-related form. The maximin design MMDm in Figure 3b is more similar to a rapid event-related design than the maximin design MMDGA. The maximin design MMDCI for the constant ISI designs is the slow event-related design with 17.5 s ISI (see Fig. 3c) and the maximin design MMDB for the blocked designs has block length 25 s and one stimulus block at the end (see Fig. 3d). The maximin geometric ISI design MMDgeo in Figure 3e is the design with ISImin = ISIstep = 2.5 s, p = 0.5 and the maximin design MMDuni shown in Figure 3f is the design with ISIs 2.5 s, 7.5 s and 12.5 s.

Maximin designs and optimal designs, white indicates a stimulus, black indicates no stimulus. The time between two time points is here 2.5 s which is the employed minimum ISI. TR was equal to 2 s.
The properties of the maximin designs are presented in Table III. Furthermore, the minimum relative efficiency of the maximin designs within their own design class and the range of relative efficiencies against the MMDGA over the expansion points are given. The range of relative efficiencies against the maximin design MMDGA is also illustrated in Figure 2. Further details will now be discussed per design type.
Genetic algorithm
The maximin design MMDGA has a high frequency of ISI 2.5 s and some longer ISIs of 5 s, 7.5 s, 10 s, 12.5 s, 15 s and 27.5 s as can be seen in Figure 4. The longer ISIs indicate null blocks. Null events had a slightly lower frequency than stimulus events in the maximin design MMDGA (Table III). This was also the case for all the locally optimal designs, except two which had equal frequencies. The minimum relative efficiencies of the 825 locally optimal designs were on average 0.87, and the range was from 0.80 to 0.93. The maximin design MMDGA was obtained for a1 = 4.8, b1 = 1.1, c=4, a2 = 15.5 and b2 = 1.1, and its minimum relative efficiency was equal to 0.93. The minimum relative efficiency of the locally optimal design for the canonical expansion point (a1 = 5, b1 = 1, c = 6.0, a2 = 15 and b2 = 1) was equal to 0.88. In Figure 5 the convergence of the GA for all expansion points is shown. It can be seen that for most expansion points the GA converged very quickly to 99% of its maximum and final value Fmax obtained for 10,000 generations. For some expansion points however reaching 99% of Fmax needed more generations. The worst convergence was for expansion point number 668 with 3507 generations to reach 99% of Fmax.
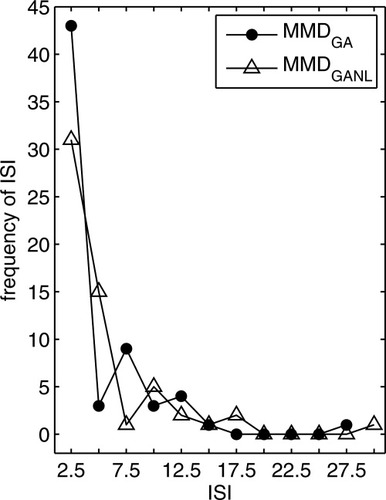
Frequency of ISI for maximin designs MMDGA and MMDGANL.
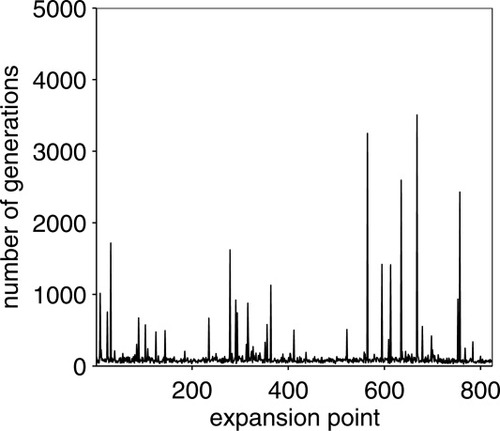
Convergence of the genetic algorithm for all expansion points. The number of generations is shown which is needed at a given expansion point to reach 99% of the final value Fmax (maximum value of design criterion F) after 10,000 generations. On the x-axis the expansion points are given and on the y-axis the number of generations is shown.
M-sequence, constant ISI designs, blocked designs
The maximin design MMDGA was compared to the maximin design MMDm of the m-sequences by calculating the relative efficiency as in Eq. (14) of the maximin design MMDm versus MMDGA at each expansion point. Likewise, the relative efficiency of the maximin design MMDB and MMDCI versus MMDGA was determined. Figure 2a shows that the maximin design MMDm was slightly less efficient than the maximin design MMDGA at all expansion points. It can be seen in Figure 2a that the maximin design MMDCI had a low relative efficiency and the maximin design MMDB a medium relative efficiency.
Geometric distribution
In Figure 6 the minimum relative efficiencies of the 5400 random sequences versus the locally optimal designs are presented. On the x-axis the 27 designs with geometric distribution for ISI are given (see Table I) and on the y-axis the range of minimum relative efficiencies is indicated. For each design a boxplot of the 200 minimum relative efficiencies for this design is shown. The vertical lines between the boxplots indicate the three sets of nine designs which have the same ISImin and ISIstep but differ in probability p. Figure 6 shows that for the geometric distribution, designs with middle probability around p = 0.5 perform better with respect to minimum relative efficiency than designs with high and low p as long as the other factors such as ISImin are kept constant. Furthermore, designs with high or low p have more variability in the minimum relative efficiencies. A small ISImin is more efficient than a higher ISImin. The maximin design for the geometric distribution which is shown in Figure 3e had an ISImin of 2.5 s with possible ISIs in steps of 2.5 s and p was equal to 0.5 (design G5 in Fig. 6). This results in a theoretical mean ISI of 5 s. Figure 2b illustrates that the maximin design MMDgeo performs well against the maximin design MMDGA.
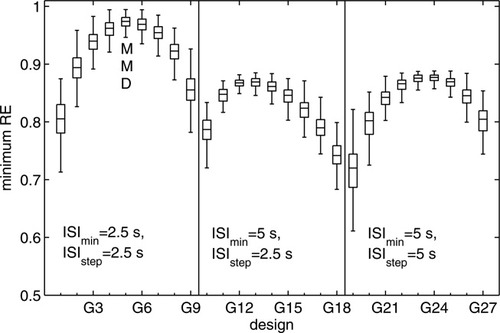
Boxplots of minimum relative efficiency (RE) for designs with a geometric distribution for ISI. On the x-axis the 27 designs G1 till G27 are indicated (see Table I for further information). The boxes give the median and 25% and 75% percentile of the 200 minimum relative efficiencies (realizations) per design versus the locally optimal designs. The whiskers show the most extreme data points (minimum relative efficiencies) which differ from the median by maximally 1.5 interquartile range. MMD denotes the maximin design and refers to the design G5 with ISImin = 2.5 s, ISIstep = 2.5 s and p = 0.5.
Uniform distribution
In Figure 7 the boxplots of minimum relative efficiencies for each of the 13 uniform designs are shown. The minimum relative efficiencies are calculated by comparison of the 5200 random sequences versus the locally optimal sequences. The maximin design in Figure 3f for the uniform distribution was the design with ISIs 2.5 s, 7.5 s and 12.5 s (design U6 in Fig. 7). Figure 7 illustrates that designs with minimum ISI 2.5 s have higher minimum relative efficiencies. The maximin design MMDuni performs well versus MMDGA but not as well as MMDgeo, see Figure 2c.
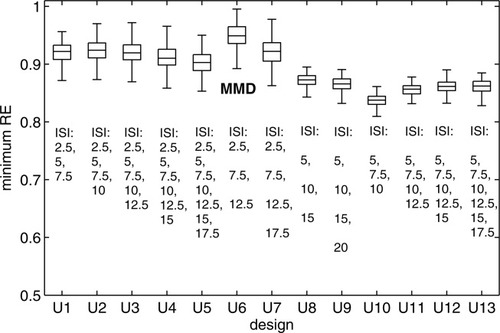
Boxplots of minimum relative efficiency (RE) for designs with a uniform distribution for ISI. On the x-axis the different 13 designs U1 till U13 are given (see Table II). The boxes give the median and 25% and 75% percentile of the 400 minimum relative efficiencies (realizations) per design versus the locally optimal designs. The whiskers show the most extreme data points (minimum relative efficiencies) which differ from the median by maximally 1.5 interquartile range. MMD denotes the maximin design U6 with ISIs 2.5, 7.5, and 12.5 s.
Nonlinearity of HRF
The properties of the maximin designs, their minimum relative efficiencies within their own design class and their relative efficiencies versus the maximin design MMDGANL can be seen in Table IV. The main difference between the results for linearity and nonlinearity was that the maximin design for the GA MMDGANL and the maximin design based on the geometric distribution MMDgeoNL (p=0.4, ISImin=2.5 s, ISIstep=2.5 s) had a higher mean ISI than the corresponding maximin designs MMDGA and MMDgeo for linearity. This can be explained by the fact than an ISI of 2.5 s is less efficient under nonlinearity and thus less frequent in the design MMDgeoNL and the maximin design MMDGANL. Among the 18 possible m-sequences 4.96 s was the highest mean ISI and both maximin designs MMDmNL and MMDm had this mean ISI. For the maximin design MMDuniNL, the mean ISI was lower than for the maximin design MMDuni which is in contrast to the designs mentioned above. This different relation in mean ISI might be explained by our specific samples. Generating another 400 realizations of the maximin uniform designs resulted in different mean ISIs, and the mean ISI was lower for the new maximin design MMDuni than for the new maximin design MMDuniNL. The original uniform design MMDuniNL had as for linearity the ISIs 2.5 s, 7.5 s and 12.5 s. The distribution of ISI for the maximin design MMDGANL can be seen in Figure 4.
The other maximin designs under nonlinearity of the HRF were as follows. The maximin constant ISI design had an ISI of 17.5 s and was thus unaffected by the nonlinearity for ISIs 2.5 s and 5 s. Another minor difference between linearity and nonlinearity was that the maximin blocked design MMDBNL had block length 22.5 s instead of 25 s. Like for linearity, the blocked design MMDBNL had a stimulus block at the end.
Optimal Designs for Estimation Efficiency and Detection Power
The optimal design for detection power was obtained assuming the canonical HRF in Eq.
(1) (a1 = 5, b1 = 1, c = 6, a2 = 15, b2 = 1 in Eq. (2)) with duration of 32 s and maximizing the D-optimality criterion
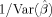 . The optimal design for estimation efficiency was obtained by maximizing the D-optimality criterion det(Cov(ĥ))−1/k where ĥ is the GLS estimator for h, the hemodynamic response vector sampled at k = 32/0.5+1 = 65 time points and the entries of h represent the height of the HRF at the k time points. The model for estimation efficiency is obtained by replacing h(θ)β in Eq.
(1) with the vector h. In comparison to h(θ)β, h can result in more flexible forms of the HRF and does not depend on the double gamma parameter vector θ. The parameters ρ, TR, ISI and the number of events N had the same values as in the calculation for the locally optimal designs and maximin designs.
. The optimal design for estimation efficiency was obtained by maximizing the D-optimality criterion det(Cov(ĥ))−1/k where ĥ is the GLS estimator for h, the hemodynamic response vector sampled at k = 32/0.5+1 = 65 time points and the entries of h represent the height of the HRF at the k time points. The model for estimation efficiency is obtained by replacing h(θ)β in Eq.
(1) with the vector h. In comparison to h(θ)β, h can result in more flexible forms of the HRF and does not depend on the double gamma parameter vector θ. The parameters ρ, TR, ISI and the number of events N had the same values as in the calculation for the locally optimal designs and maximin designs.
We determined the optimal designs for estimation efficiency Optest and detection power Optdet by the GA. The optimal designs can be seen in Figures 3g and 3h, and their properties are given in Table V. As expected, the optimal design for estimation efficiency is an event-related design whereas the optimal design for detection power is a blocked design. Figure 2d shows the relative efficiencies versus the MMDGA at the different expansion points. These relative efficiencies are based on Eq.
(14) with the estimators
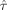 being the GLS estimators for nonlinear estimation of the double gamma function. Figure 2d illustrates that the optimal design for estimation efficiency performs better versus the MMDGA than the optimal design for detection power. This is similar to the previous results for blocked designs and rapid event-related designs, i.e., m-sequences, random event-related designs with geometric or uniform distribution for the ISI. In Figure 2 it is also seen that the maximin blocked design has lower relative efficiencies than the maximin m-sequence, maximin geometric ISI design or maximin uniform ISI design.
being the GLS estimators for nonlinear estimation of the double gamma function. Figure 2d illustrates that the optimal design for estimation efficiency performs better versus the MMDGA than the optimal design for detection power. This is similar to the previous results for blocked designs and rapid event-related designs, i.e., m-sequences, random event-related designs with geometric or uniform distribution for the ISI. In Figure 2 it is also seen that the maximin blocked design has lower relative efficiencies than the maximin m-sequence, maximin geometric ISI design or maximin uniform ISI design.
| Mean BL (s) | Mean ISI (s) | Frequency |
RE versus MMDGA based on model in Eq. (6) |
RE of MMDGA versus optimal design based on EE or DP model | ||
|---|---|---|---|---|---|---|
| Optest | 0 | 4.21 | 4.63 | 0.46 | 0.73–0.97 | 0.54 |
| A | 4.93 | 0.54 | ||||
| Optdet | 0 | 15.50 | 4.88 | 0.48 | 0.49–0.57 | 0.62 |
| A | 15.00 | 0.52 |
When determining the relative efficiency of the MMDGA versus the optimal designs for estimation efficiency and detection power, it is seen in Table V that in general the maximin design MMDGA is not very efficient for estimation efficiency and detection power. These relative efficiencies are based on Eq.
(14) with GLS estimators for an estimation efficiency model, i.e.,
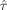 is replaced by ĥ, or detection power model, i.e.,
is replaced by ĥ, or detection power model, i.e.,
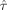 is replaced by
is replaced by
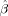 . By optimizing for the nonlinear parameters in the HRF and the amplitude β simultaneously, the ability of the maximin design MMDGA to detect only activation, that is to estimate only the parameter β efficiently, is considerably reduced. Although optimal designs for estimation efficiency, e.g., m-sequences and Optest, had a high efficiency versus the MMDGA for the model in Eq.
(6) and were thus efficient to estimate the nonlinear parameters and the amplitude β, the design MMDGA cannot be recommended for linear HRF estimation.
. By optimizing for the nonlinear parameters in the HRF and the amplitude β simultaneously, the ability of the maximin design MMDGA to detect only activation, that is to estimate only the parameter β efficiently, is considerably reduced. Although optimal designs for estimation efficiency, e.g., m-sequences and Optest, had a high efficiency versus the MMDGA for the model in Eq.
(6) and were thus efficient to estimate the nonlinear parameters and the amplitude β, the design MMDGA cannot be recommended for linear HRF estimation.
Comparing Table III with V, it is seen that the mean block length and the mean ISI of the maximin design MMDGA are between those of the designs Optest and Optdet. The maximin design MMDGA is thus more blocked than the design Optest but its mean block length is still closer to the mean block length of Optest than to the mean block length of Optdet. Thus, MMDGA is only slightly more blocked than Optest.
DISCUSSION
The general advantage of using a maximin design for nonlinear models is that the maximin criterion chooses a design which performs well within the range of possible values for the unknown parameters. The unknown parameters in our study were the parameters of the double gamma function. The main result was that the maximin design based on the GA performed best. However, due to less computation time maximin designs based on m-sequences, random event-related designs with a uniform or geometric distribution for ISI or even an optimal design for estimation efficiency can be recommended as an alternative to a maximin design obtained by the GA. It was furthermore found that the maximin design MMDGA, the most efficient design, is between a blocked design and a rapid event-related design. In the following we will discuss the results per design types and finalize this discussion with the properties of an optimal design for the nonlinear model.
Buračas and Boynton ( 2002) showed that m-sequences performed in general better for estimation efficiency than randomly generated sequences, and Kao et al. (2009) found that for estimation efficiency the design obtained by the GA was more efficient than m-sequences. The results of both papers are based on a linear model to estimate the HRF time points and are thus not directly comparable to our results from a model to estimate the amplitude of the HRF and the nonlinear parameters of the double gamma function. However, some similarities can be found between our results and their results. Under the assumption of empirically estimated correlated noise and for one stimulus type, Buračas and Boynton (2002) found randomly generated sequences which were more efficient than m-sequences. Similarly in our study, the best random sequence with a geometric distribution for ISI was more efficient than the best m-sequence when compared to the maximin design MMDGA (Fig. 2) but of course several realizations of the random sequences are necessary to find an efficient sequence. Furthermore, it is noticeable that in this article and in Kao et al. (2009) m-sequences performed well with relative efficiencies versus designs obtained from the GA from 0.8 to almost 1.
The major advantage of m-sequences is that the computation time for calculation of MMDm is much less than the computation time for calculation of the maximin design MMDGA based on the GA (Table III). This advantage in computation time of the MMDm comes along with a slightly lower efficiency of the MMDm in comparison to the MMDGA for one stimulus type. Generally, m-sequences are only available for certain sequence lengths N and number of stimulus types Q, i.e., N+1 and Q+1 have to be a prime or power of a prime. The problem of the sequence length can be handled by concatenating several m-sequences or truncating m-sequences so that the obtained sequence still maintains to a high degree desirable properties of m-sequences. These properties, which lead to a high efficiency of m-sequences especially for estimation of the HRF, are almost perfect counterbalancing, equal number of trials for different stimulus types and orthogonality of the m-sequence to cyclically shifted versions of itself (Buračas and Boynton, 2002). The estimation efficiency of m-sequences seems to be robust to truncation [Liu, 2004]. Liu (2004) also generated clustered m-sequences which are constructed from m-sequences by clustering events of the same stimulus type and provide a trade off between estimation efficiency and detection power. The possibility of constructing efficient sequences from m-sequences widens the applicability of m-sequences. To our knowledge not much research has been done to construct alternative efficient sequences from m-sequences when m-sequences are not available for a given number of stimulus types.
Our results for the geometric distribution showed that an event occurrence probability of about p = 0.5 was optimal. This probability is similar to previous results for estimation efficiency and detection power by Friston et al. ( 1999), Birn et al. (2002) and Zarahn and Friston (2002). For the uniform distribution, a smallest ISI of 2.5 s together with ISIs which were 5 s apart from each other, i.e., 2.5 s, 7.5 s, 12.5 s, 17.5 s, proved to be efficient, and the maximin design had ISIs 2.5 s, 7.5 s and 12.5 s for linearity as well as nonlinearity. The maximin designs MMDgeo and MMDuni are useful because they have a high relative efficiency, needed less computation time than the maximin design MMDGA in our situation (Table III) and they are above all available for any number of stimulus types in contrast to m-sequences. However, it is necessary to simulate several random sequences for the maximin design MMDgeo or MMDuni and choose the best one among these sequences in terms of its minimum relative efficiency as not any randomly generated sequence might be efficient. The least efficient designs were the maximin blocked design and the maximin constant ISI design. The maximin blocked design had a block length of 25 s for linearity and a block length of 22.5 s for nonlinearity. To avoid nonlinearity completely and if one wants to use a constant ISI design, the maximin constant ISI design with 17.5 s can be recommended.
Optimal designs for estimation and detection power were studied to show how much efficiency is lost by choosing the incorrect model and optimization criterion for the final data analysis. It was seen that optimal designs for one purpose might not be efficient for another purpose. For example, the optimal design for detection power Optdet had a medium relative efficiency compared to the maximin design MMDGA based on the nonlinear model. In addition, the maximin design MMDGA did not perform well for estimation efficiency or detection power. It is thus relevant to specify the model and the optimization criterion in consistency with the final analysis.
The properties of the optimal design for nonlinear estimation can be determined from the most efficient and most flexible design MMDGA. The maximin design MMDGA had a stimulus frequency close to 0.5 which was also the optimal stimulus frequency for the geometric distribution under linearity. It can thus be concluded that for one stimulus type and under linearity of the HRF the optimal stimulus frequency for the design for nonlinear estimation is 0.5 or a close value. This frequency 0.5 equals the D-optimal frequency for detection power and estimation efficiency pD = 1/(Q+1) for Q=1 and uncorrelated errors [Maus et al., 2010]. Under linearity a mean ISI of 5 s can be recommended while under nonlinearity the mean ISI should be slightly higher.
Furthermore, a mixture of a blocked and a rapid event-related design seems to be the optimal design for nonlinear estimation. The explanation for this might be that the nonlinear parameters of the double gamma function push the optimal design into another direction than the amplitude parameter β. The optimal estimation for the nonlinear double gamma parameters and the optimal estimation of the second till sixth entry in τ, which are products of the nonlinear parameters with the amplitude parameter β, may demand a rapid event-related design. In contrast, the first parameter of τ in Eq. (6), the amplitude parameter β, may be efficiently estimated by a blocked design.
One restriction of our study could be that a limited range for the HRF parameters was considered. The high minimum relative efficiencies above 0.8 of the locally optimal designs obtained by the GA could be due to the limited range for the HRF parameters. Additional numerical calculations were performed with a broader range of the HRF parameters a1 and b1, while the parameters for the undershoot were set to the canonical value of a2 = 15, b2 = 1 and c = 6. Moreover, results were obtained for a broader range of the parameters for the undershoot with the parameters of the peak a1 and b1 fixed to a standard value of a1 = 5 and b1 = 1. For these two parameter spaces, the minimum relative efficiencies of the locally optimal designs obtained by the GA were all above 0.78 which is similar to the results in the section on the genetic algorithm for the limited simultaneous parameter space of all HRF parameters.
Another restriction might be that we considered only one stimulus type, and that the results may not extend to multiple trial types. However, to estimate the subject-specific parameters of a nonlinear HRF model like the double gamma function, it would be useful to perform a run of a simple design with only one stimulus type. From this run, the active voxels or regions can be localized and the HRF parameters can be estimated such that they can be used for further data analyses from experiments with more stimulus types. Our code for the GA can also be used for multiple trial types assuming that the HRFs of these different trial types have the same double gamma function parameters and differ only in amplitude. In the following, we will discuss which results are expected to be valid for more than one stimulus type. Further work is nevertheless needed to draw firm conclusions on optimal designs with multiple trial types for nonlinear estimation of the HRF.
The best maximin design seems to be a mixture of a blocked and a rapid event-related design, and the optimal trade off between “blockiness” and “event-relatedness” can best be achieved by an open search in the design space as performed by the GA. As a consequence, we expect that the following order of efficiency from most efficient to least efficient will extend to multiple trial types: MMDGA, MMDm/MMDgeo/MMDuni/Optest, MMDB/Optdet, MMDCI. The computation time for the maximin designs is expected to be from highest to lowest: MMDGA, MMDgeo/MMDuni, MMDm/MMDB/MMDCI.
The optimal stimulus frequency in this article was close to 1/(Q+1) and may extend to higher number of stimulus types Q. The reason for this extension is that the optimality criterion for nonlinear estimation favors a mixture of a blocked design and a rapid event-related design and seems thus to behave like a multiobjective criterion combining detection power and estimation efficiency [Wager and Nichols, 2003; Kao et al., 2009]. The D-optimal stimulus frequency for detection power and for estimation efficiency is 1/(Q+1) and a combined criterion should have the same D-optimal frequency [Maus et al., 2010]. Furthermore, as the MMDGA is presumed to be between a blocked design and a rapid event-related design, the mean block length of the maximin design MMDGA is expected to be between the mean block length of the optimal design for estimation efficiency and detection power.
We presented a common method in optimal design theory to determine optimal designs for nonlinear models. A Taylor approximation was used to linearize the nonlinear model and the maximin design was chosen from the locally D-optimal designs. This method can be used to perform further research on optimal designs for estimation of the nonlinear parameters of the double gamma function or parameters of other nonlinear models in fMRI data analysis.