The neuro/PsyGRID calibration experiment
Identifying sources of variance and bias in multicenter MRI studies
Abstract
Calibration experiments precede multicenter trials to identify potential sources of variance and bias. In support of future imaging studies of mental health disorders and their treatment, the Neuro/PsyGRID consortium commissioned a calibration experiment to acquire functional and structural MRI from twelve healthy volunteers attending five centers on two occasions. Measures were derived of task activation from a working memory paradigm, fractal scaling (Hurst exponent) from resting fMRI, and grey matter distributions from T1-weighted sequences. At each intracerebral voxel a fixed-effects analysis of variance estimated components of variance corresponding to factors of center, subject, occasion, and within-occasion order, and interactions of center-by-occasion, subject-by-occasion, and center-by-subject, the latter (since there is no intervention) a surrogate of the expected variance of the treatment effect standard error across centers. A rank order test of between-center differences was indicative of crossover or noncrossover subject-by-center interactions. In general, factors of center, subject and error variance constituted >90% of the total variance, whereas occasion, order, and all interactions were generally <5%. Subject was the primary source of variance (70%–80%) for grey-matter, with error variance the dominant component for fMRI-derived measures. Spatially, variance was broadly homogenous with the exception of fractal scaling measures which delineated white matter, related to the flip angle of the EPI sequence. Maps of P values for the associated F-tests were also derived. Rank tests were highly significant indicating the order of measures across centers was preserved. In summary, center effects should be modeled at the voxel-level using existing and long-standing statistical recommendations. Hum Brain Mapp, 2012. © 2011 Wiley Periodicals, Inc.
INTRODUCTION
In what is widely recognized as the first reported randomized controlled trial (RCT), the streptomycin treatment of pulmonary tuberculosis [Wilson,1948] collected X-ray films from patients in seven hospitals around the United Kingdom. Since that time, multicenter study designs have become the predominant approach to clinical trials as they both improve statistical power through increases in sample sizes and permit a more general interpretation of results through sampling populations in several locations and with a broader demographic profile.
Magnetic resonance imaging (MRI) has made little impact on the diagnosis and monitoring of psychiatric disorders in individual patients, primarily due to small effect sizes [Matthews et al.,2006], although there is significant potential [Lennox,2009]. However, population studies have revealed widespread anatomic and functional changes in the brain. The now routine use of imaging for clinical diagnostic and treatment monitoring purposes in many other diseases has encouraged the use of these techniques as biomarkers for RCTs of therapeutic interventions [Bermel et al.,2008; Ciumas et al.,2008; Greenwood et al.,2009; Hillman and Gatsonis,2008; Leach et al.,2005]. However, including MRI endpoints in the design of multicenter RCTs is complicated by the often uncalibrated nature of the data acquired and the unique interaction between the magnetic fields produced by the scanner and the physical presence of the individual being scanned, leading to difficult to predict spatial sensitivity. Although more sophisticated methods involving multiple acquisitions [Deoni et al.,2008] can yield quantitative values, translating them to different scanners can prove problematic when installed on hardware from different manufacturers.
Recognizing these issues, a number of notable efforts have been made to estimate the consequences of multicenter data acquisition by characterizing the scanners that would be putatively involved in any subsequent RCT. In such calibration studies a cohort of healthy volunteers is scanned at each participating center with similar acquisition protocols and data processed in a common analysis pipeline. Although their primary purpose is to provide comparative information on scanner performance, they are also an opportunity to organize and improve the operational aspects of the multicenter approach; an important factor that should not be underestimated.
The Biomedical Informatics Research Network (BIRN; available at: http://www.birncommunity.org/) has been the most ambitious calibration study to date, with five healthy males scanned with 10 scanners at nine centers on two occasions. Functional (fMRI) [Friedman and Glover,2006a,b; Friedman et al.,2006] and structural MRI (sMRI) [Han et al.,2006] datasets were assessed for reliability in terms of derived parameters: blood oxygenation level dependant (BOLD) signal change and cortical thickness, respectively. Analysis of variance modeled within- and between-center factors, with within-center reliability being relatively much greater, and enumerated the between-center differences in a number of key metrics. Other calibration studies have been reported [Costafreda et al.,2007; Deoni et al.,2008; Gountouna et al.,2009; Moorhead et al.,2009; Suckling et al.,2008], with similar outcomes from comparable analyses.
-
For a particular study design, what combination of parameters—sample size, number of centers, and recruitment profile across centers—is needed to detect a hypothesized effect size?
-
Which statistical model accounts for a multicenter design?
-
Are there specific consequences of introducing multiple centers?
The first goal has been previously considered [Suckling et al.,2010] with image-based power calculations drawing upon within-center variance estimates of grey matter from tissue segmentation of T1-weighted, high-resolution structural MRI, where it was concluded that multicenter recruitment strategies have no detrimental effects on sample sizes. The same approach could also be applied to metrics from any imaging modality.
This article is concerned with the second and third goals. As a point of reference we begin with the guidelines of the Steering Committee of the International Conference on Health Research [ICH,1999; Lewis,1999]. Their recommendations for the analysis of multicenter data suggest that in the initial modeling, the treatment effect should accommodate center differences, but not treatment-by-center interactions. If treatment effects are discovered, however, an exploration of these effects across centers is prescribed. Thus, if a study is planned to detect a hypothesized effect then any preceding calibration study should attempt to investigate the possibility of a treatment-by-center interaction and understanding the nature of the interaction is of vital importance.
Two types of interaction are possible [Peto,1982]. The first is a change in the magnitude of the treatment effect across factor levels, but not a change in the direction of the effect. This is known as a quantitative (noncrossover) interaction, commonly observed in trials and represents the natural variability of the treatment effect and/or the measuring device. The other type, and most undesirable, is a qualitative (crossover) interaction that occurs when the direction of the treatment effect changes from one factor level to another. To put this into the context of a multicenter RCT, if such interactions were to be detected on MRI derived measures that could not be explained by trial management or the characteristics of the participants, it would undermine the use of MRI in these designs.
Although calibration experiments are clearly incapable of directly detecting treatment-by-center interactions since data are only acquired from a cohort of normal participants, it is possible to assess the prospect of qualitative and quantitative interactions arising from the scanning device. Effect size is defined by the difference in the means between treatments divided by the standard error of the difference. Using the general linear model, a subject-by-center interaction term will provide an indication of how the standard error of this difference varies from center-to-center and a rank order test is a proxy for between-center differences that may result in a qualitative interaction arising from the scanners at each center.
In this article, the functional and structural MRI data acquisition from the Neuro/PsyGRID calibration study is described. A fixed-effects linear model was regressed at each intra-cerebral voxel to estimate the partitioning of variance between the factors that were considered, a priori, to be potentially important, namely: center, subject, occasion, within-occasion order as well as interactions of center-by-occasion, subject-by-occasion and center-by-subject. Rank order tests of imaging variables acquired on each occasion are also presented. In doing so, we comprehensively describe the variance structure that might be expected in multicenter imaging studies as well as suggest an analysis to guard against failure to explain results in subsequent RCTs due to qualitative interactions.
MATERIALS AND METHODS
Participants and Data Acquisition
Twelve male, right-handed healthy participants (mean age = 25 ± 6 years; range: 19–34 years) gave informed consent to take part. All participants were screened for medications, recreational drug use, history of head injury or loss of consciousness and contraindication to MRI, which were ineligibility criteria.
Participants were scanned twice (although only 11 of the 12 participants were scanned on the second occasion) with a mean time between occasions of 7.8 ± 1.9 months (range: 6.3–13.1 months). Five centers participated as part of the PsyGRID consortium (available at: http://www.psygrid. org/) and the NeuroPsyGrid collaborative project (available at: http://www.neuropsygrid.org/): The Wolfson Brain Imaging Centre (University of Cambridge), Magnetic Resonance Imaging Facility (University of Manchester), the Institute of Psychiatry (Kings College, London), the Departments of Clinical Neurosciences at the Universities of Edinburgh and Glasgow, and the Centre for Clinical Magnetic Resonance Research, (University of Oxford). The study was approved by the University of Manchester Ethics Committee and ratified by the appropriate committees at each of the participating centers.
Centers operated contemporary 3T systems from three of the major manufacturers (Table I). In general, the variety of technology constrained the consistency of sequence parameter values, but was typical of those generally encountered.
| Center | MRI scanner | Head-coil | Reduction factor | Nyquist ghost correction | B0 field corrections | K-space apodization | Additional filtering | Software version |
|---|---|---|---|---|---|---|---|---|
| V | Siemens 3T TimTrio | 8-Channel | No | Yes | Yes | Raw filter | No | VB15A |
| W | GE 3T HD | 8-Channel | No | Yes | Yes | Gibbs filter | Fermi filter on k-space | V12M5 |
| X | GE 3T HDx | 8-Channel | ASSET factor 2 | Yes | No | Fermi filter | Fermi filter on k-space | V14.0M5 |
| Y | Philips 3T Intera-Achieva | 8-Channel | SENSE factor 2 | Yes | Yes | Yes | No | V2.6.3.3 |
| Z | Siemens 3T TimTrio | 12-Channel | No | No | Yes | Raw filter | No | VB15 |
Participants were scanned with a schedule that was not perfectly counterbalanced across centers, but disrupted by the availability of the scanners and participants. Although there was no prior expectation of order effects for some image variables, these were subsequently universally modelled.
Structural MRI Acquisition and Preprocessing
At every center, on both occasions, a T1-weighted, high-resolution three-dimensional image was acquired with the sequence acquisition parameters given in Table II.
| Center | Voxel size: x, y, z (mm) | Matrix size: x, y, z | TR (ms) | TE (ms) | TI (ms) | Flip angle (°) |
|---|---|---|---|---|---|---|
| V | 1 × 1 × 1 | 256 × 256 × 160 | 9.0 | 2.98 | 900 | 9 |
| W | 1.1 × 1.1 × 1 | 260 × 260 × 160 | 6.5 | 1.50 | 500 | 12 |
| X | 1.1 × 1.1 × 1 | 260 × 260 × 160 | 7.0 | 2.85 | 650 | 8 |
| Y | 1 × 1 × 1 | 256 × 256 × 160 | 8.2 | 3.80 | 885 | 8 |
| Z | 1 × 1 × 1 | 256 × 256 × 160 | 9.4 | 4.66 | 900 | 8 |
Grey matter partial volume maps were constructed for each image using the current version of FSLVBM (available at: http://www.fmrib.ox.ac.uk/fsl/fslvbm/index. html) and an additional step for correction of field nonuniformities [Sled et al.,1998]. First, structural images were brain-extracted using the brain extraction tool (BET) [Smith,2002] with the additional option of removing slices that included excessive data below the cerebellum. Next the N3 [Sled et al.,1998] algorithm was applied before tissue-type segmentation was carried out using FAST4 [Zhang et al.,2001]. The resulting grey-matter partial volume maps were then aligned to the Montreal Neurological Institute (MNI) stereotactic coordinate system with the affine registration tool FLIRT [Jenkinson et al.,2002] followed by a nonlinear registration using FNIRT which uses a b-spline representation of the registration warp field [Rueckert et al.,1999]. The resulting images were averaged to create a study-specific template (using all the images acquired), to which the native grey matter maps were then nonlinearly reregistered. The registered partial volume images were then modulated (to correct for local expansion or contraction) by dividing by the Jacobian of the warp field.
Task-Activated (Working Memory) fMRI Acquisition and Preprocessing
At four of the five centers, BOLD-sensitive T2*-weighted images were continuously acquired whilst participants engaged in a working memory paradigm. Compatible facilities to run the specific fMRI task paradigms were not available at one of the centers at the time scanning commenced, and thus all subsequent discussion of the working memory paradigm refers to data acquired from only four centers, omitting center Z (Table I).
In total, 230 three-dimensional volumes were acquired during the paradigm, with the first six images discarded. The time between volumes (i.e. the repetition time, TR) was 2 s. Center-specific acquisition parameters are given in Table III. Scans were not performed with identical sequence parameters at each site because of differences between the manufacturers and acquisition software. Even in the case of scanners of the same model the standard protocols for each center differed because of local operator preferences.
| Center | Voxel size: x, y, z (mm) | Matrix size: x, y, z | TR (ms) | TE (ms) | Flip angle (°) |
|---|---|---|---|---|---|
| V | 3.437 × 3.437 × 4.5 | 64 × 64 × 25 | 2,000 | 30 | 78 |
| W | 3.125 × 3.125 × 4.5 | 64 × 64 × 23 | 2,000 | 30 | 70 |
| X | 3.437 × 3.437 × 4.5 | 64 × 64 × 25 | 2,000 | 30 | 75 |
| Y | 3.437 × 3.437 × 4.5 | 64 × 64 × 23 | 2,000 | 40 | 79 |
| Z | 3 × 3 × 4.5 | 64 × 64 × 28 | 2,000 | 30 | 90 |
A detailed description of the working memory task has previously been published [Callicott et al.,2003]. In brief, each visual stimulus was both probe and target and consisted of a sequence of single numbers between 1 and 4 appearing every 1,800 ms for 500 ms at set locations at the points of a diamond-shaped box. Instructions displayed above the diamond informed participants to recall the stimulus seen N presentations previously. This was done by pressing the button corresponding to the location of the appropriate number using a four-button box, the configuration of which varied across centers. The task was presented in a blocked-periodic design with 16 × 30 s blocks of alternating zero-back trials (that is, locate the current probe on the screen; eight blocks) and either one-back (four blocks) or two-back (four blocks) trials.
Data were processed using the Cambridge Brain Analysis (CamBA) analysis suite (available at: http://www-bmu.psychiatry.cam.ac.uk/software) version 2.3.
Full details of the processing pipeline are given in the Supporting Information. In brief, following spatial and temporal correction for participant motion and removal of the global signal, a regression of the general linear model [Suckling et al.,2006] estimated the contrast of one-back and two-back working memory active task blocks versus zero-back blocks. Maps of the estimated responses, β (linear model coefficients), and standardized responses, β/SE(β), (i.e. model coefficients divided by their standard errors; a t-statistic) were registered into MNI stereotactic space by an affine transformation maximizing the intra-cerebral correlation between the image and the “EPI” template (available at: http://www.fil.ion.ucl.ac.uk/spm) [Suckling et al.,2006].
To assess the within-group task-related activation, median responses were statistically tested against the two-tailed null-hypothesis of no stimulus related activation based on permutation of the original time-series [Brammer et al.,1997; Bullmore et al.,2001]. Probabilistic thresholds at the cluster level were set such that the expected number of Type I clusters was less than one under the null hypothesis [Bullmore et al.,1999].
Reaction time (RT) of responses was recorded for each participant. The working memory paradigm response data from site Y (Table I) for all participants on the first occasion was unavailable due to button-box malfunction. Also, data from site V (Table I) for five participants on the second occasion were also corrupted due to a software reset of the stimulus delivery device. Accuracy (percent correct) was also recorded, although ceiling effects led to considerable deviation from normal distributions that underpin parametric significance testing. Thus, accuracy was not statistically modeled.
Resting fMRI Acquisition and Preprocessing
At all five centers participants were asked to lie quietly with their eyes closed and avoid falling asleep. Five hundred and eighteen BOLD sensitive, T2*-weighted volumes were acquired with the same protocol as that used for the task-activation paradigm. The first six volumes were discarded leaving 512 volumes for subsequent processing.
Data were processed using the Cambridge Brain Analysis (CamBA) analysis suite (available at: http://www-bmu.psychiatry.cam.ac.uk/software) version 2.3.
Resting fMRI data were characterized by the Hurst Exponent (H), a fractal measure related to the autocorrelational properties of the signal. Functional MRI time-series typically demonstrate a positive autocorrelation function over a large number of lags and a corresponding spectral density function with a 1/f form: S(f) ∼ fg, where f is the frequency. The slope of a straight line fitted to the log-log plot is defined as the spectral exponent, i.e., log S(f) ∼ g log f. The spectral exponent g is related to the Hurst exponent, H = 2g + 1, of the process (see [Bullmore et al.,2004] for a review).
Following temporal and spatial motion correction, maps of H in acquisition space for each participant were estimated by maximum likelihood in the wavelet domain [Maxim et al.,2005] and registered into MNI standard space with an affine spatial transformation.
Components of Variance Using Fixed-Effects ANOVA
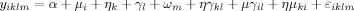 (1)
(1)The sum-of-squares for each of the components of the model was calculated and expressed as a proportion of the total sum-of-squares to assess its relative contribution to the overall observed variance. Maps of variance partitions for main effects and interactions are displayed graphically. Note that the center-by-subject interaction is a surrogate of the expected variance of the treatment effect standard error across centers induced by the differences in the scanning equipment and environment.
Total variance and variance component maps were calculated for: grey matter partial volume, estimated from T1-weighted structural images; task-related responses to the working memory paradigm, β; normalized task-related responses to the working memory paradigm, β/SE(β), and the Hurst exponent, H, estimated from fMRI datasets acquired during rest. In addition, for each imaging variable P values for the associated F-test of the main effect of center and the subject-by-center interaction were calculated.
Mean reaction time across all levels of the working memory paradigm were also modeled with the fixed effects analysis of variance of Eq. (1) and associated F-tests declared significant at P < 0.05.
Rank Order Tests
Between-center differences in the rank order of measurements of a participant across centers are indicative of quantitative or qualitative subject-by-center interactions. If significant rank order changes are observed from one center to another, then the null-hypothesis that the samples from each center come from the same population cannot be rejected and a qualitative interaction is possible.
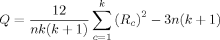
Friedman's Q was calculated at each intra-cerebral voxel of standard MNI stereotactic space for each of the image variables acquired on the first occasion (n = 12) for: grey matter partial volume (k = 5); task-related responses to the working memory paradigm (k = 4); normalized task-related responses to a working memory paradigm (k = 4); and the Hurst exponent (k = 5).
RESULTS
Components of Variance Using Fixed-Effects ANOVA
Maps of the variance components [Eq. (1)] in a single slice at Z = +16 mm of the MNI standard space (Fig. 1) is shown in Figure 2. A more extensive set of slices is displayed in the Supporting Information.
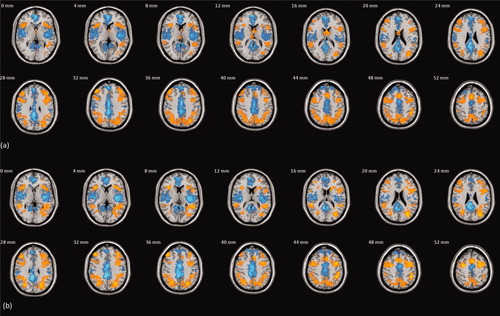
Task induced within-group activation patterns from the 1-back and 2-back versus 0-back contrast of the working memory paradigm. Statistical thresholds with cluster-level inference were set such that the average number of Type I errors <1 (equivalent P = 0.00177). Patterns with (a) β and (b) β/SE(β)as the derived image variable. Slice locations are given in MNI stereotactic space. The left-hand side of the image is the right-hand side of the brain.
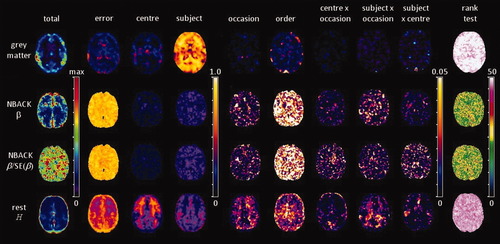
Total variance and components of variance for each of the derived image variables. The illustrated slice is at Z = +16 mm anatomical slice of MNI stereotactic space. The color scales refer to images to their left.
The spatial distribution of the total variance is strongly influenced by the dependent variable. In summary: grey matter segmentations of T1-weighted MR images have local peaks in variance in bilateral temporal regions; similar spatial inhomogeneity is observed with estimates of β from the working memory task, in regions coincident with task-activation (Fig. 1), particularly the caudate, anterior and posterior cingulate; a homogenous pattern that no longer reflects the pattern of task-activation is evident after normalization of estimates of β by the within-subject standard error; and estimates of H from BOLD time-series during rest show homogenous total variance across the entire brain parenchyma.
Decomposing the total variance into its components, there are marked similarities and differences between the imaging variables. In all cases, the main effects of center and subject along with the error variance made up the majority (>90%) of the total variance, whilst the main effects of occasion and order as well as all the interactions had components of variance that were generally <5%, and in many cases much smaller. Grey matter segmentations derived from sMRI had variance distributed primarily in the main effect of subject (70%–80%), whilst measurements derived from both task-activated and resting fMRI experiments had a large proportion of variance represented by the error (residual) variance component.
Variance components were generally spatially homogeneous. A notable exception is the main effect of center for estimates of H, where there was high variance in white matter regions strongly delineating the internal capsule with foci in the anterior forceps and tapetum of the corpus callosum. In the component represented by the main effect of subject, around 40% to 50% of the variance was located close to the mastoid processes, an area known to be prone to magnetic susceptibility artefacts in rapid acquisition echo-planar imaging sequences.
To explore this effect more thoroughly, mean H was extracted from each individual at each center on each occasion in regions where the proportion of variance of the main effect of center was >0.68 (high H; 1048 voxels) and <0.025 (low H; 1069 voxels). For both of these three-dimensional regions, two linear regression models were separately regressed that predicted mean H from the flip angle of the EPI sequence; the only sequence parameter that varied between all centers (Table III). Each model also had factors for subject, occasion and within-occasion order.
The model for the region of low H was nonsignificant (F(4,110) = 2.3, P = 0.062), as was the coefficient associated with the effect of flip angle (t(112) = 0.736, P = 0.463). For the high H region however, the model was highly significant (F(4,110) = 35.3, P < 10−18) as was the flip angle (t(112) = 11.4, P < 10−19) where there was a negative relationship; i.e. large flip angles lead to a reduction in H (Fig. 4).
The subject-by-center variance component was small (<4%) for all dependent variables with distributions apparently unrelated to the underlying anatomy or image features, although the estimate of H did show a similar pattern to that observed in the orthogonal component of the main effect of subject.
Although variance components may be small in magnitude this should not be taken to mean that there are no significant differences in the means of the levels of the factors. In the context of a study to understand the effect of introducing multiple centers, an F-test for the main effect of center and the subject-by-center interaction was calculated and plotted on a log10 scale (Fig. 3). A strong main effect of center was observed in grey matter segmentations, although the smallest P values were in white matter regions where of course, the segmented grey matter values are small. Strong effects of center (P < 10−4) were also apparent in the estimates of H from resting fMRI across much of the parenchyma. In contrast, estimates of task activation (i.e. β and β/SE(β)) did not demonstrate a main effect of center. The subject-by-center interaction is generally characterized by P values around 10−1 to 10−3 for all imaging variables.
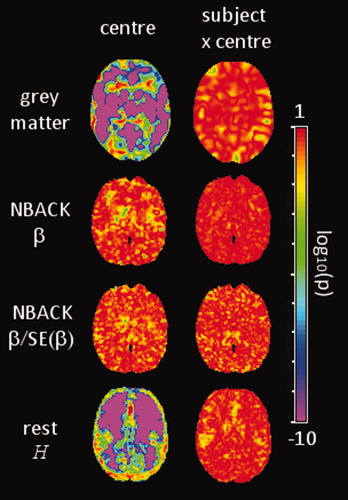
Maps of log10 of the P values of the F-tests associated with the center effect (left column) and subject-by-center interaction (right column) for each of the derived image variables. The illustrated slice is at Z = +16 mm anatomical slice of MNI stereotactic space (see Fig. 1).
Fixed-Effects Analysis of Working Memory Behavioral Data
For mean RT there were significant effects of center (F = (3,159) = 5.85; P = 0.001), subject F(11,159) = 6.99; P = 1.39 × 10−10, and subject-by-occasion F(10,159) = 2.27; P = 0.004. This is consistent with the variability in button-box design at each center, differential performance between subjects and different rates of improvement (or deterioration) in performance between the two occasions. Similar effects were seen in a previous two-center calibration study [Suckling et al.,2008].
Between-Center Rank Sum Statistics
Rank tests (Fig. 2) also did not show any remarkable spatial patterns, although the mean intra-cerebral value of Q did vary across imaging variables. Recalling that high values of Q relate to consistent rank ordering at each center, the highest values were seen with grey matter segmentations; Q = 49.95 ± 2.12. Estimates of H generated Q = 47.65 ± 1.11 and β and β/SE(β) estimates where both similar with Q = 23.84 ± 6.46 and Q = 24.13 ± 6.40 respectively. For comparison, at a Type I error rate of 0.001 χ2 (df = 4, appropriate for the five centers contributing to the structural and resting acquisitions) = 18.47 and χ2 (df = 3, appropriate for the four centers contributing to the task-activation paradigm) = 16.27.
Rank tests were also computed for the data acquired on the second occasion (11 participants) without any substantive changes in the results.
DISCUSSION
Clinical trials with imaging derived biomarkers remain sufficiently novel to consider specific calibration experiments before embarking on these labor intensive studies. However, calibration experiments consume considerable resources and their value is compromised if they are not conducted in a timely manner prior to opening the subsequent trial to recruitment; it is thus tempting to omit them altogether. Of course these experiments may be undertaken as part of the convocation of a consortium of centers for subsequent, yet unplanned, multicenter RCTs, but extended periods between the calibration experiment and any later study may erode the authority of their findings. In short, the value of calibration experiments in this context has yet to be clearly articulated.
From a statistical point-of-view, data from a calibration experiment can support decisions on how models are constructed that account for the increased variance introduced by a between-center factor and, importantly, whether there are particular biases across centers that may lead to a qualitative interaction of treatment-by-center; that is, reversals of the direction of the treatment effect from center-to-center.
Our initial premise was that statistics derived from imaging data would not be dissimilar in their between-center characteristics from other variables commonly used in RCTs: behavioral reaction times, clinical outcomes, blood test results and so on. However, in comparison to these measures a unique feature of MRI is the uncalibrated nature of the voxel values unlike, say, positron emission tomography or X-ray computed tomography which have units related, directly or indirectly, to physical quantities. Thus, without recourse to a graduated scale it remains possible that MRI scanners manufactured with varying operating principles and technology might well produce data with little correspondence between them. Furthermore, the spatial inhomogeneity of the signal across the sensitive volume of the receiving coil, dependent upon its design, could lead to localized between-center biases and qualitative interactions and a more difficult situation to effectively model.
This article describes a calibration experiment involving five centers subtending major conurbations of England and Scotland. The approach to analysis was based on well-known statistical models: fixed effects analysis of variance and rank sum statistics, but eschewed significance tests that seek to demonstrate consistency by acceptance of the null-hypothesis of no between-center differences. Clearly the interpretation of such approaches is bounded by the statistical power of the test, which is determined by the cohort size. Instead, we have reported the partitioning of the total variance across the factors of center, subject, occasion, within-occasion order, and the interactions of center-by-occasion, subject-by-occasion and center-by-subject (Fig. 2). Broadly speaking, fMRI derived variables concentrate variance in the error component, whilst grey matter segmentation of sMRI has the majority of variance in the subject component. Main effects of occasion and order were relatively small. Center-by-occasion modeled changes in center performance between the two scanning occasions due to local practices or hardware and software upgrades to the scanner. Subject-by-occasion models natural changes in functional response or brain structure that may confound the treatment effects observed longitudinally in an RCT. In both cases, these interactions contributed just a few percent of the total variance. In particular, we focused on the main effect of center and the subject-by-center interaction, for which the raw P values of the associated F-tests have also been presented (Fig. 3), as the factors that inform the key issues affecting the ability of any subsequent study to detect a treatment effect.
Which Statistical Model Accounts for a Multicenter Design?
The factor modeling center broadly accounts for up to 15% of the total variance for all the imaging variables tested in this treatment. In particular, for the response estimates to task activation this proportion was spatially homogeneous and uniformly small (<5%) (Fig. 2) as well as associated with large P values (Fig. 3). Behavioral measures exhibited a strong between-center difference that can be attributed to differences in stimulus delivery equipment, although significant between-center effects have been observed with identical facilities [Suckling et al.,2008]. Furthermore, there is no apparent relationship between the fMRI activation patterns (Fig. 1) and center variance, or indeed any other component. These findings are consistent with a previous region-of-interest analysis of similar imaging data from task-activated fMRI [Suckling et al.,2008].
Data driven methods of analysis, i.e. tissue segmentation of sMRI and fractal scaling of endogenous oscillations from resting fMRI, have low proportional center variance across the brain parenchyma, but do have some localized regions of higher center variance that coincide with brain structures (Fig. 2). The thalamus and areas of bilateral insula were associated with variance proportions of 80% for grey matter partial volume segmentations from structural data. In fact, there are more anatomically widespread differences in center, with very small P values associated with these regions along with the posterior cingulate and mid-line structures of the occipital lobe (Fig. 3). Estimates of partial volume were derived by the FAST algorithm with a hidden Markov random field method that incorporates spatial information [Zhang et al.,2001] to model the prior probabilities relating image intensities to tissue classification. In this scheme, increased contrast between grey and white leads to improved separation of the prior probability distributions (for fixed distribution variance) and thus differing estimates of tissue partial volumes. Between-center differences in grey:white tissue contrast thus leads to differences in estimated partial volume, related to the acquisition sequence parameters.
Estimates of H from resting state fMRI had high variance widely distributed, but orientated towards frontal regions, a pattern reminiscent of the variance of low frequency power derived from a large database of resting state fMRI [Biswal et al.,2010]. Notably, there was a marked correspondence between increased center variance and differences between centers in white matter (Figs. 2 and 3). Subsequent post-hoc analysis demonstrated a highly significant negative linear relationship between mean H extracted from regions of high variance (white matter) and the flip angle of the EPI sequence (Fig. 4). The flip angle of the EPI sequence is generally set to the Ernst angle [Ernst,1966], with a value determined by the assumed spin-lattice (T1) relaxation time and TR. At static field strengths of 3T, the temporal signal-to-noise ratio has been shown to be both theoretically and empirically insensitive to changes in flip angle over the small range used at the centers involved in this study (Table III) [Triantafyllou et al.,2005]. Furthermore, the contribution of intravascular flow is small relative to the BOLD effect for EPI [Gao et al.,1996]. There is little or no literature on the sensitivity of the spectral or autocorrelation properties of time-series under the influence of the flip angle. Confounding factors of flip angle and scanner manufacturer make it difficult to deduce the origins of the effects from this dataset. Instead, systematic study of resting state dynamics as a function of scan parameters is indicated.
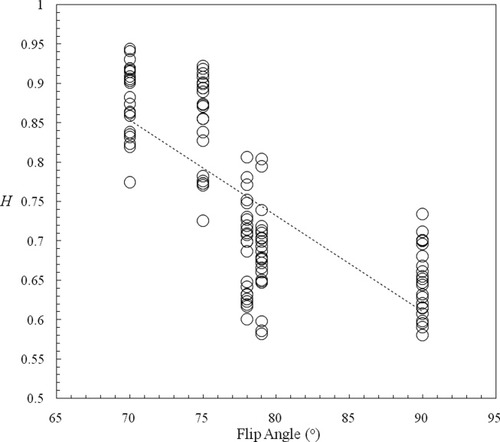
Plot of mean H extracted from a regions-of-interest representing white matter as a function of flip angle of the EPI sequence for fMRI acquisitions. The dotted line is the regressed linear model.
An immediate consequence from this observation is that multicenter studies of resting state dynamics or so-called default mode networks should take into account their apparent sensitivity to the EPI sequence flip angle in white matter. More generally, these results illustrate that center effects may be spatially inhomogenous and delineate anatomical boundaries and where this is the case, between-center differences in means is highly significant (Fig. 3). It is therefore crucial that center effects are modeled on a voxelwise basis, prior to a regional or network-level analysis.
It is usually obvious that the cluster of participants that constitute a “center” in a multicenter imaging trial refers to the location at which they were scanned. However, in RCTs center is more naturally represented by the location where a participant receives treatment, and balancing sample sizes across treatment arms is done by randomizing participants within center. This hierarchical organization of the center factor may be modeled explicitly, but generally compounds uneven within-center variance across centers. Indeed, if a scanning center only contributes a small number of participants to overall recruitment, then in the absence of sufficient data to properly estimate the effect of that center, it may be necessary to pool these data with those from other scanning centers based on proximity, similarity of the samples, scanner manufacturer, acquisition sequences, and so on. If, as is commonplace in imaging studies, the general linear model (GLM) is the statistical tool deployed, unequal sample sizes lead to differences in statistical analysis depending upon the method of calculation [Localio et al.,2001; Senn,1998], although there is currently no consensus on the most appropriate approach [Worthington,2004].
In the fMRI literature the use of terms “fixed” and “random” effects have taken the meaning of “subject-level” and “group-level” effects, respectively. In the more general statistical sense, a fixed effect refers to a variable with specific levels, in this case including the subject effect, as we are interested in within-subject (repeated measures at multiple centers) effects. A random effect has levels drawn from a population and is therefore concerned with making inferences about the effects, rather than the levels, on participants in general. Choice of one model over another is a source of controversy in the literature with suggestions that a random effects approach is parsimonious [Fedorov and Jones,2005], a fixed effects model is the majority recommendation [Worthington,2004], and that fixed and random effects models give similar results, with a random effects model preferable when the number of centers is large (≫20) [Vierron and Giraudeau,2007]. Fixed effect models were used in this study primarily to obtain variance components that were consistent (i.e. sum to exactly 1) and robust with a small (relative to conventional RCTs) number of centers. But the choice was also influenced by knowledge that random sampling of centers does not normally take place. Furthermore, random effects models are often promoted as generalizing to the population, rather than being restricted to the sample. However, it should be recognized that this interpretation cannot be extended beyond the boundaries of the sample and, in the case of center being modeled as a random effect, could not be generalised to samples including different scanner manufacturers or imaging sequences.
Are There Specific Consequences of Introducing Multiple Centers?
The answer to this question is embodied in the treatment-by-center interaction, which describes the modification of the treatment effect by center. It is worth mentioning here that this interaction is still present in single center trials when treatment of same individual at the same center on two occasions leads to different effects, and in fact degrades statistical power to a greater degree [Senn,1998].
In the context of the GLM a selection can be made from a number of approaches to assess this interaction: (a) analyze the full model including a center factor and the treatment-by-center interaction; (b) refit the model without an interaction term should its level of significance in the full model fall below some criteria; (c) begin with a model without an interaction and add it if the center factor is significant, the ICH recommendation [ICH,1999]. Treatment-by-center interactions may occur due to natural variation in both the measuring device and the sample demographics from center-to-center, or when the association between treatment and outcome varies with the level of another factor that is biased across centers.
Typically the size of the treatment effect varies, but retains the same direction across centers in a quantitative interaction, leading to inflation of variance associated with the treatment effect. A much more serious situation is when the direction reverses between centers in a qualitative interaction. This clearly affects the generalizabiliy of the conclusions if the treatment is only shown to be effective in certain centers and ICH guidelines are vociferous in the caution required when interpreting such results and in recommending additional effort to find an explanation in the conduct of the trial or in differences in the samples at each center [Lewis,1999].
As there is no treatment administered in a calibration study, a direct measure of the treatment-by-center interaction is, of course, not possible. In this experiment the subject-by-center interaction was used as a surrogate to identify any likely problems with inflated variance. In fact, this component made only a relatively minor contribution of 1% to 4% depending on the imaging variable, is broadly spatially homogenous (Fig. 2) and is not associated with particularly small P values (Fig. 3). Estimates of fractal scaling exponent, H, from resting state fMRI do show a slight increase in variance (to around 4%) coinciding with the mastoid processes. This area is well known to be liable to modulation of the BOLD signal due to the adjacency of tissues with widely differing magnetic susceptibility properties. It seems reasonable to deduce that the elevated between-subject and subject-by-center variances in this area are thus due to the differential sensitivity and/or local distortion of the scanners as a result of different hardware and sequence parameters.
Qualitative interactions are not easily visualized from the corresponding variance components without graphical presentation of the underlying data, an unrealistic prospect to achieve at the many thousands of intracerebral voxels. The rank test of imaging variables at each center (Fig. 2) allows assessment of the possibility of the reversal of the treatment direction as a result of the differential performance of the scanners. That is, if all scanners perform under the same principles, the magnitude of the measurements may differ, but the ordering across subjects should remain. Our results indicate that ordering is indeed highly preserved across centers, in particular in those imaging variables derived from data driven methods, i.e. H and grey matter partial volume estimates, relative to those from GLM models of task-related activation. Of course, investing confidence from this result to subsequent RCTs neglects the possibility of qualitative interactions due to, for example, environmental factors or local deviations from treatment protocols. This is a shortcoming of calibration studies.
Relationship to Other Calibration Experiments
Datasets from calibration experiments can also be usefully employed in a range of other analyses to support future studies. An accurate estimate of the sample sizes required to observe the hypothesised effects is essential to confidently deploy the considerable resources necessary to complete a multicenter RCT involving imaging. Moreover, underpowered studies are difficult to justify ethically. Maps of within-center variance derived from calibration experiments of the type described here are suitable for power calculations that predict key parameters of trial design [Suckling et al.,2008,2010]. Furthermore, choice of acquisition protocol or data processing pipeline can be made based on outcomes of the power calculations. By making these calculations on a voxelwise basis, the predictions are also adaptable to specific neurobiological hypotheses that may include regions with a range of within-center variances that in turn impact on organisational decisions [Suckling et al.,2010].
Detailed investigations of between-center effects have been made by the BIRN consortium, focussing on differences engendered by the static magnetic field strength of scanners, their manufacturers and differences in acquisition protocols [Friedman and Glover,2006a; Friedman et al.,2006; Han et al.,2006]. With pooling of images as the goal, between-center interclass correlation coefficients (ICC) from regions-of-interest associated with task-induced BOLD activation were improved by dilating the regions, removing centers contributing outlying data, and using contrast-to-noise measures rather than signal change alone [Friedman et al.,2008]. The replacement of β with β/SE(β) in the analysis of fMRI data here resulted in little difference in the distribution of variance across the components or in magnitude of the rank tests (Fig. 2). However, a striking change in the pattern of total variance was observed, with the normalized statistic (analogous to contrast-to-noise ratio) being more spatially homogenous and thus less sensitive to acquisition protocols and variance introduced by data processing, resulting in a possible manifestation of the same effect as that seen by Friedman et al. [Friedman et al.,2008]. Their study also assessed empirical calculations of image smoothness to adjust the statistical model. This may be a useful metric, in lieu of a center factor, made directly from images acquired during the subsequent trial without the need for a calibration study. Extending these encouraging findings to imaging methods other than task-induced activation warrants exploration.
Justification for pooling of imaging data has also been sought for reproducibility of task-induced fMRI activation patterns, dependent on the applied statistical threshold and the details of the task stimuli [Gountouna et al.,2009; Vlieger et al.2003] and comparison within activated regions of within- and between-center variance components [Costafreda et al.2007; Gountouna et al.,2009). Similar regional analyses have also been conducted on tissue segmentations of sMRI [Moorhead et al.,2009; van Haren et al.,2003]. The broad consensus can be summarized as a cautious willingness to combine datasets, whilst stressing the need for experimentation in individual cases.
Relationship to MRI Image Analysis
Based on data acquired from a calibration experiment, the treatment described in this article aims to assess the models considered for the statistical analysis of a RCT that might be pursued within the same centers. This has been achieved through a voxelwise variance component analysis of imaging variables derived from data-driven processing of sMRI and resting fMRI as well as model parameters estimated from regression of the GLM in task-induced activation (Fig. 2).
Clear differences between the distribution of variance amongst imaging variables is seen comparing fMRI, where error variance is the dominant component, to sMRI, where the between-subject factor represents by far the largest proportion. This would suggest that the factors and interactions used in the models do not adequately model the variance in the BOLD signal, particularly in GLM modeling of task activation and to a lesser extent, estimates of BOLD dynamics (H). In turn, the implication is that BOLD is a stable process in humans, but is incompletely modelled by those variables commonly reported. In contrast, error variance is very small in segmented sMRI indicating that this is an adequate representation of the distribution of grey matter, and that variance is concentrated in the between-subject component.
The spatial inhomogeneity of the total variance (Fig. 2) is locally elevated in grey matter segmentations, presumably related to natural variation arising from various sources including gender and age [Pell et al.,2008], and in areas associated with maxima of the modeled effect-size (β) associated in working memory, a pattern seen in other paradigms [Nichols and Holmes,2002]. Normalization of β by the within-subject error is known to enhance statistical power [Nichols and Holmes,2002], which is here reflected in activation that more closely resembles the pattern resulting from a meta-analysis [Owen et al.,2005] (Fig. 1). It also generates a more homogeneous variance profile across the brain, although the division amongst the components is very similar to that observed with β. This is consistent with a more complete modeling of the sources of variance in task-activation fMRI reducing structured noise [Lund et al.,2006]. Estimates of BOLD signal dynamics (H) also show remarkable homogeneity in total variance. Prior data demonstrated that H delineates grey and white matter [Maxim et al.,2005; Wink et al.,2008] and the inability to distinguish this border in the total variance map can be ascribed to the introduction of a between-center (change in flip angle) factor as described above.
CONCLUSION
Contemporary MRI scanners installed in centers familiar with the particular acquisition protocols are now of sufficient and consistent quality that between-center and subject-by-center variances are small irrespective of the type of imaging variable. Conversely, spatial inhomogeneity associated with the underlying neurobiology is apparent and between-center differences in means can be significant. Consequently, center effects should always be modeled at the voxel-level before analyses on a more macroscopic scale using existing and long-standing recommendations for multicenter clinical trials [ICH,1999]. In other words, variables derived from MRI are not a special case other than the definition of center arises from the measuring device rather than the populations from which the participants are recruited.
Calibration experiments are a useful, but not an essential precursor to multicenter RCTs involving MRI. Their value lies primarily in the opportunity to gain operational experience, build logistical frameworks and convergent acquisition and processing protocols. For this they are indispensible.
Acknowledgements
The authors thank the participants, radiographic and administrative staff in each of the centers for their concerted and sustained support throughout this project.




