A Whole-Genome Simulator Capable of Modeling High-Order Epistasis for Complex Disease
ABSTRACT
Genome-wide association studies (GWAS) have been successful in finding numerous new risk variants for complex diseases, but the results almost exclusively rely on single-marker scans. Methods that can analyze joint effects of many variants in GWAS data are still being developed and trialed. To evaluate the performance of such methods it is essential to have a GWAS data simulator that can rapidly simulate a large number of samples, and capture key features of real GWAS data such as linkage disequilibrium (LD) among single-nucleotide polymorphisms (SNPs) and joint effects of multiple loci (multilocus epistasis). In the current study, we combine techniques for specifying high-order epistasis among risk SNPs with an existing program GWAsimulator [Li and Li, 2008] to achieve rapid whole-genome simulation with accurate modeling of complex interactions. We considered various approaches to specifying interaction models including the following: departure from product of marginal effects for pairwise interactions, product terms in logistic regression models for low-order interactions, and penetrance tables conforming to marginal effect constraints for high-order interactions or prescribing known biological interactions. Methods for conversion among different model specifications are developed using penetrance table as the fundamental characterization of disease models. The new program, called simGWA, is capable of efficiently generating large samples of GWAS data with high precision. We show that data simulated by simGWA are faithful to template LD structures, and conform to prespecified diseases models with (or without) interactions.
Introduction
In the past few years, waves of genome-wide association studies (GWAS) have identified numerous genetic risk factors of complex diseases [Hindorff et al., 2013; Manolio, 2013; O'Seaghdha and Fox, 2011; Willer and Mohlke, 2012]. Although published GWAS analyses rely almost exclusively on single-marker scans, the importance of joint effects of multiple risk variants is increasingly recognized by both methodologists and practitioners of the field [Aschard et al., 2012; Cordell, 2009; Kirino et al., 2013; Lucas et al., 2012; Ma et al., 2012; MacLellan et al., 2012; Pandey et al., 2012]. Many statistical methods have been attempted for analyzing such joint effects, from multiple regression models to haplotype-based tests, and to tests for interactions of multiple loci (within a genomic region or across the whole genome) [Gao et al., 2013; Gyenesei et al., 2012; Hahn et al., 2003; Jin et al., 2010; Oh et al., 2012; Wan et al., 2010; Wu et al., 2010; Yang et al., 2011, 2012; Yang and Gu, 2013]. To facilitate development of new statistical methods and better understand high-order gene-gene interactions (epistasis), it is essential to have a GWAS data simulator that can not only simulate huge amounts of genotype data with realistic genome-wide linkage disequilibrium (LD) structure in reasonable computational time, but also correctly model complex interactions among many risk loci.
A rapid whole-genome simulator called GWAsimulator [Li and Li, 2008] does a great job in simulating marginal effects using “retrospective sampling” [Durrant et al., 2004] (first sampling genotypes at risk loci conditional on disease status, then generating haplotypes by a moving-window algorithm). The algorithm simply copies and binds small pieces of haplotypes templates from real-world populations, making it possible to generate very large datasets in reasonable time, and at the same time, making it capable of simulating realistic LD structure by using real-population haplotype templates such as those from the HapMap project [Gibbs et al., 2003]. However, the algorithm lacks a way to correctly handle multilocus interactions, which restricts its utility in studying complex diseases models with complex interactions.
A general way to specify higher order effects of multiple single-nucleotide polymorphisms (SNPs) is to use a penetrance table. The penetrance at the risk locus is the conditional probability that an individual with a given genotype is affected by the disease of interest. A penetrance table consists of penetrance values for all possible combinations of multilocus risk genotypes, which, in conjunction with the genotype frequencies, fully characterizes the joint distribution of disease status and genotypes at the risk loci. We had previously developed a novel method [Yang and Gu, 2008] for generating complex penetrance tables involving high-order interactions for any given set of marginal effects of risk loci and risk alleles frequencies.
In the present study, we combine improved interaction model specification with GWAsimulator's retrospective sampling to achieve rapid whole-genome simulation of GWAS data with accurate modeling of complex interactions. The resulting new algorithm is implemented in an R package called simGWA, which allows convenient and accurate specification of high-order effects using various approaches, including (1) departure from product of marginal effects for pairwise interactions, (2) logistic regression models for low-order interactions, (3) penetrance tables conforming to given marginal constraints for high-order interactions, and (4) special penetrance tables prescribing known biological interactions. Penetrance table is used as the canonical characterization of complex disease models and to simulate genotypes at the disease loci. We will first introduce how penetrance tables are used in the simulation. Then, we describe GWAsimulator's disease modeling and its limitation in specifying interactions, followed by description of our approaches to generate correct penetrance tables for complex disease models. Finally we give an overview of the implementation of simGWA and the evaluation of its performance.
Methods
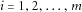 ),
),  (= 0, 1, or 2) is the risk allele count and
(= 0, 1, or 2) is the risk allele count and  is the risk allele frequency. For a multilocus genotype combination
is the risk allele frequency. For a multilocus genotype combination 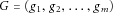 , denote the penetrance by
, denote the penetrance by 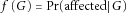 , which is the probability of being affected conditional on genotype G. Then, for a case subject, the probability that it has genotype G0 is
, which is the probability of being affected conditional on genotype G. Then, for a case subject, the probability that it has genotype G0 is
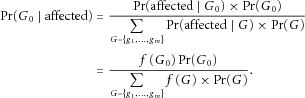 (1)
(1)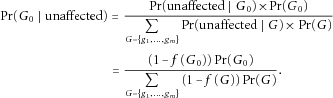 (2)
(2)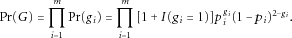 (3)
(3)Thus, given the full penetrance table  and allele frequencies
and allele frequencies  of all risk loci, it is straightforward to determine the distribution of genotypes in cases and controls using equations 1 and 2. These equations form the basis for “retrospective sampling” (sampling genotypes or haplotypes of subjects conditional on the disease status) used by GWAsimulator [Li and Li, 2008]. It is more efficient than a “prospective” approach, where multisite joint disease genotypes are randomly generated, but only accepted at a probability equal to the penetrance of that genotype combination [Peng and Amos, 2010; Pinelli et al., 2012].
of all risk loci, it is straightforward to determine the distribution of genotypes in cases and controls using equations 1 and 2. These equations form the basis for “retrospective sampling” (sampling genotypes or haplotypes of subjects conditional on the disease status) used by GWAsimulator [Li and Li, 2008]. It is more efficient than a “prospective” approach, where multisite joint disease genotypes are randomly generated, but only accepted at a probability equal to the penetrance of that genotype combination [Peng and Amos, 2010; Pinelli et al., 2012].
After determining genotypes at the disease loci from retrospective sampling, genotypes at neighboring positions on the same chromosome are simulated one by one using a moving-window algorithm [Durrant et al., 2004]. Simply speaking, for each partially simulated haplotype, the algorithm first finds haplotypes that match the already simulated haplotype in a small window among the haplotype templates. In these matched template haplotypes, the alleles at the next unsimulated position are counted and used to get the probability to simulate the allele at this position. This process is then repeated again to get the next allele on the template, until the whole chromosome is simulated.
Using templates ensures that the simulated chromosomes bear LD structures similar to the population of interest. Such templates may be generated from existing GWAS data, or easily retrieved from the HapMap [Gibbs et al., 2003] website, where phased data are provided for Caucasians (Utah residents with ancestry from northern and western Europe dataset), Africans (Yoruba in Ibadan dataset), and East Asians (Han Chinese in Beijing + Japanese in Tokyo). Naturally, the accuracy and resolution of the simulated LD structures depend on the sample sizes and data quality of the original template-generating samples.
Model Specification Used by GWAsimulator
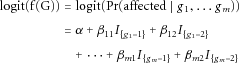 (4)
(4)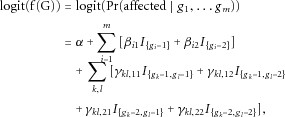 (5)
(5) , α is the constant coefficient;
, α is the constant coefficient;  and
and  are the coefficients for the effects of having one copy of targeted allele and two copies of the allele at the ith risk SNP, respectively;
are the coefficients for the effects of having one copy of targeted allele and two copies of the allele at the ith risk SNP, respectively; 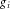 is the number of copies of the targeted allele at SNP i, and
is the number of copies of the targeted allele at SNP i, and  is an indicator function of whether the copies of the allele is n;
is an indicator function of whether the copies of the allele is n; 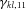 ,
,  ,
,  , and
, and  are coefficients for the interaction between SNP k and SNP l, associated to four genotype combinations of the two SNPs. If the coefficients are known, penetrances for every possible genotype combination could be determined from the logistic models and then used for data generation.
are coefficients for the interaction between SNP k and SNP l, associated to four genotype combinations of the two SNPs. If the coefficients are known, penetrances for every possible genotype combination could be determined from the logistic models and then used for data generation. and
and  , where
, where  is the penetrance function. When pairwise interactions exist, in addition to the RRs at each locus, departure of RRs for genotype combinations from the product of corresponding marginal RRs is also specified. For interaction between SNP k and SNP l, departure from product of marginal RRs is defined as
is the penetrance function. When pairwise interactions exist, in addition to the RRs at each locus, departure of RRs for genotype combinations from the product of corresponding marginal RRs is also specified. For interaction between SNP k and SNP l, departure from product of marginal RRs is defined as

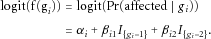 (6)
(6) (7)
(7)In GWAsimulator, β coefficients are calculated from 6, regardless of whether interactions are involved. After that, γ coefficients for interaction terms are obtained from the two-locus model (7) with the same β coefficients obtained previously. This simple two-step estimation is not always appropriate. If there are interaction effects, the estimation of β from (6) ignoring the interaction terms might not be correct. Besides this, equation 7 does not always hold true, either. A simple example is that when a risk SNP is involved in interactions with multiple SNPs, it is not possible to single out this SNP with a single interacting SNP to estimate the pairwise interaction coefficients.
A General Modeling Approach Using Penetrance Tables in simGWA
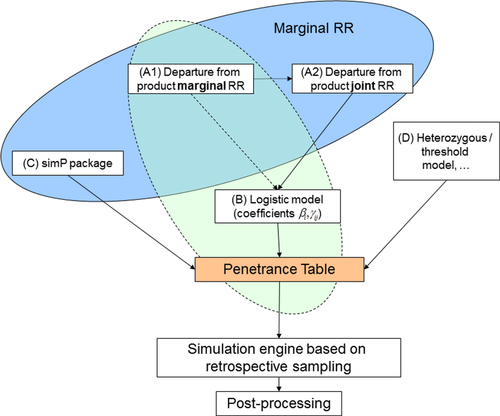
In the present work, we provide and evaluate methods to correctly specify multilocus disease models with or without epistatic effects, and with either pairwise or high-order interactions. Because penetrance tables are a more general and flexible way to precisely characterize complex joint effects of multiple risk loci, methods for conversion among different model specification methods are developed using penetrance table as the primary characterization of disease models. All methods described below are implemented in an R package called simGWA that produces the correct multilocus penetrance table, and then simulates disease loci genotypes and applies retrospective sampling by a modified GWAsimulator engine to rapidly generate genome-wide marker genotype data (see Fig. 1).
Correctly Modeling Pairwise Interactions Using RRs
Our first method addresses the misspecification problem of GWAsimulator when interaction exists, by correctly calculating the logistic model coefficients from given values of RRs. Because direct estimation requires solving high-dimensional nonlinear functions that can quickly become intractable, we developed an iterative approach to circumvent the problem. First, the departure from product of marginal RRs is converted to departure from the product of two “boundary” joint RRs involving reference genotypes at individual disease locus (see definition of  below). Then, values of the latter are used in iterative numerical computation to obtain the logistic model coefficients and the full penetrance table. This procedure is option 1 shown in Figure 1 as path from (A1) to (A2) and then to (B).
below). Then, values of the latter are used in iterative numerical computation to obtain the logistic model coefficients and the full penetrance table. This procedure is option 1 shown in Figure 1 as path from (A1) to (A2) and then to (B).
Marginal RR and Joint RR
Marginal RR is commonly used when describing the effects of individual SNPs. However, when it comes to interactions, joint RR (the risk ratio of a joint genotype  to the reference
to the reference  :
: 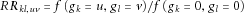 ) gives a better characterization of the RRs comparing genotype combinations.
) gives a better characterization of the RRs comparing genotype combinations.

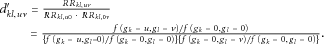
For a given set of values of  , the values of
, the values of  can be determined by solving a system of linear equations.
can be determined by solving a system of linear equations.
Numerical Algorithm to Estimate Coefficients and Penetrance Table
Assuming logistic model in formula 5, the coefficients needed to estimate are α,  , and
, and  , and for all interacting SNP pairs between SNPs k and l,
, and for all interacting SNP pairs between SNPs k and l,  ,
,  ,
,  and
and  . The estimation is achieved by iteratively calculating the coefficients and constructing the penetrance table. At each iteration, we first construct the full penetrance table from the current set of coefficients. From the full penetrance table, the joint RR and marginal RR values are calculated and compared with those specified originally in the model. The difference between the current RR values to those from the model specifications is used to update the logistic model coefficients accordingly to reduce the difference. After many iterations, the full penetrance table conforms well to all joint RR and marginal RR constraints with neglectable bias.
. The estimation is achieved by iteratively calculating the coefficients and constructing the penetrance table. At each iteration, we first construct the full penetrance table from the current set of coefficients. From the full penetrance table, the joint RR and marginal RR values are calculated and compared with those specified originally in the model. The difference between the current RR values to those from the model specifications is used to update the logistic model coefficients accordingly to reduce the difference. After many iterations, the full penetrance table conforms well to all joint RR and marginal RR constraints with neglectable bias.
 and all SNP coefficients
and all SNP coefficients  and
and  equal to 0. The penetrance for each genotype is then a constant,
equal to 0. The penetrance for each genotype is then a constant,  . Suppose at iteration s, the previously estimated coefficients are
. Suppose at iteration s, the previously estimated coefficients are  ,
,  ,
, 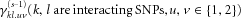 , and the penetrance table calculated from the coefficients is
, and the penetrance table calculated from the coefficients is  . The following steps are taken to update their values in the iteration.
. The following steps are taken to update their values in the iteration.
- Step 1: For each
 , update
, update  and penetrance table f. From the full penetrance table
and penetrance table f. From the full penetrance table  , the marginal penetrances at locus i are calculated by weighed average of all penetrances involving a certain genotype at this locus, and the weight is the corresponding multilocus genotype frequency. Denote the derived marginal penetrances as
, the marginal penetrances at locus i are calculated by weighed average of all penetrances involving a certain genotype at this locus, and the weight is the corresponding multilocus genotype frequency. Denote the derived marginal penetrances as  ,
,  , and
, and  for the three genotypes at SNP i. Then update
for the three genotypes at SNP i. Then update 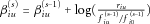 , and update the penetrance table based on the new set of coefficients. Denote the final penetrance table after updating
, and update the penetrance table based on the new set of coefficients. Denote the final penetrance table after updating  for all SNPs as
for all SNPs as 
- Step 2: Update the value of a. After step 1, the disease prevalence might not equal to K. From penetrance table
 , calculate the current disease prevalence
, calculate the current disease prevalence  , then a is updated to
, then a is updated to  . Accordingly, the new penetrance table from the coefficients is now
. Accordingly, the new penetrance table from the coefficients is now  .
. - Step 3: For each pair of interacting SNPs k and l, update the values of
 . In this step, we estimate departure from joint RRs from
. In this step, we estimate departure from joint RRs from  . Estimations are
. Estimations are  . Then the updated γ values are
. Then the updated γ values are 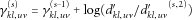 . Denote the penetrance table after updating for all
. Denote the penetrance table after updating for all  as
as  .
. - Step 4: Update the value of a as in step 2. After this updating, the logistic model coefficients are now
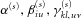 , and the penetrance table calculated from them is
, and the penetrance table calculated from them is 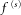 .
. - Step 5: Check the maximum change of values to all coefficients in steps 1–4 against a preset tolerance threshold (default value of 10−10 is used for results shown below). Iterations of steps 1–4 are repeated until the maximum change is below tolerance or the maximum number of iterations is reached.
Effectively Modeling Higher Order Interactions
High-order interactions can be modeled in simGWA either by logistic models (this is option 2 marked in Fig. 1 as (B)) or by sampling penetrance tables generated using the previously developed simP R package [Yang and Gu, 2008] (this is option 3 marked in Fig. 1 as (C)). For the logistic model approach (option 2), a formula similar to equation 4 is used to determine the penetrances of multilocus genotypes, with additional higher order product terms for interactions among multiple risk SNPs. Users need to specify all coefficients in the model. The simGWA package automatically calculates the penetrance table when interactions are limited between pairs of SNPs. Going beyond pairwise interactions, the users have to calculate and specify each penetrance values. Although the calculation is straightforward, we discourage the use of this approach when modeling higher than pairwise interactions because the biologically interpretation of the higher order product terms becomes less clear. Instead, we recommend directly assign multilocus penetrances conforming to assigned marginal effects. This can be done by simP [Yang and Gu, 2008] (option 3), a previously developed R package that can perform two very useful functions. First, it can generate unlimited number of random penetrance tables that satisfy a given set of marginal RR constraints. Second, for any given penetrance table, it quickly evaluates the effects of single SNPs, collective effects of interactions, and the fraction of disease variation explained by the corresponding genetic model. This information could aid selecting interesting interaction models for data simulation. For example, using simP, we were able to generate hundreds of genetic models with null marginal effects for all risk SNPs, but their joint effects account for a substantial amount of disease variability.
Special Penetrance Tables Prescribing Known Biological Models
- Heterozygous model. Occurrence of any risk genotype from different loci causes the disease. In Table 1, occurrence of AA genotype or any B allele causes the disease (penetrance is 1).
- Threshold model. Disease phenotype manifests (penetrance is 1) when the total number of risk alleles/genotypes reaches a threshold.
| bb | bB | BB | |
|---|---|---|---|
| aa | 0 | 1 | 1 |
| aA | 0 | 1 | 1 |
| AA | 1 | 1 | 1 |
- Occurrence of risk genotype AA or allele B results in a penetrance of 1.
Evaluation of simGWA Performances
To evaluate the performances of simGWA, we applied the simulator over a range of genetic models of multilocus interactions and used HapMap phased data for Caucasians (CEU) as template. The simulated GWAS datasets include a total of 676,565 SNPs on the Affymetrix Genome-Wide Human SNP Array 6.0 to mimic the real genotyping platform.
The GWAS data were simulated for a binary trait with five risk SNPs. They locate on five randomly selected chromosomes. Among the five SNPs, SNP1, SNP3, and SNP4 have no marginal effect at all; SNP2 has a multiplicative effect, and the RRs of genotypes with one and two copies of risk alleles (compared with that of no copy) are 1.5 and 2.25, respectively; SNP5 has a dominant effect, and the RR of both risk genotypes is 2. Namely,  ;
;  ,
,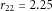 ;
;  ;
;  ; and
; and  .
.
Assuming the marginal effects described above, two types of models were considered in terms of SNP-SNP interactions: one with no interaction at all, and the other with pairwise interactions between two SNP pairs (SNP1 interacting with SNP2, SNP3 with SNP4). In the latter, the effect sizes of the pairwise interactions, as measured by departure from product of marginal RRs, are  ,
,  ,
,  ,
,  ;
;  ,
,  ,
,  ,
,  . For each model, we generated datasets containing 676,565 SNPs for 2,000 cases and 2,000 controls using simGWA, by (1) converting the marginal RR model to joint RR model, (2) numerically calculating logistic model coefficients and generating the penetrance table, and (3) generating genetic data. To compare performance, we also generated datasets using GWAsimulator and the same parameters for disease models with or without pairwise interactions. Under each of the two models, 1,000 replication datasets were generated by simGWA and GWAsimulator, respectively.
. For each model, we generated datasets containing 676,565 SNPs for 2,000 cases and 2,000 controls using simGWA, by (1) converting the marginal RR model to joint RR model, (2) numerically calculating logistic model coefficients and generating the penetrance table, and (3) generating genetic data. To compare performance, we also generated datasets using GWAsimulator and the same parameters for disease models with or without pairwise interactions. Under each of the two models, 1,000 replication datasets were generated by simGWA and GWAsimulator, respectively.
Results
Comparable Performance in Terms of Local LD Structure and Computational Time
Both programs took about 52 min to simulate genotypes of 676,565 SNPs for 4,000 subjects with a single thread on a Linux machine with two CPUs of Intel Xeon 5430 Quad Core 2.66 GHz and 32 GB of memory. For both simGWA and GWAsimulator, genome-wide LD structures in the simulated data were comparable to those in the real population of HapMap CEU. A typical example is given in Figure 2, which confirms that local LD structures by HaploView [Barrett et al., 2005] were faithfully maintained in both datasets generated by the two simulators.

Agreement Between simGWA and the GWAsimulator When There Is No Interaction
The two simulators handle parameters for disease models differently. However, we may compare effect sizes of each risk SNP estimated based on the simulated penetrance tables. Table 2 summarizes the comparisons when interactions exist or not, expressed in terms of genetic information loss (the reduction in explained heritability) if an individual SNP was ignored. When there is absolutely no interaction (“pure marginal effect” model), marginal effect sizes of individual risk SNPs were almost identical by both simulators.
| Information loss by ignoring a SNP | |||||||
|---|---|---|---|---|---|---|---|
| h2 | SNP1 | SNP2 | SNP3 | SNP4 | SNP5 | ||
| Pure marginal effect | simGWA | 0.04 | 0.00 | 0.27 | 0.00 | 0.00 | 0.74 |
| GWAsimulator | 0.04 | 0.00 | 0.26 | 0.00 | 0.00 | 0.75 | |
| Interaction model | simGWA | 0.19 | 0.54 | 0.60 | 0.26 | 0.26 | 0.20 |
| GWAsimulator | 0.08 | 0.31 | 0.32 | 0.20 | 0.20 | 0.39 | |
- Models were built using simGWA and the GWAsimulator when there was no interaction or there were two interacting SNP pairs (SNP1 and SNP2, SNP3 and SNP4). Of the five SNPs, three do not have any marginal effect (SNP1, SNP3, SNP4). The third column (h2) in the table shows the proportion of disease variation that is explainable by the joint effect of all five SNPs (heritability of disease). The next few columns summarize the genetic information loss by ignoring any of the five SNPs.
For every pair of datasets generated by the two simulators, difference in genotype distributions was tested by χ2 at each risk SNP, in cases and in controls separately. There were 5,000 tests comparing the genotypes at five risk SNPs in 1,000 cases datasets, and another 5,000 tests in 1,000 controls datasets. The smallest P-value from the 10,000 tests was 0.070. This confirms that the distributions of risk genotypes were not different in datasets generated by the two simulators. Further tests were carried out comparing distributions of all two-locus combined genotypes; the similarity still holds.
simGWA Correctly Simulates Pairwise Interactions
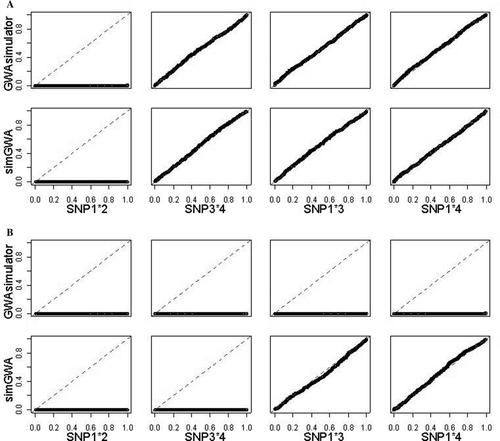
When there were interactions, simGWA correctly calculated all interaction terms in the penetrance table, which could differ substantially from those used by GWAsimulator even though the disease model is specified in the same manner. This is clearly seen in the bottom half of Table 2: there were differences both in the total heritabilities calculated by the two methods, and in the effect sizes of the risk SNPs (measured as the decrease in explained disease variation when a risk SNP was ignored). The differences were due to overly simplified specification of the logistic model coefficients in GWAsimulator for SNPs involved in interactions, as demonstrated in Table 3. If two SNPs have no marginal effect or interaction between them, their combined effects should be null, such as in the case of SNP1 and SNP3, or SNP1 and SNP4. However, as shown in Table 3, while the penetrance table calculated by simGWA resulted in a correct value of 0 for the combined effects of two such pairs of SNPs, substantial nonzero values (0.13 for both pairs) were assigned by GWAsimulator. This is supported by association test results on the simulated datasets. Single-SNP association test P-values should approximately follow the uniform distribution when the SNP has no marginal effect. As seen in Figure 3, under models of no interaction, distributions of single-SNP tests for SNP1, SNP3, and SNP4 in both simGWA- and GWAsimulator-generated datasets follow perfectly the uniform distribution (panel A); however, under interaction models, the distributions in GWAsimulator-generated datasets completely diverged from the uniform (panel B) even though these SNPs had no marginal effects. Similar observations were made for joint tests and displayed in Figure 4. Again, under pure marginal effect models, P-values of 2-SNP joint tests for SNP1-SNP3 and SNP1-SNP4 correctly follow the uniform distribution in both simGWA- and GWAsimulator-generated datasets. But when there were interactions, the distributions in GWAsimulator-generated datasets completely diverged from the uniform (panel B) even though no interaction effects were simulated for these SNP pairs.
| SNP1×2 | SNP3×4 | SNP1×3 | SNP1×4 | ||
|---|---|---|---|---|---|
| Joint effects of SNP pairs | simGWA | 0.55 | 0.22 | 0.00 | 0.00 |
| GWAsimulator | 0.35 | 0.25 | 0.13 | 0.13 | |
| Interactions effects of SNP pairs | simGWA | 0.49 | 0.22 | 0.00 | 0.00 |
| GWAsimulator | 0.23 | 0.10 | 0.00 | 0.00 |
- Models were built using simGWA and the GWAsimulator when there were two pairs of SNPs with pairwise interactions (SNP1 and SNP2, SNP3 and SNP4). For the two SNP pairs that really interact (SNP1×2, SNP3×4), and two other SNP pairs that entail no interactions (SNP1×3, SNP1×4), the interaction effects in the penetrance tables are summarized. “Information in SNP pairs” shows the proportion of variance in the total heritability that is explainable by only considering the SNP pair (joint effect). The last two rows of the tables show the variance explainable by the pairwise interaction of the two SNPs.

Discussion
We presented a novel method for correctly specifying SNP interaction effects and an improved GWAS data simulator using the method called simGWA. Penetrance table is used as the fundamental characterization of disease models, and commonly used means for interaction model specification (deviation from product of RRs or logistic model coefficients) are converted to use correct penetrance tables. A general-purpose penetrance generator (simP) or arbitrary logistic models were used to generate penetrance tables for high-order interactions.
Genotype simulation in simGWA is built on the highly efficient GWAsimulator [Li and Li, 2008]. Before GWAsimulator, many used the coalescent model [Donnelly and Tavare 1995; Hudson, 2002] of population genetics or forward-time simulation [Peng and Amos, 2010; Pinelli et al., 2012] to reconstruct the evolutionary history. Although the approach works well for sampling a theoretical population that follows the Wright–Fisher model [Hudson, 2002], the simulators are generally not as efficient for GWAS data simulation. Moreover, GWAsimulator adopts an empirical approach and the “retrospective sampling” based on real-population templates, and works excellently when there are no interactions. simGWA takes full advantage of its efficient simulation engine and by employing new methods to correctly specify SNP interaction effects. This resulted in a useful tool for rapid generation of GWAS data under complex interaction models for studying complex disease.
Existing methods such as Gene-Environment iNteraction Simulator (GENS) [Amato et al., 2010] and GENS2 [Pinelli et al., 2012] also used multilocus penetrance tables to model gene-environment interactions. These methods were limited to G × E interactions involving at most two disease loci and a single environment factor. It would be interesting to see if the methods can be combined with that of simGWA to simulate G × E interactions involving more environment variables and higher order penetrance tables.
Although the present work is focused on simulating GWAS data for binary traits, it is possible to extend simGWA to simulate GWAS data for quantitative traits for studies using population-based sampling. However, correct modeling of higher order interactions for sampling based on quantitative trait values will not be straightforward and deserves further investigation.
We note that simGWA has some limitations similar to GWAsimulator. For example, flaws in the template phase data (e.g., ascertainment bias) would be passed to the generated data. Also, long-range LDs are not considered; and it allows only one disease locus on each chromosome. These flaws may be remediable in many situations. For example, if there is need to simulate multiple disease loci on the same chromosome in different LD blocks, one can simulate that chromosome in multiple chunks, each harboring a risk SNP, with possibly slight loss of LD information at the ends connecting the chunks.
In summary, simGWA provides a rapid GWAS data simulator that is able to mimic realistic LD and correctly model complex interactions among risk SNPs. As more and more efforts are put to in-depth analysis of GWAS data to find “missing heritability,” many sophisticated analytical methods are in development and we anticipate that simGWA will provide a useful tool for method evaluation.
Acknowledgment
This research was supported in part by NIH grants HL091028, HL071782, and DA027995, and an AHA grant 0855626G.
The authors have declared no conflict of interests.




