A Shrinkage Method for Testing the Hardy–Weinberg Equilibrium in Case-Control Studies
ABSTRACT
Testing for the Hardy–Weinberg equilibrium (HWE) is often used as an initial step for checking the quality of genotyping. When testing the HWE for case-control data, the impact of a potential genetic association between the marker and the disease must be controlled for otherwise the results may be biased. Li and Li [2008] proposed a likelihood ratio test (LRT) that accounts for this potential genetic association and it is more powerful than the commonly used control-only χ2 test. However, the LRT is not efficient when the marker is independent of the disease, and also requires numerical optimization to calculate the test statistic. In this article, we propose a novel shrinkage test for assessing the HWE. The proposed shrinkage test yields higher statistical power than the LRT when the marker is independent of or weakly associated with the disease, and converges to the LRT when the marker is strongly associated with the disease. In addition, the proposed shrinkage test has a closed form and can be easily used to test the HWE for large datasets that result from genome-wide association studies. We compare the performance of the shrinkage test with existing methods using simulation studies, and apply the shrinkage test to a genome-wide association dataset for Alzheimer's disease.
Introduction
The Hardy–Weinberg equilibrium (HWE) is one of the most important properties in population genetics. More than a century ago, G. H. Hardy and W. Weinberg individually noted that for a large, self-contained, and randomly mating population, assuming a bi-allelic locus with alleles A and a and corresponding allele frequencies p and q, the genotype frequencies are p2,  and q2 for genotypes
and q2 for genotypes  ,
,  and
and  , respectively [Hardy, 1908; Weinberg, 1908]. As genotyping errors distort the genotype distribution and thus break the HWE, testing for this equilibrium has been routinely conducted as a way of checking the quality of genotyping [Gomes et al., 1999; Hosking et al., 2004; Xu et al., 2002]. Deviation from the HWE often indicates a poor quality of genotyping.
, respectively [Hardy, 1908; Weinberg, 1908]. As genotyping errors distort the genotype distribution and thus break the HWE, testing for this equilibrium has been routinely conducted as a way of checking the quality of genotyping [Gomes et al., 1999; Hosking et al., 2004; Xu et al., 2002]. Deviation from the HWE often indicates a poor quality of genotyping.
A straightforward way to test the HWE is the χ2 test, which is based on pooling samples from the cases and controls [Weir, 1996]. We refer to this test as the pooled χ2 test in order to distinguish it from other versions of χ2 tests described later. The pooled χ2 test has high statistical power but requires the subjects under investigation to be a random sample from the target population. For case-control data, subjects are retrospectively ascertained based on their disease status. Therefore, if a candidate marker is associated with the disease, the corresponding genotypes in the case-control sample are no longer representative of the target population. Consequently, the pooled χ2 test may yield misleading results and mistakenly conclude a violation of the HWE when the target population is actually within the HWE [Wittke et al., 2005]. Nevertheless, it is worth noting that if the candidate marker is independent of the disease, the genotypes of the case-control samples are a random sample from the population, and thus the pooled χ2 test is a valid and efficient test for assessing the HWE.
Many methods have been proposed to test the HWE for case-control samples without making the strong assumption that the candidate marker is independent of the disease. A widely used approach is to conduct the χ2 test using only the controls, while discarding the cases. Unfortunately, this control-only χ2 test is (approximately) valid only when the disease prevalence is low, and therefore the controls provide a good approximation of the general population. When the disease prevalence is moderate or high, the control-only χ2 test leads to inflated type I errors [Li and Li, 2008]. In addition, because of discarding the information obtained from cases, the control-only χ2 test is not efficient. To address these issues, Li and Li [2008] developed a likelihood ratio test (LRT) to assess the HWE using data from both cases and controls, while taking into account the potential association between the marker and the disease. Compared to the control-only χ2 test, the LRT is more powerful for detecting departures from the HWE for common diseases and has comparable power for use in analyzing rare diseases. Yu et al. [2009] proposed a similar test based on the likelihood ratio framework. Wang and Shete [2010] developed a bootstrapping test that also accounts for the underlying genetic association. Because the performances of these tests are quite comparable, herein we focus on the LRT.
Although the LRT is valid and more powerful than the control-only χ2 test, it has two limitations. First, because the LRT requires the estimation of extra nuisance parameters (e.g. penetrances), it can be substantially less powerful than the pooled χ2 test if the marker actually is independent of the disease. This is a concern for some genetic studies, such as a genome-wide association study (GWAS), in which most of the markers are expected to be weakly or not associated with the disease. In addition, the LRT typically requires numerical optimization to calculate the test statistic (i.e. the maximum likelihood estimates); therefore it can be time consuming to apply the LRT to large-scale case-control studies, e.g. a GWAS, in which hundreds of thousands of single nucleotide polymorphisms (SNPs) need to be tested.
In this article, we propose a novel shrinkage test to circumvent the limitations of the LRT. Toward this goal, we first propose an extension of the pooled χ2 test, called the generalized χ2 test, for assessing the HWE. The generalized χ2 test is valid regardless of whether or not the marker is associated with the disease. Based on that characteristic, we then propose a shrinkage test statistic, which takes a form of the weighted average of the pooled χ2 test statistic and the generalized χ2 test statistic. When the marker is independent of the disease, the proposed shrinkage test converges to the pooled χ2 test, and therefore achieves high statistical power. When the marker is associated with the disease, the proposed shrinkage test converges to the generalized χ2 test, and therefore remains statistically valid. A simulation study shows that, compared to the LRT, the shrinkage test is more powerful to detect departures from the HWE when the marker is weakly or not associated with the disease, and has comparable power when the marker is strongly associated with the disease. In addition, as the proposed shrinkage test has a closed form, it is easy to calculate and is particularly suitable for testing the HWE for large case-control datasets.
The remainder of this article is organized as follows. We first briefly review the pooled χ2 test, and then propose the generalized χ2 test and the shrinkage test. We compare the performances of the proposed test to existing methods using simulation studies and a GWAS dataset. We conclude the article with a brief discussion.
Methods
Consider a bi-allelic candidate marker with two alleles, A and a, having frequencies p and 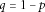 , respectively, where p is the minor allele frequency (MAF). Denote three genotypes by
, respectively, where p is the minor allele frequency (MAF). Denote three genotypes by  ,
,  and
and  with genotype frequencies
with genotype frequencies  for
for  When the HWE holds,
When the HWE holds,  ,
,  and
and  . Denote the penetrance by
. Denote the penetrance by  , and the disease prevalence by
, and the disease prevalence by  , then the genotype frequencies in the cases and controls are given by
, then the genotype frequencies in the cases and controls are given by  and
and  , respectively, for
, respectively, for  . Define the genetic relative risks (GRRs) as
. Define the genetic relative risks (GRRs) as  ,
, 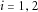 , to characterize the underlying genetic association. When the candidate marker is not associated with the disease,
, to characterize the underlying genetic association. When the candidate marker is not associated with the disease,  ; otherwise,
; otherwise,  with at least one inequality holding. When the genetic association is present, the genetic model can be used to describe the relationship between
with at least one inequality holding. When the genetic association is present, the genetic model can be used to describe the relationship between  's. A genetic model is called recessive (REC) if
's. A genetic model is called recessive (REC) if  and
and  ; additive (ADD) if
; additive (ADD) if  and
and  , and dominant (DOM) if
, and dominant (DOM) if  and
and  [Sasieni, 1997].
[Sasieni, 1997].
Consider case-control data consisting of r cases and s controls. Let  and
and  denote the genotype counts of G0, G1, and G2 in cases and controls, respectively. Let
denote the genotype counts of G0, G1, and G2 in cases and controls, respectively. Let  ,
,  ,
,  and
and  . The genotype counts for the cases and controls are displayed in Table 1.
. The genotype counts for the cases and controls are displayed in Table 1.
 |
 |
 |
Total | |
|---|---|---|---|---|
| Case | r0 | r1 | r2 | r |
| Control | s0 | s1 | s2 | s |
| Total | n0 | n1 | n2 | n |
The Pooled χ2 Test

 when the HWE holds. For case-control data, when the candidate marker is not associated with the disease, genotypes in the case-control samples are a random sample from the general population. Therefore, we can pool the cases and controls together and estimate
when the HWE holds. For case-control data, when the candidate marker is not associated with the disease, genotypes in the case-control samples are a random sample from the general population. Therefore, we can pool the cases and controls together and estimate  ,
,  , and
, and

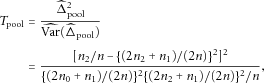
The pooled χ2 test is efficient and possesses high statistical power because of the use of the pooled data from cases and controls. However, when the candidate marker is associated with the disease, the χ2 test is invalid because the genotypes in the case-control sample are no longer a random sample from the general population and therefore  ,
,  , and
, and 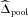 are biased. Under this circumstance, the control-only χ2 test, which uses only control data, is often used to examine the HWE.
are biased. Under this circumstance, the control-only χ2 test, which uses only control data, is often used to examine the HWE.
The Generalized χ2 Test

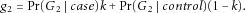
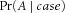 ,
,  ,
, 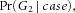 and
and 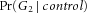 can be consistently estimated by
can be consistently estimated by  ,
,  ,
,  and
and  , respectively. Therefore, we estimate p and g2 by
, respectively. Therefore, we estimate p and g2 by
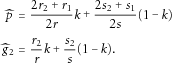
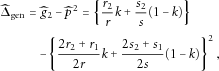
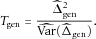
 ) Under the null hypothesis that the HWE holds, Tgen asymptotically follows a χ2 distribution with 1 degree of freedom.
) Under the null hypothesis that the HWE holds, Tgen asymptotically follows a χ2 distribution with 1 degree of freedom.Because the development of the generalized χ2 test does not require any assumptions of the association between the marker and the disease, this test is generally applicable to case-control samples. Actually, the generalized χ2 test is a Wald test that is asymptotically equivalent to the LRT. Compared to the LRT, the main advantage of the generalized χ2 test is its computational simplicity. The generalized χ2 test statistic has a closed form and thus is more suitable to test the HWE for modern large-scale case-control studies involving millions of markers. However, like the LRT, if the marker is not associated with the disease, the generalized χ2 test is less powerful than the pooled χ2 test. To address this issue, we propose a shrinkage test as follows.
The Shrinkage Test

 and pooled estimate of the HWD coefficient
and pooled estimate of the HWD coefficient 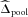 . The shrinkage factor or weight w (
. The shrinkage factor or weight w ( ) controls how much
) controls how much  shrinks toward
shrinks toward  or
or 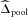 . As described later, we select w in a data-adaptive way so that
. As described later, we select w in a data-adaptive way so that  inherits the merits from both the pooled χ2 test and the generalized χ2 test. Specifically, we require that when the marker is associated with the disease, w goes to 1 and thus
inherits the merits from both the pooled χ2 test and the generalized χ2 test. Specifically, we require that when the marker is associated with the disease, w goes to 1 and thus  converges to
converges to  to ensure the validity of the test; and when the marker is not associated with the disease, w goes to 0 and thus
to ensure the validity of the test; and when the marker is not associated with the disease, w goes to 0 and thus  converges to
converges to  to achieve the high statistical power of the pooled χ2 test.
to achieve the high statistical power of the pooled χ2 test.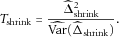
 can be obtained through the Delta method (see the Appendix for details). Under the null hypothesis that the HWE holds, Tshrink follows a χ2 distribution with 1 degree of freedom.
can be obtained through the Delta method (see the Appendix for details). Under the null hypothesis that the HWE holds, Tshrink follows a χ2 distribution with 1 degree of freedom.We now discuss how to construct the shrinkage factor w. In order to ensure that the value of w adaptively changes with the strength of the marker-disease association, we first define a measure of the marker-disease association and then use that as a basis for constructing the shrinkage factor.
We measure the strength of the marker-disease association using the Bayes factor. The Bayes factor is the cornerstone of Bayesian hypothesis testing [Jeffreys, 1961; Kass and Raftery, 1995] and provides an evidence-based measure of the likelihood of a hypothesis being true. As the standard Bayes factor involves high-dimensional integration and is sensitive to the prior of the unknown parameters, we herein adopt a variation of the Bayes factor, called the approximate Bayes factor (ABF; Wakefield [2007]; Xu et al. [2012]). The main difference between the ABF and the standard Bayes factor is that the ABF is based on the likelihood of a test statistic, whereas the standard Bayes factor is based on the likelihood of the observed data [Johnson, 2005; Wakefield, 2007].
 vs. the alternative
vs. the alternative  , and assuming that the distribution of T depends only on θ, the ABF is defined as
, and assuming that the distribution of T depends only on θ, the ABF is defined as
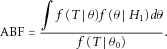
 denote the prior odds of H1 vs. H0 being true, the posterior probability of H1 being true is
denote the prior odds of H1 vs. H0 being true, the posterior probability of H1 being true is
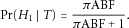 (1)
(1)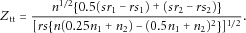
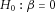 (no marker-disease association) and
(no marker-disease association) and 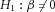 (having marker-disease association). Under H0,
(having marker-disease association). Under H0,  and under H1,
and under H1, 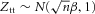 . Following Xu et al. [2012], we assign β a normal prior distribution
. Following Xu et al. [2012], we assign β a normal prior distribution 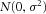 with
with 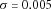 . The ABF based on Ztt is given by
. The ABF based on Ztt is given by
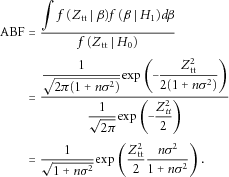
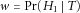 as given in (1), because of its appealing feature that
as given in (1), because of its appealing feature that  in the presence of a marker-disease association (as
in the presence of a marker-disease association (as  goes to 1) and
goes to 1) and  in the absence of such an association (as
in the absence of such an association (as  goes to 0). To use this shrinkage factor, we found that the conventional noninformative prior
goes to 0). To use this shrinkage factor, we found that the conventional noninformative prior  (i.e. there is an equal prior probability that the marker is associated or not associated with the disease) did not work well in finite samples and led to inflated type I errors (see Table 1 in the Supplementary Materials). This is because in finite samples, the value of
(i.e. there is an equal prior probability that the marker is associated or not associated with the disease) did not work well in finite samples and led to inflated type I errors (see Table 1 in the Supplementary Materials). This is because in finite samples, the value of  can be substantially smaller than 1 under H1 although it asymptotically converge to 1. As a result, even there is a marker-disease association, Tpool still contributes to Tshrink, which causes inflated type I errors. One way to address this issue is to assign a higher prior probability to H1, thus a lower prior weight to Tpool, to control the influence of Tpool. Based on the simulation study, we recommend
can be substantially smaller than 1 under H1 although it asymptotically converge to 1. As a result, even there is a marker-disease association, Tpool still contributes to Tshrink, which causes inflated type I errors. One way to address this issue is to assign a higher prior probability to H1, thus a lower prior weight to Tpool, to control the influence of Tpool. Based on the simulation study, we recommend  with an addition set-off of 0.1 for w because it consistently yields good operating characteristics in terms of both the type I error and power. That is,
with an addition set-off of 0.1 for w because it consistently yields good operating characteristics in terms of both the type I error and power. That is,

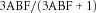 is very close to 1. In this case, we simply round w to 1 so that
is very close to 1. In this case, we simply round w to 1 so that  .
.Simulation Studies
We carried out comprehensive simulation studies to investigate the performance of the proposed shrinkage test and compare our proposed approach to the control-only χ2 test and the LRT. We first investigated the type I error rate of the different methods under the null hypothesis that the HWE holds. We assumed the MAF  , disease prevalence
, disease prevalence 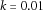 or 0.1, GRR
or 0.1, GRR  , 1.5 or 2.0, and sample size
, 1.5 or 2.0, and sample size  . We considered three genetic models, including REC, ADD, and DOM, under which the values of λ1 were determined.
. We considered three genetic models, including REC, ADD, and DOM, under which the values of λ1 were determined.
The genotype distributions among the case and control groups were determined according to p, λ1, λ2, and k under the constraint of the HWE. Under each simulation condition, 10,000 replicates were used to evaluate the empirical type I error rate for the tests.
To evaluate the power of the methods to detect different departures from the HWE, following Li and Li [2008], we simulated case-control data from two genotyping error models (denoted as S1 and S2) introduced by Leal [2005]. Model S1 assumes that heterozygosity may be incorrectly genotyped as homozygosity. In this case, given the MAF p and error rate δ, the observed genotype probabilities are 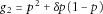 ,
,  and
and 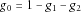 . In S2, homozygosity may be incorrectly genotyped as heterozygosity with
. In S2, homozygosity may be incorrectly genotyped as heterozygosity with  ,
,  and
and 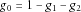 . The parameters setting for evaluating the power were the same as those for evaluating the type I error rate except that we considered
. The parameters setting for evaluating the power were the same as those for evaluating the type I error rate except that we considered  , 1.25 or 1.5. We specified an error rate of
, 1.25 or 1.5. We specified an error rate of 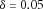 or 0.075 and evaluated the empirical power using 10,000 replicates under a significance level 0.05.
or 0.075 and evaluated the empirical power using 10,000 replicates under a significance level 0.05.
Figure 1 shows the type I error rates of the control-only χ2 test, LRT and shrinkage test under different simulation conditions. We can see that the LRT and the shrinkage test consistently controlled the type I error rates at the nominal value (5%) across all conditions. In contrast, although the control-only χ2 test performed reasonably well when the disease prevalence was low 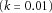 , it led to inflated type I error rates under REC and DOM with modest disease prevalence and strong genetic association (e.g.
, it led to inflated type I error rates under REC and DOM with modest disease prevalence and strong genetic association (e.g.  ,
, 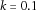 ). For example, the type I error rate of the control-only χ2 test was inflated up to 10.84% under REC with
). For example, the type I error rate of the control-only χ2 test was inflated up to 10.84% under REC with  and
and 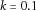 . Therefore, if we were to use the control-only χ2 test to evaluate the genotyping quality for large-sample studies (e.g. GWAS), we might falsely exclude the important candidate markers from further study.
. Therefore, if we were to use the control-only χ2 test to evaluate the genotyping quality for large-sample studies (e.g. GWAS), we might falsely exclude the important candidate markers from further study.

In terms of power to detect departures from the HWE, the proposed shrinkage test outperformed the LRT and control-only χ2 test, especially when the marker was weakly or not associated with the disease, as shown in Table 2. For example, when the marker is not associated with the disease, under genotyping error model S2 with disease prevalence 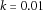 , the power of the shrinkage test was about 12% and 14% higher than that of the LRT when the error rates are
, the power of the shrinkage test was about 12% and 14% higher than that of the LRT when the error rates are 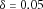 and 0.075, respectively. Such improvement stems from the fact that the shrinkage test automatically converged toward the pooled χ2 test in the absence of a marker-disease association.
and 0.075, respectively. Such improvement stems from the fact that the shrinkage test automatically converged toward the pooled χ2 test in the absence of a marker-disease association.
 |
 |
||||||||
| Genetic | Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| model | λ2 | model | δ | Control | LRT | Shrinkage | Control | LRT | Shrinkage |
| No | 1.0 | S1 | 0.05 | 34.2 | 34.2 | 43.2 | 35.4 | 41.1 | 48.6 |
| association | 0.075 | 65.7 | 66.0 | 78.4 | 65.1 | 73.2 | 82.4 | ||
| S2 | 0.05 | 35.0 | 35.8 | 47.8 | 35.6 | 41.8 | 51.4 | ||
| 0.075 | 65.3 | 66.5 | 80.9 | 65.5 | 74.2 | 84.4 | |||
| REC | 1.25 | S1 | 0.05 | 35.0 | 35.2 | 52.2 | 28.5 | 41.6 | 54.5 |
| 0.075 | 63.8 | 65.7 | 79.3 | 57.6 | 73.5 | 83.7 | |||
| S2 | 0.05 | 35.7 | 36.0 | 37.0 | 41.2 | 41.5 | 41.6 | ||
| 0.075 | 66.1 | 67.1 | 71.3 | 71.9 | 74.8 | 77.4 | |||
| 1.5 | S1 | 0.05 | 33.2 | 34.5 | 43.1 | 22.3 | 40.1 | 46.5 | |
| 0.075 | 63.9 | 65.9 | 71.8 | 50.9 | 74.9 | 78.1 | |||
| S2 | 0.05 | 36.6 | 36.5 | 34.5 | 49.2 | 43.0 | 41.4 | ||
| 0.075 | 67.6 | 66.4 | 67.2 | 77.3 | 74.8 | 77.5 | |||
| ADD | 1.25 | S1 | 0.05 | 34.3 | 34.3 | 38.4 | 34.6 | 41.3 | 43.8 |
| 0.075 | 65.0 | 65.2 | 70.6 | 64.7 | 73.6 | 76.6 | |||
| S2 | 0.05 | 35.1 | 36.2 | 43.7 | 35.3 | 42.6 | 48.2 | ||
| 0.075 | 64.6 | 65.9 | 74.6 | 65.1 | 75.2 | 80.3 | |||
| 1.5 | S1 | 0.05 | 33.9 | 33.9 | 33.8 | 33.7 | 40.6 | 39.9 | |
| 0.075 | 65.0 | 65.6 | 65.5 | 62.7 | 72.7 | 72.2 | |||
| S2 | 0.05 | 35.3 | 35.9 | 38.8 | 34.7 | 42.4 | 44.1 | ||
| 0.075 | 66.3 | 66.8 | 70.0 | 65.7 | 75.7 | 77.5 | |||
| DOM | 1.25 | S1 | 0.05 | 35.4 | 34.8 | 33.8 | 40.6 | 40.7 | 39.4 |
| 0.075 | 66.1 | 65.8 | 66.2 | 69.9 | 72.9 | 72.8 | |||
| S2 | 0.05 | 34.3 | 36.0 | 43.4 | 29.5 | 41.8 | 47.3 | ||
| 0.075 | 66.4 | 67.7 | 74.8 | 59.4 | 75.5 | 79.9 | |||
| 1.5 | S1 | 0.05 | 35.8 | 34.9 | 34.5 | 45.7 | 40.7 | 39.6 | |
| 0.075 | 66.1 | 65.3 | 64.6 | 73.6 | 73.2 | 72.8 | |||
| S2 | 0.05 | 33.5 | 35.2 | 36.9 | 25.5 | 42.3 | 44.0 | ||
| 0.075 | 65.1 | 67.5 | 69.1 | 54.1 | 75.7 | 76.7 | |||
As the association between the marker and the disease becomes stronger (e.g.  or 1.5), the power gain using the shrinkage test becomes smaller because the shrinkage test converges toward the generalized χ2 test, which is asymptotically equivalent to the LRT. Even so, in general, we observed that the shrinkage test was slightly more powerful than the LRT in many cases, especially under the S2 genotyping error model. For instance, under the ADD and the moderate association with
or 1.5), the power gain using the shrinkage test becomes smaller because the shrinkage test converges toward the generalized χ2 test, which is asymptotically equivalent to the LRT. Even so, in general, we observed that the shrinkage test was slightly more powerful than the LRT in many cases, especially under the S2 genotyping error model. For instance, under the ADD and the moderate association with  and disease prevalence
and disease prevalence  , the shrinkage test was 7.5% and 8.7% more powerful than the LRT when the error rates were
, the shrinkage test was 7.5% and 8.7% more powerful than the LRT when the error rates were 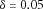 and 0.075 under genotyping error model S2.
and 0.075 under genotyping error model S2.
The proposed shrinkage test also has a substantial edge over the LRT in terms of computing time. It took about 4 min to conduct 10,000 simulations using the LRT; whereas it took only 15 seconds using the proposed shrinkage test on a personal computer with a 3.20 GHZ Intel Core i5 CPU and 4.00 GB memory.
To further understand the behavior of the proposed shrinkage test, we investigated the relationship between the shrinkage factor w and strength of the marker-disease association (i.e. λ2). As shown in Figure 2, across different genetic models, the value of the shrinkage factor w automatically adjusted according to the strength of the marker-disease association. When the association was weak (i.e. the value of λ2 was close to 1), the value of the shrinkage factor w was small, thereby strongly converging the shrinkage test toward the pooled χ2 test to achieve high statistical power. When λ2 increased, the shrinkage factor w approached 1, thereby converging the shrinkage test toward the generalized χ2 test to maintain the validity of the test. These results explain the underlying reason the shrinkage test yields higher power than the LRT, while also controlling the type I error rate at the nominal value, as described previously.
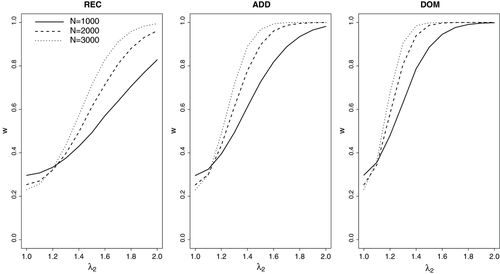
In this simulation studies, we focus on the single-SNP case-control studies. Actually, the proposed shrinkage test can also be used in the GWAS study where millions of SNPs are being tested. The only modification is that we should select a much stricter significance level (i.e. 0.0001) for the GWAS study due to the multiple comparison issue. In the following section, we applied the shrinkage test to a real GWAS dataset to investigate its performance in the GWAS study.
Application
We applied the proposed method to a GWAS dataset from the Genome Medicine Database of Japan (GeMDBJ) [Yoshida et al., 2003]. This dataset contains information from 763 patients diagnosed with Alzheimer's disease and 1,422 healthy volunteers from Japan. A total of 577,728 SNPs were genotyped to identify patterns of genomic variation associated with Alzheimer's disease. According to Matsui et al. [2009], the incidence rate of Alzheimer's disease was 14.6/1,000 persons in the Japanese population. To assess the genotyping quality of the data, we applied the proposed method to the SNPs. We first screened out the SNPs with estimated MAF < 0.05, and then applied the LRT and the shrinkage test to assess the HWE for the remaining 469,225 SNPs.
As shown in Table 3, across different cutoffs (of the p-value) for significance, compared to the LRT, the proposed shrinkage test identified more SNPs that had significant departure from the HWE, which suggests that the shrinkage test has higher power than the LRT. For example, with 0.05 as the significance cutoff, the LRT detected 33,006 significant SNPs, whereas the shrinkage test detected 34,952 significant SNPs. To obtain more insight into the variations in performance between the shrinkage test and the LRT, we calculated the p-values of the SNP-disease association for each of the SNPs based on the trend test (e.g. PVassoc), and then stratified the SNPs into four groups according to PVassoc; see Table 4. Consistent with our simulation results, compared to the statistical power of the LRT, the power gained by using the shrinkage test depended on the strength of the SNP-disease association. When the SNP-disease association was weak (i.e. PVassoc ⩾ 0.05), the shrinkage test identified 1,896 more significant SNPs than the LRT (31,268 vs. 33,164). As the strength of the association became stronger, the difference between these two methods diminished. The shrinkage test identified 41, 8, and 1 more significant SNPs than the LRT when 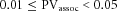 and
and  , and
, and  , respectively. Given the fact that most candidate SNPs in the GWAS are not associated with the disease, the shrinkage test is preferred to the LRT for checking the quality of genotyping in the GWAS. In addition, the proposed shrinkage test required a substantially shorter computing time. To analyze this dataset, the LRT took more than 2.5 hr, whereas the shrinkage test took only about 10 min.
, respectively. Given the fact that most candidate SNPs in the GWAS are not associated with the disease, the shrinkage test is preferred to the LRT for checking the quality of genotyping in the GWAS. In addition, the proposed shrinkage test required a substantially shorter computing time. To analyze this dataset, the LRT took more than 2.5 hr, whereas the shrinkage test took only about 10 min.
| p-value less than | |||||
|---|---|---|---|---|---|
| Method |  |
 |
 |
 |
 |
| LRT | 396 | 437 | 673 | 2,636 | 33,006 |
| Shrinkage | 1,411 | 1,669 | 2,149 | 4,605 | 34,952 |
| p-value for marker-disease association | |||||
|---|---|---|---|---|---|
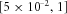
| Method | [0, 10−4) |  |
 |
 |
Total |
| LRT | 3 | 374 | 1,361 | 31,268 | 33,006 |
| Shrinkage | 4 | 382 | 1,402 | 33,164 | 34,952 |
Conclusion
In this article, we propose a shrinkage test for assessing the HWE in case-control data. The proposed shrinkage test is more powerful than the LRT when the marker is independent of or weakly associated with the disease, and remains valid when the marker is strongly associated with the disease. Specifically, we propose a generalized χ2 test that is asymptotically equivalent to the LRT but easier to calculate. Then, we develop a shrinkage test that takes the form of the weighted average of the pooled χ2 test and the generalized χ2 test. We construct the weight (or shrinkage factor) based on the ABF so that the weight adaptively shrinks the test toward the pooled χ2 test or the generalized χ2 test according to the strength of the marker-disease association. When the marker is independent of the disease, the shrinkage test converges to the pooled χ2 test to achieve high statistical power; and when the marker is associated with the disease, the shrinkage test converges to the generalized χ2 test to guarantee the validity of the test. In addition, the shrinkage test has a closed form and is easy to use. A simulation study and real data application show that the shrinkage test outperforms the existing methods with higher statistical power to detect departures from the HWE. The associated R code to implement the proposed shrinkage test can be downloaded from http://odin.mdacc.tmc.edu/yyuan/Software_release/HWE/simu.R
Acknowledgments
The authors thank two referees for their helpful comments and LeeAnn Chastain for her editorial assistance.
Appendix
Expressions for  and
and 
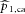 ,
, 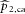 ,
,  and
and 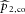 to represent
to represent  ,
,  ,
,  and
and  respectively and denote
respectively and denote 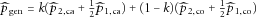 . Thus,
. Thus,  can be rewritten as
can be rewritten as
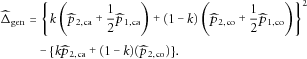
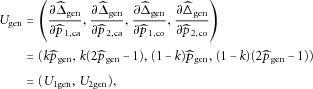
 as
as
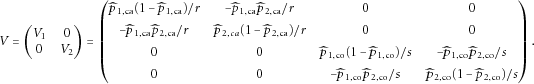
 can be expressed as
can be expressed as
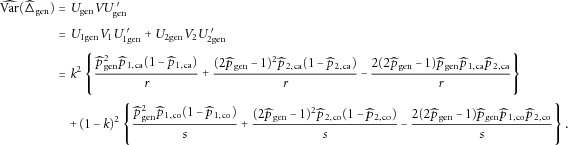
 that can be considered as the estimated “disease prevalence” from the case-control sample, we have
that can be considered as the estimated “disease prevalence” from the case-control sample, we have
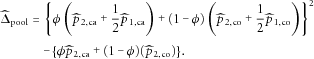
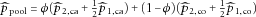 , then
, then
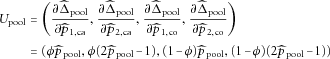
 can be expressed as
can be expressed as
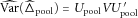
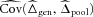 can be obtained as
can be obtained as

 ca be derived as
ca be derived as





