A Kernel Regression Approach to Gene-Gene Interaction Detection for Case-Control Studies
ABSTRACT
Gene-gene interactions are increasingly being addressed as a potentially important contributor to the variability of complex traits. Consequently, attentions have moved beyond single locus analysis of association to more complex genetic models. Although several single-marker approaches toward interaction analysis have been developed, such methods suffer from very high testing dimensionality and do not take advantage of existing information, notably the definition of genes as functional units. Here, we propose a comprehensive family of gene-level score tests for identifying genetic elements of disease risk, in particular pairwise gene-gene interactions. Using kernel machine methods, we devise score-based variance component tests under a generalized linear mixed model framework. We conducted simulations based upon coalescent genetic models to evaluate the performance of our approach under a variety of disease models. These simulations indicate that our methods are generally higher powered than alternative gene-level approaches and at worst competitive with exhaustive SNP-level (where SNP is single-nucleotide polymorphism) analyses. Furthermore, we observe that simulated epistatic effects resulted in significant marginal testing results for the involved genes regardless of whether or not true main effects were present. We detail the benefits of our methods and discuss potential genome-wide analysis strategies for gene-gene interaction analysis in a case-control study design.
Introduction
Genome-wide association studies (GWAS) are a popular approach toward investigating the genetic component of complex diseases. Through the use high-throughput genotyping chips, GWAS can simultaneously characterize hundreds of thousands of single-nucleotide polymorphisms (SNPs) for a given subject. Analysis of GWAS data typically involves the isolated evaluation of individual SNPs for association with a given phenotype. Despite much success in identification of associated loci [Hindorff et al., 2009], such findings generally are of modest effect and often explain only a small proportion of heritability in complex phenotypes [Manolio et al., 2009]. This “missing heritability” has prompted investigators to consider alternative sources of genetic variation in association analysis.
It is well established that coding products of some genes interact with one another molecularly in complex networks, such as enzymatic reactions and signaling cascades [Bonetta, 2010]. Such interactions may contribute to the genetic variation of complex traits [Moore, 2003], with multiple examples documented [Howard et al., 2002; Li et al., 2012; Moore and Williams, 2002; Sima et al., 2012]. Statistically, gene-gene interactions are defined as deviations from additive marginal effects of individual genes [Kempthorne, 1954], and our reference of gene-gene interactions hereafter is with respect to such. In regard to genotyping data, pairwise gene-gene interactions can be considered at the SNP level as statistical interactions between two SNPs in respective genes of interest. Similar to single marker regression analysis, SNP-SNP interaction analysis can be framed as a traditional regression-based analysis by including pairwise interaction terms into a generalized linear model. It is important to note that this definition of interaction does necessarily coincide with the biological interpretation of interaction, and that one does not necessarily imply the other [Greenland, 2009]. Although the utility of identifying such interactions with respect to explaining missing heritability is contentious [Aschard et al., 2012; Moore and Williams, 2009], such interactions can at the very least contribute to our understanding of complex disease etiology.
Advancements in both genotyping technology and imputation methodology have increased the density of genotyped markers in the coding regions of genes. Moreover, large-scale next-generation sequencing technologies, such as whole exome/genome sequencing, interrogate all genetic variation within regions of interest. Unlike traditional GWAS, these tools yield dense genotype data. Under such conditions, exhaustive genome-wide evaluation of SNP-level pairwise interaction is computationally burdensome [Moore and Ritchie, 2004]. Thus, the development of statistically powerful and computationally efficient algorithms for detecting these interactions is of great interest. A comprehensive review of gene-gene interaction analysis can be found by Cordell [2009].
Gene-level testing has recently grown in popularity due to its dimensional reduction and biological interpretability [Jorgenson and Witte, 2006; Neale and Sham, 2004]. In contrast to single-SNP analyses, such tests allow for all of the SNPs within the region of a gene to be modeled jointly as a set and can take into account the linkage disequilibrium (LD) structure within the gene. By grouping SNPs based upon prior biological information, SNP-set testing may improve power and increase the chance of reproducible significant findings [Wu et al., 2010], particularly when multiple causal SNPs are present in a given gene. Although SNP-set approaches are not necessarily restricted to gene-level definition, the gene as a functional unit is a natural choice and provides an intuitive decomposition of the genome.
Kernel machine methods in particular have provided a successful tool in SNP-set association testing [Kwee et al., 2008; Wu et al., 2010, 2011]. Such approaches determine genetic association through representations of genomic similarity between pairs of subjects [Schaid, 2010a, 2010b]. Recently, Li and Cui presented a gene-level interaction approach for continuously valued quantitative traits using a kernel machine smoothing-spline ANOVA model, which they refer to as SPA3G [Li and Cui, 2012]. An application of this method for a binary response, such as disease status, presents unique challenges that preclude a direct application of SPA3G, notably that the response can no longer be assumed to be Gaussian distributed. These challenges motivated our work to adapt the methods within SPA3G to be applicable to case-control studies.
In this paper, we outline a comprehensive approach toward hypothesis testing for marginal and interaction effects of genes in association analysis for dichotomous responses using regression-based score tests. In addition to detailing omnibus and marginal tests, we define a kernel regression approach toward gene-gene interaction detection for a dichotomous response under a generalized linear mixed model (GLMM) framework. We evaluate the performance of these testing approaches using coalescent simulation data under a variety of experimental conditions and investigate their relation to one another within the context of multiple epistatic models. We also compare our approach to exhaustive SNP-SNP logistic regression and two leading gene-level gene-gene interaction methods. Finally, we discuss the implications of our findings and suggest future directions for further development.
Methods
Consider a case-control association study involving N individuals, such that N is composed of NCase cases and NCont controls. Let  be a binary representation of case-control status, such that
be a binary representation of case-control status, such that  if the jth subject is designated a case and 0 otherwise. Let
if the jth subject is designated a case and 0 otherwise. Let  be an
be an  set of any additional covariate data, and
set of any additional covariate data, and 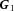 and
and 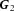 be respective
be respective  and
and  matrices of genotypes for markers contained within the regions of genes 1 and 2, where q1 and q2 correspond to the number of respective markers within each gene. It is assumed that these regions are defined a priori based upon some relevant biological criteria. We define genotypes under an additive model, such that
matrices of genotypes for markers contained within the regions of genes 1 and 2, where q1 and q2 correspond to the number of respective markers within each gene. It is assumed that these regions are defined a priori based upon some relevant biological criteria. We define genotypes under an additive model, such that  is the integer count of minor alleles observed at marker k in gene i for subject j.
is the integer count of minor alleles observed at marker k in gene i for subject j.
 , we can map
, we can map 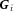 to some Hilbert space through the mapping
to some Hilbert space through the mapping  such that
such that  is an inner product space. This is accomplished through the “kernel trick” [Schölkopf and Smola, 2002] that calculates inner products in
is an inner product space. This is accomplished through the “kernel trick” [Schölkopf and Smola, 2002] that calculates inner products in  through the given kernel function, such that
through the given kernel function, such that

 represents all the marker genotypes for gene i for subject j. The kernel function circumvents the necessity to calculate the explicit mappings
represents all the marker genotypes for gene i for subject j. The kernel function circumvents the necessity to calculate the explicit mappings 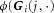 , yielding the kernel space mapping
, yielding the kernel space mapping  of the respective original genotype matrix
of the respective original genotype matrix 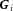 . This kernel matrix
. This kernel matrix  is an
is an  full Gram matrix, such that the element-wise definition is given as
full Gram matrix, such that the element-wise definition is given as 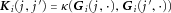 for
for  . From Aronszajn [1950], we also define the interaction kernel matrix
. From Aronszajn [1950], we also define the interaction kernel matrix 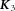 as
as  , where the operator ○ represents the Hadamard, or element-wise, product. Through
, where the operator ○ represents the Hadamard, or element-wise, product. Through 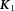 ,
,  , and
, and 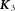 , the genetic effect of the two genes of interest on the phenotypic variation is decomposed into main and interaction effects. These matrices in turn can be applied in a mixed-model context as underlying covariance structures for variance components. Let
, the genetic effect of the two genes of interest on the phenotypic variation is decomposed into main and interaction effects. These matrices in turn can be applied in a mixed-model context as underlying covariance structures for variance components. Let 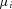 represent the probability that the ith observation is a case, and
represent the probability that the ith observation is a case, and 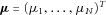 . We consider a mixed effects logistic model for
. We consider a mixed effects logistic model for  , such that
, such that

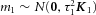 ,
, 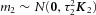 , and
, and 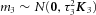 are independent
are independent  random effect vectors, and
random effect vectors, and  .
.Global Hypothesis Test
Define the omnibus, or global, hypothesis of no genetic effect such that  . The score statistic is defined as
. The score statistic is defined as 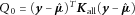 , where
, where  and
and 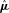 are the fitted values of μ on
are the fitted values of μ on  under H0. Under the null hypothesis, Q0 is asymptotically distributed as a weighted mixture of chi-square distributions [Liu et al., 2008]. Although there are a number of methods to characterize this distribution for purposes of hypothesis testing, we employ Pearson's three-moment approach [Imhof, 1961] because the approximation error can be bounded.
under H0. Under the null hypothesis, Q0 is asymptotically distributed as a weighted mixture of chi-square distributions [Liu et al., 2008]. Although there are a number of methods to characterize this distribution for purposes of hypothesis testing, we employ Pearson's three-moment approach [Imhof, 1961] because the approximation error can be bounded.
Marginal and Interaction Hypothesis Tests
It is possible to test for the presence of marginal effects of each gene individually by using the respective kernel matrix in the framework of the score statistic, such that 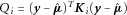 for
for 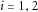 . This is equivalent to the sequence kernel association test (SKAT) [Wu et al., 2011]. If there are no marginal effects present (
. This is equivalent to the sequence kernel association test (SKAT) [Wu et al., 2011]. If there are no marginal effects present ( ,
,  ), we can also test specifically for a statistical interaction between genes 1 and 2 via the score statistic
), we can also test specifically for a statistical interaction between genes 1 and 2 via the score statistic 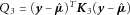 , which we refer to as the interaction test. For any of these tests, we again approximate the null distribution of
, which we refer to as the interaction test. For any of these tests, we again approximate the null distribution of 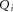 by the Pearson's approximation.
by the Pearson's approximation.
Composite Hypothesis Test
We also define a test specifically for an interaction effect adjusting for the presence of marginal gene effects ( ), such that
), such that  . This requires fitting the null GLMM that includes the main effects of the two genes, which may be conducted using penalized quasi-likelihood (PQL) [Breslow and Clayton, 1993]. Maximum likelihood approaches toward fitting GLMMs involve intractable integration of high dimension, and PQL utilizes Laplace approximation in order to accommodate this integration through iterative estimation of the fixed and random model components. For our purposes, we fit this model using the glmmPQL function from the MASS library in R [Venables and Ripley, 2002].
. This requires fitting the null GLMM that includes the main effects of the two genes, which may be conducted using penalized quasi-likelihood (PQL) [Breslow and Clayton, 1993]. Maximum likelihood approaches toward fitting GLMMs involve intractable integration of high dimension, and PQL utilizes Laplace approximation in order to accommodate this integration through iterative estimation of the fixed and random model components. For our purposes, we fit this model using the glmmPQL function from the MASS library in R [Venables and Ripley, 2002].
 and
and  to be diagonal
to be diagonal  matrices with corresponding diagonal elements
matrices with corresponding diagonal elements

 is the link function in the GLMM,
is the link function in the GLMM,  denotes the first derivative of
denotes the first derivative of  with respect to
with respect to 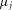 ,
,  is the corresponding variance function, and
is the corresponding variance function, and 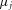 is the mean for the jth subject under the null model. Because we apply the canonical logit link function, it follows that
is the mean for the jth subject under the null model. Because we apply the canonical logit link function, it follows that  . From Lin [1997], we define
. From Lin [1997], we define 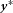 to be the PQL working vector under the null GLMM, such that
to be the PQL working vector under the null GLMM, such that


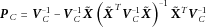 is the null projection matrix and
is the null projection matrix and  is the estimated null covariance matrix with variance component parameter estimates
is the estimated null covariance matrix with variance component parameter estimates  and
and  . Although Lin goes on to define a normalized version of the score statistic, our early findings indicated strong biases for a dichotomous response under the null. Similar to the global and marginal score tests, we derive the null distribution for
. Although Lin goes on to define a normalized version of the score statistic, our early findings indicated strong biases for a dichotomous response under the null. Similar to the global and marginal score tests, we derive the null distribution for  using the Pearson's approximation.
using the Pearson's approximation.Computational Considerations
Fitting the composite null model using PQL requires that 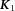 and
and 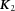 be decomposed into corresponding square-root matrices
be decomposed into corresponding square-root matrices  and
and  , such that
, such that 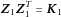 and
and 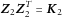 . When a linear (or weighted linear) kernel is used, this is easily accommodated because
. When a linear (or weighted linear) kernel is used, this is easily accommodated because 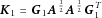 , where
, where  is a diagonal weight matrix, such that
is a diagonal weight matrix, such that 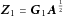 . If a nonlinear kernel function, such as the Gaussian kernel, is used, then this may be completed using the incomplete Cholesky decomposition [Kershaw, 1978] of
. If a nonlinear kernel function, such as the Gaussian kernel, is used, then this may be completed using the incomplete Cholesky decomposition [Kershaw, 1978] of  , whereby
, whereby  is the lower triangle matrix. Then, the random effects
is the lower triangle matrix. Then, the random effects 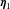 and
and 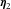 are modeled as
are modeled as 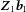 and
and  , such that
, such that  and
and  . Because such decompositions can be computationally intensive, there is initial appeal to the use of some form of linear kernel for this application, particularly when the number of markers per gene is relatively small.
. Because such decompositions can be computationally intensive, there is initial appeal to the use of some form of linear kernel for this application, particularly when the number of markers per gene is relatively small.
Algorithms for approximating the null distribution of the score statistics (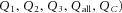 are dependent upon deriving the eigenvalues of
are dependent upon deriving the eigenvalues of  for the respective kernel matrix K and projection matrix P of each test, which always will be
for the respective kernel matrix K and projection matrix P of each test, which always will be  . This can be computationally demanding, as such decompositions are in practice
. This can be computationally demanding, as such decompositions are in practice  . However, equivalent eigenvalues can be derived from
. However, equivalent eigenvalues can be derived from  . This form is more appealing for two reasons: (1) it is guaranteed to be positive definite, which can be exploited by decomposition algorithms; and (2) if
. This form is more appealing for two reasons: (1) it is guaranteed to be positive definite, which can be exploited by decomposition algorithms; and (2) if  , the computational burden of this eigendecomposition is greatly reduced. This can motivate the use of low-rank approximations of
, the computational burden of this eigendecomposition is greatly reduced. This can motivate the use of low-rank approximations of  , although we leave this topic to future research.
, although we leave this topic to future research.
Kernel Selection
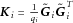 where
where
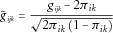
Simulation Study
In order to assess the properties of type I error rate control and statistical power for our hypothesis tests, we devised a comprehensive simulation study. Our basic simulation strategy was to simulate haplotypes and randomly combine haplotypes to create a large population of genotypes. Then, under a given genetic disease model and prevalence, we simulated disease status and performed case-control sampling to obtain our test data. The details of our simulation are given below.
To simulate genotypic data, we used the calibrated coalescent model simulation software COSI [Schifano et al., 2012] to generate two independent sets of ten thousand 50 kb regions, each representative of a distinct gene. Recombination maps were based upon observed LD structure in samples of European ancestry. A derived minor allele frequency (dMAF) was calculated for each marker based upon its frequency in the haplotype population to represent a population-based value. From these pools of haplotypes, we generated a large population of Npop genotype profiles for simulated individuals by combining two randomly selected haplotypes. The two gene-wise datasets had 1,017 and 1,040 polymorphic sites, respectively, with 116 and 164 being common SNPs (dMAF ⩾0.05). We then selected a subset of common SNPs for each gene to represent our simulation genotyped marker data, such that the maximum pairwise Pearson correlation between any two SNPs in a given gene was ⩽0.50. This resulted in 12 and 25 genotyped SNPs for genes 1 and 2, respectively, ranging in dMAF from 0.05 to 0.49. LD plots of both SNP sets are found in Figure 1.

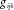 to corresponding genotype weights,
to corresponding genotype weights,  , which are based upon the dMAF of the respective SNPs. Let Ω1 and Ω2 respectively define the subsets of gene 1 and gene 2 SNPs selected to be causal. Dichotomous phenotypes are then simulated via a log-linear model with probability of occurrence
, which are based upon the dMAF of the respective SNPs. Let Ω1 and Ω2 respectively define the subsets of gene 1 and gene 2 SNPs selected to be causal. Dichotomous phenotypes are then simulated via a log-linear model with probability of occurrence 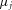 , such that for subject j
, such that for subject j

 and
and  the marginal effects for the respective SNPs, and
the marginal effects for the respective SNPs, and  the interaction effect between SNP l in gene 1 and SNP m in gene 2, with
the interaction effect between SNP l in gene 1 and SNP m in gene 2, with 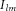 (0 or 1) an indicator for the presence of that specific interaction. The genotype weights
(0 or 1) an indicator for the presence of that specific interaction. The genotype weights  are functions of the population-level MAF (dMAF) of the respective SNPs, and are defined such that the expected effect of each interaction term conditional on a specific genotype at one locus is always equal to 0 (see Aschard et al. [2012] for details). We let all marginal effects be randomly selected uniformly between log(1.1) and log (1.3) to reflect realistic relative risk (RR) values observed in GWAS. By setting various effect components to be null, we also control which genetic effects are present in our disease model. For each simulation, we generated a population of
are functions of the population-level MAF (dMAF) of the respective SNPs, and are defined such that the expected effect of each interaction term conditional on a specific genotype at one locus is always equal to 0 (see Aschard et al. [2012] for details). We let all marginal effects be randomly selected uniformly between log(1.1) and log (1.3) to reflect realistic relative risk (RR) values observed in GWAS. By setting various effect components to be null, we also control which genetic effects are present in our disease model. For each simulation, we generated a population of  genotypes and performed case-controls sampling, with disease prevalence fixed at 0.10. All causal SNPs were randomly selected for each simulation replication.
genotypes and performed case-controls sampling, with disease prevalence fixed at 0.10. All causal SNPs were randomly selected for each simulation replication.Finally, given that gene-gene interaction analysis is an active area of research, we compared the power of our testing procedures to gene-based Bonferroni-adjusted single SNP-SNP logistic regression, along with two leading gene-level approaches: kernel canonical correlation analysis (KCCA) [Larson et al., 2013; Yuan et al., 2012] and principal component (PC) analysis-based logistic regression modeling (PC-LR). KCCA is an LD-based procedure, which uses kernelized canonical correlation analysis to test for differences in association between genes across case-control status using a Gaussian kernel function. Variations of PC-LR [Bhattacharjee et al., 2010; He et al., 2011; Wang and Abbott, 2008] have been shown to be powerful approaches for gene-level interaction analysis by reducing the marker data for a given gene to a few leading PCs. For our PC-LR analysis, we derive the lead PC term from each gene and test the statistical significance of their interaction in the presence of their marginal effects within a basic logistic regression model.
Results
Type I Error
We examined type I error rate control for sample sizes of 1,000, 1,500, and 2,000, with balanced numbers of cases and controls. For the global, marginal, and interaction tests, a total of 100,000 simulation runs were run for each sample size, with type I error rates evaluated at α levels of 0.001 and 0.0001. Table 1 presents the type I error simulation results for these tests, along with Figure 2 presenting QQ plots of the respective −log10 transformed p-values. These tests exhibit near nominal type I error rates across all α levels, with the interaction test tending toward being more conservative for smaller sample sizes.
| Global test | Marginal test | Interaction test | ||||
|---|---|---|---|---|---|---|
| N | α = 1 × 10−3 | α = 1 × 10−4 | α = 1 × 10−3 | α = 1 × 10−4 | α = 1 × 10−3 | α = 1 × 10−4 |
| 1,000 | 8.3 × 10−4 | 5.0 × 10−5 | 9.3 × 10−4 | 6.0 × 10−5 | 3.7 × 10−4 | 1.0 × 10−5 |
| 1,500 | 8.0 × 10−4 | 6.0 × 10−5 | 1.1 × 10−3 | 1.1 × 10−4 | 5.4 × 10−4 | 3.0 × 10−5 |
| 2,000 | 8.7 × 10−4 | 6.0 × 10−5 | 1.1 × 10−3 | 1.2 × 10−4 | 7.0 × 10−4 | 4.0 × 10−5 |
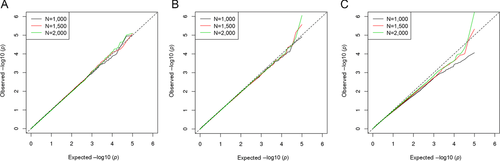
We also examined type I error rate control for the composite test when marginal effects are present in both genes but there is no interaction ( , and contrast it with that of the interaction test where such marginal effects are not taken into account. We considered disease models where the number of causal markers per gene was 1 or 2, and ran 4,000 replications. Results for the error rates of the two tests can be found in Table 2 at α levels of 0.05 and 0.01. Interestingly, the findings indicate that both the interaction test and composite test control the type I error rate under both models despite the lack of marginal effect adjustment for the interaction test.
, and contrast it with that of the interaction test where such marginal effects are not taken into account. We considered disease models where the number of causal markers per gene was 1 or 2, and ran 4,000 replications. Results for the error rates of the two tests can be found in Table 2 at α levels of 0.05 and 0.01. Interestingly, the findings indicate that both the interaction test and composite test control the type I error rate under both models despite the lack of marginal effect adjustment for the interaction test.
| 1 Causal SNP per gene | 2 Causal SNPs per gene | |||||||
|---|---|---|---|---|---|---|---|---|
| Interaction (Q3) | Composite  |
Interaction (Q3) | Composite  |
|||||
| N | α = 0.05 | α = 0.01 | α = 0.05 | α = 0.01 | α = 0.05 | α = 0.01 | α = 0.05 | α = 0.01 |
| 1,000 | 0.0390 | 0.0090 | 0.0398 | 0.0088 | 0.0355 | 0.0058 | 0.0378 | 0.0050 |
| 1,500 | 0.0385 | 0.0065 | 0.0375 | 0.0063 | 0.0408 | 0.0070 | 0.0398 | 0.0070 |
| 2,000 | 0.0420 | 0.0063 | 0.0438 | 0.0068 | 0.0440 | 0.0108 | 0.0445 | 0.0108 |
Power
We first considered a set of simulations in which there were single causal interacting SNPs in each gene for sample sizes of  , 1,500, and 2,000. Because there is specific interest in being able to detect interacting loci in the absence of marginal effects, we considered simulation conditions with and without marginal effects present. We examined four specific values of γ12 [log(1.5), log(2.0), log(2.5), log(3.0)] in our simulations, and ran 500 replications for each unique set of conditions, reporting empirical power at an α level of 0.05. Figure 3 presents our findings for all of our score-based tests along with the SNP-SNP, PC-LR, and KCCA approaches under these simulation conditions. The results show that when marginal effects are present, the various score tests generally perform best, especially at lower values of γ12. When marginal effects were absent, KCCA and the global test had the highest power at lower effect sizes as well. Interestingly, the marginal tests indicate power levels above the type I error rate despite no marginal effects being explicitly modeled.
, 1,500, and 2,000. Because there is specific interest in being able to detect interacting loci in the absence of marginal effects, we considered simulation conditions with and without marginal effects present. We examined four specific values of γ12 [log(1.5), log(2.0), log(2.5), log(3.0)] in our simulations, and ran 500 replications for each unique set of conditions, reporting empirical power at an α level of 0.05. Figure 3 presents our findings for all of our score-based tests along with the SNP-SNP, PC-LR, and KCCA approaches under these simulation conditions. The results show that when marginal effects are present, the various score tests generally perform best, especially at lower values of γ12. When marginal effects were absent, KCCA and the global test had the highest power at lower effect sizes as well. Interestingly, the marginal tests indicate power levels above the type I error rate despite no marginal effects being explicitly modeled.

 as a function of interaction effect size exp(γ12), for the global, marginal, interaction, and composite tests, along with SNP-SNP logistic regression, PCA, and KCCA methods. Results are shown with marginal effects present for sample sizes (A)
as a function of interaction effect size exp(γ12), for the global, marginal, interaction, and composite tests, along with SNP-SNP logistic regression, PCA, and KCCA methods. Results are shown with marginal effects present for sample sizes (A) 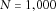 , (B)
, (B) 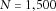 , and (C)
, and (C)  , and with marginal effects absent for sample sizes (D)
, and with marginal effects absent for sample sizes (D)  , (E)
, (E)  , and (F)
, and (F)  .
.In all simulations, the SNP-SNP approach tended to be best (or at least competitive) when the interaction effect size was most extreme, regardless of whether or not marginal effects were present. This corroborates previous findings that have found SNP-SNP methods to be competitively powerful when the gene-level interaction is isolated to a single pair of SNPs [He et al., 2011; Li and Cui, 2010].
We also considered an additional set of simulations where two pairs of interacting SNPs were present across genes, and values of  were randomly sampled uniformly from the interval [log(1.5), log(2.0)]. All other simulation conditions were the same as previously defined and 1,000 replications were run per unique set of conditions. A barplot of these results can be found in Figure 4. These findings indicate that even in the absence of marginal effects, the global test is the most powerful approach for identifying the presence of interaction. The interaction and composite tests were relatively close in their empirical power, and performed similarly to the SNP-SNP testing. The KCCA approach performed comparably to the previously mentioned test when no marginal effects were present, but was less powerful when marginal effects were included.
were randomly sampled uniformly from the interval [log(1.5), log(2.0)]. All other simulation conditions were the same as previously defined and 1,000 replications were run per unique set of conditions. A barplot of these results can be found in Figure 4. These findings indicate that even in the absence of marginal effects, the global test is the most powerful approach for identifying the presence of interaction. The interaction and composite tests were relatively close in their empirical power, and performed similarly to the SNP-SNP testing. The KCCA approach performed comparably to the previously mentioned test when no marginal effects were present, but was less powerful when marginal effects were included.

 for hypothesis testing when the number of causal SNPs per gene is two, where interaction effects
for hypothesis testing when the number of causal SNPs per gene is two, where interaction effects  are uniformly drawn from [log(1.5), log(2.0)]. Results are presented for sample sizes of
are uniformly drawn from [log(1.5), log(2.0)]. Results are presented for sample sizes of 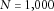 , 1,500, and 2,000, with marginal effects either present (Marg = T) or absent (Marg = F).
, 1,500, and 2,000, with marginal effects either present (Marg = T) or absent (Marg = F).It is important to note that under all simulations, the interaction test was more powerful than the composite test regardless of the inclusion of marginal effects.
Discussion
Gene-gene interactions are becoming an increasingly common component to genomic association analysis. Increasing GWAS chip sizes, imputation, and next-generation sequencing platforms will continue to increase the number of genotyped intragenic SNPs, and the need for computationally efficient strategies for exploratory interaction analysis among loci has grown in response. In this paper, we have detailed a comprehensive approach toward detecting the presence of genetic effects, specifically gene-gene interactions, for case-control genetic association studies. We have devised a global test for detecting the presence of gene-level associations via kernel matrix representations of marker data. Using a simulation study based upon realistic genotype data, we have demonstrated that it is a powerful approach toward detecting the presence of both main and interaction effects of gene-level risk association. By adapting the work of Li and Cui for quantitative traits to binary traits using GLMMs, we have also defined a score test, the composite test, for detecting gene-gene interactions after adjusting for main effects.
As Figures 3 and 4 indicate, the global test is a powerful approach toward detecting gene-gene interactions even in the absence of marginal effects. Given that the global test only requires fitting a single null regression model, it is a computationally attractive screening procedure for possible interactions and can rapidly be implemented in a genome-wide analysis. Subsequent testing performed on significant findings can then be applied to identify the particular architecture of the genetic association. We also found that marginal tests result in significant findings despite the exclusion of marginal effects from our simulations. Although lower powered than the global test, conducting solely marginal tests (SKAT) could be an effective alternative strategy in contrast to the testing burden of exhaustive pairwise exploratory analysis.
As per Table 2, the interaction test (Q3) does not incur any quantifiable bias when multiple SNPs with true marginal effects are present in the simulation model. Although the included simulations are restricted to a relatively small number of total SNPs per gene as well as marginal effects of modest size, this is a surprising result that raises the question of whether or not the interaction test can be used as a proxy for the composite test. More surprising is that the interaction test is more powerful than the composite test in all of our simulations. Although we refrain from recommending the composite test be abandoned for the interaction test, it is computationally appealing prospect which warrants further investigation.
With increasing numbers of polymorphic sites being either genotyped or imputed in association studies, computational burden is of particular importance, especially relative to SNP-level testing. For example, on a modern workstation with an Intel® Core™ i5 3.10 Ghz processor and 4 GB of RAM, running all possible pairwise SNP-SNP tests for our simulation required 7.914 sec per simulation replication when  . Running the global score test, meanwhile, requires only 2.595 sec. This discrepancy in computational burden is further evidenced if we increase SNP-level testing burden, as such analyses scale poorly as the number of included SNPs increases. If we consider a simple data simulation where genotypes are independently sampled from a binomial distribution, and set the number of genotyped SNPs per gene to 100, the respective compute times for exhaustive SNP-SNP testing and the global test are 236.54 and 22.00 sec, respectively. It is important to note, however, that the computational burden of the kernel-based tests scales largely with respect to sample size N, as this requires decomposition of larger and larger kernel Gram matrices. Respective compute times for the SNP-SNP tests and the global test when
. Running the global score test, meanwhile, requires only 2.595 sec. This discrepancy in computational burden is further evidenced if we increase SNP-level testing burden, as such analyses scale poorly as the number of included SNPs increases. If we consider a simple data simulation where genotypes are independently sampled from a binomial distribution, and set the number of genotyped SNPs per gene to 100, the respective compute times for exhaustive SNP-SNP testing and the global test are 236.54 and 22.00 sec, respectively. It is important to note, however, that the computational burden of the kernel-based tests scales largely with respect to sample size N, as this requires decomposition of larger and larger kernel Gram matrices. Respective compute times for the SNP-SNP tests and the global test when  on our COSI simulation data are 12.123 and 34.044 sec, respectively. This burden can be mitigated with varying strategies, however, including low-rank decompositions [Bach and Jordan, 2005], which could significantly reduce computational times. More work is necessary to explore the utility of these approaches.
on our COSI simulation data are 12.123 and 34.044 sec, respectively. This burden can be mitigated with varying strategies, however, including low-rank decompositions [Bach and Jordan, 2005], which could significantly reduce computational times. More work is necessary to explore the utility of these approaches.
Even with computationally efficient implementations of our gene-level interaction tests, exhaustive pairwise analysis of a genome with 25,000 genes would require
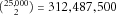 hypothesis tests, which is generally infeasible with respect to both computational and multiple testing burdens. Efficient strategies for implementing agnostic genome-wide analysis thus should be dependent in part on prior functional information. One strategy would be to utilize protein-protein interaction (PPI) databases to define a body of potential gene-gene interaction pairs, greatly reducing the testing space. For example, we downloaded the protein interaction network analysis [Wu et al., 2009] PPI dataset for binary interactions in Homo sapiens (accessed February 2013). This information was reduced to the gene level (HUGO designation) and redundant pairs were removed. This resulted in 106,004 unique gene pairs between 14,784 individual genes, a substantially reduced testing multiplicity. Stricter inclusion criteria, such as experimental validation, can further reduce this testing set.
hypothesis tests, which is generally infeasible with respect to both computational and multiple testing burdens. Efficient strategies for implementing agnostic genome-wide analysis thus should be dependent in part on prior functional information. One strategy would be to utilize protein-protein interaction (PPI) databases to define a body of potential gene-gene interaction pairs, greatly reducing the testing space. For example, we downloaded the protein interaction network analysis [Wu et al., 2009] PPI dataset for binary interactions in Homo sapiens (accessed February 2013). This information was reduced to the gene level (HUGO designation) and redundant pairs were removed. This resulted in 106,004 unique gene pairs between 14,784 individual genes, a substantially reduced testing multiplicity. Stricter inclusion criteria, such as experimental validation, can further reduce this testing set.
Although there are a number of benefits to gene-level testing, questions remain as to how to interpret replicability of specific findings, because it is possible different sets of interacting SNPs may yield the same significant gene pair. This requires a paradigm shift in how gene-level association is considered relative to individual SNPs, being more akin to gene-set types of analyses. Moreover, special considerations will be necessary for multiple testing, because there is a clear issue of dependence among test statistics where a given gene is a member of multiple gene pairs being evaluated. Additional work is necessary to evaluate the effects of such dependence on multiple testing correction.
Power analysis for multilocus approaches, such as gene-level testing, is complicated by a number of factors, including the quantity of total and interacting SNPs, their respective MAFs, overall LD structure of the genotyped SNPs themselves, and underlying models of epistasis [Marchini et al., 2005]. Although our random selection of causal SNPs in our simulations averages over a number of these factors, our simulations are by no means exhaustive and systematic influences on power will remain. The kernel function itself may also impact statistical power, as the polygenic kernel is just one of many possible options and alternative selections may behave differently from our findings. Although it is not within the scope of this paper to investigate the impact of the kernel function itself, we acknowledge that strategic kernel selection may impact hypothesis-testing performance. Influence of kernel selection under differing epistatic models is a focus of future work, particularly with respect to its comparative performance with KCCA, which is specifically capable of nonlinear interaction detection.
Although we have presented this work strictly within the context of a dichotomous trait, we note that the theoretical adaptation of our approach from SPA3G could be modified to account for any non-Gaussian response with a presumed exponential family distribution with little difficulty. We also foresee this testing framework being expanded to address pathway analysis applications and higher order interactions through linear combinations of gene-level kernel matrices and their Hadamard products.
Acknowledgments
This research was supported by the U.S. Public Health Service, National Institutes of Health, contract number GM065450. We also thank the anonymous reviewers for their constructive comments. The authors declare no conflict of interest.




