The Value of Statistical or Bioinformatics Annotation for Rare Variant Association With Quantitative Trait
ABSTRACT
In the past few years, a plethora of methods for rare variant association with phenotype have been proposed. These methods aggregate information from multiple rare variants across genomic region(s), but there is little consensus as to which method is most effective. The weighting scheme adopted when aggregating information across variants is one of the primary determinants of effectiveness. Here we present a systematic evaluation of multiple weighting schemes through a series of simulations intended to mimic large sequencing studies of a quantitative trait. We evaluate existing phenotype-independent and phenotype-dependent methods, as well as weights estimated by penalized regression approaches including Lasso, Elastic Net, and SCAD. We find that the difference in power between phenotype-dependent schemes is negligible when high-quality functional annotations are available. When functional annotations are unavailable or incomplete, all methods suffer from power loss; however, the variable selection methods outperform the others at the cost of increased computational time. Therefore, in the absence of good annotation, we recommend variable selection methods (which can be viewed as “statistical annotation”) on top of regions implicated by a phenotype-independent weighting scheme. Further, once a region is implicated, variable selection can help to identify potential causal single nucleotide polymorphisms for biological validation. These findings are supported by an analysis of a high coverage targeted sequencing study of 1,898 individuals.
Introduction
Recent studies have shown that rare variants may be important to the underlying etiology of complex traits [Cohen et al., 2004; Dickson et al., 2010; Gorlov et al., 2008; Haase et al., 2012; Nelson et al., 2012; Zawistowski et al., 2010] and that they may account for part of the “missing heritability” [Eichler et al., 2010; Gibson, 2010; Maher, 2008; Manolio et al., 2009] left by genome-wide association studies (GWAS). Conventional association analysis methods, which evaluate each variant independently of all others, lack the statistical power to evaluate rare variants given the sample size of sequencing data currently available. However, there is increasing evidence that the combined effects of rare variants in the same exon, gene, region, or biological pathway can be used to elucidate complex phenotypes [Cohen et al., 2004; Nejentsev et al., 2009; Sanna et al., 2011]. Where the effect size of a single variant may not be large enough to detect with the sample sizes available, a collection of variants with small effect size, taken together, may be detectable. In order to explore the potential effects of rare variants in present-day genomic data, a large number of methods [Bacanu et al., 2011; Cheung et al., 2012; Lee et al., 2012; Li and Leal, 2008; Li et al., 2010a; Madsen and Browning, 2009; Mao et al., 2013; Neale et al., 2011; Price et al., 2010; Tzeng et al., 2011; Wu et al., 2011; Xu et al., 2012; Yi et al., 2011] for aggregating information across variants have emerged. However there is little consensus on which method is most effective. The weighting scheme adopted when aggregating across variants is an important consideration, as is the use of functional or bioinformatics information when available.
We present an evaluation of multiple weighting schemes through a series of simulations. We evaluate several existing phenotype-independent [Cohen et al., 2004; Madsen and Browning, 2009; Morgenthaler and Thilly, 2007] and phenotype-dependent weighting schemes [Wu et al., 2011; Xu et al., 2012], as well as weighting schemes determined by linear regression, penalized regression, and variable selection methods, including Lasso [Tibshirani, 1996], Elastic Net (EN) [Zou and Hastie, 2005], and SCAD [Xie and Huang, 2009]. We conduct simulations under a variety of scenarios with different numbers of true causal variants, mixtures of direction of effect, and availability of functional information, mimicking sequencing studies of a quantitative trait. We then apply each of these methods to a set of high coverage targeted sequencing data [Nelson et al., 2012] of 1,898 individuals from the CoLaus population-based cohort [Firmann et al., 2008].
Materials and Methods
Over the last few years, numerous sensible weighting schemes have been proposed. In most of these methods a genomic region or variant set is assigned a weighted sum over the variants meant to describe the burden of potentially influential variants carried by each individual. We call this weighted sum Si. Further, we assume there are N individuals under study, indexed by i, and for each individual we have M variants in the region or variant set, indexed by j.
Phenotype-Independent Weighting Schemes
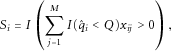
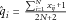is the estimated MAF of variant j in the data with pseudocounts and Q is the MAF threshold. In this work, we consider Q = 0.05.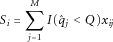
being the estimated MAF, as defined above.
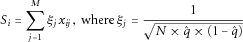
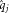as above. In the original Madsen and Browning framework for case-control studies, MAFs are estimated using controls only. However, in this paper, the outcome of interest is quantitative and we estimate MAF using the entire sample, which makes the method phenotype-independent in this context.Phenotype-Dependent Weighting Schemes
for each variant j separately and independently and then take the fitted values 
to be our weights.
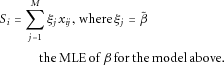
Though imperfect, this weighting scheme allows investigators to test for associations with multiple rare variants in cases where N < M and begin to follow up on individual variants that may potentially be of interest.
Second, we consider weights from ordinary multiple regression, modeling all of the M variants simultaneously. That is, we fit the model Y = Xβ +ε, where the (i, j)th element of the matrix X = xij, the minor allele count for individual i at variant j. We then take Si to be as above, with the fitted values from this multiple regression, 
[Lin and Tang, 2011; Xu et al., 2012].
We also consider weights from several variable selection methods. Such methods are appealing because we expect the majority of rare variants not to influence the quantitative trait of interest. Use of penalized regression is therefore expected to reduce the number of nonzero weights. Similar strategies were recently proposed in the context of rare variant association testing [Turkmen and Lin, 2012; Zhou et al., 2010]. In penalized regression, we solve for the 
, which best fit the data, subject to some constraint(s) or penalty. That is, instead of minimizing the sum of squared error, 
, we aim to minimize the sum of squared errors and an additional penalty term,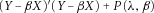 
. In general, the greater the number of parameters included in the model, the greater the penalty. A number of penalty functions have been proposed and extensively studied in the recent statistical literature [Heckman and Ramsay, 2000; Hesterberg et al., 2008; Kyung et al., 2010; Wu and Lange, 2008]. Of these, we chose three: the Lasso, which imposes a linear penalty [Tibshirani, 1996], EN, which imposes a quadratic penalty [Zou and Hastie, 2005], and SCAD, which is designed to penalize smaller coefficients more heavily than larger coefficients [Xie and Huang, 2009].
For Lasso and SCAD, only one tuning parameter, λ, is required. We used the R packages lars [Efron et al., 2004] and ncvreg [Breheny and Huang, 2011] with default parameter values, which is to choose the optimal λ among a grid of 100 possible values equally spaced on the log-scale. For EN, there are two tuning parameters, one for the linear component and one for the quadratic component. The linear term, λ1, is chosen in the same way as the λ parameter for the Lasso and SCAD methods, discussed above. The quadratic parameter, λ2, was set to 1 in all simulations and for the real data. We used the R package elasticnet to fit the EN models [Zou and Hastie, 2005]. After model fitting, we then use estimated coefficients from each of these variable selection methods as weights. The number of nonzero coefficients included is upper-bounded by 100 for each of these schemes throughout this work.
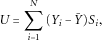
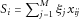, in which N is the number of individuals under study, and Yi is the quantitative trait value for the ith individual. Si is the genetic score for the ith individual, a weighted sum across multiple variants. Specifically, xij is the number of minor alleles observed for individual i at variant j, where xij are not normalized. M is the number of variants in the region under study (discovered through sequencing in our context) and ξj is the weight of variant j under one of the above weighting schemes. The analytical distribution for this statistic is not generally known in this context, so significance must be assessed empirically by permutation.Additionally, we apply the similarity-based method SKAT [Wu et al., 2011] to each of our simulated data sets and the real data set for comparison. We use weights based on the default beta distribution implemented in the SKAT package, version 0.79. We will comment in the Discussion section on the conceptual differences between the weighting schemes we consider in this work and the SKAT methodology.
Simulation Setup
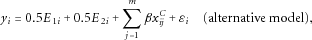
is the number of minor alleles individual i has at causal variant j. The link function F takes one of the following forms:
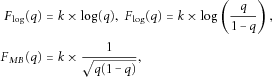
To assess significance in each simulated setting, score test statistic from each weighting scheme is compared to the empirical distribution of the test statistic obtained under the null simulations. We assess the significance of each test at the α = 0.01 level using the empirical null distribution, which we approximate using 100,000 data sets simulated under the null hypothesis of no variant contributing to the quantitative trait.
Simulation of Data Sets Under the Null Hypothesis
For each of the 100 regions we simulate, we randomly select 100 samples of 2,000 chromosomes (forming 1,000 diploid individuals). We then assign quantitative trait values under the null model specified above. Using these 100 × 100 = 10,000 data sets simulated under the null hypothesis, we obtain the empirical null distribution of the test statistics for each method.
Simulation of Data Sets Under Different Alternative Hypotheses
For each choice of r, m, and F(·), we select 2,000 chromosomes from the population of 45,000 chromosomes again via simple random sampling. Again, we randomly pair these chromosomes to form diploid individuals and replicate 100 times for each region. For each replicate, we randomly select m rare variants to be causal. Each causal variant is assigned a direction in which to exert its effect (positive with probability r and negative with probability 1 ‒ r).
Simulation of “Good” Functional Annotation
In each simulated data set, we annotate variants as “functional” or “non-functional.” We assume that we have a reasonably good bioinformatics tool such that a true causal variant has 90% probability to be annotated as “functional.” Even a perfect bioinformatics tool can only predict functionality, not causality or association with a particular trait of interest. Because of this, we annotate an additional random number of W noncausal variants as “functional.” Kryukov et al. [2009] have estimated that approximately one-third of de novo missense mutations (that would be predicted as functional by a sensible bioinformatics tool) have no effect on phenotypic traits. We therefore used 1/3 as the lower bound for the fraction of noncausal variants annotated and simulated 
, rounded to the nearest integer. We evaluate the performance of each of these weighting schemes both using all variants without the help of the bioinformatics tool, and using only the “functional” variants annotated. Under the null distribution, W variants are selected at random.
Simulation of GWAS Data Sets
We use the same choice of causal variants in each region as in the simulated sequencing data. Consequently, the direction of association and true effect size of each of these are unchanged. In order to simulate GWAS SNPs, we select 1,000 chromosomes from the total 45,000 to mimic the 1000 Genomes [Abecasis et al., 2012] sample. The simulated 1000 Genomes sample is used to define LD, based on which GWAS SNPs are selected. For each region, we choose 75 GWAS SNPs consisting of the first 70 tagSNPs (SNPs with the highest number of LD buddies where an LD buddy is an SNP for which the r2 > 0.8) and five SNPs at random from the remaining set of SNPs, mimicking the Illumina Omni5 or Affymetrix Axiom high-density SNP genotyping platforms.
Results
In the Absence of a Bioinformatics Tool
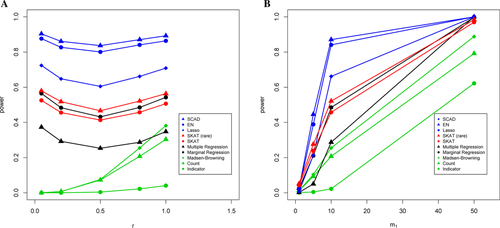
Throughout our simulations, we observe several consistent patterns. First, when we apply these methods in the absence of a bioinformatics tool (thus, all variants are included in analysis), variable selection schemes (most noticeably Lasso and EN) outperform other methods, including SKAT, in nearly all situations (notable exceptions are discussed below). For example, under the simulated setting of 10 causal variants, among which five are expected to increase quantitative trait value, the power is 80.0% and 83.7% for Lasso and EN, and is 0.4%, 7.3%, 7.6%, 43.2%, 25.3%, 60.5%, 41.3%, and 46.6% for Indicator, Count, MB, Marginal Regression, Multiple Regression, SCAD, SKAT (all variants), and SKAT (rare variants only), respectively (Fig. 1a). Under the simulated setting of 50 causal variants among which 40 are expected to increase quantitative trait value, power is 100% for both Lasso and EN, and is 0.03%, 0.19%, 0.07%, 99.63%, 100%, 100%, 96.9%, and 98.5% for Indicator, Count, MB, Marginal Regression, Multiple Regression, SCAD, SKAT (all variants), and SKAT (rare variants only), respectively (Fig. 1b).
In the Presence of a Good Bioinformatics Tool
In the presence of a good bioinformatics tool (as introduced in the Materials and Methods section) the power increases for each of the methods previously discussed. Most notably, the phenotype-independent methods show a substantial gain in power once the bioinformatics tool is applied. For example, under the simulated setting of 10 causal variants, among which five are expected to increase the quantitative trait value, the power is 99.83% and 99.80% for Lasso and EN, and is 23.91%, 17.15%, 18.85%, 97.87%, 99.73%, 99.76%, 98.49%, and 98.34% for Indicator, Count, MB, Marginal Regression, Multiple Regression, SCAD, SKAT (all variants), and SKAT (rare variants only), respectively (Fig. 2a). Under the simulated setting of 50 causal variants, among which 40 increase quantitative trait value, power is 100% for both Lasso and EN, and is 99.38%, 98.89%, 96.51%, 100%, 100%, 100%, 100%, and 100% for Indicator, Count, MB, Marginal Regression, Multiple Regression, SCAD, SKAT (all variants), and SKAT (rare variants only), respectively (Fig. 2b). Although power increases for all methods, the relative performance of the methods changes little from that under the absence of a bioinformatics tool.
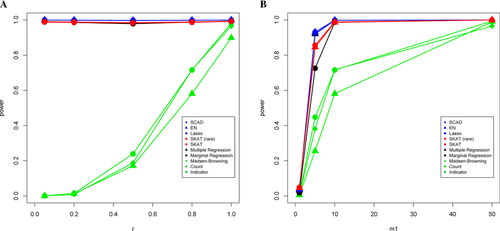
Effect of m (the Number of Causal Variants) and r (Percent of Positive Causal Variants)
As the number of true causal variants (m) increases, so does power for all methods. This is to be expected because adding more causal variants increases the signal-to-noise ratio. When the number of true causal variants is very small, none of the methods have adequate power. Interestingly, it is in these situations where m is very small that SKAT manifests its advantage over other methods examined. As r gets smaller (i.e., the probability that a causal variant will contribute positively to the quantitative trait values gets smaller), the power of the phenotype-independent methods decreases. For example, the phenotype-independent methods have close to 0 power when r = 0.05; while the phenotype-dependent methods are relatively unaffected by changing values of r (Figs. 1a and 2a). We also observe a slight dip in power in all of the phenotype-dependent schemes when r = 0.5 and no bioinformatics information is used (Fig. 1a), which is to be expected because the signals from different directions are canceling one another. Similar trends are seen in all simulations with all four link functions (shown in supplementary materials).
Weight Estimation Accuracy for Individual Variants
Table 1 shows the correlation between the true and estimated values of the weights for each method under the simulation settings in which the number of truly causal variants, m, is 10 and the proportion of variants contributing in the positive direction, r, is 80%. Of note, the correlation between true and estimated weights increases for all methods with the addition of bioinformatics filtering. The EN and Lasso yield the highest correlations between estimated and true weights, both in situations where we restrict to variants that are likely to be functional (Pearson correlations of 0.285 and 0.355), and when we do not (Pearson correlations of 0.744 and 778).
| Method | All markers | Limited to functional markers |
|---|---|---|
| Indicator | – | – |
| Count | 0.0126 | 0.2386 |
| Madsen-Browning | 0.0591 | 0.1225 |
| Marginal Regression | 0.1588 | 0.6490 |
| Multiple Regression | 0.0883 | 0.6537 |
| Lasso | 0.2852 | 0.7436 |
| EN | 0.3555 | 0.7787 |
| SCAD | 0.2301 | 0.7344 |
| SKAT (all) | – | – |
| SKAT (rare only) | – | – |
Identification of Individual Causal Variants
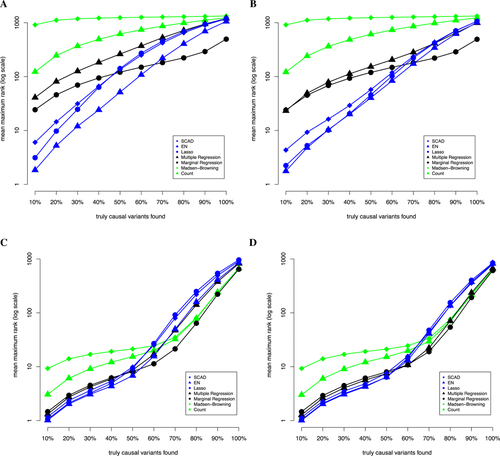
When using variable selection schemes, we have the opportunity to identify individual causal variants within the region or variant set under study. Figure 3 illustrates the accuracy with which the causal variant(s) can be identified by each weighting scheme. Note that the causal variant(s) are not always 100% identified, but in many cases, the causal variant, or a variant in high LD (r2 > 0.8), has estimated nonzero weights. For example, if we fix m = 10, r = 0.8, and the logit link function, without considering LD buddies, we need to consider the top 696 (109 and 12) variants in order to detect 90% (60%, 30%) of the causal variants using EN (Fig. 3a); taking LD buddies into consideration, the numbers decrease to 378 (14 and 4; Fig. 3b). While considering functional information we consider fewer variants and narrow the field to include a higher proportion of truly causal variants. In this case, we need to consider the top 408 (16 and 4) variants in order to detect 90% (60%, 30%) of the causal variants (Fig. 3c) without considering LD buddies; with LD buddies taken into consideration, the numbers decrease to 374 (13 and 3; Fig. 3d).
Results With GWAS Data Sets
Studies that sequence a portion or the entirety of the genome are becoming increasingly common, but still much more GWAS data exist than sequencing data. Imputation has been shown to accurately predict genotypes at untyped variants from GWAS data in a variety of circumstances [Auer et al., 2012; de Bakker et al., 2008; Li et al., 2009b; Li et al. 2010a; Liu et al., 2012; Marchini and Howie, 2010]. Using our simulated GWAS data and simulated reference, we observe that variable selection can improve power for GWAS data as well. However, the power is consistently lower than that under the sequencing setting due to the imperfect rescue of information through imputation (comparing Fig. 1 with supplementary Fig. S3). In our simulations, the imputation accuracy is 99.66% for all variants and 99.98% for rare variants, but most of the inaccuracies are due to missed rare variants. In fact, among variants with MAF < 0.001 nearly all inaccuracies are due to failure to identify the minor allele. Specifically, the squared Pearson correlation between the imputed genotypes (continuous, ranging from 0 to 2) and the true underlying genotypes (coded as 0, 1, and 2) is only 0.2397 for variants with MAF < 0.001. Supplementary Figure S3 shows the relative power of these weighting schemes over a range of r (supplementary Fig. S3a) and m (supplementary Fig. S3b).
Results With Real Data Set
Of the over 6,000 individuals in the CoLaus cohort [Firmann et al., 2008], 1,898 had recorded total cholesterol and targeted sequence data in 202 drug target genes [Nelson et al., 2012]. Sequencing was done at moderately high coverage (with median coverage 27X) and genotype calls were obtained using SOAP-SNP [Li et al., 2009a]. Sporadic missing genotypes were imputed with MaCH [Li et al., 2010b]. One gene previously known to be associated with total cholesterol in these data is used as a positive control. We test each of the 172 autosomal genes with and without removing nonfunctional variants using ANNOVAR [Wang et al., 2010]. For each method, we estimate weights in association with total cholesterol and, for the methods that accommodate covariates, we adjust for age, age2, sex, and the first five principal components. For the phenotype-independent methods, no covariate adjustment is performed and significance is assessed by permutation of the Yi's. For methods allowing covariates (marginal and multiple regression, Lasso, EN, and SCAD), permutation of outcomes alone is not appropriate. For these methods, we fit a regression model, Yi ∼ Zi, where Z is the matrix of covariates and then obtain residuals, 
. The 
's are then randomly permuted to obtain a set of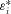 
's, the permuted residuals. For each permutation, we fit the model 
in order to re-estimate the weights ξj and scores Si as in Davidson and Hinkley, [1997]. We do 10,000 such permutations and, from these, obtain a null distribution of statistics with which to assess significance. Because SKAT produces analytical P-values shown to preserve type I error [Wu et al., 2011], we use the SKAT analytical P-values without permutation.
When all variants regardless of bioinformatics prediction are included, the variable selection methods Lasso and EN yield the smallest P-values compared to other methods for the previously implicated gene. However, the previously implicated gene is not the most significant among the 172 genes tested. Using ANNOVAR annotations [Wang et al., 2010], we restrict to nonsynonymous variants in coding regions of the genome only. When considering only these functional variants, most weighting schemes identify the correct gene with highly significant P-values (Table 2 and supplementary Fig. S4).
| Method | All variants (491) | Limited to functional variants (13) |
|---|---|---|
| Indicator | 0.208 | 0.00057 |
| Count | 0.068 | 0.00017b |
| Madsen-Browning | 0.090 | 0.00041c |
| Marginal Regression | 0.166 | 0.00420 |
| Multiple Regression | 0.136 | 0.00395 |
| Lasso | 0.017c | 0.00053 |
| EN | 0.008b | 0.00059 |
| SCAD | 0.111 | 0.00078 |
| SKAT (all) | 0.329 | 0.00142 |
| SKAT (rare only) | 0.348 | 0.00142 |
- a Except for SKAT(all) and SKAT(rare only).
- b Most significant P-value under each column is in bold, italicized.
- c Second most significant P-value under each column is in bold.
Discussion
In summary, through extensive simulation studies with varying number, model, and direction of causal variant(s) contributing to a quantitative trait, we find that functional annotations derived from good set of bioinformatics tools can substantially boost power for rare variant association testing. In the absence of good bioinformatics tools, “statistical” annotation based on phenotype-dependent weighting of the variants, particularly through variable selection based methods to both select potentially causal/associated variants and estimate their effect sizes, manifests advantages. This observation holds for both sequencing-based studies or studies based on a combination of genotyping, sequencing, and imputation. We also find supporting evidence from application to a real sequencing-based data set.
The price one has to pay for adopting phenotype-dependent methods is the necessity of permutation, which can be easily performed through permuting of residuals for the analysis of quantitative traits [Davidson and Hinkley, 1997; Lin, 2005] or using the BiasedUrn method [Epstein et al., 2012] recently proposed for binary traits. This, in turn, increases computational costs. Therefore, we recommend primarily using phenotype-dependent weighting for refining the level of significance. That is, we recommend applying phenotype-dependent weighting only to genomic regions or variant sets that have strong evidence of association (but not necessarily reaching genome-wide significance) from methods that do not require permutation (e.g., SKAT [Wu et al., 2011]).
We note that testing over a region by aggregating information across variants is a different task from estimating effect sizes of individual variant (as measured by the variant weights in our work). Perfection in the latter (i.e., being able to estimate weights for each individual variants accurately) leads to perfection in the former (i.e., maximal testing power over the region harboring those variants), but not vice versa. Based on our simulations where we know the true contribution (effect size) of each individual variant, we find that individual effect sizes cannot be well estimated (Pearson correlation between true and estimated effect sizes <0.5 even for the best variable selection based methods). However, these methods can still increase power of region or variant set association analysis without accurate estimation of individual variant effect sizes. In addition, these methods are able to identify the vast majority of the causal variants, particularly when LD buddies are considered.
In this paper, we mainly consider aggregation of information at the genotype level (where we first obtain a regional genotype score via a weighted sum of genotype scores for individual variants and then assess the association between the regional genotype score and the phenotype of interest), which underlies the largest number of rare variant association methods published. In contrast, there are methods that aggregate information at the effect size level (e.g., SKAT [Wu et al., 2011] where the final regional score test statistic is a weighted sum of the test statistics for individual variants) or at the P-value level, for example, in Cheung et al. [2012]. Our comparisons with SKAT suggest that the same conclusions apply to aggregation methods at levels other than genotype.
Lastly, although one could potentially argue that the phenotype-dependent methods require an undesirable computing-power trade-off in the presence of good bioinformatics tools, in practice, we rarely (if ever) get perfect bioinformatics tools. In addition, even perfect bioinformatics tools can only predict functionality but not causality or association with particular phenotypic trait(s) of interest. Therefore, we view that the application of “statistical annotation” through phenotype-dependent weighting, particularly using variable selection based methods, to top regions or variant sets implicated by computationally efficient phenotype-independent methods, is valuable.
Acknowledgments
We thank GlaxoSmithKline, especially Drs. Margaret G. Ehm, Matthew R. Nelson, Li Li, and Liling Warren for sharing the targeted sequencing data. We also thank our CoLaus collaborators for providing the phenotypic data. The research is supported by R01HG006292, R01HG006703 (awarded to Y.L.), and R01HG004517, R01HG005854 (to M.L.).
