Prediction of soil sorption coefficients with a conductor-like screening model for real solvents
Abstract
Using a general theory for partition coefficients based on a quantum chemically derived conductor-like screening model for real solvents σ-moment descriptors, the logarithmic soil sorption coefficients log KOC of a database of 440 compounds has been successfully correlated, achieving a standard deviation (root-means-squared [RMS]) of 0.62 log-units on the training set and a predictive RMS of 0.72 log-units on a more demanding test set. The quality of this generally applicable predictive approach is almost the same as that of a regression of log KOC with experimental log KOW values, which are the best correlations currently available. The error of this new predictive method is only approximately 43% of the error of a recently published model using a different quantum chemically based approach.
INTRODUCTION
 (1)
(1)The experimental measurement of KOC is expensive, time-consuming, and often related to considerable experimental error or noise resulting from differences in soils and, sometimes, in temperature. Hence, a great need exists for reliable calculation methods that can be used to predict the KOC for new pesticides or to validate experimental data. Many methods have been reported based on correlations of log KOC with other experimental data, especially with experimental log KOW data, water solubilities, melting points, etc. [1-3].
In the present study, we specially focus on pure predictive methods that do not depend on other experimental data for the special compound under consideration. The advantages of such methods are that no time-consuming and expensive measurements have to be done for a new pesticide and, even more, that they can be applied even for pesticide candidates that have not yet been synthesized. Methods of this kind have mainly been developed based on topological indices [2-5]. Meylan et al. [6] introduced a much broader applicable combination of topological indices with group contributions for polar groups (called PC-KOCWIN). This method appears to have considerable predictive power. Nevertheless, it can only be applied to such polar fragments, for which no group contributions have been fitted before. Thus, it is not applicable to pesticides with new heterocycles or with other rare polar groups.
Recently, Winget et al. [7] published a study in which they tried to predict KOC using the universal solvation model SMx, which is based on quantum chemical calculations in combination with a dielectric continuum model. In that study, 440 compounds were considered. The advantage of this approach is that it can be applied to almost any neutral organic compound because of the generality of the underlying quantum chemistry, but the reported predictive accuracy of approximately 1.6 log-units (root-mean-square [RMS]) is much worse than that of other methods currently available.
In the present study, we present a new model for the prediction of KOC, which is based on another universal solvation model, the conductor-like screening model for real solvents (COSMO-RS) [8-11], which is more rigorous than the SMx models used by Winget et al. [7] in two regards. First, the COSMO-RS is based on density functional calculations, which are more reliable than the semiempirical and Hartree-Fock quantum chemical methods used in the context of SMx by Winget et al. [7]. Second, the COSMO-RS is based on a quite rigorous thermodynamic concept for molecular interaction, which replaces the insufficient dielectric approximation [9, 10]. Thus, it enables the treatment of mixtures and of variable temperature without the need for new solvent parameters.
The COSMO-RS has successfully been used for accurate prediction of many kinds of thermodynamic liquid-liquid and liquid-vapor equilibrium properties, including vapor pressure, solubility, and many kinds of partition coefficients. By a generalization of the COSMO-RS theory [12], it has been shown that any kind of logarithmic partition coefficient can be expressed as a linear function of a small number of COSMO-RS descriptors, the s-moments (see below). Whereas the direct calculation of partition coefficients can only be used for solvent phases of known molecular composition, the σ-moment approach is applicable to situations of chemically less well-defined phases. In this way, physiological partition coefficients [12] and adsorption coefficients to activated carbon [13] have been successfully correlated.
MATERIALS AND METHODS
KOC data
The data sets used in the present study are exactly the same as those used in the study by Winget et al. [7]. They consist of a training set of 387 compounds (set 1) that arises from a data collection by Meylan et al. [6] and a test of 53 compounds (set 2) selected from a data set by Sabljic [2]. At one place, a subset (SetPOW) of 316 compounds out of set 1 is used, which is defined by the availability of experimental octanol-water partition coefficients (SetPOW) according to Winget et al. [7].
The full data set includes neutral compounds of very different classes spanning the typical range of pesticide compounds. The elements C, H, N, O, S, P, F, Cl, Br, and I are represented in the data set. Molecular weights are rather equally distributed in the range of 50 to 400, with a minimum value of 32 and a maximum value of 546. Most experimental values of log KOC are in the range of 1.5 to 5, and the extremes are 0 and 6.5.
COSMO and COSMO-RS
The COSMO-RS [8-11] is a theory combining quantum theory, dielectric continuum models, the concept of surface interactions, and statistical thermodynamics. Because a full derivation of the COSMO-RS theory is beyond the scope of this article, a short summary of the essentials will be given here. (For further details, see [8-11].) The COSMO-RS considers a liquid system to be an ensemble of molecules of different kinds, including solvent and solute. For each kind of molecule X, a density functional calculation with the dielectric continuum solvation model COSMO [8] is performed to get the total energy E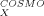 and the polarization (or screening) charge density (SCD) σ that the dielectric continuum or conductor, respectively, produces on the molecular surface. The σ value is a good local descriptor of molecular surface polarity [12].
and the polarization (or screening) charge density (SCD) σ that the dielectric continuum or conductor, respectively, produces on the molecular surface. The σ value is a good local descriptor of molecular surface polarity [12].
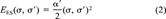 (2)
(2)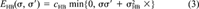 (3)
(3)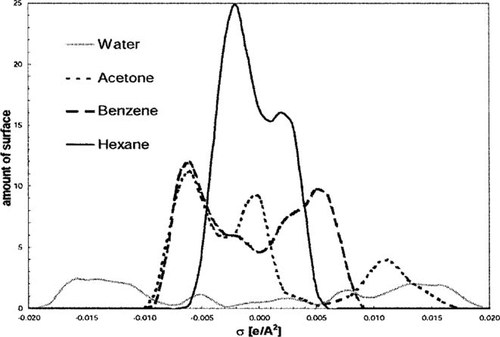
σ Profiles of different solvents. These profiles show the amount of molecular surface in a given interval of polarization charge density σ.
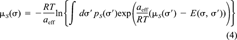 (4)
(4)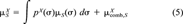 (5)
(5)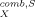 in Equation 5 takes into account size and shape effects of solute and solvent [11]. Usually, it is small compared to the first term in Equation 5 that results from the surface interactions. It is sufficient here to consider the combinatorial part as a solvent-specific constant.
in Equation 5 takes into account size and shape effects of solute and solvent [11]. Usually, it is small compared to the first term in Equation 5 that results from the surface interactions. It is sufficient here to consider the combinatorial part as a solvent-specific constant.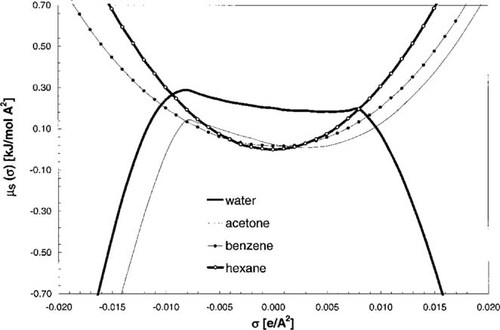
σ Potentials of solvents. These curves show the chemical potential (y-axis) of a piece of surface of polarization charge density σ in a solvent. Thus, they quantify the affinity of a solvent for surface of polarity σ.
As a result of this series of relatively simple steps, we found, starting from a quantum chemical calculation for each compound, a general expression for the chemical potential of a compound X in any solvent S, which may be a pure compound or a mixture. This allows us to calculate any partition coefficient as well as solubility. Based on density functional COSMO calculations, the few parameters required in COSMO-RS have been fitted to a large set of experimental data [9] covering 215 diverse chemical compounds and the Gibbs free energy of hydration (ΔGhydr), the logarithmic vapor pressure (log Pvapor), and the aqueous partition coefficients with octanol, hexane, benzene, and ether. Note that the properties ΔGhydr and log Pvapor involve the gas phase, which requires a small addendum to the steps given above that is not of interest here. However, because the logarithmic aqueous solubility (log Saq) is the difference of ΔGhydr/RT and ln Pvapor, aqueous solubility was implicitly taken into account in the parameterization of COSMO-RS. The initial COSMO-RS parameterization yielded a RMS of 0.3 log-units for the diverse partition and solubility properties of small- and medium-sized molecules [9]. In recent parameterizations, the error has been reduced to approximately 0.23 log-units.
Extension of COSMO-RS to chemically undefined phases
As shown in the COSMO and COSMO-RS section, COSMO-RS is a reliable method for the a priori prediction of thermophysical data and phase equilibria of pure fluids and liquid mixtures of well-defined composition. Nevertheless, several thermodynamic equilibria of industrial importance involve one or more phases that are either chemically less defined, are disordered but not really liquid, or both. Because in such phases no surface composition function pS(σ) is available, the σ-potential μS(σ) of the phase S and the chemical potentials μ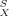 of solutes X in these phases cannot be directly calculated by COSMO-RS. However, an indirect treatment of such phases by COSMO-RS is enabled by the following extension.
of solutes X in these phases cannot be directly calculated by COSMO-RS. However, an indirect treatment of such phases by COSMO-RS is enabled by the following extension.
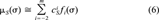 (6)
(6)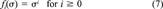 (7)
(7)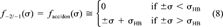 (8)
(8)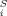 . Obviously, and difference between the σ potentials of two solvents is of the same kind of expansion, with coefficients c
. Obviously, and difference between the σ potentials of two solvents is of the same kind of expansion, with coefficients c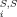 ' being just the difference of the coefficients of the two solvents. Partition coefficients are connected with the pseudochemical potentials by the equation
' being just the difference of the coefficients of the two solvents. Partition coefficients are connected with the pseudochemical potentials by the equation
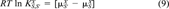 (9)
(9)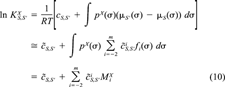 (10)
(10)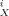 of the solute X are defined by
of the solute X are defined by
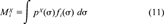 (11)
(11)Equation 10 implies that any logarithmic partition coefficient can be represented as a linear combination of σ moments. As a consequence, the set of σ-moments M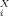 , i = 0,2,3, complemented by the hydrogen-bond moments MXacc (=M
, i = 0,2,3, complemented by the hydrogen-bond moments MXacc (=M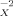 ) and M
) and M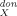 (=MX−1) should be a very good and almost complete set of molecular descriptors for a linear regression analysis of any partition problem. Note that the first moment M
(=MX−1) should be a very good and almost complete set of molecular descriptors for a linear regression analysis of any partition problem. Note that the first moment M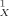 usually is of no importance, because it is just the negative of the total charge of the molecule. Hence, for neutral compounds, M
usually is of no importance, because it is just the negative of the total charge of the molecule. Hence, for neutral compounds, M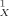 trivially vanishes. By definition of the σ profiles, the zero-th moment M
trivially vanishes. By definition of the σ profiles, the zero-th moment M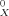 is identical with the molecular surface. The second moment is an excellent measure of the overall electrostatic polarity of the solute, and the third moment is a measure of the asymmetry of the σ profile. The hydrogen-bond moments are quantitative measures of the acceptor and donor capacities of the compound X. Because the organic soil phase involved in the soil sorption coefficients is of unknown chemical composition, this σ-moment approach is well suited to generate a predictive KOC model.
is identical with the molecular surface. The second moment is an excellent measure of the overall electrostatic polarity of the solute, and the third moment is a measure of the asymmetry of the σ profile. The hydrogen-bond moments are quantitative measures of the acceptor and donor capacities of the compound X. Because the organic soil phase involved in the soil sorption coefficients is of unknown chemical composition, this σ-moment approach is well suited to generate a predictive KOC model.
Calculations
Density functional COSMO calculations have been done for all compounds. Starting from the optimized geometries used by Winget et al. [7], the geometries of all compounds have been optimized by the semiempirical AM1/COSMO [8, 14] method using the MOPAC2000 program [15]. Using the geometries thus optimized, the COSMO polarization charge densities σ on the molecular surfaces have been computed on density functional level with the COSMO extension of the Turbomole program package (University of Karlsruhe, Karlsruhe, Germany) [16, 17] using Becke-Perdew density functional theory [18, 19] with split-valence polarization basis set. Finally, the s moments have been calculated using the COSMOtherm program [20]. The s moments of all 440 compounds considered in the present study are provided as supplemental material [SETAC Supplemental Data Archive, Item ETC-21–12–001; http://etc.allenpress.com] together with calculated and experimental values of log KOW and log KOC.
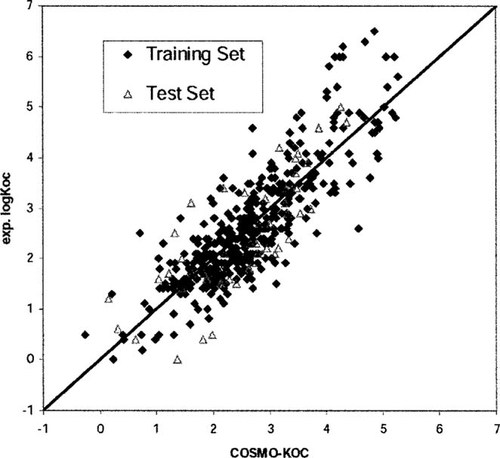
Experimental versus calculated soil sorption coefficients. Values on x-axis are by the conducter-like screening model (COSMO)-KOC model (see Eqn. 12).
A multilinear regression was performed on the 387 compounds of the training set (set 1) using a self-written, multilinear regression routine that automatically evaluates the predictivity of the model by leave-one-out cross-validation. The regression coefficients and standard deviations are referred to as r2 and RMS, and their analogs from cross-validation are noted as q2 and QMS.
RESULTS AND DISCUSSION
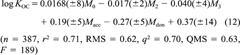 (12)
(12)This model will be referred to as COSMO-KOC. The results are graphically shown in Figure 3. On the more chemically demanding test set of 53 compounds, COSMO-KOC achieves a RMS deviation of 0.72. These results are significantly better than those achieved by Winget et al. [7], who obtained a RMS of 1.36 on the training set and of 1.62 on the test set. Note that the number of adjusted parameters is very similar in both models (five in their model and six in COSMO-KOC). The applicability of COSMO-KOC can be assumed to be even broader than that of the method of Winget et al.
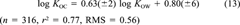 (13)
(13)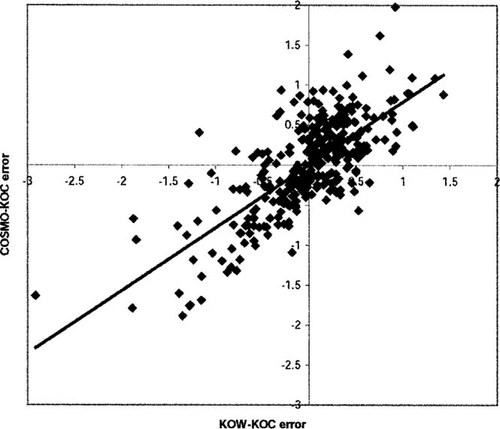
We call this the KOW-KOC model. On the same subset, COSMO-KOC yields a RMS of 0.59 (without refitting). Thus, both models can be considered as almost equally accurate. In Figure 4, an analysis of the error distribution of both models is given. The deviations from experiment of the two methods are clearly correlated (r2 = 0.54). Because the COSMO-KOC and KOW-KOC models are absolutely independent, this error correlation may be caused either by a common systematic error of the models or be an experimental error or experimental noise resulting from different soil samples and, eventually, different temperatures. We consider the latter to be more likely, because the intrinsic accuracy of the COSMO-RS approach for logarithmic partition coefficients is approximately 0.3 log-units (RMS). Keep in mind, however, that both COSMO-KOC and KOW-KOC derive the log KOC values from models of liquid partition. Hence, some chance exist, that special effects arising from the fact that soil is a solid phase may be missed by both models.
The error distribution curve of COSMO-KOC for all 440 compounds would be best described by a Gaussian error function centered at δ = COSMO-KOC -log KOC,exp = 0.06 log-units and having a width of 0.83 log-units. Whereas on the positive side the error distribution is very close to this Gaussian distribution, significantly more large negative deviations (i.e., large underestimations) are found than would be expected from a purely Gaussian distribution. A large number of these large underestimations arise from polycyclic aromatic hydrocarbons and their aza-derivatives. Interestingly, these classes show approximately the same underestimation in the KOW-KOC model. Hence, some special adsorption effects likely are present in soil sorption of large, rigid compounds like polycyclic aromatic hydrocarbons that are not captured in pseudoliquid partition models. Surprisingly, simple alcohols appear to get overestimated systematically by approximately 0.8 log-units, without a significant trend in chain lengths. Again, the same feature can be found in the KOW-KOC model, with an even larger deviation of approximately 1.0 log-unit. For the 35 phosphate compounds in the dataset, COSMO-KOC tends to overestimate the log KOC significantly. The overall largest overestimation (two log-units) is for phosalone, which is a phosphate. Because we have carefully checked the conformation of this outlier, no reason for this overestimation is obvious to us at the moment.
We also compared our method with the PC-KOCWIN estimation method of Meylan et al. [6]. For this, we used a list of 430 estimated log KOC values from PC-KOCWIN, which have been made available for this study by Meylan (Syracuse Research Corporation, NY, USA). On all 430 compounds, the RMS of PC-KOCWIN is 0.48. On a subset of 368 compounds, which we could merge with the structures of our data set, we found RMS deviation of 0.49, whereas COSMO-KOC gave a RMS error of 0.62 on this set. It is remarkable that almost no error correlation (r2 = 0.04) is found between these two methods. For some compounds for which COSMO-KOC and KOW-KOC consistently find a large deviation from the experimental results, PC-KOCWIN finds almost zero error. Others for which COSMO-KOC and KOW-KOC are in reasonable agreement with experiment are large outliers in PC-KOCWIN. This behavior probably arises from the bias in the development of PC-KOCWIN. Polar fragment corrections have been defined only as necessary by the apparent necessity (i.e., based on the deviations to experiment). This procedure carries the danger that some experimental error has been fitted into polar group corrections and that, for other compounds, necessary corrections are missing. Because KOW-KOC and COSMO-KOC have no group-specific contributions, they are not subject to such bias.
CONCLUSIONS
The COSMO-KOC is a new and almost generally applicable method for the a priori prediction of soil sorption coefficients. It is based on σ moments as molecular descriptors, which are derived from quantum chemical density functional calculations combined with the continuum solvation model COSMO. The underlying s-moment approach is theoretically well justified and has been successfully validated for other partition coefficients. The RMS of COSMO-KOC from experimental data is approximately 0.65 log-units. Hence, it is approximately as accurate as prediction methods based on experimental values of log KOW. A large portion of the deviations likely arises from experimental error.
Acknowledgements
We are grateful to Chris Cramer for sending us the 440 chemical structures considered in their work in electronic format and to Bill Meylan for sending us a table of estimated log KOC values.




