Selecting internally consistent physicochemical properties of organic compounds
Abstract
Methods are presented for selecting values of chemical properties of vapor pressure, water solubility, Henry's law constant, and octanol—water and octanol—air partition coefficients, which are subject to thermodynamic constraints, while taking advantage of all measurements. The aim of the mathematical procedures is to find the one set of internally consistent partitioning parameters that is minimally divergent from the experimental values. Information about the reliability or uncertainty of reported values can be accounted for by weighing factors. A similar approach is applied to the temperature dependence of these properties. The influence of partial miscibility of the octanol—water system is discussed and a correction is suggested for this effect. The selection method is applied to 50 mostly aromatic chemicals for which multiple measured partitioning data are available. The resulting sets of consistent property data are presented and discussed.
INTRODUCTION
The environmental partitioning behavior of organic chemicals usually is described on the basis of the partitioning between the pure liquid phase, the gas phase, and the dissolved phases in water and n-octanol. This partitioning behavior finds quantitative expressions in the use of the six partitioning coefficients between these phases, such as the vapor pressure, solubility in water, and octanol-water partition coefficient (KOW). In addition, enthalpies or heats of phase change, such as the heat of solution, are used to express the temperature dependence of these partition coefficients. Cole and Mackay [1] set out the fundamental thermodynamic relationships between these properties, which enable properties to be derived from each other. One common example is Henry's law coefficient (H), which is often estimated as the ratio of saturation vapor pressure (Ps) and water solubility (Sw) [2], thus avoiding the necessity of measuring all three quantities. A check of consistency is possible if all three measurements are available. When measured or estimated data are available for all three properties, they usually are not fully consistent with these constraints. However, when performing model calculations, internally consistent substance data are needed. Those consistent data usually were obtained by calculating data from others, even if measurements of the property are available. For instance, the suggested Henry's law coefficients are always calculated from Ps and Sw by Mackay et al. [2]. Although this approach yields internally consistent chemical properties, it omits available information and it requires judgement, because one could also calculate the water solubility from H and Ps to get consistent data. Here, we address the issue of analyzing such reported values to obtain a consistent set of data, while taking advantage of all measured properties and exploiting the fundamental thermodynamic constraints to which they are subject. The suggested procedure has the additional advantage that it avoids any judgment by the user, and hence the procedure can be incorporated into automated data processing.
When approaching this issue, we need to be aware that the thermodynamic relationships between these properties are not necessarily absolute. For example, when estimating KAW as the ratio of the saturation vapor pressure and water solubility, we assume that this ratio approximates the air-water partition coefficient at much more dilute conditions. Measurements of KAW are typically conducted at conditions far from saturation, and environmental conditions usually are also far from saturation in both gas and aqueous phase. Schwarzenbach et al. [3] showed that this rests on the assumption that the aqueous solution activity coefficient does not change as a function of solute concentration, and concluded that this is a reasonable approximation for compounds that are slightly or even moderately soluble in water (<1.5 mol/L).
AN EXAMPLE OF WATER SOLUBILITY, VAPOR PRESSURE, AND HENRY'S LAW CONSTANT
In the following, the suggested approach of obtaining consistent values for Ps, Sw, and H is derived by using 4,4′-dichlorobiphenyl (polychlorinated biphenyl [PCB] 15) as an example. First, the assumption is made that only one measured value exists for each chemical property. If more than one measurement exists for a given property, the most reliable value can be selected or a weighted mean of all values can be calculated. Measured properties at 25°C for PCB 15 are presented in Table 1. The Henry's law coefficient derived from the vapor pressure and water solubility is 17.49 Pa m3/mol, which deviates from the two measured values of 9.66 and 18.94 Pa m3/mol. The actual value probably lies in the range 9 to 20 Pa m3/mol.
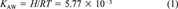 (1)
(1)Here R is the gas constant 8.314 J/(mol K) and T is absolute temperature (298.15 K in this case).
| Compound | P (Pa) (Pa) |
References | (mol/m3) | References | SOI (mol/m3) | References | KAW | References | log KOW | References | log KOA | References |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PCB 15 | 7.26 × 10−2 | [18] | 4.06 × 10−3 | [11] | NA | 5.77 × 10−3 | [26, 27] | 5.23 | [19] | 7.66b | [6] | |
| PCB 28 | 3.41 × 10−2 | [18] | 9.28 × 10−4 | [11] | NA | 1.17 × 10−2 | [9]c | 5.71 | [19] | NA | ||
| PCB 29 | 4.47 × 10−2 | [18] | 2.18 × 10−3 | [11] | NA | 1.12 × 10−2 | [9]c | 5.75d | [19] | 7.95b | [6] | |
| PCB 30 | 9.69 × 10−2 | [18] | 1.63 × 10−3 | [11] | NA | 2.71 × 10−2 | [26] | 5.52d | [19] | NA | ||
| PCB 31 | 3.46 × 10−2 | [18] | 8.63 × 10−4 | [2] | NA | 7.77 × 10−3 | [28] | 5.68 | [19] | 7.92e | [7] | |
| PCB 33 | 2.64 × 10−2 | [18] | 6.90 × 10−4 | [2] | NA | NA | 5.71 | [19] | NA | |||
| PCB 44 | 1.28 × 10−2 | [18] | 5.65 × 10−4 | [2] | NA | 1.06 × 10−2 | [9]c | 5.73 | [19] | 8.36 | [7] | |
| PCB 47 | 1.53 × 10−2 | [18] | 1.15 × 10−3 | [2] | NA | 7.77 × 10−3 | [28] | 5.94 | [19] | NA | ||
| PCB 52 | 1.61 × 10−2 | [18] | 3.25 × 10−4 | [11] | 7.43 × 102 | [5] | 1.30 × 10−2 | [9]c | 5.79 | [19] | 8.22 | [7] |
| PCB 61 | 1.21 × 10−2 | [18] | 4.42 × 10−4 | [11] | 9.12 × 102 | [5] | 1.08 × 10−2 | [26] | 6.15d | [19] | 8.73b | [6] |
| PCB 77 | 2.20 × 10−3 | [18] | 8.39 × 10−5 | [11] | NA | 4.02 × 10−3 | [9]c | 6.1 ld | [19] | 9.70b | [20] | |
| PCB 95 | 5.32 × 10−3 | [18] | NA | NA | 4.91 × 10−3e | [28] | 5.92 | [19] | 8.75 | [7, 20] | ||
| PCB 101 | 3.39 × 10−3 | [18] | 1.40 × 10−4 | [11] | NA | 1.02 × 10−2 | [9]c | 6.39d | [19] | 8.93e | [7, 20] | |
| PCB 105 | 8.74 × 10−4 | [18] | NA | NA | 4.07 × 10−3 | [9]c | 6.79 | [19] | 10.01 | [20] | ||
| PCB 110 | 1.83 × 10−3 | [18] | 4.15 × 10−5 | [2] | NA | NA | 6.20 | [19] | 9.06 | [7] | ||
| PCB 116 | 2.31 × 10−3 | [18] | 2.33 × 10−4 | [2] | NA | 1.26 × 10−2 | [26] | 6.46d | [19] | NA | ||
| PCB 118 | 1.19 × 10−3 | [18] | NA | NA | 9.86 × 10−3 | [9]c | 6.57 | [19] | 9.82 | [20] | ||
| PCB 126 | 4.87 × 10−4 | [18] | NA | NA | 3.34 × 10−3 | [9]c | 6.67d | [19] | 10.35 | [20] | ||
| PCB 138 | 5.14 × 10−4 | [18] | NA | NA | 5.32 × 10−3 | [9]c | 6.73 | [19] | 9.66e | [7, 20] | ||
| PCB 153 | 6.83 × 10−4 | [18] | 1.37 × 10−5 | [11] | NA | 6.98 × 10−3 | [9]c | 6.80 | [19] | 9.55 | [7, 20] | |
| PCB 180 | 1.32 × 10−4 | [18] | NA | NA | 8.33 × 10−3 | [9]c | 7.21 | [19] | 10.20 | [7, 20] | ||
| p,p′-DDT | 3.08 × 10−4 | [2] | 2.39 × 10−4 | [2] | 1.61 × 103 | [5] | 5.28 × 10−4 | [29] | 6.19 | [2] | 9.81 | [21] |
| p,p′-DDE | 4.82 × 10−3 | [2] | 5.40 × 10−4 | [2] | NA | 1.70 × 10−3 | 5.70 | [30] | 9.67 | [21] | ||
| α-HCH | 1.42 × 10−1 | [2] | 1.15 × 10−1 | [2] | NA | 3.09 × 10−4 | [12] | 3.81 | [2] | 7.61 | [21] | |
| γ-HCH | 3.23 × 10−2 | [2] | 1.84 × 10−1 | [2] | 1.57 × 103 | [5] | 1.43 × 10−4 | [12] | 3.70 | [2] | 7.84 | [21] |
| trans-Chlordane | 5.78 × 10−3 | [2] | 8.30 × 10−4 | [2] | NA | NA | 6.00 | [2] | 8.86 | [21] | ||
| cis-Chlordane | 4.71 × 10−3 | [2] | 9.07 × 10−4 | [2] | NA | NA | 6.00 | [2] | 8.91 | [21] | ||
| Chlorobenzene | 1.58 × 103 | [11] | 4.30 × 100 | [11] | NA | 1.48 × 10−1 | [12] | 2.80 | [2] | NA | ||
| 1,2,4,5-TetraCBz | 1.08 × 101 | [11] | 4.16 × 10−2 | [11] | 1.80 × 103 | [5] | 4.07 × 10−2 | [31] | 4.50 | [2] | 5.65c | [6] |
| 1,2,3,5-TetraCBz | 1.02 × 101 | [11] | 3.32 × 10−2 | [11] | 2.82 × 103 | [5] | 6.45 × 10−2 | [32] | 4.50 | [2] | NA | |
| Pentachlorobenzene | 9.02 × 10−1 | [11] | 8.19 × 10−3 | [11] | 1.13 × 103 | [5] | 2.86 × 10−2 | [12] | 5.00 | [2] | 6.28c | [6] |
| Hexachlorobenzene | 9.37 × 10−2 | [11] | 7.15 × 10−4 | [11] | 5.63 × 102 | [5] | 1.79 × 10−2 | [12] | 5.50 | [2] | 7.38 | [21] |
| Naphthalene | 3.36 × 101 | [10] | 7.95 × 10−1 | [10] | 2.29 × 103 | [5] | 1.72 × 10−2 | [12] | 3.37 | [2] | NA | |
| Biphenyl | 3.51 × 100 | [10] | 1.26 × 10−1 | [10] | 2.00 × 103 | [5] | 1.26 × 10−2 | [32] | 3.90 | [2] | NA | |
| Acenaphthene | 1.60 × 100 | [10] | 1.31 × 10−1 | [10] | 1.37 × 103 | [5] | 7.46 × 10−3 | [8] | 3.92 | [2] | NA | |
| Fluorene | 5.96 × 10−1 | [10] | 7.57 × 10−2 | [10] | 1.59 × 103 | [5] | 3.96 × 10−3 | [8] | 4.18 | [2] | 6.79 | [33] |
| Phenanthrene | 8.87 × 10−2 | [10] | 2.74 × 10−2 | [10] | 1.57 × 103 | [5] | 1.73 × 10−3 | [8] | 4.57 | [2] | 7.60 | [33] |
| Anthracene | 1.73 × 10−2 | [10] | 2.18 × 10−2 | [10] | 1.06 × 103 | [5] | 2.28 × 10−3 | [8] | 4.54 | [2] | NA | |
| Fluoranthene | 5.23 × 10−3 | [10] | 6.73 × 10−3 | [10] | 9.09 × 102 | [5] | 7.91 × 10−4 | [8] | 5.22 | [2] | 8.87 | [33] |
| Pyrene | 1.09 × 10−2 | [10] | 1.18 × 10−2 | [10] | 2.28 × 103 | [5] | 6.90 × 10−4 | [8] | 5.18 | [2] | 8.81 | [33] |
| Benzo[a]pyrene | 7.35 × 10−6 | [10] | 1.25 × 10−4 | [10] | 2.64 × 102 | [5] | 1.86 × 10−5 | [12] | 6.04 | [2] | NA | |
| Benz[a]anthracene | 4.42 × 10−4 | [10] | 7.61 × 10−4 | [10] | NA | 4.92 × 10−4 | [8] | 5.91 | [2] | NA | ||
| Chrysene | 1.03 × 10−4 | [10] | 1.58 × 10−3 | [10] | 4.53 × 102 | [5] | 4.28 × 10−5 | [34] | 5.60 | [2] | NA | |
| 2,3,7,8-TetraCDF | 2.77 × 10−3 | [35] | 5.32 × 10−4 | [11] | NA | 6.86 × 10−4 | [36] | 6.10 | [2] | 10.01 | [35] | |
| 1-MonoCDD | 3.59 × 10−1 | [11] | 5.70 × 10−2 | [11] | NA | NA | 4.75 | [2] | 7.85 | [35] | ||
| 1,2,3,4-TetraCDD | 1.14 × 10−3 | [35] | 1.51 × 10−4 | [11] | NA | 8.15 × 10−4 | [36] | 6.60 | [2] | 9.70 | [35] | |
| 2,3,7,8-TetraCDD | 2.17 × 10−3 | [35] | 1.46 × 10−4 | [11] | NA | NA | 6.80 | [2] | 10.04 | [35] | ||
| 1,2,3,4,7-PentaCDD | 1.53 × 10−3 | [35] | 1.65 × 10−4 | [11] | NA | NA | 7.40 | [2] | 10.66 | [35] | ||
| 1,2,3,4,7,8-HexaCDD | 8.78 × 10−4 | [35] | 7.58 × 10−5 | [11] | NA | NA | 7.80 | [2] | 11.11 | [35] | ||
| 1,2,3,4,6,7,8-HeptaCDD | 5.99 × 10−4 | [35] | 9.18 × 10−5 | [11] | NA | NA | 8.00 | [2] | 11.42 | [35] |
- a PCB = polychlorinated biphenyl; NA = not available; DDE = dichlorodiphenyldichloroethylene; HCH = hexachlorocyclohexane; CBz = chlorobenzene; CDF = chlorodibenzofuran; CDD = chlorodibenzo-p-dioxin.
- b Not measured above 20°C (extrapolated to 25°C).
- c Median value of all values cited in Bamford et al. [9].
- d Calculated.
- e Parameter from Kömp et al. [7] measured with coeluting congener. Value selected for main component of Aroclor mixture.
- f Standard with more than 95% PCB-95 used for measurement.
 (2)
(2)It is important that all solubilities apply to the same state, that is, either to the liquid or the solid state of the solute. Generally, the liquid state is preferred because it better represents the conditions of chemicals in solution at low environmental concentrations [4] and liquid or supercooled liquid properties are used in quantitative structure-property relationships. Thus, we used the data applicable to the liquid or supercooled liquid state.
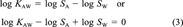 (3)
(3)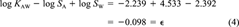 (4)
(4)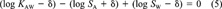 (5)
(5)The adjustment term δ is therefore -0.033. Note that log SA is increased because it is subtracted from the other properties in Equation 4. Subtracting or adding this δ adjustment term on the log-scale implies dividing or multiplying all parameters by a factor of 10, that is, 0.927. This assumes that all parameters are subject to the same relative or fractional error and all are changed by the same incremental value on a log-scale. The results for PCB 15 are included in Table 2. Adjusting the given KAW, SA, and SW in this way has the advantage that it avoids any judgment on the part of the user and that it takes into account all measured properties. Calculating the KAW from measured SA and SW would also yield consistent properties, but neglects measurements of KAW.
INCORPORATING RELIABILITY
Some measurements likely are known to be more accurate than others. For example, it may be easier to determine KAW than solubility in water or vapor pressure for hydrophobic compounds of low volatility. When selecting consistent values of these parameters, assigning greater weight to KAW may then be desirable. We suggest that a factor μi is assigned to each property which ranges from 0 (known with high accuracy) to 5 (highly uncertain). This could be termed an uncertainty factor. The adjustment factor δ is then modified and calculated for each property i as δi = ∈.ui/Σui, where the summation is over all n quantities. Clearly, if all ui values are equal, this reduces to ∈/n. Any scale can be selected for ui (e.g., 0 to 1 or 1 to 10) as long as it is consistent. The factors can be assigned depending on the nature of the property measured, the method of determination, the use of standards, and the number of determinations. Of course, judgment is involved in the assignment of reliability but in our view this judgment is best applied to the reported determination, not to the final selected parameter value.
APPLICATION TO OCTANOL PARTITIONING
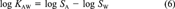 (6)
(6)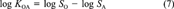 (7)
(7)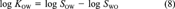 (8)
(8)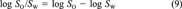 (9)
(9)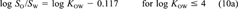 (10)
(10)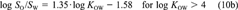 (11)
(11)P (Pa) (Pa) |
%b | SWl (mol/L) | % | SOl (mol/L) | % | KAW | % | Kow | % | KOA | % | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PCB 15 | 6.47 × 10−2 | −7 | 4.38 × 10−3 | 8 | 1.33 × 103 | 6.21 × 10−3 | 8 | 1.61 × 105 | −5 | 4.89 × 107 | 7 | |
| PCB 28 | 3.15 × 10−2 | −8 | 1.00 × 10−3 | 8 | 1.47 × 103 | 1.27 × 10−2 | 8 | 5.13 × 105 | 1.16 × 108 | |||
| PCB 29 | 5.28 × 10−2 | 18 | 1.85 × 10−3 | −15 | 2.39 × 103 | 1.15 × 10−2 | 3 | 4.68 × 105 | −16 | 1.12 × 108 | 26 | |
| PCB 30 | 1.01 × 10−1 | 4 | 1.57 × 10−3 | −4 | 1.26 × 103 | 2.60 × 10−2 | −4 | 3.29 × 105 | 3.08 × 107 | |||
| PCB 31 | 2.71 × 10−2 | −22 | 1.10 × 10−3 | 28 | 1.16 × 103 | 9.90 × 10−3 | 28 | 4.01 × 105 | −16 | 1.06 × 108 | 27 | |
| PCB 33 | 2.64 × 10−2 | 6.90 × 10−4 | 1.01 × 103 | 1.55 × 10−2 | 5.13 × 105 | 9.47 × 107 | ||||||
| PCB 44 | 1.31 × 10−2 | 3 | 5.51 × 10−4 | −2 | 1.02 × 103 | 9.57 × 10−3 | −9 | 6.09 × 105 | 13 | 1.93 × 108 | −16 | |
| PCB 47 | 1.73 × 10−2 | 13 | 1.02 × 10−3 | −12 | 3.06 × 103 | 6.87 × 10−3 | −12 | 8.71 × 105 | 4.38 × 108 | |||
| PCB 52 | 1.37 × 10−2 | −15 | 3.68 × 10−4 | 13 | 7.69 × 102 | 4 | 1.50 × 10−2 | 15 | 6.66 × 105 | 8 | 1.39 × 108 | −16 |
| PCB 61 | 9.76 × 10−3 | −19 | 3.62 × 10−4 | −18 | 1.38 × 103 | 52 | 1.09 × 10−2 | 1 | 1.04 × 106 | −26 | 3.51 × 108 | −34 |
| PCB 77 | 1.31 × 10−3 | −40 | 1.41 × 10−4 | 68 | 1.38 × 103 | 3.76 × 10−3 | −6 | 2.08 × 106 | 61 | 2.61 × 109 | −48 | |
| PCB 95 | 5.32 × 10−3 | 4.34 × 10−4 | 1.22 × 103 | 4.94 × 10−3 | 1 | 8.28 × 105 | 0 | 5.69 × 108 | 1 | |||
| PCB 101 | 3.57 × 10−3 | 5 | 1.33 × 10−4 | −5 | 1.43 × 103 | 1.08 × 10−2 | 5 | 2.22 × 106 | −11 | 9.94 × 108 | 16 | |
| PCB 105 | 8.74 × 10−4 | 8.56 × 10−5 | 3.65 × 103 | 4.12 × 10−3 | 1 | 6.12 × 106 | −1 | 1.03 × 1010 | 1 | |||
| PCB 110 | 1.39 × 10−3 | −24 | 5.47 × 10−5 | 32 | 4.89 × 102 | 1.03 × 10−2 | 1.94 × 106 | 22 | 8.72 × 108 | −24 | ||
| PCB 116 | 3.38 × 10−3 | 47 | 1.59 × 10−4 | −32 | 2.40 × 103 | 8.59 × 10−3 | −32 | 2.86 × 106 | 1.76 × 109 | |||
| PCB 118 | 1.19 × 10−3 | 7.05 × 10−5 | 2.20 × 103 | 6.83 × 10−3 | −31 | 4.87 × 106 | 31 | 4.58 × 109 | −31 | |||
| PCB 126 | 4.87 × 10−4 | 8.00 × 10−5 | 3.26 × 103 | 2.45 × 10−3 | −27 | 5.91 × 106 | 26 | 1.66 × 1010 | −27 | |||
| PCB 138 | 5.14 × 10−4 | 3.42 × 10−5 | 1.07 × 103 | 6.06 × 10−3 | 14 | 4.88 × 106 | −9 | 5.17 × 109 | 14 | |||
| PCB 153 | 4.62 × 10−4 | −32 | 2.03 × 10−5 | 48 | 7.71 × 102 | 9.18 × 10−3 | 32 | 5.62 × 106 | −11 | 4.14 × 109 | 17 | |
| PCB 180 | 1.32 × 10−4 | 5.95 × 10−6 | 8.91 × 102 | 8.92 × 10−3 | 7 | 1.54 × 107 | −5 | 1.68 × 1010 | 7 | |||
| p,p′-DDT | 3.56 × 10−4 | 15 | 2.40 × 10−4 | 0 | 1.40 × 103 | −14 | 5.99 × 10−4 | 13 | 1.42 × 106 | −9 | 9.72 × 109 | 51 |
| p,p′-DDE | 3.05 × 10−3 | −37 | 8.52 × 10−4 | 58 | 2.63 × 103 | 1.45 × 10−3 | −15 | 8.88 × 105 | 77 | 2.13 × 109 | −54 | |
| α-HCH | 1.05 × 10−1 | −26 | 1.55 × 10−1 | 35 | 1.01 × 103 | 2.75 × 10−4 | −11 | 9.55 × 103 | 48 | 2.37 × 107 | −41 | |
| γ-HCH | 4.15 × 10−2 | −28 | 2.01 × 10−1 | 9 | 1.12 × 103 | −29 | 8.32 × 10−5 | −42 | 8.52 × 103 | 70 | 6.69 × 107 | −4 |
| trans-Chlordane | 6.66 × 10−3 | 15 | 7.20 × 10−4 | −13 | 2.27 × 103 | 3.73 × 10−3 | 9.00 × 105 | −10 | 8.43 × 108 | 15 | ||
| cis-Chlordane | 5.70 × 10−3 | 21 | 7.49 × 10−4 | −17 | 2.25 × 103 | 3.07 × 10−3 | 8.69 × 105 | −13 | 9.77 × 108 | 21 | ||
| Chlorobenzene | 1.58 × 103 | 0 | 4.30 × 100 | 0 | 6.94 × 102 | 1.48 × 10−1 | 0 | 6.31 × 102 | 1.09 × 103 | |||
| 1,2,4,5-TetraCBz | 8.78 × 100 | −19 | 5.30 × 10−2 | 27 | 1.73 × 103 | −4 | 6.69 × 10−2 | 64 | 3.14 × 104 | −1 | 4.89 × 105 | 9 |
| 1,2,3,5-TetraCBz | 8.39 × 100 | −17 | 4.33 × 10−2 | 30 | 2.01 × 103 | −29 | 7.82 × 10−2 | 21 | 4.05 × 104 | 28 | 5.94 × 105 | |
| Pentachlorobenzene | 9.09 × 10−1 | 1 | 8.70 × 10−3 | 6 | 1.06 × 103 | −7 | 4.22 × 10−2 | 47 | 8.21 × 104 | −18 | 2.88 × 106 | 50 |
| Hexachlorobenzene | 6.87 × 10−2 | −27 | 8.95 × 10−4 | 25 | 6.14 × 102 | 9 | 3.10 × 10−2 | 73 | 2.94 × 105 | −7 | 2.22 × 107 | −7 |
| Naphthalene | 3.70 × 101 | 10 | 9.52 × 10−1 | 20 | 1.45 × 103 | −37 | 1.57 × 10−2 | −9 | 3.28 × 103 | 40 | 9.71 × 104 | |
| Biphenyl | 4.05 × 100 | 15 | 1.50 × 10−1 | 19 | 1.23 × 103 | −38 | 1.09 × 10−2 | −13 | 1.14 × 104 | 43 | 7.54 × 105 | |
| Acenaphthene | 2.01 × 100 | 26 | 1.37 × 10−1 | 4 | 1.00 × 103 | −27 | 5.93 × 10−3 | −21 | 1.04 × 104 | 26 | 1.24 × 106 | |
| Fluorene | 6.32 × 10−1 | 6 | 8.08 × 10−2 | 7 | 1.40 × 103 | −12 | 3.15 × 10−3 | −20 | 1.97 × 104 | 30 | 5.51 × 106 | −11 |
| Phenanthrene | 9.57 × 10−2 | 8 | 2.77 × 10−2 | 1 | 1.44 × 103 | −8 | 1.39 × 10−3 | −19 | 4.42 × 104 | 19 | 3.74 × 107 | −6 |
| Anthracene | 4.00 × 10−2 | 132 | 1.64 × 10−2 | −25 | 8.09 × 102 | −24 | 9.83 × 10−4 | −57 | 4.24 × 104 | 22 | 5.02 × 107 | |
| Fluoranthene | 5.63 × 10−3 | 8 | 4.72 × 10−3 | −30 | 1.20 × 103 | 32 | 4.82 × 10−4 | −39 | 1.42 × 105 | −15 | 5.29 × 108 | −29 |
| Pyrene | 1.18 × 10−2 | 9 | 9.69 × 10−3 | −18 | 2.56 × 103 | 12 | 4.91 × 10−4 | −29 | 1.45 × 105 | −4 | 5.37 × 108 | −16 |
| Benzo[a]pyrene | 6.28 × 10−6 | −15 | 1.16 × 10−4 | −7 | 3.55 × 102 | 35 | 2.17 × 10−5 | 17 | 8.80 × 105 | −20 | 1.40 × 1011 | |
| Benz[a]anthracene | 5.66 × 10−4 | 28 | 5.94 × 10−4 | −22 | 1.63 × 103 | 3.84 × 10−4 | −22 | 8.13 × 105 | 7.13 × 109 | |||
| Chrysene | 1.13 × 10−4 | 10 | 1.18 × 10−3 | −26 | 7.44 × 102 | 64 | 3.88 × 10−5 | −9 | 2.77 × 105 | −31 | 1.63 × 1010 | |
| 2,3,7,8-TetraCDF | 1.69 × 10−3 | −39 | 8.72 × 10−4 | 64 | 5.46 × 103 | 7.81 × 10−4 | 14 | 1.49 × 106 | 19 | 8.02 × 109 | −21 | |
| 1-MonoCDD | 2.85 × 10−1 | −20 | 7.17 × 10−2 | 26 | 6.53 × 103 | 1.61 × 10−3 | 6.65 × 104 | 18 | 5.67 × 107 | −20 | ||
| 1,2,3,4-TetraCDD | 7.62 × 10−4 | −33 | 2.26 × 10−4 | 49 | 2.86 × 103 | 1.36 × 10−3 | 67 | 2.51 × 106 | −37 | 9.32 × 109 | 87 | |
| 2,3,7,8-TetraCDD | 1.96 × 10−3 | −10 | 1.61 × 10−4 | 11 | 7.91 × 103 | 4.92 × 10−3 | 6.79 × 106 | 8 | 1.00 × 1010 | −10 | ||
| 1,2,3,4,7-PentaCDD | 1.75 × 10−3 | 14 | 1.45 × 10−4 | −12 | 3.70 × 104 | 4.87 × 10−3 | 2.28 × 107 | −9 | 5.24 × 1010 | 14 | ||
| 1,2,3,4,7,8-HexaCDD | 1.00 × 10−3 | 14 | 6.63 × 10−5 | −12 | 5.91 × 104 | 6.10 × 10−3 | 5.72 × 107 | −9 | 1.46 × 1011 | 14 | ||
| 1,2,3,4,6,7,8-HeptaCDD | 7.74 × 10−4 | 29 | 7.11 × 10−5 | −23 | 1.05 × 105 | 4.39 × 10−3 | 8.29 × 107 | −17 | 3.36 × 1011 | 29 |
- a PCB = polychlorinated biphenyl; DDE = dichlorodiphenyldichloroethylene; HCH = hexachlorocyclohexane; CBz = chlorobenzene; CDF = chlorodibenzofuran; CDD = chlorodibenzo-p-dioxin.
- b Percentages indicate deviation from selected values in Table 1.
P (Pa) (Pa) |
%b | 5Wl (mol/L) | % | 5Ol (mol/L) | % | KAW | % | KOW | % | KOA | % | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PCB 15 | 6.74 × 10−2 | −7 | 4.38 × 10−3 | 8 | 1.33 × 103 | 6.21 × 10−3 | 8 | 1.61 × 105 | −5 | 4.89 × 107 | 7 | |
| PCB 28 | 3.15 × 10−2 | −8 | 1.00 × 10−3 | 8 | 1.47 × 103 | 1.27 × 10−2 | 8 | 5.13 × 105 | 1.16 × 108 | |||
| PCB 29 | 5.28 × 10−2 | 18 | 1.85 × 10−3 | −15 | 2.39 × 103 | 1.15 × 10−2 | 3 | 4.68 × 105 | −16 | 1.12 × 108 | 26 | |
| PCB 30 | 1.01 × 10−1 | 4 | 1.57 × 10−3 | −4 | 1.26 × 103 | 2.60 × 10−2 | −4 | 3.29 × 105 | 3.08 × 107 | |||
| PCB 31 | 2.71 × 10−2 | −22 | 1.10 × 10−3 | 28 | 1.16 × 103 | 9.90 × 10−3 | 28 | 4.01 × 105 | −16 | 1.06 × 108 | 27 | |
| PCB 33 | 2.64 × 10−2 | 6.90 × 10−4 | 1.01 × 103 | 1.55 × 10−2 | 5.13 × 105 | 9.47 × 107 | ||||||
| PCB 44 | 1.31 × 10−2 | 3 | 5.51 × 10−4 | −2 | 1.02 × 103 | 9.57 × 10−3 | −9 | 6.09 × 105 | 13 | 1.93 × 108 | −16 | |
| PCB 47 | 1.73 × 10−2 | 13 | 1.02 × 10−3 | −12 | 3.06 × 103 | 6.87 × 10−3 | −12 | 8.71 × 105 | 4.38 × 108 | |||
| PCB 52 | 1.59 × 10−2 | −1 | 3.61 × 10−4 | 11 | 7.65 × 10-2 | 3 | 1.78 × 10−2 | 37 | 6.73 × 105 | 9 | 1.19 × 108 | −28 |
| PCB 61 | 1.44 × 10−2 | 19 | 3.74 × 10−4 | −15 | 1.29 × 103 | 41 | 1.55 × 10−2 | 44 | 9.63 × 105 | −31 | 2.23 × 108 | −58 |
| PCB 77 | 1.31 × 10−3 | −40 | 1.41 × 10−4 | 68 | 1.38 × 103 | 3.76 × 10−3 | −6 | 2.08 × 106 | 61 | 2.61 × 109 | −48 | |
| PCB 95 | 5.32 × 10−3 | 4.34 × 10−4 | 1.22 × 103 | 4.94 × 10−3 | 1 | 8.28 × 105 | 0 | 5.69 × 108 | 1 | |||
| PCB 101 | 3.57 × 10−3 | 5 | 1.33 × 10−4 | −5 | 1.43 × 103 | 1.08 × 10−2 | 5 | 2.22 × 106 | −11 | 9.94 × 108 | 16 | |
| PCB 105 | 8.74 × 10−4 | 8.56 × 10−5 | 3.65 × 103 | 4.12 × 10−3 | 1 | 6.12 × 106 | −1 | 1.03 × 1010 | 1 | |||
| PCB 110 | 1.39 × 10−3 | −24 | 5.47 × 10−5 | 32 | 4.89 × 102 | 1.03 × 10−2 | 1.94 × 106 | 22 | 8.72 × 108 | −24 | ||
| PCB 116 | 3.38 × 10−3 | 47 | 1.59 × 10−4 | −32 | 2.40 × 103 | 8.59 × 10−3 | −32 | 2.86 × 106 | 1.76 × 109 | |||
| PCB 118 | 1.19 × 10−3 | 7.05 × 10−5 | 2.20 × 103 | 6.83 × 10−3 | −31 | 4.87 × 106 | 31 | 4.58 × 109 | −31 | |||
| PCB 126 | 4.87 × 10−4 | 8.00 × 10−5 | 3.26 × 103 | 2.45 × 10−3 | −27 | 5.91 × 106 | 26 | 1.66 × 1010 | −27 | |||
| PCB 138 | 5.14 × 10−4 | 3.42 × 10−5 | 1.07 × 103 | 6.06 × 10−3 | 14 | 4.88 × 106 | −9 | 5.17 × 109 | 14 | |||
| PCB 153 | 4.62 × 10−4 | −32 | 2.03 × 10−5 | 48 | 7.71 × 102 | 9.18 × 10−3 | 32 | 5.62 × 106 | −11 | 4.14 × 109 | 17 | |
| PCB 180 | 1.32 × 10−4 | 5.95 × 10−6 | 8.91 × 102 | 8.92 × 10−3 | 7 | 1.54 × 107 | −5 | 1.68 × 1010 | 7 | |||
| p,p′-DDT | 2.75 × 10−4 | −11 | 2.39 × 10−4 | 0 | 1.43 × 103 | −11 | 4.63 × 10−4 | −12 | 1.44 × 106 | −7 | 1.29 × 1010 | 100 |
| p,p′-DDE | 3.05 × 10−3 | −37 | 8.52 × 10−4 | 58 | 2.63 × 103 | 1.45 × 10−3 | −15 | 8.88 × 105 | 77 | 2.13 × 109 | −54 | |
| α-HCH | 1.05 × 10−1 | −26 | 1.55 × 10−1 | 35 | 1.01 × 103 | 2.75 × 10−4 | −11 | 9.55 × 103 | 48 | 2.37 × 107 | −41 | |
| γ-HCH | 3.32 × 10−2 | 3 | 1.98 × 10−1 | 8 | 1.18 × 103 | −25 | 6.74 × 10−5 | −53 | 8.98 × 103 | 79 | 8.86 × 107 | 27 |
| trans-Chlordane | 6.66 × 10−3 | 15 | 7.20 × 10−4 | −13 | 2.27 × 103 | 3.73 × 10−3 | 9.00 × 105 | −10 | 8.43 × 108 | 15 | ||
| cis-Chlordane | 5.70 × 10−3 | 21 | 7.49 × 10−4 | −17 | 2.25 × 103 | 3.07 × 10−3 | 8.69 × 105 | −13 | 9.77 × 108 | 21 | ||
| Chlorobenzene | 1.58 × 103 | 0 | 4.30 × 100 | 0 | 6.94 × 102 | 1.48 × 10−1 | 0 | 6.31 × 102 | 1.09 × 103 | |||
| 1,2,4,5-TetraCBz | 9.34 × 100 | −13 | 5.09 × 10−2 | 22 | 1.74 × 103 | −3 | 7.40 × 10−2 | 82 | 3.24 × 104 | 3 | 4.63 × 105 | 3 |
| 1,2,3,5-TetraCBz | 8.39 × 100 | −17 | 4.33 × 10−2 | 30 | 2.01 × 103 | −29 | 7.82 × 10−2 | 21 | 4.05 × 104 | 28 | 5.94 × 105 | |
| Pentachlorobenzene | 7.74 × 10−1 | −14 | 8.62 × 10−3 | 5 | 1.07 × 103 | −6 | 3.62 × 10−2 | 27 | 8.34 × 104 | −17 | 3.42 × 106 | 78 |
| Hexachlorobenzene | 8.47 × 10−2 | −10 | 8.62 × 10−4 | 20 | 6.05 × 102 | 8 | 3.97 × 10−2 | 121 | 2.99 × 105 | −6 | 1.77 × 107 | −26 |
| Naphthalene | 3.70 × 101 | 10 | 9.52 × 10−1 | 20 | 1.45 × 103 | −37 | 1.57 × 10−2 | −9 | 3.28 × 103 | 40 | 9.71 × 104 | |
| Biphenyl | 4.05 × 100 | 15 | 1.50 × 10−1 | 19 | 1.23 × 103 | −38 | 1.09 × 10−2 | −13 | 1.14 × 104 | 43 | 7.54 × 105 | |
| Acenaphthene | 2.01 × 100 | 26 | 1.37 × 10−1 | 4 | 1.00 × 103 | −27 | 5.93 × 10−3 | −21 | 1.04 × 104 | 26 | 1.24 × 106 | |
| Fluorene | 6.11 × 10−1 | 3 | 7.99 × 10−2 | 6 | 1.43 × 103 | −10 | 3.08 × 10−3 | −22 | 2.01 × 104 | 33 | 5.82 × 106 | −6 |
| Phenanthrene | 9.15 × 10−2 | 3 | 2.76 × 10−2 | 1 | 1.47 × 103 | −7 | 1.34 × 10−3 | −23 | 4.47 × 104 | 20 | 3.79 × 107 | −1 |
| Anthracene | 4.00 × 10−2 | 132 | 1.64 × 10−2 | −25 | 8.09 × 102 | −24 | 9.83 × 10−4 | −57 | 4.24 × 104 | 22 | 5.02 × 107 | |
| Fluoranthene | 6.69 × 10−3 | 28 | 5.01 × 10−3 | −26 | 1.15 × 103 | 26 | 5.39 × 10−4 | −32 | 1.31 × 105 | −21 | 4.25 × 108 | −43 |
| Pyrene | 1.25 × 10−2 | 15 | 1.00 × 10−2 | −15 | 2.51 × 103 | 10 | 5.02 × 10−4 | −27 | 1.40 × 105 | −8 | 4.99 × 108 | −22 |
| Benzo[a]pyrene | 6.28 × 10−6 | −15 | 1.16 × 10−4 | −7 | 3.55 × 102 | 35 | 2.17 × 10−5 | 17 | 8.80 × 105 | −20 | 1.40 × 1011 | |
| Benz[a]anthracene | 5.66 × 10−4 | 28 | 5.94 × 10−4 | −22 | 1.65 × 103 | 3.84 × 10−4 | −22 | 8.13 × 105 | 7.13 × 109 | |||
| Chrysene | 1.13 × 10−4 | 10 | 1.18 × 10−3 | −26 | 7.44 × 102 | 64 | 3.88 × 10−5 | −9 | 2.77 × 105 | −31 | 1.63 × 1010 | |
| 2,3,7,8-TetraCDF | 1.69 × 10−3 | −39 | 8.72 × 10−4 | 64 | 5.46 × 103 | 7.81 × 10−4 | 14 | 1.49 × 106 | 19 | 8.02 × 109 | −21 | |
| 1-MonoCDD | 2.85 × 10−1 | −20 | 7.17 × 10−2 | 26 | 6.53 × 103 | 1.61 × 10−3 | 6.65 × 104 | 18 | 5.67 × 107 | −20 | ||
| 1,2,3,4-TetraCDD | 7.62 × 10−4 | −33 | 2.26 × 10−4 | 49 | 2.86 × 103 | 1.36 × 10−3 | 67 | 2.51 × 106 | −37 | 9.32 × 109 | 87 | |
| 2,3,7,8-TetraCDD | 1.96 × 10−3 | −10 | 1.61 × 10−4 | 11 | 7.91 × 103 | 4.92 × 10−3 | 6.79 × 106 | 8 | 1.00 × 1010 | −10 | ||
| 1,2,3,4,7-PentaCDD | 1.75 × 10−3 | 14 | 1.45 × 10−4 | −12 | 3.70 × 104 | 4.87 × 10−3 | 2.28 × 107 | −9 | 5.24 × 1010 | 14 | ||
| 1,2,3,4,7,8-HexaCDD | 1.00 × 10−3 | 14 | 6.63 × 10−5 | −12 | 5.91 × 104 | 6.10 × 10−3 | 5.72 × 107 | −9 | 1.46 × 1011 | 14 | ||
| 1,2,3,4,6,7,8-HeptaCDD | 7.74 × 10−4 | 29 | 7.11 × 10−5 | −23 | 1.50 × 105 | 4.39 × 10−3 | 8.29 × 107 | −17 | 3.36 × 1011 | 29 |
- a PCB = polychlorinated biphenyl; DDE = dichlorodiphenyldichloroethylene; HCH = hexachlorocyclohexane; CBz = chlorobenzene; CDF = chlorodibenzofuran; CDD = chlorodibenzo-p-dioxin.
- b Percentages indicate deviation from selected values in Table 1.
ΔU |
References | References | ΔUAW | References | ΔUOW | References | ΔUOA | References | ||
|---|---|---|---|---|---|---|---|---|---|---|
| PCB 15 | 73.633 | [18] | 17.066 | [17] | NA | −20.9 | [37] | −72.597 | [6] | |
| PCB 28 | 75.624 | [18] | NA | 47.230 | [12] | NA | NA | |||
| PCB 29 | 74.322 | [18] | 14.098 | [17] | NA | NA | −72.597 | [6] | ||
| PCB 30 | 72.006 | [18] | 16.815 | [38] | NA | −20.4 | [37] | NA | ||
| PCB 31 | 75.298 | [18] | NA | NA | NA | −83 | [7] | |||
| PCB 33 | 75.624 | [18] | NA | NA | NA | NA | ||||
| PCB 44 | 78.572 | [18] | NA | NA | NA | −86 | [7] | |||
| PCB 47 | 78.572 | [18] | 13 | [39] | NA | [12] | NA | NA | ||
| PCB 52 | 78.400 | [18] | NA | 48.437 | NA | −86 | [7] | |||
| PCB 61 | 81.501 | [18] | 16.100 | [17] | NA | −24.0 | [37] | −66.318 | [6] | |
| PCB 77 | 84.756 | [18] | 25.800 | [13, 38] | NA | NA | −73.287 | [20] | ||
| PCB 95 | 81.827 | [18] | NA | NA | NA | −82.371 | [7, 20] | |||
| PCB 101 | 84.029 | [18] | 13.070 | [13, 38] | NA | NA | −79.768 | [7, 20] | ||
| PCB 105 | 88.700 | [18] | NA | NA | NA | −89.560 | [20] | |||
| PCB 110 | 84.182 | [18] | NA | NA | NA | −89 | [7] | |||
| PCB 116 | 84.182 | [18] | NA | NA | NA | NA | ||||
| PCB 118 | 86.900 | [18] | NA | NA | NA | −89.847 | [20] | |||
| PCB 126 | 92.491 | [18] | NA | NA | NA | −93.236 | [20] | |||
| PCB 138 | 89.504 | [18] | NA | NA | NA | −86.880 | [7, 20] | |||
| PCB 153 | 89.025 | [18] | 18.059 | [38] | NA | NA | −88.443 | [7, 20] | ||
| PCB 180 | 94.137 | [18] | NA | NA | NA | −82.411 | [7, 20] | |||
| p,p′-DDT | 90.748 | [40] | NA | NA | NA | −88.124 | [21] | |||
| p,p′-DDE | 84.794 | [40] | NA | NA | NA | −97.945 | [21] | |||
| α-HCH | 66.052 | [40] | NA | 51.347 | [12] | NA | −61.857 | [21] | ||
| γ-HCH | 68.062 | [40] | NA | 43.153 | [12] | NA | −65.380 | [21] | ||
| trans-Chlordane | 78.323 | [40] | NA | NA | NA | −96.414 | [21] | |||
| cis-Chlordane | 79.625 | [40] | NA | NA | NA | −98.156 | [21] | |||
| Chlorobenzene | 45.709 | [41] | NA | 28.851 | [12] | −15.0 | [37] | NA | ||
| 1,2,4,5-TetraCBz | 55.648 | [11] | 6.700 | [17] | NA | −19.3 | [37] | NA | ||
| 1,2,3,5-TetraCBz | 55.024 | [11] | 7.300 | [17] | NA | −19.9 | [37] | NA | ||
| Pentachlorobenzene | 69.486 | [11] | 12.300 | [17] | 40.817 | [12] | −22.0 | [37] | −71.257 | [6] |
| Hexachlorobenzene | 75.728 | [40, 41] | 11.142 | [17] | 45.507 | [12] | −24.3 | [37] | −55.788 | [21] |
| Naphthalene | 70.340 | [42] | NA | 44.646 | [12] | −15.7 | [37] | NA | ||
| Biphenyl | 81.886 | [43] | 15.500 | [13] | NA | NA | NA | |||
| Acenaphthene | 80.609 | [44] | NA | 51.9 | [8] | NA | NA | |||
| Fluorene | 85.983 | [44] | NA | 48.8 | [8] | −19.0 | [37] | −82.936 | [33] | |
| Phenanthrene | 68.751 | [40] | NA | 51.900 | [8, 12] | −19.0 | [37] | −75.469 | [33] | |
| Anthracene | 67.334 | [40] | NA | 48.800 | [8, 12] | −19.7 | [37] | NA | ||
| Fluoranthene | 74.954 | [40] | NA | 54.907 | [12] | −20.8 | [37] | −84.563 | [33] | |
| Pyrene | 76.217 | [40] | NA | 42.9 | [8] | −19.2 | [37] | −76.292 | [33] | |
| Benzo[a]pyrene | 93.122 | [40] | NA | 36.892 | [12] | −25.4 | [37] | NA | ||
| Benz[a]anthracene | 88.394 | [40] | NA | 66.4 | [8] | −23.3 | [37] | NA | ||
| Chrysene | NA | NA | 100.9 | [8] | −22.7 | [37] | NA | |||
| 2,3,7,8-TetraCDF | 85.813d | [45] | NA | NA | NA | −85.195 | [35] | |||
| 1-MonoCDD | 74.759 | [22] | 19.450 | [46] | NA | NA | −61.264 | [35] | ||
| 1,2,3,4-TetraCDD | 86.371d | [45] | 15.600 | [38, 46, 47] | NA | NA | −83.663 | [35] | ||
| 2,3,7,8-TetraCDD | 81.710 | [22] | NA | NA | NA | −92.661 | [35] | |||
| 1,2,3,4,7-PentaCDD | 92.628e | [22] | 5.100 | [48] | NA | NA | −104.531 | [35] | ||
| 1,2,3,4,7,8-HexaCDD | 99.132d | [45] | −2.600 | [48] | NA | NA | −98.788 | [35] | ||
| 1,2,3,4,6,7,8-HeptaCDD | 103.602d | [45] | −11.500 | [48] | NA | NA | −85.195 | [35] |
- a ΔU = heat of phase transition; A = air; W = water; AW = air—water; OW = octanol—water; OA = octanol—air; PCB = polychlorinated biphenyl; NA = not available; DDE = dichlorodiphenyldichloroethylene; HCH = hexachlorocyclohexane; CBz = chlorobenzene; CDF = chlorodibenzofuran; CDD = chlorodibenzo-p-dioxin.
- b ΔUA is obtained by subtracting 2.391 kJ/mol from the enthalpy reported for vapor pressure (ΔHvp). See text for details.
- c Literature values changed to apply to the supercooled liquid state.
- d Calculated from relative retention times, with p,p′-DDT as reference compound.
- e Calculated.
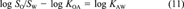 (12)
(12)In this example, all available data can be related to each other in one constraining equation. This is always the case if not more than three or four of the six partitioning properties have been measured. Then ∈ and δ can be calculated as shown. When measured data are available for more than four of the parameters, two constraining equations will be needed to relate all properties. A common example is when data are available for KAW, KOW, KOA, SA, and SW but not SO (which is the case for PCB 15). Equations 6 and 11 may then be used. One option is to apply one equation, deduce the adjustment factor δ, then apply the corrected values to the second. This is problematic because the result will depend on the order in which the equations are applied.
A more rigorous approach is to apply iterations, that is, use both equations to deduce two different values of ∈ and hence δi for one property (e.g., KAW), and adjust the parameters separately by using both equations, then use these adjusted values to deduce new values of ∈. By repeating this iteration, the parameter values will converge to a set consistent with both equations. A third strategy is to calculate the adjustment factors δi for both equations separately and to apply mean corrections to the property that occurs in both equations. For example, KAW, which occurs in Equations 6 and 11, is changed by the mean adjustment according to both equations. Then, KOW, KOA, SA, and SW are altered to account for the remaining error in Equations 6 and 11. Inserting the values of PCB 15 from Table 1, the correction of log KAW is -0.0325 (Eqn. 6) and -0.0311 (Eqn. 11), hence log KAW is corrected by the mean of both (i.e., -0.0318). Both log SA and log SW now must be altered to account for the remaining error in Equation 6, which is -0.0975 + 0.0318, that is, -0.0657. If this remaining error is shared among the two properties, both are changed by -0.03285, thus log SA becomes -4.566 and log SW becomes -2.359. Adjustment factors for KOW and KOA are determined accordingly. This analytic approach yields adjustment factors that can directly be derived from the substance properties without any numerical iteration. The disadvantage of this approach is that it sometimes yields larger δi for one property, whereas other properties are changed by a smaller δi. Hence, for some properties the absolute deviation from the measurement may be larger as if using the iterative approach.
Strategies two and three have been applied to the data given in Table 1. VisualBasic code used for the two adjustment procedures can be downloaded free of charge from http://www.usf.uos.de/projects/elpos. Tables 2 and 3 report consistent sets of parameters that were obtained by applying the iterative approach (method two) and the analytical approach (method three), respectively. A comparison shows that both approaches generally yield similar results. A deviation between the two methods occurs only if six measured parameters are available. Thus, the adjusted properties of the example chemical PCB 15 are the same when applying both approaches. The deviation between the two selection procedures becomes larger if the measured data lead to larger deviations in Equations 6 through 9. However, large deviations point to inconsistent or erroneous data, suggesting that such data should not be used. Hence, assuming that the input data were measured and selected appropriately, the difference between the two selection strategies is expected to be negligible for applications in the field of environmental research.
TEMPERATURE DEPENDENCE
When attempting to apply chemical fate models to real situations, the temperature dependence of physicochemical properties obviously is of high importance. Recently, several authors have compiled sets of temperature-dependent data [8-12] that must be subjected to the same procedure as the properties at standard temperature. Similar thermodynamic relations constraining the temperature slopes are used for this purpose [1, 13].
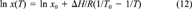 (13)
(13)| ΔUA | %b | ΔUW | % | ΔUO | % | ΔUAW | % | ΔUOW | % | ΔUOA | % | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PCB 15 | 72.42 | −2 | 18.28 | 7 | −1.40 | 54.13 | −19.68 | −6 | −73.81 | 2 | ||
| PCB 28 | 75.62 | 28.39 | 0.00c | 47.23 | −28.39c | −75.62c | ||||||
| PCB 29 | 74.32 | 14.10 | 1.72 | 60.22 | −12.37 | −72.60 | ||||||
| PCB 30 | 72.01 | 16.82 | −3.59 | 55.19 | −20.40 | −75.59 | ||||||
| PCB 31 | 75.30 | 20.00c | −7.70 | 55.30c | −27.70c | −83.00 | ||||||
| PCB 33 | 75.62 | 20.00c | 0.00c | 55.62c | −20.00c | −75.62c | ||||||
| PCB 44 | 78.57 | 20.00c | −7.43 | 58.57c | −27.43c | −86.00 | ||||||
| PCB 47 | 78.57 | 13.00 | 0.00c | 65.57 | −13.00c | −78.57c | ||||||
| PCB 52 | 78.40 | 29.96 | −7.60 | 48.44 | −37.56 | −86.00 | ||||||
| PCB 61 | 75.73 | −7 | 21.87 | 36 | 3.64 | 53.86 | −18.23 | −24 | −72.09 | 9 | ||
| PCB 77 | 84.76 | 25.80 | 11.47 | 58.96 | −14.33 | −73.29 | ||||||
| PCB 95 | 81.83 | 20.00c | −0.54 | 61.83c | −20.54= | −82.37 | ||||||
| PCB 101 | 84.03 | 13.07 | 4.26 | 70.96 | −8.81 | −79.77 | ||||||
| PCB 105 | 88.70 | 20.00c | −0.86 | 68.70c | −20.86c | −89.56 | ||||||
| PCB 110 | 84.18 | 20.00c | −4.82 | 64.18c | −24.82c | −89.00 | ||||||
| PCB 116 | 84.18 | 20.00c | 0.00c | 64.18c | −20.00c | −84.18c | ||||||
| PCB 118 | 86.90 | 20.00c | −2.95 | 66.90c | −22.95c | −89.85 | ||||||
| PCB 126 | 92.49 | 20.00c | −0.74 | 72.49c | −20.74c | −93.24 | ||||||
| PCB 138 | 89.50 | 20.00c | 2.62 | 69.50c | −17.38c | −86.88 | ||||||
| PCB 153 | 89.03 | 18.06 | 0.58 | 70.97 | −17.48 | −88.44 | ||||||
| PCB 180 | 94.14 | 20.00c | 11.73 | 74.14c | −8.27c | −82.41 | ||||||
| p,p′-DDT | 90.75 | NA | 2.62 | NA | NA | −88.12 | ||||||
| p,p′-DDE | 84.79 | NA | −13.15 | NA | NA | −97.95 | ||||||
| α-HCH | 66.05 | 14.70 | 4.19 | 51.35 | −10.51 | −61.86 | ||||||
| γ-HCH | 68.06 | 24.91 | 2.68 | 43.15 | −22.23 | −65.38 | ||||||
| trans-Chlordane | 78.32 | NA | −18.09 | NA | NA | −96.41 | ||||||
| cis-Chlordane | 79.63 | NA | −18.53 | NA | NA | −98.16 | ||||||
| Chlorobenzene | 45.71 | 16.86 | 1.86 | 28.85 | −15.00 | −43.85 | ||||||
| 1,2,4,5-TetraCBz | 55.65 | 6.70 | −12.60 | 48.95 | −19.30 | −68.25 | ||||||
| 1,2,3,5-TetraCBz | 55.02 | 7.30 | −12.60 | 47.72 | −19.90 | −67.62 | ||||||
| Pentachlorobenzene | 63.37 | −9 | 18.42 | 50 | −5.736 | 44.95 | 10 | −24.15 | 10 | −69.10 | −3 | |
| Hexachlorobenzene | 66.61 | −12 | 20.26 | 82 | 3.39 | 46.35 | 2 | −16.87 | −31 | −63.22 | 13 | |
| Naphthalene | 70.34 | 25.69 | 9.99 | 44.65 | −15.70 | −60.35 | ||||||
| Biphenyl | 81.89 | 15.50 | 0.00c | 66.39 | −15.50c | −81.89c | ||||||
| Acenaphthene | 80.61 | 28.71 | 0.00c | 51.90 | −28.71c | −80.61c | ||||||
| Fluorene | 85.98 | 32.14 | 8.09 | 53.85 | 10 | −24.05 | 27 | −77.89 | −6 | |||
| Phenanthrene | 68.75 | 15.33 | −5.20 | 53.42 | 3 | −20.52 | 8 | −73.95 | −2 | |||
| Anthracene | 67.33 | 18.53 | −1.17 | 48.80 | −19.70 | −68.50 | ||||||
| Fluoranthene | 74.95 | 17.09 | −6.66 | 57.86 | 5 | −23.75 | 14 | −81.61 | −3 | |||
| Pyrene | 76.22 | 28.59 | 4.66 | 47.63 | 11 | −23.93 | 25 | −71.56 | −6 | |||
| Benzo[a]pyrene | 93.12 | 56.23 | 30.83 | 36.89 | −25.40 | −62.29 | ||||||
| Benz[a]anthracene | 88.39 | 21.99 | −1.31 | 66.40 | −23.30 | −89.70 | ||||||
| Chrysene | 123.60c | 22.70c | 0.00c | 100.90 | −22.70 | −123.60 | ||||||
| 2,3,7,8-TetraCDF | 85.81 | NA | 0.62 | NA | NA | −85.19 | ||||||
| 1-MonoCDD | 74.76 | 19.45 | 13.50 | 55.31 | −5.95 | −61.26 | ||||||
| 1,2,3,4-TetraCDD | 86.37 | 15.60 | 2.71 | 70.77 | −12.89 | −83.66 | ||||||
| 2,3,7,8-TetraCDD | 81.71 | 15.60c | −2.62 | 74.44c | −18.22c | −92.66 | ||||||
| 1,2,3,4,7-PentaCDD | 92.63 | 5.10 | −11.90 | 87.53 | −17.00 | −104.53 | ||||||
| 1,2,3,4,7,8-HexaCDD | 99.13 | −2.60 | 0.34 | 101.73 | 2.94 | −98.79 | ||||||
| 1,2,3,4,6,7,8-HeptaCDD | 103.60 | −11.50 | 18.41 | 115.10 | 29.91 | −85.19 |
- a PCB = polychlorinated biphenyl; NA = not available; DDE = dichlorodiphenyldichloroethylene; HCH = hexachlorocyclohexane; CBz = chlorobenzene; CDF = chlorodibenzofuran; CDD = chlorodibenzo-p-dioxin.
- b Percentages indicate deviation from selected values in Table 3.
- c Default value used or calculated by using default value of another property.
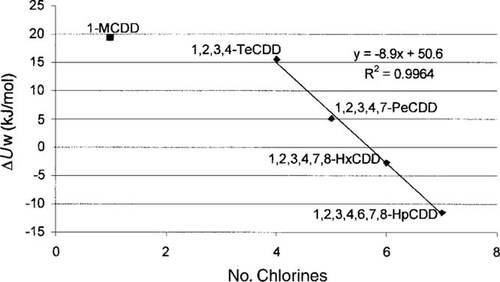
Plot of measured internal energy change in water (ΔUW in kJ/mol) of chlorinated dibenzo-p-dioxins versus number of chlorines. HpCDD = heptachlorodibenzo-p-dioxin; HxCDD = hexachlorodibenzo-p-dioxin; MCDD = monochlorodibenzo-p-dioxin; PeCDD = pentachlorodibenzo-p-dioxin; TeCDD = tetrachlorodibenzo-p-dioxin.
 (14)
(14) (15)
(15)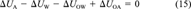 (16)
(16)In the case of the temperature slopes ΔU, the adjustment is applied to the absolute quantity rather than to the logarithmic quantity. This is preferable when the error is judged to be normally rather than log-normally distributed. Uncertainty factors can be applied as before. Selected heats of phase transfer are presented in Table 5.

APPLICATION TO 50 CHEMICALS
Vapor pressure, water solubility, octanol solubility, KAW, KOW, and KOA have been compiled from the literature for 50 chemicals, along with data on their temperature dependence (Tables 1 and 3). The set of chemicals contains mainly aromatic compounds of environmental interest covering a broad range of chemical properties. Subcooled liquid-phase vapor pressures range from 10−5 Pa to 104 Pa and log KOW values range from 2 to 8. Mainly measured data were taken (Table 1) and corrected to be thermodynamically consistent (Tables 2 and 3). The assumptions for this adjustment procedure are as follows: All properties apply to the same solute state (liquid or solid). All properties apply to the same temperature. Concentrations are dilute. Solubility is independent of solute concentration (or activity coefficients do not change as function of solute concentration). Deviations from ideal thermodynamic relationships are small. Equations 10a and 10b can be used to transform KOW to SO/SOW. Temperature dependence can be approximated by exponential relationship (Eqn. 12). Values of ΔH and ΔU are constant over the considered temperature range. The parameter ΔHVp can be transformed to ΔUA by subtracting 2,391 J/mol. Several recent compilations of physicochemical properties of organic compounds were used to select most of the properties. The selection procedure was as follows. If only one measurement existed for a given property, this datum was taken. If more than one measurement existed and if a value was suggested in one of the recent reviews, the suggested value was taken. If the chemical was considered in an older review, the suggested value was omitted only if newer measurements suggested a different value, that is, more recent publications of new data were taken into account. When no suggestion existed, either a typical value of all values was selected or the mean or median of all measurements was taken, based on judgment.
Two recent publications by Shiu and Ma [10, 11] provided most of the data for the vapor pressures and water solubilities at 25°C. The suggested values for the Henry's law constants in Shiu and Ma [10, 11] were derived from the selected values for vapor pressure and water solubilities. Because this approach neglects measurements of Henry's law constants, these values were not taken. Therefore, a selection of typical, measured KAW values was made, based on the available data. The selected log KOWs are mostly taken from Mackay et al. [2] and Makino [19]. For most of the log KOAs, only one measurement exists. If two values exist from two different studies [7, 20] the mean was selected, because it is not yet possible to decide which of the measurements is more reliable. In case of p,p′-DDT and hexachlorobenzene, two measurements by the same group exist [6, 21] and the newer values were selected.
The approach taken for the temperature slopes was the same. Most temperature slopes were measured between 5 and 30°C. Exceptions existed only for KOA and are indicated in Table 4. The temperature dependence of vapor pressures was determined indirectly via the gas chromatography retention time method in all cases, except for three polychlorinated dibenzo-p-dioxins (PCDDs) for which heats of vaporization were taken from Rordorf [22].
Data gaps were filled by deriving missing values from others whenever possible. However, in some cases, it was necessary to use values derived from molecular structure information to fill data gaps, which is indicated in Tables 1 and 4. Transformations from solid to supercooled liquid state were performed with substance specific entropies of fusion and melting point temperatures whenever possible. If no entropy of fusion was reported, a default value of 56 J/(mol K) was assumed [2].
The numbers from Tables 1 and 4 were used to either derive missing values or apply the corrections from above if possible. The resulting values along with their relative changes are reported in Tables 2, 3, and 5. The relative changes are mostly less than 50%; however, some exceptions did occur. In most cases the change is well within the range of reported measurements.
The resulting set of data at 25°C is complete (Tables 2 and 3), whereas temperature slopes are not available for all chemicals in Table 4. For the PCBs, Shiu et al. [17] suggested using a mean value of 35 kJ/mol for the solid-phase water solubility. The average ΔUW for the water solubility of supercooled liquid PCBs in Table 4 is 20 kJ/mol, which agrees well with the value suggested by Shiu et al. [17]. The ΔUW of PCBs was therefore set to 20 kJ/mol if it could not be derived from measured data. Plotting the measured ΔUW of PCDDs with four or more chlorine atoms from Table 4 versus the number of chlorines yields a good correlation (R2 = 0.996; Fig. 1). Analysis of the available data suggests that ΔUW is mainly determined by the number of chlorines. Because the measured ΔUW values also include 2,3,7,8-substituted congeners, the assumption can be made that the ΔUW of 2,3,7,8-tetrachlorodibenzo-p-dioxin (2,3,7,8-TeCDD) is relatively close to the value of 1,2,3,4-TeCDD. Hence, a ΔUW of 15.6 kJ/mol is assumed for 2,3,7,8-TeCDD.
If the temperature dependence of KOW or KOA is known, one can derive temperature slopes for the octanol solubility. Kömp and McLachlan [7] as well as Harner and Bidleman [20] calculated internal energy changes of the octanol solubility ΔUO for PCBs from temperature slopes of KOA and vapor pressure. Although a systematic difference seems to exist between the studies [7], the absolute calculated ΔUO values were always less than 20 kJ/mol, that is, relatively close to zero. This also holds for the corrected values in Table 5. In fact they are even closer to zero than the values reported by Harner and Bidleman [20] and Kömp and McLachlan [7]. The same is true for most other chemicals; the only exception is benzo[a]pyrene, which has a ΔUO of 31 kJ/mol. Thus, assuming a ΔUO equal to zero seems reasonable, if deriving the value from measured data is impossible. Hence, by assuming standard internal energy changes for water solubilities and octanol solubilities, estimating most partitioning data as a function of temperature is possible, although with variable accuracy.
CONCLUSIONS
We suggest that when selecting chemical property data for use in chemical fate models, all available data be taken into account and processed with the methods described here to obtain an internally consistent set of data. Perceived accuracy can be taken into account. We believe that by adopting this approach, not only will more accurate data be obtained, but the determination of key properties that can improve accuracy of selected values may be encouraged. Most problematic is the relationship between KOW and SO/SW, as derived in the Appendix. More data must be gathered to improve this relationship.
Acknowledgements
Funding by the German Federal Environmental Agency, Berlin (R&D Project FKZ 299 65 402); the Natural Sciences and Engineering Research Council of Canada; and the consortium of chemical companies that support the Canadian Environmental Modelling Centre; and helpful comments by two anonymous reviewers are gratefully acknowledged. We especially thank Tom Harner for providing us with his KOA data for organochlorine pesticides before publication.
APPENDIX
Measured octanol-air partition coefficients (KOA) have been compared to the ratio KOW/KAW [6, 7]. Systematic deviations between the calculated KOA and measured values have been attributed to the fact that the KOW expresses the equilibrium between water-saturated octanol and octanol-saturated water, whereas the KOA refers to pure phases. Similarly, a deviation between directly measured KOW and KOW calculated as the ratio of octanol and water solubilities has been observed [5].
 (17)
(17) (18)
(18)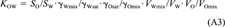 (19)
(19) (20)
(20)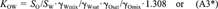 (21)
(21)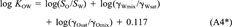 (22)
(22)This equation shows that even if the activity coefficients of the solute in water and octanol are unaffected by the mutual solubility of the two solvents or the concentration of the solute. KOW is not exactly equal to SO/SW, but would be larger by 0.117 log units.
The extent to which SO/SW, additionally differs from KOW depends on how the activity coefficients of the solute in the water and octanol phases are influenced by the concentration of the solute (i.e., solute-solute interaction) and the presence of the other solvent. The first effect results in a deviation of γW/γWsat and γO/γOsat from one; the second effect causes γW/γWmix and γO/γOmix to be different from unity.
Solute—solute interaction
The activity coefficients γWsat and γOsat are necessarily measured at saturation concentration or solubility limit. At lower concentrations and ultimately at infinite dilution, the activity coefficients γW and γO are probably greater because of reduced solute-solute interactions (e.g., self-association). The magnitude of this effect is likely to be small in aqueous solutions for hydrophobic substances that are sparingly soluble in water, but the effect may be significant for solutions in octanol [23]. Unfortunately, data are insufficient to permit the magnitude of these effects to be quantified.
If solute-solute interactions occur in the saturated solutions, the terms γW/γWsat and γOsat/γO in Equation A4* would not equal one. The effect of increasing the concentration of nonpolar solutes in water is to encourage their solute-solute interactions in the aqueous phase [23]. This would imply that for such solutes, γWsat is smaller than γW, thus γW/γWsat is larger than 1 and log (γW/γWsat) is positive. However, significant interaction of sparingly soluble aqueous solutes is rather unlikely even in saturated solutions, that is, for most practical purposes γW = γWsat. Yalkowsky et al. [23] suggested that solute-solute interactions of polar solutes at high concentration in octanol generally will increase the ability of octanol to accommodate the solute. This would imply that γOsat is lower than γO, thus γOsat/γO is smaller than 1, and log (γOsat/γO) is negative.
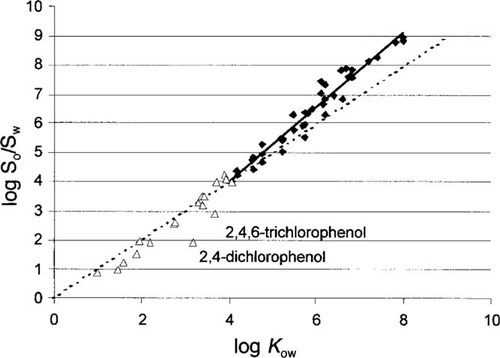
Plot of calculated ratios of octanol and water solubility versus measured log octanol-water partition coefficient (KOW). The set of 70 chemicals contains polyaromatic hydrocarbons, polychlorinated biphenyls, polychlorinated dibenzo-p-dioxins and dibenzofurans, chlorobenzenes, various organic pesticides, organic acids, and two chlorinated phenols. The regression applying to chemicals with log KOW greater than 4 (squares) has a coefficient of determination of 0.953 (n = 40). Chemicals with log KOW less than 4 are displayed as triangles.
Effect of binary solvents
Li and Andren [24] measured the effect of octanol on the solubilities of PCBs in water and could not identify a significant difference between the solubilities in pure water and octanol-saturated water. On the other hand, Chiu et al. [25] found that the presence of octanol in water increased the solubility of hydrophobic substances in water. Taking both studies into account, the conclusion can be made that the ratio γWmix/γW is either close to 1 or below 1 and log (γWmix/γW) is zero or negative, respectively. If the presence of water in octanol decreases the solubility of the solute in octanol, γOmix is larger than the activity coefficient in pure octanol. Hence, γO/γOmix is smaller than 1, and log (γO/γOmix) is negative. This implies that the mixing of water and octanol causes SO/SW to be larger relative to KOW.
Relationship between KOW and SO/SW
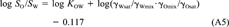 (23)
(23)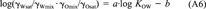 (24)
(24)The currently available data are insufficient to separate the different factors resulting in the deviation between SO/SW and KOW. For instance, evidence exists that γWsat/γWmix is equal to one, that is, the entire deviation is caused by effects in the octanol phase. Therefore, the empirical relationship between SO/SW and KOW is preliminary and we suggest that further research be undertaken to improve the suggested relationship.




