Long-term bioconcentration kinetics of hydrophobic chemicals in Selenastrum capricornutum and Microcystis aeruginosa
Abstract
The bioconcentration of two chlorobenzenes (CBs) and of seven polychlorobiphenyls (PCBs) to Selenastrum capricornutum and Microcystis aeruginosa was studied with accumulation experiments followed by gas purge elimination experiments. Henry's law constants at 10°C were needed to interpret the gas purge results and were measured in control experiments. For the M. aeruginosa culture, steady-state uptake was reached within days, whereas uptake by S. capricornutum took several weeks. The relationships between the log bioconcentration factors (BCF) and log octanol–water partition coefficients (Kow) were nonlinear, with relatively low values for the more hydrophobic PCBs. Rate constants for the elimination of CBs and PCBs from the algal cells were shown to be larger than 1 per day when calculated with a one-compartment model. With such large rate constants, it is unlikely that the curvature observed for these species is caused by slow kinetics or that algal growth affects BCF by dilution of CB or PCB concentrations. The log BCF–log Kow relationships could be described by a simple three-phase model that accounted for the binding of CBs and PCBs to dissolved organic carbon (DOC). Modeling bioconcentration of hydrophobic chemicals in phytoplankton should account for the binding to DOC.
INTRODUCTION
Algal cells and detritus may form a major fraction of particles in aquatic systems. They are important carriers of hydrophobic organic compounds (HOCs) and are the primary pathway through which HOCs enter the food chain. Therefore, bioconcentration in phytoplankton plays an important role in the aquatic fate of HOCs [1-3]. In recent studies, bioconcentration in phytoplankton has received attention because of (1) the interspecies differences in accumulation rates [4] and (2) the curvature of the relationship between apparent polychlorobiphenyl log BCF values and log Kow [4, 5]. Interspecies differences seem to be related to differences in lipid content and character [4] and to different algal sizes and shapes [6]. To explain the curvature in log BCF–log Kow relationships, two mechanisms have been suggested: slow elimination kinetics or binding of the hydrophobic chemicals to dissolved organic carbon (DOC) remaining in the aqueous phase after phase separation [4, 5, 7]. These mechanisms affect the BCF as follows. When the elimination kinetics are slow, algal growth may cause a continuous dilution of the chemical concentration in the cells and may thus influence steady-state BCF values. After separation of the algal cells from the medium, dissolved, or colloidal, organic carbon (DOC; e.g., exudates) remains in the aqueous phase. Exudation is the result of metabolic activity and is therefore also related to growth [8]. The rates of extracellular release are highly variable and have been reported to range from 1 to 100% of the rate of carbon fixation [8]. As a result of the binding of HOCs to DOC [9], aqueous concentrations are overestimated, and BCFs are underestimated. The slow kinetics and the binding strength (to DOC) are functions of hydrophobicity, so both mechanisms may explain the nonlinearity of log BCF–log Kow relationship. In earlier work [6, 10, 11], rate parameters for chlorobenzene bioconcentration to phytoplankton were measured using gas purge experiments. For the chlorobenzenes, kinetics were fast enough to exclude the slow-kinetics hypothesis as an explanation for nonlinear log BCF–log Kow relationships. However, for the larger and more hydrophobic PCBs, this issue has not yet been settled.
The aim of this study was to assess the adequacy of the hypothesis of slow elimination kinetics for two common species, Selenastrum capricornutum and Microcystis aeruginosa. A secondary aim was to evaluate the possible role of the binding of the hydrophobic chemicals to DOC. The common methodology in bioconcentration research is batchwise equilibration followed by (incomplete) phase separation (e.g., Stange and Swackhamer [4] and Swackhamer and Skoglund [5]) and analysis of algal and aqueous phase concentrations. With this method, it is impossible to discriminate between the two mechanisms mentioned above. Therefore, we combined batchwise equilibration of HOCs at low temperature with subsequent gas purge–induced elimination experiments. The first method minimizes the potential affect of algal growth on the HOC concentration in the cells. The latter method minimizes the influence both of growth and of exudates (or DOC) on the apparent BCF or kinetic constants, because phase separation is not required [10, 11].
Gas purging is a technique used to measure aqueous fugacities [12], Henry's law constants (H) [13-16], or equilibrium and rate characteristics as a result of HOC binding to DOC [17, 18], algae [6, 10, 11], or sediments [19-21]. So far, no gas purge experiment results concerning PCB bioconcentration in phytoplankton have been published.
The bioconcentration experiments consisted of a 5-week batchwise accumulation period that was followed immediately by 5- or 6-week gas purge–induced elimination. Algal characteristics and DOC were monitored extensively during accumulation and elimination. Experiments were performed at both 10 and 20°C. The lower temperature was chosen in order to assure comparability with the data from earlier reports [4, 5] was possible. Henry's law constants are required for gas purge data analysis and were taken from the literature (20°C) or were measured (10°C).
METHODS
Algae
Cultures of S. capricornutum (NIVA-CHL1, Rhaphidocelis subcapitata) and M. aeruginosa (NIVA-CYA043) were supplied by the Norwegian Institute for Water Research (NIVA). The algae were cultured in a 25% Z8 mineral medium [22], prepared axenically in 0.2 μm filtrated Nanopure water (Sybron-Barnstead, Dubuque, IA, USA). The light regime was 16: 8 h light: dark at 100 μE/m2. Temperature was 20 ± 2°C. Algal subsamples were used for bioconcentration experiments after the stationary growth stage had been reached.
Monitoring of algal density during culturing, CB and PCB bioconcentration, and elimination
Dry weight (DW; mg/L) was measured by drying at 105°C until constant weight was reached. Cell numbers and particle size distribution were measured with a Coulter Multisizer II (Coulter Electronics, Mijdrecht, The Netherlands). Total organic carbon (TOC) was measured in unfiltered samples (mg/L) and in 0.45 μm filtrated samples (DOC; mg/L) with an OIC (College Station, TX, USA) Model 700 TOC analyzer. Particulate carbon concentrations (POC; mg/L) were calculated from TOC and DOC by differencing. Organic carbon fractions of the algal cells were calculated as POC/DW. Comparability of subsamples was assured by using a Retsch (Dassel, Germany) suspensions divider.
Chemicals
1,2,3,4-Tetrachlorobenzene (TeCB; 98%) and pentachlorobenzene (QCB; 98%) were obtained from Aldrich (Zwijndrecht, The Netherlands); hexachlorobenzene (HCB; >98%) was obtained from BDH Chemicals (Poole, UK), and 2,4,4′-trichlorobiphenyl (PCB28), 2,2′,5,5′-tetrachlorobiphenyl (PCB52), 2,2′,4,5,5′-pentachlorobiphenyl (PCB101), 2,3′,4,4′,5′-pentachlorobiphenyl (PCB118), 2,2′,3,4,4′,5′-hexachlorobiphenyl (PCB138), 2,2′,4,4′,5,5′-hexachlorobiphenyl (PCB153), and 2,2′,3,4,4′,5,5′-heptachlorobiphenyl (PCB180) were obtained from Dr. Ehrenstorfer (Augsburg, Germany). Nanograde organic solvents (acetone, diethyl ether, 2,2,4-trimethylpentane) were obtained from Promochem (Wesel, Germany) and from Mallinckrodt (Paris, KY, USA).
Bioconcentration experiments
Quadruplicate BCFs were determined for TeCB, HCB, PCB28, PCB52, PCB101, PCB118, PCB138, PCB153, and PCB180 at the following conditions: (1) M. aeruginosa, 10°C; (2) S. capricornutum, 10°C; and (3) S. capricornutum, 20°C. The algal cultures (10 L) were spiked with 200 μL of a solution of each test compound in acetone. To avoid saturation with respect to the HOC aqueous solubilities, the spike solution was added to the continuously stirred cultures in several equal portions over a 5-h period. The spiked suspensions were incubated for 5 or 6 weeks at 10 ± 1°C or at 20 ± 2°C. At incremental time intervals, triplicate 0.6-L subsamples were taken for monitoring algal density, size, growth, and concentrations of the test compounds in/on algal cells. After equilibration, aqueousphase HOC analysis in 0.45-μm filtrates (glass fiber, Whattmann GF/C, Maidstone, UK) were performed. After the bioconcentration experiments, gas purge–induced desorption experiments (n = 3) were performed immediately.
Gas purge experiments
General explanation. The gas purge method involves bubble generation in water with HOCs (determination of Henry's law constant) or in the algal suspension incubated with HOCs (elimination studies). If the bubbles remain in solution for a sufficient period of time, HOC transfer from the water to the bubbles will occur until equilibrium is attained. With algae, the depletion of HOCs in the aqueous phase causes HOC elimination from the cells. The resultant HOC concentration in the gas leaving the headspace then depends on Henry's law constant, as measured in controls without algae, and on the HOC elimination rate (from the cells). The HOC concentration in the gas can be measured with a trap.
Gas purge procedure. The purge procedure was described earlier [10], but it is briefly explained here. Three 0.8-L subsamples from equilibrated cultures were placed in a thermostatted (10 ± 0.1°C), glass-stoppered, 0.9-L bottle. The HOCs were purged onto 11 to 14 Tenax traps (40–60 mesh, Chrompack, Bergen op Zoom, The Netherlands) in 5 or 6 weeks at a flow of 0.5 L/min under continuous stirring. The gas flow (constant within 2%) was adjusted with flow controllers and was passed through vessels containing water to prevent volume reduction in the algal suspensions. Tenax traps (trap efficiency, 100%) were replaced at incremental intervals, and these consisted of glass tubes containing glass wool and approximately 0.2 g Tenax. After purging, HOCs in the algae were analyzed so that we could account for remaining HOC fractions. Mass balances were calculated from the amounts of test compound that were found in the Tenax traps, in the algae, and on the container walls after purging based on the amount initially added to the systems. Before and after purging, a full characterization, including DW, DOC, and TOC, was performed.
For the determination of Henry's law constants, the HOCs were purged from Nanopure water at 10 ± 0.1°C. Spike volume was 5 μL. Equilibration and purge time were 1.5 h and 5 d, respectively.
HOC cleanup and analysis
HOCs were isolated from the filtered algae by multiple extractions with acetone. Combined acetone extracts were shaken with diethyl ether. Acetone was removed by extractions with water. The organic fraction was separated, and the aqueous phase was extracted again with diethyl ether. Both diethyl ether fractions were combined and were shaken again with water. The organic fraction was separated, dried with potassium sulphate (p.a.), concentrated to 5 ml on a Kuderna-Danish apparatus, (Wheaton Science Products, Millville, NJ, USA) and finally concentrated to 1 ml under nitrogen. The resultant solution was cleaned by eluting with diethyl ether over deactivated alumina. The extract was concentrated to 2 ml after addition of 2 ml 2,2,4-trimethylpentane with QCB as an internal standard.
Hydrophobic organic compounds were isolated from water samples by extraction with diethyl ether. After drying with p.a., the samples were concentrated and cleaned, as described above. Hydrophobic organic compounds were desorbed from container walls by thorough rinsing with acetone. Acetone fractions were extracted, concentrated, and cleaned as described above. Hydrophobic organic compounds were extracted from Tenax traps with 15 ml diethyl ether (100% recovery). The extracts were concentrated to 2 ml under nitrogen after addition of 2 ml 2,2,4-trimethylpentane with QCB as an internal standard.
A Hewlett-Packard (Avondale, PA, USA) 5890 double-column gas chromatography system equipped with two 63Ni electron capture detectors was used for CB and PCB quantification. Further details of the analytical procedure were described in previous studies [6, 10].
Data analysis
Recoveries were calculated for the S. capricornutum and M. aeruginosa accumulation experiments. After incubation, bioconcentration factors on a DW basis (BCFbatchDW), were calculated from solid phase and aqueous concentrations. The purge data were analyzed using first-order compartment models, which are briefly explained below. For a full discussion of these models, we refer to our earlier publications [6, 10]. This analysis also yields DW-based BCF (BCFGPDW) and kinetic data.
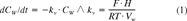 (1)
(1)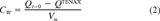 (2)
(2)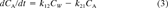 (3)
(3) (4)
(4) (5)
(5)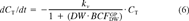 (6)
(6)RESULTS
Algal density
Because of the low temperatures, average growth rates in doublings per day, based on cell numbers, were low during batch incubation: 0.002 ± 0.003 per day for M. aeruginosa at 10°C, 0.0036 0.009 for S. capricornutum at 10°C, and 0.005 ± 0.004 for S. capricornutum at 20°C. Characteristics of the cultures are summarized in Table 1. During gas purging, no losses of cells were observed for S. capricornutum at both temperatures. However, the density of the M. aeruginosa culture gradually decreased during gas purging. The DOC concentrations indicate significant exudation for S. capricornutum at 10°C. Particle size distributions remained similar in all cases except for that of S. capricornutum at the end of the incubation, during which a second peak occurred at 3.5 μm.
Henry's law constant determinations
Henry's law constant values at 108C were calculated from the cumulative mass purged from solution, except in the cases of PCB118 and PCB180. For PCB118 and PCB180, the mass purged was too small to allow direct fitting to Equations 1 and 2. Following Murray and Andren [23], the H values for PCB118 and PCB180 were calculated directly as the ratio of gas-phase concentration at time t = (QTENAX/[F.t]) and at initial aqueous concentration, assuming that the aqueous concentration did not change significantly during the first hours of purging. Estimated H values are presented in Table 2.
Uptake of chlorobenzenes and PCBs
The total recovery of individual homologues varied from 50 to 100%. Balances were less complete for the least and for the most hydrophobic chemicals. Uptake was monitored to check whether equilibrium had been reached, and it was not the subject of detailed study. The graphs of the uptake data are available on request. For all three experiments, accumulation was rapid in the first week. For S. capricornutum (20°C) and M. aeruginosa, no further uptake occurred. Selenastrum capricornutum cells at 10°C still accumulated some PCBs in the last week of the experiment.
| Sample | Cells (×109/L) | Diameter (μm) | DWb (mg/L) | TOCc (mg/L) | DOCd (mg/L) | f∝ |
|---|---|---|---|---|---|---|
| Microcystis aeruginosa, 10°C | ||||||
| Day 0 | 3.4 | 24.4 ± 0.57 | 16.4 ± 0.44 | 6.2 ± 0.01 | 0.41 ± 0.03 | |
| Day 36e | 3.55 | 3.4 | 26.1 ± 3.3 | 23.4 ± 0.08 | 4.8 ± 0.02 | 0.71 ± 0.07 |
| Day 69f | 0.45 | — | 8.3 ± 1.2 | 8.9 ± 0.50 | 7.2 ± 0.34 | 0.20 ± 0.04 |
| Selenastrum capricomutum, 10°C | ||||||
| Day 0 | 1.28 | 4.5 | 32.7 ± 2.49 | 54.8 ± 1.3 | 25.6 ± 2.2 | 0.89 ± 0.10 |
| Day 33e | 2.40 | 3.5/4.8 | 30.7 ± 2.1 | 81.0 ± 2.0 | 65.6 ± 4.2 | 0.50 ± 0.16 |
| Day 77f | 2.31 | — | 35.4 ± 0.79 | 16.9 ± 1.0 | 5.2 ± 0.47 | 0.32 ± 0.04 |
| Selenastrum capricomutum, 20°C | ||||||
| Day 0 | 0.60 | 3.8 | 33.7 ± 2.4 | 20.6 ± 0.23 | 6.2 ± 0.06 | 0.34 ± 0.02 |
| Day 34e | 0.77 | 4.1 | 57.8 ± 4.0 | 21.2 ± 1.15 | 3.9 ± 0.01 | 0.32 ± 0.03 |
| Day 71f | 0.62 | 4.3 | — | 26.6 ± 9.3 | 7.2 ± 0.93 | — |
- aErrors relate to 1 SD.
- bDW = dry weight.
- cTOC = total organic carbon.
- dDOC = dissolved (<0.45 μm) organic carbon.
- eAfter batch equilibration.
- fAfter batch equlibration and gas purge elimination.
Bioconcentration factors
Apparent BCFs were calculated from algal and aqueous phase measurements after 33, 34, or 36 d (see Table 1). The log BCFDW−log Kow curves (Fig. 1A), as determined by batchwise equilibration, were nonlinear and had a maximum at log Kow = 6.5 to 7. No clear difference was found for the log BCF values measured at 10 and 20°C (Fig. 1A). Note that no decisive conclusions regarding a temperature effect can be drawn. The differences in apparent BCF values were also influenced by differences in DOC concentration and probably by the degree of equilibration.
Gas purge–induced elimination
The removal curves were fitted to the first-order one-compartment model and are presented in Figures 2 and 3 (upper curves). For the experiments at 10°C, Equation 6 fitted the experimental data very well (Fig. 2A and B and Fig. 3, upper curves). At 20°C (Fig. 2C), the fit for the more hydrophobic PCBs is slightly worse.
The BCFGPDW values determined by gas purging (Eq. 6) are presented in Figure 1B. Because of the low volatility of the higher chlorinated PCBs, data for compounds with log Kow > 7 were not available for this graph, so the curvature seen in Figure 1A is not observed. Figure 1B shows that the difference in bioconcentration between the two species is reduced. If binding to algal exudates is significant, the reduction may be explained by the fact that theBCFGPDW values relate to the free aqueous HOC concentrations. The relationship of the pooled log BCF values to the log Kow values up to log Kow = 7 is fairly linear (r2 = 0.743; p = 4 × 10−6; n = 17).
| Temperature | |||||||
|---|---|---|---|---|---|---|---|
| Compound | 10°Ca | 10.4°Cb | 20°Cb | 20°c | 20°Cd | 25°Ce | 25°Cf |
| TeCB | 3.6 | 6.2 | 6.9 | ||||
| HCB | 2.0 | 4.1 | 4.8 | ||||
| PCB28 | 0.65 | 0.87 | 2.1 | 3.16 | |||
| PCB52 | 0.47 | 0.86 | 1.6 | 1.2 | 3.42 | ||
| PCB101 | 0.16 | 0.7 | 2.51 | ||||
| PCB118 | 0.056 | 0.76 | |||||
| PCB138 | 0.16 | ||||||
| PCB153 | 0.16 | 0.6 | 1.32 | ||||
| PCB 180 | 0.0091 | 0.32 | |||||
DISCUSSION
Henry's law constant
Estimated H values were compared to literature data in Table 2 [14-16, 20, 24]. The results are similar to those presented by Ten Hulscher et al. [16]. For the PCBs, the general decrease with increasing molecular weight and the decrease of H with the decreasing degree of ortho-chlorine substitution (e.g., PCB118 vs PCB101) agree with previous reports [15].
Uptake of chlorobenzenes and PCBs
The mass balances for the uptake experiment were less complete for the least and the most hydrophobic chemicals. The same pattern and ranges of recoveries were reported by Stange and Swackhamer [4], who presented a discussion on possible sinks in this type of experiments. Following their arguments, we explain that the low recoveries for the more volatile and less adsorbing chlorobenzenes and PCBs are likely the result of evaporation losses during sampling and gas leakage. Poor recoveries for the more hydrophobic PCBs may relate to the stronger associations with the container walls. Incomplete recoveries did not interfere with the data interpretation of BCF, as they were based on measured concentrations in the media and the algae rather than on a procedure that required us to measure one and calculate the other by difference.
The observed rate of uptake (data not shown) is similar to that of earlier reports. Chlorobenzenes and PCBs have been found to reach equilibrium over a time period of days [6, 10] or weeks [4, 5], respectively. The net PCB uptake by S. capricornutum cells at 10°C may have been retarded by an increase in the elimination of PCBs due to exudation of DOC. For the S. capricornutum experiments, the PCB180 concentration decreased after the first week. Among the test compounds, PCB180 had the highest affinity to DOC or algal exudates [9, 25]. For this very hydrophobic compound, the enhanced elimination may have overcompensated the uptake.
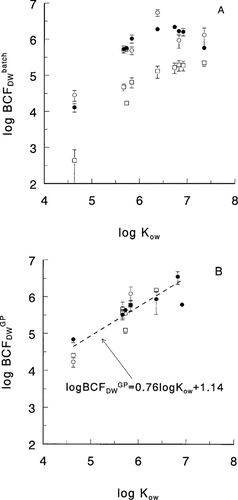
Log BCF versus log Kow for Microcystis aeruginosa at 10°C (□), Selenastrum capricornutum at 10°C (•), and S. capricornutum at 20°C (○). (A) BCF on a dry weight basis determined by batch equilibration. Error bars relate to 1 SD (N = 4). (B) BCF on a dry weight basis determined by gas purge–induced elimination. Error bars relate to 1 SD. (N = 3).
Bioconcentration factors
The log BCFDW−log Kow curves (Fig. 1A), as determined by batch equilibration at 10°C, agree closely with those previously reported by Stange and Swackhamer [4]. First, they found a maximum log BCF at log Kow 6.5 for S. capricornutum, which is comparable to our values for the same species. Second, they found a slight increase of log BCF with log Kow at log Kow > 6.5 for the cyanobacterium Anabaena, as observed for the cyanobacterium M. aeruginosa in the present study. Third, they found relatively low log BCF values for the cyanobacterium at log Kow < 6.5, which is also observed here. The main difference is that our values are one-half a log unit higher. Two explanations for this may be offered. First, in the current study, incubation times were longer (33–36 d) as compared with 12 d in Stange and Swackhamer [4]. Second, in our experiments DOC levels were relatively low (Table 1) as compared with those in Stange and Swackhamer [4] (70–120 mg/L). This may have resulted in a larger bioavailability of PCBs in our experiments.
Gas purge–induced elimination
The good fit of the first-order one-compartment model (Fig. 2A and B and Fig. 3, upper curves) suggests that for both species, uptake and elimination kinetics at 10°C are sufficiently fast, with respect to the volatilization rate kvCw, to maintain equilibrium between HOCs in the algae and the water. At 10°C, this volatilization rate is very low because of low Henry's law constants. At 20°C (Fig. 2C) the fit is worse but is not severe enough to make a two-compartment model statistically preferable. Although no alterations were detected visually, it is possible that the algal suspensions may have changed during gas purging. Besides physiological changes related to aging, such as changes in lipid content, exudates may have been formed (e.g., S. capricornutum) because of metabolic activity. For M. aeruginosa, gas purging removed cells from the bulk of the suspension. The excellent fit of the one-compartment model throughout the entire 5- or 6-week elimination period suggests that the changes, observed or not, had no significant effect on the overall sorptive properties of the population. During the M. aeruginosa experiments, cells appeared to accumulate in a liquid film on the inner surface of the flasks and near the outlet to the Tenax traps. No cells or cell fragments were detected in the Tenax traps themselves. We assume that the transport of the test compounds from this film to the Tenax traps occurred at the same rate as did transport from the bulk suspension. Hence, the amounts trapped in the Tenax were not significantly affected by the loss of cells.
The effect of slow accumulation kinetics on the apparent BCF
The aim of this study was to assess the possible influence of slow kinetics on the magnitude of the steady-state BCF for PCBs. First, minimum values for the uptake and elimination rate constants, which were still consistent with the results of the purge experiments, were calculated. Second, the maximum values of the rate constants at which the slow kinetics hypothesis was still consistent with the apparent BCF values reported in this study and in the literature were calculated. Finally, the calculated constants were compared. The calculations were performed on the data for PCB138 and PCB153 in the S. capricornutum experiment at 10°C. This experiment offered the greatest degree of comparability with literature data [4, 5] and showed no loss of cells.
Calculation of lower limits for rate constants from purge data. The fitting of Equation 6 yielded estimates of BCFGPDW that were equal to the ratio k21/k12. When the magnitudes of these rate constants were larger than certain minimum values, then the elimination from the algae was not rate limiting with respect to the known volatilization rate, and equilibrium was maintained. However, had the constants been lower than these minimum values, the elimination would have been rate limiting, and the continuous equilibrium state would not have been observed. Using Equations 3 and 4, the elimination of PCB138 and PCB153 from S. capricornutum cells was simulated for various magnitudes of k21, keeping the ratio k21/k12 (=BCFGPDW) constant at the value obtained with Equation 6. The DW volatilization rate constants for PCB138 and PCB153 were approximately 1 per day. The numerical integration of the differential equations was carried out using the simulation software package TUTSIM (Meerman Automation, The Netherlands). The results (Fig. 3) indicate that the equilibrium binding situation found in our experiments implies k21 values that are larger than 1.5 per day (PCB138 and PCB153) and k12 values that are larger than 250 per day (PCB138) and 30 per day (PCB153). At lower k values, the observed equilibrium would not have occurred, and the model would no longer fit the data (Fig. 3). Equilibrium binding was also observed for the other PCBs. In our experiments, the kv values had a constant ratio to the Henry's law constant and were all of the same order of magnitude. Therefore, a value of 1 per day is a safe minimum value for k21 for all PCBs and species considered in this study.
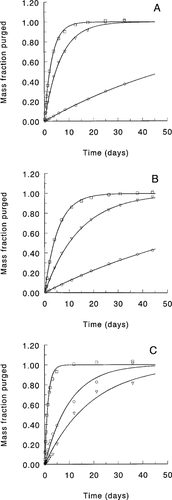
Elimination of PCB28 (□), PCB52 (∇), and PCB101 (○). Lines represent the best fit of the one-compartment first-order model as condensed in Equation 6. (A) Microcystis aeruginosa, 10°C; (B) Selenastrum capricornutum, 10°C; (C) S. capricornutum, 20°C.
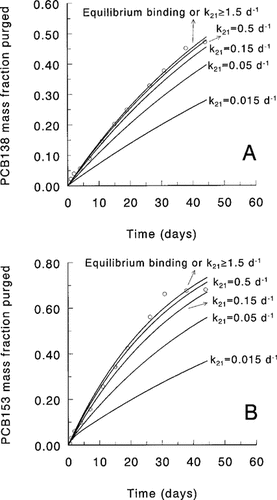
Recently, Axelman et al. [26] found evidence from field data that algal cell size has an effect on bioconcentration rate constants. They estimated the effect of algal cell size on elimination rate constants using radial diffusion model concepts. Following their method (eqns. 1–7 in [26]), we obtained values for k21 in the range of 10 to 50 per day for k21 for the pentachloro- and hexachlorobiphenyls under our experimental conditions (10°C; cell diameter 4–5 μm; log Koc = 7−7.5). These high values are consistent with the current results from our purge experiments.
 (7)
(7)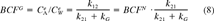 (8)
(8)For PCBs with hydrophobicity similar to that of PCB138 and PCB153 (log Kow of 6.8-7.0), Swackhamer and Skoglund reported lipid-normalized log BCFG values of approximately 107 for Scenedesmus sp. at low growth rate (fig. 1 in ref [5]). For the same species and log Kow range, they found log BCFG values of approximately 106 at a growth rate of 0.13 per day (fig. 2 in ref [5]), which represents a factor 10 decrease of BCF. The same authors also report a factor 10 reduction of BCF in the 6.8 to 7.0 log Kow range for a summer field collection of mixed algae (higher growth rate), as compared with a winter field collection (low growth rate). It follows from Equation 8 that a factor 10 reduction of BCF as a result of growth at a rate of 0.13 per day requires an elimination rate constant of 0.014 per day.
Recently, Skoglund et al. [27] evaluated laboratory- and field-derived BCF values for PCBs using a two-compartment kinetics model for bioconcentration in growing phytoplankton. In their experiments, DOC concentrations were considerably higher (S. capricornutum: 45–93 mg/L) and were acknowledged to affect the BCF values, but they were not taken into account in the data analysis because the quality of the DOC measurements was in question [27]. Elimination (depuration) rate constants for the slow accumulating fraction were less than 0.06 per day for all species studied and approximately 0.001 per day for S. capricornutum. These were calculated from equation 5 in Skoglund et al. [27], using uptake rate constants at log Kow = 6.8-7 from figure 1 in Skoglund et al. [27], and using surface adsorption partitioning coefficients from table 2 in Skoglund et al. [27].
The above analysis shows that the hypothesis of slow bioconcentration kinetics requires very low rate constants and therefore cannot explain the curvature of log BCF−log Kow plots for S. capricornutum and M. aeruginosa unicells. If elimination from S. capricornutum cells had been as slow as the rate constants suggested, no equilibrium binding would have occurred in our purge experiments. The k21 value measured for PCB138 or for PCB153 by gas purging is at least factor 100 to 500 higher than the value derived from steadystate BCFs reported in Swackhamer and Skoglund [5]. The recent analysis by Skoglund et al. [27], which used a kinetics model, requires elimination rate constants that are at least three orders of magnitude lower than the minimum value of 1.5 per day. We therefore suggest that both the effect of growth on BCF and the curvature of log BCF−log Kow plots may need another explanation.
The effect on the apparent BCF of binding to DOC
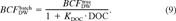 (9)
(9) (10)
(10) (11)
(11)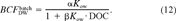 (12)
(12)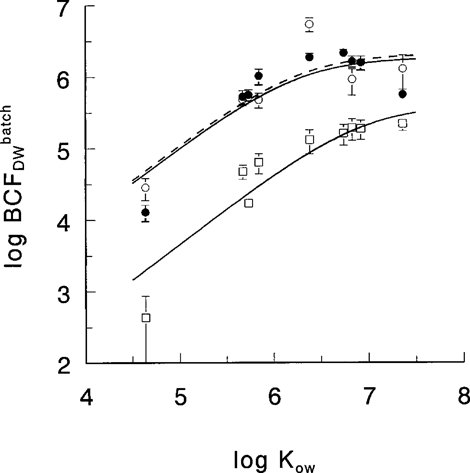
Relationship between log BCF (±1 SD) and log Kow for Microcystis aeruginosa at 10°C (□—□), Selenastrum capricornutum at 10°C (•—•), and S. capricornutum at 20°C (○–––○). Curves represent the best fit of a three-phase model accounting for binding to exudates (Eq. 12).
| Species (temperature) | αb | βc | r2 | pd |
|---|---|---|---|---|
| I. Microcystis aeruginosa (10°C) | 0.05 | 0.02 | 0.858 | 0.00925 |
| II. Selenastrum capricornutum (10°C) | 1.06 | 0.01 | 0.776 | 0.0317 |
| III. Selenastrum capricornutum (20°C) | 1.06 | 0.14 | 0.990 | 0.00005 |
- aAccording to the model as condensed in Equation 12.
- bRatio BCFtrueDW/Kow.
- cRatio KDOC/Kow.
- dF-test on residual error.
CONCLUSIONS
In three gas purge elimination experiments (S. capricornutum at 10°C and 20°C and M. aeruginosa at 10°C), the rate constants for elimination of PCBs from algal cells were shown to be larger than 1 per day. For such high rate constants, BCF values for PCBs in natural waters are not influenced by slow accumulation and/or elimination kinetics, even at high rates of algal growth. The relationships between apparent log BCF and log Kow after 5 to 6 weeks of batchwise equilibration were curved. The curvature could satisfactorily be described by a simple three-phase model that accounts for the binding of test compounds with DOC. This leaves the binding of PCBs to algal exudates as the most plausible explanation for the observed slow uptake and nonlinear log BCF−log Kow plots in this study. Apparently, models quantifying the bioconcentration of HOCs by phytoplankton in natural waters do not need a kinetic framework alone. Instead, modeling efforts should focus on process descriptions that quantify the exudation rate and the binding of HOCs to the algal exudates.
Acknowledgements
We thank Frits Gillissen, who took care of the GC analysis, and Morten Grum, who provided linguistic advice.




