Soil-to-indoor air exposure models for volatile organic compounds: The effect of soil moisture†
This article does not represent the policy of the New Jersey Department of Environmental Protection.
Abstract
Two finite-source models that calculate volatilization of contaminants from soil to indoor air were used to study the effect of soil moisture on indoor air concentrations and inhaled doses, using a representative model volatile organic chemical. A hypothetical scenario was used that assumed that subsurface contaminant diffuses through a layer of clean soil and is then swept into the building interior via advection. Both models simulated depletion of source contaminant via volatilization and degradation. One was an analytical model adapted from the behavior assessment model of Jury et al., which could be used to calculate time-dependent volatilization rates (and indoor air concentrations) as a function of constant soil moisture contents and steady-state moisture advection. The second model, the Integrated Moisture Plus Contaminant Transport (IMPACT) model, had the additional capability of simulating daily and seasonal variations in soil moisture behavior from actual daily temperature and rainfall data. Predicted indoor air concentrations and inhaled doses for the model contaminant varied by up to seven orders of magnitude, depending on the soil moisture conditions and whether or not contaminant degradation was considered. Over extended time periods, inhaled doses predicted under conditions of daily and seasonal variations in soil moisture were in general agreement with those predicted using average soil moistures or average moisture fluxes, suggesting that simplified treatment of soil moisture behavior may be adequate if accurate soil moisture data are available.
INTRODUCTION
In a previous publication, Sanders and Stern presented an analytical model for calculating indoor air concentrations and inhalation exposures for carcinogenic volatile organic compounds (VOCs) that originate in subsurface soil [1]. The model was adapted from the behavior assessment model of Jury et al., a one-dimensional analytical screening model that calculates both leaching and volatilization of organic chemicals from the unsaturated soil zone [2-6]. When used in accordance with transport assumptions described by Little et al. [7], Jury's model may be coupled to appropriate equations that calculate indoor air concentrations and inhalation exposures [1]. This approach offers two advantages not available in other existing indoor air exposure models. First, it calculates time-dependent flux rates of the contaminant entering a building based on a finite source of contamination. Second, it allows for the finite source to be additionally depleted through the use of a first-order degradation rate. Nonetheless, the analytical model still required the simplifying assumption that soil properties are homogeneous throughout the soil column. This contrasts with conditions in the field, in which a soil's texture, total porosity, organic matter content, and other properties may vary significantly as a function of depth. Although all soil parameters affect volatilization of contaminants, not all are of equal importance. Bulk densities for soils tend not to vary greatly, typically being near 1.3 g/ml [8]. Porosity usually varies within a factor of two, from about 0.3 to 0.5 (v/v) [9]. Considered alone, these two parameters do not vary sufficiently to have a large effect on volatilization. Soil organic carbon contents vary over a wider range [10]; however organic carbon partition coefficients (Kocs) for VOCs are relatively small, and significant mobility of these chemicals would be expected even at higher levels of organic carbon [11].
The soil property that is perhaps the most difficult to assess, and that can have a large effect on volatilization, is soil moisture. The soil moisture content affects the available pore space for chemical volatilization in the vapor phase, and moisture content may vary from near zero, which allows for maximum volatilization (as long as the soil is hydrated), to saturation, which greatly reduces volatilization by eliminating air-filled pore space. Soil moisture also has a temporal character. Other soil properties may vary spatially, but they will remain constant as a function of time. Soil moisture content and soil moisture movement (advection) can vary significantly on a daily and seasonal basis [12]. The model of Jury et al. assumes a constant soil moisture content and constant soil moisture advection. The adaptation of Jury's model by Sanders and Stern was limited further by assuming that soil moisture advection did not occur. The lack of soil moisture movement in the adapted model meant that chemical movement through the soil occurred solely via molecular diffusion.
In this paper, the sensitivity of calculated indoor air concentrations and inhalation exposures to variations in soil moisture content and soil moisture advection is described, using a model volatile organic contaminant that originates in subsurface soil. First, the model of Jury et al. is used to investigate the effect of varying soil moisture levels, both in the presence and absence of constant soil moisture advection. The compounding effect of including a degradation rate for the model chemical is also studied. Although sensitivity analyses have already been described by Jury et al. for his volatilization model [3], a more detailed analysis of the soil moisture effect is presented here from the perspective of potential indoor air concentrations and exposures. Following this analysis, the Jury model is compared to the Integrated Moisture Plus Contaminant Transport (IMPACT) model, a numerical model that more realistically simulates day-to-day and seasonal variations in soil moisture content and advection [13-16]. The IMPACT model allows for simulation of two-dimensional contaminant transport in the unsaturated soil zone. In this study, the model was used in a one-dimensional mode for comparison with the model of Jury et al.
METHODS
Hypothetical environmental scenario
A building foundation (including the zone of influence [7], discussed below) was assumed to be 1.83 m (6 ft) above a contaminated zone of soil that was 1.22 m (4 ft) thick. The contaminated zone was assumed to contain a model volatile organic chemical at an initial concentration of 1 μg/g. The soil between the foundation and the contaminated zone was assumed to be initially contaminant-free. The soil texture was assumed to be sandy loam. Base values for soil properties were taken as follows: bulk density of soil, 1,300 kg/m3; total porosity, 0.41 (v/v); soil organic carbon content, 0.1%. Additional soil properties, used only by the IMPACT model, are shown in the appendix. The area of the zone of influence subject to contaminant entry was assumed to be 52 m2, and the building ventilation rate was 46 m3/h. Physicochemical properties for the model contaminant were set at representative values for VOCs. The Koc was 100 ml/g and the dimensionless Henry's law constant was set at 0.222. These values correspond to those reported for benzene; they were also close to median values for 30 environmentally significant VOCs [17]. Air and water diffusion coefficients were set at representative values of 5 × 10−6 and 5 × 10−10m2/s, respectively [6]. The chemical half-life in soil, when used, was set at 16 or 180 d. The shorter half-life has been reported for benzene in soil, and is representative of rapidly degrading VOCs, such as nonhalogenated chemicals [18]. The longer half-life is more representative of halogenated chemicals [18].
Calculation of volatilization flux—Jury model
The indoor air exposure model previously presented by Sanders and Stern used a simplified form of the volatilization model of Jury et al., which assumed no soil moisture movement [1]. In this study, the full Jury model (Equations 18, 21, and A2, see Jury et al. [6]) was used, which allowed determination of the effect of soil moisture advection. The model of Jury et al. calculates a time-dependent volatilization flux of a chemical from the soil surface, assuming that a finite source of the chemical is originally contained within a specified depth range beneath the soil surface [6]. First-order degradation of the chemical can also be included. Transport of chemical is accomplished via both diffusive and advective processes. The diffusive component is controlled by a soil diffusion coefficient, which is a function of the Henry's law constant, the diffusion coefficient of the chemical in both air and water, the adsorption coefficient of the chemical to the soil, soil water content, porosity, and bulk density [2]. Partitioning of chemical between the vapor, aqueous, and sorbed phases is assumed to be at equilibrium at all times. The advective component is controlled by a user-specified soil moisture flux rate, which is held constant as a function of time.
Calculation of volatilization flux—IMPACT model
The IMPACT model is specifically designed for the calculation of soil cleanup criteria for hazardous waste sites as controlled by the soil-to-groundwater pathway [14-16]; however, the model also includes, as a mechanism of contaminant loss, the volatilization pathway.
The IMPACT model incorporates equilibrium partitioning, diffusive, degradation, and mass-balance processes equivalent to those employed by the Jury model, but includes the additional process of hydrodynamic dispersion. These processes are assembled into an advection-dispersion equation representing contaminant transport through the soil column, expressed in terms of the aqueous phase concentration [13, 15, 16]. The equation is similar to that of Baehr [19]. The most significant capability included in the IMPACT model that is not available in the Jury model is the ability to simulate soil moisture contents and moisture transport on a day-to-day basis. This is done using the moisture form of the Richards equation to describe moisture transport [20], and Darcy's law to describe moisture flux [21]. To evaluate these equations, the hydraulic conductivity expression of Campbell is used [22], and soil moisture retention and soil diffusivities are calculated according to the empirical expression proposed by Clapp and Hornberger [23]. To solve the contaminant transport and moisture flow equations, the soil column is divided into imaginary layers (0.30 m thick in this study). The moisture flow equation is solved using a fully implicit finite difference technique [24]. The advection-dispersion equation is solved numerically using Hamming's modified predictor/corrector method [24]. A 1-d time step was used in this study.
The IMPACT model was executed in two modes. First, soil moistures and moisture advection rates were held constant at various levels to allow comparison of the output of this model with that of the Jury model, which can only accomodate constant soil moisture advection. Second, the model was run in the default simulation mode, using actual daily temperature and rainfall records for Newark, New Jersey, USA, from 1959 to 1989 [13]. When run in this mode, initial net infiltration was calculated using a mass balance expression accommodating evapotranspiration, precipitation, and surface runoff. Evapotranspiration rates were calculated using Thornthwaite's method [25, 26]. Potential evapotranspiration was first calculated as a function of temperature and percentage sunshine [25]. Actual evapotranspiration was then calculated by the water balance method of Thornthwaite and Mather [26]. Surface runoff rates were calculated using the Soil Conservation Service runoff curve number [27]. Recharge (advection) of soil moisture to the water table was then transiently calculated using the net infiltration as a boundary condition at the top of the soil zone [13]. A limitation of the one-dimensional hydrologic approach used in this study is that it does not take into account shielding of impacting precipitation by the building, which may reduce recharge rates directly under the structure. To more realistically determine absolute moisture advection rates from a specific climate or rainfall history, a two-dimensional model would be required.
Seasonal and short-term temperature fluctuations in nearsurface soil would affect the magnitude of some contaminant chemical parameters, particularly the Henry's law constant and the first-order degradation constant. The IMPACT model does not allow for adjustment of contaminant properties as a function of temperature; daily temperature and rainfall data were used only for calculating moisture transport. The model may therefore underestimate the fluctuations in near-surface contaminant transport and degradation processes when it is used in the natural environmental simulation mode.
Transformation of volatilization flux values into air concentrations and doses
 (1)
(1) (2)
(2)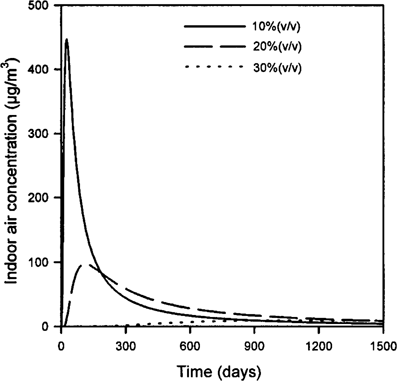
Effect of soil moisture on calculated indoor air concentrations using the model of Jury et al. [2-6] and the transport assumptions of Little et al. [7], in the absence of soil moisture advection and chemical degradation. All parameters other than soil moisture are baseline values as given in the text. Initial concentration of the model contaminant was 1 μg/g.
RESULTS AND DISCUSSION
Sensitivity analysis of the model of Jury et al.—No soil moisture advection
Soil moisture contents vary considerably, ranging from <0.05 (v/v) to nearly saturation values (approximately 0.5 [v/v]), depending on soil texture and environmental conditions. The sensitivity of indoor air concentrations and cumulative inhaled doses to soil moisture content, in the absence of soil moisture movement or chemical degradation, was investigated using the Jury model (Figs. Fig. 1., Fig. 2. and Table 1). The magnitude of the indoor air concentration peak, and the time at which this peak occurred, varied significantly with soil moisture. As soil moisture was increased from 10 to 30% (v/v), peak indoor air concentrations decreased from 450 μg/m3 to 9 μg/m3, and the time of the peak concentration increased from 25 d to 1,100 d (Fig. 1 and Table 1). Because cumulative dose is proportional to the area under the indoor air concentration curve with respect to time, the soil moisture variation also had a substantial effect on cumulative dose in the early stages of exposure (Fig. 2). However, the effect of soil moisture on the long-term 30-year cumulative dose was less dramatic, varying by less than a factor of two (Table 1). The model of Jury et al. predicted that all chemical would eventually volatilize into the building foundation if chemical degradation and soil moisture advection are not modeled (Fig. 2). If the exposure period entirely brackets the entire volatilization time-course of the chemical, the total dose of inhaled chemical will remain constant. If the exposure time period is shorter than the time for complete volatilization, the total dose will be dependent on soil moisture.
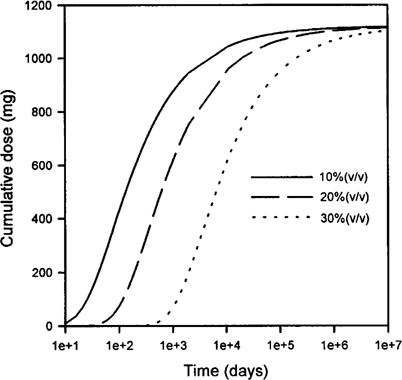
Effect of soil moisture on cumulative dose inhaled using the model of Jury et al. [2-6] and the transport assumptions of Little et al. [7], in the absence of soil moisture advection and chemical degradation. All parameters other than soil moisture are baseline values as given in the text. Initial concentration of the model contaminant was 1 μg/g.
| No degradation | Half-life = 180 d | Half-life = 16 d | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil moisture (%) (v/v) | Soil moisture advection (cm/d) | Model | Time to peak concn. (d) | Peak concn. (μg/m3) | Dose (mg) | Time to peak concn. (d) | Peak concn. (μg/m3) | Dose (mg) | Time to peak concn. (d) | Peak concn.(μg/m3) | Dose (mg) |
| 10 | 0 | Jury | 25 | 450 | 1,045 | 22 | 409 | 521 | 16 | 198 | 90 |
| 10 | 0 | IMPACT | 67 | 410 | 990 | 65 | 380 | 820 | 47 | 185 | 230 |
| 20 | 0 | Jury | 110 | 97 | 960 | 87 | 66 | 220 | 42 | 7 | 6 |
| 30 | 0 | Jury | 1,100 | 9 | 633 | 445 | 0.8 | 7 | 150 | 0.0001 | 0.0002 |
| 19 | 0 | Jury | 100 | 116 | 975 | 75 | 84 | 251 | 38 | 12 | 9 |
| 19 | 0.016 | Jury | 100 | 110 | 919 | 75 | 80 | 240 | 38 | 11 | 9 |
| 19 | 0.016 | IMPACT | 350 | 89 | b | 260 | 49 | 390 | 100 | 2 | 5 |
| 21 | 0 | Jury | 140 | 81 | 941 | 100 | 52 | 189 | 47 | 4 | 4 |
| 21 | 0.056 | Jury | 140 | 63 | 661 | 100 | 41 | 145 | 46 | 3 | 3 |
| 21 | 0.056 | IMPACT | 420 | 31 | 700 | 290 | 15 | 125 | 100 | 0.5 | 1 |
| 22 | 0.12 | Jury | 150 | 32 | 310 | 110 | 19 | 75 | 50 | 1.1 | 1 |
| 22 | 0.12 | IMPACT | 320 | 8 | 90 | 245 | 4 | 28 | 100 | 0.2 | 0.3 |
| 24 | 0 | Jury | 220 | 47 | 874 | 155 | 23 | 111 | 63 | 0.7 | 0.7 |
| 24 | 0.27 | Jury | 160 | 4 | 20 | 125 | 3 | 7 | 60 | 0.1 | 0.08 |
| 24 | 0.27 | IMPACT | 185 | 1.5 | 8 | 160 | 1 | 4 | 80 | 0.09 | 0.1 |
| Simulated | Simulated | IMPACT | 270 | 68 | 160 | 270 | 40 | 65 | 150 | 0.8 | 0.8 |
- a For each run, parameters other than those indicated were set at the base value.
- b An accurate dose could not be calculated for this run because of mass balance errors at long time periods.
When chemical degradation was included, the dose accumulation curve reached a final plateau quickly relative to long-term exposure periods (Fig. 3). When compared to simulations without degradation, peak indoor air concentrations occurred earlier, were lower, and decreased more dramatically as the soil moisture was increased (Table 1). The 30-year cumulative doses, relative to doses obtained without degradation, were reduced by as much as seven orders of magnitude relative to the dose inhaled with 10% soil moisture and no chemical degradation (Table 1). Clearly, the soil moisture content and the chemical degradation rate are critical factors to be considered when assessing the indoor air exposure pathway using an environmental scenario similar to that employed in this study.
Sensitivity analysis of the model of Jury et al.—Soil moisture advection included
When soil moisture is present at a level above field capacity, advection of moisture towards the water table will occur. Using a sandy loam soil texture and soil moisture contents of 19, 21, and 24%, hydrologically appropriate steady-state rates of soil moisture flow were calculated using the IMPACT model as described below (Table 1). This range of soil moisture contents spanned most of the normal annual range of soil moisture for this soil texture. The paired moisture contents and moisture flow rates were then used in the Jury model. At a lower moisture content (19%), the downward advection of soil moisture had little effect on the time course and magnitude of indoor air concentrations, or on the dose accumulated (Table 1). Under these conditions, diffusive transport was the dominant transport mechanism because of the relatively large volume of airspace available in the soil and the low rate of soil moisture advection (0.016 cm/d). As the soil moisture was increased to 24%, advection of soil moisture increased by over a factor of 10, to 0.27 cm/d (Table 1). The increased advection and the reduced pore space for available diffusive transport significantly reduced the peak indoor air concentration of the chemical in the building airspace and the long-term dose inhaled (Table 1). These results indicate that the moisture content of the soil should be compared to its field capacity and saturation volume when deciding whether or not to model soil moisture movement.
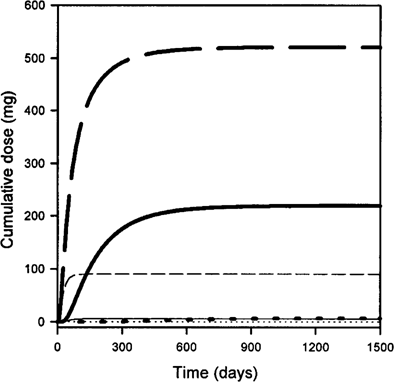
Effect of soil moisture on cumulative dose inhaled using the model of Jury et al. [2-6] and the transport assumptions of Little et al. [7] when chemical degradation is included (moisture advection not included). All parameters other than soil moisture and degradation rates are baseline values as given in the text. Initial concentration of the model contaminant was 1 μg/g. Thick lines represent simulations using contaminant half-life of 180 d, thin lines are simulations using 16-d half-life. Soil moisture contents for dashed, solid, and dotted lines are 10, 20, and 30% (v/v), respectively.
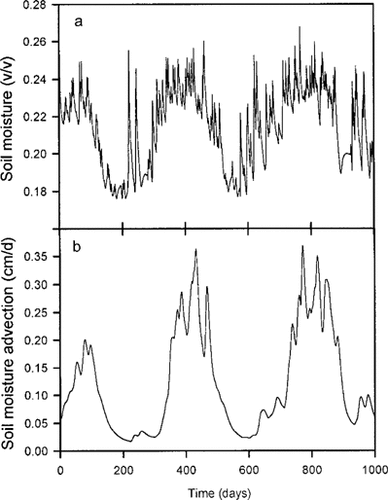
Daily and seasonal variations in moisture contents and moisture advection for a sandy loam soil as calculated by the Integrated Moisture Plus Contaminant Transport (IMPACT) model. Input parameters correspond to baseline environmental scenario as given in text. Daily precipitation and rainfall records from Newark, New Jersey, USA, were used, starting in January 1959. (a) Moisture content of top soil layer, (b) Moisture advection in bottom soil layer.
Comparison of the model of Jury et al. to the IMPACT model under steady-state soil moisture conditions
The IMPACT simulation model was designed to calculate daily and seasonal variations in soil moisture movement and soil moisture content. However, the model could also be executed in a mode that allowed for constant soil moisture content and advection, thus allowing comparison with the model of Jury et al. under equivalent conditions. Through trial and error, the steady-state downward moisture flux that matched a given constant soil moisture profile was determined, as controlled by the Richards equation and Darcy's law (Table 1). The range of volumetric soil moisture contents modeled (19, 21, and 24% [v/v]) spanned the range predicted for a sandy loam soil when the IMPACT model was run in the default simulation mode, in which daily and seasonal variations in soil moisture properties were modeled as a function of daily precipitation and temperature records (Fig. 4).
The volatilization of the model contaminant into indoor air was calculated using both the Jury and IMPACT models, using the three steady-state soil moisture conditions described above. The models were also run at a soil moisture content equal to the soil's field capacity (10% [v/v]), to determine their behavior when no soil moisture advection occurred. Simulations were initially conducted in the absence of chemical degradation. Under field capacity conditions, peak indoor air concentrations were nearly the same for both models, although the peak time for the IMPACT model was slightly later (Fig. 5a). This is attributed to the value of the spatial increment used in the numerical solution scheme. Calculated long-term doses using each model were nearly the same (Table 1). At the annual average moisture for this soil (21%), when both advection and diffusive transport of the model contaminant were significant, the IMPACT model yielded a peak indoor air concentration that was one-half that predicted by the Jury model, and which occurred at a substantially later time-point (Fig. 5b). However, the long-term estimated doses were nearly the same for both models (Table 1). At a moisture content near the upper limit of the range predicted for this soil (24%), in which advection dominates, the time of the peak indoor air concentration was nearly the same for both models, whereas the magnitude of the peak indoor air concentration was lower using the IMPACT model (Fig. 5c). The cumulative long-term dose, although quite small for both models, was lower using the IMPACT model (Table 1).
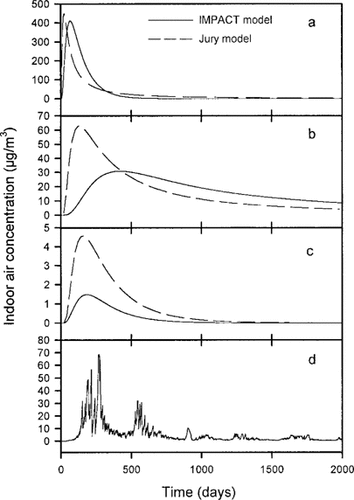
Indoor air concentrations as a function of time using the volatilization model of Jury et al. [2-6] and the Integrated Moisture Plus Contaminant Transport (IMPACT) model. Initial concentration of the model contaminant was 1 μg/g and no degradation was considered. Parameters other than soil moisture were for the baseline environmental scenario as given in the text. (a) 10% soil moisture, no advection. (b) 21% soil moisture, advection = 0.056 cm/d. (c) 24% soil moisture, advection = 0.27 cm/d. (d) IMPACT model; soil moisture and advection simulated using daily precipitation and temperature data.
The Jury and IMPACT models both incorporate similar assumptions regarding the contaminant diffusion process (the Millington and Quirk model [30]), and soil moisture advection was matched between the two models. Additionally, assumptions regarding the overall contaminant transport process were similar for both models, in that diffusion of chemical through the soil to the zone of influence around the building foundation was considered to be the rate-limiting step. However, important differences exist between the two models. First, mechanical dispersion is not modeled in the Jury model. This may partly explain the observation that the IMPACT model gave peak concentrations that were somewhat lower and broader than those observed using the Jury model. Second, although most transport assumptions were similar for both models, the assembly of these processes into an overall transport equation varied. The Jury model is an analytical solution containing the advection and diffusion transport assumptions described by Jury et al. [2, 6], whereas the IMPACT model uses an advection-dispersion equation, incorporating an additional term for mechanical dispersion [13, 15, 16]. Finally, it is possible that the numerical methods used in the IMPACT model may have introduced some perturbations in predicted results. The IMPACT model output has been compared to an analytical solution of the advection-dispersion equation in the case of steady-state flow conditions, and agreement was found to be excellent [13]. However, the comparison was restricted to predicting the concentration profile of the contaminant in the soil zone.
When comparing model predictions with environmental measurements, an order of magnitude agreement is frequently considered to be adequate [31]. The same criterion could be applied when determining whether or not there is adequate agreement between different models [17]. Using this criterion, the models gave comparable results, because peak heights, peak times, and calculated doses agreed to within a factor of three, and were nearly equivalent in several cases. From this perspective, either model could be used for investigating the soil-to-indoor air pathway under constant soil moisture flow conditions.
The Jury model and the IMPACT model were also compared when chemical degradation was included, with the half-life for the model contaminant set at 16 or 180 d. Degradation assumptions differed between the two models, in that the Jury model considers degradation to occur in all three phases, whereas the IMPACT model assumes that degradation occurs in the liquid phase only, an assumption that is probably more realistic. Given the partitioning assumptions of this study, significant levels of contaminant will exist in both the sorbed and aqueous phases (at 20% soil moisture, about 60% in the aqueous phase and 40% in the sorbed phase). Therefore, when a given half-life is entered for the two models, the overall degradation rate will be somewhat lower for the IMPACT model, depending on the level of soil moisture. At the field capacity (10%), the IMPACT model doses became progressively higher than the Jury model doses as the half-life was decreased (Table 1), because the low soil moisture restricted the amount of possible aqueous phase degradation. At an intermediate soil moisture (21%), doses using the IMPACT model were one-third of those determined using the Jury model when a 16-d half-life was used, whereas the doses were nearly equivalent between the two models in the absence of degradation (Table 1). The reason for this observation is that the significantly longer transport time for the model contaminant using the IMPACT model (Fig. 5b) allowed more time for chemical to degrade before volatilizing, despite the slower overall rate of degradation of the model relative to the model of Jury et al. At the highest soil moisture (24%), transport times using both models were similar, and the IMPACT model dose again increased relative to the Jury model dose as the half-life decreased, becoming equal at a 16-d half-life (Table 1). Despite the mechanistic differences in the degradation process between the two models, peak times, peak concentrations, and calculated doses still agreed to within a factor of three (with one exception) when a 180-d half-life was used, and to within a factor of three (with two exceptions) when a 16-d half-life was used (Table 1), indicating that the models were roughly comparable.
IMPACT simulation under natural environmental conditions
When the IMPACT model was run under natural environmental conditions, using daily temperature and precipitation records for Newark, New Jersey, USA, soil moisture levels and soil moisture movement varied considerably both day-today and seasonally (Fig. 4). The short-term peaks and valleys resulted from particular storm events and were a function of the magnitude and duration of rain storms. The longer term rises and falls were due to seasonal variations in soil surface temperatures. In winter, evapotranspiration decreases and soil moisture contents and moisture movement increase. An opposite effect occurs during the warm season.
When indoor air concentrations were investigated under natural environmental conditions, similar day-to-day and seasonal variations can be seen, although the magnitude of these effects taper off with time as the bulk of the chemical is volatilized from the soil (Fig. 5d). Volatilization increased during periods of low soil moisture and moisture advection, and decreased when moisture levels and moisture advection increased (Figs. Fig. 4., Fig. 5.), with shorter term spikes and troughs corresponding to individual storm events.
Although the concentration trace of the natural environmental simulation is difficult to compare directly to the simplified moisture runs, it was observed to fall within the range of concentration traces predicted using simplified moisture conditions that span the annual range of moisture calculated for this soil (Table 1 and Fig. 5). Over the longer term, the accumulated dose should be comparable to a run under steady-state conditions using average soil moistures. The average soil moisture simulated using the IMPACT model was 21%, which could be maintained using a steady-state soil moisture advection of 0.056 cm/d. However, the average soil moisture advection was calculated to be about 0.12 cm/d, which under steady-state conditions required a constant soil moisture of 22%. Although this 1% difference in soil moisture seems small, it corresponded to a doubling in the soil moisture advection rate, and a significant decrease in the calculated total dose (Table 1). When steady-state simulations were run at a soil moisture of 22%, the Jury model dose decreased relative to the dose at 21% moisture by a factor of two to three (from 661 to 310 mg, in the absence of degradation, Table 1). The IMPACT model dose decreased by a factor of three to seven (from 700 to 90 mg, in the absence of degradation, Table 1). This illustrates the extreme sensitivity of predicted indoor air concentrations and exposures to even small variations in soil moisture behavior. Under the conditions of this study, the dose resulting from the simulation carried out under natural environmental conditions fell in between the two doses predicted by the IMPACT model using the average moisture content of 21% or the average moisture advection of 0.12 cm/d (Table 1). When chemical degradation was not considered, the IM-PACT model dose under natural environmental conditions was within a factor of two of those calculated using the Jury model under average soil moisture advection conditions (0.12 cm/d). When degradation was included, the doses were nearly the same (Table 1).
Comparisons with steady-state conditions are more difficult to interpret when contaminant degradation is included. Because the IMPACT model assumes that degradation is first-order with time, the effect of degradation will be somewhat dependent on the season in which the simulation is started. The simulation in this study began in January, during a period of low volatilization, so degradation was able to act upon the initial mass of contaminant for 2 to 3 months before significant volatilization occurred. Nonetheless, over the longer term, this effect appeared to be minimal.
CONCLUSIONS
The sensitivity of predicted indoor air concentrations to soil moisture conditions indicates that care should be taken to accurately determine the soil moisture behavior when a site-specific assessment is made for the soil-to-indoor air pathway. The U.S. EPA, in its recently released guidance on screening sites with contaminated soils, has pointed out that moisture contents measured at a single time point should not be used [32]. Because moisture advection rates vary significantly with slight variations in soil moisture, use of average moisture advection rates, rather than average soil moisture levels, appears to be prudent if simulations are to be carried out under steady-state soil moisture conditions. If this information is not readily available, utilization of a model that simulates soil moisture behavior from more easily obtainable parameters (e.g., precipitation, temperature, soil texture) may be best.
The models used in this study do not include mechanisms for modeling the transport of nonaqueous phase contaminants. Therefore, the models are best suited for assessing potential inhalation exposures from low levels of VOCs that would remain after cleanup of contaminated soil to specified criteria. When high levels of soil contaminants are present, nonaqueous phase contamination may result in steady-state indoor air concentrations. In these cases, the models of Little et al. [7] and Johnson and Ettinger [33] may be more appropriate for assessing potential exposures.
Heavier soils, such as those with significant clay content, tend to retain higher levels of moisture than sandy soils. This study showed that chemical degradation in combination with higher soil moistures could greatly reduce indoor air concentrations, because the contaminant may never reach the building foundation. This effect of a lower diffusivity layer (e.g., clay) has been observed by others in the field [34]. In cases such as these involving a lower diffusivity layer, the rate-limiting step for transport may be migration through this layer. The presence of such a soil layer may enable a relatively simple approach for modeling heterogenous soils, in that relatively simple analytical models, such as that of Jury et al., could be applied to the rate-limiting layer.
According to recent reports, atmospheric pressure fluctuations may largely control volatilization of subsurface VOCs in some cases [35]. This proposed mechanism of control illustrates the uncertainty that accompanies all volatilization models at this time.
In a previous study, large variations in indoor air concentrations and inhaled doses resulted when finite source and infinite source volatilization models were compared, with results that varied by several orders of magnitude [1]. When the variations observed in that previous study and the current study are considered together, it is clear that careful consideration should be given to modeling assumptions and the selection of soil moisture values when assessing the soil-to-indoor air exposure pathway.
Appendix
| Parameter | Value |
|---|---|
| Contamination depth range (m) | 1.83–3.05 |
| Groundwater depth (m) | 3.05 |
| Bulk density of dry soil (kg/m3) | 1,300 |
| Saturation volume of soil (v/v) | 0.41 |
| Field capacity of soil (v/v)ab | 0.10 |
| Wilt point of soil (%, v/v)ab | 7.0 |
| Air dry moisture content (v/v)ab | 0.05 |
| Initial moisture content of soil (v/v)c | 0.21 |
| Organic carbon content of soil (%, w/w) | 0.1 |
| Air diffusion coefficient of contaminant (m2/s) | 5 × 10−6 |
| Water diffusion coefficient of contaminant (m2/s) | 5 × 10−10 |
| Soil Conservation Service runoff curve number (AMCII) [27]ab | 82 |
| Saturated hydraulic conductivity (m/d)ab | 3.00 |
| m Coefficient (Campbell's hydraulic conductivity equation [22])ab | 12.8 |
| b Coefficient (Clapp and Hornberger's soil diffusivity and soil moisture retention equations [23])ab | 4.9 |
| Saturation suction head (m; Clapp and Hornberger equations [23])ab | 0.219 |
| Time increment (d)a | 1 |
| Spatial increment (m)a | 0.30 |
| Convergence criteriaa | 0.001 |
| Root zone depth (m)a | 0.91 |
| Soil dispersivity (m)a | 0.30 |
- a Used by Integrated Moisture Plus Contaminant Transport (IMPACT) model only.
- b Set as recommended by IMPACT model guidance for sandy loam soil [13].
- c This value used for simulation under natural moisture conditions.




