Test of significant toxicity: A statistical application for assessing whether an effluent or site water is truly toxic
Abstract
The U.S. Environmental Protection Agency (U.S. EPA) and state agencies implement the Clean Water Act, in part, by evaluating the toxicity of effluent and surface water samples. A common goal for both regulatory authorities and permittees is confidence in an individual test result (e.g., no-observed-effect concentration [NOEC], pass/fail, 25% effective concentration [EC25]), which is used to make regulatory decisions, such as reasonable potential determinations, permit compliance, and watershed assessments. This paper discusses an additional statistical approach (test of significant toxicity [TST]), based on bioequivalence hypothesis testing, or, more appropriately, test of noninferiority, which examines whether there is a nontoxic effect at a single concentration of concern compared with a control. Unlike the traditional hypothesis testing approach in whole effluent toxicity (WET) testing, TST is designed to incorporate explicitly both α and β error rates at levels of toxicity that are unacceptable and acceptable, given routine laboratory test performance for a given test method. Regulatory management decisions are used to identify unacceptable toxicity levels for acute and chronic tests, and the null hypothesis is constructed such that test power is associated with the ability to declare correctly a truly nontoxic sample as acceptable. This approach provides a positive incentive to generate high-quality WET data to make informed decisions regarding regulatory decisions. This paper illustrates how α and β error rates were established for specific test method designs and tests the TST approach using both simulation analyses and actual WET data. In general, those WET test endpoints having higher routine (e.g., 50th percentile) within-test control variation, on average, have higher method-specific α values (type I error rate), to maintain a desired type II error rate. This paper delineates the technical underpinnings of this approach and demonstrates the benefits to both regulatory authorities and permitted entities. Environ. Toxicol. Chem. 2011; 30:1117–1126. © 2011 SETAC
INTRODUCTION
Within the National Pollutant Discharge Elimination System (NPDES) Program in the United States, acute and chronic whole effluent toxicity (WET) tests are analyzed using either hypothesis testing (e.g., no-observed-effect concentration [NOEC], pass or fail determinations) or point estimate techniques (e.g., effect concentration to 25% of test organisms [EC25]) 1-4. Hypothesis testing can generate statistical endpoints (NOEC) for multiconcentration tests (e.g., effluent discharge testing, chemical registration testing) as well as a standard t test analysis for two concentration test designs (e.g., storm water or receiving water testing). Many researchers have identified advantages and disadvantages with both hypothesis and point estimate analysis approaches, particularly as they apply in a regulatory compliance setting, along with suggestions for enhancements 5-7. This article does not address the advantages and disadvantages of either approach, and U.S. Environmental Protection Agency (U.S. EPA) toxicity testing method manuals 1-4 allow the choice of either hypothesis testing or point estimate techniques for developing permit conditions (e.g., limits, monitoring triggers). The hypothesis testing approach is commonly used in the NPDES WET program and is the only viable statistical approach to use in receiving water quality monitoring programs, in which organism responses in the sample are compared with responses in a control or reference site sample. Furthermore, one of the key recommendations from a multistakeholder Society of Environmental Toxicology and Chemistry Pellston workshop on WET was to evaluate improvements in the statistical analysis of WET data and, in particular, the bioequivalence statistical approach 5. This article delineates the technical underpinnings of this approach and demonstrates the benefits to both regulatory authorities and permitted entities.
In terms of the WET program, the hypothesis approach may lend itself more to the way in which permitting is typically considered. State programs seek to determine whether the effluent or receiving water exhibits unacceptable effects (toxicity) at the critical concentration (often termed either instream waste concentration [IWC] or receiving water concentration [RWC]). Indeed, in terms of the NPDES WET program in the United States, WET limits or triggers are expressed in terms of an effect endpoint at the IWC (e.g., NOEC = IWC) as recommended in the U.S. EPA guidance 8.
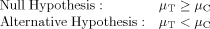(1)where µC refers to the true mean for the biological measure in the control water and µT refers to the true mean for this measure in the effluent sample. Thus, the traditional WET null hypothesis assumes that the effluent sample is not toxic, and appropriate statistical tests are used to determine whether the null hypothesis is rejected in favor of the alternative hypothesis, that is, that any apparent toxicity based on the sample means is real and not simply a reflection of random variation. Such statistical tests are part of current recommended practice in the WET testing program in the United States.
Two common concerns with the traditional hypothesis testing approach in the WET program are precise test control replication (small coefficient of variation [CV]), resulting in an effluent being declared toxic when in fact the difference observed between the response at the critical concentration and the control is too little to be considered unacceptable environmentally, and very imprecise test control replication, resulting in an unacceptably toxic effluent sample being incorrectly classified as not toxic 5. The first limitation arises because the null hypothesis is defined around µT ≥ µC, so the goal is to declare an effluent toxic if µT < µC, no matter how small the difference. The second concern is that the current WET hypothesis testing approach currently does not explicitly address the type II error rate (β; i.e., the error of accepting the null hypothesis when it should have been rejected) and thus does not address requirements regarding the power of the test to detect an unacceptably toxic sample. By not establishing an appropriate β and test power in the WET program, a permittee has no incentive to increase the precision of a WET test (e.g., incorporating additional replicates within a test), when using the traditional hypothesis approach (and using the point estimation approach as well). As illustrated in Figure 1, greater precision simply results in a sample being declared toxic and can lead to high rejection rates for effluents with low levels of toxicity that might be considered acceptable.
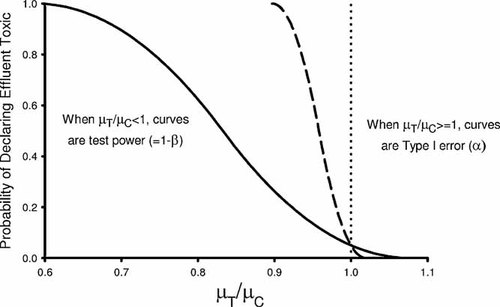
Example test performance curves for traditional whole effluent toxicity hypothesis tests. The dotted line marks where the true mean biological measure in the effluent equals that in the control. The solid curve is for a high-variability test, and the dashed curve is for a low-variability test.
This article presents an alternative statistical approach that attempts to improve upon the current hypothesis testing approach, specifically addressing and incorporating both type I and type II error rates, and thereby test power, and establish the a priori selection of an effect level that is considered unacceptably toxic (similar to the point estimate approach) while providing appropriate incentives for permittees to collect high-quality WET test data. This alternative statistical approach is applicable to an individual effluent, storm water, or receiving water. Therefore, in the present study, the term sample is used to apply to any of these types of water matrices for which WET test methods are currently used to assess toxicity. A more detailed discussion of this approach as well as all results applying this approach can be found in U.S. EPA document EPA/833-R-10-004 9.
MATERIALS AND METHODS
(2)Consistent with the noninferiority approach, TST hypotheses incorporate two important distinctions compared with the traditional WET hypothesis approach. First, a specific value for the ratio µT/µC, designated b (where b is a constant, 0.0 < b < 1.0), is included to delineate unacceptable and acceptable levels of toxicity, allowing a risk management decision about what level of toxicity should be allowed if the true means were known. Second, the inequalities are reversed so that it is assumed that the sample has an unacceptable level of toxicity until demonstrated otherwise. As a result of this reversal of the inequalities, the meanings of α and β under the TST hypotheses are reversed from those under the traditional hypothesis approach (Table 1). Under the TST approach, α or type I error rate is associated with the error of declaring a toxic sample as acceptable; β or type II error rate is associated with the error of declaring a sample toxic when it is truly acceptable; and statistical test power, using the TST approach, is the ability to conclude correctly that true organism response levels are acceptable. A sample would be considered not toxic under the TST approach when the null hypothesis is rejected. By reversing the inequalities and referencing them to b, the TST approach also results in more precise tests having lower type II errors (Fig. 2). Thus a sample with a true response level that is acceptably low is declared toxic with less frequency as within-test precision increases, a desirable attribute for the WET program. This provides permittees with a clear incentive to improve the precision of test results. Thus, using the TST approach in the NPDES program, a permittee has to demonstrate with some confidence that the effluent has effects within an acceptable range but can also improve testing procedures as needed (that is, increase replicates or decrease within-test variability).
| Statistical test result | True condition | |
|---|---|---|
| µT ≤ b · µC (sample is toxic) | µT > b · µC (sample is nontoxic) | |
| µT ≤ b · µC (sample is toxic) | Correct decision (1 − α) | Type II error (β) |
| µT ≤ b · µC (sample is not toxic) | Type I error (α) | Correct decision test power (1 − β) |
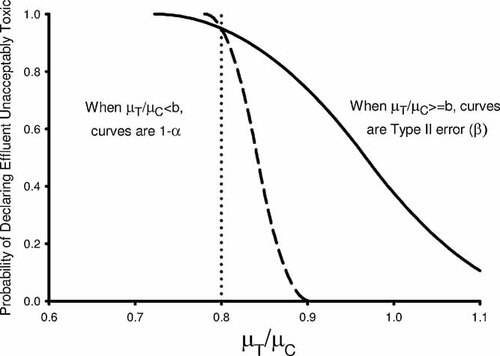
Example test performance curves for test of significant toxicity whole effluent toxicity test hypothesis tests. For this example, b is set to 0.8 (denoted by dotted line), with α = 0.05. The two curves represent test performance for tests with high (solid line) and low (dashed line) variability.
TST regulatory management decisions
In presenting a similar bioequivalence approach for WET analysis, Erickson and MacDonald 10 recognized that a clear regulatory management decision was lacking regarding what is or is not acceptable in terms of an effect in WET tests (i.e., b was not explicitly defined). Without such a regulatory decision threshold, a bioequivalence approach cannot be readily implemented in a WET or receiving water monitoring program. The TST approach establishes regulatory management decisions (RMDs), which are incorporated into the TST methodology by selecting bioequivalence values for b and a low mean effect level, for distinguishing unacceptable and acceptable toxicity, respectively, as well as the α error rate when βT = b · µC.
The selection of b is a biologically based decision that should reflect what is considered ecologically unacceptable in terms of toxicological effects and is therefore independent of WET test method performance 10, 12, 14. For all chronic WET test methods, the RMD using TST is to set b = 0.75. This b value (25% effect in the critical effluent concentration or b = 0.75) is consistent with U.S. EPA's use of the 25% inhibiting concentration (IC25) in point estimation methods for examining chronic WET data. Chronic effects less than 25% would be considered to have a lower risk potential. Because of the more severe environmental implications of acute toxicity (organism death), the RMD for acute WET test methods using TST is to set b higher than that for chronic WET test methods, at 0.80 (20% mortality or organism immobility in the effluent).
For a given level of test precision and b value, selecting a value for α completely determines both type I and type II error rates at all toxicity levels, such as the curves shown in Figure 2. However, the value selected for α does not have to be based just on consideration of the desired error rate when µT = b · µC. Rather, α can be selected on the basis of balancing goals regarding this type I error rate with goals for type II error rates at lower levels of toxicity. Therefore, a different α can be assigned for different types of WET toxicity test methods based on routine test control precision and on specific goals regarding type I and II error rates.
With regard to type I error rates, the U.S. EPA's goal is to identify unacceptable toxicity in WET tests most of the time when it occurs. It is a preference to set α at the typical 0.05 level (if µT = b · µC, the sample will be declared unacceptable 95% of the time). However, for tests with lower routine control precision (resulting from the type of test endpoint measured or the minimum acceptable test design in the U.S. EPA test method), setting α equal to 0.05 could result in a high type II error rate (declaring samples unacceptable or toxic) when toxicity is truly low or absent (Fig. 2). Therefore, values of α (type I) up to 0.25 were allowed, as needed to meet the goal regarding type II error rates discussed below. Thus, the type I error rate RMD is 0.05 ≤ α ≤ 0.25, so that there is at least a 0.75 probability that a sample with unacceptable toxicity at the IWC (µT ≤ b · µC) will be declared toxic. Note, the traditional hypothesis testing approach used to analyze WET data had not established this error rate (the error to the environment, missing truly toxic samples).
With regard to type II error probabilities, the goal of the U.S. EPA is to have a low error rate when toxicity is negligible. It is necessary to define negligible as a second, smaller level of effect that is acceptable because the latter includes toxicity as high as that represented by b, at which point the false-positive error rate always will approach 1 − α. To address this, the TST approach defines negligible as 10% effect or less and specifies that the type II error probability be no higher than 0.05 at a 10% mean effect in the effluent at the IWC. Note, this error rate is set at the same level as the traditional hypothesis testing approach. The assignment of a 10% effect as negligible is consistent with the allowance of a 10% effect in acute WET tests and is often indistinguishable from the control response in chronic WET tests as well. Thus, the type II error RMD is β ≤ 0.05 at µT/µC = 0.90, given that type I error RMD is α = 0.25 when µT < b · µC. It should be emphasized that this RMD relates to only one point in the range of toxicity considered acceptable and that the type II error rate will vary within this range (Fig. 2). Type II error rates will be lower when toxicity is lower than 10%, dropping to near zero when toxicity is absent, and will be higher when toxicity values are greater than negligible but still acceptable, rising to 1 − α as the toxicity approaches the unacceptable level.
Therefore, the overall RMD for α (type I error rate when µT/µC = b) is to set it to the lowest value that results in β ≤ 0.05 (the type II error rate) when the true toxicity at µT/µC = 0.90, but that α will be no lower than 0.05 and no higher than 0.25. This selection of α is primarily a function of routine method within-test variability (control CV), which is a function of the minimum required test design for a given WET test method and the types of endpoints measured as described in the next section.
WET test data
Initially, nine U.S. EPA WET test methods commonly used by regulatory authorities (Table 2) were evaluated in this project. Three additional water column WET test methods (acute Ceriodaphnia and Hyalella survival and chronic Selenastrum growth tests) were evaluated using TST in subsequent analyses with the same process as described herein and in U.S. EPA/833-R-10-004 9. Preference was given to valid WET data generated using the U.S. EPA 1995 WET test methods for the EPA West Coast marine species 4 and for test species in U.S. EPA WET test methods 1-3. These test methods are representative of the range of U.S. EPA WET test methods commonly required of permittees in terms of types of toxicity endpoints written into NPDES permits and test designs followed by permittee's testing laboratories. Whole effluent toxicity data were received from several reliable sources 9 to identify baseline test method statistics (e.g., control CV percentiles, mean control response percentiles) that were used in simulation analyses and to identify appropriate α values for each test method. Nearly 2,000 valid WET tests (tests meeting U.S. EPA's test acceptability criteria) of interest were incorporated, representing over 50 dischargers and 30 laboratories 9. Only post-1995 data were used in analyses of West Coast WET test methods 4, and data for other WET test methods were obtained mostly after 2002, the year in which those test methods were substantially refined 15. Furthermore, laboratories had more experience with all chronic test methods after 1995 as evidenced by significantly more precise data from 1996 onward compared with pre-1995 (mean CV = 0.45 and 0.30, respectively, F = 5.40, p < 0.05 9).
| Percentile | C.d. | P.p.-G | A.b. | H.r. | M.p. | D.e. and S.p. | P.p.-A |
|---|---|---|---|---|---|---|---|
| 25th | 21.2 (0.10) | 0.43 (0.06) | 0.25 (0.10) | 0.900 (0.021) | 0.859 (0.027) | 0.875 (0.012) | 1.00 (0.000) |
| 50th | 25.5 (0.15) | 0.62 (0.09) | 0.30 (0.14) | 0.938 (0.031) | 0.908 (0.038) | 0.953 (0.027) | 1.00 (0.000) |
| 75th | 29.4 (0.24) | 0.79 (0.13) | 0.38 (0.18) | 0.968 (0.045) | 0.940 (0.051) | 0.978 (0.065) | 1.00 (0.000) |
| 90th | 33.3 (0.35) | 0.89 (0.17) | 0.43 (0.27) | 0.982 (0.062) | 0.965 (0.065) | 0.993 (0.107) | 1.00 (0.12) |
- a C.d. = Ceriodaphnia dubia reproduction; P.p.-G = Pimephales promelas growth; A.b. = Americamysis bahia growth; H.r. = Haliotis rufescens larval development; M.p. = Macrocystis pyrifera germination; D.e. and S.p. = Dendraster excentricus and Strongylocentrotus purpuratus egg fertilization; P.p.-A = Pimephales promelas acute survival.
For each of the test methods examined, control CV was calculated on the basis of WET test control data compiled. Cumulative frequency plots were used to identify various percentiles of observed method-specific control CVs (25th, 50th, 75th percentiles). These measures were calculated to characterize typical achievable test performance in terms of control variability. A similar analysis was performed for the control endpoint responses for each of the test methods (mean offspring per female in the chronic Ceriodaphnia dubia test method) to characterize typical achievable test performance in terms of control response.
Selection of WET test method α values
Monte Carlo simulation analysis was used to estimate the percentage of WET tests that would be declared toxic using TST as a function of different α levels (type I error rate), within-test control variability, and mean percentage effect level. This analysis identified probable β (type II) error rates (declaring an effluent toxic when in fact it is acceptable) as a function of the α error rate, mean effect in the effluent, and control CV.
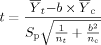(3)
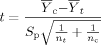(4)
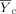= mean for the control; 
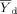= mean for the IWC; nc = number of replicates for the control; nt = number of replicates for the IWC; b = 0.75 for chronic tests and 0.80 for acute WET tests;
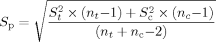(5)S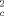
= estimate of the variance for the control; and S
= estimate of the variance for the IWC.
By simulating thousands of WET tests for a given scenario (mean percentage effect, control CV, and α level), the percentage of tests declared toxic could be calculated and compared among scenarios and between the TST and the traditional hypothesis testing approach. Simulations were based on a two-treatment analysis (control and a sample concentration). At the present time, TST has not been extended to a multiconcentration analysis because of the complexities involved in identifying true error rates using a bioequivalence approach in a multicomparison analysis 16.
Probabilities of accepting the null hypothesis for the traditional hypothesis and TST approaches will differ according to differences in population variances, number of replicates, α level, and effect size (fraction of the control response). Each of these factors was varied in simulation analysis, as summarized in Table 3. Sample sizes (N) of control and sample were randomly selected from a population having a specified control CV, mean ratio of response between control and the sample, and α level. The TST t statistic and the traditional t statistic were then calculated for each test using Equations 3 and 4, respectively. The one-tailed probabilities of declaring the test toxic using the traditional t test and the TST t test were calculated and saved. This simulation was repeated 10,000 times for each combination of effect level, CV, and α level. The percentage of tests declared toxic (β error rate) was then calculated for each simulation setting.
| Factor | Range of values used in simulation | Comments |
|---|---|---|
| Population variance | 10th, 25th, 50th, 75th, 90th percentile CVs; some test methods examined additional CVs as well | Based on CV percentiles obtained from actual WET data for a given WET test method and endpoint; the population mean was set to the median value of observed control mean values from actual effluent tests. N samples (representing the minimum number of replicates required in the test method) from the control population were selected for each simulation |
| Effect size | Five different effect sizes from 10% to 30% of the control mean | For example, when the control mean = 25 and the effect size =10%, N samples (corresponding to the minimum number of replicates required in the test method) were picked at random from a population with mean = 25 · ([100 − 10]%) |
| Sample size (N) | For certain WET test methods, sample size for each test method was increased up to double the minimum number of replicates required for a given test method | For example, number of replicates for the chronic Ceriodaphnia dubia test ranged from 10 to 20 in simulation analyses; this provided useful information indicating potential benefits to a permittee if they conducted a WET test method with additional replicates, given a specified mean percent effect level and control CV observed, and a specified α level |
| α Error | Different levels ranging from 0.05 to 0.30 (six values) | Results of these analyses indicated potential β error rates (probability of declaring a sample toxic when it is acceptable) given a specified mean percent effect in the effluent and control CV |
- a CV = coefficient of variation.
Once β error rates were identified for a WET method given different α levels, control CVs, and percentage mean effect levels, bivariate plots were used to compare the percentage of tests declared toxic as a function of α and the ratio of effluent mean: control mean at various within-test CV percentiles (25th, 50th, 75th) and the RMD effect thresholds identified as either toxic (25% effect for chronic and 20% for acute) or negligible (10% mean effect). The results were then used to identify an appropriate α error rate for a test method given the RMDs.
RESULTS AND DISCUSSION
Figures 3 and 4 summarize results of simulations for the Ceriodaphnia reproduction test endpoint and for the Haliotis rufescens (red abalone) percentage larval development endpoint, respectively, as two examples demonstrating the range in results observed. All simulation results can be obtained from the U.S. EPA 9. It is understood that using normally distributed data and equal variances is a simplification for some WET test endpoints that are prone to nonnormality or heterogeneous variances, such as acute fathead minnow survival. Extensive analyses in this research indicated that the bioequivalence t test of Erickson and McDonald 10 results in a very small (<0.01) departure of the nominal α error rate using TST with data that have even a ninefold difference between control and effluent variances (which is greater than most variance ratios observed in nearly 2,000 WET tests) and with data that were nonnormally distributed 9. Thus, results of simulation analyses should be applicable to the types of nonnormality and variance heterogeneity encountered in WET tests. This was further supported by additional research 9 showing that WET test data distributions are typically not highly skewed or long tailed, two factors known to affect reliability of the t statistic 17-19. This is due to the way in which WET tests are designed and because there are boundaries for test acceptability criteria (i.e., control response) that truncate the potential data range within a test and, consequently, the difference in variance one observes between control and a sample response. A review of the statistical literature as well as additional analyses in developing the TST approach confirmed that Welch's t test is appropriate for the types of nonnormal data distributions encountered in actual effluent WET tests as well as for normally distributed data 9, 20-22.
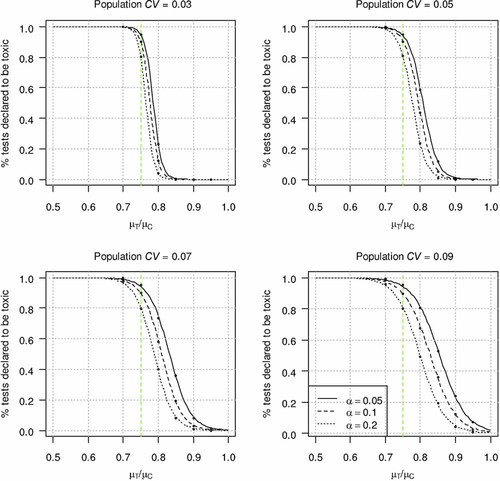
Power curves showing the percentage of tests declared toxic as a function of the ratio of effluent mean to control mean response and α level categorized by the level of control within-test variability. Coefficients of variation (CV) of 0.1, 0.15, 0.2, and 0.25 correspond to the approximate 25th, 50th, 70th, and 75th percentiles for the chronic Ceriodaphnia reproduction whole effluent toxicity test method. The dashed line indicates the 75% mean effect level, which is the decision threshold for chronic tests. [Color figure can be seen in the online version of this article, available at wileyonlinelibrary.com]
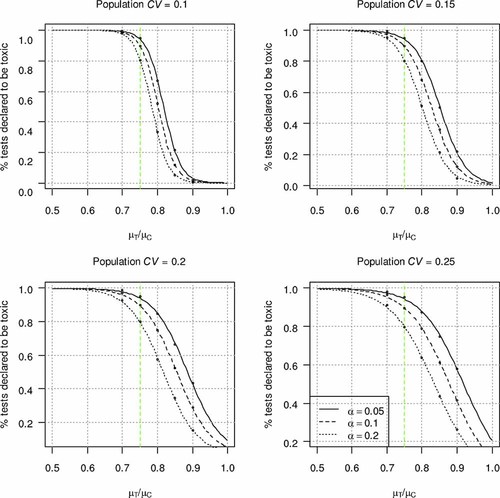
Power curves showing the percentage of tests declared toxic as a function of the ratio of effluent mean to control mean response and α level categorized by the level of control within-test variability. Coefficients of variation (CV) correspond to the 25th, 50th, 75th, and 98th percentiles for the chronic red abalone whole effluent toxicity test method. The dashed line indicates the 75% mean effect level, which is the decision threshold for chronic tests. [Color figure can be seen in the online version of this article, available at wileyonlinelibrary.com]
Results using select α values are plotted in each graph illustrating how the percentage tests declared toxic using TST vary with the mean effect (expressed in the graphs as the mean ratio of response between the control and a sample) given a specified control CV. As noted in the RMDs described previously, for each test method, the lowest α level was selected that declared ≥75% of tests toxic when there was a 25% effect in the effluent (ratio µT/µC = 0.75) for chronic test endpoints or when there was a 20% effect in the effluent (ratio µT/µC = 0.80) for acute test endpoints and also declared ≤5% tests toxic when there was a 10% effect in the effluent (ratio µT/µC = 0.90) for all test endpoints (i.e., β ≤ 0.05).
Figure 3 illustrates two fundamental concepts using the TST approach. First, at mean effect levels less than the RMD unacceptable toxicity threshold, there are differing probabilities of a sample being declared toxic (different actual β error rates) depending on within-test variability and the difference in mean responses observed between control and the sample. For some WET test methods and endpoints such as the Ceriodaphnia reproduction endpoint, a sample with a mean effect lower than the chronic RMD threshold of 25% may have some probability of being declared toxic. For example, at an α = 0.20 and the 75th percentile CV for Ceriodaphnia reproduction of approximately 0.25 (Table 2), simulation analysis indicated that an effluent demonstrating a 15% effect (i.e., µT/µC = 0.85) could be declared toxic up to 42% of the time for this test endpoint (Fig. 3). Analyses of actual effluent data indicate that the percentage of tests declared toxic is much lower for this endpoint (<10%; unpublished data), and a 10% effect would be declared toxic less than 5% of the time. Note that as the control CV is lower, for example, the 50th percentile CV of 0.15 for this test endpoint (Table 2), simulation analyses indicate that a 15% effect would be declared toxic less frequently (∼20% of the time), and a 10% effect would be declared toxic less than 5% of the time (Fig. 3). Again, analyses of actual effluent data have indicated much lower rates of tests declared toxic at a 15 or 10% mean effect for this endpoint given routine test performance. Thus, given routine within-test control variability, defined as the 50th percentile CV for this test endpoint based on many laboratories using the current approved WET test method, α = 0.20 would satisfy the RMDs for the Ceriodaphnia reproduction endpoint using the TST approach (≥75% of the tests declared toxic at a 25% effect [α] and ≤5% tests declared toxic at a 10% effect [β]).
A second fundamental result demonstrated in Figure 3 is that, for certain WET test methods, such as the Ceriodaphnia reproduction test, there is some probability of declaring a test not toxic when the mean effect in the effluent exceeds the RMD threshold of 25%; for example, at an α = 0.20 and the 75th percentile CV for Ceriodaphnia reproduction, a 30% mean effect in the effluent (µT/µC = 0.70) might not be declared toxic as much as 10% of the time (Fig. 3). Similar results were observed for the Americamysis bahia growth and Pimephales promelas growth endpoints 9.
In contrast, a relatively low α value (α = 0.05) met the RMDs specified using the TST approach for the red abalone larval development chronic test (Fig. 4). At an α = 0.05, both a low type II error rate (<5% of the tests are declared toxic at a 10% mean effect in the effluent) and low type I error rate (>95% tests are declared toxic at a 25% effect in the effluent) are observed, even at a population CV somewhat higher than the 75th percentile CV (0.05) for this test method (Fig. 4). Similar results were observed for several of the other West Coast chronic WET methods examined, such as the echinoderm egg fertilization test and the giant kelp germination test 9.
In general, those WET test endpoints having higher routine (for example, 50th percentile CV) within-test control CVs on average have higher method-specific α values so as to maintain a desired low type II error rate (<5% type II error rate at a 10% mean effect in the sample). This result is a consequence of the minimum test designs specified for those WET test methods.
Table 4 summarizes the α levels identified for each WET test method examined based on the RMDs established using the TST approach. In total 14 unique WET test endpoints are represented in Table 4. These method-specific α values apply to all test endpoints for a given U.S. EPA WET test method (e.g., reproduction for the chronic Ceriodaphnia test). Results obtained from the TST analyses using the U.S. EPA WET test methods in Table 4 should be applicable to other U.S. EPA WET methods not examined that use the same test design and measure the same endpoint as one of the tests evaluated. For example, results generated for the fish Pimephales survival and growth test can be extrapolated to other U.S. EPA fish survival and growth tests (such as Menidia sp., Cyprinus variegates, Atherinops affinis) because the test methods use a similar test design (e.g., number of replicates, number of organisms tested) and measure the same biological endpoints. Similar extrapolations are indicated for the East Coast echinoderm species (for example, Arbacia punctulata) in relation to those observed for the West Coast echinoderm species and for other fish species acute test methods using a design similar to the P. promelas acute method evaluated.
| U.S. Environmental Protection Agency WET test method | b Value | Probability of declaring a toxic effluent nontoxic (type I [α] error)a |
|---|---|---|
| Chronic freshwater and East Coast marine methods | ||
| Ceriodaphnia dubia (water flea) survival and reproduction | 0.75 | 0.20 |
| Pimephales promelas (fathead minnow) survival and growth | 0.75 | 0.25 |
| Selenastrum capricornutum (green algae) growth | 0.75 | 0.25 |
| Americamysis bahia (mysid shrimp) survival and growth | 0.75 | 0.15 |
| Arbacia punctulata (Echinoderm) fertilization | 0.75 | 0.05 |
| Cyprinodon variegatus (sheepshead minnow) and Menidia beryllina (inland silverside) survival and growth | 0.75 | 0.25 |
| Chronic West Coast marine methods | ||
| Dendraster excentricus and Strongylocentrotus purpuratus (Echinoderm) fertilization | 0.75 | 0.05 |
| Atherinops affinis (topsmelt) survival and growth | 0.75 | 0.25 |
| Haliotis rufescens (red abalone), Crassostrea gigas (oyster), Dendraster excentricus, Strongylocentrotus purpuratus (Echinoderm) and Mytilus sp. (mussel) larval development methods | 0.75 | 0.05 |
| Macrocystis pyrifera (giant kelp) germination and germ-tube length | 0.75 | 0.05 |
| Acute methods | ||
| Pimephales promelas (fathead minnow), Cyprinodon variegatus (sheepshead minnow), Atherinops affinis (topsmelt), Menidia beryllina (inland silverside) survivalb | 0.80 | 0.10 |
| Ceriodaphnia dubia, Daphnia magna, Daphnia pulex, Americamysis bahia acute survival; Hyalella azteca survival | 0.80 | 0.10 |
- a Desired regulatory management decision (RMD) ≤25% effect at the critical effluent concentration or 0.25; i.e., ≥75% of samples above the RMD are declared toxic and ≤5% of samples with effect at critical effluent concentration = 10% are declared toxic.
- b Based on four replicate test designs.
One of the intended benefits of the TST approach is that increasing the precision (decreasing within-test variability) and power of the test increases the chances of rejecting the null hypothesis and declaring a truly acceptable sample (as defined by the TST RMDs) as not toxic. This increases the permittee's ability to demonstrate that a sample is acceptable (not toxic). Results for the Ceriodaphnia reproduction test method (Fig. 5) indicate the benefits of increased replication within a test, especially when the mean effect of the sample is ≤25%. As expected, increasing test replication (and thereby the power of the test) results in a higher rate of tests declared toxic using the traditional hypothesis testing approach but a lower rate of tests declared toxic using the TST approach. Similar results were observed for the mysid chronic growth test (A. bahia) and for the chronic fish growth test (P. promelas 9). For these WET test methods, adding two more replicates to the control and the critical concentration of the sample often increased test power sufficiently such that a true difference of 25% was declared not toxic 95% of the time using TST.
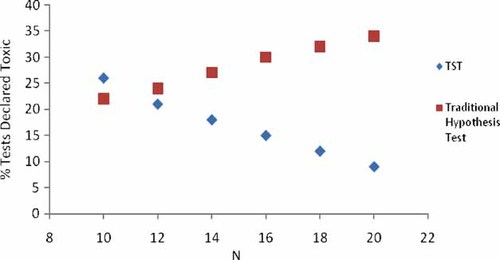
Percentage of chronic Ceriodaphnia tests declared toxic using test of significant toxicity (TST) having a mean effluent effect of 10% and above average control variability and α = 0.20, as a function of the number of test replicates. Result using the traditional hypothesis approach (α = 0.05) is shown as well. [Color figure can be seen in the online version of this article, available at wileyonlinelibrary.com]
For those WET tests that have relatively small mean effect based on test design (high number of organisms per replicate and sufficient replication), such as the echinoderm egg fertilization test and the red abalone larval development test, test power is relatively high using the minimum test design requirements (number of replicates) as specified in the test method. For those methods, TST performs as expected with relatively low α and β error rates and thereby high test power. For these methods, additional replication is probably not needed to determine with fairly high confidence whether an effluent is acceptable or not using TST.
Examples illustrating results using TST analysis
The discussion above relies primarily on simulated test data, although actual WET data were used to inform the simulations and identify appropriate α rates. Here we demonstrate the TST approach using actual WET data to illustrate how results compare with the traditional hypothesis test approach currently used in chronic WET testing in the United States and in many other countries. In these examples, it is evident that, when the mean percentage effect in the critical effluent concentration equals or exceeds the RMD threshold (25% effect or 0.25 in these examples),TST declares the test toxic, whereas the traditional hypothesis approach may or may not depending on within-test variability (examples 2, 4, 6, and 7; Table 5). We would note that these particular tests would have been declared toxic using the point estimate IC25 approach as well.
| Test species | Endpoint | Control mean | Control CV | Effluent mean | Effluent CV | Percentage effect | NOEC | TST |
|---|---|---|---|---|---|---|---|---|
| 1. Ceriodaphnia dubia | Reproduction | 31.5 | 0.242 | 25.7 | 0.255 | 18.5 | NT | T |
| 2. Ceriodaphnia dubia | Reproduction | 28.0 | 0.225 | 20.0 | 0.395 | 28.6 | NT | T |
| 3. Pimephales promelas | Growth | 0.686 | 0.063 | 0.593 | 0.071 | 13.5 | T | NT |
| 4. Pimephales promelas | Growth | 0.541 | 0.089 | 0.301 | 0.242 | 44.3 | T | T |
| 5. Pimephales promelas | Growth | 0.518 | 0.017 | 0.425 | 0.169 | 17.9 | NT | NT |
| 6. Pimephales promelas | Percentage survival | 1.459b | 0 | 1.143b | 0.283b | 26.6 | NT | T |
| 7. Pimephales promelas | Percentage survival | 1.459b | 0 | 1.114b | 0.095b | 29.1 | T | T |
| 8. Dendraster excentricus | Percentage fertilization | 1.350b | 0.062b | 1.110b | 0.189b | 15.5 | T | NT |
- a NT = nontoxic, T = toxic, CV = coefficient of variation. All results are based on the minimum test design (number of replicates, organisms per replicate) required by the respective methods.
- b Based on arc sine square root-transformed data. The percentage effect is calculated based on untransformed data.
Examples 1 and 6 illustrate the effect of lack of test power on TST and NOEC results. In both of these examples, the control CV is within the 50th percentile of the observed range, but the effluent CV exceeds the 90th percentile of the range of control CVs observed, indicating high variability among replicates in the effluent treatment. The result is that the test is declared toxic using TST but not toxic using the NOEC method. As discussed previously, high within-test variability favors a finding of no effect using the traditional hypothesis approach (not rejecting the null hypothesis that the control and effluent responses are equal). This is not the case using TST. Examples 3 and 8 illustrate the opposite effect: because of the high precision in these tests (control CVs are <25th percentile and approximately equal to the 50th percentile in examples 3 and 8, respectively), the NOEC declares both tests toxic despite a mean effect <16% (Table 5). Because of the high precision in these tests, TST declares both tests nontoxic, insofar as neither exceeded the 25% unacceptable toxicity RMD.
Finally, both NOEC and TST (and the IC25 approach) will yield similar conclusions either when a large mean effect is observed (all approaches declare the test toxic as in examples 4 and 7) or when a small mean effect is observed and test precision is average (all approaches declare the test not toxic as in example 5; Table 5). These examples illustrate that TST is responsive to test power such that mean effects approaching the RMD threshold for unacceptable toxicity will be declared toxic if test power is low in comparison with routine test performance. Greater test replication or decreasing within-test control variability via other means will counteract this effect by increasing test power. These examples also illustrate that responses at both ends of the spectrum (either a small effect or a large effect in the test sample) will yield conclusions in line with common sense: small effects will be declared not toxic and large effects will be declared toxic regardless of within-test precision.
Shukla et al. 12 proposed an approach similar to the TST approach for WET testing, in which the bioequivalence factor b was applied as a difference between treatment and control means (µT > µC − b) rather than as a ratio, as in our approach. Many other researchers have proposed an approach similar to that described by Shukla et al. 12, often referred to as the test of noninferiority 23, which has been used in the pharmaceutical registration process by the U.S. Food and Drug administration 24-26 and other applications 14, 27, 28. As pointed out by Shukla et al., the small sample sizes typically used in WET tests will tend to produce tests of normality that have fairly low power in either the original or the log scale, which may lead to an equivocal verdict regarding the distributional property of the data 12. With these conditions, Shukla et al. 12 determined that either the ratio or the difference hypothesis can be used for WET analysis.
However, the approach used by Shukla et al. 12 did not use an a priori value for b as in our approach. Rather, they determined the b value by maximizing concordance of results (i.e., the percentage of WET tests that would be declared toxic) between the bioequivalence and the traditional hypothesis testing approach using the Ceriodaphnia reproduction endpoint as an example. A concern with this approach is that the WET methods have not established the β error rate, so the b value, using their approach, is tied to method performance rather than a risk management decision. Method performance is a factor in the TST approach insofar as helping to set an achievable α and β value for a given WET test method design and endpoint but not in setting the risk management decision of what should be considered unacceptable toxicity 12, 13.
As in any hypothesis testing approach, TST is not applicable if the toxicity test endpoint does not use a traditional replicated experimental design. For example, the U.S. EPA's Ceriodaphnia survival and reproduction test method uses one organism per replicate for each treatment (control and IWC). This experimental design of having only one organism per replicate does not lend itself to either the traditional hypothesis approach or TST for the survival endpoint. For most other WET test endpoints, this is not an issue. In terms of the WET program or receiving water toxicity testing programs, it may be sufficient to analyze only the sublethal endpoint in chronic tests because that endpoint is generally as sensitive as or more sensitive than survival. Indeed, for the U.S. EPA chronic fish WET test method (P. promelas survival and growth test), the biomass endpoint already incorporates survival as well 1.
Results using TST for effluent and receiving water toxicity analyses indicate that it is a viable additional approach for analyzing valid acute and chronic toxicity test data. Given the RMDs and test-method-specific α values specified in the TST approach, TST provides a transparent methodology for demonstrating whether a sample is acceptable under the NPDES effluent, storm water, and receiving water programs. Although similar results could be obtained using the traditional hypothesis approach by requiring a certain power in a given test, the advantage of the TST approach is that it provides a framework in which to analyze toxicity test results that is easy to calculate, understand, and implement in regulatory program setting.
CONCLUSIONS
In conclusion, the TST approach applies already documented statistical tests to WET data analysis via the incorporation of regulatory management decisions that define acceptable and unacceptable toxicity and error rates that apply at those decision levels. TST could be a useful statistical alternative for analyzing WET data, for both regulatory compliance (effluent and storm water) and ambient monitoring (e.g., sediment or water column toxicity assessments), because it explicitly incorporates both type I and type II error rates and provides clear incentives for generating high-quality test data. In addition, because TST is designed as a two-treatment statistical analysis (control compared with a critical concentration), opportunities to provide higher test power (via more replicates or smaller effect size in treatments, for example) are less costly than they would be in a multiconcentration analysis (point estimate approach such as IC25). For those WET tests that have relatively small mean effect based on test design (high number of organisms per replicate and sufficient replication), such as the echinoderm egg fertilization test and the red abalone larval development test, test power is relatively high using the minimum test design requirements (number of replicates) as specified in the test method. For those methods, TST performs as expected, with relatively low α and β error rates and thereby high test power. For these methods, additional replication is probably not needed to determine with fairly high confidence whether a sample (effluent, storm water, ambient water) is acceptable or not using TST. Thus, the TST approach should provide incentives to generate less variable data (achievable within-test precision based on the experience of many laboratories), thereby providing more confidence in the interpretation of WET data.
Acknowledgements
Russell Erickson and John Fox provided statistical and analytical guidance in this research. J. Gilliam, J. Roberts, and M. Bowersox provided assistance on data compilation, database organization, and data presentation. This document has been reviewed in accordance with U.S. EPA policy and approved for publication. Approval does not signify that the contents necessarily reflect the views or policies of the Agency, nor does mention of trade names or commercial products constitute endorsement or recommendation for use.
